2. 浙江省微纳卫星研究重点实验室(浙江大学),杭州 310027
2. Key Laboratory of Micro-satellite Research of Zhejiang Province (Zhejiang University), Hangzhou 310027, China
近年来,随着航天器编队飞行技术特别是卫星编队组网技术逐渐热门[1],微小卫星编队因其研发周期短、研发成本低、小体积、轻质量、快速度等特点,被广泛应用于光学干涉测量、定位及导航、微波合成孔径雷达等领域[2]。微小卫星编队技术是通过多颗小卫星的协同来实现传统卫星的功能拓展,如图 1所示给出了卫星协同工作示意,小卫星之间通过建立星间链路进行相互通信或相对测量等操作,进而实现较为复杂的功能[3]。

|
图 1 多卫星协同示意 Fig. 1 Schematic diagram of multi-satellite cooperation |
在常用的信息传输方式中,扩频通信因其隐蔽性、抗衰落能力、抗干扰性能等方面的优势,被广泛应用于星间通信、全球定位、无线传感等系统中[4]。扩频通信中代表性的直接序列扩展频谱(Direct sequence spread spectrum, DSSS)系统,其原理是发射端利用高速率伪码序列对数据进行频谱展宽,而接收端则通过伪码捕获、解扩等操作完成信号中的伪码剥离,因此,伪码序列的捕获是建立扩频通信链路的先决条件。并且,由于微小卫星终端的发射功率小、信号突发性强、信号传输距离远等因素,星间扩频通信对信号处理算法有着高灵敏度、快速捕获的针对性需求。
本文针对搭载于天平二号卫星的星间通信机,面向星间链路的应用环境与任务指标,在提高星间通信效率与可靠性的设计需求下,以传统的快速傅里叶变换(Fast Fourier transform, FFT)码相位捕获法为基础,对于传统算法存在的灵敏度与捕获速度不足等缺点,提出多路并行架构、特殊同步序列、非相干累加机制等改进策略,并对改进后的FFT快速捕获法进行了性能分析、仿真与硬件平台测试。
1 传统捕获算法扩频系统捕获原理基于扩频码良好的自相关性,利用本地伪码与接收信号的相关峰值判定两者是否对齐,当两者码片相位基本对齐时,才可实现信号的伪码剥离。然而,在实际星间通信系统中,除了收发端的码片相位差,还存在着因收发端的相对运动、时钟晶振偏差产生的载波多普勒频偏[5],多普勒频偏会使接受信号与本地伪码的相关值衰减,因此,信号捕获的关键就是对多普勒频偏和伪码相位的估计[6]。
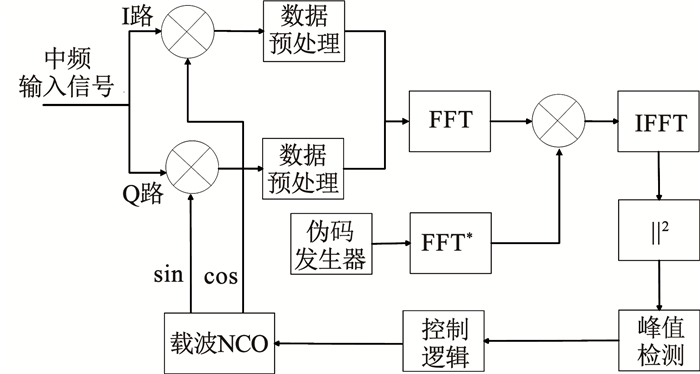
目前说来,常用的伪码捕获方法有串行滑动相关法、匹配滤波法和FFT码相位捕获法等。串行捕获法对多普勒频偏和伪码相位进行二维串行搜索,故其结构较为简单,但捕获速度慢[7];匹配滤波法通过设置与伪码长度相同阶数的滤波器来完成伪码相位的搜索,所以该算法捕获速度快但资源消耗巨大[8];FFT码相位捕获法则是对信号在频域进行处理,其结构如图 2所示,通过信号与伪码的FFT及IFFT操作可以直接获取两者的码片相位差,故其码片搜索速度较快[9]。
|
图 2 FFT码相位捕获法 Fig. 2 FFT code phase acquisition algorithm |
由上述比较可得,FFT码相位捕获法在资源消耗与搜索速度方面较为适中,然而,面对星间通信需求,传统的FFT码相位捕获法亦存在许多局限性:该方法对多普勒频偏进行串行搜索,所以捕获时间较长,并且算法容易受到数据比特跳变的影响,因而接收灵敏度不足。因此,针对天平二号卫星星间链路任务需求,需要对传统的FFT码相位捕获法进行优化,即首先要提高捕获算法的极限灵敏度以适应星间弱信号,其次要加快算法的捕获速度以提高通信效率。
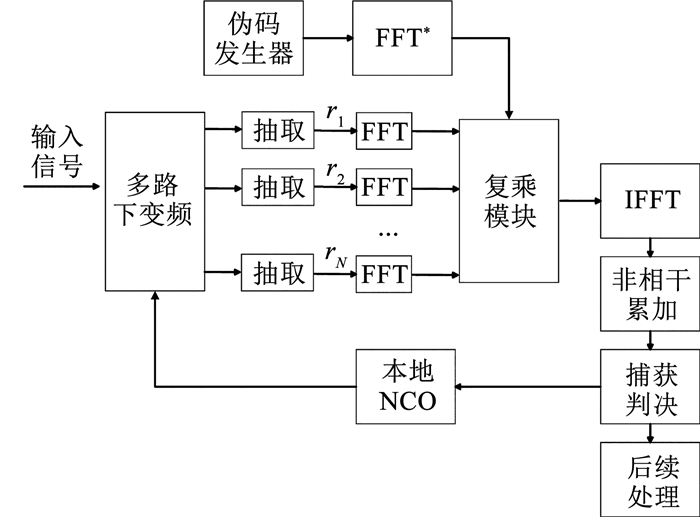
2 改进的FFT码相位捕获法为了使算法适应星间链路通信需求,本文对传统的码相位算法架构改进如图 3所示,其主要优化策略为:
|
图 3 改进的捕获算法结构 Fig. 3 Structure of improved acquisition algorithm |
1) 采用特殊的同步引导序列以避免信号数据跳变从而提高捕获算法的灵敏度,同时在接收端实现了通信数据的符号速率自适应估计。
2) 采用多路并行架构,在每个频率搜索区间内设置多路频差一定的本地数字控制振荡器(Numerically controlled oscillator, NCO),对多路信号分别进行下变频和后续算法处理,该架构有效提高了多普勒频偏搜索速度。
3) 当本地伪码和接收信号的快速傅里叶变换结果乘积进行快速傅里叶逆变换(Inverse fast Fourier transform, IFFT)时,对数据进行降速率抽取—非干累加操作,降速率抽取操作可以降低运算复杂度、提高运算速度,非相干累加操作则能提高信号的信噪比,加强算法对于弱信号的捕获性能。
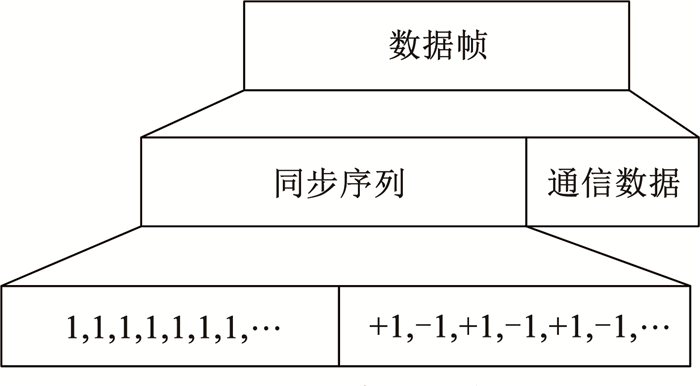
2.1 特殊同步序列设计图 4给出了改进算法在通信帧前添加的同步序列结构,系统对数据帧添加的同步引导序列包括全1序列,和±1交替序列。
|
图 4 同步序列结构 Fig. 4 Structure of synchronization sequence |
同步序列中全1序列的添加可避免数据跳变对直接扩频信号捕获造成的影响,由于捕获机制的原理实际是将本地伪码与接收信号进行相关,相关公式为
| $ R_{\text {corr }}(\tau)=\sum\limits_{n=-N}^{+N} r_{\text {local }}(n) r_{\text {sig }}(n-\tau) \times g(n-\tau) $ | (1) |
式中: N=NFFT/2,NFFT为FFT点数, rlocal(n)为本地伪码序列。在DSSS系统中,接收信号由伪码序列rsig(n)与通信序列g(n)两部分构成,根据在相关期间内通信序列g(n)是否发生跳转式(1)可进一步表示为
| $ R_{\text {corr }}(\tau)=\left\{\begin{array}{l} k \sum\limits_{n=-N}^{+N} r_{\text {local }}(n) r_{\text {sig }}(n-\tau), g(n) {\text { 无跳转 }} \\ k \sum\limits_{n=-N}^i r_{\text {local }}(n) r_{\text {sig }}(n-\tau)- \\ k \sum\limits_{n=i+1}^N r_{\text {local }}(n) r_{\text {sig }}(n-\tau), g(n) {\text { 有跳转 }} \end{array}\right. $ | (2) |
式中: k为双极性序列的数值,即k=±1。式(2)对比可见,当通信序列g(n)在相关期间i处发生跳转时,最终的相关峰值相对于通信序列未跳转情况下的相关峰值有明显衰减。因此,在同步序列中添加全1序列可以保证捕获相关时的峰值更加明显,从而能有效提高算法的极限捕获灵敏度。
同步序列中除了包含全1序列外,还使用了与信息码元长度对应的±1交替的序列实现对不同符号速率信号的区分。当数据到达接收端时,接收端在全1同步序列时间内完成对信号的捕获,在信号捕获完成以后对信号进行符号速率估计,算法对解扩信号进行采样并进行符号判断,统计过零点数量,进而根据过零点数量估计数据的符号速率。故该同步序列的添加不仅提高了算法的极限灵敏度,更同时在接收端完成了对数据码元速率的自适应估计,节省了常规的测控机制来通知卫星通信码元速率所需时间,极大提高了卫星通信效率与灵活性。
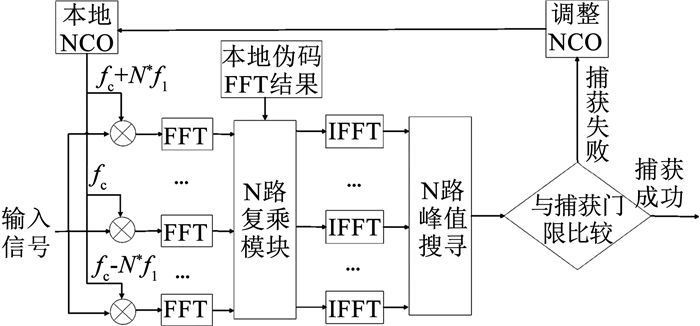
2.2 多路并行架构为了优化算法的捕获速度,方案采用多路并行架构以实现算法对于多普勒频偏以及伪码相位的二维搜索。图 5给出了高灵敏度快速捕获算法的多路并行架构示意,其算法可简述如下。
|
图 5 多路并行捕获架构 Fig. 5 Architecture of multiple parallel acquisition |
Step 1 信号经过N路NCO进行下变频,下变频后得到多路信号x1(m), x2(m), …, xN(m),多路信号之间的频率差为f1。
Step 2 将多路信号分别进行快速傅里叶变换,即
Step 3 将本地伪码傅里叶变换结果取共轭并与信号傅里叶变换结果对应相乘,即R(k)=X(k)·C*(k),将乘积结果进行傅里叶逆变换r(m)=IFFT[R(k)]。
Step 4 将多路乘积结果ri(m)非相干累加Ni次以提高信号的信噪比,并将多路的累加结果分别进行峰值搜索,取多路IFFT结果中峰值最大的一路rmax(m)。
Step 5 将rmax(m)路的峰值与设定的捕获门限比较:
If Max{rmax(m)} > THERESHOLD_SET
将信号进行后续处理;
Else
调整NCO的中心频率,并返回Step1;
End
该多路并行架构在实际应用中可通过设计多路并行数N,默认频率搜索区间的中心频率fc,多路之间的固定频差f1,多普勒搜索区间间隔fΔ来面对不同的应用环境与扩频信号要求,相对于传统FFT码相位捕获法,其捕获速度提升了N倍。
2.3 降速率抽取—非相干累加机制由于FFT码相位捕获算法需要对数据进行傅里叶变换,而N点的FFT需要进行
然而,对于卫星通信的弱信号来说,抽取操作会带来相关值能量的降低,进而影响FFT算法中频谱峰值的正确搜寻,因此改进的算法中采用非相干累加的方式来提高信号的相关能量。非相干累加对算法IFFT后输出的信号相关值进行多次累加以降低数据抖动,从而提高相关精度,非相干积分的信噪比增益可以表示为[11]
| $ G_{{\mathrm{i}}}\left(N_{{\mathrm{i}}}\right)=G_{{\mathrm{c}}}\left(N_{{\mathrm{i}}}\right)-L\left(N_{{\mathrm{i}}}\right) $ | (3) |
式中: Gc(Ni)为非相干积分增益, L(Ni)为非相干积分损耗,而且:
| $ G_{{\mathrm{c}}}\left(N_{{\mathrm{i}}}\right)=10 \lg \left(N_{{\mathrm{i}}}\right) $ | (4) |
| $ L\left(N_{{\mathrm{i}}}\right)=10 \lg \left[\frac{1+\sqrt{1+9.2 \times N_{{\mathrm{i}}} / D_{{\mathrm{c}}}(1)}}{1+\sqrt{1+9.2 / D_{{\mathrm{c}}}(1)}}\right] $ | (5) |
| $ D_{{\mathrm{c}}}(1)=\left({\mathrm{erf}}^{-1}\left(1-2 P_{{\mathrm{fa}}}\right)-{\mathrm{erf}}^{-1}\left(1-2 P_{{\mathrm{d}}}\right)\right)^2 $ | (6) |
式中: Ni为非相干积分次数, Pfa为捕获检测的虚警概率, Pd为检测概率。当非相干累加次数增加时,单次搜索时间也会增加,最终也会使得捕获时间变长,因此在进行算法设计中需要根据任务需求合理选择非相干累加次数。
3 算法性能分析 3.1 极限灵敏度理论推导卫星的接收端信号经过与数控振荡器控制本地载波进行下变频、滤波、降采样等操作后得到I、Q两路信号:
| $ x_{{\mathrm{I}}}(n)=\frac{\sqrt{2 P}}{2} d(n) c(n-\gamma) \cos (\varphi)+\frac{n_{{\mathrm{I}}}(n)}{2} $ | (7) |
| $ x_{\rm{Q}}(n)=\frac{\sqrt{2 P}}{2} d(n) c(n-\gamma) \sin (\varphi)+\frac{n_{\rm{Q}}(n)}{2} $ | (8) |
式中: P为信号功率, d(n)为基带信息数据, c(n-γ)为接收伪码, γ为接受伪码序列与本地伪码序列的相位差, nI(n)、nQ(n)表示均值为0,方差为σ2的相互独立的窄带高斯白噪声。为降低计算复杂度,采用FFT来计算相关值,将同相信号xI(n)和正交信号xQ(n)两项作为复序列进行FFT,同时对接收端本地伪码序列c(n)进行FFT并取其共轭,将两者FFT结果相乘并最终进行IFFT,该过程的相关值可表示为
| $ y(m)={\mathrm{IFFT}}\left[X(k) \cdot C^*(k)\right]=y_{{\mathrm{I}}}(m)+{\mathrm{j}} y_{\rm{Q}}(m) $ | (9) |
式中: X(k)=FFT[xI(n)+jxQ(n)]为接收信号的傅里叶变换值,C*(k)=FFT[c(n)]*为本地伪码傅里叶变换值的共轭,且相关结果的实部与虚部分别为:
| $ \begin{aligned} y_{{\mathrm{I}}}(m)= & \frac{\sqrt{2 P}}{2} \cos \varphi \sum\limits_{n=0}^{N-1} c(n) c(n-\gamma+m)+ \\ & \frac{1}{2} \sum\limits_{n=0}^{N-1} n_{{\mathrm{I}}}(n) c(n+m) \end{aligned} $ | (10) |
| $ \begin{aligned} y_{\rm{Q}}(m)= & \frac{\sqrt{2 P}}{2} \sin \varphi \sum\limits_{n=0}^{N-1} c(n) c(n-\gamma+m)+ \\ & \frac{1}{2} \sum\limits_{n=0}^{N-1} n_{\rm{Q}}(n) c(n+m) \end{aligned} $ | (11) |
式中: yI(m)、yQ(m)为相互独立的高斯随机变量,相关值包络r(m)在服从莱斯分布H1与服从瑞利分布H0时的概率密度函数分别为:
| $ f\left(r \mid H_1\right)=\frac{r}{\sigma_{{\mathrm{n}}}^2} \exp \left(-\frac{r^2+\frac{P \times N^2}{2}}{2 \sigma_{{\mathrm{n}}}^2}\right) I_0\left(\frac{N \sqrt{2 P}}{2 \sigma_{{\mathrm{n}}}^2} r\right) $ | (12) |
| $ f\left(r \mid H_0\right)=\frac{r}{\sigma_{{\mathrm{n}}}^2} \exp \left(-\frac{r^2}{2 \sigma_{{\mathrm{n}}}^2}\right) $ | (13) |
式中:I0(·)为修正的零阶第一类贝塞尔函数,σn2为非相干累加归一化以后的信号噪声方差。
因此误判概率PFA可以表示为
| $ P_{{\mathrm{FA}}}=\int_{T_{{\mathrm{h}}}}^{\infty} \frac{r}{\sigma_{{\mathrm{n}}}^2} {\mathrm{e}}^{-\frac{r^2}{2 \sigma_{{\mathrm{n}}}^2}} {\mathrm{~d}} r=\int_{\frac{T_{{\mathrm{h}}}^2}{2 \sigma_{{\mathrm{n}}}^2}}^{\infty} {\mathrm{e}}^{-y} {\mathrm{~d}} y={\mathrm{e}}^{-\frac{T_{{\mathrm{h}}}^2}{2 \sigma_{{\mathrm{n}}}^2}} $ | (14) |
式中Th为门限,
| $ P_{{\mathrm{fa}}}=1-\left(1-P_{{\mathrm{FA}}}\right)^{N_{{\mathrm{FFT}}}} $ | (15) |
式中: NFFT为FFT运算点数,且检测概率Pd可表示为[12]
| $ \begin{aligned} P_{{\mathrm{d}}}= & \int_{T_{{\mathrm{h}}}}^{\infty} \frac{r}{\sigma_{{\mathrm{n}}}^2} {\mathrm{e}}^{-\frac{r^2+v^2}{2 \sigma_{{\mathrm{n}}}^2}} I_0\left(\frac{r v}{\sigma_{{\mathrm{n}}}^2}\right) {\mathrm{d}} r= \\ & \int_{T_{{\mathrm{h}}}}^{\infty} \frac{r}{\sigma_{{\mathrm{n}}}^2} {\mathrm{e}}^{-\left(\frac{r^2}{2 \sigma_{{\mathrm{n}}}^2}+R_{{\mathrm{SN}}}\right)} I_0\left(\frac{r \sqrt{2 R_{{\mathrm{SN}}}}}{\sigma_{{\mathrm{n}}}}\right) {\mathrm{d}} r \end{aligned} $ | (16) |
式中:
| $ R_{{\mathrm{SN}}}=\frac{v^2}{2 \sigma_{{\mathrm{n}}}^2} $ | (17) |
由于高斯噪声方差σn2可通过统计方法测算出,故可视作常数,将Th2/2σn2视为门限参数,虚警概率Pfa与检测概率Pd均与Th2/2σn2直接相关。Th2/2σn2增加时,虚警概率Pfa不断减小,经式(14)、(15)计算,门限参数大于17时,满足虚警概率Pfa>10-4的要求。
然而,门限的增大同时会导致检测概率Pd下降,由于Pd接近于1,使用1-Pd表示漏检概率。同理,经式(16)计算可得在门限参数为18,检测门限信噪比为16 dB时,满足设计上常用的虚警概率小于10-4要求和漏检概率小于0.01的要求。输入载噪比RCN与检测门限信噪比RSN的关系为[13]
| $ R_{{\mathrm{CN}}}=R_{{\mathrm{SN}}}-G_{{\mathrm{i}}}-G_{{\mathrm{c}}}-L_{{\mathrm{rc}}}-L_{{\mathrm{s}}}+10 \lg \left(f_{{\mathrm{pn}}}\right) $ | (18) |
式中: Gi为非相干增益, Gc为相干积分增益, Lrc为伪码相位损耗, Ls为扫频损耗, fpn为伪码速率,针对天平二号的典型应用环境通过式(18)计算可得在门限信噪比条件下输入载噪比RCN=37.54 dB-Hz。灵敏度Pas和载噪比RCN的换算关系为[14]
| $ P_{{\mathrm{as}}}=-174+N_{{\mathrm{R}}}+R_{{\mathrm{CN}}} $ | (19) |
式中:Pas为捕获灵敏度,NR为接收机噪声系数。将RCN=37.54 dB-Hz代入式(19)可以获得在天平二号的典型应用环境下该算法的理论极限捕获灵敏度约为-133.46 dBm。
3.2 抗干扰能力分析抗干扰容限[15]Mj是衡量接收机处于多大功率干扰下依然能够正常工作的能力,计算式为
| $ M_{{\mathrm{j}}}=G_{{\mathrm{p}}}-\left[L+R_{{\mathrm{SN}}}\right] $ | (20) |
式中:L为接收机内部损耗,Gp为接收机增益,RSN为接收机最小输出信噪比,取满足虚警概率与检测概率要求下的门限信噪比16 dB。
因此在改进的捕获算法下,接收机的抗干扰容限可计算为
| $ \begin{aligned} M_{{\mathrm{j}}}= & G_{{\mathrm{p}}}-\left[L+R_{{\mathrm{SN}}}\right]=\left[G_{{\mathrm{c}}}+G_{{\mathrm{i}}}\right]- \\ & {\left[\left|L_{{\mathrm{s}}}\right|+\left|L_{{\mathrm{rc}}}\right|+R_{{\mathrm{SN}}}\right] \approx 25.33 {\mathrm{~dB}} } \end{aligned} $ | (21) |
式(21)表明,当接收机前端的干信比高于25.33 dB时,就超过了接收机所承受的最大干扰范围使得接收机无法正常进行工作。
3.3 理论捕获时间计算一般来说,在直接序列扩频通信中,伪码并行-频偏串行搜索的最大捕获时间可以表示为[16]
| $ \bar{T}_{{\mathrm{acq}}}=\frac{\left(2-P_{{\mathrm{d}}}\right)\left(1+K P_{{\mathrm{fa}}}\right)}{P_{{\mathrm{d}}}} \cdot m \cdot \tau_{{\mathrm{D}}} $ | (22) |
式中: K为发生虚警时额外增加的搜索次数,m为最差情况下捕获所需的扫频次数, τD为一次搜索需要的时间,若考虑到算法中FFT实际的运算时间,则
| $ \tau_{{\mathrm{D}}}=N_{{\mathrm{i}}} \cdot {\mathrm{Max}}\left\{T_{\text {coh }}, T_{\text {delay }}\right\} $ | (23) |
式中:Ni为非相干次数,Tcoh为相干积分时间,Tdelay为FFT运算时间,可近似认为检测概率Pd≈1,虚警概率Pfa≈0,由此式(17)可近似表示为
| $ \bar{T}_{\text {acq }}=m \times N_{{\mathrm{i}}} \times {\mathrm{Max}}\left\{T_{\text {coh }}, T_{\text {delay }}\right\} $ | (24) |
当采用多路并行架构时,通过合理设计多路并行数N与多路固定频差f1可使载波多普勒频偏落在多路并行搜索范围内,此时则不需要多次扫频,故m=1。当算法在芯片硬件中实现时,芯片条件不同,FFT运算时间Tdelay也会不同,在目前主流芯片的计算能力下,Tdelay可以控制与Tcoh相同数量级,相关时间Tcoh在参数设计下为亚毫秒量级,所以最终的捕获时间可控制在毫秒级。
4 性能仿真与实测 4.1 算法性能仿真表 1给出了针对天平二号任务需求所设置的仿真环境参数,兼容算法的资源消耗与捕获性能考虑,设置算法的并行路数N=3,非相干累加次数Ni=256。
| 表 1 仿真参数设置 Tab. 1 Simulation parameter settings |
在该仿真环境下,接收机在受到不同强度干扰时的相关情况如图 6所示。

|
图 6 干扰下算法相关情况 Fig. 6 Correlation value of algorithm under interference |
观察图 6可以发现,信号受21 dB单音干扰与21 dB多址干扰的情况时,仍有明显的相关峰出现,即可以实现成功捕获;而当信号受22 dB单音干扰与22 dB多址干扰时,信号出现误判,即此时已经超过了算法的抗干扰容限。
图 7给出了当设置接收信号的功率电平为-130 dBm时传统的FFT码相位捕获法与改进捕获算法的对比,从图中可以看出,在该灵敏度下,传统的FFT码相位捕获法未检测出明显相关峰,即捕获没有成功;但改进的算法相关结果中有着比较明显的峰值,可以实现成功捕获。

|
图 7 算法对比 Fig. 7 Algorithm comparison |
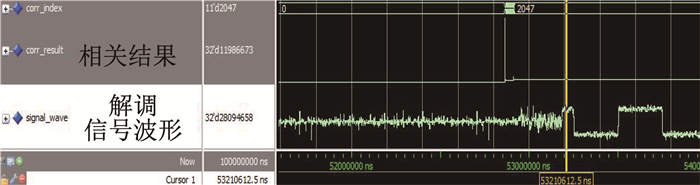
最后将算法的捕获时间进行FPGA的硬件级仿真,如图 8所示,最终信号在53 ms左右完成了对信号的捕获,相关峰值明显,最终解扩的信号波形分明。
|
图 8 硬件仿真结果 Fig. 8 Hardware simulation result |
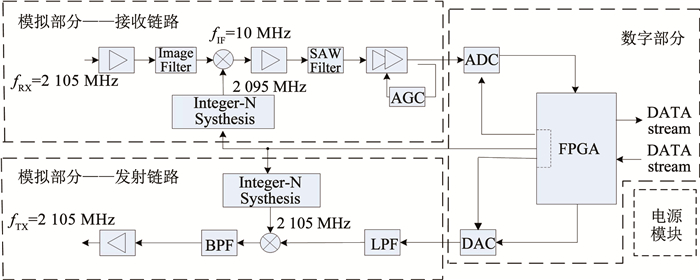
天平二号B星与C星主要用于地面雷达设备标校和RCS测量,两颗卫星通过星间链路建立通信以实现协同工作,图 9给出了基于天平二号卫星任务需求设计的S波段星间通信机架构,改进的捕获算法则利用硬件描述语言在FPGA芯片中进行实现。
|
图 9 星间通信机结构图 Fig. 9 Structure diagram of inter-satellite communicator |
搭载于天平二号卫星的星间通信机可分为射频模拟链路与数字信号处理两部分,当卫星其他协议层发来通信数据流时,FPGA芯片对通信数据进行扩频、调制等操作以后经过数模转换器(Digital to analog converter, DAC)转换为基带模拟信号,基带模拟信号经过上混频、滤波等操作后,通过功率放大及天线发射后到达星间信道;当星间信号到达接收端卫星通信机时,接收信号首先经过低噪音放大器和镜像滤波器,并下混频为中频模拟信号,中频信号经滤波器后滤除带外噪声,并通过自动增益控制(Automatic gain control, AGC)模块以控制信号电平基本恒定,最终经过模数转换器(Analog to digital converter, ADC)后信号送入FPGA芯片进行后续捕获检测等操作。
为了对算法进行实际验证,搭建星间通信测试平台如图 10所示,平台由发射端通信机、接收端通信机、可调式衰减器、射频功率计、地面站模拟设备和PC组成,其中可调式衰减器模拟星间信道衰落,地面站模拟设备增加信号干扰,射频功率计标定信号电平情况。

|
图 10 硬件测试平台结构 Fig. 10 Hardware test platform structure |
在图 10所示的硬件平台下,使用PC与串口实时观测数据传输情况,并利用ISE软件中的Chipscope功能观测算法捕获情况,表 2给出了在不同接收信号电平下多组测试所得平均数据,据表中数据可见在通信误码率BER < 10-6的任务指标下,算法极限灵敏度约为-130 dBm,多次测得平均捕获时间均小于100 ms。
| 表 2 算法测试数据 Tab. 2 Algorithm test data |
1) 本文从常用的捕获扩频算法原理出发,分析各种方法在星间链路系统中的适用性。针对传统算法捕获速度慢、捕获灵敏度不足等缺陷,以传统的FFT码相位捕获法为基础,面向天平二号卫星的应用环境,设计改进了一种可用于星间通信的高灵敏度快速捕获算法。
2) 改进的FFT快速捕获法相对于传统算法,采取了如下改进策略: 提出了多路并行结构,将捕获速度提升至N倍;利用降速率抽取—非相干累加机制来减小运算复杂度,提高相关能量;设计了特殊同步引导序列以提高系统的捕获性能与通信效率。并且,该算法能够通过选择设计非相干累加次数Ni,FFT并行支路数N,FFT并行支路固定频差f1,多普勒频率搜索间隔fΔ等参数来兼容不同应用环境的需求,算法灵活性较高。
3) 经过理论公式推导、仿真软件验证及硬件平台测试等步骤,改进后算法的各项性能得到了检验。结果表明,该算法能够在100 ms内对电平-130 dBm以上的扩频信号实现快速捕获,且抗干扰性能出色,对于长距离星间链路通信具有较强的实用性。
| [1] |
陈晓宇, 戴光明, 王茂才, 等. 一种确定性星座对地覆盖计算方法[J]. 哈尔滨工业大学学报, 2017, 49(4): 55. CHEN Xiaoyu, DAI Guangming, WANG Maocai, et al. Deterministic method for coverage of constellation to ground region[J]. Journal of Harbin Institute of Technology, 2017, 49(4): 55. DOI:10.11918/j.issn.0367-6234.201509008 |
| [2] |
孟泽民, 徐兆斌, 金小军, 等. 微小卫星星间测距在轨零值标定方法及应用[J]. 宇航学报, 2016, 37(10): 1239. MENG Zemin, XU Zhaobin, JIN Xiaojun, et al. On-orbit delay calibration of inter-satellite ranging system and its application for micro-satellite[J]. Journal of Astronautics, 2016, 37(10): 1239. DOI:10.3873/j.issn.1000-1328.2016.10.012 |
| [3] |
张仲楷, 崔高峰, 和梦敏, 等. 毫米波星间通信测距一体化技术研究[J]. 电讯技术, 2023, 63(1): 24. ZHANG Zhongkai, CUI Gaofeng, HE Mengmin, et al. Research on integrated technology of millimeter wave inter-satellite communication and ranging[J]. Telecommunication Engineering, 2023, 63(1): 24. DOI:10.20079/j.issn.1001-893x.211026002 |
| [4] |
冯永新, 任锦君, 刘芳. 双块零扩展截断相关的长码信号快速捕获算法[J]. 兵工学报, 2019, 40(3): 539. FENG Yongxin, REN Jinjun, LIU Fang. A fast acquisition algorithm with DBZP truncation correlation for the long code signal[J]. Acta Armamentarii, 2019, 40(3): 539. DOI:10.3969/j.issn.1000-1093.2019.03.012 |
| [5] |
朱军, 李秋瑾, 李凯, 等. 卫星组网系统下的多普勒频移估计与补偿[J]. 北京邮电大学学报, 2020, 43(3): 66. ZHU Jun, LI Qiujin, LI Kai, et al. Doppler shift estimation and compensation under satellite networking system[J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(3): 66. DOI:10.13190/j.jbupt.2019-178 |
| [6] |
王爱珍, 栾美松, 胡姣, 等. 高码率扩频系统的快速捕获算法研究[J]. 系统仿真学报, 2019, 31(8): 1727. WANG Aizhen, LUAN Meisong, HU Jiao, et al. Research on fast acquisition algorithm for high bit rate spread spectrum system[J]. Journal of System Simulation, 2019, 31(8): 1727. DOI:10.16182/j.issn1004731x.joss.19-0109 |
| [7] |
赵琳, 罗治斌, 丁继成, 等. GNSS接收机导航滤波器辅助捕获技术[J]. 哈尔滨工业大学学报, 2020, 52(3): 165. ZHAO Lin, LUO Zhibin, DING Jicheng, et al. Signal acquisition technique aided by navigation filter in GNSS receiver[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 165. DOI:10.11918/201810175 |
| [8] |
LI Ruitao, LI Songlin, LIU Gang. Research and implementation of GPS pseudo-code fast acquisition based on matched filter and FFT[C]//2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC). Xiamen, China: IEEE, 2020: 1. DOI: 10.1109/GNCC42960.2018.9019015.
|
| [9] |
RAO H, LIANG X F, SHEN M, et al. Fast acquisition scheme of the spread spectrum signals for satellite communications[J]. Journal of Communications Technology and Electronics, 2020, 65(4): 449. DOI:10.1134/S1064226920040063 |
| [10] |
卢迪, 郑世超. 混频前端抽取FFT伪码并行捕获算法[J]. 弹箭与制导学报, 2017, 37(5): 131. LU Di, ZHENG Shichao. FFT pseudo-code parallel acquisition algorithm for extracting at mixing front-end[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2017, 37(5): 131. DOI:10.15892/j.cnki.djzdxb.2017.05.031 |
| [11] |
田拓, 张风国, 陈奇东, 等. 一种改进的基于FFT的GPS弱信号捕获算法[J]. 全球定位系统, 2016, 41(6): 30. TIAN Tuo, ZHANG Fengguo, CHEN Qidong, et al. An improved weak GPS signal acquisition algorithm based on FFT[J]. GNSS World of China, 2016, 41(6): 30. DOI:10.13442/j.gnss.1008-9268.2016.06.007 |
| [12] |
SHEN Yuyao, WANG Yongqing, CHEN Jingyao, et al. High sensitivity acquisition algorithm for DSSS signal with data modulation[J]. China Communications, 2015, 12(4): 76. DOI:10.1109/CC.2015.7114072 |
| [13] |
邬志影, 常青, 尚梦云. 基于FFT的二维并行长码捕获算法[J]. 太赫兹科学与电子信息学报, 2015, 13(5): 757. WU Zhiying, CHANG Qing, SHANG Mengyun. Two-dimensional parallel long code acquisition algorithm based on FFT[J]. Journal of Terahertz Science and Electronic Information Technology, 2015, 13(5): 757. DOI:10.11805/TKYDA201505.0757 |
| [14] |
莫杭斌. 微纳卫星星间链路可靠通联设计与实现[D]. 杭州: 浙江大学, 2020 MO Hangbin. Design and implementation of reliable communication in inter-satellite link of micro-nano satellites[D]. Hangzhou: Zhejiang University, 2020. DOI: 10.27461/d.cnki.gzjdx.2020.001369 |
| [15] |
瞿智, 杨俊, 陈建云. 伪码测距抗干扰容限分析[J]. 宇航学报, 2014, 35(12): 1450. QU Zhi, YANG Jun, CHEN Jianyun. Analysis of anti-jamming margin of pseudo-random code ranging[J]. Journal of Astronautics, 2014, 35(12): 1450. DOI:10.3873/j.issn.1000-1328.2014.12.015 |
| [16] |
TA T H, DOVIS F, MARGARIA D, et al. Comparative study on joint data/pilot strategies for high sensitivity Galileo E1 open service signal acquisition[J]. IET Radar, Sonar & Navigation, 2010, 4(6): 764. DOI:10.1049/iet-rsn.2009.0256 |
 2023, Vol. 55
2023, Vol. 55


