T型橡胶减振器是航天系统中最常用的减振装置,如惯组、飞控装置和伺服等设备的减振。实际使用时,在设备支座与安装台面之间布置一组上、下对接的T型橡胶减振垫,实现对设备的支承和减振功能。由此,保障设备在长时大振动、短时强冲击和持续高过载等恶劣环境下能够可靠、安全的工作[1]。然而,使用过程中经常会发现,T型橡胶减振器在飞行环境下的动态特性变化非常显著,很容易超出其设计范围,进而引发与其他设备或弹箭系统平台的耦合共振。这样将会影响设备的使用寿命和电气性能,更为严重的情况还会导致飞行器的姿态失稳,甚至飞行失败。因此,研究T型橡胶减振器在动态环境下的非线性特性具有十分重要的意义。
当前,国内、外橡胶减振器非线性动特性的研究在试验分析、理论建模和数值仿真等方面都已经相当成熟。刘辉等[2]、Shoyama等[3]和韩德宝等[4]分别研究了振动频率、振幅和预压缩量对橡胶减振器动刚度和阻尼系数的影响,表明其具有较强的非线性特性。潘孝勇等[5]构建了基于超弹性、分数导数和摩擦模型的橡胶减振器非线性动力学模型,较好地表征了其弹性、振动频率相关性和振幅相关性。李峙岳等[6]综合考虑了橡胶材料的高弹特性、频率相关特性和摩擦特性及形状因素,提出了一种基于鬃毛摩擦理论的减振器动态迟滞特性模型。杨盛林等[7]推导了橡胶材料硬度参数和动态弹性模量的等价关系式,建立了适合于工程仿真分析的橡胶减振装置数学模型,较好地模拟了动态环境下系统的真实响应。已有研究工作主要涉及橡胶的材料应变率效应与刚度滞回特性和减振器的几何非线性。
针对T型橡胶减振器,由于其上、下对接的特殊设计,还存在着因结构设计型式带来的非线性。郭铁能等[8-9]采用迟滞回线法和时域最小二乘法及频域解析法辨识得到了ZN-35T型橡胶减振垫在不同振动频率下的刚度和阻尼参数,但没有研究振幅和预压缩量对其非线性动特性的影响。同时,这些研究仅针对橡胶减振器小变形情况,实际飞行环境中大变形工况也是不可避免的。
为研究飞行大过载、强振动环境对T型橡胶减振器非线性动特性的影响,本文将T型减振器简化为一组双向承压、不承拉弹簧-阻尼元件,建立了含分段线性刚度及阻尼和立方刚度的双层级非线性动力学模型。随后,采用谐波平衡法分别数值模拟了外部载荷正弦扫频激励下分段线性刚度系统和立方刚度系统的非线性频响函数。同时,采用基础位移正弦扫频激励方式进行了T型橡胶减振系统非线性传递特性试验,表明其具有渐软刚度和渐小阻尼的非线性特性。通过计算结果与试验结果的比对分析,验证了本文双层级非线性动力学模型的合理性和正确性。最后,从航天工程应用的角度提出了基于飞行环境进行预压缩量设计的方法。
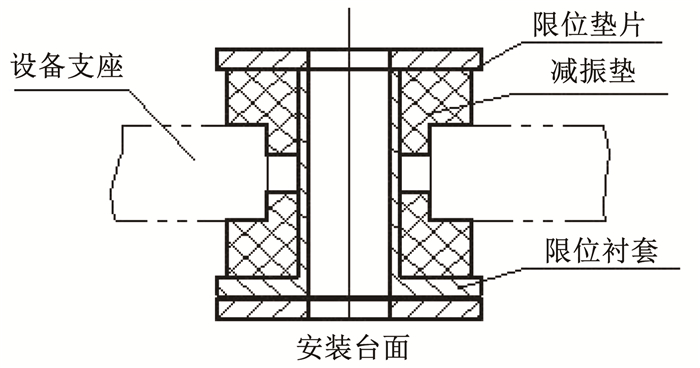
1 T型橡胶减振系统动力学模型 1.1 模型简化T型橡胶减振器通常由上减振垫、下减振垫、限位垫片和限位衬套等组成。如图 1结构示意图中,设备支座夹在上、下减振垫之间,限位衬套和限位垫片将减振垫轴向和径向压紧,减振器螺接到设备安装台面上。考虑到设备和安装台面相对减振垫均较为刚硬,因而可处理为刚体。由此,设备、减振器和台面组成的系统可简化为由一个质量块和两个承压、不承拉弹簧-阻尼元件组成的双边约束单自由度系统,如图 2所示。
|
图 1 T型橡胶减振器结构示意图 Fig. 1 Structure diagram of T-shape rubber damper |

|
图 2 单自由度系统模型 Fig. 2 Single degree of freedom system model |
图 2中,坐标原点位于设备质心处,设备质量为m;上、下减振垫简化为无质量的单向承压、不承拉弹簧-阻尼元件,弹簧刚度分别为kl和kr,阻尼系数分别为cl和cr;台面处理为基础边界。
| $ \left\{\begin{array}{l} m \ddot{x}+f_{c}(x, \dot{x})+f_{k}(x)=F(t) \\ f_{c}(x, \dot{x})=f_{c}^{l}(x, \dot{x})+f_{c}^{r}(x, \dot{x}) \\ f_{k}(x)=f_{k}^{l}(x)+f_{k}^{r}(x) \end{array}\right. $ | (1) |
式中:
| $ \begin{aligned} & f_{c}^{l}(x, \dot{x})= \begin{cases}c_{l} \dot{x}, & x \leqslant 0, \dot{x}<0 \\ 0, & x \leqslant 0, \dot{x} \geqslant 0 \\ 0, & x>0\end{cases} \\ & f_{c}^{r}(x, \dot{x})= \begin{cases}0, & x \leqslant 0 \\ 0, & x>0, \dot{x} \leqslant 0 \\ c_{r} \dot{x}, &x>0, \dot{x}>0\end{cases} \end{aligned} $ | (2) |
| $ \begin{aligned} & f_{k}^{l}(x)= \begin{cases}k_{l} x, & x \leqslant 0 \\ 0, & x>0\end{cases} \\ & f_{k}^{r}(x)= \begin{cases}0, & x \leqslant 0 \\ k_{r} x, & x>0\end{cases} \end{aligned} $ | (3) |
工程设计中,上、下减振垫通常选用同一规格,且严格要求其刚度和阻尼特性保持一致。因此,这里令cl=cr=c和kl=kr=k,将式(2)、(3)代入式(1)可得
| $ m \ddot{x}+c_{e} \dot{x}+k_{e} x=F(t) $ | (4) |
式(4)表明,图 2所示系统是一个由质量m、等效弹簧ke和等效阻尼ce组成的线性单自由度系统。实际上,由于系统在平衡位置x=0处是不连续的,因此其本质上是一个非线性系统。
1.2 考虑预压缩设计实际使用过程中,设备将做上、下往复运动,因而减振器将承受设备带来的正向或负向惯性力,进而单向压缩上或下减振垫,由此将在上、下减振垫之间引入间隙。过载导致单向静态间隙,振动引发双向动态间隙。若出现这样的情况,设备和减振器组成的系统将变为间隙碰撞振动系统[11],进而引发噪声、磨损和碰撞振动的现象以致损坏设备,同时导致系统表现出强非线性、非连续性和非光滑性的复杂特性。
为解决上述问题,工程上根据橡胶材料具有的超弹特性,采用预先压缩的方式来消除间隙。如此,式(3)可修正为:
| $ \begin{aligned} f_{k}^{l}(x, p) & = \begin{cases}k(x-p), & x \leqslant p \\ 0, & x>p\end{cases} \\ f_{k}^{r}(x, p) & = \begin{cases}0, & x \leqslant-p \\ k(x+p), & x>-p\end{cases} \end{aligned} $ | (5) |
式中:p为单个减振垫的预压缩量。将式(5)代入弹性恢复力fk,可修正为
| $ f_{k}(x, p)=f_{k}^{l}(x, p)+f_{k}^{r}(x, p)= \begin{cases}k(x-p), & x \leqslant-p \\ 2 k x, & |x|<p \\ k(x+p), & x \geqslant p\end{cases} $ | (6) |
式(6)表明,弹性恢复力fk是一个分段线性函数,如图 3所示。

|
图 3 非线性弹性恢复力 Fig. 3 Nonlinear elastic restoring force |
同理,可将阻尼力fc修正为
| $ \begin{aligned} f_{c}(x, \dot{x}, p)= & f_{c}^{l}(x, \dot{x}, p)+f_{c}^{r}(x, \dot{x}, p)= \\ & \left\{\begin{array}{l} c \dot{x}, x \leqslant-p, \dot{x}<0 \\ 0, x \leqslant-p, \dot{x}>0 \\ c \dot{x}, -p<x<p \\ 0, x \geqslant p, \dot{x}<0 \\ c \dot{x}, x \geqslant p, \dot{x}>0 \end{array}\right. \end{aligned} $ | (7) |
采用等价线性化方法,设在一次近似的情况下,式(1)的近似解为x=Asin θ,由此
| $ k_{e}=\frac{1}{{\rm{ \mathsf{ π}}} A} \int_{0}^{2 {\rm{ \mathsf{ π}}}} f_{k}(A \sin \theta, p) \sin \theta \mathrm{d} \theta $ | (8) |
| $ c_{e}=\frac{1}{{\rm{ \mathsf{ π}}} A \omega} \int_{0}^{2 {\rm{ \mathsf{ π}}}} f_{c}(A \sin \theta, A \omega \cos \theta, p) \cos \theta \mathrm{d} \theta $ | (9) |
式中:A为振幅,θ为相位角,ω为频率。将式(6)、(7)分别代入式(8)、(9),经推导可得:
| $ k_{e}=k+\frac{2 k}{{\rm{ \mathsf{ π}}}}\left(\theta_{p}+\frac{\sin 2 \theta_{p}}{2}\right) $ | (10) |
| $ c_{e}=\frac{c}{2}+\frac{c}{{\rm{ \mathsf{ π}}}}\left(\theta_{p}+\frac{\sin 2 \theta_{p}}{2}\right) $ | (11) |
式中:θp为预压缩量p对应的相位角,且θp=
综合式(1)、式(6)、(7)可以发现:1)若振幅A位于预压缩量p范围内,则系统可看作是由质量m、弹簧2k和阻尼c组成的线性单自由度系统;2)若振幅A位于预压缩量p范围外,则由于在x=p和x=-p处不连续,系统变成分段线性系统。图 4中随着振幅A相对预压缩量p的不断变大,弹簧刚度表现出非常明显的渐近软化特性,同时阻尼系数也随之减小,这是由T型减振器结构型式的特点所决定的。

|
图 4 等效刚度和等效阻尼随预压缩量与振幅之比的变化曲线 Fig. 4 Curves of equivalent stiffness and damping with the ratio of precompression to amplitude |
已有试验结果[1, 12]表明,橡胶减振垫具有非常明显的动态软化特性,即随着振幅的逐级增大,减振系统峰值频率逐渐减小。动力学建模时,通常将弹性恢复力fk处理为包含线性弹性力和三次方非线性弹性力的方程[13]。由此,式(5)可修正为:
| $ \begin{aligned} f_{k}^{l}(x, p) & = \begin{cases}k(x-p)+k_{2}(x-p)^{3} & , x \leqslant p \\ 0, & x>p\end{cases} \\ f_{k}^{r}(x, p) & = \begin{cases}0, & x \leqslant-p \\ k(x+p)+k_{2}(x+p)^{3}, & x>-p\end{cases} \end{aligned} $ | (12) |
式中:k2为三次方刚度,且k2<0。由此,非线性弹性恢复力fk可表示为
| $ f_{k}(x, p)=\left\{\begin{array}{l}k(x-p)+k_{2}(x-p)^{3}, x \leqslant-p \\ 2 k x+6 k_{2} x p^{2}+2 k_{2} x^{3}, \quad-p<x<p \\ k(x+p)+k_{2}(x+p)^{3}, x \geqslant p\end{array}\right. $ | (13) |
式(13)表明,弹性恢复力fk是一个含分段线性刚度和立方刚度的双层级非线性函数。
2 数值模拟令图 2中质量块承受的外部载荷激励输入为F(t)=F0sin(ωt)的简谐形式,并代入式(1)可得运动微分方程:
| $ m \ddot{x}+f_{c}(x, \dot{x})+f_{k}(x)=F_{0} \sin (\omega t) $ | (14) |
采用谐波平衡法对式(14)所描述系统进行分析,研究其在不同激励幅值下的非线性频响特性。本文研究中,T型橡胶减振垫的基本参数为:线性刚度系数k=8.21×105 N/m,非线性刚度系数k2=-2.46×109 N/m3,阻尼系数c=2 050 N·s/m,预压缩量p=0.5 mm, 设备质量特性参数m=16 kg。
2.1 仅模拟分段线性刚度令式(14)中

|
图 5 分段线性刚度系统的非线性频响函数 Fig. 5 Nonlinear frequency-response functions of piecewise linear stiffness system |
令式(14)中:

|
图 6 立方刚度系统的非线性频响函数 Fig. 6 Nonlinear frequency-response functions of cubic stiffness system |
通常采用单自由度激励的方式研究减振系统的传递特性,其原理性试验系统如图 7所示。

|
图 7 减振系统基础激励试验原理 Fig. 7 Basic excitation test principle of vibration isolation system |
设备通过减振器连接在振动平台上,电动振动台对振动平台施加正弦扫频激励。振动控制点在振动平台上,通过控制传感器的安装位置和响应量级实现常幅激励。设备上安装监测加速度传感器测量减振后信号。
由此,图 2系统将承受简谐形式的基础位移激励输入xi(t)=x0sin(ωt),将其代入式(1)可得运动微分方程:
| $ m \ddot{x}+f_{c}\left(x-x_{i}, \dot{x}-\dot{x}_{i}\right)+f_{k}\left(x-x_{i}\right)=0 $ | (15) |
令式(15)中fc取修正式(7),fk取修正式(13),由此演化为考虑分段线性刚度及阻尼和立方刚度的双层级非线性动力学系统。采用谐波平衡法对上述系统进行分析,研究其在不同激励幅值下的非线性传递特性。T型橡胶减振垫参数和设备参数取值同文中数值模拟的参数取值。
图 8给出了式(15)数值计算结果与真实系统正弦扫频试验结果的对比,二者吻合良好。利用数据统计分析可知,不同激励幅值下计算结果与试验结果均值偏差最大仅为3.1%,矢量偏差最大仅为11.5%,二者相关度最小也达到了93.0%,吻合度最小也有99.3%。由此表明,本文构建的T型橡胶减振器动力学模型和模型参数可以真实地表征系统传递特性,能够很好地应用于工程实际。

|
图 8 T型橡胶减振器的非线性传递特性 Fig. 8 Nonlinear transfer characteristics of T-shape rubber damper |
对比图 5、6仿真结果可见,350 N外载荷激励就可导致T型减振器结构型式上的渐进软化特性,而3 000 N外载荷激励才能引发橡胶减振器本身具有的动态软化特性。由此,为避免或降低T型结构型式带来的渐软刚度和渐小阻尼的非线性特性,设计合理的预压缩量是非常必要的。
当前,T型橡胶减振器预压缩量的设计是带有经验性的[14]、经过多次试验反复试错确定的,即费时又费力,有时还得不到满意的结果。预压缩量的设计主要应考虑设备工作过程中承受的飞行环境,即大过载和强振动环境,通过研究减振器对过载和振动环境的响应,综合、设计出合理的预压缩量。
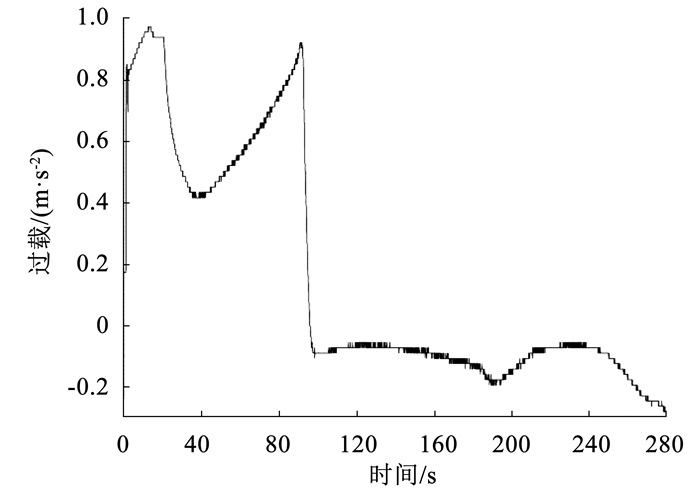
导弹飞行过程中典型的过载和振动时程曲线,分别见图 9、10所示。图 9、10中包含了导弹发动机工作主动段、滑行段和再入段等典型飞行剖面。
|
图 9 过载时程曲线 Fig. 9 Overload time history curve |

|
图 10 振动时程曲线 Fig. 10 Vibration time history curve |
根据图 9过载时程曲线可获取飞行最大过载gmax,计算得到减振垫最大承载力F0=m·gmax。随后,在图 11减振垫载荷-位移曲线中,选取F0对应的位移作为静态预压缩量p0,通过计算数据点(p0, F0)位置的切线值作为减振垫平衡态下的刚度k。

|
图 11 减振垫刚度曲线 Fig. 11 Stiffness curve of damping pad |
采用谱平滑和谱平均技术[15-16]对图 10中多个时段振动平稳数据进行加速度功率谱密度分析,通过将谱密度数据进行综合包络得到加速度最大谱[17],借助功率谱密度转换方法[18]得到位移最大谱,如图 12所示。图 12中加速度谱突出反应了高频分量的变化,位移谱则反应了低频分量的变化,300 Hz位移谱值相对20 Hz位移谱值衰减了40 dB,表明高频分量对位移的贡献基本可以忽略。航天工程中,20 Hz以内低频分量通常包含在图 9过载测量数据中。因此,可选取20~300 Hz频带内位移谱值,估算得到振动位移均值drms,进而选作动态预压缩量p1=3drms。

|
图 12 功率谱密度曲线 Fig. 12 Power spectral density curve |
由此,较为合理的预压缩设计量为
| $ p=p_0+p_1 $ | (16) |
本文预压缩量是基于飞行大过载、强振动环境的设计包络值。实际使用时,若发现减振器减振效率较低,可根据飞行时域数据开展分时段设计,得到随飞行时间变化的预压缩设计量。据此,在传递特性和减振效率之间综合考虑,选取较为合理的设计值。
5 结论1) 基于T型橡胶减振器结构型式导致分段线性刚度及阻尼和橡胶材料具有立方刚度特性的认识,构建了含分段线性刚度及阻尼和立方刚度的双层级非线性动力学模型,模拟T型橡胶减振器的渐软刚度和渐小阻尼的非线性特性。
2) 采用谐波平衡法分别模拟了外载正弦扫频激励下分段线性刚度系统和立方刚度系统的渐进软化特性,研究了不同激励幅值对T型橡胶减振器非线性频响函数和传递特性的影响,结果表明:较低的激励幅值即可导致T型减振器结构型式上的渐进软化特性,而较大的激励幅值才能引发橡胶减振器本身具有的动态软化特性;合理的预压缩设计量可以避免或降低T型结构型式导致的非线性特性。
3) 利用试验和数值方法获取了基础位移正弦扫频激励下T型橡胶减振系统的非线性传递特性,二者结果的对比分析表明,本文构建的双层级非线性动力学模型工程应用简便、方法正确、合理可信。
| [1] |
商霖, 张海瑞, 赵晓宁. 惯组小系统动力学建模与非线性特性分析[J]. 中国惯性技术学报, 2021, 29(1): 126. SHANG Lin, ZHANG Hairui, ZHAO Xiaoning. Dynamic modeling and nonlinear characteristic analysis of inertial navigation system[J]. Journal of Chinese Inertial Technology, 2021, 29(1): 126. DOI:10.13695/j.cnki.12-1222/o3.2021.01.020 |
| [2] |
刘辉, 胡晓东, 胡煦. 某橡胶减振器动态振动特性试验研究[J]. 特种橡胶制品, 2020, 41(6): 44. LIU Hui, HU Xiaodong, HU Xu. Experimental study on dynamic vibration characteristics of a rubber shock absorber[J]. Special Purpose Rubber Products, 2020, 41(6): 44. DOI:10.16574/j.cnki.issn1005-4030.2020.06.011 |
| [3] |
SHOYAMA T, FUJIMOTO K. Direct measurement of high-frequency viscoelastic properties of pre-deformed rubber[J]. Polymer Testing, 2018, 67: 399. DOI:10.1016/j.polymertesting.2018.03.011 |
| [4] |
韩德宝, 宋希庚, 薛冬新. 橡胶减振器非线性动态特性的试验研究[J]. 振动工程学报, 2008, 21(1): 102. HAN Debao, SONG Xigeng, XUE Dongxin. Experiment on nonlinear dynamic characteristics of rubber isolator[J]. Journal of Vibration Engineering, 2008, 21(1): 102. DOI:10.16385/j.cnki.issn.1004-4523.2008.01.006 |
| [5] |
潘孝勇, 上官文斌, 柴国钟, 等. 基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模[J]. 振动与冲击, 2007, 26(10): 6. PAN Xiaoyong, SHANGGUAN Wenbin, CHAI Guozhong, et al. Dynamic modeling for carbon-filled rubber isolators based on hyperelastic ity, fractional derivative and a generalized frictional model[J]. Journal of Vibration and Shock, 2007, 26(10): 6. DOI:10.3969/j.issn.1000-3835.2007.10.002 |
| [6] |
李峙岳, 朱如鹏, 李苗苗. 基于鬃毛摩擦理论的环形橡胶减振器动态迟滞特性模型[J]. 航空动力学报, 2018, 33(5): 1136. LI Zhiyue, ZHU Rupeng, LI Miaomiao. Dynamic hysteresis characteristics model of rubber damping ring based on bristle friction theory[J]. Journal of Aerospace Power, 2018, 33(5): 1136. DOI:10.13224/j.cnki.jasp.2018.05.014 |
| [7] |
杨盛林, 芈小龙, 王晓丹, 等. 基于橡胶等效动态模量的惯导减振装置设计方法[J]. 中国惯性技术学报, 2019, 27(5): 695. YANG Shenglin, MI Xiaolong, WANG Xiaodan, et al. A design method of inertial navigation's damping device based on rubber equivalent dynamic Young's Modulus[J]. Journal of Chinese Inertial Technology, 2019, 27(5): 695. DOI:10.13695/j.cnki.12-1222/o3.2019.05.020 |
| [8] |
郭铁能, 彭立伟, 周成, 等. ZN-35橡胶减振垫迟滞回线与刚度阻尼参数[J]. 北京工业大学学报, 2022, 48(1): 1. GUO Tieneng, PENG Liwei, ZHOU Cheng, et al. Hysteresis loop and stiffness and damping parameters of ZN-35 rubber damping pad[J]. Journal of Beijing University of Technology, 2022, 48(1): 1. DOI:10.11936/bjutxb2020070005 |
| [9] |
郭铁能, 杨涛. ZN-35橡胶减振垫动力学参数试验研究[J]. 特种橡胶制品, 2020, 41(5): 34. GUO Tieneng, YANG Tao. Experimental research of dyanamic parameters of ZN-35 rubber damping PAD[J]. Special Purpose Rubber Products, 2020, 41(5): 34. DOI:10.16574/j.cnki.issn1005-4030.2020.05.009 |
| [10] |
闻邦椿, 李以农, 韩清凯, 等. 非线性振动理论中的解析方法及工程应用[M]. 沈阳: 东北大学出版社, 2001. WEN Bangchun, LI Yinong, HAN Qingkai, et al. Analytical method in nonlinear vibration theory and its engineering application[M]. Shenyang: Northeast University Press, 2001. |
| [11] |
张艳龙, 唐斌斌, 王丽, 等. 动摩擦作用下含间隙碰撞振动系统的动力学分析[J]. 振动与冲击, 2017, 36(24): 58. ZHANG Yanlong, TANG Binbin, WANG Li, et al. Dynamic analysis for a vibro-impact system with clearance under kinetic friction[J]. Journal of Vibration and Shock, 2017, 36(24): 58. DOI:10.13465/j.cnki.jvs.2017.24.009 |
| [12] |
张鹏飞, 苏华昌, 吴家驹. 基于奇异值分解的惯性测量组合减振系统非线性刚度识别[J]. 导弹与航天运载技术, 2016(3): 68. ZHANG Pengfei, SU Huachang, WU Jiaju. Identification of nonlinear stiffness of inertial measurement unit with vibration absorber system based on singular value decomposition[J]. Missiles and Space Vehicles, 2016(3): 68. DOI:10.7654/j.issn.1004-7182.20160316 |
| [13] |
王丹, 张亚红, 白长青, 等. 新型橡胶隔振器参数辨识及动力学特性研究[J]. 应用力学学报, 2017, 34(3): 410. WANG Dan, ZHANG Yahong, BAI Changqing, et al. Study on parameter identification and dynamic performance of a novel rubber isolator[J]. Chinese Journal of Applied Mechanics, 2017, 34(3): 410. DOI:10.11776/cjam.34.03.C014 |
| [14] |
刘家燕, 程志峰, 王平. 机载光电吊舱橡胶减振器的设计与应用[J]. 中国机械工程, 2014, 25(10): 1308. LIU Jiayan, CHENG Zhifeng, WANG Ping. Design and applications of rubber shock absorber in airborne photoelectric pod[J]. China Mechanical Engineering, 2014, 25(10): 1308. DOI:10.3969/j.issn.1004-132X.2014.10.007 |
| [15] |
(比)沃德· 海伦(Ward Heylen)等. 模态分析理论与试验[M]. 白化同, 郭继忠, 译. 北京: 北京理工大学出版社, 2001 Heylen W, et al. Theory and experiment of modal analysis[M]. BAI Huatong, GUO Jizhong. Beijing: Beijing Institute of Technology Press, 2001 |
| [16] |
黄怀德. 振动工程[M]. 北京: 中国宇航出版社, 2005. HUANG Huaide. Vibration engineering[M]. Beijing: China Aerospace Publishing House, 2005. |
| [17] |
HARRIS C M, PIERSOL A G. 冲击与振动手册[M]. 刘树林, 王金东, 李凤明, 等译. 5版. 北京: 中国石化出版社, 2007 HARRIS C M, PIERSOL A G. Shock and vibration manual[M]. LIU Shulin, WANG Jindong, LI Fengming, et al. 5th ed. Beijing: China Petrochemical Press, 2007 |
| [18] |
商霖, 李璞, 廖选平. OMEGA算法在导弹振动工程中的应用[J]. 装备环境工程, 2015, 12(3): 58. SHANG Lin, LI Pu, LIAO Xuanping. Application of OMEGA algorithm in missile vibration engineering[J]. Equipment Environmental Engineering, 2015, 12(3): 58. DOI:10.7643/issn.1672-9242.2015.03.011 |
 2023, Vol. 55
2023, Vol. 55


