入水问题广泛存在于自然界和工程的众多领域,如导弹入水[1]、船舶砰击[2]、滑坡涌浪[3]甚至打水漂[4]等,具有重要的实际应用价值。然而,入水问题的精确高效数值仿真仍面临艰巨的技术挑战。当具有复杂几何外形的结构撞击水面时,固体大运动边界的处理成为首要难点;同时,运动物体对液面挤压与排开,必然伴随一系列的自由液面剧烈演化过程,如液面飞溅、空泡和射流[5]等现象,给数值模拟带来额外的困难;另外,结构的运动决定流场的演化,流场的演化又反过来影响结构的运动特性,呈现流固之间强烈的耦合效应。归纳起来,结构移动边界的合理描述、剧烈变形自由液面的准确捕捉及各相之间耦合作用的精细刻画是入水现象数值仿真面临的核心难题。
为解决结构入水过程中的移动边界问题,王永虎等[6]运用动网格技术,严格按照结构边界构造贴体网格,并随边界移动进行网格变形或重建,构建了三维圆柱自由入水模型;然而,当结构发生大位移时,动网格逐时间步的网格更新消耗大,还可能产生网格扭曲等问题。Ma等[7]、谢路毅等[8]采用嵌套网格方法,采用固定的背景网格离散计算域,无需实时更新,但需采取合理的挖洞措施,且难以考虑多体情况下子网格间的相互作用。相比之下,采用固定笛卡尔网格,并利用拉格朗日点来表征复杂结构边界的浸入边界法(IBM)[9]更加简洁:通过在流体动量方程中附加体力项来施加固体边界条件,IBM物理概念明确,网格生成简单,对于结构复杂外形与大幅位移问题处理优势显著,目前已被广泛应用于包含复杂边界的流固耦合问题[10]。
针对强非线性的自由面问题,Kleefsman等[11]采用单相流简化,仅考虑水相演化并构造自由面边界条件以描述气相的影响。然而,单相流简化无法反映实际入水过程中气液两相剧烈的相互掺杂,也不能解释气液耦合流动的潜在机制。目前常用的多相流界面捕捉方法为VOF方法[12]和LS(level set)方法[13]。VOF方法通过构造流体体积函数捕捉界面,以其高度守恒性得到广泛应用,但需要复杂的界面重构技术。LS方法概念简单,通过距离指示函数隐式追踪界面,但具有严重的质量损失问题。Olsson等[14]提出守恒式LS(CLS)方法,采用双曲正切函数,以保守的方式对流,显著提高了质量守恒性,然而,该方法界面边缘法向对扰动极为敏感,可能使法向计算失准。据此,Zhao等[15]提出改进的守恒式LS方法(ICLS),以CLS方法捕获界面,并以LS方法获得界面信息,在保证方法简单性的同时兼顾了守恒性及界面参数的准确性要求。
结构入水冲击过程中的流固耦合机制十分复杂。何春涛等[16]采用常速入水模型,只考虑结构位移对流体的作用,实际上只求解了包含动边界的纯流体力学问题。而工程中以自由入水为主,结构运动轨迹及流体的响应事先未知,有学者考虑流固耦合效应开展了对自由入水问题的探索。如Calderer等[10]结合曲线IBM及LS方法提出流固耦合模型,预测浮体与自由面的相互作用;Sun等[17]采用光滑粒子动力学方法处理自由面与刚体间的耦合作用。然而,现有研究普遍局限于单体入水,王聪等[18]虽对双体入水作出尝试,但均不考虑固体间的碰撞。对于滑坡体入水或抛石等问题,散体材料自身的相互作用描述也是不可或缺的。
为合理考虑包含离散介质相互作用的流固耦合问题,有学者采用流体动力学-离散单元法(CFD-DEM)[19]。CFD-DEM方法虽引入了接触模型考虑离散介质的物理碰撞,但流固耦合作用力通过Di Felice[20]提出的经验公式估算,只适用于圆形颗粒,无法准确满足流固耦合边界条件,流场也是非解析的。底瑛棠等[21]曾提出高解析度CFD-DEM-IBM方法解决了上述问题,但缺乏对自由面的合理描述,不适用于入水现象仿真。
为实现具有普遍工程适用价值的入水问题数值仿真,本文提出一种解析的CFD-DEM-IBM方法,通过Navier-Stokes方程描述流体,采用固定的笛卡尔网格离散计算域,依据距离势离散单元法分析固体运动特性并有效处理固体间的相互作用,引入隐式直接力IBM追踪固体移动边界并展开相间作用力的精确求解,确保同时满足固体表面无滑移边界条件及连续性条件,并采用ICLS方法捕捉自由液面,在保证守恒性的前提下获得准确的界面信息。为实现流固间的强耦合,将变量通过插值函数与分布函数在流固耦合面上传递,采用交错迭代格式求解流固耦合系统,在每个时间步内反复迭代多次以精确满足收敛条件。从而,本文所提出的CFD-DEM-IBM方法不仅能够获得准确的耦合作用力及高解析度的流场信息,克服入水问题数值仿真固有的困难,还能够合理反映离散块体间的碰撞,深入描述多体入水现象的复杂行为特征,为相关工程解答提供可靠的技术支撑。
1 数值计算方法 1.1 流体控制方程 1.1.1 Navier-Stokes方程与浸入边界法流体运动由不可压缩Navier-Stokes方程描述:
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\nabla \cdot(\boldsymbol{u} \boldsymbol{u})=-\frac{1}{\rho} \nabla p+\frac{1}{\rho} \nabla \cdot \boldsymbol{\tau}+\boldsymbol{f}_{\mathrm{b}}+\boldsymbol{f} $ | (1) |
| $ \nabla \cdot \boldsymbol{u}=0 $ | (2) |
式中:u为流速,t为时间,ρ为密度,p为压力,τ=μ(∇u+∇Tu) 为黏性应力张量,μ为动力黏度,fb为体力项,f为附加体力项,反映固体边界对流体的作用。
根据CBS(Characteristic-based split scheme)算法[22],时间离散后式(1)可以写作下式:
| $ \Delta \boldsymbol{u}=\boldsymbol{G}^{n}+\boldsymbol{H}^{n+1}+\boldsymbol{f}^{n+1} \Delta t $ | (3) |
式中:
如图 1所示,固体由分布在其边界上的浸入边界(IB)点来表征,流体域则采用固定的笛卡尔网格离散,流体网格无需随固体运动实时更新。根据直接力浸入边界法[23],流固耦合面上需满足无滑移边界条件Vn+1=Un+1,其中Vn+1是IB点的期望速度,Un+1为同一点由周围流体网格节点插值得到的速度。定义分布函数D将IB点上的物理量分布到网格节点及插值函数I将网格节点上的物理量插值到IB点[24],结合式可得
| $ \boldsymbol{V}^{n+1}=\boldsymbol{U}^{n+1}=I\left(\boldsymbol{u}^{n}+\boldsymbol{G}^{n}+\boldsymbol{H}^{n+1}+\boldsymbol{f}^{n+1} \Delta t\right) $ | (4) |

|
图 1 入水问题的CFD-DEM-IBM方法示意 Fig. 1 Sketch of the CFD-DEM-IBM for water entry problems |
从而可以将附加体力项写作下式:
| $ \boldsymbol{f}^{n+1} \Delta t=D\left[\boldsymbol{V}^{n+1}-I\left(\boldsymbol{u}^{n}+\boldsymbol{G}^{n}+\boldsymbol{H}^{n+1}\right)\right] $ | (5) |
ICLS方法[15]融合LS及CLS方法的优势,采用守恒性好的CLS方法对流运输和捕捉界面,LS方法计算准确的界面法向。CLS方法中双曲正切函数H为
| $ H(\phi)=\frac{1}{2}\left(1+\tanh \left(\frac{\phi}{2 \varepsilon}\right)\right) $ | (6) |
式中:ϕ为符号距离函数,ε为H的弥散宽度。
CLS方法的对流输运及重新初始化方程分别为:
| $ \frac{\partial H}{\partial t}+\nabla \cdot(\boldsymbol{u} H)=0 $ | (7) |
| $ \frac{\partial H}{\partial \tau}+\nabla \cdot(H(1-H) \boldsymbol{n})=\nabla \cdot(\varepsilon(\nabla H \cdot \boldsymbol{n}) \boldsymbol{n}) $ | (8) |
式中:τ为虚拟时间步,n为重新初始化开始时刻的界面法向。n可由下式计算:
| $ \boldsymbol{n}=\left\{\begin{array}{l} \nabla \phi /|\nabla \phi|, \text { if }|\phi|>\delta \\ \nabla H /|\nabla H|, \text { if }|\phi| \leqslant \delta \end{array}\right. $ | (9) |
式中δ为给定距离,与界面附近网格尺寸Δh有关。
LS方法中ϕ的对流输运及重新初始化方程为:
| $ \frac{\partial \phi}{\partial t}+\nabla \cdot(\boldsymbol{u} \phi)=0 $ | (10) |
| $ \frac{\partial \phi}{\partial \tau}+\nabla \cdot(\tilde{\boldsymbol{u}} \phi)=S\left(\phi^{n}\right)+\phi \nabla \cdot \tilde{\boldsymbol{u}} $ | (11) |
式中:名义流速
界面附近ϕ值根据式(6)由H反算:
| $ \phi=2 \varepsilon \tanh ^{-1}(2 H-1) $ | (12) |
流体密度ρ=ρ1+(ρ2-ρ1)H(ϕ)和黏性系数μ=μ1+(μ2-μ1)H(ϕ)等材料性质即可由H计算,其中,下标1和2分别为第1种和第2种流体。
1.2 固体控制方程刚性块体的运动符合牛顿第二定律:
| $ m \ddot{\boldsymbol{\delta}} ={\mathit{\Sigma}} \boldsymbol{F} $ | (13) |
| $ I_{\mathrm{M}} \ddot{\boldsymbol{\theta}} ={\mathit{\Sigma}} \boldsymbol{M} $ | (14) |
式中:合力
根据势函数离散单元法[25],接触力Fc由法向接触力Fcn和切向接触力Fct构成:
| $ \boldsymbol{F}_{\mathrm{cn}}=p \int_{S_{\beta_{\mathrm{c}} \cap \beta_{\mathrm{t}}}} \boldsymbol{n}_{S_{\beta_{\mathrm{c}} \cap \beta_{\mathrm{t}}}}\left(\boldsymbol{\varphi}_{\mathrm{c}}-\boldsymbol{\varphi}_{\mathrm{t}}\right) \mathrm{d} S $ | (15) |
| $ \boldsymbol{F}_{\mathrm{ct}}=\boldsymbol{R} \boldsymbol{F}_{\mathrm{ct}}^{\prime}+k_{\mathrm{t}} \cdot {\mathit{\Delta}} \boldsymbol{\delta}_{\mathrm{ct}} $ | (16) |
式中:p为罚函数,βc、βt分别为接触块体和目标块体,Sβc∩βt为两块体重叠区域βc∩βt的边界,n为该边界的单位外法向向量,φc、φt分别为接触块体和目标块体内的势函数值,R为旋转矩阵,用以将上一时间步的切向接触力F′ct等值转换至当前时间步切向接触力方向,kt为切向刚度系数,Δδct为切向位移增量。
根据库仑摩擦定律,切向力需要满足下式:
| $ \left(\boldsymbol{F}_{\mathrm{ct}}\right)_{\text {max }}=\boldsymbol{F}_{\mathrm{cn}} \cdot \tan \varphi_{\mu} $ | (17) |
式中:(Fct)max为最大允许静摩擦,φμ为最大静摩擦角。
注意 流体施加在固体上的耦合作用力Ff是基于拉格朗日描述作用在IB点上的,与式中欧拉描述下施加于网格节点上的附加体力f不同。由文献[26]有
| $ \boldsymbol{F}_{\mathrm{f}}=\int_{\Omega^{\prime \prime}}\left(\frac{\partial \boldsymbol{u}}{\partial t}-\boldsymbol{f}_{\mathrm{b}}\right) \mathrm{d} {\mathit{\Omega}}-\int_{{\mathit{\Omega}}^{\prime}} f \mathrm{~d} {\mathit{\Omega}} $ | (18) |
式中:Ω″为边界Γs所围固体域,Ω为计算域边界Γout以内、固体边界Γs以外的流体域,Ω′为由流体域Ω及固体域Ω″共同组成的整个计算域,如图 1所示。
1.3 流固耦合系统迭代求解方案由式(5)可见,引入浸入边界法后,流体速度、压力及体力三者相耦合,需要进行迭代计算。本文采用分区强耦合算法求解流固耦合系统,在一个时间步内迭代数次以满足收敛条件,提高解的收敛性与稳定性。现假设第n步的计算已经完成,第n+1步的第k次迭代步骤如图 2所示,图中‖·‖为任一范数,ζ可以是u、p或δ,εζ为对应项给定的小值。

|
图 2 CFD-DEM-IBM方法迭代求解步骤 Fig. 2 Iterative scheme of the CFD-DEM-IBM approach |
依据标准伽辽金有限单元法[27]对流体控制方程进行空间离散、速度Verlet算法[28]对固体控制方程离散,流固控制方程的迭代格式分别为:
| $ \left(\Delta \boldsymbol{u}^{n, k}, \Delta p^{n, k}\right)=R_{\mathrm{f}}\left(\boldsymbol{u}^{n}, p^{n}, \boldsymbol{\delta}^{n+1, k-1}\right) $ | (19) |
| $ \Delta \boldsymbol{\delta}^{n, k}=R_{\mathrm{s}}\left(\boldsymbol{\delta}^{n}, \boldsymbol{u}^{n+1, k}, p^{n+1, k}\right) $ | (20) |
式中: Rf、Rs分别为流体方程与固体方程的右端项。当耦合系统迭代过程满足收敛条件时,跳出循环,否则执行第n+1步第k+1次迭代。
采用投影法[29]求解流体相,将速度增量拆分为中间速度场增量Δu*=Gn+fn+1和速度增量的修正量Δu**=Hn+1,如图 2所示,中间速度场u*, k不含压力和附加体力项。内循环中的附加体力fn+1, k, i由下式计算:
| $ \begin{gathered} \boldsymbol{f}^{n+1, k, i} \Delta t=\boldsymbol{f}^{n+1, k, i-1} \Delta t+ \\ D\left[\boldsymbol{V}^{n+1}-I\left(\boldsymbol{u}^{n}+\boldsymbol{G}^{n}+\boldsymbol{H}^{n+\theta_{2}}+\boldsymbol{f}^{n+1, k, i-1} \Delta t\right)\right] \end{gathered} $ | (21) |
内、外循环的收敛判断条件分别由下式给出:
| $ \left\|\boldsymbol{V}^{n+1}-I\left(\boldsymbol{u}^{n}+\boldsymbol{G}^{n}+\boldsymbol{H}^{n+\theta_{2}}+\boldsymbol{f}^{n+1, k, i-1} \Delta t\right)\right\| <\varepsilon $ | (22) |
| $ \| I\left(\boldsymbol{u}^{n}+\boldsymbol{K}^{n}+\boldsymbol{R}^{n+\theta_{2}, k}\right)-I\left(\boldsymbol{u}^{n}+\boldsymbol{K}^{n}+\boldsymbol{R}^{n+\theta_{2}, k-1}\right) \|<\varepsilon $ | (23) |
式中ε为容差。若满足收敛性要求则退出迭代,否则继续执行下一迭代步的计算。
2 数值仿真结果 2.1 圆柱常速入水为验证CFD-DEM-IBM方法对自由面的准确捕捉及高解析度流场的反映,开展文献[10, 30]中圆柱常速入水现象仿真。半径1 m圆柱以v=1 m/s的速度入水,初始时刻圆心距离水面h=1.25 m,水深20 m,水体密度与黏度分别为1 kg/m3和1.0×10-3 Pa·s,对应气体取值为1×10-3 kg/m3和1.8×10-5 Pa·s,重力加速度设为1 m/s2。计算域宽40 m,高30 m,依据文献[10],将计算域剖分为600×480个单元,圆柱运动路径附近采用Δx=Δy=0.025 m的均匀网格,圆柱表面布置502个IB点,计算域边界均为无滑移固壁。
图 3给出了圆柱入水的自由液面位置及涡量云图,T=vt/h为量纲一的时间。当圆柱接触静止水面时,水面由于固体边界的挤压而变形,产生沿圆柱边界的两股射流;随着圆柱浸入,射流逐渐变陡并与圆柱表面分离,直至圆柱完全浸没在水面以下时,液面呈现凹陷状态;随后,不稳定的液面持续变形并最终合并,在中间形成向上的飞溅。图 3成功再现了圆柱入水全过程,与文献[10, 30]中的数值结果符合,涡量在自由液面曲率发展的区域及圆柱附近产生,与文献[10]吻合,验证了本文方法能够获得高解析度流场,精细描述流场结构。

|
图 3 圆柱入水自由液面位置及涡量云图 Fig. 3 Positions of the free water surface and vorticity contours for water entry of a cylinder |
为详细论证本文方法捕获自由液面的准确性,图 4对比了文献[10, 30]中的数值结果与本文得到的不同时刻界面轮廓。注意到T=3.0时刻的差异以及T=4.0时刻空腔关闭时产生的气泡可能与接触角边界条件的设置有关,在文献[10, 30]中均有所提及。考虑到自由液面的网格敏感性,网格分辨率也对计算结果存在影响。总的来说,文中结果与以往研究符合较好,展示了本文方法准确刻画瞬态演化自由液面的能力。

|
图 4 圆柱入水自由液面形态对比 Fig. 4 Comparison of the free water surface profiles for water entry of a cylinder |
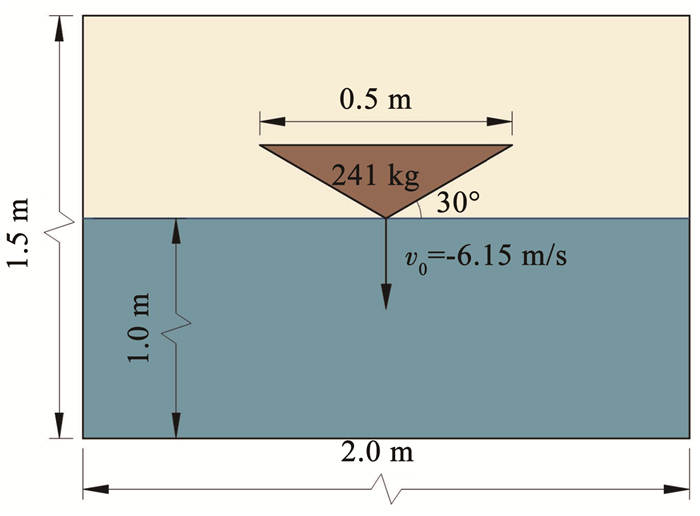
圆柱常速入水实际只是包含移动边界的纯流体力学问题。本文开展对称楔形体垂直自由入水数值仿真,旨在揭示本文方法处理入水问题时对强烈的流固耦合作用的准确反映及自由液面与移动边界的妥善处理能力。算例取自文献[11, 31-34],计算参数如图 5所示,水体密度与黏度分别为1 000 kg/m3和1.0×10-3 Pa·s,对应空气取值为1 kg/m3及1.8× 10-5 Pa·s。三维楔形体长1 m,其中测量截面长度为0.2 m,本文依据文献[31-32]将该三维入水问题简化为二维考虑,仅考虑竖向自由度。参照文献[32],将计算域剖分为520×280个网格,楔形体边界上布置862个IB点,边界条件设置同圆柱常速入水。
|
图 5 楔形体垂直入水初始时刻示意 Fig. 5 Sketch of the vertical free fall of a wedge at t=0 s |
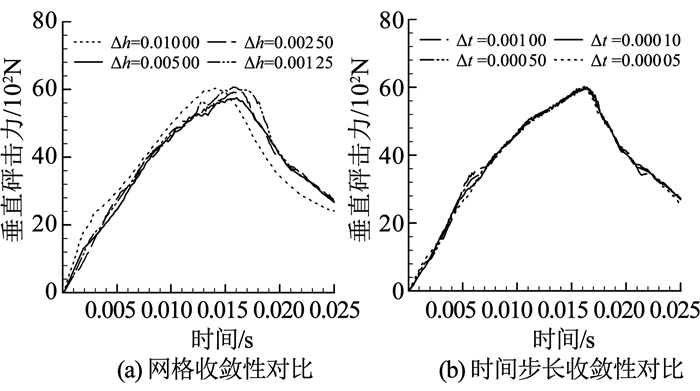
楔形体起初由静止距离水面2.0 m处自由下落,接触水面时具有6.15 m/s的初速度。为了验证数值方法的网格收敛性,保持其他条件不变,对时间步长为Δt=0.000 1 s,最小网格尺寸Δh分别为0.010 00、0.005 00、0.002 50、0.001 25 m 4种情况下的楔形体入水砰击力进行计算,结果如图 6(a)所示。由图 6(a)可见,本文方法具有良好的网格收敛性,4种不同网格尺寸得到的计算结果基本一致,后续计算选取Δh=0.002 50 m。
|
图 6 数值方法时空离散收敛性验证 Fig. 6 Convergence verification of the proposed numerical method |
同样地,为验证本文方法的时间步长收敛性,保持其他条件不变,采用最小网格尺寸Δh=0.002 50 m,对比Δt分别为0.001 00、0.000 50、0.000 10、0.000 05 s 4种时间步长下的楔形体入水砰击力。如图 6(b)所示,本文所提出的高解析度CFD-DEM-IBM方法具有良好的时间步长收敛性,分别采用4种时间步长计算得到的结果吻合度高。后续数值计算的时间步长统一选为Δt=0.000 10 s。
本文计算得到的自由液面及压力云图如图 7所示,可以看出,楔形体入水后,在楔形体两侧激起两股射流,随后射流沿楔形体边界上升并在重力作用下发生弯曲,与边界表面发生分离;压力峰值在入水初期位于楔形体底部尖端附近,随后移动到射流区根部并逐渐降低。总的来说,压力分布与Oger等[31]的数值结果具有较高的一致性。

|
图 7 楔形体对称入水自由液面及压力云图 Fig. 7 Positions of the free water surface and pressure contours for water entry of a wedge |
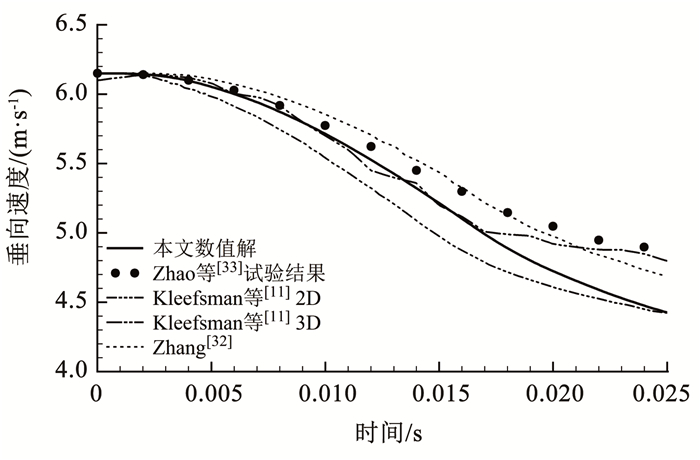
图 8、9分别给出了垂向砰击力和楔形体下落速度的定量对比。由图 8、9可见,楔形体入水过程经历了两个阶段:第1阶段(0 s<t<0.016 s)楔形体撞击自由水面,造成自身速度的急剧下降和砰击力的快速上升并达到峰值,随后在第2阶段(0.016 s< t<0.025 s),楔形体入水速度缓慢降低,并最终完全浸没在水中。如图 8、9所示,本文方法对入水砰击力的预测相比试验偏大,造成楔形体速度偏小,这可能与楔形体入水的三维效应有关[31]。总体上,曲线的趋势和幅值与以往数值与试验结果[11, 31-33]吻合,验证了本文方法的正确性、准确性与可靠性。

|
图 8 楔形体对称入水垂向砰击力时程图 Fig. 8 Time history of the vertical slamming force |
|
图 9 楔形体对称入水垂向速度时程图 Fig. 9 Time history of the vertical velocity of the wedge |
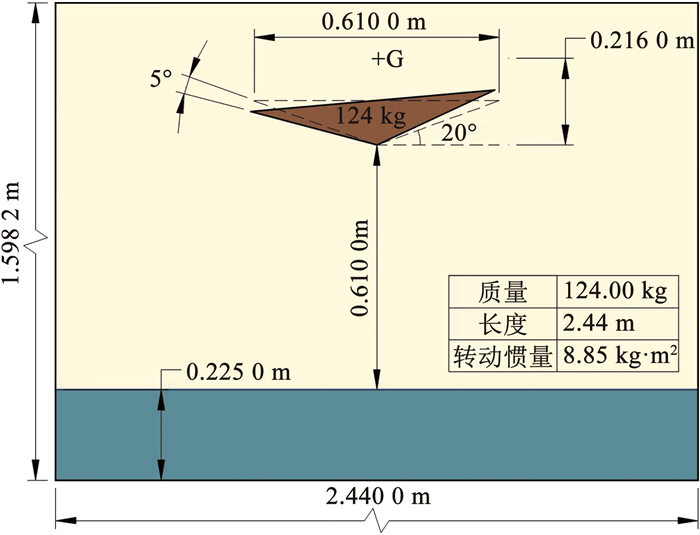
本文对三自由度倾斜楔形体自由入水问题展开仿真。计算参数与文献[35]一致,如图 10所示。水体和空气的密度分别为1 000 kg/m3和1.2 kg/m3,黏度分别为1.0×10-3 Pa·s和1.8×10-5 Pa·s。楔形体表面分布1 511个IB点,计算域剖分为796×464个单元,边界均为无滑固壁。
|
图 10 楔形体斜入水初始时刻示意 Fig. 10 Sketch of the inclined fall of a wedge at t=0 s |
楔形体初始由静止在距离水面0.610 0 m处受重力自由下落,自由液面及涡量云图如图 11所示。当楔形体在空气中下落时,其左、右尖端处形成涡结构并逐渐脱落,至楔形体撞击水面时,大的涡结构与液面相互作用破碎成小涡,与文献[35]的数值结果符合,表明本文方法能够精细刻画流体结构,获得高解析度流场信息。非对称楔形体入水造成非对称的液面飞溅,及楔形体由倾斜“回正”的现象也与文献[31]的数值结果描述相符。

|
图 11 楔形体斜入水自由液面与涡量云图 Fig. 11 Position of the free water surface and vorticity contours for water entry of a wedge |
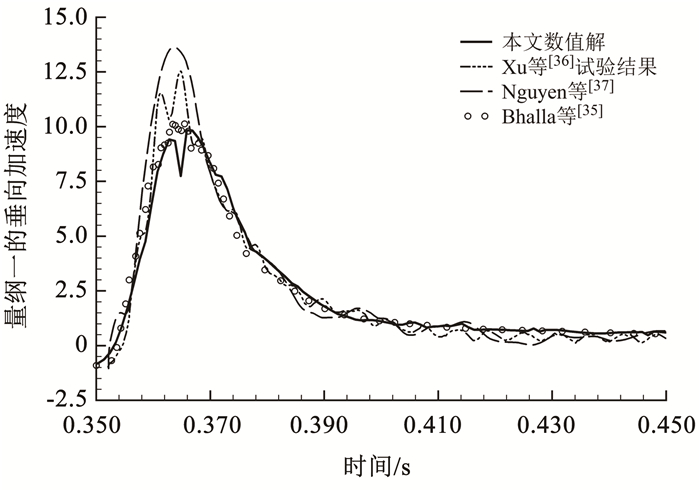
为定量对比计算结果,图 12、13分别将量纲一的垂向加速度与角加速度与已有文献结果展开比较。其中,量纲一的垂向加速度
|
图 12
斜入水楔形体量纲一的加速度( |
|
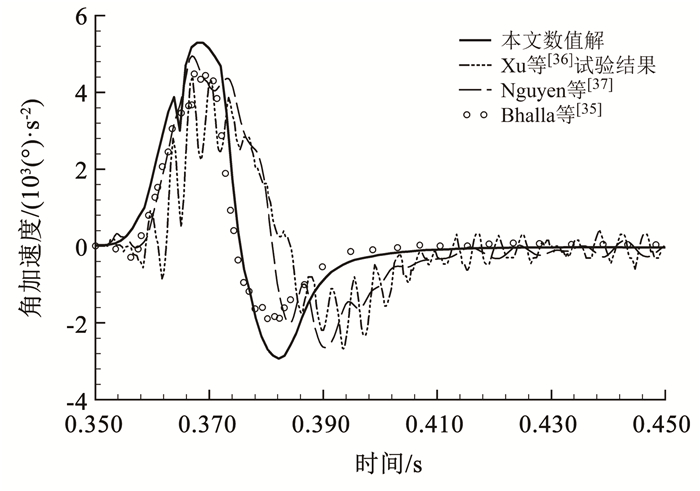
图 13 斜入水楔形体角加速度时程图 Fig. 13 Time history of the angular acceleration of the wedge |
涉及块体间相互作用的多体入水问题数值仿真尤为复杂,在以往的研究中鲜见报道。本文针对5个相同刚性圆柱的入水问题展开模拟,以揭示本文方法对复杂多体入水问题乃至更一般的工程问题的适用性。计算参数如图 14所示,固体密度为2 500 kg/m3,各圆柱表面布置471个浸入边界点,计算域由500×400个单元离散,流体特性与边界条件设置同楔形体非对称斜入水。圆柱的最大静摩擦角取为0,法向与切向刚度系数均取为2×107 N/m。

|
图 14 多圆柱入水初始时刻示意 Fig. 14 Sketch of water entry of multiple bodies at t=0 s |
图 15给出了多圆柱入水过程中的自由水面和压力云图。初始时刻,5个分散的圆柱在一定排列方式下由静止受重力作用下落,如图 15(a)所示;随后在t=0.638 s时刻,底部3个圆柱撞击自由水面,产生巨大的砰击力,如图 15(b)中圆柱底部呈现高压区;从而,底部圆柱速度骤降,而上方圆柱仍持续下落,造成原来分散的5个圆柱发生碰撞,如图 15(c)所示,此时水面发生变形,出现水花飞溅现象;紧接着,不稳定的自由面持续变形,如图 15(d)所示,由于复杂的流固耦合作用及固体间的碰撞,压力的分布与单体入水时全然不同,下方圆柱间飞溅的液面也由于上方圆柱的阻碍发生变形弯曲,并推动上方圆柱,使5个圆柱重新变得分散。总之,本文对多体入水时剧烈的自由面演化、块体间的碰撞及强烈的流固耦合效应都得到了很好的反映,验证了本文CFD-DEM-IBM方法处理多体入水问题的灵活性与普适性。

|
图 15 多圆柱入水自由液面与压力云图 Fig. 15 Position of the free water surface and pressure contours for water entry of multiple cylinders |
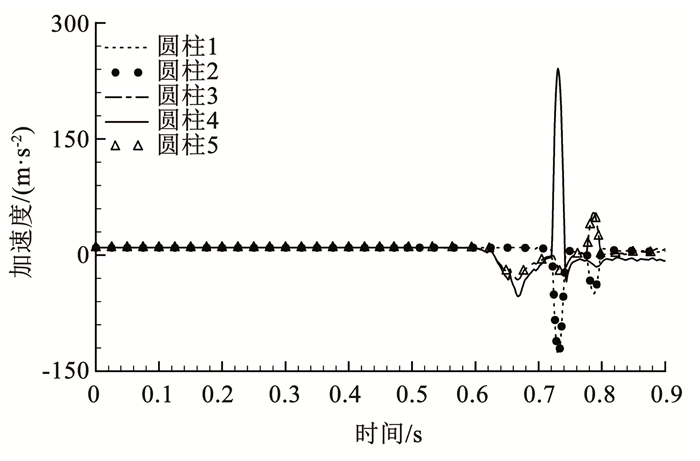
图 16给出了圆柱的加速度时程图。由图 16可见,初始5个圆柱在重力作用下匀加速规则下落;t=0.620 s时下方圆柱砰击水面急剧减速,而上方圆柱仍保持以重力加速度向下运动;t=0.730 s时刻,下方3个圆柱在中间射流作用下分散,从而上方圆柱与圆柱4发生碰撞,使得上方圆柱速度骤降而圆柱4受到高速撞击加速下落;在t=0.780 s时,圆柱间发生第2次碰撞,下方两侧圆柱受到上方圆柱的撞击后开始加速下落。结合图 15可见,多体入水现象呈现出高度对称性,且在不同入水阶段存在不同的力的主导趋势,而本文所提出的CFD-DEM-IBM方法能够兼顾离散体间的碰撞处理、自由液面的瞬态演化及复杂的流固耦合效应描述,在涉及固体间相互作用的多体入水问题求解方面优势显著。
|
图 16 入水圆柱加速度时程图 Fig. 16 Time history of the accelerations of multiple cylinders |
1) 高解析度CFD-DEM-IBM方法能够合理描述结构移动边界,准确计算流固耦合作用力,获得高解析度流场,实现对自由面演化过程的精细刻画。
2) 通过4种不同网格尺寸与时间步长的敏感性分析,验证了CFD-DEM-IBM方法在处理入水问题方面具有良好的收敛性。
3) 本文再现了圆柱1 m/s常速入水、底升角30°的楔形体对称自由入水及底升角20°的楔形体非对称自由入水过程,与以往研究符合较好,揭示了本文方法对入水问题数值仿真的准确性与可靠性。
4) 多体入水与单体入水现象迥异,通过设计5个圆柱入水过程仿真,证明了CFD-DEM-IBM方法能够合理考虑固体间的碰撞,在处理复杂多体入水问题方面具有独到的优越性,能够推广应用于更加一般的实际工程问题。
| [1] |
侯宇, 黄振贵, 郭则庆, 等. 超空泡射弹小入水角高速斜入水试验研究[J]. 兵工学报, 2020, 41(2): 332. HOU Yu, HUANG Zhengui, GUO Zeqing, et al. Experimental investigation on shallow-angle oblique water-entry of a high-speed supercavitating projectile[J]. Acta Armamentarii, 2020, 41(2): 332. DOI:10.3969/j.issn.1000-1093.2020.02.015 |
| [2] |
XIE Hang, LIU Fang, TANG Haoyun, et al. Numerical study on the dynamic response of a truncated ship-hull structure under asymmetrical slamming[J]. Marine Structures, 2020, 72: 102767. DOI:10.1016/j.marstruc.2020.102767 |
| [3] |
徐文杰. 滑坡涌浪流-固耦合分析方法与应用[J]. 岩石力学与工程学报, 2020, 39(7): 1420. XU Wenjie. Fluid-solid coupling method of landslide tsunamis and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(7): 1420. DOI:10.13722/j.cnki.jrme.2020.0061 |
| [4] |
CLANET C, HERSEN F, BOCQUET L. Secrets of successful stone-skipping[J]. Nature, 2004, 427(6969): 29. DOI:10.1038/427029a |
| [5] |
张佳悦, 李达钦, 吴钦, 等. 航行体回收垂直入水空泡流场及水动力特性研究[J]. 力学学报, 2019, 51(3): 803. ZHANG Jiayue, LI Daqin, WU Qin, et al. Numerical investigation on cavity structures and hyrodynamics of the vehicle during vertical water-entry[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 803. DOI:10.6052/0459-1879-18-364 |
| [6] |
王永虎, 林天龙. 基于k-ε湍流模型的结构物水流中跌落过程数值分析[J]. 重庆交通大学学报(自然科学版), 2019, 38(2): 144. WANG Yonghu, LIN Tianlong. Numerical analysis on the structure falling in water flow based on k-ε viscous model[J]. Journal of Chongqing Jiaotong University (Natural Science), 2019, 38(2): 144. DOI:10.3969/j.issn.1674-0696.2019.02.21 |
| [7] |
MA Z H, QIAN L, MARTÍNEZ-FERRER P J, et al. An overset mesh based multiphase flow solver for water entry problems[J]. Computers & Fluids, 2018, 172: 689. DOI:10.1016/j.compfluid.2018.01.025 |
| [8] |
谢路毅, 曹留帅, 万德成. 基于重叠网格方法模拟双圆柱入水过程[J]. 水动力学研究与进展(A辑), 2021, 36(2): 244. XIE Luyi, CAO Liushuai, WAN Decheng. Simulation of twin-cylinder water entry process based on overset grid method[J]. Chinese Journal of Hydrodynamics, 2021, 36(2): 244. DOI:10.16076/j.cnki.cjhd.2021.02.011 |
| [9] |
PESKIN C S. Flow patterns around heart valves: A numerical method[J]. Journal of Computational Physics, 1972, 10(2): 252. DOI:10.1016/0021-9991(72)90065-4 |
| [10] |
CALDERER A, KANG S, SOTIROPOULOS F. Level set immersed boundary method for coupled simulation of air/water interaction with complex floating structures[J]. Journal of Computational Physics, 2014, 277: 201. DOI:10.1016/j.jcp.2014.08.010 |
| [11] |
KLEEFSMAN K M T, FEKKEN G, VELDMAN A E P, et al. A Volume-of-Fluid based simulation method for wave impact problems[J]. Journal of Computational Physics, 2005, 206(1): 363. DOI:10.1016/j.jcp.2004.12.007 |
| [12] |
王易君, 李明海, 张中礼, 等. 基于VOF法的平底结构自由落体入水砰击载荷模拟[J]. 振动与冲击, 2017, 36(2): 185. WANG Yijun, LI Minghai, ZHANG Zhongli, et al. Numerical simulation on the slamming load in the water-entry process of flatted-bottom body based on the method VOF[J]. Journal of Vibration and Shock, 2017, 36(2): 185. DOI:10.13465/j.cnki.jvs.2017.02.030 |
| [13] |
OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12. DOI:10.1016/0021-9991(88)90002-2 |
| [14] |
OLSSON E, KREISS G. A conservative level set method for two phase flow[J]. Journal of Computational Physics, 2005, 210(1): 225. DOI:10.1016/j.jcp.2005.04.007 |
| [15] |
ZHAO Lanhao, MAO Jia, LIU Xiaoqing, et al. Improved conservative level set method for free surface flow simulation[J]. Journal of Hydrodynamics, Ser B, 2014, 26(2): 316. DOI:10.1016/S1001-6058(14)60035-4 |
| [16] |
何春涛, 王聪, 闵景新, 等. 回转体匀速垂直入水早期空泡数值模拟研究[J]. 工程力学, 2012, 29(4): 237. HE Chuntao, WANG Cong, MIN Jingxin, et al. Numerical simulation of early air-cavity of cylinder cone with vertical water-entry[J]. Engineering Mechanics, 2012, 29(4): 237. |
| [17] |
SUN Pengnan, MING Furen, ZHANG Aman. Numerical simulation of interactions between free surface and rigid body using a robust SPH method[J]. Ocean Engineering, 2015, 98: 32. DOI:10.1016/j.oceaneng.2015.01.019 |
| [18] |
王聪, 何超杰, 余德磊. 回转体并联入水运动状态预测[J]. 哈尔滨工业大学学报, 2021, 53(6): 21. WANG Cong, HE Chaojie, Yu Delei. Prediction of the state of revolution bodies entering water in parallel[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 21. DOI:10.11918/201906068 |
| [19] |
王胤, 艾军, 杨庆. 考虑粒间滚动阻力的CFD-DEM流-固耦合数值模拟方法[J]. 岩土力学, 2017, 38(6): 1771. WANG Yin, AI Jun, YANG Qing. A CFD-DEM coupled method incorporating soil inter-particle rolling resistance[J]. Rock and Soil Mechanics, 2017, 38(6): 1771. DOI:10.16285/j.rsm.2017.06.027 |
| [20] |
DI FELICE R. The voidage function for fluid-particle interaction systems[J]. International Journal of Multiphase Flow, 1994, 20(1): 153. DOI:10.1016/0301-9322(94)90011-6 |
| [21] |
底瑛棠, 赵兰浩, 毛佳. 颗粒沉降问题的高解析度CFD-DEM-IBM流固耦合数值模拟方法[J]. 水科学进展, 2021, 32(2): 286. DI Yingtang, ZHAO Lanhao, MAO Jia. A CFD-DEM-IBM method for sedimentation of particles with high resolution[J]. Advances in Water Science, 2021, 32(2): 286. DOI:10.14042/j.cnki.32.1309.2021.02.014 |
| [22] |
ZIENKIEWICZ O C, WU J. A general explicit or semi-explicit algorithm for compressible and incompressible flows[J]. International Journal for Numerical Methods in Engineering, 1992, 35(3): 457. DOI:10.1002/nme.1620350303 |
| [23] |
JI C, MUNJIZA A, WILLIAMS J J R. A novel iterative direct-forcing immersed boundary method and its finite volume applications[J]. Journal of Computational Physics, 2012, 231(4): 1797. DOI:10.1016/j.jcp.2011.11.010 |
| [24] |
MAO Jia, ZHAO Lanhao, LIU Xunnan, et al. An iterative divergence-free immersed boundary method in the finite element framework for moving bodies[J]. Computers & Fluids, 2020, 208: 104630. DOI:10.1016/j.compfluid.2020.104630 |
| [25] |
ZHAO Lanhao, LIU Xunnan, MAO Jia, et al. A novel discrete element method based on the distance potential for arbitrary 2D convex elements[J]. International Journal for Numerical Methods in Engineering, 2018, 115(2): 238. DOI:10.1002/nme.5803 |
| [26] |
SHEN Linwei, CHAN E S, LIN Pengzhi. Calculation of hydrodynamic forces acting on a submerged moving object using immersed boundary method[J]. Computers & Fluids, 2009, 38(3): 691. DOI:10.1016/j.compfluid.2008.07.002 |
| [27] |
ZHOU Chuan, LI Jianhua, WANG Huaan, et al. A divergence-free immersed boundary method and its finite element applications[J]. Journal of Mechanics, 2020, 36(6): 901. DOI:10.1017/jmech.2020.23 |
| [28] |
ALLEN M P, TILDESLEY D J. Computer simulation of liquids[M]. USA: Oxford University Press, 1987.
|
| [29] |
CHORIN A J. A numerical method for solving incompressible viscous flow problems[J]. Journal of Computational Physics, 1967, 2(1): 12. DOI:10.1016/0021-9991(67)90037-x |
| [30] |
YANG Jianming, STERN F. Sharp interface immersed-boundary/level-set method for wave-body interactions[J]. Journal of Computational Physics, 2009, 228(17): 6590. DOI:10.1016/j.jcp.2009.05.047 |
| [31] |
OGER G, DORING M, ALESSANDRINI B, et al. Two-dimensional SPH simulations of wedge water entries[J]. Journal of Computational Physics, 2006, 213(2): 803. DOI:10.1016/j.jcp.2005.09.004 |
| [32] |
ZHANG Yali. A level set immersed boundary method for water entry and exit[J]. Communications in Computational Physics, 2019, 8(2): 265. DOI:10.4208/cicp.060709.060110a |
| [33] |
ZHAO R, FALTINSEN O, AARSNES J. Water entry of arbitrary two-dimensional sections with and without flow separation[C]//Proceedings of the 21st Symposium on Naval Hydrodynamics. Trondheim, Norway: [s. n. ], 1996: 408
|
| [34] |
YANG Qingyong, QIU Wei. Numerical simulation of water impact for 2D and 3D bodies[J]. Ocean Engineering, 2012, 43: 82. DOI:10.1016/j.oceaneng.2012.01.008 |
| [35] |
BHALLA A P S, NANGIA N, DAFNAKIS P, et al. Simulating water-entry/exit problems using Eulerian-Lagrangian and fully-Eulerian fictitious domain methods within the open-source IBAMR library[J]. Applied Ocean Research, 2020, 94: 101932. DOI:10.1016/j.apor.2019.101932 |
| [36] |
XU L, TROESCH A W, PETERSON R. Asymmetric hydrodynamic impact and dynamic response of vessels[J]. Journal of Offshore Mechanics and Arctic Engineering, 1999, 121(2): 83. DOI:10.1115/1.2830082 |
| [37] |
NGUYEN V T, VU D T, PARK W G, et al. Navier-Stokes solver for water entry bodies with moving Chimera grid method in 6DOF motions[J]. Computers & Fluids, 2016, 140: 19. DOI:10.1016/j.compfluid.2016.09.005 |
 2023, Vol. 55
2023, Vol. 55


