用实验数据作为精确的参考数据来改进有限元预测,称为有限元模型修正[1]。当前多数模型修正方法属于确定性方法,没有考虑结构参数和响应的不确定性,降低了其工程实际应用价值。然而,大多数实际工程结构的材料参数、几何尺寸和试验数据的不确定性广泛存在。因此,研究涉及不确定性分析的有限元模型修正非常必要[2-3]。
在模型修正过程中,使用代理模型代替有限元模型可减小计算量,是解决复杂工程结构优化问题的有效途径之一[4]。常见的代理模型中,径向基(Radial basis function, RBF)模型结构简单,预测精度高,广泛应用于土木、航天和机械等领域[5]。因此,本文选用RBF模型为模型修正的代理模型。
近年来,众多学者研究了考虑不确定性的模型修正方法,并取得了一定的成果。不确定性有限元模型修正主要可分为概率和非概率方法,基于概率的模型修正一般为随机模型修正方法,基于非概率的模型修正有模糊方法和区间分析方法[6]。概率方法需要丰富的试验数据以得到较准确的统计信息,计算成本高[7];基于模糊数学的模糊方法在确定隶属函数时容易引入额外的不确定性[8];区间分析方法对数据要求低,适用于缺乏数据信息的情况[9]。Fang等[10]将区间响应面模型用于区间模型修正,实现参数和响应的区间估计。骆勇鹏等[11]提出一种基于响应面的灵敏度模态区间分析方法,通过比较相对模态区间灵敏度判断结构响应对参数的敏感程度。姜东等[12]采用区间扩张理论与灵敏度方法,用于不确定性和初始有限元模型误差均较小情况的有限元模型修正。Deng等[13]提出了一种利用一阶摄动法和RBF神经网络进行结构参数区间识别的两步确定性修正方法。Wang等[14]提出了一种改进的参数摄动法来预测不确定结构的特征值区间,该方法考虑了计算效率,但它依赖于区间变量的初始值和不确定程度。Deng等[15]提出了一种结构不确定性度量区间识别策略,可以得到系统响应的精确区间估计。Zheng等[8]提出了一种利用泛灰数学和高斯过程回归模型的两步区间模型修正方法。上述区间模型修正研究均以结构振动的模态参数作为响应量,相比于模态参数,结构振动的频响函数(Frequency response function,FRF)则包含了更充分的结构信息,能够更加准确地反映结构的动力学特性。同时,采用FRF进行模型修正可以有效避免由模态分析所引入的误差[16-17]。此外,小波变换是进行信号时频研究的重要工具,可以聚焦信号的细节特征,已被广泛应用于水文、地震勘探、生态保护和经济管理等领域的预测研究[18]。本文对加速度FRF小波变换提取低频小波系数作为响应特征量进行模型修正。
综上所述,本文提出了基于加速度频响函数的区间有限元模型修正方法。首先构造RBF代理模型并对RBF模型方差值进行了优选;然后利用区间重叠率和巴氏距离分别构造两步和同步修正所需要的目标函数,用来度量两个样本区间分布的相似性和相异性;最后结合灰色数学方法,运用花朵授粉算法分别进行两步和同步待修正参数区间的求解。通过支撑框架结构,空间桁架结构和简支梁结构验证所提方法的有效性。
1 小波变换小波变换通过伸缩平移运算对信号多尺度细化,最终高频处时间细分,低频处频率细分,凸显问题某些方面的特征。对一维信号y(t)的小波变换,给定一个基函数,令
| $ \psi_{a, b}(t)=\frac{1}{\sqrt{a}} \psi\left(\frac{t-b}{a}\right) $ | (1) |
式中:a为伸缩因子且大于0,b为平移因子。为了计算方便,在实际分析和应用中需要将连续小波及小波系数进行离散化处理,则y(t)的小波变换为
| $ W T_{y}(a, b)=\frac{1}{\sqrt{a}} \sum\limits_{t=1}^{n} y(t) \psi\left(\frac{t-b}{a}\right), t=1, 2, \cdots, n $ | (2) |
式中,WTy(a, b)为y(t)的小波系数。在一定的频率点数下,小波分解层数过少会使每层小波系数过多,计算量过高,反之,分解层数过多会使每层小波系数过少而影响模型修正效果。通过对比多次试验效果,本文设定基函数为db3,分解层数为4、5层。对加速度FRF进行小波变换,提取低频小波系数作为构造RBF模型的输出,也作为加速度FRF的响应特征量进行模型修正。
2 RBF模型的构造 2.1 RBF神经网络的基本原理在d维设计空间中生成一组数量为N的初始样本点x=[x1, x2, …, xN]∈ Rd,目标的真实响应值为y(x1), y(x2), …, y(xN),RBF插值函数的数学形式为
| $ s(x)=\sum\limits_{k=1}^{N} w_{k} \varphi\left(\left\|x-x_{k}\right\|\right) $ | (3) |
式中:N为样本点个数,wk为权值系数,‖·‖为欧氏距离,φ(·)为基函数。
由s(xk)=y(xk) 可得:Φ·W=Y,即W=Φ-1·Y,其中
| $ \boldsymbol{\varPhi}=\left(\begin{array}{ccc} \varphi\left(\left\|x_{1}-x_{1}\right\|\right) & \cdots & \varphi\left(\left\|x_{1}-x_{k}\right\|\right) \\ \vdots & \ddots & \vdots \\ \varphi\left(\left\|x_{k}-x_{1}\right\|\right) & \cdots & \varphi\left(\left\|x_{k}-x_{k}\right\|\right) \end{array}\right) $ |
式中:W=(w1, w2, …, wk)T为权系数向量,Y=[y(x1), y(x2), …, y(xk)]T为样本点的真实响应向量。选用应用较广的高斯插值基函数,表达式为
| $ \varphi(r, \sigma)=\mathrm{e}^{-\frac{r^{2}}{2 \sigma^{2}}} $ | (4) |
式中:r=‖x-xk‖为当前预测点与任意样本点之间的欧氏距离,σ2为方差。
2.2 RBF模型的构造及验证建立一个严格RBF模型,需要先设定高斯插值基函数的方差值,方差直接影响模型预测精度。通过鲸鱼优化算法(Whale optimization algorithm,WOA)优选最佳方差值。WOA以泡泡网搜索策略为灵感,主要步骤为包围猎物、气泡网攻击和搜索猎物[19]。
采用拉丁超立方抽样方法抽取初始待修正参数±20%区间内的样本,将其分为训练集和测试集。建立目标函数:
| $ \operatorname{obj}_{\sigma}=\sum\limits_{k=1}^{K} \sum\limits_{s=1}^{S}\left(y_{s}^{\mathrm{a}}-y_{s}^{\mathrm{res}}\right)^{2} $ | (5) |
式中:ysres为测试集RBF模型预测的响应特征量,ysa为测试集有限元模型响应特征量,S为测试集样本数,K为响应特征量数目。设置WOA中搜索代理为30,最大迭代次数为50, 参数上、下界分别为50.00和0.01,通过WOA以式(5)为目标函数确定RBF模型的最优方差值,建立RBF模型。然后,计算测试集的RBF模型预测值和有限元模型真实值之间的均方根误差值(RMSE)来评估RBF模型的预测精度,RMSE表达式为
| $ \operatorname{RMSE}=\frac{1}{{S \hat y_{s}^{\mathrm{a}}}} \sqrt{\sum\limits_{s=1}^{S}\left(y_{s}^{\mathrm{a}}-y_{s}^{\mathrm{res}}\right)^{2}} $ | (6) |
式中
实际工程结构中所能获得的样本信息非常有限,且具有不确定性。灰色数学方法需要的样本量小,主观依赖性小,具有效率高和精度高的优点[9]。在工程问题中,不确定信息可以使用灰色数学方法来获得实际值的区间估计,其基本原理如下。
对一组初始不规则数据:
| $ \boldsymbol{Y}=\{y(c), c=1, 2, \cdots, n\} $ | (7) |
将数据从小到大排列,得到:
| $ \boldsymbol{Y}^{(0)}=\left\{y^{(0)}(c), c=1, 2, \cdots, n\right\} $ | (8) |
把Y(0)的元素按顺序相加,得到一个新的Y(1)序列:
| $ \begin{array}{l} \boldsymbol{Y}^{(1)}=\left\{y^{(1)}(c), c=1, 2, \cdots, n\right\}=\left\{y^{(0)}(1), y^{(0)}(1)+\right.\\ \;\;\;\;\;\;\;\;\;\left.y^{(0)}(2), \cdots, y^{(0)}(1)+y^{(0)}(2)+\cdots+y^{(0)}(n)\right\} \end{array} $ | (9) |
定义:
| $ \left\{\begin{array}{l} \Delta(c)=\frac{y^{(1)}(n)}{n} c-y^{(1)}(c) \\ \Delta_{\max }=\max (\Delta(1), \Delta(2), \cdots, \Delta(n)) \\ g=h \frac{\Delta_{\max }}{n} \end{array}\right. $ | (10) |
式中:h为恒定灰色系数,通常取值2.5;g为基于灰色估计的不确定性估计标准差;数据的区间为
不确定度量用以表征理论分析响应和测量响应之间的区间一致性,反映两个区间分布的相似性和相异性,它直接影响模型修正的精度。
4.1 区间重叠率连续区间
| $ \operatorname{len}(P)=\bar{p}-\underline p, \operatorname{len}(Q)=\bar{q}-\underline q $ | (11) |
定义区间P和区间Q的区间重叠率(Interval overlap ratio, IOR)[15]为
| $ \operatorname{IOR}(P \mid Q)=\frac{\operatorname{len}(P \cap Q)-\operatorname{len}((P \cup Q)-(P \cap Q))}{\operatorname{len}(Q)} $ | (12) |
式中:运算符∪、∩分别为并集、交集;len(P∩Q)、len((P∪Q)-(P∩Q))分别为表征区间P和区间Q之间的相似程度和不相似程度。由式(12)可知,在P=Q的情况下,IOR(P|Q)=1。对于区间模型修正问题,利用IOR(P|Q)可以度量理论分析数据和测量数据之间区间分布的相似性。
4.2 区间巴氏距离巴氏距离用来度量两个概率分布之间的相似性,巴氏距离越小,表示两个概率分布越相似[20]。在高斯分布下U=N(mU, θU)和V=N(mV, θV)的巴氏距离为
| $ \begin{aligned} \mathrm{BD}(U, V)= & \frac{1}{8}\left(m_{U}-m_{V}\right)^{\mathrm{T}} \theta^{-1}\left(m_{U}-m_{V}\right)+ \\ & \frac{1}{2} \ln \left(\frac{\operatorname{det} \theta}{\sqrt{\operatorname{det} \theta_{U} \operatorname{det} \theta_{V}}}\right) \end{aligned} $ | (13) |
式中:θ=(θU+θV)/2。本文将式(13)中概率分布的均值和方差定义为区间分布的区间中点和半径。将高斯分布下的巴氏距离推广应用于区间有限元模型修正,度量两个区间分布的相似性,称为区间巴氏距离,表示为
| $ \begin{aligned} \operatorname{obj}_{x}= & \frac{1}{8}\left(\tilde{\boldsymbol{y}}^{\text {res }}-\tilde{\boldsymbol{y}}^{\mathrm{e}}\right)^{\mathrm{T}} \boldsymbol{\delta}^{-1}\left(\tilde{\boldsymbol{y}}^{\text {res }}-\tilde{\boldsymbol{y}}^{\mathrm{e}}\right)+ \\ & \frac{1}{2} \ln \left(\frac{\operatorname{det}(\boldsymbol{\delta})}{\sqrt{\operatorname{det}\left(\operatorname{diag}\left(\Delta \boldsymbol{y}^{\text {res }}\right)\right) \operatorname{det}\left(\operatorname{diag}\left(\Delta \boldsymbol{y}^{\mathrm{e}}\right)\right)}}\right) \end{aligned} $ | (14) |
式中:δ=(diag(Δyres)+diag(Δye))/2,
花朵授粉算法(Flower pollination algorithm, FPA)具有异花授粉(全局寻优)和自花授粉(局部寻优)两大特性。异花授粉过程可以逃离任何局部景观,进而探索更大的空间;自花授粉过程使相似的解被更频繁地选择,本质上是指数收敛,收敛速度更高,性能优于遗传算法和粒子群算法[21]。本文运用FPA分别进行两步和同步的区间有限元模型修正。
结构待修正参数具有不确定性,将其描述为实数域R内的一个闭区间:
| $ \boldsymbol{x}^{\mathrm{I}}=[\underline{\boldsymbol{x}}, \overline{\boldsymbol{x}}]=[\tilde{\boldsymbol{x}}-\Delta \boldsymbol{x}, \tilde{\boldsymbol{x}}+\Delta \boldsymbol{x}] $ | (15) |
式中:上标I为该参数为区间参数,
1) 两步修正参数区间中点和半径。第1步求解结构待修正参数的区间中点。建立目标函数:
| $ \operatorname{obj}_{\tilde{x}}=\sum\limits_{k=1}^{K}\left|y_{k}^{\mathrm{res}}-\tilde{y}_{k}^{\mathrm{e}}\right| $ | (16) |
式中:ykres为RBF模型预测的响应特征量,
| $ \operatorname{obj}_{\Delta x}=\sum\limits_{k=1}^{K}\left|1-\operatorname{IOR}\left(y_{k}^{\text {Ires }} \mid y_{k}^{\text {Ie }}\right)\right| $ | (17) |
式中:ykIres为灰色数学方法估计RBF模型预测响应特征量的区间,ykIe为灰色数学方法估计试验模型响应特征量的区间。其中,在每次求解参数区间半径迭代过程中,根据已修正的区间中点,采用拉丁超立方抽取200个区间样本参与模型修正。两步模型修正流程如图 1所示。

|
图 1 两步模型修正流程 Fig. 1 Flow chart of two-step model updating |
2) 同步修正参数区间中点和半径。首先抽取200个参数区间样本,通过已构造的RBF模型预测样本响应特征量;然后使用灰色数学方法估计响应特征量区间中点和半径;最后运用FPA直接以式(14)为目标函数同时求解待修正参数区间中点和半径。其中,在每次同时求解参数区间中点和半径迭代过程中,同样抽取200个区间样本参与有限元模型修正。值得说明,式(14)完全可以替换式(17),实现两步修正参数区间中点和半径,由于篇幅所限,不再详细说明。
6 算例 6.1 数值算例1如图 2所示支撑框架结构,采用空间刚架单元模拟该结构的有限元模型。该结构共有54个节点,144个自由度,70个梁单元和6个边界支撑。其中,1~6为边界上的固定节点。箭头表示激励位置,⊗表示测点位置。选择结构弹性模量E和材料密度d的区间中点及半径为模型待修正参数,初始有限元模型E和d的区间中点分别为231 GPa和7 020 kg/m3,试验模型E和d的区间中点分别为210 GPa和7 800 kg/m3,区间半径分别为3 GPa和100 kg/m3。初始有限元模型和试验模型E和d的区间中点的相对误差分别为10%和-10%。

|
图 2 支撑框架结构 Fig. 2 Supporting frame structure |
本算例中选择500个频率点,设定小波变换分解层数为5。根据所述方法,通过WOA优化确定最佳方差值来建立RBF模型,得到RBF模型的方差值为0.089 3。然后计算得到RMSE为9.29×10-5,说明构造的RBF模型预测精度较高。为进一步评估RBF模型的预测精度,图 3给出了测试集样本第2和第10响应特征量的有限元模型计算值和RBF模型预测值,从图 3可以看到,有限元模型计算值和RBF模型预测值几乎全部重合,可以代替有限元模型。

|
图 3 测试集样本的预测值和真实值 Fig. 3 Predicted value and true value of test set sample |
以试验模型参数区间中点和半径抽取50个样本进行计算有限元模型加速度FRF,通过小波变换并提取第5层低频小波系数作为仿真试验响应特征量,使用灰色数学方法评估响应特征量区间。然后按照所述两步修正过程,通过FPA第1步迭代求解结构参数区间中点,第2步迭代求解待修正参数的区间半径,修正后的结构参数结果见表 1。
| 表 1 结构修正前、后的参数区间 Tab. 1 Initial and updated parameter interval of structure |
从表 1可以看出,修正后的相对误差较小,表明所提两步进行区间模型修正取得了很好的效果,对结构参数区间的修正是精确的,也表明了所提方法可以有效地解决试验小样本的区间模型修正问题。为进一步验证修正效果,使用表 1中修正后的结构参数区间抽取50个样本分别计算修正后的有限元模型加速度FRF(称为RBF模型FRF)和响应特征量。其中,FRF区间收敛如图 4所示,计算修正后有限元模型第4和第12响应特征量样本与试验模型响应特征量数据比较的散点如图 5所示。

|
图 4 频响函数区间收敛 Fig. 4 Interval convergence of FRF |

|
图 5 响应特征量区间散点图 Fig. 5 Scatter plot of response characteristics interval |
从图 4、5可以看出,修正后的有限元模型和试验模型的FRF区间吻合良好,修正后的有限元模型响应特征量计算样本和试验模型响应特征量数据也吻合良好。综上所述,验证了所提两步进行区间有限元模型修正的有效性。
6.1.2 同步修正按照所述同步修正过程,使用与两步修正相同的仿真试验数据,通过FPA同时迭代求解结构参数区间中点和半径,修正后的结果见表 2。
| 表 2 结构修正前、后的参数区间 Tab. 2 Initial and updated parameter interval of structure |
从表 2可以看出,同步修正与两步修正具有相同的修正效果。同样,为进一步验证修正效果,使用表 2中修正后的结构参数区间抽取50个样本分别计算修正后的有限元模型FRF和响应特征量。其中,FRF区间收敛如图 6所示,计算修正后有限元模型第4和第12响应特征量样本与试验模型响应特征量数据比较的散点如图 7所示。从图 6、7可以看出,修正后的有限元模型和试验模型的FRF区间及响应特征量区间样本同样吻合良好。综上所述,验证了所提同步进行区间有限元模型修正的有效性。
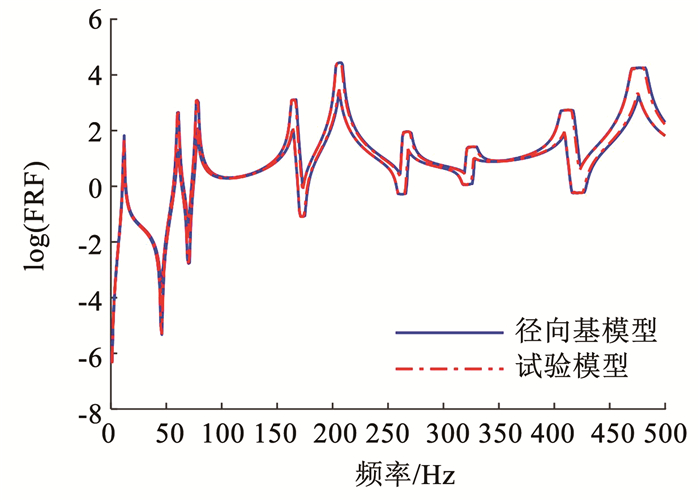
|
图 6 频响函数区间收敛 Fig. 6 Interval convergence of FRF |
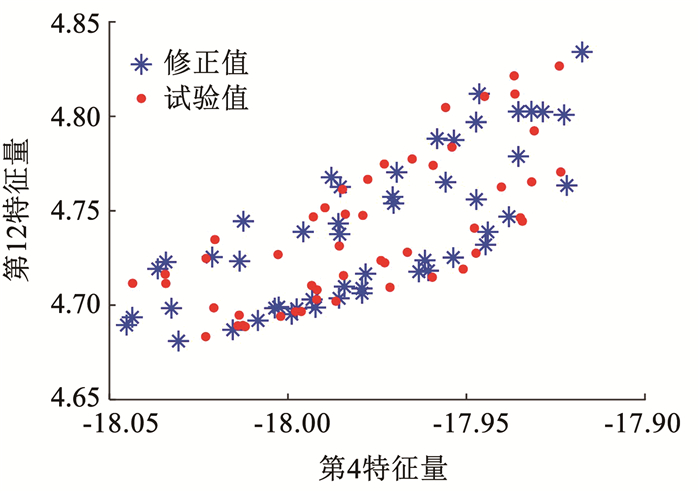
|
图 7 响应特征量区间散点图 Fig. 7 Scatter plot of response characteristics interval |
如图 8所示空间桁架结构,该桁架模型由72个杆单元组成,共有20个节点和48个自由度。单元横截面积为1 cm2,箭头表示激励位置,×表示测点位置。选择结构弹性模量E1(直杆)、E2(斜杆)和材料密度d的区间中点及半径为模型待修正参数。初始有限元模型E1、E2和d的区间中点分别为231、209 GPa和7 020 kg/m3,试验模型E1、E2和d的区间中点分别设定为210、190 GPa和7 800 kg/m3,初始有限元模型和试验模型E1、E2和d的区间中点的相对误差分别为10 %、10 %和-10 %。设定两种不同的试验参数区间半径工况来验证所提模型修正方法的有效性。工况1为试验模型参数E1、E2和d区间半径分别设定为3、2 GPa和60 kg/m3;工况2为试验模型参数E1、E2和d区间半径分别设定为6、5 GPa和200 kg/m3。

|
图 8 空间桁架结构 Fig. 8 Space truss structure |
本算例中选择500个频率点,设定小波变换分解层数为5。采用RBF模型的构造及验证所述方法建立RBF模型,得到RBF模型的方差值为0.246 9,迭代情况如图 9所示。为进一步评估RBF模型的预测精度,图 10给出了测试集样本第7和第15响应特征量的有限元模型计算值和RBF模型预测值,从图 10可以看到,有限元模型计算值和RBF模型预测值几乎全部重合,可以代替有限元模型。
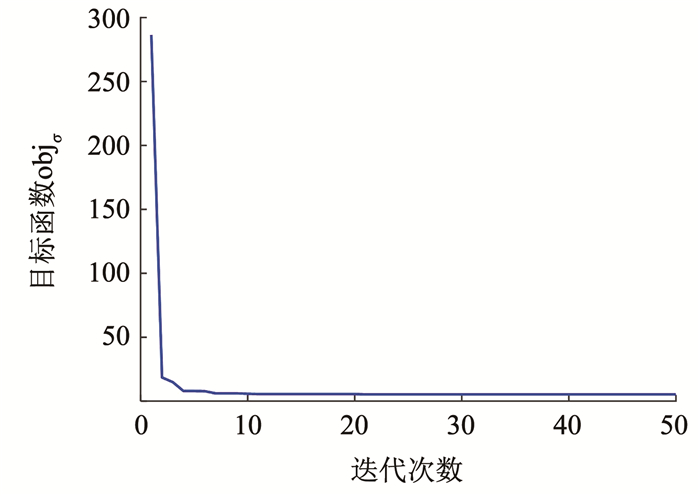
|
图 9 鲸鱼优化算法迭代曲线 Fig. 9 Iteration curve of WOA |
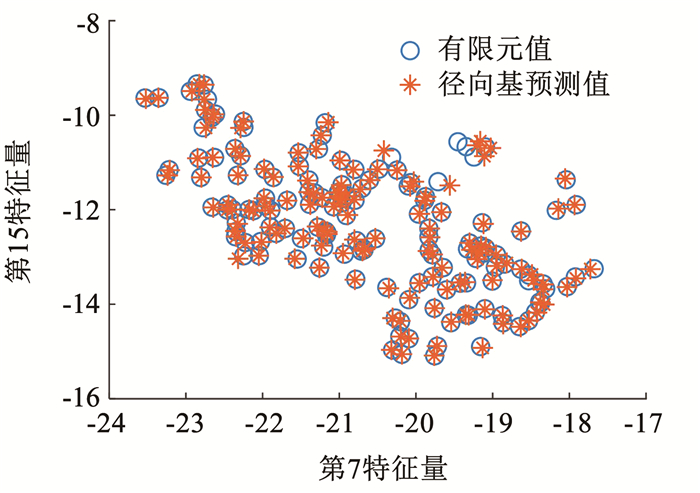
|
图 10 测试集样本的预测值和真实值 Fig. 10 Predicted value and true value of test set sample |
以试验模型参数区间中点和半径抽取100个样本进行计算有限元模型加速度FRF,通过小波变换并提取第5层低频小波系数作为仿真试验响应特征量,并使用灰色数学方法估计响应特征量区间。然后根据所述两步修正方法进行区间模型修正。其中,工况1结构参数区间中点和半径的迭代情况分别如图 11、12所示,修正结果见表 3,工况2结构参数区间修正结果见表 4。
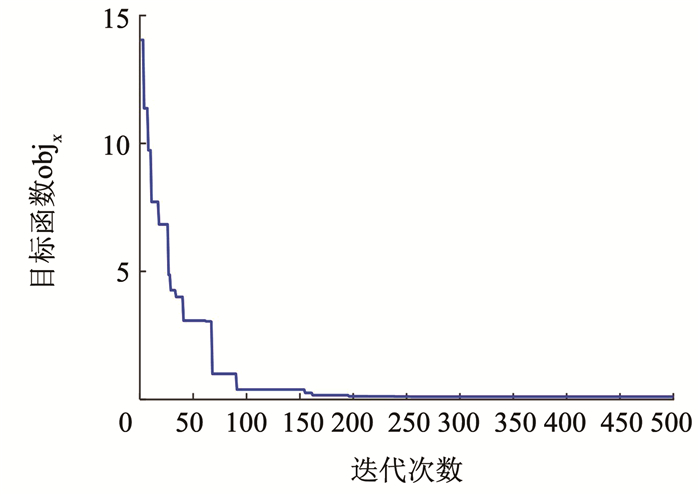
|
图 11 花朵授粉算法求解参数区间中点 Fig. 11 Interval midpoint iteration curve of FPA |
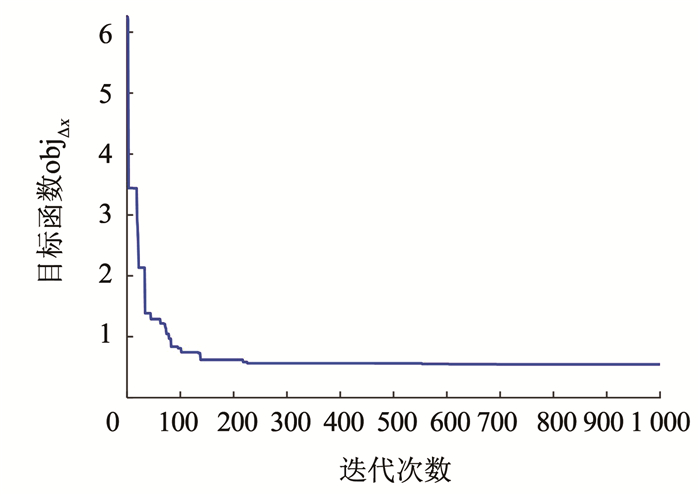
|
图 12 花朵授粉算法求解参数区间半径 Fig. 12 Interval radius iteration curve of FPA |
| 表 3 空间桁架结构修正前、后参数区间(工况1) Tab. 3 Initial and updated parameters interval of space truss structure (case 1) |
| 表 4 空间桁架结构修正前、后参数区间(工况2) Tab. 4 Initial and updated parameters interval of space truss structure (case 2) |
由表 3、4可以看出,对两种工况参数区间修正的相对误差值都较小,表明所提两步修正方法取得很好的效果,且在不同试验响应区间下对参数区间的修正具有鲁棒性。进一步验证修正效果,使用表 3、4中修正后的结构参数区间分别抽取100个样本计算两种工况修正后的有限元模型FRF和响应特征量。其中,工况2的FRF区间收敛如图 13所示,计算工况1修正后的有限元模型第8和第16响应特征量样本与试验模型响应特征量数据比较的散点如图 14所示。从图 13、14可以看出,修正后的有限元模型和试验模型的FRF区间及响应特征量区间样本吻合良好。

|
图 13 频响函数区间收敛 Fig. 13 Interval convergence of FRF |

|
图 14 响应特征量区间散点图 Fig. 14 Scatter plot of response characteristics interval |
根据所提同步修正方法,使用与两步修正相同的仿真试验数据来同时求解参数区间中点和半径。其中,工况1结构参数区间中点和半径同步修正的迭代情况如图 15所示。两种工况的结构参数修正结果分别见表 5、6。

|
图 15 花朵授粉算法同时求解参数区间中点和半径 Fig. 15 Interval midpoint and radius iteration curve of FPA |
| 表 5 空间桁架结构修正前、后参数区间(工况1) Tab. 5 Initial and updated parameters interval of space truss structure (case 1) |
| 表 6 空间桁架结构修正前、后参数区间(工况2) Tab. 6 Initial and updated parameters interval of space truss structure (case 2) |
由表 5、6可以看出,在两种工况下同步修正参数区间的相对误差值都较小,表明在不同试验响应区间下对参数区间的修正具有鲁棒性,说明所提同步修正方法与两步修正方法具有相同的效果。再由图 11、12和图 15相比可以看出,同步修正参数区间迭代350次之前就已收敛,而两步修正参数区间的第2步迭代收敛就需500次以上,因此在时间上同步修正相比两步修正节省了许多。同样进一步验证修正效果,使用表 5、6修正参数区间分别抽取100个样本计算修正后两种工况的FRF和响应特征量。工况2的FRF区间收敛如图 16所示,计算工况1修正后的有限元模型第8和第16响应特征量样本与试验模型响应特征量数据比较的散点如图 17所示。从图 16、17可以看出,修正后的有限元模型与试验模型的FRF区间和响应特征量区间样本同样吻合良好。

|
图 16 频响函数区间收敛 Fig. 16 Interval convergence of FRF |

|
图 17 响应特征量区间散点图 Fig. 17 Scatter plot of response characteristics interval |
如图 18所示,对长2 000 mm,宽100 mm,高10 mm的简支梁结构进行试验研究。该梁材料为Q235钢,将其划分为20个单元和21个节点。选择16节点为激励位置,选择5、8、11、14、和17节点为测量位置。选择结构弹性模量E和材料密度d的区间中点及半径为结构待修正参数。根据Q235钢材料参数范围,设置初始有限元模型E和d的区间中点分别为205 GPa和7 850 kg/m3。

|
图 18 简支梁 Fig. 18 Simply supported beam |
测试试验过程通过东方所的DASP软件进行50次试验,设置采样通道为6,采样频率为4 000 Hz,采样点数为4 096,直接采集加速度响应数据和加速度FRF数据。图 19给出了一次试验的16节点激励与11节点响应的加速度响应曲线,图 20给出了16节点激励与11节点响应的初始有限元模型和实际测量的加速度FRF中值曲线。
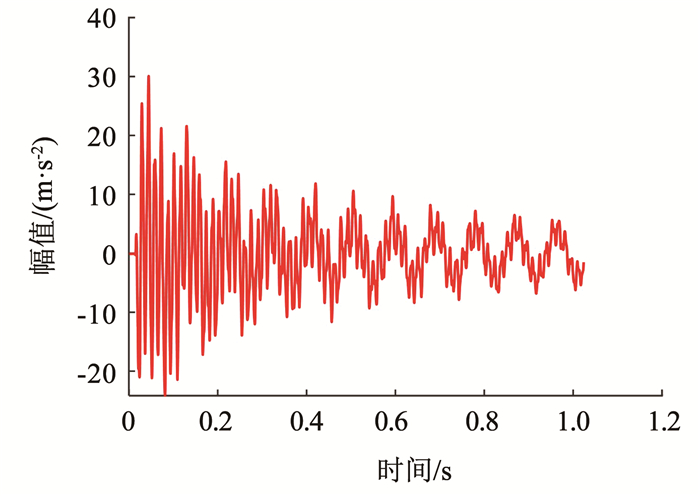
|
图 19 实测加速度响应 Fig. 19 Measured acceleration response |

|
图 20 加速度频响函数 Fig. 20 Acceleration FRF |
本试验算例中选择250个频率点,设定分解层数为4。将16节点激励与11节点响应的加速度FRF经过小波变换并提取第4层低频小波系数作为试验响应特征量,通过灰色数学方法评估试验响应特征量区间。然后按照两步修正过程,通过FPA第1步迭代求解结构参数区间中点,第2步迭代求解待修正参数的区间半径,修正后结果见表 7。
| 表 7 简支梁修正后的参数值 Tab. 7 Parameters of simply supported beam after updating |
为验证修正效果,使用表 7中修正后的结构参数区间抽取50个样本计算修正后的有限元模型加速度FRF。图 21给出了16节点激励与11节点响应的修正前、后的有限元模型加速度FRF中值曲线和试验加速度FRF中值曲线,从图 21可以看出修正后的有限元模型加速度FRF中值曲线和试验加速度FRF中值曲线大致吻合。图 22给出了16节点激励与11节点响应的加速度FRF区间收敛,从图 22可以看出修正后的有限元模型加速度FRF区间与试验加速度FRF区间大致吻合。
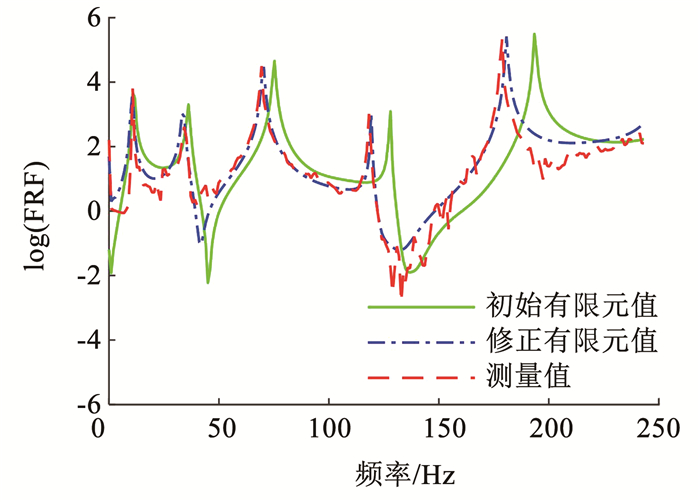
|
图 21 加速度频响函数 Fig. 21 Acceleration FRF |

|
图 22 频响函数区间收敛 Fig. 22 Interval convergence of FRF |
为进一步验证修正效果,测量不同位置的加速度FRF与修正后的有限元模型相对应位置的加速度FRF进行比较。图 23给出了16节点激励与17节点响应的修正前、后有限元模型加速度FRF中值曲线和试验加速度FRF中值曲线,从图 23可以看出修正后的有限元模型加速度FRF中值曲线与试验加速度FRF中值曲线大致吻合。图 24给出了16节点激励与17节点响应的修正后有限元模型加速度FRF区间收敛和试验加速度FRF区间收敛。从图 24可以看出,修正后的有限元模型加速度FRF区间和试验加速度FRF区间大致吻合。综上所述,验证了所提两步进行区间有限元模型修正的有效性。
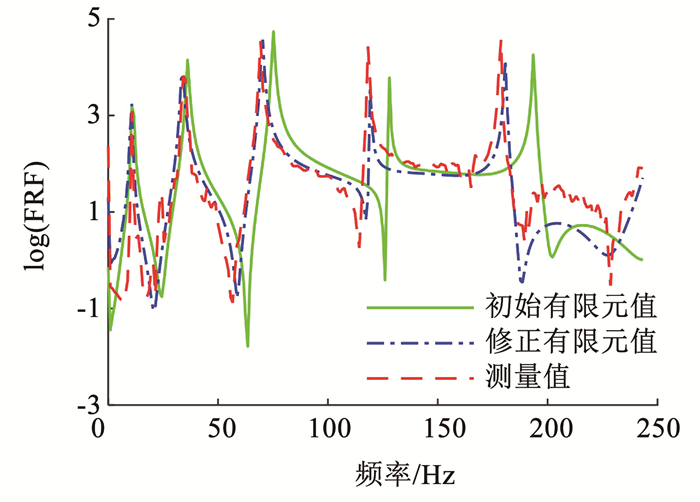
|
图 23 加速度频响函数 Fig. 23 Acceleration FRF |
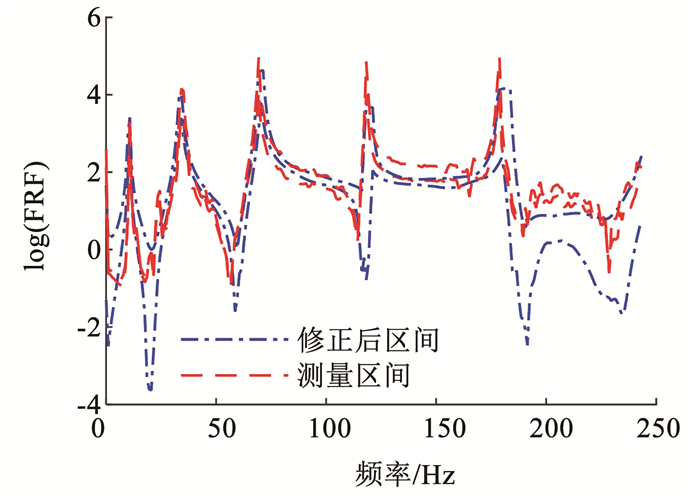
|
图 24 频响函数区间收敛 Fig. 24 Interval convergence of FRF |
按照所述同步修正过程,使用与两步修正相同的试验数据,通过FPA同时迭代求解结构参数区间中点和半径,修正后的结果见表 8。
| 表 8 简支梁结构修正后的参数值 Tab. 8 Parameter values of simply supported beam structure after updating |
同样为验证修正效果修正,使用表 8中修正后的结构参数区间抽取50个样本计算修正后的有限元模型加速度FRF。图 25、26分别给出了16节点激励与11节点响应的有限元模型与试验加速度FRF中值曲线和区间收敛,从图 25、26可以看出修正后的有限元模型与试验加速度FRF中值曲线和区间大致吻合。

|
图 25 加速度频响函数 Fig. 25 Acceleration FRF |
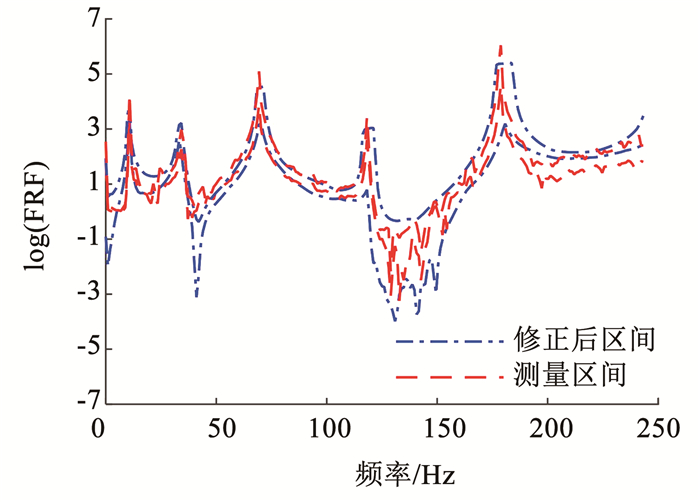
|
图 26 频响函数区间收敛 Fig. 26 Interval convergence of FRF |
同样为进一步验证修正效果,测量不同位置的加速度FRF进行比较,图 27、28分别给出了16节点激励与17节点响应的有限元模型与试验加速度FRF中值曲线和区间收敛,可以看出修正后的有限元模型与试验加速度FRF中值曲线和区间大致吻合。综上所述,验证了所提同步进行区间有限元模型修正的有效性。
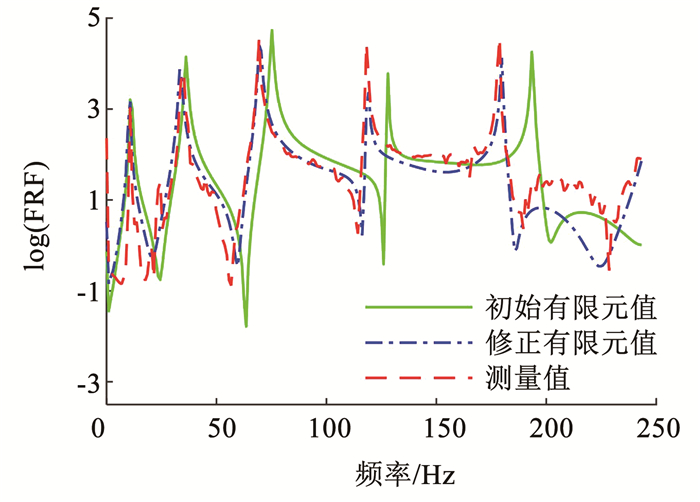
|
图 27 加速度频响函数 Fig. 27 Acceleration FRF |

|
图 28 频响函数区间收敛 Fig. 28 Interval convergence of FRF |
1) 考虑参数不确定性对于结构响应的影响,提出了以结构参数区间中点和半径为修正目标的两步和同步的区间模型修正方法,可以较好地修正结构参数的区间中点和半径,且在不同试验响应区间下对参数区间的修正都具有鲁棒性。同时,可以有效地解决试验小样本的不确定性模型修正问题。
2) 算例表明,两步和同步修正都可以达到相同的效果,且在迭代求解过程中表征区间进行模型修正的参数样本量较小,提高了模型修正效率。但在时间上同步修正相比两步修正节省了许多。
3) 在使用参数样本参与不确定性模型修正时构造了RBF模型,并采用WOA优选了RBF模型的方差值,使所构造的RBF模型具有良好的拟合精度和预测能力,能代替有限元模型进行迭代计算,提高模型修正效率。
4) 将加速度FRF经过小波变换,提取低频小波系数作为区间模型修正的响应特征量,具有保留FRF特性的优点,且可以大量减少输出响应数目,提高了模型修正计算效率。
| [1] |
JIN S S, JUNG H J. Sequential surrogate modeling for efficient finite element model updating[J]. Computers & Structures, 2016, 168: 30. DOI:10.1016/j.compstruc.2016.02.005 |
| [2] |
陈光宋, 钱林方, 王明明, 等. 基于统计信息的多体系统区间不确定性分析[J]. 振动与冲击, 2019, 38(8): 117. CHEN Guangsong, QIAN Linfang, WANG Mingming, et al. An interval analysis method based on statistical information for a multibody system with uncertainty[J]. Journal of Vibration and Shock, 2019, 38(8): 117. DOI:10.13465/j.cnki.jvs.2019.08.018 |
| [3] |
陈学前, 沈展鹏, 刘信恩. 基于响应面与灵敏度分析的区间不确定性参数识别方法[J]. 振动与冲击, 2019, 38(16): 267. CHEN Xueqian, SHEN Zhanpeng, LIU Xin'en. A method of interval uncertain parameter identification based on a response surface model and sensitivity analysis[J]. Journal of Vibration and Shock, 2019, 38(16): 267. DOI:10.13465/j.cnki.jvs.2019.16.038 |
| [4] |
杨修铭, 郭杏林, 李东升. 基于Kriging模型的频响函数有限元模型修正方法[J]. 计算力学学报, 2018, 35(4): 487. YANG Xiuming, GUO Xinglin, LI Dongsheng. Kriging model based finite element model updating method using frequency response function[J]. Chinese Journal of Computational Mechanics, 2018, 35(4): 487. DOI:10.7511/jslx20170303001 |
| [5] |
魏锋涛, 卢凤仪, 郑建明. 基于多策略的改进径向基代理模型方法[J]. 计算机集成制造系统, 2019, 25(3): 764. WEI Fengtao, LU Fengyi, ZHENG Jianming. Augmented radial basis function metamodel method based on multi-strategy[J]. Computer Integrated Manufacturing Systems, 2019, 25(3): 764. DOI:10.13196/j.cims.2019.03.023 |
| [6] |
CHEN Xueqian, SHEN Zhanpeng, LIU Xin'en. A copula-based and Monte Carlo sampling approach for structural dynamics model updating with interval uncertainty[J]. Shock and Vibration, 2018, 2018: 1. DOI:10.1155/2018/3958016 |
| [7] |
DENG Zhongmin, GUO Zhaopu, ZHANG Xuede. Non-probabilistic set-theoretic models for transient heat conduction of thermal protection systems with uncertain parameters[J]. Applied Thermal Engineering, 2016, 95: 10. DOI:10.1016/j.applthermaleng.2015.10.152 |
| [8] |
ZHENG Bowen, YU Kaiping, LIU Shuaishuai, et al. Interval model updating using universal grey mathematics and Gaussian process regression model[J]. Mechanical Systems and Signal Processing, 2020, 141: 106455. DOI:10.1016/j.ymssp.2019.106455 |
| [9] |
SHI Qinghe, WANG Xiaojun, WANG Ruixing. An interval updating model for composite structures optimization[J]. Composite Structures, 2019, 209: 177. DOI:10.1016/j.compstruct.2018.10.055 |
| [10] |
FANG Shengen, ZHANG Qiuhu, REN Weixin. An interval model updating strategy using interval response surface models[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 909. DOI:10.1016/j.ymssp.2015.01.016 |
| [11] |
骆勇鹏, 黄方林, 韩建平, 等. 灵敏度的模态区间分析方法及其在不确定性参数识别中的应用[J]. 振动工程学报, 2016, 29(4): 577. LUO Yongpeng, HUANG Fanglin, HAN Jianping, et al. A sensitivity modal interval analysis method and its application to uncertain parameter identification[J]. Journal of Vibration Engineering, 2016, 29(4): 577. DOI:10.16385/j.cnki.issn.1004-4523.2016.04.003 |
| [12] |
姜东, 费庆国, 吴邵庆. 基于区间分析的不确定性结构动力学模型修正方法[J]. 振动工程学报, 2015, 28(3): 352. JIANG Dong, FEI Qingguo, WU Shaoqing. Updating of structural dynamics model with uncertainty based on interval analysis[J]. Journal of Vibration Engineering, 2015, 28(3): 352. DOI:10.16385/j.cnki.issn.1004-4523.2015.03.003 |
| [13] |
DENG Zhongmin, GUO Zhaopu, ZHANG Xinjie. Interval model updating using perturbation method and Radial Basis Function neural networks[J]. Mechanical Systems and Signal Processing, 2017, 84: 699. DOI:10.1016/j.ymssp.2016.09.001 |
| [14] |
WANG Chong, QIU Zhiping. Modified perturbation method for eigenvalues of structure with interval parameters[J]. Science China Physics, Mechanics & Astronomy, 2015, 58(1): 1. DOI:10.1007/s11433-013-5328-6 |
| [15] |
DENG Zhongmin, GUO Zhaopu. Interval identification of structural parameters using interval overlap ratio and Monte Carlo simulation[J]. Advances in Engineering Software, 2018, 121: 120. DOI:10.1016/j.advengsoft.2018.04.006 |
| [16] |
邓振鸿, 张保强, 苏国强, 等. 基于近似似然的频响函数不确定性模型修正[J]. 振动、测试与诊断, 2020, 40(3): 548. DENG Zhenhong, ZHANG Baoqiang, SU Guoqiang, et al. Uncertainty model updating of frequency response function based on approximate likelihood function[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(3): 548. DOI:10.16450/j.cnki.issn.1004-6801.2020.03.018 |
| [17] |
王巨涛, 王春洁, 宋顺广. 结构加速度频响函数模型修正的Kriging方法[J]. 工程科学学报, 2017, 39(7): 1087. WANG Jutao, WANG Chunjie, SONG Shunguang. Structural model updating of acceleration frequency response function based on Kriging method[J]. Chinese Journal of Engineering, 2017, 39(7): 1087. DOI:10.13374/j.issn2095-9389.2017.07.015 |
| [18] |
张娜, 雷明. 基于小波变换的小样本随机振荡序列灰色预测模型[J]. 数学的实践与认识, 2020, 50(9): 28. ZHANG Na, LEI Ming. Grey prediction model of sample random oscillation sequence based on wavelet transform[J]. Mathematics in Practice and Theory, 2020, 50(9): 28. |
| [19] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51. DOI:10.1016/j.advengsoft.2016.01.008 |
| [20] |
BI Sifeng, BROGGI M, BEER M. The role of the Bhattacharyya distance in stochastic model updating[J]. Mechanical Systems and Signal Processing, 2019, 117: 437. DOI:10.1016/j.ymssp.2018.08.017 |
| [21] |
YANG Xinshe. Flower pollination algorithm for global optimization[C]// International Conference on Unconventional Computing and Natural Computation. Berlin Heidelberg: Springer, 2012: 240. DOI: 10.1007/978-3-642-32894-7_27
|
 2023, Vol. 55
2023, Vol. 55


