船舶与海洋工程结构物在服役期间遭受交变环境载荷作用,疲劳破坏是其结构失效的主要模式之一。目前,疲劳损伤分析方法主要分为时域方法和频域方法。基于雨流计数法的时域方法计算精度高且应用范围广,因此常被作为评价其他计算方法准确性的基准。然而,在实际工程应用中使用时域方法的计算代价往往过于庞大,与此相比,通过结构物的应力响应功率谱来计算疲劳损伤的频域方法则更为可行、有效[1-2]。
当结构的随机应力响应过程在频域下为窄带且服从高斯分布时,其应力幅值服从Rayleigh分布,疲劳损伤存在解析解。然而,对于宽带高斯随机应力过程,仍采用理想窄带假设方法计算疲劳损伤则难以保证准确性。因此,学者们提出了一系列近似方法进行宽带随机应力疲劳损伤的评估,例如SM(single-moment)方法[3]、Dirlik方法[4]以及TB(Tovo- benasciutti)方法[5]等。对于船海结构物,其结构应力响应在功率谱上常常呈现出两个分开的显著峰值即高斯双模态特征[6-8]。高斯双模态随机过程作为宽带随机过程的一种特例,需要专门处理此类问题的疲劳损伤频域计算方法。
目前,高斯双模态随机过程疲劳损伤频域分析方法中,最早的理论模型由Jiao等[9]提出,称为JM方法。JM方法从雨流应力循环的角度出发,将疲劳损伤来源划分为大应力循环和小应力循环两个部分。在该理论框架下,Fu等[10]改进了大、小循环的计数规则,认为大循环与小循环的总循环次数等于高频过程的循环次数,而大循环的循环次数则与低频过程循环次数相等,从而提出了FC方法。Benasciutti等[11]对FC方法进行了修正,将大循环计数单独修正为JM法的计数规则。Low[12]通过引入相位角参数进一步反映了低频分量与高频分量间的相互作用,使得Low方法的精度较JM方法有了大幅提升,但该方法需要计算变上限三重积分,导致其难以在实际工程中得到广泛应用。
近年来,有学者[13-15]从功率谱分割的思想出发,提出了一系列新的高斯双模态疲劳损伤分析方法。Benasciutti等[13]率先提出了功率谱分割法,即将功率谱离散为许多份足够窄的频带,认为每个窄带过程均为服从Rayleigh分布的理想窄带高斯随机过程,并利用PbP(projection-by-projection)准则对每个窄带过程的损伤进行组合来计算总疲劳损伤。Gao等[14]指出基于PbP准则的功率谱分割法忽略了低频模态与高频模态间的耦合作用,通过引入模态耦合系数对原有功率谱分割法[13]进行了改进,提出GZ方法。类似于功率谱分割法,Braccesi等[15]将功率谱离散后得到的各个窄带视作相互独立的随机变量,从随机变量叠加和损伤等效的角度出发提出了频带法(Bands method,BM)。该方法的计算过程仅涉及零阶谱矩,便于编程且计算量少,适合在实际工程中应用。
然而,采用现有频带法计算高斯双模态疲劳损伤时,由于未能考虑到有别于一般宽带过程的双模态特征,随着高频模态与低频模态能量比的降低和特征频率比的增大,频带法结果与雨流法结果的差异逐渐增大[15]。针对该问题,本文在频带法基础上考虑了双模态过程中高频模态与低频模态间的相互作用,提出了一种适用于高斯双模态随机疲劳损伤分析的改进频带法。首先,针对双模态过程中的高频模态和低频模态分别利用频带法进行等效转换得到相应的等效窄带过程。然后,将高频等效窄带过程向低频等效窄带过程再次进行等效转换,同时引入与频率比γ、能量比β以及S-N曲线材料参数m有关的修正因子μ对第2次等效过程中的高频零阶谱矩进行修正。最后,可利用基于窄带假设的疲劳损伤解析解计算的等效窄带过程的疲劳损伤即高斯双模态随机过程的总疲劳损伤。
1 窄带高斯随机过程疲劳损伤分析基本理论 1.1 随机过程的谱参数对于一个平稳高斯随机过程X(t)而言,其单边功率谱密度函数为SXX(ω),则其n阶谱矩定义如下:
| $ \lambda_{n}=\int\limits_{0}^{\infty} \omega^{n} \cdot S_{X X}(\omega) \mathrm{d} \omega, n=0, 1, 2, \cdots $ | (1) |
式中ω为角频率,rad/s。谱矩可以对随机过程的带宽进行表征,工程中常用的Vanmarcke带宽系数δ[16]定义为
| $ \delta=\sqrt{1-\frac{\lambda_{1}^{2}}{\lambda_{0} \lambda_{2}}} $ | (2) |
式中δ的取值范围为[0, 1.0]。当δ越趋近于0时,表明该随机过程越趋近于理想窄带随机过程,反之则为宽带随机过程。工程上一般认为δ<0.1时,可将一个随机过程近似看作窄带随机过程。
根据随机过程理论,X(t)的平均跨零率ν0和平均峰值率νp也可以利用谱矩进行表示:
| $ \nu_{0}=\frac{1}{2 {\rm{ \mathsf{ π} }}} \sqrt{\frac{\lambda_{2}}{\lambda_{0}}}, \nu_{\mathrm{p}}=\frac{1}{2 {\rm{ \mathsf{ π} }}} \sqrt{\frac{\lambda_{4}}{\lambda_{2}}} $ | (3) |
根据Palmgren-Miner线性累积损伤理论,随机应力过程在作用时间T下的疲劳损伤可表示为
| $ D=\frac{\nu_{\mathrm{p}} \cdot T}{K} \int\limits_{0}^{\infty} s^{m} \cdot f_{S}(s) \mathrm{d} s $ | (4) |
式中:νp为单位时间内应力循环数,即平均峰值率;fS(s)为应力范围S的概率密度函数;m、K分别为S-N曲线中的材料参数,其中N=K·S-m,表示在应力范围在S这一水平下,材料发生疲劳破坏所需的应力循环数为N。
对于一个零均值窄带高斯随机过程X(t),其应力峰值服从Rayleigh分布,且应力峰值和谷值在每一个循环中对称出现,由此可知应力幅值R服从Rayleigh分布如下:
| $ f_{R}(r)=\frac{r}{\lambda_{0}} \exp \left(-\frac{r^{2}}{2 \lambda_{0}}\right) $ | (5) |
由于应力范围S是应力幅值R的2倍,也服从Rayleigh分布,并且平均峰值率νp等于平均跨零率ν0,由式(4)、(5)可得时间T范围内的窄带疲劳损伤的解析解为
| $ D=\frac{\nu_{0} T}{K}\left(2 \sqrt{2 \lambda_{0}}\right)^{m} \mathit{\Gamma}\left(\frac{m}{2}+1\right) $ | (6) |
式中Γ(·)为gamma函数。
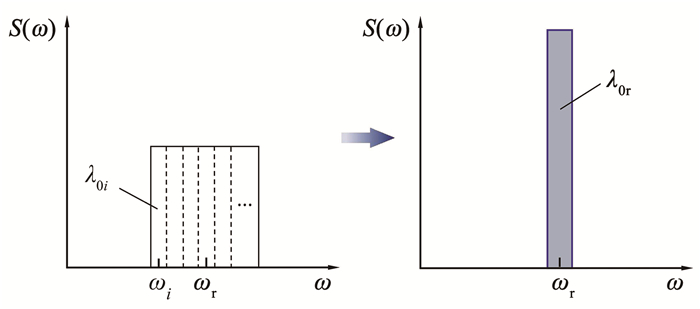
2 基于改进频带法的高斯双模态疲劳损伤分析方法 2.1 频带法基本原理Braccesi等[15]于2015年提出了一种基于频带法的疲劳损伤频域评估方法。将一个高斯随机过程的功率谱切分为n份足够窄的频带,每一频带由其中心频率ωi表征,其应力幅值服从Rayleigh分布,并将它们看作是n个相互独立的随机变量。对于窄带随机过程,平均跨零率ν0i与其中心频率ωi之间关系为ν0i=ωi/2π,每一个窄带频段的平均跨零率ν0i都不相同。因此需要将这些窄带过程按照一定规则进行等效转换后,计算等效过程的零阶谱矩再进行叠加得到一个总的零阶谱矩,进而可利用基于窄带假设的解析解计算总疲劳损伤。
由于每个窄带的中心频率并不相等,在进行零阶谱矩加和之前需要将这些窄带的中心频率ωi“移动”至某一固定频率处,即参考频率ωr。由Braccesi等[15]的研究可知,该参考频率可任意取值且对计算结果无影响。如图 1所示,根据损伤等效原则将第i个窄带频段中心频率ωi移动至参考频率ωr后,存在如下关系:
| $ \begin{aligned} d_{i}= & \frac{2^{m / 2} \cdot T}{K} \mathit{\Gamma}\left(\frac{m}{2}+1\right) \nu_{0 i} \lambda_{0 i}^{m / 2}= \\ & \frac{2^{m / 2} \cdot T}{K} \mathit{\Gamma}\left(\frac{m}{2}+1\right) \nu_{0 \mathrm{r}} \lambda_{0 \mathrm{r} i}^{m / 2} \end{aligned} $ | (7) |
|
图 1 频带法示意图 Fig. 1 Schematic illustration of the bands method |
式中:ν0i、λ0i分别为第i个窄带的平均跨零率和零阶谱矩,ν0r为在参考频率处等效频带的平均跨零率,λ0ri为第i个窄带等效后的零阶谱矩。由式(7)可得
| $ \lambda_{0 \mathrm{r} i}=\left(\frac{\nu_{0 i}}{\nu_{0 \mathrm{r}}}\right)^{2 / m} \lambda_{0 i} $ | (8) |
考虑ν0i=ωi/2π和ν0r=ωr/2π,式(8)可改写为
| $ \lambda_{0 \mathrm{r} i}=\left(\frac{\omega_{i}}{\omega_{\mathrm{r}}}\right)^{2 / m} \lambda_{0 i} $ | (9) |
对每一个窄带频段进行上述等效操作之后,可得到一个中心频率为参考频率ωr且零阶谱矩为等效零阶谱矩总和λ0r的等效窄带过程,如图 1所示。等效窄带过程的零阶谱矩可由下式计算:
| $ \lambda_{0 \mathrm{r}}=\sum\limits_{i}^{n} \lambda_{0 \mathrm{r}i}=\sum\limits_{i}^{n}\left(\frac{\nu_{0 i}}{\nu_{0 \mathrm{r}}}\right)^{2 / m} \lambda_{0 i} $ | (10) |
将式(10)代入式(6)可得到等效窄带过程的疲劳损伤为
| $ D=\frac{\nu_{0 \mathrm{r}} T}{K}\left(2 \sqrt{2 \lambda_{0 \mathrm{r}}}\right)^{m} \mathit{\Gamma}\left(\frac{m}{2}+1\right) $ | (11) |
对于双模态功率谱,当高频模态和低频模态中心频率相距较远或存在宽带模态时,整个功率谱的带宽系数会较大,采用现有频带法进行损伤等效转换而产生的误差会明显增大。因此,本文在原有频带法的基础上,通过引入修正因子以考虑双模态过程中高频模态与低频模态之间的相互作用,从而提出改进频带法。
改进频带法的具体计算步骤如下:首先,采用频带法分别对双模态功率谱中的低频模态和高频模态进行第1次等效转换,计算它们的等效窄带过程零阶谱矩λ0rLF和λ0rHF,如图 2所示;然后,将等效后中心频率为ωrHF的高频窄带过程向低频等效窄带过程再进行一次等效转换,即将高频模态的等效零阶谱矩λ0rHF由中心频率ωrHF移动至ωrLF,与此同时乘以一个修正因子μ,从而得到一个可代替原双模态过程的总的等效窄带过程(如图 2所示),其零阶谱矩λ0, total的计算如式(12);最后,将式(12)代入窄带疲劳损伤闭合解式(6)中,即可计算双模态随机过程的总疲劳损伤值为:
| $ \begin{array}{l} \lambda_{0, \text { total }}=\lambda_{0 \mathrm{r}}^{\mathrm{LF}}+\lambda_{0 \mathrm{r}}^{\mathrm{LFHF}}= \\ \;\;\;\;\;\;\;\;\;\; \lambda_{0 \mathrm{r}}^{\mathrm{LF}}+\left(\frac{\nu_{0 \mathrm{r}}^{\mathrm{HF}}}{\nu_{0 \mathrm{r}}^{\mathrm{LF}}}\right)^{2 / m} \cdot \lambda_{0 \mathrm{r}}^{\mathrm{HF}} \cdot \mu \end{array} $ | (12) |
| $ D_{\text {totoal }}=\frac{\nu_{0 \mathrm{r}}^{\mathrm{LF}} T}{K}\left(2 \sqrt{2 \lambda_{0, \text { total }}}\right)^{m} \mathit{\Gamma}\left(\frac{m}{2}+1\right) $ | (13) |

|
图 2 针对双模态过程的改进频带法示意图 Fig. 2 Illustration of the improved bands method proposed for bimodal process |
通过理论推导得到修正因子μ的具体表达式是十分困难的。因此,本文以高、低频模态均为矩形谱的双模态随机过程为研究对象(如图 3所示),通过时域模拟结果拟合修正因子μ的近似表达式。其中,ωcLF、ωcHF分别为低频模态和高频模态的中心频率,λ0LF、λ0HF则分别为其0阶谱矩。定义高、低频模态间的频率比γ=ωcHF/ωcLF,能量比β=λ0HF/λ0LF。基于双模态功率谱特征和疲劳损伤相关理论,修正因子μ主要与频率比γ、能量比β以及S-N曲线中材料参数m相关。因此,针对3个参数选取不同数值进行组合,通过逆傅里叶变换法模拟生成大量的高斯双模态随机时间序列。采用时域方法计算雨流损伤值,将其代入式(13)左侧反推出相应的μ值,再由非线性拟合方法得到修正因子μ的经验表达式。

|
图 3 理想矩形双模态功率谱 Fig. 3 Ideal rectangular bimodal power spectral |
本文以船舶与海洋工程结构为研究对象,选取的特征参数γ、β和m的具体取值如下: γ=3, 4, 5, …, 15,β=0.1, 0.2, …, 1.0, 2.0, …, 10.0,m=3, 4, 5。需要指出,在已往研究中发现,采用由理想矩形双模态功率谱确定修正因子μ时,需要根据计算工况中的高频模态是窄带过程或是宽带过程进行区分。对于计算工况为“窄带低频+窄带高频”和“宽带低频+窄带高频”两种情况,采用双窄带功率谱拟合修正因子μ,其中高频和低频模态的Vanmarcke带宽系数均设为0.03以保证其满足窄带假设。对于计算工况为“窄带低频+宽带高频”和“宽带低频+宽带高频”的情况,则采用高频和低频模态的Vanmarcke带宽系数均设为0.3的双宽带功率谱进行拟合。
在建立μ值与特征参数γ、β和m之间的关系式时,参考Gao等[14]的工作,在固定材料参数m的前提下建立修正因子μ以γ和β为自变量的函数式如下:
| $ \begin{array}{l} \mu=\left[P_{1}+P_{2} \cdot \ln (\gamma)+P_{3} \cdot \ln (\beta)+P_{4} \cdot[\ln (\gamma)]^{2}+\right.\\ \;\; \;\; \;\; \;\; \left.P_{5} \cdot[\ln (\beta)]^{2}+P_{6} \cdot \ln (\gamma) \cdot \ln (\beta)\right] /\\ \;\; \;\; \;\; \;\; \left[1+P_{7} \cdot \ln (\gamma)+P_{8} \cdot \ln (\beta)+P_{9} \cdot[\ln (\gamma)] 2+P_{10} \cdot\right.\\ \;\; \;\; \;\; \;\; \left.[\ln (\beta)]^{2}+P_{11} \cdot \ln (\gamma) \cdot \ln (\beta)\right] \end{array} $ | (14) |
式中,P1~P11为11个待定拟合系数。此外,当材料参数m不同时,μ与γ和β的非线性关系是存在差异的,拟合系数P1~P11也相应有所变化。因此针对高频模态为窄带或是宽带,不同m值对应的拟合系数P1~P11的数值见表 1。在船舶与海洋工程结构物领域,m=3, 4, 5为较为常见的S-N曲线材料参数。
| 表 1 拟合系数P1至P11 Tab. 1 Fitted coefficients P1 to P11 |
本文先以理想矩形双模态功率谱为算例,以时域方法计算雨流损伤值作为参考值对本文提出的改进频带法进行计算精度验证,并与Low法[12]、GZ法[14]、TB法[5]以及频带法(BM法)[15]进行对比。如修正因子μ的确定中提到,窄带高频的修正因子μ对于“窄带低频+窄带高频”和“宽带低频+窄带高频”两种情况是同样适用的,而宽带高频的修正因子μ适用于“窄带低频+宽带高频”和“宽带低频+宽带高频”的组合,即两组修正因子对于低频为窄带或宽带过程并不敏感。由于篇幅考虑,本文仅展示“窄带低频+窄带高频”和“宽带低频+宽带高频”两种双模态矩形谱的验证结果。
对于“窄带低频+窄带高频”的双模态矩形谱验证算例,低频和高频模态的Vanmarcke带宽系数设为δLF=δHF=0.052 4。图 4给出了S-N曲线材料系数K=1,m=3和m=5,频率比γ=3、6、9,能量比β=0.1、0.5、1.0、2.0、5.0、10.0的“窄带低频+窄带高频”双模态矩形谱各频域方法结果与时域雨流法结果的相对误差。相对误差的定义为
| $ \rho=\left(\frac{D-D_{\mathrm{RFC}}}{D_{\mathrm{RFC}}}\right) \times 100 \% $ | (15) |

|
图 4 窄带低频+窄带高频矩形谱下各方法计算结果相对于雨流法的相对误差 Fig. 4 Relative errors of different methods compared with RFC method for NB-LF & NB-HF rectangular spectra |
式中,D、DRFC分别为频域方法和时域雨流法所计算得到的疲劳损伤值。
由图 4可知,当m=3时,由于频带法忽略了高频与低频间的相互作用,其在能量比β=0.10时的计算误差与其他方法相比要大的多。相比之下,本文所提出的改进频带法在计算精度上有显著提升,且与Low法和GZ法精度相当。此外,作为通用宽带谱方法的TB法在处理双模态问题时精度略差。当m=5时,因为疲劳损伤与应力循环的非线性关系会随着m的增大而增强,此时TB法与频带法的误差都明显增大。同样,Low法的精度与m=3时相比略微下降。只有GZ法和本文的改进频带法依然保持较好的计算精度,最大误差均在3%以内。
对于“宽带低频+宽带高频”的双模态矩形谱验证算例,低频和高频模态的Vanmarcke带宽系数分别设为δLF=0.148 0和δHF=0.256 4。图 5展示了S-N曲线材料系数K=1,m=3和m=5,频率比γ=3、6、9,能量比β=0.1、0.5、1.0、2.0、5.0、10.0的“宽带低频+宽带高频”双模态矩形谱的分析结果,其中GZ(M=4)表示采用GZ方法处理高频模态时需要划分4个子模态[14]。

|
图 5 宽带低频+宽带高频矩形谱下各方法计算结果相对于雨流法的相对误差 Fig. 5 Relative errors of different methods compared with RFC method for WB-LF & WB-HF rectangular spectra |
由图 5可知,当m=3时,频带法在能量比β≤1.0时的计算误差仍是5种方法中最大的,最大误差达到了-16%。尽管Low法是基于双窄带假设推导的,但是对于双宽带工况在m=3时,依然保持较为准确的精度,最大误差约为-9%。TB法的计算精度尚可,误差均在7%以内。参照Gao等[14],采用GZ法时将宽带高频模态划分为4个子模态后,可以得到非常准确的计算结果,绝大多数误差都在3%以内。相比于其他4种方法,本文提出的改进频带法的计算精度最好,误差均在1%以内。当m=5时,Low法、TB法和频带法与雨流法相比均出现了较大的偏差,最大误差分别为-19%、-22%和-28%。GZ法的计算结果依然保持很好的精度,绝大部分结果误差控制在5%以内,最大误差也未超过8%。相比之下,改进频带法对于双宽带工况依然保持良好的精度,最大误差未超过2%。
3.2 真实双模态应力谱由于理想双模态矩形谱和真实双模态应力谱仍存在一定的差异,因此有必要选取船舶与海洋工程结构遭受的一些真实响应谱对本文所提出方法的有效性进一步进行验证。第1个算例为如图 6所示的“佛蒂尼”号远洋散货船实船测得的应力响应谱[7],其中包含了两个比较明显的峰值,第1个峰值对应波频响应,第2个峰值为该船的二阶共振频率。该功率谱中双模态的参数信息见表 2,其中低频模态带宽系数δLF=0.344 7,高频模态带宽系数δHF=0.076 1。因此,该双模态功率谱为“宽带低频+窄带高频”的组合,应采用修正因子μ的确定中窄带高频对应的修正因子μ。分别采用改进频带法、Low法、GZ法、TB法以及频带法对实测应力谱进行疲劳损伤评估,各方法计算结果与雨流法结果的误差见表 3。可以看出在m=3, 4, 5时,Low方法、GZ法和改进频带法的计算结果与雨流法结果非常接近,相对误差均在1%以内,优于TB法和频带法。
| 表 2 功率谱中各模态参数信息 Tab. 2 Spectral characteristics of each mode in spectrum |
| 表 3 算例1中各频域方法结果相对于雨流法结果的相对误差 Tab. 3 Relative errors of different methods in Case 1 |
第2个算例为如图 7所示的某海洋工程结构的双模态响应谱[8],低频模态对应涌浪响应,高频模态对应波频响应。该功率谱中双模态的参数信息见表 2,其中低频模态带宽系数δLF=0.090 2,高频模态带宽系数δHF=0.319 5。因此,该双模态功率谱为“窄带低频+宽带高频”的组合,应采用修正因子μ的确定中宽带高频对应的修正因子μ。表 4给出了当m=3, 4, 5时,Low法、TB法、GZ法、频带法以及改进频带法的计算结果与雨流法结果的对比误差。可以看出,对于该工况Low法的计算误差在5种方法中是最大的,最大误差已达到-22.97%。与Low法相比,TB法和频带法的计算精度略好,最大误差分别为-11.59%和-7.21%。GZ法和改进频带法给出的结果仍然与雨流结果非常接近,相对误差均在3%以内。
| 表 4 算例2中各频域方法结果相对于雨流法结果的相对误差 Tab. 4 Relative errors of different methods in Case 2 |
1) 现有频带法在计算高斯双模态随机过程疲劳损伤时仍然保持一定的准确性。但当双模态过程的能量比变小和频率比变大时,该方法与雨流结果之间的误差逐渐增大,最大误差可达到-30%左右。
2) 与现有频带法相比,本文提出的改进频带法通过引入与频率比、能量比以及S-N曲线材料参数m有关的修正因子μ对计算结果进行修正使其与雨流结果更加接近,计算精度明显提高。
3) 对于高斯双模态随机过程,改进频带法中修正因子μ的经验公式适用范围为频率比γ=3~15,能量比β=0.1~10.0和S-N曲线材料参数m=3, 4, 5。通过大量数值试验对改进频带法的有效性进行了验证,并与Low法、TB法、GZ法以及频带法进行对比,结果表明本文提出的新方法具有精度高、适用性强的优点,并且理论简单、易于编程实现。
| [1] |
康海贵, 田茂金, 龙丽吉, 等. 基于谱分析方法的海上风机支撑结构疲劳寿命分析[J]. 可再生能源, 2013, 31(7): 41. KANG Haigui, TIAN Maojin, LONG Liji, et al. Spectral-based fatigue analysis of a support structure for offshore wind turbines[J]. Renewable Energy Resources, 2013, 31(7): 41. DOI:10.13941/j.cnki.21-1469/tk.2013.07.009 |
| [2] |
秦培江, 马永亮, 韩超帅, 等. 海上风机支撑结构的频域疲劳评估方法研究[J]. 浙江大学学报(工学版), 2017, 51(9): 1712. QIN Peijiang, MA Yongliang, HAN Chaoshuai, et al. Frequency-domain fatigue assessment of support structure for offshore wind turbine[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(9): 1712. DOI:10.3785/j.issn.1008-973X.2017.09.005 |
| [3] |
LARSEN C E, LUTES L D. Predicting the fatigue life of offshore structures by the single-moment spectral method[J]. Probabilistic Engineering Mechanics, 1991, 6(2): 96. DOI:10.1016/0266-8920(91)90023-W |
| [4] |
DIRLIK T. Application of computers in fatigue analysis[D]. Coventry, West Midlands, UK: University of Warwick, 1985
|
| [5] |
BENASCIUTTI D, TOVO R. Spectral methods for lifetime prediction under wide-band stationary random processes[J]. International Journal of Fatigue, 2005, 27(8): 867. DOI:10.1016/j.ijfatigue.2004.10.007 |
| [6] |
郑向远, 高山, 李炜. 一种新的高斯多模态随机疲劳损伤频域分析方法[J]. 哈尔滨工业大学学报, 2020, 52(10): 85. ZHENG Xiangyuan, GAO Shan, LI Wei. A new frequency-domain method for analysis of Gaussian multi-modal random fatigue damage[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 85. DOI:10.11918/201908054 |
| [7] |
STIANSEN S G, MANSOUR A E. Ship primary strength based on statistical data analysis[C]// Annual Meeting of the Society of Naval Architects and Marine Engineers. New York: Society of Naval Architects and Marine Engineers, 1975
|
| [8] |
OLAGNON M, GUÉDÉ Z. Rainflow fatigue analysis for loads with multimodal power spectral densities[J]. Marine Structures, 2008, 21(2/3): 160. DOI:10.1016/j.marstruc.2007.12.004 |
| [9] |
JIAO G, MOAN T. Probabilistic analysis of fatigue due to Gaussian load processes[J]. Probabilistic Engineering Mechanics, 1990, 5(2): 76. DOI:10.1016/0266-8920(90)90010-H |
| [10] |
FU T T, CEBON D. Predicting fatigue lives for bi-modal stress spectral densities[J]. International Journal of Fatigue, 2000, 22(1): 11. DOI:10.1016/S0142-1123(99)00113-9 |
| [11] |
BENASCIUTTI D, TOVO R. On fatigue damage assessment in bimodal random processes[J]. International Journal of Fatigue, 2007, 29(2): 232. DOI:10.1016/j.ijfatigue.2006.03.013 |
| [12] |
LOW Y M. A method for accurate estimation of the fatigue damage induced by bimodal processes[J]. Probabilistic Engineering Mechanics, 2010, 25(1): 75. DOI:10.1016/j.probengmech.2009.08.001 |
| [13] |
BENASCIUTTI D, CRISTOFORI A, TOVO R. Analogies between spectral methods and multiaxial criteria in fatigue damage evaluation[J]. Probabilistic Engineering Mechanics, 2013, 31: 39. DOI:10.1016/j.probengmech.2012.12.002 |
| [14] |
GAO Shan, ZHENG Xiangyuan. An improved spectral discretization method for fatigue damage assessment of bimodal Gaussian processes[J]. International Journal of Fatigue, 2019, 119: 268. DOI:10.1016/j.ijfatigue.2018.09.027 |
| [15] |
BRACCESI C, CIANETTI F, TOMASSINI L. Random fatigue. A new frequency domain criterion for the damage evaluation of mechanical components[J]. International Journal of Fatigue, 2015, 70: 417. DOI:10.1016/j.ijfatigue.2014.07.005 |
| [16] |
VANMARCKE E H. Properties of spectral moments with applications to random vibration[J]. Journal of the Engineering Mechanics Division, 1972, 98(2): 425. DOI:10.1061/jmcea3.0001593 |
 2023, Vol. 55
2023, Vol. 55




