2. 中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration (Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
基岩上覆土层对地震动的放大已被广泛认知,一些场地指标(例如,场地类别、一定深度内的平均剪切波速、卓越周期等)被用于量化、表征场地放大程度。其中,地表以下介质30 m内的平均剪切波速(VS30)因其概念清晰、计算简便并且与周期依赖的场地放大幅值相关性较强,是应用较多的一个指标参数。各国规范,例如美国的IBC和NEHRP、欧洲的Eurocode、智利的DS61等,都将其作为定义场地类别的核心参数之一。目前常用的地震动预测模型(例如,NGA项目开发的多个模型[1-3],国内地震动衰减关系[4])大都采用VS30作为场地项的参数之一,用以反映场地的线性和非线性效应。通常情况下,VS30最为合理的获取方式是通过真实的钻孔剖面数据计算获得。然而,由于受经济性、勘测环境、规范要求等因素影响,钻孔深度往往达不到30 m。例如,日本K-NET的强震动台站仅对钻孔20 m深度以内的场地条件进行了波速测试。
中国的抗震设计规范采用覆盖层厚度和等效剪切波速(计算深度取覆盖层厚度与20 m两者较小值)“双指标”进行场地分类。依据规范要求,实际操作中许多工程场地的钻探深度不到30 m就已达基岩层(规范定义剪切波速达到500 m/s),无需再往下钻进。这种情况下,无法通过实际钻孔剖面资料直接计算出真实VS30值,通常可利用经验外推模型对VS30值进行估算。常速度外推模型(BCV,也称作“底部常速度模型”)将钻孔最底层的波速直接按常数外推至30 m处,因其操作方便而应用广泛[5-7]。已有研究表明,土层剪切波速与埋深大致总体上呈正相关的趋势[8],这也符合浅层土层沉积年代较近,剪切波速较小,深层土层或基岩沉积年代久远,剪切波速较大的规律。因此,BCV模型理论上会低估VS30值。另一种经验外推模型是速度梯度外推模型,认为VSz(Z m以内的平均剪切波速,Z<30 m)和VS30之间存在一定的对数线性关系[9]或者二次多项式关系[10]。随着距地表深度的不断增大,地下介质通常由剪切波速较小的土壤层和剪切波速较大的基岩层组成,对数线性和二次多项式模型都要求场地的波速梯度变化不大,若30 m深度内存在坚硬的岩石层则会引起较大的估计误差。文献[11-12]提出了依据两个不同深度的平均剪切波速(VSz1和VSz2)估算VS30的方法,称为双深度外推法,其优点是不需要事先针对大量钻孔数据建立回归模型,并且不存在区域依赖性。但缺点是结果受选取的双深度z1和z2影响较大,同一场地可产生多个外推值,偶然误差较大。
因此,针对中国广泛存在的钻孔深度低于30 m且存在基岩层的工程场地,目前并不存在适合的VS30经验估计模型,利用日本KiK-net台站钻孔数据,在BCV模型基础上,试图基于最优子集方法提出一种修正方法,建立修正函数,并通过预测VS30值与实测值的残差分布验证函数的修正效果。最终利用新疆地区的钻孔数据,验证修正函数在该地区的适用性,以期望得到该地区合理的VS30值估计。
1 修正方法描述鉴于钻孔深度低于30 m且已至基岩层的工程场地,速度梯度外推模型并不适用。尽管BCV模型会低估预测结果,但BCV模型较为实用,无需事先对模型参数进行回归。因此,设想针对BCV模型的预测结果进行修正,使其尽可能的接近真实的VS30值。方法基本思路:
1) 采用BCV模型对钻孔VS30进行估计
| $V_{\mathrm{S} 30-\mathrm{BCV}}=30 /\left(\sum\limits_{i=1}^n h_i / V_{\mathrm{S} i}+\left(30-d_{\mathrm{f}}\right) / V_{\mathrm{S}\left(Z=d_{\mathrm{S}}\right)}\right)$ | (1) |
式中:VS30-BCV表示估计值;df表示需要外推钻孔的终孔深度;hi和VSi分别为第i层的厚度和剪切波速;n为土层层数;VS(Z=dS)为覆盖土层下卧基岩面的剪切波速,也就是基岩层的剪切波速,Z表示深度,假设dS至30 m内的剪切波速值都等于此。
2) 国内建筑工程场地上的工程钻孔的普遍如下特点:勘测工程钻孔的主要目的是判断所在场地条件的场地类别,从而确定地震动参数。依据中国抗震设计规范的场地类别判定条件,结合作者收集到的国内钻孔数据发现,国内大多数钻孔只打到20 m或到剪切波速超过500 m/s的层就停止,即达成判定场地类别的基本条件就停止向下钻探。故选取一批钻孔深度大于30 m(便于得到真实VS30值),并具有上述特点的钻孔进行回归分析,探究相关规律。
3) 计算VS30真实值与估计值之间的残差
| $\sigma_{\mathrm{BCV}}=V_{\mathrm{S} 30-\mathrm{REL}}-V_{\mathrm{S} 30-\mathrm{BCV}}$ | (2) |
式中σBCV为真实VS30与估计VS30之间的残差,VS30-REL表示真实值。其中计算常数外推VS30值时,将钻孔基岩层首层(剪切波速首次超过500 m/s的岩层)的底部深度假定为式(1)中的df。
4) 建立σBCV与体现场地特征的典型参数之间的经验关系,给出修正模型。
2 数据选取为了建立修正模型,从日本KiK-net台站数据库中选择合适的钻孔数据。为了计算真实VS30值,钻孔终孔深度(db)必须大于30 m。为了能够还原中国常见的钻孔深度低于30 m且已至基岩层的相似情况,要求钻孔基岩层首层(剪切波速首次超过500 m/s的岩层)的底部深度Zrock1须小于30 m。钻孔数据选取条件:1)db≥30 m;2)Zrock1 < 30 m;3)钻孔剖面不存在明显的软弱夹层。
其中条件3)所述的软弱夹层可能出现在具有多项沉积的场地条件下,该类场地下钻孔剖面的各层剪切波速并非严格与钻孔深度呈正相关趋势。若软弱夹层存在于外推深度范围内,常数外推VS30值与真实值的偏差会变大,为排除此类少数特殊场地条件下钻孔对修正效果的影响,规定此类钻孔暂不适用于该方法。
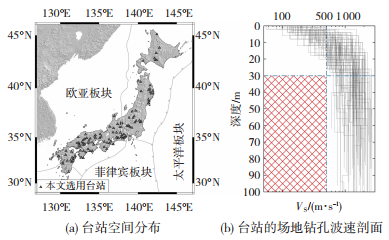
最终收集到满足上述条件的钻孔共计109个,其地理空间分布见图 1(a),所有钻孔的波速剖面见图 1(b)。图 1(b)中阴影部分区域为满足上述筛选条件的钻孔的剪切波速剖面线不与阴影区域相交的判定区域。图 1可见,选取的109个台站钻孔较均匀地分布在日本境内,所有钻孔30 m以下无剪切波速小于500 m/s的土层或基岩层,即各钻孔剪切波速随深度分布曲线均没有穿过图中阴影部分,确保了与上文的钻孔数据选取条件一致。
|
图 1 本研究所选的日本KiK-net台站的地理分布及钻孔场地的剪切波速剖面 Fig. 1 Geographic distribution of KiK-net stations selected in this study and corresponding shear wave velocity profiles |
图 2绘制了所选取109个钻孔的终孔深度db和Zrock1的分布,大多数钻孔的db都在40 m以上,主要集中在50~90 m,保证了每个用于研究的钻孔都能得到真实的VS30值,Zrock1较为均匀分布在10~30 m范围内。

|
图 2 本研究所选的日本KiK-net台站场地钻孔深度统计分布 Fig. 2 Statistics of borehole depths for KiK-net stations selected in this study |
在建立模型之前,须确定与σBCV相关的可反映场地特征的参数。针对中国常见的钻孔深度低于30 m且已下探至基岩层的情况,确定了5个可计算的备选参数,见表 1。
| $\bar{V}_{\mathrm{S}(\text { soil })}=d_{\mathrm{S}} / \sum\limits_{i=1}^n\left(h_i / V_{\mathrm{S} i}\right)$ | (3) |
| $\eta=\frac{V_{\mathrm{S}\left(Z=d_{\mathrm{S}}\right)}}{\bar{V}_{\mathrm{S}(\text { soil })}}$ | (4) |
| $T_0=\sum\limits_{i=1}^n \frac{4 h_i}{V_{\mathrm{S} i}}$ | (5) |
| 表 1 反映场地特征的备选参数 Tab. 1 Optional parameters reflecting site characteristics |
多个自变量中存在两个或多个变量线性相关的现象称为自变量的共线性。在多元回归分析中,存在一条基本假设是各自变量间不存在明显的线性相关关系。其中3个或者更多变量之间相互线性相关的情况又称为变量的多重共线性。变量的共线性会造成回归方程中变量的冗余,增加了回归模型的不稳定性,样本的微小扰动都可能带来回归模型参数很大的变化。因此在回归前需要剔除相应的共线性变量。
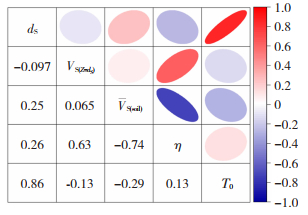
为了消除变量间共线性对回归模型的影响,将上述5个变量的对数值进行相关性分析,若出现两个变量的相关系数值大于0.7,则剔除其中一个变量。通过计算各变量间的相关系数,绘制各参数的相关系数矩阵,见图 3,图 3椭圆长轴与水平向右方向夹角为45°时,表示该图形在水平与数值方向所对应的两个变量间的相关关系呈现正相关,反之,当椭圆长轴与水平向右方向夹角为135°时,该关系为负相关。同时,椭圆的长轴与短轴之比越大,相关系数越大。可以发现,dS与T0具有很强的相关性,相关系数高达0.86;VS(soil)与η也具有较强相关性,相关系数达到0.74。考虑到变量获取的难易程度和回归方程的易用性,选择通过剔除T0和η来消除变量的共线性问题,即最终参与模型回归分析的3个变量分别为dS、VS(soil)和VS(Z=dS)。
|
图 3 所选5个场地特征参数的相关系数矩阵 Fig. 3 Correlation coefficient matrix of five site characteristic parameters |
最优子集法(又称作最优子集回归)是一种筛选多个线性回归模型中最优模型的特征筛选方法,目的是从所有解释变量中依据残差平方和最小的原则选择出不同变量个数的变量组合,最终从包含不同变量个数的方程集合中选择出最优模型。最优子集法中选择最优参数子集的具体步骤:
1) 建立全体回归变量X1,X2,…,Xm对因变量Y的回归方程Em;
2) 分别剔除X1,X2,…,Xm,对余下参数建立回归方程,得到m个回归方程Em1、Em2、…、Emm,分别求出每一个回归方程所对应的残差平方和,其中残差平方和最小值所对应的方程定义为Em-1;
3) Em、Em-1、Em-2、…、E1即为不同参数个数下的最优参数子集,由上文可知,通过对变量去除多重共线性后,有效变量个数为3,因此m=3。
为了从中选择最优的回归模型,采用调整后R2(R2为回归模型的拟合优度)、贝叶斯信息准则(BIC准则)和k倍交叉验证3种方法对最优参数子集对应的回归方程进行特征选择。
调整后R2按下式计算:
| $R_{\mathrm{Adj}}^2=1-\frac{\left(1-R^2\right)(N-1)}{N-p-1}$ | (6) |
式中p为预测变量的个数,N为总样本容量。
从式(6)可看出,RAdj2考虑了样本容量N和回归方程中的预测变量个数的影响,这使得RAdj2不会像R2一样随着预测变量个数的增加而增大,使其更适合评价回归方程的拟合效果。RAdj2越大,方程的回归效果越好,故选择最大的RAdj2所对应的回归方程作为该特征选择条件下的最优方程。
贝叶斯信息准则(BIC)是衡量统计模型拟合程度的一种标准,当回归方程时,随着预测变量的不断增加,模型的复杂程度不断增加,似然函数也随之增大。ξBIC按下式计算:
| $\xi_{\mathrm{BIC}}=p \ln (N)-2 \ln (L)$ | (7) |
式中p、N含义同上,L为极大似然函数值。
针对回归得到的多个较为合理的模型,通常考虑模型对数据集的描述能力(极大似然函数值)与模型的复杂程度(模型中变量个数)来判断各方程是否为最优方程。一般来说,当用于回归模型的数据集越大,模型的拟合优度越大,似然函数也越大;当预测变量个数p过大时,似然函数增速减缓,使得BIC公式中第一项的值变小。因此BIC最小的模型是平衡了模型复杂度和对数据集的描述能力的最优模型。即ξBIC值最小的方程是在模型拟合度(极大似然函数值)尽可能大的前提下,选择模型的参数尽可能的少的拟合方程。因此,BIC准则就是筛选ξBIC值最小的回归模型作为最优方程。
交叉验证是测试通过训练集确定的预测方程在新测试集中使用效果的方法。由于模型在回归过程中整个数据集是确定的,因此使用一种运用数据集的子集作为测试集来验证模型准确性的方法——k倍交叉验证。该方法将整个数据集随机拆分成k个子集,分别选取k个子集作为测试集,并每次使用其余未被选择的子集作为训练集进行回归方程,通过计算k组数据的均方根误差(ERMS)和平均绝对误差(EMA)来评价模型的好坏,ERMS和EMA值越小表明模型越优。统计学上一般将测试集的容量占比定为20%左右,因此根据日本KiK-net钻孔数据集容量,同时为保证每一个子集尽可能有足够的钻孔个数,k值取为5。
3.4 最优回归方程选择通过最优子集法对日本109个台站钻孔的3个参数的对数进行最优参数子集的计算,最终得到分别具有1个、2个、3个参数的方程1、方程2、方程3,各方程的参数选择结果及对应回归方程的回归系数见表 2,其中“—”表示该变量不是该最优参数子集中的元素。接下来将通过3种特征选择方法选择整体最优的回归方程。
| 表 2 由最优子集法确定的各方程参数及线性方程回归系数 Tab. 2 Equation parameters determined by optimized subset method and regression coefficients of linear equations |
依据上述公式及原理,各参数子集的特征值计算结果见表 3。
| 表 3 各方程的特征选择参数值 Tab. 3 Feature selecting parameters of equations |
采用RAdj2筛选原则和k倍交叉验证筛选方法,最优回归方程为方程3:
| $\begin{array}{r}\log \left(\sigma_{\mathrm{BCV}}\right)=2.006-1.782 \times \log \left(d_{\mathrm{S}}\right)+0.983 \times \\ \log \left(\bar{V}_{\mathrm{S}(\text { soil })}\right)-0.422 \times \log \left(V_{\mathrm{S}\left(Z=d_{\mathrm{S}}\right)}\right)\end{array}$ | (8) |
采用BIC准则,最优回归方程为方程2:
| $\begin{aligned} \log \left(\sigma_{\mathrm{BCV}}\right)= & 0.859-1.758 \times \log \left(d_{\mathrm{S}}\right)+0.948 \times \\ & \log \left(\bar{V}_{\mathrm{S}(\text { soil })}\right)\end{aligned}$ | (9) |
上节通过最优子集法与不同的拟合优度评价方法得到了两个不同的最优回归方程,本节将通过KiK-net钻孔数据验证这两个方程的修正效果来分析其孰优孰劣。
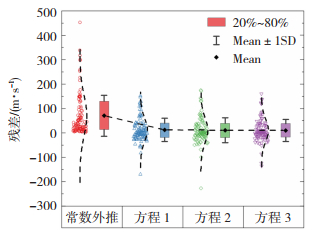
图 4绘制了前文KiK-net钻孔的σBCV和通过3个修正方程计算得到的VS30残差分布散点箱型图,图 4虚线表示VS30残差散点的正态分布曲线,箱体表示散点20%~80%的分布范围,触须线的上下限分别表示各组数据的正负一倍标准差。图 4可见,σBCV分布集中在0 m/s以上,具有明显偏分布特点,说明常数外推法对VS30的估计有系统性偏差,这符合常数外推法系统性低估的原理。通过各修正方程对VS30外推值的修正后,可以发现修正后的VS30残差基本呈现正态分布,均值接近0 m/s,相较于σBCV,3个方程的整体残差平均值更趋于稳定。因此,可以认为这3个方程均能有效地修正常数外推模型的系统偏差。
|
图 4 常数外推VS30预测值和3个方程修正后的VS30预测值的残差分布 Fig. 4 Residuals of VS30 predicted by BCV model and three correction methods |
将上文筛选出两个最优方程与方程1对比发现:3个方程针对常数外推VS30值进行修正后,新得到的修正后VS30值相对于真实VS30的残差分布均值相差不大,但是使用方程2与方程3修正后的残差值在分布的标准差上略有改善;从方程使用的变量上看,方程2与方程3相对于方程1依此添加了变量VS(soil)和VS(Z=dS),针对某些处于特殊场地条件的钻孔(例如,地表覆盖土层较浅且下卧基岩硬度较大、各层性质变化不大的土层结构等),这两个参数更能表现出这些特殊场地的波速分布特性。单纯从统计学的角度上看,方程2与方程3针对常数外推VS30值的修正效果几乎一样。综合考虑以上各项因素,同时考虑模型的易操作性,推荐使用方程2作为常数外推VS30值的修正函数,即所述的特定场地下的VS30预测值(VS30-COR)可通过式(10)计算:
| $V_{\mathrm{S} 30-\mathrm{COR}}=V_{\mathrm{S} 30-\mathrm{BCV}}+\sigma_{\mathrm{BCV}}$ | (10) |
式中VS30-BCV和σBCV分别通过式(1)和式(9)计算。
式(10)适用的钻孔须符合以下条件:1)钻孔终孔深度db≤30 m,并存在基岩层(剪切波速VS>500 m/s) 的钻孔;2)钻孔所在场地为非多相沉积场地条件。
4 修正函数在新疆地区的适用性检验鉴于上述修正函数是利用日本KiK-net钻孔数据建立的,是否适用于中国,需要检验。下面以中国新疆地区为例,进行适用性检验,具体步骤:
1) 筛选出新疆地区符合第2节所述数据筛选要求的钻孔共计821个;
2) 将步骤1中筛选得到的钻孔数据使用式(9)计算BCV模型的修正值σBCV;
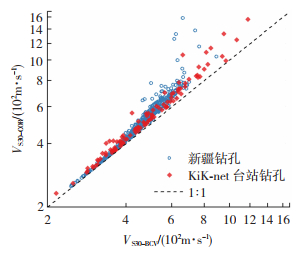
3) 利用式(1)和式(10)分别计算每一个钻孔的VS30-BCV和VS30-COR,与KiK-net台站的相应计算结果一并绘制散点图,见图 5。
|
图 5 KiK-net台站钻孔与新疆地区钻孔VS30常数外推值以及修正值的散点分布 Fig. 5 Scatter distribution of predicted VS30 values by BCV model versus their corrected values for boreholes from KiK-net stations and Xinjiang region |
由图 5可知,对于KiK-net钻孔,随着VS30-BCV的增大,VS30-COR偏离VS30-BCV也越大,新疆地区钻孔也呈现出这种趋势。这是由于VS30较大的钻孔往往具有较小的覆盖层厚度,大部分情况是较浅的表层覆盖土下卧硬度较大的基岩层,由式(9)可知,随着dS的减小,回归得到的σBCV也逐渐增大。图 5新疆地区的散点分布与KiK-net散点的分布整体上基本重叠,两者并未出现系统性偏差,为进一步说明这种现象,图 6绘制了这两个地区VS30-BCV与VS30-COR的直方分布图。图 6可见,两个地区的VS30-BCV值主要分布于300~600 m/s范围内,KiK-net的VS30-BCV在700~1 200 m/s范围内均有分布,而新疆地区在这一范围内几乎无数据;相比较VS30-BCV,VS30-COR在两个地区的分布规律差别与VS30-BCV基本一致。因此,一定程度上说明大多数情况下采用日本钻孔数据建立的修正函数在新疆地区是可以适用的。针对图 5中在较大的剪切波速段(VS30-BCV>600 m/s)的异常点进行追溯原始钻孔数据文件分析可知,该类钻孔覆盖层厚度很小(筛选出5个异常点,dS分别为1.7、2、2、2、2.5 m),通过提出的修正方程修正,由式(9)可知,较小的dS值提供了较大的σBCV,造成图中该类点离散到正常范围外,从而导致最终修正后的VS30-COR误差较大。为提高该模型在新疆地区使用的合理性及准确性,对该修正函数在新疆地区的使用增加一个使用条件:当钻孔的覆盖层厚度dS≥3 m时,该模型可以用于新疆地区钻孔的外推修正。

|
图 6 KiK-net台站钻孔与新疆地区钻孔VS30常数外推值以及修正值的直方分布 Fig. 6 Histograms of predicted VS30 values by BCV model versus their corrected values for boreholes from KiK-net stations and Xinjiang region |
不同地区的土层结构分布是存在区域性差异的,经验模型通常存在区域适用性,图 5、6只能粗略地说明模型区域依赖性影响较小,未来还需要在新疆地区或国内其他地区收集更多满足条件的钻孔数据,以验证上述修正函数的适用性,或者构建本地区的经验修正函数。
5 结论1) 选取5个可反映钻孔剖面特征的参数,通过相关系数矩阵排除共线性问题,确定其中3个参数,包括覆盖土层厚度、覆盖土层下卧基岩面的剪切波速和覆盖土层的平均剪切波速作为修正函数的回归参数。
2) 挑选适用的日本KiK-net台站钻孔数据,利用最优子集法建立了常数外推模型的VS30残差σBCV与上述3个参数的优选函数关系,通过调整后R2、贝叶斯信息准则和k倍交叉验证3种特征选择方法确定其中的最优关系。
3) 根据修正后预测VS30与实际观测VS30间残差均值和标准差的分布,同时考虑模型的易操作性,给出了推荐的常数外推模型修正函数。最后,利用收集的钻孔数据,验证了修正函数在中国新疆地区具有一定适用性。
| [1] |
ABRAHAMSON N, SILVA W. Summary of the Abrahamson & Silva NGA ground-motion relations[J]. Earthquake Spectra, 2008, 24(1): 72. DOI:10.1193/1.2924360 |
| [2] |
BOORE D M, STEWART J P, SEYHAN E, et al. NGA-West2 equations for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes[J]. Earthquake Spectra, 2014, 30(3): 1065. DOI:10.1193/070113EQS184M |
| [3] |
SI Hongjun, MIDORIKAWA S, KISHIDA T. Development of NGA-sub ground-motion model of 5%-damped pseudo-spectral acceleration based on database for subduction earthquakes in Japan[R]. Berkeley: University of California, Berkeley, 2020
|
| [4] |
喻畑, 李小军. 基于NGA模型的汶川地震区地震动衰减关系[J]. 岩土工程学报, 2012, 34(3): 554. |
| [5] |
KUO C H, WEN K L, HSIEH H H, et al. Evaluating empirical regression equations for Vs and estimating VS30 in northeastern Taiwan[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(3): 433. DOI:10.1016/j.soildyn.2010.09.012 |
| [6] |
XIE Junju, ZIMMARO P, LI Xiaojun, et al. VS30 empirical prediction relationships based on a new soil-profile database for the Beijing plain area, China[J]. Bulletin of the Seismological Society of America, 2016, 106(6): 2845. DOI:10.1785/0120160053 |
| [7] |
江志杰, 彭艳菊, 方怡, 等. 北京平原地区VS30估算模型适用性研究[J]. 震灾防御技术, 2018, 13(1): 76. |
| [8] |
宋健, 师黎静, 党鹏飞, 等. 哈尔滨市剪切波速与埋深相关性分析[J]. 建筑结构, 2020, 50: 1089. |
| [9] |
BOORE D M. Estimating VS(30)(or NEHRP site classes) from shallow velocity models (depths<30 m)[J]. Bulletin of the Seismological Society of America, 2004, 94(2): 591. DOI:10.1785/0120030105 |
| [10] |
BOORE D M, THOMPSON E M, CADET H. Regional correlations of VS30 and velocities averaged over depths less than and greater than 30 meters[J]. Bulletin of the Seismological Society of America, 2012, 101(6): 3050. DOI:10.1785/0120110071 |
| [11] |
WANG Haiyun, WANG Suyang. A new method for estimating VS(30) from a shallow shear-wave velocity profile (depth<30 m)[J]. Bulletin of the Seismological Society of America, 2015, 105(3): 1362. DOI:10.1785/0120140103 |
| [12] |
WANG Suyang, WANG Haiyun, LI Qiang. An alternative method for estimating VS(30) from a shallow shear-wave velocity profile (depth<30 m)[J]. Soil Dynamics and Earthquake Engineering, 2017, 99: 70. DOI:10.1016/j.soildyn.2017.05.002 |
 2023, Vol. 55
2023, Vol. 55


