2. 中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration (Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
现行建筑抗震设计规范[1]以及多数地震动预测模型[2]给出的反应谱一般针对5%阻尼比的情况。建筑抗震设计规范[1]提供抗震设计是基于承载力的抗震设计,结构滞回恢复力(或弹性恢复力)是标定抗震设计谱的依据,工程实践中最常用的是利用阻尼修正系数(damping modification factor, DMF) 对5%阻尼比反应谱进行调整,通常被定义为阻尼比为ζ的加速度反应谱与5%阻尼比加速度反应谱的比值。
DMF的研究可以追溯到1982年Newmark等[3]的经典著作,其研究利用1973年以前美国加州14条地震动的水平和竖向分量,提出了阻尼比低于20%情况下的DMF模型,得出的结果已在很多规范和指南中得到应用。早期的研究[3-4]大多只考虑阻尼比的影响,Liu等[5]计算了各影响因素(阻尼比、谱周期、震级、距离等)与DMF的Spearman秩相关系数,发现阻尼比对DMF的影响显著大于其他因素,早期模型因形式简单,计算方便,被广泛应于各国规范及规程中。近年研究表明,仅考虑阻尼比影响的模型很难预测更精确的谱值,除阻尼比外,DMF还受谱周期和地震动参数的影响。Castillo等[6]、Fernandez等[7]、Miranda等[8]、Zhou等[9-10]分别针对墨西哥、秘鲁、智利、日本地区建立了考虑阻尼比、谱周期以及场地类别的DMF模型。而Lin等[11]、Daneshvar等[12]、Rezaeian等[13]认为场地类别对DMF的影响很小,可以忽略。Lin等[14]、Cameron等[15]和Zhao等[16]认为需要单独研究加速度谱DMF和位移谱DMF,若结构阻尼来源于滞回特性,塑性铰的产生,应选择加速度谱DMF;而结构阻尼由附加消能装置产生的,应选择位移谱DMF。苏开潍等[17]、姜明秀等[18]、张潇男等[19]分别对日本俯冲带地震建立加速度谱DMF模型,张衡等[20]、杨新格[21]和李恒等[22]利用日本地震动台网记录的地震记录建立了位移谱DMF模型。一些学者认识到地震动持续时间对能量耗散的重要性,Bommer等[23]发现DMF随地震动持续时间的增大而减小。但地震动持续时间不是一个设计工程师容易得到的参数,有些模型中包含了其他参数作为地震动持续时间的替代,如Rezaeian等[13]利用矩震级和震源距代替地震动持续时间的影响,建立了与阻尼比、谱周期、震级和距离有关的全球俯冲带地震DMF模型。
随着海洋工程的兴建、很多海洋结构的阻尼比并非5%,例如,海底沉管隧道、海底管道、海洋石油平台、储油罐、跨海桥梁等海洋工程结构的阻尼比一般小于5%,装有隔震支座的建筑和桥梁的阻尼比要大于5%。结构体系和外部环境介质相互作用时,产生的阻尼也不一致,如地震烈度较大时海底管道与土之间产生相对滑动,其结构阻尼比往往大于5%,储液晃动的储油罐远小于5%。目前海域工程的抗震设计主要参考陆地相关抗震规范提供的地震动参数,没有考虑海域地震动的特殊性[24-26]。在海域地震动模型方面,仅Hu等[27]根据日本相模湾海底地震记录探讨了6个台站的海域水平向地震动加速度峰值和5%阻尼比反应谱的地震动模型,表明海陆地震动模型存在较大差异。相对于研究较多的陆地DMF模型,目前没有基于海域地震动建立DMF模型。因此,本研究基于日本S-net海底地震大量水平向地震动,研究其影响因素,提出海域DMF模型,为调整海域地震动的反应谱,以及海域工程抗震设计和地震安全性评估提供参考。
1 海域地震动数据集S-net台网是日本的大型海底观测网络,用于观测研究以及预警发生在该海域的地震和海啸。2011年东北太平洋地震后,日本防灾科学技术研究所在从北海道海岸到千叶县博索半岛外的太平洋海底安装了150个由地震仪、水压计和倾斜仪组成的观测系统。该系统以网状方式布设,平均每30 km设置约25个观测点,观测点的数据通过海底电缆传输到地面台站。
本研究选取2016年9月到2021年7月S-net台网记录的矩震级大于4.0的地震记录,经过地震数据的筛选与处理,获得了415次地震的5 680条海底地震动记录。考虑到日本所处复杂板块的震源特征,根据Zhao等[28]提出的日本俯冲带地震分类方法,结合Hayes等[29]提出的俯冲板块模型,将地震动数据集分成40次浅层壳内地震的604条地震动记录,90次上地幔地震的1 235条地震动记录,103次俯冲带板间地震的1 590条地震动记录,182次俯冲带板内地震的2 251条地震动记录,见表 1。
| 表 1 各地震类别的地震事件数以及地震动记录数 Tab. 1 Number of events and records for each earthquake category |
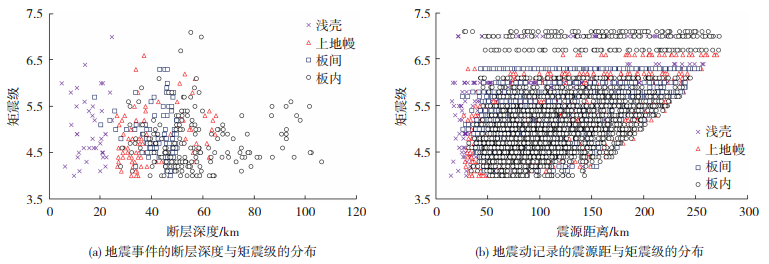
图 1显示了选取的地震事件的断层深度与矩震级的分布,以及地震动记录的震源距与矩震级的分布。由图 1可见,矩震级在4~7.1范围内变化,断层深度最小为4.90 km,最大为106.49 km,震源距最小为14.33 km,最大为272.88 km。为了避免未触发台站的影响,对于特定震级的地震事件,超过一定震源距的记录需要剔除,本研究采用了与矩震级相关的距离截断,且最大的震源距设置为300 km。
|
图 1 地震事件及地震动记录分布 Fig. 1 Distribution of events and ground motion records |
在结构的性态抗震设计中,常采用相应阻尼比的设计反应谱,例如高阻尼谱用于直接基于位移的抗震设计、使用能力谱法时的目标位移估计、耗能装置或隔震系统的抗震设计等,而低阻尼谱用于非结构部件的抗震设计。本研究根据5 680条地震记录计算了包含高阻尼比(>5%)和低阻尼比(< 5%)共14个阻尼比(1% ~30%)和36个谱周期(0.01~5.0 s)的2 862 720条加速度反应谱,计算得到了相应阻尼比下的DMF值,并求出为建立DMF模型所用的DMF均值。
2 DMF的影响因素相比于陆地地震动,海域地震动受到的影响因素更多、更复杂。在建立海域地震动DMF模型时,首先需要分析影响和控制DMF的主要因素,以便于计算DMF并使得建立的模型便于工程应用。因此,需要首先明确是否:1)有必要针对每类地震单独建立模型;2)需要将震源、路径和场地效应纳入到模型中。
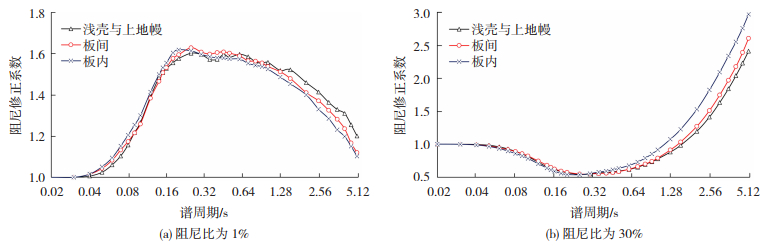
图 2比较了3组地震在阻尼比1%和30%时的DMF。由于浅层壳内地震的记录较少,且浅层壳内地震与上地幔地震有相似的衰减特征[2],本研究将两者归为一组。浅壳与上地幔记录数为1 839,板间为1 590,板内为2 251。由图可见在谱周期小于0.6 s时,地震类型对DMF的影响很小,随谱周期的增大差异逐渐增大,且阻尼比为30%的差异(5.0 s处板内为2.97,浅壳与上地幔为2.41,相差0.56)大于阻尼比为1%的情况。阻尼比为1%时(图 2(a))的中长周期,浅壳与上地幔地震的DMF略大于板间和板内地震的DMF,这与Zhao等[2]认为相比浅壳与上地幔和板内地震,板间地震的DMF略大的结论不同。
|
图 2 不同地震类型DMF变化趋势 Fig. 2 Variation of DMF for different earthquake types |
为了分类研究地震动参数对DMF的影响,本研究用统计的方法[30]分析了震源参数(矩震级和断层深度)、震源距和沉积层厚度对加速度谱DMF的影响,表 2、3分别给出了基于矩震级、震源距和基于断层深度、沉积层厚度的地震动记录分组。图 3、4给出了所有地震动记录的加速度谱DMF,根据矩震级大小划分了4个震级组,分别为小震组(4.0~4.8),中震组(4.9~5.5和5.5~6.5),大震组(>6.5);参照Zhao等[2]对深度的分段点并根据本研究数据集的分布,划分了3个断层深度组,分别为小深度组(< 40 km),中深度组(40~70 km),大深度组(>70 km);根据路径效应中近场项和远场项,划分了4个震源距组,分别为近场组(< 70 km),中远场组(70~120 km和120~200 km),远场组(>200 km);Morikawa等[31]认为沉积层厚度大于250 m会对地震动衰减有影响且随沉积层厚度的增加影响增大,本研究沉积层厚度小于250 m的记录只有137条,因此选取了3个沉积层厚度组,分别为浅沉积层厚度组(1.0 km),较深沉积层厚度组(1.0~1.5 km)和深沉积层厚度组(>1.5 km)。
| 表 2 基于矩震级和震源距的地震动记录分组 Tab. 2 Classification of ground motion records based on moment magnitude and source distance |
| 表 3 基于断层深度和沉积层厚度的地震动记录分组 Tab. 3 Classification of ground motion records based on fault depth and sediment thickness |

|
图 3 DMF值随矩震级和断层深度的变化趋势 Fig. 3 Variation of DMF values with moment magditude and fault depth |
|
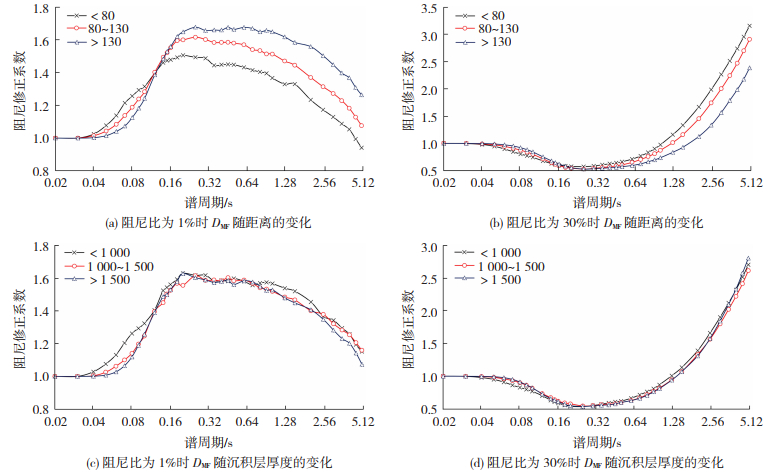
图 4 DMF值随距离和沉积层厚度的变化趋势 Fig. 4 Variation of DMF values with distance and sediment thickness |
图 3给出了DMF随矩震级和断层深度的变化,从图 3(a)可看出在阻尼比为1%时,在谱周期小于0.2 s时,DMF几乎不受矩震级的影响,仅小震组比中震和大震组略大,小震级组随谱周期的增大迅速降低,在谱周期大于3.0 s后DMF < 1.0,大震组值始终大于1.6且变化不大;在阻尼比为30%时(图 3(b)),在谱周期小于0.4 s时,DMF随矩震级的增大而增大,但不同震级组的DMF差异很小,小震级组随谱周期的增大迅速增加,在5.0 s处达到最大值3.95,大震组增加缓慢且始终小于1.0。这表明除短周期外,矩震级对DMF值的影响显著,低阻尼DMF随矩震级的增大而增大,而高阻尼DMF随矩震级的增大而降低。由图 3(c)和(d)可见不同深度组DMF的差异不大,在长周期阶段小深度组值略小,与中深度和大深度组的最大差异为0.1(图 3(d)),表明断层深度对DMF影响很小。
图 4给出了DMF随断层距和沉积层厚度的变化,从图 4(a)可看出当阻尼比为1%时,在谱周期小于0.12 s时,近场组最大且与中远场组和远场组的差异在0.13以内,中远场组(120~200 km)和远场组相似,短距离组随谱周期的增大迅速降低,在5.0 s时DMF < 1.0,为0.94,远场组在长周期时略有下降,仅在1.6~1.8的区间变化;当阻尼比为30%时(图 4(b)),在谱周期小于0.5 s,DMF几乎不受距离的影响,不同震源距组的DMF随谱周期增加差异在增大,在5.0 s处远场组与近场组差异达到最大值1.85。
这表明震源距对DMF值的影响显著,在长周期阶段低阻尼DMF会随震源距的增大而增加,而高阻尼DMF随震源距的增大而降低。由图 4(c)可以看出在阻尼比为1%时,相比较深和深沉积层厚度组,在短周期阶段浅沉积层厚度组略大、长周期阶段浅沉积层厚度组略小,但从整体来看沉积层厚度对DMF值的影响甚微。
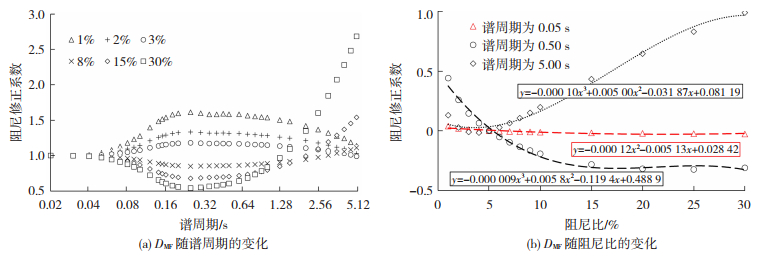
图 5给出了DMF均值的变化趋势,从阻尼比为1%、2%、3%、8%、15%、30%的DMF均值关于谱周期的分布,可看出以下特点:1)谱周期小于0.04 s时,DMF趋近于1.0,这是因为单自由度结构固有频率非常高时,该结构的最大加速度等于输入地震动的最大加速度,即与阻尼比无关,在建模型时可不考虑该谱周期范围,DMF值默认为1.0;2)谱周期处于0.03~1.0 s时,阻尼比越大,DMF越小,这说明在这个周期范围内增加阻尼比能有效减小结构加速度反应;3)在长周期阶段,高阻尼DMF会大于1.0,即长周期高阻尼比结构的加速度值大于5%阻尼比结构的加速度值。该现象是因为单自由结构加速度等于惯性力除以结构质量,惯性力等于结构变形所需的力(弹性力)加上阻尼力,在短周期和小阻尼比时,结构速度引起阻尼力相对很小,加速度主要是用弹性力来平衡,而阻尼比较大的结构长周期下其阻尼力不可忽略不计,故导致长周期高阻尼下加速度谱值偏大。Zhao等[32-33]研究表明为减少结构的加速度反应,在设计隔震结构时应限制其阻尼比在20%以内。图 5(b)给出了谱周期为0.05 s、0.5 s、5.0 s的DMF均值对数关于阻尼比的分布, 图中散点为DMF均值的对数,曲线为对应散点的趋势线,可见在短周期可采用阻尼比的二次多项式进行拟合,而长周期可采用三次多项式拟合,其他谱周期有相同结论。
|
图 5 DMF均值的变化趋势 Fig. 5 Variation of mean DMF |
由上可知,不同震级和距离组之间DMF的差异显著,且矩震级和震源距对DMF的影响效果相同,断层深度以及沉积层厚度对DMF影响甚微。另外地震类型对DMF也有影响,但与陆域地震动[16]有所不同,本研究表明,阻尼比为1%的中长周期浅壳与上地幔海域地震动的DMF略大于板间和板内海域地震动的DMF。根据DMF特性,谱周期和阻尼比是影响DMF的主要参数。如果需要考虑外部因素,可以优先考虑矩震级和震源距的影响。由于以往的模型普遍不能满足边界约束,且不同谱周期下的回归系数不同,不适合实际应用。研究者对地震动参数的影响程度存在分歧,且地震动参数的不可预测性,不能准确表达影响因素,难以适应统一的形式。本研究通过非线性回归提出了一个只考虑阻尼比和谱周期的DMF模型,目的是应用于大多数矩震级和震源距情况下的反应谱,因此本研究没有考虑矩震级和震源距的影响。
3 DMF模型 3.1 DMF模型的建立根据上述分析以及相应参考文献[34-35],本研究考虑谱周期和阻尼比的影响提出海域地震动加速度谱DMF的模型形式为
| $\ln \left[\bar{D}_{\mathrm{MF}}(T, \zeta)\right]=\left\{\begin{array}{l}\sum\limits_{i=1}^3 \sum\limits_{j=0}^4 a_{i, j} \beta^j \alpha^i, T>0.1 \mathrm{~s} \\ \sum\limits_{i=1}^2 \sum\limits_{j=0}^3 b_{i, j} \beta^j \alpha^i, T \leqslant 0.1 \mathrm{~s}\end{array}\right.$ | (1) |
式中ai, j和bi, j为谱周期项系数。α与β取值分别为:
| $\begin{gathered}\alpha=\ln (\zeta)-\ln (5) \\ \beta=\ln (T)\end{gathered}$ |
可以看出满足阻尼比5%时DMF为1.0的边界条件。并采用两步回归方法得到回归系数,首先采用最小二乘法对阻尼比的多项式进行回归,得到与谱周期相关的回归系数;然后对回归系数关于谱周期进行拟合得到谱周期项系数ai, j和bi, j。表 4给出了谱周期T>0.1 s时模型系数ai, j的百分数;表 5给出了谱周期T≤0.1 s时系数bi, j的百分数。
| 表 4 谱周期T>0.1 s时系数ai, j Tab. 4 Coefficient ai, j when T>0.1 s |
| 表 5 谱周期T≤ 0.1 s时系数bi, j Tab. 5 Coefficient bi, j when T ≤0.1 s |
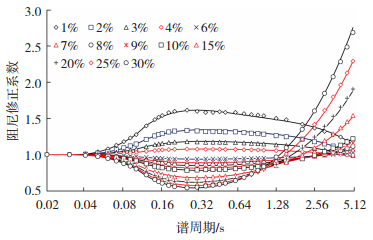
图 6给出了海域DMF模型曲线与实际DMF几何均值的对比,曲线为DMF模型,散点为计算DMF均值。可见,平滑曲线在所有谱周期和阻尼比内都能很好的拟合,在长周期阶段高阻尼DMF > 1.0且超过低阻尼DMF,交叉周期随阻尼比的增大而提前,这是由于惯性力是由弹性力和阻尼力共同组成,高阻尼情况下阻尼力大大增加,从而导致由惯性力标定的绝对加速度谱增大。
|
图 6 DMF模型与DMF均值的对比 Fig. 6 Comparison between DMF model and mean DMF |
近年来,相关研究提出了大量基于陆域不同地区、不同类型地震以及不同数据集的DMF模型,但是并没有可供比较的海域地震动DMF模型。本研究建立的DMF模型是针对海域地震动加速度谱推导的,因此本研究分别选取基于日本相近区域数据和全球数据的两个陆地加速度谱DMF模型进行比较,分别为Zhao等[16]与Liu等[5]。Zhao等[16]利用日本KiK-net和K-NET的俯冲带板间地震4 695条的地震动记录建立了考虑场地类别、谱周期和阻尼比的模型;Liu等[5]利用太平洋数据库的1 586条地震动记录建立了考虑谱周期和阻尼比的模型。
图 7给出了阻尼比为2%和20%时本研究模型与Zhao等[16]和Liu等[5]的对比,比较发现谱周期小于0.1 s时,本研究模型明显小于后两者,谱周期大于2.0 s时本研究模型的增长速度速率最快且最大,该现象可能是由于海域地震动的长周期成分很丰富以及海底的沉积层的放大作用。虽然这3个模型来自不同区域的地震动数据,但不同DMF模型的变化趋势相似,阻尼比2%时在谱周期0.1 s后比较相近,阻尼比30%时3个模型DMF计算值都出现了在1.0处交叉现象,即在长周期高阻尼比情况下模型值大于1.0。

|
图 7 DMF模型与陆域DMF模型的对比 Fig. 7 Comparison between proposed DMF model and onshore DMF models |
本研究针对的海底地震动,其他模型针对陆域地震动。由于海陆数据集的平均震级、断层深度以及震源距不同以及海域地震动特性,导致模型预测存在差异,因此很有必要专门对海底地震动建立DMF模型。
4 结论面向海域工程抗震设计的需求,本研究利用2016年9月到2021年7月S-net台网获取的5 680条海底地震动水平向地震记录,分析不同地震动参数对DMF的影响,建立考虑阻尼比和谱周期的DMF模型,与现有陆地模型进行了对比,验证了本文DMF的合理性,主要结论如下:
1) 海域地震动不同震级和距离组之间DMF的差异显著,且矩震级和震源距对DMF的影响效果相同,即低阻尼DMF会随之增大而增加,高阻尼DMF随之增大而降低,而断层深度以及沉积层厚度对DMF几乎无影响。地震类型对DMF也有影响,但影响效果与陆域地震有所不同,在阻尼比为1%的中长周期浅壳与上地幔地震的DMF略大于板间和板内地震的DMF。
2) 建立了海域地震动反应谱DMF模型,谱周期大于0.1 s时,可用三次多项式模拟阻尼比对DMF的影响,谱周期的影响可用四次多项式表示;谱周期小于0.1 s时,阻尼比对DMF的影响可用二次多项式模拟,谱周期的影响可用三次多项式表示。
3) 由于海陆地震动特性的差异,数据集的平均震级、断层深度以及震源距不同,导致海域地震动DMF模型与陆域模型在不同周期上差异明显,因此面向海域工程抗震设计,采用基于海域地震动建立的DMF模型更合理。致谢
致谢
感谢日本国家地球科学与抗灾研究所的S-net地震动台网(https://hinetwww11.bosai.go.jp/auth/download/cont/?LANG=en.)为本文提供的海域地震动记录。
| [1] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版, 2016 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architectur & Building Press, 2016 |
| [2] |
ZHAO J X, ZHOU Shuanglin, ZHOU Jun, et al. Ground-motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bulletin of the Seismological Society of America, 2016, 106(4): 1558. DOI:10.1785/0120200383 |
| [3] |
NEWMARK N M, HALL W J. Earthquake spectra and design[J]. Engineering Monographs on Earthquake Criteria, 1982, 8(1): 5. |
| [4] |
ASHOUR S A. Elastic seismic response of buildings with supplemental damping[D]. Ann Arbor: University of Michigan, 1987
|
| [5] |
LIU Tao, WANG Wenze, WANG Huakun, et al. Improved damping reduction factor models for different response spectra[J]. Engineering Structures, 2021, 246(1): 118. DOI:10.1016/j.engstruct.2021.113012 |
| [6] |
CASTILLO T, RUIZ S E. Reduction factors for seismic design spectra for structures with viscous energy dampers[J]. Journal of Earthquake Engineering, 2014, 18(3): 328. DOI:10.1080/13632469.2013.860932 |
| [7] |
FERNANDEZ V I, MENDO A R. Damping modification factors for the design of seismic isolation systems in Peru[J]. Earthquake Spectra, 2020, 36(4): 2062. DOI:10.1177/8755293020926189 |
| [8] |
MIRANDA S, MIRANDA E, CARLOS J. The effect of spectral shape on damping modification factors[J]. Earthquake Spectra, 2020, 36(4): 2089. DOI:10.1177/8755293020936691 |
| [9] |
ZHOU Jun, ZHAO J X. A damping modification factor prediction model for horizontal displacement spectrum from subduction slab earthquakes in Japan accounting for site conditions[J]. Bulletin of the Seismological Society of America, 2020, 110(2): 650. DOI:10.1785/0120190156 |
| [10] |
ZHOU Jun, ZHAO J X. A damping modification factor prediction model for horizontal displacement spectrum from subduction interface earthquakes in Japan accounting for site conditions[J]. Bulletin of the Seismological Society of America, 2020, 110(3): 1241. DOI:10.1785/0120190275 |
| [11] |
LIN Yuyuan, CHANG Kuochung. Effects of site classes on damping reduction factors[J]. Journal of Structural Engineering, 2004, 130(11): 1671. DOI:10.1061/(asce)0733-9445(2004)130:11(1667) |
| [12] |
DANESHVAR P, BOUAANANI N, GODA K, et al. Damping reduction factors for crustal, inslab, and interface earthquakes characterizing seismic hazard in southwestern British Columbia, Canada[J]. Earthquake Spectra, 2016, 32(1): 49. DOI:10.1193/061414EQS086M |
| [13] |
REZAEIAN S, ATIK L, KUEHN N M, et al. Spectral damping scaling factors for horizontal components of ground motions from subduction earthquakes using NGA-Subduction data[J]. Earthquake Spectra, 2021, 37(4): 2467. DOI:10.1177/87552930211027903 |
| [14] |
LIN Yuyuan, CHANG Kuochung. Study on damping reduction factor for buildings under earthquake ground motions[J]. Journal of Structural Engineering, 2003, 129(2): 210. DOI:10.1061/(ASCE)0733-9445(2003)129:2(206) |
| [15] |
CAMERON W I, GREEN R A. Damping correction factors for horizontal ground-motion response spectra[J]. Bulletin of the Seismological Society of America, 2007, 97(3): 951. DOI:10.1785/0120060034 |
| [16] |
ZHAO J X, YANG Qingsong, SU Kaiwei, et al. Effects of earthquake source, path, and site conditions on damping modification factor for the response spectrum of the horizontal component from subduction earthquakes[J]. Bulletin of the Seismological Society of America, 2019, 109(6): 2601. DOI:10.1785/0120190105 |
| [17] |
苏开潍, 杨青松, 梁基冠. 浅壳与上地幔地震的水平加速度谱阻尼修正系数模型[J]. 地震学报, 2019, 41(6): 780. SU Kaiwei, YANG Qingsong, LIANG Jiguan. Damping correction coefficient model of horizontal acceleration spectrum for shallow crust and upper mantle earthquakes[J]. Acta Seismologica Sinica, 2019, 41(6): 780. |
| [18] |
姜明秀, 张潇男, 康莉莉. 俯冲带板内地震水平加速度谱的阻尼比修正系数模型研究[J]. 地震工程与工程振动, 2019, 39(4): 131. JIANG Mingxiu, ZHANG Xiaonan, KANG Lili. Study on damping ratio correction coefficient model of seismic horizontal acceleration spectrum in subduction zone[J]. Earthquake Engineering and Engineering Dynamic, 2019, 39(4): 131. |
| [19] |
张潇男, 姜明秀, 康莉莉. 俯冲带板间地震水平加速度谱阻尼修正系数研究[J]. 世界地震工程, 2019, 35(4): 85. ZHANG Xiaonan, JIANG Mingxiu, KANG Lili. Study on damping correction coefficient of seismic horizontal acceleration spectrum between plates in subduction zone[J]. World Earthquake Engineering, 2019, 35(4): 85. |
| [20] |
张衡, 朱敏, 杨新格. 俯冲带板内地震的位移谱阻尼修正系数研究[J]. 地震工程与工程振动, 2018, 38(6): 208. ZHANG Heng, ZHU Min, YANG Xinge. Study on displacement spectrum damping correction coefficient of in plate earthquake in subduction zone[J]. Earthquake Engineering and Engineering Dynamic, 2018, 38(6): 208. |
| [21] |
杨新格. 俯冲带板间地震的位移谱阻尼比修正系数研究[D]. 成都: 西南交通大学, 2018 YANG Xinge. Study on correction coefficient of displacement spectrum damping ratio of inter plate earthquake in subduction zone[D]. Chengdu: Southwest Jiaotong University, 2018 |
| [22] |
李恒, 吴建超, 雷霆. 地震动位移反应谱阻尼修正系数研究[J]. 土木工程学报, 2018, 51(7): 65. LI Heng, WU Jianchao, LEI Ting. Study on damping correction coefficient of ground motion displacement response spectrum[J]. China Civil Engineering Journal, 2018, 51(7): 65. |
| [23] |
BOMMER J J, MENDIS R. Scaling of spectral displacement ordinates with damping ratios[J]. Earthquake Engineering & Structural Dynamics, 2005, 34(2): 148. DOI:10.1002/eqe.414 |
| [24] |
胡进军, 杨泽西, 谢礼立. 海域地震动研究现状分析[J]. 世界地震工程, 2019, 35(3): 31. HU Jinjun, YANG Zexi, XIE Lili. Analysis of current research situation of sea area ground motion[J]. World Earthquake Engineering, 2019, 35(3): 31. |
| [25] |
谭景阳, 胡进军, 周旭彤, 等. 海底与陆地地震动反应谱比定量分析[J]. 振动与冲击, 2021, 40(2): 215. TAN Jingyang, HU Jinjun, ZHOU Xutong, et al. Quantitative analysis of seismic response spectrum ratio of seabed and land[J]. Joumal of Vibration and Shock, 2021, 40(2): 215. |
| [26] |
DIAO Hongqi, HU Jinjun, XIE Lili. Effect of seawater on incident plane P and SV waves at ocean bottom and engineering characteristics of offshore ground motion records off the coast of southern California, USA[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(2): 188. DOI:10.1007/s11803-014-0222-4 |
| [27] |
HU Jinjun, TAN Jingyang, ZHAO J X. New GMPEs for the Sagami Bay region in Japan for moderate magnitude events with emphasis on differences on site amplifications at the seafloor and land seismic stations of K-NET[J]. Bulletin of the Seismological Society of America, 2020, 110(5): 2580. DOI:10.1785/0120190305 |
| [28] |
ZHAO J X, ZHOU Shuanglin, GAO Pingjun, et al. An earthquake classification scheme adapted for Japan determined by the goodness of fit for ground-motion prediction equations[J]. Bulletin of the Seismological Society of America, 2015, 105(5): 2761. DOI:10.1785/0120150013 |
| [29] |
HAYES G P, MOORE G L, PORTNER D E, et al. Slab2, a comprehensive subduction zone geometry model[J]. Science, 2018, 362(6410): 58. DOI:10.1126/science.aat4723 |
| [30] |
HAO Anmin, ZHOU Deyuan, LI Yaming, et al. Effects of moment magnitude, site conditions and closest distance on damping modification factors[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(9): 1239. DOI:10.1016/j.soildyn.2011.05.002 |
| [31] |
MORIKAWA N, FUJIWARA H. A new ground motion prediction equation for Japan applicable up to M9 mega-earthquake[J]. Journal of Disaster Research, 2013, 8(5): 880. DOI:10.20965/jdr.2013.p0878 |
| [32] |
ZHAO J X, ZHANG Jian. Inelastic demand spectra for bi-linear seismic isolation systems based on nonlinear time history analyses and the response of lead-rubber bearing isolation systems subjected to near-source ground motions[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2007, 40(1): 11. DOI:10.5459/bnzsee.40.1.7-17 |
| [33] |
ZHAO J X. Response of seismically isolated buildings with buffers subjected to near-source ground motions and possible alternative isolation systems[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2004, 37(3): 118. DOI:10.5459/bnzsee.37.3.111-133 |
| [34] |
刘名吉, 张洪博, 康莉莉. 俯冲带浅壳和上地幔地震竖向位移谱阻尼修正系数模型[J]. 地震工程与工程振动, 2020, 40(4): 209. LIU Mingji, ZHANG Hongbo, KANG Lili. Damping correction coefficient model of seismic vertical displacement spectrum of shallow shell and upper mantle in subduction zone[J]. Earthquake Engineering and Engineering Dynamic, 2020, 40(4): 209. |
| [35] |
张洪博, 刘名吉, 康莉莉. 浅壳与上地幔地震竖向加速度谱阻尼修正系数模型[J]. 世界地震工程, 2021, 37(3): 158. ZHANG Hongbo, LIU Mingji, KANG Lili. Damping correction coefficient model of seismic vertical acceleration spectrum of shallow crust and upper mantle[J]. World Earthquake Engineering, 2021, 37(3): 158. |
| [36] |
ZHAO J X, JIANG Mingxiu, ZHANG Xiaonan, et al. A damping modification factor for horizontal acceleration spectrum from subduction slab earthquakes in Japan accounting for site conditions[J]. Bulletin of the Seismological Society of America, 2020, 110(4): 1948. DOI:10.1785/0120190242 |
 2023, Vol. 55
2023, Vol. 55


