2. 道路与铁道工程安全保障教育部重点实验室(石家庄铁道大学),石家庄 050043
2. Key Lab of Roads and Railway Engineering Safety Control (Shijiazhuang Tiedao University), Ministry of Education, Shijiazhuang 050043, China
隔震结构[1]的抗震性能试验测试方法主要有两种:一是对隔震支座进行拟静力试验[2-3]以获取其力学性能,但拟静力试验无法模拟动力特性,单独对隔震支座进行试验也无法准确评价整体隔震结构的抗震性能;第二种是将隔震支座与被隔震结构一起进行振动台试验[4-6],受振动台尺寸和承载能力的限制,往往需要大比例缩尺才能对整体隔震结构进行动力测试,尤其对于隔震支座这种力学性能受竖向荷载影响大的构件,大比例缩尺可能会导致试验失真。
近年来,实时子结构试验技术[7-8]发展迅速。该试验方法将整体结构分为两部分,将非线性特征明显,难以建模的部分作为物理子结构,用以真实试验加载,其余部分作为数值子结构,利用计算机进行数值分析,两者之间通过实时数据交互实现边界的协调统一,以完成对整体结构的动力分析。该方法不需要将整个隔震系统进行物理试验,可实现大尺寸甚至足尺试验,为隔震结构的抗震性能研究[9-10]提供了新思路。数值子结构建模误差会影响实时子结构试验结果的准确性,目前提高数值模型精度的主要方法是模型更新[11-14],在试验过程中通过识别物理子结构试验加载的观测数据来更新数值子结构的本构模型。该方法能在一定情况下较好的提高数值模型的精度,但模型更新的前提需要数值子结构和物理子结构具有相同的本构特性[15],对于隔震结构来说,隔震层和被隔震结构的动力性能明显不同,模型更新难以适用。对此,本文提出一种两阶段实时子结构试验方法,通过仿真和试验验证,该方法在保证隔震支座力学性能真实性的前提下,可以提高隔震支座的模型精度,有效实现对隔震结构的抗震性能研究。
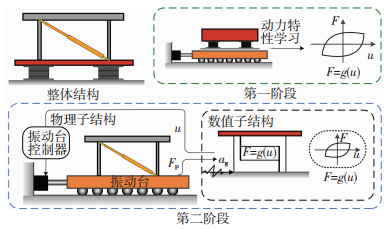
1 试验原理两阶段实时子结构试验原理见图 1,将隔震层作为数值子结构,上部被隔震结构作为物理子结构,整个试验过程分为两个阶段。第一阶段对隔震支座单独进行动力试验,试验中隔震支座受到的竖向荷载为该支座在原结构中所受真实荷载。利用试验数据训练神经网络,使其学习隔震支座的动力特性,基于神经网络建立隔震支座的精确数值模型。由于隔震支座恢复力和阻尼力都具有明显的非线性特征且难以分别测量,因此将恢复力和阻尼力作为整体考虑;第二阶段将基于神经网络建立的隔震支座数值模型作为数值子结构,被隔震结构作为物理子结构安装在振动台上进行物理试验,以此通过实时子结构试验完成对整体隔震结构的抗震性能测试。
|
图 1 两阶段实时子结构试验原理 Fig. 1 Schematic of two-stage real-time hybrid testing |
第一阶段中隔震支座单独的动力分析方程为
| $m_{\mathrm{n}} a_{\mathrm{n}}+c_{\mathrm{n}} v_{\mathrm{n}}+k_{\mathrm{n}} u_{\mathrm{n}}=-m_{\mathrm{n}} a_{\mathrm{g}}$ | (1) |
式中:mn、cn、kn分别为数值子结构的质量、阻尼、刚度,an、vn、un分别为数值子结构的加速度、速度、位移,ag为地震加速度。通过神经网络学习恢复力和阻尼力和位移的非线性关系g(·)为
| $g(u)=c_{\mathrm{n}} v_{\mathrm{n}}+k_{\mathrm{n}} u_{\mathrm{n}}$ | (2) |
试验中恢复力和阻尼力难以分别测量,隔震支座可看作单自由度系统,根据式(1)可知,其恢复力和阻尼力之和与绝对惯性力大小相等,方向相反,因此式(2)中神经网络的学习可以通过式(3)实现。
| $g(u)=-m_{\mathrm{n}}\left(a_{\mathrm{n}}+a_{\mathrm{g}}\right)$ | (3) |
基于神经网络建立隔震支座的数值模型,然后联合物理子结构试验加载,将物理子结构反力Fp反馈给数值子结构进行动力分析,以完成两阶段实时子结构试验,数值子结构的动力平衡方程为
| $\left\{\begin{array}{l}m_{\mathrm{n}} a_{\mathrm{n}}+F=-m_{\mathrm{n}} a_{\mathrm{g}}+F_{\mathrm{p}} \\ F=g(u)\end{array}\right.$ | (4) |
式中F为神经网络预测数值子结构刚度恢复力与阻尼力之和。
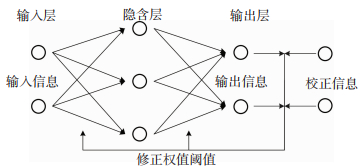
2 神经网络模型本文采用一种按误差逆传播算法训练的多层前馈网络(BP神经网络)作为数值子结构动力特性的学习方法,BP神经网络的拓扑结构见图 2。
|
图 2 BP神经网络拓扑结构 Fig. 2 Topology of BP neural network |
BP神经网络的结构包括输入层、隐含层、输出层。训练样本信息从输入层输入,经隐含层逐层处理,最后输出预测结果。计算预测信息与校正信息的误差,当大于期望误差时,误差信号反向传播,根据学习算法调整网络结构中的权值和阈值,再次将训练样本输入修正后的神经网络,循环以上步骤直到误差精度满足要求。
原始BP神经网络的训练算法为梯度下降法,参数沿着误差梯度相反的方向移动,直到取得极小值,但该算法线性收敛速度较慢,本文中神经网络学习算法选取Levenberg-Marquardt(LM)[16]算法,LM算法属于近似二阶算法,是梯度下降法与高斯-牛顿法的结合,相比于梯度下降法,其收敛速度更快,函数陷入局部极小值的概率更小,LM算法的权值修正规则为
| $\boldsymbol{W}_{i+1}=\boldsymbol{W}_i-\left[\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}+\mu \boldsymbol{I}\right]^{-1} \boldsymbol{J}^{\mathrm{T}} \boldsymbol{e}$ | (5) |
式中:Wi+1为第i+1步权值修正向量,e为误差向量,J为误差向量e对权值求导的Jacobian矩阵,I为单位矩阵,μ为正参数,当μ较大时,LM算法接近梯度下降法,当μ较小时,LM算法接近高斯-牛顿法。
本文采用的神经网络模型输入特征向量[17]为6个变量:当前时刻和前一时刻的数值子结构的位移ui、ui-1;前一时刻数值子结构的内力Fi-1;前一时刻数值子结构内力与位移的乘积Fi-1×ui-1;前一时刻数值子结构内力与位移增量的符号函数的乘积Ai-1=Fi-1×sign(ui-ui-1);以及一个时间步内的能量消耗Ei-1=(Fi-1+Fi-2)(ui-1-ui-2)/2。输出变量为当前时刻数值子结构内力Fi,神经网络计算过程为
| $F=h(\boldsymbol{w} \times \cdots b(\boldsymbol{w} \times \boldsymbol{x}+\boldsymbol{\theta})+\boldsymbol{\theta})$ | (6) |
式中:x为输入特征向量,w、θ分别为各隐含层和输出层的权值向量和阈值向量,b(·)、h(·)分别为隐含层和输出层的激活函数。
3 数值仿真 3.1 仿真方案为了验证两阶段实时子结构试验的可行性,选用如图 3所示的两自由度非线性模型进行数值仿真。上部结构作为物理子结构,其结构参数为质量3 t,阻尼比5%,物理子结构恢复力模型采用双折线模型,初始刚度k1=90 kN/m,屈服刚度k2=k1/10。隔震层作为数值子结构,其结构参数为质量6 t,阻尼比5%,数值子结构恢复力模型采用Bouc-Wen[18]模型,其模型表达式为
| $\left\{\begin{array}{l}f=\alpha k d+(1-\alpha) k z \\ \dot{z}=v-\beta|v||z|^{n-1} z-\gamma v|z|^n\end{array}\right.$ | (7) |

|
图 3 数值仿真示意 Fig. 3 Schematic of numerical simulation |
式中:f为恢复力,k为结构初始刚度,d、v为系统输入位移和速度,z为滞变位移,α为第二刚度系数,即屈服后刚度与屈服前刚度比值。β、n、γ为控制滞回环大小和形状的参数。仿真中Bouc-Wen模型参数分别取k=90 kN/m,α=0.1,β=8,n=1,γ=5。
首先建立隔震层单独模型进行动力分析,得到隔震层的位移变形和内力响应,此动力分析过程共用10组地震波,训练样本从频谱和峰值尽量保证对激励对象的动力特性充分包络覆盖。然后整理数据训练神经网络。基于训练好的神经网络建立数值子结构模型与物理子结构完成子结构动力仿真,仿真动力方程见式(8),第i时刻,神经网络预测数值子结构内力Fn,结合地震加速度ag和物理子结构反力Fp,数值子结构积分求解得到界面响应,通过界面响应分析物理子结构动力响应,得到第i+1时刻物理子结构反力Fp,重复上述步骤完成动力时程分析。
| $\left\{\begin{array}{l}m_{\mathrm{n}} a_{\mathrm{n}}+F_{\mathrm{n}}=-m_{\mathrm{n}} a_{\mathrm{g}}+F_{\mathrm{p}} \\ m_{\mathrm{p}} a_{\mathrm{p}}+c_{\mathrm{p}} v_{\mathrm{p}}+k_{\mathrm{p}} u_{\mathrm{p}}=-m_{\mathrm{p}}\left(a_{\mathrm{g}}+a_{\mathrm{n}}\right) \\ F_{\mathrm{p}}=-m_{\mathrm{p}}\left(a_{\mathrm{g}}+a_{\mathrm{n}}+a_{\mathrm{p}}\right)\end{array}\right.$ | (8) |
式中:mn为数值子结构质量,mp、cp、kp分别代表物理子结构的质量、阻尼、刚度,an为数值子结构加速度,ap、vp、up分别为物理子结构的加速度、速度、位移,ag为地震加速度, Fn为神经网络预测的数值子结构刚度恢复力和阻尼力之和,Fp为物理子结构传递给数值子结构的反力。BP神经网络模型隐含层为2层,每层15个神经元节点,隐含层的激活函数为logsig函数,输出层的激活函数为purelin函数。
将同一激励下的两阶段实时子结构试验方法的响应结果与整体结构的仿真结果进行对比。本文选用峰值误差和相对均方根误差作为误差判别指标,其中峰值误差判断在动力响应峰值处的误差情况,其表达式见式(9),相对均方根误差判断整体时程响应的误差情况,其表达式见式(10):
| $E_{\mathrm{p}}=\frac{F_{\mathrm{m}}^{\mathrm{true}}-F_{\mathrm{m}}^{\mathrm{k}}}{F_{\mathrm{m}}^{\text {true }}}$ | (9) |
| $D_{\mathrm{RMS}}=\sqrt{\frac{\sum\limits_{i=1}^t\left(F_i^{\mathrm{true}}-F_i^{\mathrm{k}}\right)^2}{\sum\limits_{i=1}^t\left(F_i^{\mathrm{true}}\right)^2}}$ | (10) |
式中:Fitrue为第i时刻整体模型仿真的响应,Fik为第i时刻两阶段子结构动力分析的响应,Fmtrue为整体结构仿真的动力响应峰值,Fmk为两阶段子结构动力分析的对应动力响应峰值。
3.2 仿真结果对神经网络的训练精度进行验证,将隔震支座在动力仿真中的位移时程整理后输入神经网络模型,预测隔震支座对应的内力时程,并与动力仿真中隔震支座真实的内力响应进行对比,神经网络预测结果见图 4,图中仿真值曲线为仿真中的真实内力响应,预测值曲线为神经网络预测的响应结果。神经网络预测内力时程的相对均方根误差为2.49%,峰值误差为0.08%。

|
图 4 仿真数据预测精度 Fig. 4 Prediction accuracy of simulation data |
基于训练好的神经网络建立隔震层的数值子结构模型,并与物理子结构模型进行子结构动力分析,用在同一激励下的原整体结构动力响应作为对比,以El-Centro波作为地震激励,结构各层位移时程响应和加速度时程响应的对比结果见图 5,图中整体仿真曲线为整体模型仿真的动力响应,两阶段曲线为用本文所提的两阶段子结构动力分析得到的响应结果,由图 5看出结构各部分的时程响应对比曲线吻合情况较好,初步证实两阶段实时子结构试验方法的可行性。

|
图 5 仿真动力响应 Fig. 5 Dynamic response of simulation |
图 6总结了6组地震工况下的结构各层动力响应误差信息,由图可知两阶段子结构动力分析结果的峰值误差基本保持在3%以内,相对均方根误差基本保持在6%以内,精度较好。

|
图 6 仿真动力响应误差 Fig. 6 Dynamic response errors of simulation |
通过仿真初步验证,针对隔震结构的各部分非线性都比较明显的情况,可以通过两阶段实时子结构试验得到整体隔震结构在地震激励下的真实响应。
4 试验验证 4.1 试验方案试验模型及流程见图 7,整体结构为两层框架结构,底层结构作为数值子结构,其平面尺寸为250 mm×250 mm,上层结构作为物理子结构,其平面尺寸为160 mm×160 mm,各层层高为300 mm,一层楼板处集中质量为8.27 kg,二层楼板集中质量为1.49 kg,上部物理子结构为线性结构,实测物理子结构的结构参数为阻尼比1%,频率4.28 Hz。为模拟底部数值子结构非线性,在数值子结构运动方向加入斜撑。试验所用振动台为尺寸500 mm×500 mm的电磁振动台。在各层楼板处配置加速度传感器和位移传感器收集结构动力响应数据。

|
图 7 试验验证示意 Fig. 7 Schematic of experimental verification |
首先对底部数值子结构单独进行振动台试验,整理观测数据训练神经网络模型使其学习数值子结构动力特性。然后基于训练好的神经网络建立数值子结构的精确模型并与物理子结构进行实时子结构动力分析。
本文在针对数值子结构的单独振动台试验总共做了30组地震波工况,地震动数量对网络训练效果呈正相关,由于仿真训练中只需要覆盖模型的动力行为,即动力响应能对数值子结构的动力行为形成包络即可,试验训练则需要学习试件的动力行为和时变效应,需要的训练数据多于仿真,对于用神经网络学习结构的动力特性,一般训练数据越多覆盖范围越广,神经网络的学习效果越好。试验验证环节采用的BP神经网络模型共有5层隐含层,每层15个神经元节点,隐含层的激活函数为logsig函数,输出层的激活函数为purelin函数。
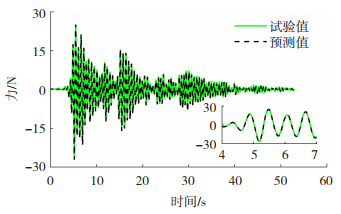
4.2 试验结果对神经网络进行精度测试,将物理子结构在振动台试验中测得的位移响应整理后作为神经网络的输入信息,将神经网络预测的内力值与振动台试验中实测内力响应进行对比,神经网络预测结果对比见图 8,图中试验值曲线为振动台试验的真实响应,预测值曲线为神经网络预测的响应结果。由图 8看出神经网络预测响应和振动台试验的真实响应二者时程曲线基本吻合,峰值误差为0.59%,相对均方根误差为7.74%,神经网络预测精度理想,神经网络预测的计算效率为单步计算需要0.05 ms,目前实时混合试验最小时间步长为1 ms,神经网络可满足实时子结构试验对计算效率的要求。
|
图 8 试验数据预测精度 Fig. 8 Predication accuracy of experimental data |
试验中物理子结构为线性模型,因此不需要进行第二阶段实时加载即可得到数值与物理子结构的全部动力响应。本文主要为了验证两阶段实时子结构试验技术的可行性,通过验证神经网络对隔震层的学习精度以及将神经网络应用到实时子结构动力分析的有效性,受试验条件的限制,上部结构为线性结构对两阶段实时子结构试验方法的验证无影响。图 9汇总了整体结构振动台试验和两阶段子结构动力分析的结构各层动力响应对比情况。整体试验曲线代表整体结构振动台试验的时程响应,两阶段曲线代表本文所提两阶段实时子结构试验得到的时程响应。由图 9看出结构各层动力响应时程曲线基本吻合。

|
图 9 试验动力响应 Fig. 9 Dynamic response of experiment |
图 10总结了结构各层的加速度响应与位移响应的峰值误差和相对均方根误差,两阶段实时子结构试验峰值误差在6%以内,相对均方根误差在10%以内,试验误差主要分为两部分原因:神经网络对数值子结构动力特性的学习精度误差;在两阶段子结构动力分析中,上部物理子结构的建模误差也会影响试验结果。结合上述试验结果证明本文所提适于隔震结构的两阶段实时子结构试验方法的有效性,该方法有效的弥补了缩尺振动台试验对隔震结构整体动力响应的模拟误差,对隔震结构在数值子结构和物理子结构均存在强非线性的情况下,能对结构动力响应进行准确测试。

|
图 10 试验动力响应误差 Fig. 10 Dynamic response errors of experiment |
为更好模拟隔震结构各个部分的非线性,研究其抗震性能,提出一种适于隔震结构的两阶段实时子结构试验方法,通过仿真和试验验证,得到以下结论:
1) 两阶段实时子结构试验将隔震支座单独离线加载,能够保障其力学性能真实性,避免欠质量的影响。
2) 神经网络学习结构动力特性的精度理想,其结构动力特性的学习精度峰值误差在1%以内,相对均方根误差在8%以内,能够有效提高数值子结构建模精度。
3) 神经网络的计算效率为单步计算耗时0.05 ms,满足实时子结构试验对实时数值求解效率的要求。
4) 本文基于两自由度模型,验证了所提出的两阶段实时子结构试验方法的可行性,后续将进一步展开该方法用于复杂隔震结构实际试验的研究。
| [1] |
孔德文, 范峰, 支旭东. 摩擦摆支座在K8型单层球面网壳结构中的隔震研究[J]. 哈尔滨工业大学学报, 2015, 47(12): 9. KONG Dewen, FAN Feng, ZHI Xudong. Isolation research of friction pendulum bearings in K8 single-layer reticulated domes[J]. Journal of Harbin Institute of Technology, 2015, 47(12): 9. DOI:10.11918/j.issn.0367-6234.2015.12.002 |
| [2] |
陈彦江, 郭凯敏, 李勇, 等. 桥梁高阻尼隔震橡胶支座性能试验研究[J]. 振动与冲击, 2015, 34(9): 136. CHEN Yanjiang, GUO Kaimin, LI Yong, et al. Behavior of high damping seismic isolation rubber bearings for bridges[J]. Journal of Vibration and Shock, 2015, 34(9): 136. DOI:10.13465/j.cnki.jvs.2015.09.025 |
| [3] |
焦驰宇, 马银强, 刘陆宇, 等. FPS支座双向加载拟静力试验与数值模拟研究[J]. 工程力学, 2019, 36(增刊1): 86. JIAO Chiyu, MA Yinqiang, LIU Luyu, et al. Study on quasi-static test and numerical simulation of FPS bearings under two-way loading[J]. Engineering Mechanics, 2019, 36(Sup.1): 86. |
| [4] |
李祥秀, 王瑶, 李小军, 等. 速度脉冲地震动作用下巨-子结构隔震体系的振动台试验研究[J]. 应用基础与工程科学学报, 2021, 29(3): 633. LI Xiangxiu, WANG Yao, LI Xiaojun, et al. Experimental studies on seismic performance of mega-sub isolation system subjected to near-fault ground motions with velocity pulse[J]. Journal of Basic Science and Engineering, 2021, 29(3): 633. DOI:10.16058/j.issn.1005-0930.2021.03.009 |
| [5] |
XU Hao, HE Wenfu, LIU Wenguang, et al. Shaking table test and rocking effect investigation of high-rise isolated structure[J]. Structures and Buildings, 2021, 8(174): 637. |
| [6] |
许伟志, 王曙光, 刘伟庆, 等. 大跨隔震结构竖向地震响应的振动台试验研究[J]. 建筑结构学报, 2020, 41(4): 19. XU Weizhi, WANG Shuguang, LIU Weiqing, et al. Shaking table test on vertical seismic responses of isolated large-span structure[J]. Journal of Building Structures, 2020, 41(4): 19. DOI:10.14006/j.jzjgxb.2018.0151 |
| [7] |
NAKASHIMA M, KATO H, TAKAOKA E. Development of real-time pseudo dynamic testing[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(1): 79. DOI:10.1002/eqe.4290210106 |
| [8] |
章红梅, 曾松, 段元锋, 等. 实时混合试验方法研究与应用综述[J]. 结构工程师, 2015, 31(1): 207. ZHANG Hongmei, ZENG Song, DUAN Yuanfeng, et al. Overview of real-time hybrid simulation with substructure[J]. Structural Engineer, 2015, 31(1): 207. DOI:10.15935/j.cnki.jggcs.2015.01.032 |
| [9] |
LIN Shuchao, WANG Jingxuan, GAO Shan, et al. Real-time hybrid test of a LNG storage tank with a variable curvature friction pendulum system[J]. Archives of Civil and Mechanical Engineering, 2021, 21(3): 1. DOI:10.1007/s43452-021-00245-z |
| [10] |
LANESE I, PAVESE A, DACARRO F. Development of software and hardware architecture for real-time dynamic hybrid testing and application to a base isolated structure[J]. Journal of Earthquake Engineering, 2012, 16(Sup.1): 65. DOI:10.1080/13632469.2012.675833 |
| [11] |
王涛, 翟绪恒, 孟丽岩, 等. 基于在线神经网络算法的混合试验方法[J]. 振动与冲击, 2017, 36(14): 1. WANG Tao, ZHAI Xuheng, MENG Liyan, et al. Hybrid testing method based on an online neural network algorithm[J]. Journal of Vibration and Shock, 2017, 36(14): 1. DOI:10.13465/j.cnki.jvs.2017.14.001 |
| [12] |
王燕华, 吕静, 吴京. 基于遗忘因子和LMBP神经网络的混合试验在线模型更新方法[J]. 振动与冲击, 2020, 39(9): 42. WANG Yanhua, LV Jing, WU Jing. On-line model updating method for hybrid testing based on the forgetting factor and LMBP neural network[J]. Journal of Vibration and Shock, 2020, 39(9): 42. DOI:10.13465/j.cnki.jvs.2020.09.006 |
| [13] |
梅竹, 吴斌, 杨格, 等. 钢筋混凝土结构的模型更新混合试验方法[J]. 工程科学与技术, 2018, 50(6): 65. MEI Zhu, WU Bin, YANG Ge, et al. Model updating hybrid simulation of reinforced concrete structures[J]. Advanced Engineering Sciences, 2018, 50(6): 65. DOI:10.15961/j.jsuese.201800616 |
| [14] |
王涛, 吴斌. 基于约束UKF模型更新的混合试验方法[J]. 地震工程与工程振动, 2013, 33(5): 100. WANG Tao, WU Bin. Hybrid testing method based on model updating with constrained unscented Kalman filter[J]. Earthquake Engineering and Engineering Dynamics, 2013, 33(5): 100. DOI:10.13197/j.eeev.2013.05.100.wangt.013 |
| [15] |
吴斌, 王贞, 许国山, 等. 工程结构混合试验技术研究与应用进展[J]. 工程力学, 2022, 39(1): 7. WU Bin, WANG Zhen, XU Guoshan, et al. Research and application progress in hybrid testing of engineering structures[J]. Engineering Mechanics, 2022, 39(1): 7. |
| [16] |
SMITH J S, WU Bo, WILAMOWSKI B M. Neural network training with Levenberg-Marquardt and adaptable weight compression[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(2): 580. DOI:10.1109/TNNLS.2018.2846775 |
| [17] |
张健. 自适应子结构拟动力试验方法[D]. 哈尔滨: 哈尔滨工业大学, 2010 ZHANG Jian. Adaptive substructure pseudo-dynamic testing method[D]. Harbin: Harbin Institute of Technology, 2010 |
| [18] |
王涛, 刘媛, 孟丽岩, 等. 基于改进粒子滤波算法的Bouc-Wen模型参数在线识别方法[J]. 重庆大学学报, 2021, 44(5): 38. WANG Tao, LIU Yuan, MENG Liyan, et al. Online parameters identification method of Bouc-Wen model based on modified particle algorithm[J]. Journal of Chongqing University, 2021, 44(5): 38. |
 2023, Vol. 55
2023, Vol. 55


