2. 建筑安全与节能教育部重点实验室(湖南大学),长沙 410082
2. Key Lab of Building Safety and Energy Conservation (Hunan University), Ministry of Education, Changsha 410082, China
混合试验是拟动力试验的进一步发展[1-2],其将完整结构中强非线性构件进行真实试验加载,其余结构进行数值模拟。混合试验方法是研究结构地震响应的一种重要试验方法,但以往的结构混合试验方法一般只考虑水平地震作用或多维地震加载仅应用于验证性的简单结构案例。研发一种在水平及竖向双向地震作用下可用于多高层RC框架结构的混合试验方法,可以进一步拓展混合试验方法的应用,同时可用以研究在水平及竖向地震作用下RC框架结构的性能。
随着结构抗震领域不断深入研究发现:竖向地震对结构破坏的影响不容忽视。白国良等[3]通过振动台试验研究发现在较高地震烈度下,竖向地震影响对结构破坏起决定性作用。易伟建等[4]通过模拟研究发现,在竖向和水平地震动同时作用下,竖向地震对于框架结构最大的影响是使框架柱轴力剧烈变化,从而影响框架柱的抗弯承载力,使得框架柱的破坏模式较为复杂。为了研究RC框架柱在竖向地震下的破坏机理,国内外学者进行了大量柱子变轴力拟静力试验[5-7],但是拟静力试验不能很好地模拟柱子在地震作用下真实加载路径。混合试验可以克服这个缺点,是可以用来研究水平和竖向地震下RC框架结构真实受力性能的良好试验方法。
近年来,国内外大量学者对混合试验方法进行研究并开发相应的混合试验平台,如OpenFresco[8]、UI-SimCor[9]、NetSLab[10-11]、HyTest[12]、MTS-OpenFresco-MATLAB[13]等。然而这些试验平台大多只考虑水平地震激励,同时由于试验设备和加载条件限制,往往只进行水平地震激励下的混合试验。例如郭玉荣等[14]利用NetSLab采用1个水平作动器对一榀BRB组合框架进行混合试验,王贞等[15]利用HyTest采用4个水平作动器对单层钢框架进行水平双向混合试验,蔡新江等[16]利用MTS-OpenFresco-MATLAB混合试验系统采用1个水平作动器完成一榀两跨三层SRC异形柱中框架的混合试验。哈尔滨工业大学近年建设了3自由度MTS加载系统,王贞等[17]在此设备基础上研究了MTS系统在混合试验中的控制与应用,曾聪等[18]开展了水平地震激励下单层单跨钢框架混合试验,试验中采用3个MTS作动器完成试验子结构柱顶3个自由度的位移加载控制。文献[17-18]的研究成果为多维加载控制的结构混合试验提供设备控制技术支持。
在水平和竖向地震同时作用下结构混合试验研究方面,钟树生[19]利用杆系模型编制水平及竖向地震联合作用的混合试验程序,并进行两层一跨钢筋混凝土框架混合试验。袁志仁[20]提出基于修正OS法的水平及竖向地震混合试验方法,同样进行两层一跨钢筋混凝土框架混合试验。文献[19-20]的试验结果均表明:在水平和竖向地震作用下框架柱中产生的变轴力将使试件位移延性显著降低,并且滞回曲线呈现明显的不对称性和不确定性,柱子会呈现多种破坏形态。总体而言,水平和竖向地震激励下结构混合试验研究还比较有限,存在数值子结构模拟效果差、时程分析计算精度低等问题。
本文首先提出一种在水平和竖向地震共同作用下RC框架结构混合试验方法,在此方法基础上开发相应的混合试验程序。混合试验程序采用有限元分析软件OpenSees进行数值子结构的非线性模拟,利用Matlab编写整体结构运动方程求解模块,并结合加载设备HNU-MUST[21]在NetSLab基础上开发混合试验控制程序。为了验证本文方法和程序的实用性与稳定性,设计并制作一根足尺RC框架柱作为试验子结构,并以一榀七层三跨RC框架作为整体结构进行混合试验。同时通过试验研究在水平和竖向地震下共同作用下RC框架柱的受力性能和破坏特征。
1 本文混合试验方法基本理论 1.1 混合试验结构振动模型对于二维平面框架结构,每个节点有3个自由度,也就意味着理想混合试验必须保证试验子结构和数值子结构之间3个自由度的边界条件协调。然而试验子结构边界条件由试验设备控制,大多数实验室因设备条件限制无法同时控制柱顶的3个自由度。因此实际试验中常常忽略柱顶转动自由度,只控制柱顶水平和竖向位移。结合试验设备HNU-MUST加载能力,本文所采用的混合试验方法只控制柱顶的水平和竖向自由度而忽略柱顶转动自由度,在试验过程中保证数值子结构和试验子结构边界的水平和竖向位移一致。
忽略柱顶转动自由度会造成数值子结构和试验子结构之间的转动边界条件不一致。为减少因转动边界条件不一致带来的误差,在混合试验中设计选取梁柱线刚度比较大的框架作为试验整体结构,并且约束试验子结构柱顶转动。因此在试验加载过程中,数值子结构梁柱节点转角较小,且试验子结构柱顶转角也较小,实现了子结构转动边界条件尽可能相近。
另一方面,忽略节点转动自由度会影响混合试验中时程分析的计算精度。但在实际工程计算中,为了降低结构时程分析计算难度,常常会忽略节点转动自由度。当框架中梁柱线刚度比大于3时,节点近似不发生转动,即节点转角近似为零[22]。在此基础上,忽略节点转动自由度所造成的时程分析计算误差就将大幅度减少。
不考虑节点转动自由度时,结构动力自由度将会被缩减。在水平和竖向地震同时作用下,结构水平及竖向运动方程分别为:
| $[\boldsymbol{M}]\{\ddot{\boldsymbol{H}}\}+\left[\boldsymbol{C}_{\mathrm{H}}\right]\{\dot{\boldsymbol{H}}\}+\left(\left[\boldsymbol{K}_{\mathrm{H}}\right]+\left[\boldsymbol{K}_{\mathrm{G}}\right]\right)\{\boldsymbol{H}\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{H}_{\mathrm{g}}$ | (1) |
| $[\boldsymbol{M}]\{\ddot{\boldsymbol{V}}\}+\left[\boldsymbol{C}_{\mathrm{v}}\right]\{\dot{\boldsymbol{V}}\}+\left[\boldsymbol{K}_{\mathrm{v}}\right]\{\boldsymbol{V}\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{V}_{\mathrm{g}}$ | (2) |
式中:[M]为质量矩阵,[CH]和[CV]分别为水平阻尼矩阵和竖向阻尼矩阵,[KH]和[KV]分别为水平刚度矩阵和竖向刚度矩阵,[KG]为几何刚度矩阵,{H}和{V}分别为水平位移列向量和竖向位移列向量,{I}为单位列向量。
可以从式(1)、(2)看出,竖向振动是独立的,而水平振动和竖向振动是耦联的。当不考虑结构几何非线性时[KG]=0,水平振动和竖向振动不耦联[23],式(1)可改写作式(3)。因此水平和竖向振动可以分别独立计算。
| $[\boldsymbol{M}]\{\ddot{\boldsymbol{H}}\}+\left[\boldsymbol{C}_{\mathrm{H}}\right]\{\dot{\boldsymbol{H}}\}+\left[\boldsymbol{K}_{\mathrm{H}}\right]\{\boldsymbol{H}\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{H}_{\mathrm{g}}$ | (3) |
由于水平和竖向振动可以分别独立计算,水平和竖向振动可以根据不同的振动特征采用不同的结构振动模型。在分析结构水平振动时,实际工程和研究中常常假定楼板平面内的刚度为无穷大,在地震作用下同一层不同节点的水平位移是相等的。由此可以将同一层的所有质量集中到一点,构成串联质点系模型,即常用的层剪模型。但由于楼板平面外刚度远小于平面内刚度同时梁刚度也相对较小,因此同一层不同节点的竖向位移不能近似相等。在分析计算结构竖向振动时,不能采用类似于串联质点系模型的简化,需要同时分析各个梁柱节点竖向位移并采用串并联多质点系模型[24]。
综上所述,在计算水平和竖向地震作用下框架结构振动响应时,将水平和竖向振动分别独立计算。并且水平振动模型采用串联质点系模型,竖向振动模型采用串并联多质点系模型,见图 1。

|
图 1 水平和竖向振动模型 Fig. 1 Horizontal and vertical vibration models |
式(1)、(3)为理想弹性框架在地震作用下运动方程,用于混合试验的运动方程需经过一定修正。实际RC框架结构在地震作用下会进入非线性状态,此时结构力位移曲线不再服从线性关系,运动方程中必须采用结构真实恢复力。同时RC框架结构在竖向会受到一定静力荷载,这部分静力荷载包括结构的恒载和活载,并且在运动方程中需要与竖向地震作用同时体现。在水平和竖向地震同时作用下RC框架混合试验的水平运动方程和竖向运动方程为:
| $[\boldsymbol{M}]\{\ddot{\boldsymbol{H}}\}+\left[\boldsymbol{C}_{\mathrm{H}}\right]\{\dot{\boldsymbol{H}}\}+\left\{\boldsymbol{f}_{\mathrm{H}}\right\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{H}_{\mathrm{g}}$ | (4) |
| $[\boldsymbol{M}]\{\ddot{\boldsymbol{V}}\}+\left[\boldsymbol{C}_{\mathrm{V}}\right]\{\dot{\boldsymbol{V}}\}+\left\{\boldsymbol{f}_{\mathrm{V}}\right\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{V}_{\mathrm{g}}+\left\{\boldsymbol{F}_{\mathrm{G}}\right\}$ | (5) |
式中:{fH}为水平恢复力列向量,{fV}为竖向恢复力列向量,{FG}为竖向静载列向量。
建立运动方程时,需要获取结构阻尼矩阵,本文方法采用瑞利阻尼。瑞利阻尼的构造见式(6)。对于竖向和水平的阻尼矩阵,分别采用对应的质量和刚度矩阵。
| $[\boldsymbol{C}]=\alpha_1[\boldsymbol{M}]+\alpha_2[\boldsymbol{K}]$ | (6) |
时程分析是混合试验中的重要核心,本文选择PC-Newmark法作为进行时程分析的数值积分方法。PC-Newmark法又被称作预测-校正Newmark法,其由隐式Newmark-β法与显式Newmark法组合而成。PC-Newmark法的预测、校正过程适用于混合试验,同时具有隐式算法的稳定性和计算精度。
PC-Newmark法分为预测和校正两部分,在一个积分步中先预测结构位移状态,再将预测状态作用于子结构以返回恢复力,最后将恢复力带入方程以校正所预测的位移状态。预测部分公式见式(7)、(8),校正部分公式见式(9)~(11)。
| $\left\{\widetilde{\boldsymbol{u}}_i\right\}=\left\{\boldsymbol{u}_{i-1}\right\}+\Delta t\left\{\dot{\boldsymbol{u}}_{i-1}\right\}+\left(\frac{1}{2}-\beta\right) \Delta t^2\left\{\ddot{\boldsymbol{u}}_{i-1}\right\}$ | (7) |
| $\left\{\tilde{\dot{\boldsymbol{u}}}_i\right\}=\left\{\dot{\boldsymbol{u}}_{i-1}\right\}+(1-\gamma) \Delta t\left\{\ddot{\boldsymbol{u}}_{i-1}\right\}$ | (8) |
| $[\boldsymbol{M}]\left\{\ddot{\boldsymbol{u}}_i\right\}+[\boldsymbol{C}]\left\{\tilde{\dot{\boldsymbol{u}}}_i\right\}+\left\{\tilde{\boldsymbol{f}}_i\right\}=-[\boldsymbol{M}]\{\boldsymbol{I}\} \ddot{u}_{\mathrm{g}, i}$ | (9) |
| $\left\{\boldsymbol{u}_i\right\}=\left\{\tilde{\boldsymbol{u}}_i\right\}+\beta \Delta t^2\left\{\ddot{\boldsymbol{u}}_i\right\}$ | (10) |
| $\left\{\dot{\boldsymbol{u}}_i\right\}=\left\{\tilde{\dot{\boldsymbol{u}}}_i\right\}+\gamma \Delta t\left\{\ddot{\boldsymbol{u}}_i\right\}$ | (11) |
式中:
混合试验主要分为3部分:试验子结构、数值子结构、结构运动方程求解模块。框架结构混合试验常常将受力复杂的框架柱作为试验子结构,而其余框架结构部分作为数值子结构。
在只受水平地震作用时,框架结构受水平倾覆力矩作用而导致框架柱轴力发生一定变化。相比于受竖向地震的结构,该轴力变化幅度不大,且呈现边柱轴力变化幅度大于中柱的特点。对于一般的水平地震下混合试验,其常常不考虑柱子轴力变化而假定轴力是恒定的。但在水平和竖向地震同时作用下,竖向地震作用会导致框架柱轴力发生持续大幅度变化。柱子轴力大幅度变化会显著影响柱子的抗弯承载力、刚度和滞回性能等受力性能特征。因此在进行水平和竖向地震同时作用下混合试验时,选取框架柱作为试验子结构进行试验加载,并且要求试验加载设备具有变轴力加载控制能力。
在混合试验每一个数值积分步中,运动方程求解模块计算出水平和竖向预测位移,将预测位移发送给数值子结构和试验子结构并返回结构恢复力。运动方程求解模块利用结构恢复力校正预测位移,然后进行下一个积分步。具体的混合试验示意见图 2。

|
图 2 水平及竖向地震作用下RC框架混合试验示意 Fig. 2 Schematic of hybrid test of RC frame under combined excitation of horizontal and vertical earthquakes |
本文所提混合试验方法具体流程如下:
步骤1构建运动方程求解模块,编制程序构建结构运动方程并求解运动方程;
步骤2构建数值子结构模块,利用有限元软件模拟数值子结构;
步骤3试验子结构准备,在实验室中安装并调试实体试验子结构柱;
步骤4正式试验开始后,运动方程求解模块根据已知的第i-1步位移状态利用式(7)、(8)计算第i步预测位移状态,并将计算出的水平和竖向预测位移发送给数值子结构和试验子结构;
步骤5数值子结构模块利用第i步的水平和竖向预测位移对各节点进行位移加载,而后获得各个构件的恢复力发送给运动方程求解模块;
步骤6试验子结构利用第i步的水平和竖向预测位移进行真实试验加载,而后获得柱子的剪力和轴力发送给运动方程求解模块;
步骤7运动方程求解模块整合数值子结构和试验子结构的恢复力,而后形成第i步的水平恢复力列向量和竖向恢复力列向量,然后利用式(9)~(11)校正第i步位移状态;
步骤8令i=i+1,重复步骤4~7,直至地震波结束。
2.2 水平和竖向地震下混合试验程序开发根据本文所提出的混合试验方法开发相应混合试验程序,该程序主要分为3个子程序:1)运动方程求解程序,利用Matlab编制相应程序建立并求解运动方程;2)数值子结构模拟程序,利用OpenSees有限元程序实现试验过程中数值子结构加载模拟;3)混合试验控制程序,利用Visual Basic编程语言编制相应程序以实现对试验设备HNU-MUST的数据通讯和控制。
Matlab作为商业数学软件拥有强大的矩阵计算和数值分析功能,利用Matlab编程语言编制程序可以精确且高效地完成求解运动方程时复杂矩阵运算和数值分析。
数值子结构模块需要对框架结构构件的非线性滞回性能进行更接近真实的数值模拟。过去混合试验常常采用经验滞回曲线模型来获取构件恢复力,当考虑轴力变化对柱子受力性能产生影响时,则滞回曲线模型参数也需要进行一定修正。采用这种方法不能更好地模拟轴力变化下的柱子受力性能,并会导致程序开发较为困难。为了更为真实地模拟数值子结构在水平和竖向地震下的受力性能以获取更为精确的恢复力,利用OpenSees纤维模型构建数值子结构,纤维模型能对构件复杂受力状态进行较好的模拟。
在NetSLab试验平台基础上开发出混合试验控制程序,该程序的操作界面见图 3。混合试验控制程序实现以下多种功能:1)试验的整体控制功能,包括试验的启动、暂停、终止等;2)试验意外终止后的数据保存和试验续航功能;3)试验加载设备的通讯、控制、调试等功能;4)与运动方程求解模块的数据通讯功能;5)试验构件力、位移数据的保存和输出功能;6)试验进行中试验构件力、位移时程的显示和水平、竖向滞回曲线的显示。

|
图 3 混合试验控制程序的操作界面 Fig. 3 Operation interface of hybrid test control program |
混合试验程序的3个子程序通过TCP/IP协议来实现程序间通讯和数据传输,运动方程求解程序作为通讯中的服务器,其余两个程序作为客户端。混合试验控制程序通过串口通信来实现与试验加载设备的通讯和数据传输。
3 RC框架混合试验概况设计一榀七层三跨RC框架作为整体结构,并取框架底层中柱作为试验子结构进行混合试验。通过试验验证本文方法的可行性和有效性,同时研究框架结构柱在水平和竖向地震下的受力性能和破坏特征。
3.1 整体结构和试验构件基本情况所设计的七层三跨RC框架见图 4,框架底层层高为4.3 m,其余层层高为3.0 m,跨度为6.0 m。该框架各层质量均设为161.18 t。柱截面和梁截面分别取为600 mm×600 mm和300 mm×700 mm。框架柱中纵筋为12 25,梁中上下部纵筋各为3 20。取底层中柱作为试验子结构,其余部分为数值子结构。

|
图 4 整体RC框架结构(mm) Fig. 4 RC frame structure (mm) |
试验子结构即为试验构件,试件截面尺寸和配筋均与整体框架柱相同。试件柱身净高3 600 mm,试件底座和顶座完全相同且各高850 mm,试件总高度为5 300 mm。柱身纵筋为12 25,配筋率1.64%,纵筋在底座和顶座中的直锚长度满足规范要求。柱身箍筋为10@100/150, 体积配箍率1.13%,在距柱底和柱顶各1 050 mm高度范围内加密。试件尺寸和配筋见图 5。

|
图 5 试件配筋(mm) Fig. 5 Specimen reinforcement (mm) |
试件底座和顶座分别采用8根高强螺杆与实验室地面和HNU-MUST加载板相连,实现试件与设备、地面的可靠连接。因此在试验过程中,柱底完全嵌固于地面,柱顶随着HNU-MUST加载板的移动实现水平和竖向位移的加载,但同时约束了柱顶转动。
试件采用C35商品混凝土一次浇筑而成,在试件浇筑养护时同条件养护10个边长150 mm立方体试块。在正式试验前测试该批混凝土试块的力学性能,见表 1。试件纵筋和箍筋均采用HRB400级钢筋,同批次测试其钢筋力学性能见表 2。
| 表 1 混凝土实测强度 Tab. 1 Measured strength of concrete |
| 表 2 钢筋实测力学性能 Tab. 2 Measured value of mechanical properties of steel |
数值子结构利用OpenSees进行模拟,梁柱模拟采用非线性梁柱单元。梁柱截面采用纤维截面,混凝土纤维本构模型为Concrete01,钢筋纤维本构模型为Steel01。混凝土截面被划分为核心区和保护层,核心区混凝土采用Mander约束混凝土模型[25]计算其峰值强度、峰值应变、残余应变等本构参数。钢筋和混凝土保护层本构模型参数采用试件实测参数,而Mander约束混凝土基于实测参数进行计算,试件材料实测参数参考表 1、2。
3.2 混合试验加载设备和加载方案本次试验加载设备为大型地震载荷模拟加载装置HNU-MUST,水平和竖向加载均采用位移控制。HNU-MUST最大特点是水平力和竖向力可以相互独立,测得的水平力和竖向力即为施加至构件的实际荷载无需修正,其改善传统加载装置的不足。根据设计,HNU-MUST具备水平和竖向混合试验加载功能。其通过与外部混合试验程序连接,可以将作用力和作用位移实时反馈,并可以接收位移和力加载指令对构件进行实时加载。HNU-MUST具有较大荷载加载能力,水平作动器加载行程为±400 mm,最大水平加载力为4 000 kN;竖向作动器加载行程为0~500 mm,最大竖向加载力为20 000 kN。构件水平加载方向以N指向S为加载正向,试件安装和加载示意见图 6。

|
图 6 试件安装和加载示意 Fig. 6 Loading condition and installation of specimen |
在本次试验中,整体框架结构梁上分布静载为39 kN/m,边节点集中静载为198.75 kN,中节点集中静载为240 kN。这部分静载参考实际建筑结构所受到的恒载和活载,为结构构件所受到的初始荷载。设框架边节点质量为32.22 t,中节点质量为48.37 t。
试验地震波选取El-Centro波水平和竖直分量,地震波持时为15 s。由于本次试验重要目的之一是检验本文混合试验方法和混合试验程序,因此最开始设定两条峰值较小的地震波。在试验开始后,时刻观察试验中数据通讯、位移加载、荷载反馈等是否稳定,是否存在未知问题。如果发现试验方法和试验程序出现错误,试验人员会立即终止试验。同时由于输入地震波较小,加载的位移峰值也较小,构件仍然处于弹性状态,错误的试验不会对构件造成破坏。待试验方法和程序改进后,仍可继续进行试验。在验证试验程序的可靠性后,输入较大峰值地震波以进行破坏性试验,研究RC框架柱在水平和竖向地震作用下的破坏特征和力学性能。试验中根据试件破坏情况,水平地震波峰值从70 cm/s2逐步加至200、800、1 100、1 500 cm/s2,竖向地震波峰值取为水平向的2/3。当输入水平地震波峰值为1 500 cm/s2时试件严重破坏,因此结束试验。
4 RC框架混合试验结果及分析 4.1 试验现象和试件破坏过程试验分别输入峰值70 cm/s2和200 cm/s2的El-Centro波以初步验证试验方法和程序的稳定性。在这两条地震波加载过程中,试验设备和混合试验程序的加载、反馈等过程稳定,数据传输未出现异常,位移和荷载时程曲线也满足预期要求。峰值为70 cm/s2的工况下,水平位移峰值仅为4.29 mm,轴力变化幅度较小,构件仍处于线弹性状态。加载结束后,试件未出现明显裂缝。峰值为200 cm/s2的工况下,水平位移峰值为12.26 mm,轴力变化幅度不大,力-位移曲线仍接近直线,构件仍处于线弹性状态。70 cm/s2和200 cm/s2工况加载结束后,试件底部出现5条细小水平裂缝。
在验证试验程序稳定性后,将El-Centro波峰值提升至800 cm/s2。800 cm/s2工况加载结束后,柱顶部和底部均出现大量水平裂缝和少量竖向裂缝,柱顶部新出现约14条水平裂缝和4条竖向裂缝,柱底部新出现约18条水平裂缝和7条竖向裂缝,同时在前面工况下出现的水平裂缝进一步发展延伸。柱底部靠近根部20 cm范围内出现混凝土剥落现象,竖向裂缝也集中出现在角部。总体而言,柱底部破坏情况较顶部严重。其中,加载方向的N和S面集中出现水平通缝,同时N和S面的角根部有部分混凝土剥落;W和E面的水平裂缝从N和S面延伸而来,只有小部分贯通整个截面,并且W和E面未出现混凝土剥落现象。
1 100 cm/s2工况加载结束后,试件表面破坏程度更加严重,柱顶部和底部水平裂缝大量贯通,顶部新出现8条水平裂缝,底部新出现7条水平裂缝。其中,N和S面水平裂缝大量贯通,竖向裂缝也进一步延伸发展。试件顶部和底部混凝土也进一步剥落,N和S面剥落较为严重,其中角部混凝土剥落最为严重。
最后1 500 cm/s2工况加载结束后,试件表面破坏程度更为严重。试件底部表面混凝土大量剥落,各个面近根部约20 cm范围内保护层混凝土基本破碎与试件失去连接。由于正负向加载的不对称性,正向加载水平位移较大而导致NW角部和NE角部破坏较为严重,其中核心区混凝土部分破碎,钢筋明显出现屈服弯曲现象。试件顶部破坏程度较底部轻,表面同样出现大量混凝土剥落现象,4个角部混凝土基本剥落,N面保护层混凝土基本与构件脱开剥落。试件最终破坏形态见图 7。

|
图 7 试件最终破坏照片 Fig. 7 Final damaged photos of specimen |
从试件加载破坏过程和最终破坏形态可以看出:1)加载过程中出现大量水平裂缝逐步发展破坏,呈明显压弯破坏现象;2)由于大幅度高水平轴力变化,在加载中由于混凝土压碎而出现较多竖向裂缝;3)由于地震波作用的不对称性,正向位移较大而导致N面损伤破坏较S面严重,破坏形态出现明显的非对称性;4)由于试验加载过程中试件上底座与设备固定螺栓会出现一定松动,其导致试件顶部不是完全转动约束,因此试件底部破坏比顶部严重。
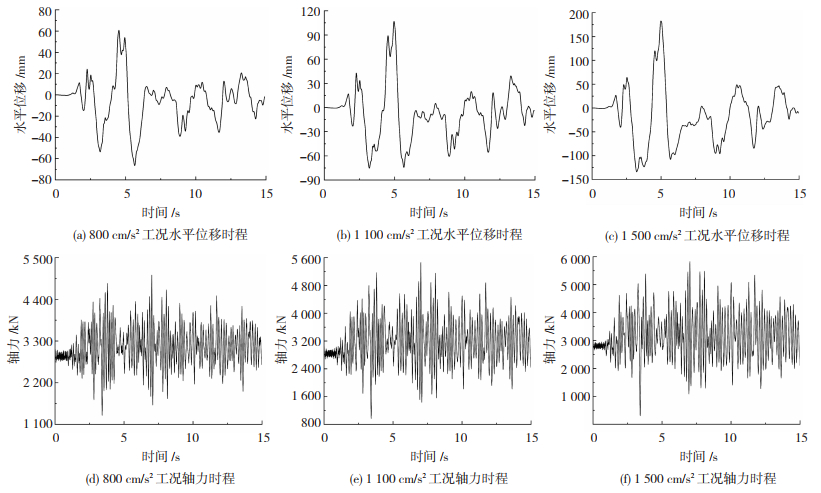
4.2 试件时程曲线和滞回曲线峰值为70 cm/s2和200 cm/s2的地震波加载时位移峰值较小,轴力变化不大,构件仍处于线弹性状态,力-位移曲线接近直线。目的在于验证混合试验方法和程序的稳定性。800、1 100、1 500 cm/s2这3种工况的柱顶水平位移时程曲线和轴力时程曲线见图 8,从图 8分析得出:1)随着地震波峰值增大,水平位移峰值和轴力峰值均增大,各工况下轴力、轴压比最值见表 3;2)水平位移加载存在不对称性,正负向水平位移存在较大差异;3)轴力变化幅度较大,加载过程中轴压比最高可达0.462,最低轴压比仅为0.024;4)竖向时程的频率远高于水平时程。原因有两点:El-Centro波符合一般地震波特点,竖向波频率高于水平波;结构构件竖向刚度远大于水平刚度,其导致竖向地震响应的频率远高于水平地震响应的频率。
| 表 3 各工况下的轴力和轴压比最值 Tab. 3 Extreme value of axial force and axial compressive ratio under different working conditions |
|
图 8 800、1 100和1 500 cm/s2工况下的水平位移和轴力时程曲线 Fig. 8 Time-history curves of horizontal displacement and axial force under working conditions 800, 1 100, and 1 500 cm/s2 |
峰值为800、1 100、1 500 cm/s2这3种工况下水平滞回曲线见图 9,从图 9分析得出:

|
图 9 800、1 100和1 500 cm/s2工况下的水平滞回曲线 Fig. 9 Horizontal hysteresis curves under working conditions 800, 1 100, and 1 500 cm/s2 |
1) 滞回曲线呈现明显不对称性,正负向滞回曲线形态存在明显差异。一方面由于正负向水平位移加载存在不对称性,在1 100 cm/s2和1 500 cm/s2工况下正向水平位移峰值大于负向水平位移峰值,同时正负向加载路径存在较大差别。另一方面由于水平、竖向地震作用,轴力出现高水平、大幅度、高频率变化,其会影响试件整体受力性能,导致构件受力更为复杂,从而使水平滞回曲线的不对称性和不规则性加剧。滞回曲线的不对称性会容易导致RC框架柱在水平、竖向地震中因某向水平位移过大而出现倾覆破坏且未发挥整体耗能能力。
2) 滞回曲线出现较多不光滑和突变现象。这是由于在竖向地震作用下轴力出现高水平、大幅度、高频率变化。剧烈而快速的轴力变化影响试件的承载能力、刚度等力学性能,使得滞回曲线出现不连续变化现象。
3) 滞回曲线不饱满且呈现一定“捏缩”效应,并且负向“捏缩”效应较正向严重。这是由于在水平和竖向地震作用下,高频且复杂的轴力变化与水平位移加载耦合削弱了试件的塑性变形能力和耗能能力。在这3种工况下负向位移时常常对应着较高的轴力水平,1 100 cm/s2和1 500 cm/s2工况下最大轴力时水平位移为负。在较高的轴力作用下,RC框架柱的延性和滞回耗能力会显著下降。这些共同导致负向“捏缩”效应较为严重。
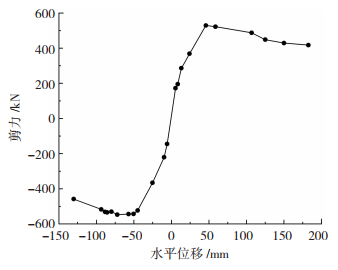
4.3 骨架曲线和延性在试件水平滞回曲线上,提取各个水平位移响应脉冲中的荷载峰值点,将各个荷载峰值点连接而成形成骨架曲线,见图 10。骨架曲线直观反映整个试验过程中RC框架柱的强度变化和延性发展。
|
图 10 所有工况的骨架曲线 Fig. 10 Skeleton curve of all working conditions |
根据骨架曲线计算试件延性系数,延性系数μ计算表达式见式(12),计算构件延性系数见表 4。
| $\mu=\frac{\varDelta_{\mathrm{u}}}{\varDelta_{\mathrm{y}}}$ | (12) |
| 表 4 试件延性系数 Tab. 4 Ductility coefficient of specimen |
式中:Δu为构件极限位移,为构件骨架曲线中水平荷载下降至峰值荷载85%时对应的位移;Δy为构件屈服位移[26]。
从图 10和表 4可看出,骨架曲线和延性呈现不对称性,正向延性较负向高。说明在水平和竖向地震作用下,RC框架柱受力性能会变得更为复杂,某一方向的延性可能会明显下降而导致构件提前破坏。
4.4 数值子结构时程曲线数值子结构在800 cm/s2和1 500 cm/s2这两种工况下基底剪力时程曲线见图 11,数值子结构在800 cm/s2和1 500 cm/s2工况下顶点位移时程曲线见图 12。从图 11、12可看出,数值子结构时程曲线变化趋势与试验子结构相似,具有类似的变化特征。

|
图 11 800 cm/s2和1 500 cm/s2工况下的基底剪力时程曲线 Fig. 11 Time-history curves of base shear force under working conditions 800 cm/s2 and 1 500 cm/s2 |

|
图 12 800 cm/s2和1 500 cm/s2工况下的顶点位移时程曲线 Fig. 12 Time-history curves of top displacement under working conditions 800 cm/s2 and 1 500 cm/s2 |
提出一种水平和竖向双向地震激励下RC框架混合试验方法,并结合大型地震加载设备HNU-MUST开发相应的混合试验程序,最后以足尺框架柱为试验子结构进行框架结构混合试验,得到以下主要结论
1) 根据框架结构振动特征,分别采用串联质点系模型和串并联多质点系模型来模拟结构水平和竖向振动,合理简化了混合试验结构运动方程。
2) 采用OpenSees模拟数值子结构非线性特性,用Matlab编写整体结构水平和竖向运动方程求解模块,采用VB语言开发整体试验控制程序,协调各个模块和试验设备之间的通讯控制。开发的混合试验程序具有较强的非线性模拟功能,良好的用户操作界面和稳定的数据通讯。
3) 设计并制作一根足尺RC框架柱为试验子结构,进行一榀七层三跨RC框架的混合试验,验证了本文混合试验程序的控制效果和稳定性。
4) 试验结果表明,在水平及竖向地震激励作用下,柱子轴力呈现高水平、大幅度、高频率的变化特征。复杂轴力变化与水平加载耦合导致框架柱受力状态更加复杂。
5) 试验柱滞回曲线和骨架曲线呈现显著的非对称性以及出现一定“捏缩”现象。说明在水平和竖向地震作用下,框架结构柱的塑性变形和耗能能力有所下降,并可能导致柱构件出现非对称破坏现象。
| [1] |
陈再现, 陈芍桥, 吴斌, 等. 缩尺模型子结构混合模拟试验方法数值模拟研究[J]. 哈尔滨工业大学学报, 2016, 48(6): 51. CHEN Zaixian, CHEN Shaoqiao, WU Bin, et al. Numerical simulation of substructure hybrid simulation test method for the scale model[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 51. |
| [2] |
吴斌, 王贞, 许国山, 等. 工程结构混合试验技术研究与应用进展[J]. 工程力学, 2022, 39(1): 2. WU Bin, WANG Zhen, XU Guoshan, et al. Research and application progress in hybrid testing of engineering structures[J]. Engineering Mechanics, 2022, 39(1): 2. |
| [3] |
白国良, 郝彬. 竖向地震作用下钢-钢筋混凝土塔式组合结构抗震性能研究[J]. 土木工程学报, 2019, 52(3): 18. BAI Guoliang, HAO Bin. Seismic performance study on steel-reinforced concrete composite tower under vertical earthquake excitation[J]. China Civil Engineering Journal, 2019, 52(3): 18. |
| [4] |
易伟建, 王维一. 近场区竖向地震动对钢筋混凝土框架结构抗震性能的影响[J]. 土木工程学报, 2012, 45(10): 87. YI Weijian, WANG Weiyi. Effect of vertical ground motion on seismic behavior of RC frame in near-fault region[J]. China Civil Engineering Journal, 2012, 45(10): 87. |
| [5] |
陈嵘, 雷俊卿. 变轴力钢筋混凝土墩柱抗震性能试验研究[J]. 振动与冲击, 2017, 36(18): 131. CHEN Rong, LEI Junqing. Experimental investigations on the seismic behaviors of RC bridge piers under variable axial loads[J]. Journal of Vibration and Shock, 2017, 36(18): 131. |
| [6] |
ESMAEILY A, XIAO Yan. Behavior of reinforced concrete columns under variable axial loads[J]. ACI Structural Journal, 2004, 102(9/10): 124. |
| [7] |
XU Guoshan, WU Bin, JIA Dedeng, et al. Quasi-static tests of RC columns under variable axial forces and rotations[J]. Engineering Structures, 2018, 162: 60. |
| [8] |
TAKAHASHI Y, FENVES G L. Software framework for distributed experimental-computational simulation of structural systems[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(3): 267. |
| [9] |
KWON O S, ELNASHAI A, SPENCER B F. A framework for distributed analytical and hybrid simulations[J]. Structural Engineering and Mechanics, 2008, 30(3): 331. |
| [10] |
肖岩, 胡庆, 郭玉荣, 等. 结构拟动力远程协同试验网络平台的开发研究[J]. 建筑结构学报, 2005, 26(3): 122. XIAO Yan, HU Qing, GUO Yurong, et al. A network platform for remote pseudo-dynamic testing[J]. Journal of Building Structures, 2005, 26(3): 122. |
| [11] |
黄民元, 郭玉荣. 子结构拟动力试验平台NetSLabOSR开发与试验应用[J]. 哈尔滨工业大学学报, 2016, 48(9): 89. HUANG Minyuan, GUO Yurong. Development and experimental application of substructure pseudo dynamic test platform NetSLabOSR[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 89. |
| [12] |
杨格, 王贞, 吴斌, 等. 建筑结构混合试验平台HyTest开发研究[J]. 建筑结构学报, 2015, 36(11): 149. YANG Ge, WANG Zhen, WU Bin, et al. Development of HyTest for structural hybrid simulation[J]. Journal of Building Structures, 2015, 36(11): 149. |
| [13] |
蔡新江, 田石柱. MTS-OpenFresco-MATLAB混合试验系统构建及验证试验[J]. 地震工程与工程振动, 2014, 34(1): 117. CAI Xinjiang, TIAN Shizhu. MTS-OpenFresco-MATLAB hybrid simulation system construction and verification test[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(1): 117. |
| [14] |
郭玉荣, 黄民元. 防屈曲耗能支撑钢管混凝土柱-钢梁组合框架子结构拟动力试验研究[J]. 建筑结构学报, 2014, 35(11): 62. GUO Yurong, HUANG Minyuan. Substructure pseudo-dynamic tests of a concrete filled steel tubular column-steel beam composite frame with buckling restrained braces[J]. Journal of Building Structures, 2014, 35(11): 62. |
| [15] |
王贞, 朱思宇, 许国山, 等. 双向混合试验方法及验证[J]. 振动与冲击, 2019, 38(9): 1. WANG Zhen, ZHU Siyu, XU Guoshan, et al. Bi-directional hybrid test method and its verification[J]. Journal of Vibration and Shock, 2019, 38(9): 1. |
| [16] |
蔡新江, 巩牧华, 贾红星, 等. 实腹式型钢混凝土十字形截面柱抗震性能拟静力及混合试验研究[J]. 建筑结构学报, 2016, 37(5): 146. CAI Xinjiang, GONG Muhua, JIA Hongxing, et al. Seismic quasi-static test and hybrid test on +-shaped section solid-web steel reinforced concrete columns[J]. Journal of Building Structures, 2016, 37(5): 146. |
| [17] |
王贞, 王照然, 杨婧, 等. MTS控制系统的二次开发及其在混合试验中的应用[J]. 地震工程与工程振动, 2015, 35(2): 22. WANG Zhen, WANG Zhaoran, YANG Jing, et al. Secondary development of MTS control system and its application to hybrid tests[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(2): 22. |
| [18] |
曾聪, 吴斌, 许国山, 等. 结构多轴抗震试验加载系统开发及控制策略研究[J]. 振动与冲击, 2014, 33(2): 2. ZENG Cong, WU Bin, XU Guoshan, et al. Multi-axial dynamic structural testing system and its control strategies[J]. Journal of Vibration and Shock, 2014, 33(2): 2. |
| [19] |
钟树生. 水平及竖向地震作用下钢筋混凝土框架柱抗震性能的试验研究[D]. 重庆: 重庆建筑大学, 1999 ZHONG Shusheng. Experimental research on the seismic behaviors of RC frame columns under combined actions of horizontal and vertical earthquake excitations[D]. Chongqing: Chongqing University of Architecture, 1999 |
| [20] |
袁志仁. 采用拟动力子结构实验方法研究钢筋混凝土框架柱在水平和竖向地震作用下的抗震性能[D]. 重庆: 重庆大学, 2001 YUAN Zhiren. Experiments on seismic behavior of RC framed columns under horizontal and vertical earthquake excitations using pseudodynamic method with substructuring techniques[D]. Chongqing: Chongqing University, 2001 |
| [21] |
肖岩, 孙意斌, 徐金俊, 等. 大型结构构件地震作用模拟装置MUST的研发及加载控制验证[J]. 建筑结构学报, 2018, 39(6): 149. XIAO Yan, SUN Yibin, XU Jinjun, et al. Development and validation of earthquake simulation testing equipment MUST for large-scale structural components[J]. Journal of Building Structures, 2018, 39(6): 149. |
| [22] |
包世华, 方鄂华. 高层建筑结构设计[M]. 北京: 清华大学出版社, 1985: 114. BAO Shihua, FANG Ehua. Structure design of high-rise buildings[M]. Beijing: Tsinghua University Press, 1985: 114. |
| [23] |
刘季, 何立民. 烟囱在水平与竖向地震动联合作用下的反应[J]. 地震工程与工程振动, 1983, 3(2): 90. LIU Ji, HE Limin. Analysis of seismic response of chimneys to combined horizontal and vertical ground motion[J]. Earthquake Engineering and Engineering Dynamics, 1983, 3(2): 90. |
| [24] |
赵西安. 高层建筑结构在竖向地震作用下的时程分析[J]. 建筑结构学报, 1994, 15(3): 6. ZHAO Xi'an. Direct dynamic analysis of tall building structures subjected to vertical earthquake action[J]. Journal of Building Structures, 1994, 15(3): 6. |
| [25] |
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Division, 1988, 114(8): 1804. |
| [26] |
PARK R, PAULAY T. Reinforced concrete structures[M]. Hoboken: John Wiley & Sons, 1975: 97.
|
 2023, Vol. 55
2023, Vol. 55


