为了满足日益增长的建筑美学和遮阳等功能需求,建筑表面设置的局部装饰构件已越来越常见。建筑表面突出的肋条、阳台、百叶板等局部构件增加了表面粗糙度,对建筑表面的风压会产生一定影响。
已有研究探讨了建筑物外附构件对局部风压的影响。Stathopoulos等[1]研究发现,迎风面上部、侧面和背风面下部的局部风压随着粗糙度的增大而减小,而其他区域的影响较小;Chand等[2]发现阳台会显著改变建筑物迎风面上的风压分布,但不会引起背风面上的明显变化;Maruta等[3]研究了不同阳台宽度对局部风压的影响,他们发现由于表面粗糙度的增加抑制了涡脱,导致分离气泡引起的脉动风压有所降低;Montazeri等[4]通过CFD模拟发现阳台可能导致建筑物风压分布发生非常强烈的变化,因为它们会在立面上引入多个流动分离和再循环区域;沈国辉等[5]研究了外部开孔装饰构件对扭曲型高层建筑风压分布的影响,研究发现装饰构件可明显降低建筑表面两侧的负压峰值;Hu等[6]发现带开口双层幕墙的侧面开口抑制了侧面的分离泡,因此可以有效降低侧面和背风面的压力;Yuan等[7]使用水平薄分流板模拟覆面构件,发现覆面构件可以降低侧面角部区域的局部负压峰值,与参考模型相比风压标准差的最大折减效率达60%;Liu等[8]用高频粒子测速技术对模型周围的流场进行了研究,发现竖向肋条可以显著地减弱分离剪切层和近尾流区的湍流强度,降低侧面和背风面的脉动风压。以上研究发现了外附粗糙构件对局部风荷载的影响,但对于常见的竖向肋条对高层建筑局部风压的研究较少。
本文通过风洞试验研究三种竖向肋条布置对高层建筑局部风压的影响,对比有无竖向肋条情况下高层建筑平均风压和脉动风压的差异,分析各工况下风压点的功率谱和风压POD模态的差异,通过风压点的分布概率密度探究竖向肋条导致风压非高斯性分布的变化,最后获得有竖向肋条情况下的高层建筑表面风压的极值。研究成果为带装饰条的高层建筑围护结构抗风设计提供参考。
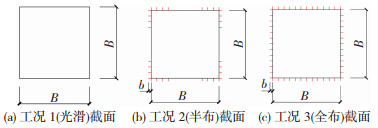
1 试验概况选取高度H=368 m的方形截面超高层建筑为研究对象,建筑边长B=48 m,模型几何缩尺比为1:400。试验模型采用ABS塑料等材料制作而成,共模拟了三种工况,其中工况1(参考工况)表面光滑,未布置竖向肋条。由于高层建筑上半部分对风压更为敏感[9],文献[7-8]也大多在上半部分布置肋条,因此工况2、工况3在表面风压较大的上半部分布置竖向肋条,肋条外伸宽度b=2 m,相对宽度b/B≈4%。由于建筑角部对负风压更加敏感,为了探究角区的肋条对建筑覆面风压的影响程度,对工况2和3设置不同的肋条分布形式,其中工况2仅在模型上半部分的角区布置竖向肋条,工况3在模型上半部分全部布置竖向肋条。基于工程项目实践,装饰条的间距为4 m,在本文设置为常量。三种工况的横截面见图 1。其中工况3的试验模型见图 2。为叙述方便,以上三种工况分别简称为光滑、半布、全布。由于对于方形截面,气流分离点不发生改变,气流分离后也不会发生再附,因此对于本试验不考虑雷诺数效应的影响。
|
图 1 三种工况截面示意 Fig. 1 Sectional layout of three cases |

|
图 2 工况3试验模型 Fig. 2 Test model of case 3 |
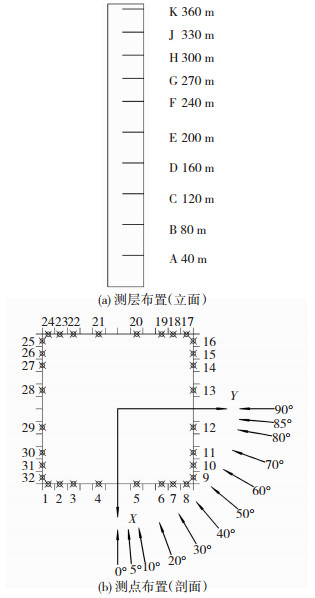
三个模型测点布置保持一致,共布置10个测层,见图 3,从下至上测层名称依次为A-H、J、K,对应高度分别为40、80、120、160、200、240、270、300、330、360 m,每一层测点布置也均相同。测点层的测点布置见图 3,每个面均布置8个测点,每层共布置32个测点,每个测点的测压管垂直建筑物表面[10]。坐标系定义见图 3(b),其中编号1-8位于X正面,编号9-16位于Y正面。由于建筑具有双轴对称性,风洞试验测试0~90°风向角,间隔为10°,并增加了5°和85°的风向角测试。
|
图 3 测点与测层布置 Fig. 3 Layout of measuring taps and layers |
风洞试验在浙江大学的ZD-1边界层风洞中进行,试验段长18 m、宽4 m、高3 m。风压测试采用美国DSM340电子扫描阀,对同一个模型的所有测点进行同步测压,采样频率为312.5 Hz,采样时长为90 s,采样点数为28 125。本次试验在来流前部布置粗糙元与尖劈来模拟B类风场。根据GB 50009—2012《建筑结构荷载规范》[11],平均风速和湍流度剖面采用如下公式:
| $ U=U_H(z / H)^\alpha $ | (1) |
| $ I_u=I_{10}(z / 10)^{-\alpha} $ | (2) |
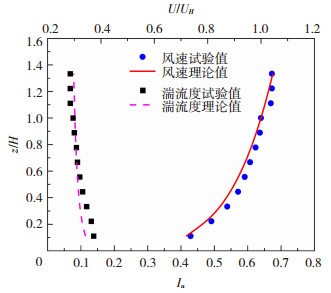
式中: UH为H高度处的风速,z为离地高度,H为建筑顶部高度,I10为10 m高度处的湍流度,α为0.15。图 4为风洞模拟值和规范要求值的比较,可以发现风洞较好地模拟了B类风场。
|
图 4 B类地貌的风场模拟 Fig. 4 Wind field simulation of terrain category B |
风洞试验获得测点的风压系数Cpi定义为
| $ C_{p i}=\frac{P_i-P_{\infty}}{0.5 \rho U_{\infty}^2} $ | (3) |
式中:Pi为测点i的风压值;P∞为参考点静压力值;ρ为空气密度;U∞为参考点的风速,选取建筑顶点H作为参考点,本次建筑模型顶部高度处的测试速度为12.50 m/s。
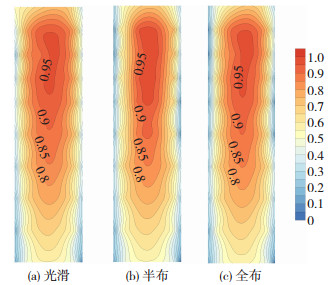
2 平均风压系数三种工况在0°风向下迎风面的平均风压系数Cp见图 5。为表示清晰,等值线图中宽度放大了一倍,下文的表达方式均同此。可以发现:1)迎风面上的平均风压系数随着高度增大总体增大;2)在楼顶处由于三维流的存在使得风压系数减小;3)同一高度下,中间的测点风压系数最大,向两边减少,且等值线密集,压力梯度较大;4)三种工况的平均风压系数非常接近,说明竖向肋条的布置对于迎风面正风压的影响很小。
|
图 5 迎风面平均风压系数分布(0°) Fig. 5 Mean wind pressure coefficient on windward side (0°) |
0°风向下侧风面的平均风压系数Cp分布见图 6,可以发现:1)受气流分离及旋涡脱落的影响,侧面承受负压;2)光滑工况下,前缘与后缘的风压差距不大,而当布置竖向肋条后,前后缘之间的风压差异变大,其原因为竖向肋条对建筑横向绕流的局部阻碍作用[12]使得前缘负压变大,而后缘负压变小;3)特别在肋条布置的分界点(180 m处),风压在上下方向和前后方向的梯度都非常大;4)半布和满布工况的平均风压系数几乎相同,可以看出中部肋条对风压分布的影响较小。

|
图 6 侧风面平均风压系数等值线(0°) Fig. 6 Mean wind pressure coefficient on side face (0°) |
0°风向下背风面的平均风压系数Cp分布见图 7,可以发现:1)背风面位于尾流区,承受负压;2)背风面中部承受负风压最小,从中部到四周的负风压绝对值逐渐增大;3)半布和满布工况的背风面风压分布非常接近,均小于光滑工况,说明布置竖向肋条使得背风面所有测点的负压都有所降低。

|
图 7 背风面平均风压系数等值线(0°) Fig. 7 Mean wind pressure coefficient on leeward side (0°) |
选取B(80 m)、E(200 m)、H(300 m)三个测层在0°风向角下的平均风压进行分析,相对高度z/H分别为0.22、0.54和0.82。三个测层各测点的平均风压系数Cp见图 8,图 8中N为测点编号,可以发现:1)B层(z/H=0.22)三种工况在迎风面的平均风压系数不变,光滑工况在侧风面和背风面平均风压系数的负压绝对值均大于半布和全布工况,说明上方的竖向肋条对该层的风荷载产生了影响, 这是相对于正压,负压对建筑表面特性更加敏感,与高度无关,即使下半部分没有布置肋条,但是也受到上半部分肋条的影响有所变化,这与文献[7-8]的研究结果类似;2)E层(z/H=0.54)位于肋条分界线(184 m)之上,半布和全布工况在侧风面的气流分离点处产生了很大的负压,而光滑工况在该位置的负风压较小,说明在肋条分界线附近,肋条导致了剧烈的气流分离,使得侧面前缘局部负风压骤然增大,特别是9、10号测点,E9测点全布工况的平均风压系数比光滑工况大83.3%;3)H层(z/H=0.82)侧风面的气流分离点由于布置肋条导致的负压增大现象依旧存在,但是增大程度远不如E层,H9测点全布工况的平均风压系数只比光滑工况大23.5%,侧面后缘与背部测点在布置肋条后风压系数有所降低;4)三个截面半布工况和全布工况的平均风压系数风压非常接近,说明中部肋条对风压分布的影响较小。

|
图 8 三个测层的平均风压系数 Fig. 8 Mean pressure coefficient on three layers |
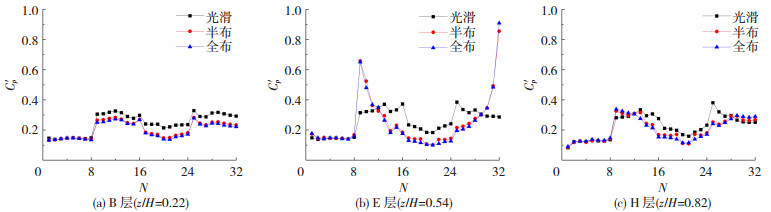
B(80 m)、E(200 m)、H(300 m)三个测层的测点在0°风向角下的风压系数标准差C′p见图 9。可以发现:1)B层(z/H=0.22)三种工况在迎风面的风压系数标准差不变,光滑工况在侧风面和背风面的风压系数标准差均大于半布和全布工况;2)E层(z/H=0.54)半布和全布工况在侧风面的气流分离点处产生了很大的风压脉动,与平均值的规律类似,肋条的布置使得侧面前缘分离引起较大的气流紊乱;3)H层(z/H=0.82)侧风面的气流分离点由于布置肋条导致的负压增大现象依旧存在,肋条布置导致的负压脉动剧烈程度有所减小;4)三个测层背风面风压系数标准差中均反映了一个规律,即半布和全布工况的标准差均小于光滑工况,说明竖向肋条会降低背风面的风压脉动值;5)三个截面半布工况和全布工况的脉动风压系数非常接近,说明中部肋条对脉动风压分布影响较小。
|
图 9 三个测层风压系数的标准差 Fig. 9 Standard deviation of wind pressure coefficients on three layers |
由前面的分析可知,在迎风面上肋条布置对平均值和脉动值几乎没有影响,因此本节主要分析侧风面、背风面的风压频谱特性。在侧风面选取B10、E10、H10三个测点分析在0°风向角不同高度测点的频谱特性,见图 10。图 10中f为频率,D为建筑宽度,fS*为无量纲化后的功率谱。由图 10可知:1)对于B10测点,受建筑上半部分的肋条影响后,半布和全布工况的谱峰值比光滑工况略小;2)对于E10测点,肋条的布置并没有改变频谱最大值所在的约化频率,这说明St=fD/U并没有改变,也说明本试验当中Re数效应可以忽略,但是肋条的存在显著改变了测点风压的功率谱幅值大小,光滑工况的风压谱能量较为集中,峰值出现在折减频率为0.1左右,而半布和全布工况的风压谱峰值明显降低,但半布和全布工况的大部分频率上的谱值均大于光滑工况;3)H10测点布置肋条后的变化规律与E10测点类似,与风压标准差的变化规律类似,肋条布置导致的负压脉动剧烈程度比E10有所减小。

|
图 10 侧风面不同高度测点的频谱 Fig. 10 Spectra of pressure along height on side face |
在背风面取B18、E18、H18三个测点分析在0°风向角的风压谱特性,见图 11,可以发现:1)对于B18测点,可以发现三种工况下的风压谱形状非常接近,半布和全布工况的风压谱在峰值处略小于光滑工况;2)对于E18和H18,均处于布置肋条的背风面区域,三种工况呈现出的规律非常接近,即三种工况均表现为单峰谱,而半布和全布工况的风压谱非常接近,均小于光滑工况的风压谱,该情况与图 9(b)和图 9(c)的风压系数标准差分布特征相吻合,说明竖向肋条会降低背风面的风压脉动幅度。

|
图 11 背风面不同高度测点的频谱 Fig. 11 Spectra of pressure along height on leeward side |
本征正交分解(proper orthogonal decomposition, POD)技术主要用于识别流动机制和压力分布模式[7]。对该建筑的两个侧面上的风压进行了POD分析,风向角为0°,获得了POD分析的各阶能量占比、主坐标和模态。
对0°风向角侧风面的脉动风压系数进行POD分解,得到各阶能量占比。图 12为不同工况各阶模态能量占比示意(以侧风面为例),图中Nm为模态数目。可以看出:1)背风面光滑工况下的第一阶能量占比为52.9%,超过50%,第一阶模态拥有较大的脉动能量;2)半布和全布的第一阶能量占比分布为37.9%和35.0%,都小于光滑工况的占比,但是一阶仍占据较大的脉动能量;3)POD分析的各阶能量占比主要集中在前三阶模态。

|
图 12 不同工况前10阶模态能量占比(侧风面) Fig. 12 Energy ratio of first 10-order modes in three cases (side face) |
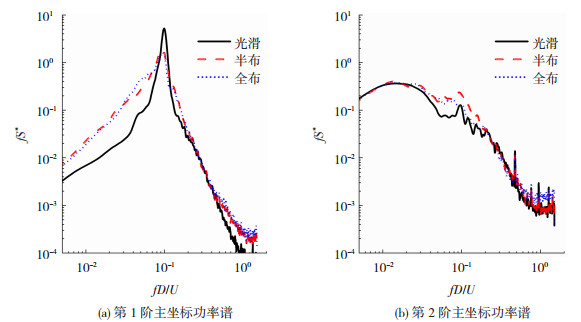
取前两阶的主坐标进行功率谱分析,图 13为POD前两阶主坐标归一化功率谱曲线。可以看出:1)第一阶主坐标呈现出单峰谱特性,在折减频率0.1附近存在尖峰,对应于涡脱频率,此时横风向气动力占主导地位,布置肋条后峰值有所降低;2)在折减频率为0.01~0.1时布置肋条的功率谱大于光滑工况;3)第二阶主坐标功率谱表现出宽带谱特性,没有明显谱峰,对应顺风向气动力。
|
图 13 前两阶主坐标归一化功率谱 Fig. 13 Normalized power spectra on first-and second-order principal coordinates |
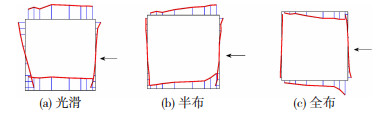
图 14给出了模型光滑工况下第一阶模态在建筑表面的分布,可以发现:1)第一阶特征模态在两侧面呈反对称分布,说明侧风面风压分布偏向一侧,合力方向垂直与来流风向,表明一阶模态主要由横风向气动激励起主导作用[13];2)当布置肋条后,在肋条分界线(184 m)以上的前缘区域位置的模态值增大较多,其他位置的模态值有所减小。
|
图 14 E层各工况1阶模态分布 Fig. 14 First-order mode distribution for each case in layer E |
由于侧风面角区受气流分离作用,使得测点风压概率分布具有非高斯性,采用峰值因子法可能会带来较大的误差。对非高斯分布的判断标准通常采用数据的三阶中心距S(偏度)与四阶中心矩K(峰度),偏度表示概率分布的对称性,峰度描述数据的突起程度,K>3表示概率密度曲线凸起程度比高斯分布大,K<3表示概率密度曲线比较平坦。标准高斯信号概率分布的偏度值和峰度值S=0、K=3。本文参考文献[14]确定划分非高斯区域的标准为:|S|>0.2且|K-3|>0.5。
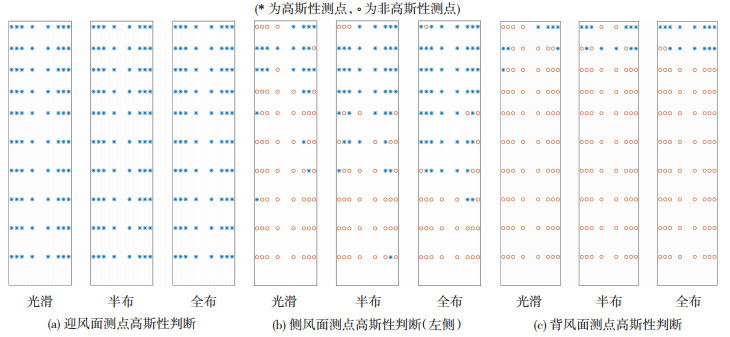
对0°风向角下迎风面、背风面、侧风面高斯和非高斯区域见图 15,可知:1)迎风面受来流正面撞击,斜度值较大,正偏,而峰态值比较小,整个立面为高斯区域,肋条的布置对高斯区域的分布没有任何影响;2)侧风面(以左侧为例)在光滑工况下,只有上部局部点风压概率密度分布为高斯性,当增加竖向肋条后,建筑中部测点的风压概率密度分布由非高斯性转化为高斯性;3)对于背风面的测点,整个立面都处于来流的尾流区,即整个背风面几乎为非高斯区域,竖向肋条的存在使得一部分测点风压概率密度分布由非高斯性转化为高斯性。
|
图 15 高斯区域与非高斯区域变化(0°) Fig. 15 Distribution changes in Gaussian region and non-Gaussian region (0°) |
鉴于侧风面和背风面的风压分布的非高斯特性,采用Cook等[15]提出的最佳线性无偏估计(best linear unbiased estimation,BLUE)极值分析法计算极值正压系数[16]。以0°风向角为例计算各个面的极值风压系数,迎风面的极值风压系数见图 16,由于迎风面为正压控制,图中只给出正的极值风压系数,可以发现:1)在楼顶处由于三维流的存在使得极值风压系数减小;2)同一高度处,中间测点的极值风压系数最大,向两边减少,且等值线密集,压力梯度较大;3)三种工况的极值正风压系数非常接近,说明竖向肋条的布置对于迎风面极值正风压的影响很小。

|
图 16 迎风面极值风压系数分布(0°) Fig. 16 Extreme wind pressure coefficient on windward side (0°) |
侧风面的风压主要为负压,因此侧风面(以左侧为例)主要分析极值负压系数,见图 17。可以发现:1)光滑工况下,前缘与后缘的极值风压差距不大,当布置竖向肋条后,前后缘之间的极值风压差异变大,其原因为竖向肋条对建筑横向绕流的局部阻碍作用使得前缘负压变大、后缘负压变小;2)在肋条布置的分界点(180 m处),极值负风压在上下方向和前后方向的梯度都非常大;3)半布和满布工况的极值风压系数几乎相同,可以看出中部肋条对侧面极值负风压分布的影响较小。

|
图 17 侧风面极值风压系数等值线(0°) Fig. 17 Extreme wind pressure coefficient on side face (0°) |
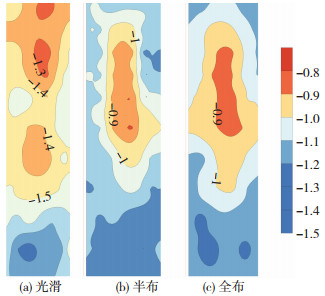
背风面的风压主要为负压,因此背风面主要分析负的极值风压系数,见图 18。可以发现:1)背风面中部承受负的极值风压最小,从中部到四周的极值负风压绝对值逐渐增大;2)半布和满布工况的背风面极值负风压分布非常接近,均小于光滑工况,说明布置竖向肋条使得背风面的极值负压有所降低。
|
图 18 背风面极值风压系数等值线图(0°) Fig. 18 Extreme wind pressure coefficient on leeward side (0°) |
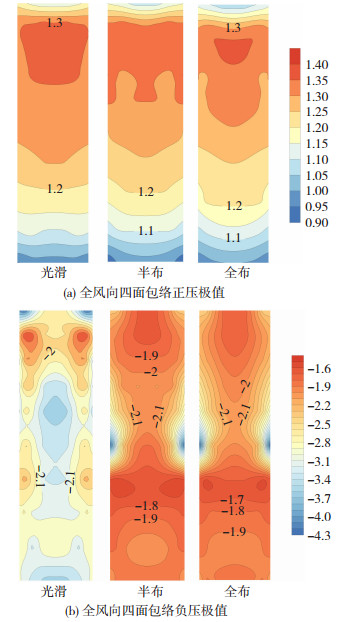
将所有风向角下风压系数极值取包络,可获得全风向的极值风压系数,根据建筑的双轴对称性,可以采用一个面的风压来表示。全风向的极值风压系数见图 19。
|
图 19 全风向风压系数极值 Fig. 19 Extreme wind pressure coefficient of omnidirectional wind |
由图 19可知:1)对于正压,三种工况的风压分布几乎一致,说明竖向肋条对正压极值几乎没有影响,风压系数极值大部分为1.1~1.3;2)对于负压,竖向肋条分界线(180 m)以下的区域,肋条布置使得负压极值都变小;对于分界线附近,肋条的存在现使得负压极值大大增大;对于顶部高度区域,肋条的存在使得负压极值略有降低。
8 结论研究竖向肋条对高层建筑局部风压的影响,通过风洞试验研究三种竖向肋条布置对高层建筑局部风压的影响,对比有无竖向肋条下情况高层建筑平均风压和脉动风压的差异,分析各工况下风压点的功率谱和风压POD模态的差异,通过风压点的分布概率密度探究竖向肋条导致风压非高斯性分布的变化,最后获得有竖向肋条情况下的高层建筑表面风压的极值,得出以下结论:
1) 肋条的布置对于迎风面测点风压的平均值和标准差没有影响;对于侧风面,分界线以上的前缘点的负压平均值和脉动值大大增加, 其他区域负压平均值和脉动值均有所降低;背风面布置肋条后平均值和脉动值降低。
2) 通过对典型测点的频谱特性也验证了脉动风压的差异。如E10点半布和全布工况的谱峰处有所降低,但风压谱积分小于光滑工况下的值。
3) 通过POD分解可知,对风场能量贡献最大的第一阶特征模态是横风向气起主导作用;布置肋条使得一阶主坐标功率谱谱峰有所降低;肋条分界线以上的前缘区域位置的模态值增大较多。
4) 当肋条增加后,在建筑侧风面中部的测点的风压概率密度分布由非高斯性转化为高斯性。迎风面、背风面基本没有变化。
5) 肋条的布置对于正压极值没有变化。分界线以上的前缘点的负压极值大大增加,其他区域的负压极值有所降低。
6) 半布和满布工况对局部风压特性造成的差异相差不大,说明中部的肋条对局部风压影响较小。
| [1] |
STATHOPOULOS T, ZHU X. Wind pressures on building with appurtenances[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 31(2): 265. DOI:10.1016/0167-6105(88)90008-6 |
| [2] |
CHAND I, BHARGAVA P K, KRISHAK N L V. Effect of balconies on ventilation inducing aeromotive force on low-rise buildings[J]. Building and Environment, 1998, 33(6): 385. DOI:10.1016/S0360-1323(97)00054-1 |
| [3] |
MARUTA E, KANDA M, SATO J. Effects on surface roughness for wind pressure on glass and cladding of buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1998, 74: 651. DOI:10.1016/S0167-6105(98)00059-2 |
| [4] |
MONTAZERI H, BLOCKEN B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: validation and sensitivity analysis[J]. Building and Environment, 2013, 60: 137. DOI:10.1016/j.buildenv.2012.11.012 |
| [5] |
沈国辉, 钱涛, 杨晓强, 等. 设有外镂空装饰结构的扭转体型高层建筑风荷载研究[J]. 建筑结构学报, 2013, 34(6): 68 SHEN Guohui, QIAN Tao, YANG Xiaoqiang, et al. Study of wind loads on torsion shaped high-rise building with outer pierced ornament structure[J]. Journal of Building Structures, 2013, 34(6): 68. DOI: 1000-6869(2013)06-0068-07 |
| [6] |
HU G, SONG J, HASSANLI S, et al. The effects of a double-skin façade on the cladding pressure around a tall building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 191: 239. DOI:10.1016/j.jweia.2019.06.005 |
| [7] |
YUAN K, HUI Y, CHEN Z. Effects of facade appurtenances on the local pressure of high-rise building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 178: 26. DOI:10.1016/j.jweia.2018.05.004 |
| [8] |
LIU J, HUI Y, YANG Q, et al. Flow field investigation for aerodynamic effects of surface mounted ribs on square-sectioned high-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2021, 211: 104551. DOI:10.1016/j.jweia.2021.104551 |
| [9] |
邓挺. 500 m以上量级典型超高层建筑风效应研究[D]. 广州: 华南理工大学, 2016: 66 DENG Ting. Research on the wind effect of typical super-tall buildings beyond 500 m[D]. Guangzhou: South China University of Technology, 2016: 66 |
| [10] |
钱涛. 不同长宽比矩形截面高层建筑的风荷载研究[D]. 杭州: 浙江大学, 2013: 16 QIAN Tao. Research on influence of length to width ratios on wind loads of rectangular sectioned high-rise buildings[D]. Hangzhou: Zhejiang University, 2013: 16 |
| [11] |
建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012: 30 Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Construction Industry Press, 2012: 30 |
| [12] |
程旭. 粗糙条围护结构对高层建筑风荷载影响的研究[D]. 成都: 西南交通大学, 2020: 21 CHENG Xu. Influence of architectural facades on wind loads of tall buildings[D]. Chengdu: Southeast Jiaotong University, 2020: 21 |
| [13] |
胡梦诗. 基于随机场分解的超高层建筑气动作用机制研究[D]. 北京: 北京交通大学, 2018: 30 HU Mengshi. Study on aerodynamic mechanism of super tall buildings based on random field decomposition[D]. Beijing: Beijing Jiaotong University, 2018: 30 |
| [14] |
李进晓. 高层建筑幕墙表面风压特性研究[D]. 杭州: 浙江大学, 2010: 62 LI Jinxiao. Study on wind pressure characteristics on curtain wall surfaces of tall buildings[D]. Hangzhou: Zhejiang University, 2010: 62 |
| [15] |
COOK N J, MAYNE J R. A novel working approach to the assessment of wind loads for equivalent static design[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1979, 4(2): 149. DOI:10.1016/0167-6105(79)90043-6 |
| [16] |
杨肖悦, 谢霁明. 建筑覆面风致连锁损坏的概率风险评估[J]. 哈尔滨工业大学学报, 2019, 51(6): 185. YANG Xiaoyue, XIE Jiming. Probabilistic risk assessment of cascading damage for building cladding in strong wind[J]. Journal of Harbin University of Technology, 2019, 51(6): 185. DOI:10.11918/j.issn.0367-6234.201811105 |
 2023, Vol. 55
2023, Vol. 55


