高层建筑上的风荷载通常被分为顺风向、横风向和扭转向3个分量。顺风向风荷载主要由来流特性决定;横风向风荷载产生原因较为复杂,一般认为是来流的湍流、尾流的旋涡脱落和侧向流动的分离再附、结构自身的气动弹性激励等共同引起的[1-2];扭转向风荷载被认为主要由侧风面风力不对称作用和背风面的脉动风压分布不均匀共同所致[3]。
建筑基底力矩系数是结构抗风设计中的重要参数,国内外学者对矩形高层建筑基底力矩系数进行了大量研究。Lin等[3]通过同步测压和高频天平测力试验,讨论了长宽比1/3~3的矩形高层建筑基底力矩系数的变化规律。Zhou等[4]对平行四边形截面、三角形截面、不同长宽比矩形截面共27个模型在开阔地貌和城市地貌下进行高频天平测力试验,将试验获得的基底力矩系数和功率谱密度储存于交互式数据库(UND),供设计和研究人员查询。唐意[5]对长宽比1/3~3的矩形高层建筑在B类和D类风场下进行同步测压试验,分析了风向角、风场类别、长宽比等因素对基底力矩系数的影响。熊勇等[6]通过高频天平测力试验,研究了高宽比4~7.5、长宽比1/5~5的矩形高层建筑的整体阻力系数特性。顾明等[7]通过高频天平测力试验,研究了长宽比1/4.7~4.7、高宽比4~14.24的矩形截面建筑在不同风场下基底扭矩系数均方根特性,给出了不同风场下建筑基底扭矩系数均方根的计算公式。全涌等[8]研究了这些建筑的横风向基底弯矩系数均方根特性,给出了不同风场下横风向基底弯矩系数均方根的计算公式。李永贵等[9]通过同步测压试验,研究了长宽比1/3~3的矩形高层建筑基底扭矩系数标准差特性,给出了相应的计算公式。张明月等[10]对长宽比1/2~2的矩形高层建筑进行了同步测压试验,讨论了3个方向基底力矩系数随长宽比变化规律。袁深根等[11]通过同步测压试验,研究了长宽比1/3~3的矩形高层建筑横风向基底弯矩标准差特性,并给出了对应的拟合公式。
为了获得更好的采光通风功能,住宅高层建筑截面多采用狭长矩形截面形式,长宽比最大达8~9,但国内外学者对矩形高层建筑基底力矩系数的研究基本局限在长宽比1/5~5的范围内。另一方面,以往文献关于来流湍流特性对基底力矩系数影响的研究都是综合考虑的,尚未见对湍流强度或湍流积分尺度的影响作单独分析的报导。各国荷载规范给出的基底扭矩系数和横风向基底弯矩系数经验公式只适用于长宽比较小的建筑,且大多没有考虑风场类别的影响[12-13]。因此有必要研究更大范围长宽比矩形高层建筑在不同风场中的基底力矩系数,为建筑结构设计和荷载规范的修订提供参考。
本文对长宽比1/9~9的矩形高层建筑在4种风场下进行同步测压试验,通过与国内外研究成果的比较,验证本次试验结果的可靠性,并考察相互之间的异同点;探讨了长宽比,湍流强度和湍流积分尺度对3个方向基底力矩系数的影响;针对4种风场提出了矩形高层建筑顺风向、横风向和扭转向基底力矩系数的拟合公式。
1 风洞试验 1.1 试验风场同步测压风洞试验在加拿大西安大略大学边界层风洞II的高速试验段中进行。关于该风洞的详细信息见文献[14]。试验按照工程科学数据库模拟了4种不同类别的风场:O1、S1、O2和S2。其中字母O和S分别表示开阔地貌和郊区地貌;数字1和2分别表示模拟较大和较小湍流积分尺度。湍流积分尺度按ESDU-74031[15]建议的公式模拟,理论值按照下式计算:
| $ L_u=\bar{U}_z \int_0^{\tau_0} \rho_{u u}(\tau) \mathrm{d} \tau $ | (1) |
式中:Lu为湍流积分尺度,Uz为高度z处的平均风速,ρuu为脉动风速自相关系数,τ为时差,τ0为自相关系数收敛至0时对应的时差。本次试验O1、S1、O2和S2风场在z=H(H为模型总高)高度处的缩尺湍流积分尺度分别为1.328、1.545、0.504和0.656 m。
平均风速剖面按照ESDU-85020[16]模拟,理论值按照下式计算:
| $ \bar{U}_z=\bar{U}_{10} \frac{\ln \left(z / z_0\right)}{\ln \left(10 / z_0\right)}+86.25 f_{\mathrm{c}} z $ | (2) |
式中:U10为10 m平均风速,z0为地表粗糙长度,fc为科里奥利力。
湍流强度剖面按照ESDU-82026[17]模拟,理论值按照下式计算:
| $ I_{u z}=\frac{7.5 \eta u\left[0.538+0.09 \ln \left(z / z_0\right)\right]^p}{\left[1+0.156 \ln \left(u / f_{\mathrm{c}} z_0\right)\right] \bar{U}_z} $ | (3) |
式中:η、p为拟合参数,u为摩擦速度。
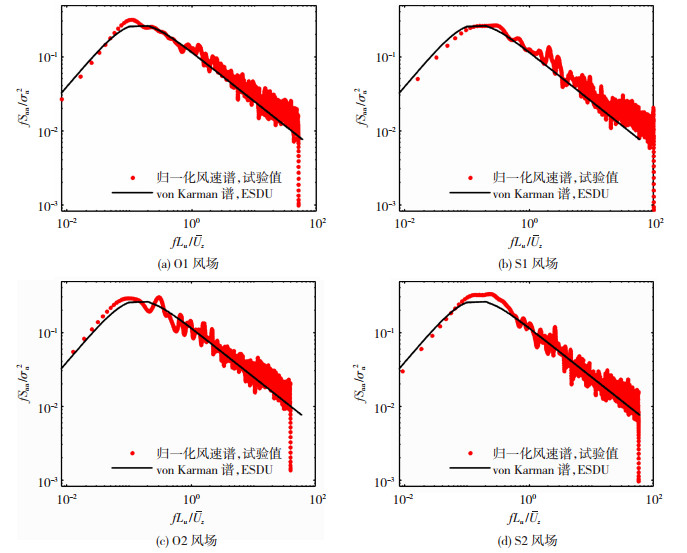
图 1给出4种风场下平均风速和湍流度剖面,试验值和理论值拟合情况良好。图 1同时给出了各风场足尺地表粗糙长度z0和指数率形式的剖面参数α。O1、S1、O2和S2风场下模型顶部平均风速分别为8.86、8.32、8.07和8.11 m/s,模型顶部的湍流强度分别为0.124、0.187、0.122和0.170。图 2给出了本次风洞试验4种风场在z=0.762H处的脉动风速谱试验值和理论值,二者吻合良好。

|
图 1 平均风速和湍流度剖面 Fig. 1 Mean velocity and turbulence intensity profiles |
|
图 2 z=0.762H高度处脉动风速谱 Fig. 2 Fluctuating velocity spectra at z=0.762H |
脉动风速谱模拟采用ESDU-74031[15]建议的von-Karman谱:
| $ \frac{f S_{u u}(f)}{\sigma_u^2}=\frac{4 f_u}{\left(1+70.8 f_u^2\right)^{5 / 6}}, f_u=\frac{f L_u}{\overline{U}_z} $ | (4) |
式中:σu为脉动风速标准差,Suu为脉动风速功率谱密度,f为频率。
1.2 试验模型试验采用刚性节段模型,缩尺比为1:200,长0.06~0.54 m,宽0.06 m,高0.5 m。模型1~6段的长宽比为0.5,7~12段的长宽比为1.0。通过不同的拼接方式可以得到长宽比(D/B,B为迎风面宽度,D为侧风面长度)为1/9~9的模型,试验模型参数和拼接方式见图 3和表 1。模型沿高度布置了7个测点层,分别位于0.1H、0.3H、0.5H、0.65H、0.8H、0.9H和0.98H高度处,每层测点的布置方式相同,测点平面布置见图 3。针对不同长宽比工况的模型进行了测压试验,获得了各测点的风压系数时程,风洞试验照片见图 4。一般来说矩形截面建筑基底力矩系数在正交风向角出现最不利情况[5],因此本文只考虑0°和90°这两个正交风向角的情况。

|
图 3 模型与测点平面布置 Fig. 3 Plane layout of model and pressure taps |
| 表 1 试验模型参数 Tab. 1 Parameters of experiment models |

|
图 4 风洞试验 Fig. 4 Wind tunnel tests |
在来流风作用下,建筑基底力矩系数平均值和标准差按下式计算:
| $ \begin{aligned} & C_{M_{\mathrm{D}}}=\frac{\bar{M}_{\mathrm{D}}}{0.5 \rho \bar{U}_H^2 B H^2}, C_{M_{\mathrm{D}}}^{\prime}=\frac{\sigma_{M_{\mathrm{D}}}}{0.5 \rho \bar{U}_H^2 B H^2} \\ & C_{M_{\mathrm{L}}}=\frac{\bar{M}_{\mathrm{L}}}{0.5 \rho \bar{U}_H^2 B H^2}, C_{M_{\mathrm{L}}}^{\prime}=\frac{\sigma_{M_{\mathrm{L}}}}{0.5 \rho \bar{U}_H^2 B H^2} \\ & C_{M_{\mathrm{T}}}=\frac{\bar{M}_{\mathrm{T}}}{0.5 \rho \bar{U}_H^2 B^2 H}, C_{M_{\mathrm{T}}}^{\prime}=\frac{\sigma_{M_{\mathrm{T}}}}{0.5 \rho \bar{U}_H^2 B^2 H} \\ & \end{aligned} $ | (5) |
式中:CMD、CML和CMT分别为顺风向、横风向和扭转向基底力矩系数平均值,C′MD、C′ML和C′MT分别为顺风向、横风向和扭转向基底力矩系数标准差。MD、ML和MT分别为顺风向、横风向和扭转向基底力矩平均值,σMD、σML和σMT分别为顺风向、横风向和扭转向基底力矩标准差。ρ为空气密度,UH为建筑顶部平均风速,B为迎风面投影宽度,H为模型总高度。
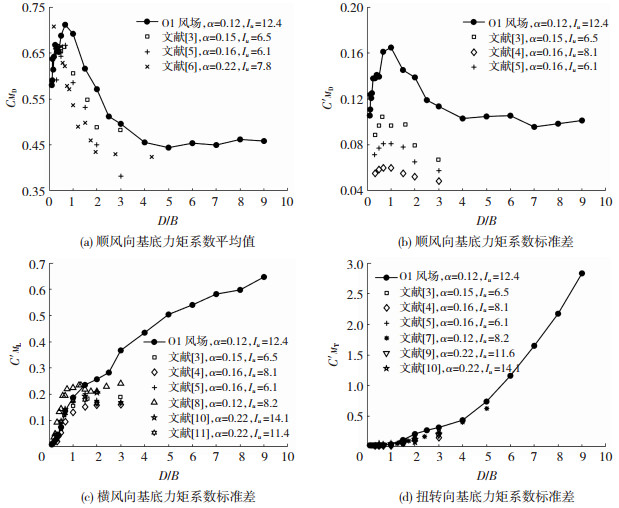
2 试验结果 2.1 与文献数据比较图 5给出了本次试验获得的O1风场下的基底力矩系数与以往文献数据的比较,图 5标出了各文献试验风场的平均风速剖面指数和模型顶部湍流强度Iu。由于在来流垂直于建筑表面时,横风向和扭转向基底力矩系数平均值接近0,故对其不做讨论。从图 5可看出,CMD、C′ML和C′MT的试验结果大小及其变化趋势与以往文献研究结果有较好的一致性。C′MD的变化趋势与以往文献结果基本一致,但数值比后者大,原因在于O1风场的湍流强度明显大于以往文献风场,而顺风向脉动风力与来流湍流强度密切相关。在已有的长宽比范围内,本次试验结果与文献结果有良好吻合,表明试验结果具有可靠性。
|
图 5 基底力矩系数与以往文献数据比较 Fig. 5 Comparison between base moment coefficients and data from previous literature |
图 6给出了4种风场条件下,建筑长宽比对基底力矩的影响。由图 6可见,所有风场类型下,顺风向基底力矩系数的平均值和标准差随长宽比的变化规律基本相同,大致可分为两个阶段:

|
图 6 长宽比对基底力矩系数的影响 Fig. 6 Effect of side ratio on base moment coefficients |
1) 当D/B≤3时,顺风向基底力矩系数随长宽比先增大后减小,平均值在D/B=0.67时取得最大值,标准差在D/B=1.0时取得最大值,这与以往文献的结果基本一致。
2) 当D/B>3时,出现了以往研究未曾发现的规律,顺风向基底力矩系数基本不再随长宽比变化。
顺风向基底力矩系数随长宽比的变化规律可以用前缘拐角处分离的自由剪切层特性来解释。分离的剪切层会在尾流区形成旋涡,在这个过程中背风面尾流区的气流被夹卷挟带,导致背风面出现负压[18]。建筑长宽比增大时,尾流区尺寸减小,同样的夹卷过程在较小的尾流区内将导致背风面负压增大。这个阶段基底力矩系数逐渐增大。当长宽比增大到0.7以上时,后缘的角部会对剪切层产生干扰,使得旋涡的夹卷减弱。此时基底力矩系数开始减小。当长宽比大于3时,分离剪切层会发生再附,并在侧风面形成沿表面滚动的涡,最后在尾流区脱落[19]。此时旋涡的夹卷能力基本不变,使得基底力矩系数基本不再随长宽比变化。
横风向基底力矩系数标准差随长宽比单调增大,但是增长速度随长宽比逐渐减小。其原因在于,对于小长宽比建筑,横风向脉动风力主要来源于尾流的旋涡脱落;随着长宽比增大,不同高度的分离剪切层相继发生再附,而再附后的剪切层是不完全稳定的,会在侧风面形成滚动的涡,最后在尾流区脱落。这些滚动的涡也会在横风向产生脉动风力。但是随长宽比增大,尾流区的旋涡脱落强度会被抑制。因此横风向基底力矩系数标准差虽然随长宽比单调增大,但是增长速度会减小。
扭转向基底力矩系数标准差随长宽比单调增大,且增长速度也随之增大。扭转向脉动风荷载由侧风面的不平衡力作用和背风面的风压分布不均匀共同产生。剪切层在前缘分离,自由剪切层再附和在侧风面形成滚动的涡,以及尾流旋涡脱落这些现象都会在侧风面产生不平衡力。随着长宽比增大,由侧风面和尾流区域复杂流动引发的脉动风压的不均匀和不平衡性趋于增大,导致扭转向基底力矩系数标准差增速变大。
2.3 湍流特性的影响从1.1节分析可知,本次试验中O1与O2风场的湍流强度相近,但湍流积分尺度相差较大;S1与O1风场的湍流积分尺度相近,而湍流强度相差较大。虽然不同风场的风速剖面也不同,但是文献[20-21]表明,风速剖面对结构风压系数和基底力矩系数的影响很小,因此在讨论湍流特性的影响时,暂忽略风速剖面的影响。为定量考察来流湍流积分尺度和湍流强度对基底力矩系数的影响,定义湍流积分尺度影响系数为O1与O2风场下基底力矩系数的比值,定义湍流强度影响系数为S1与O1风场下基底力矩系数比值,计算公式为:
| $ \begin{aligned} & R_{\mathrm{D}}^{L_u}=\frac{C_{M_{\mathrm{D}}}^{01}}{C_{M_{\mathrm{D}}}^{02}}, R_{\mathrm{D}}^{I_u}=\frac{C_{M_{\mathrm{D}}}^{\mathrm{S} 1}}{C_{M_{\mathrm{D}}}^{01}} \\ & R_{\mathrm{D}}^{\prime L_u}=\frac{C_{M_{\mathrm{D}}}^{\prime 01}}{C_{M_{\mathrm{D}}}^{\prime 02}}, R_{\mathrm{D}}^{\prime I_u}=\frac{C_{M_{\mathrm{D}}}^{\prime \mathrm{S} 1}}{C_{M_{\mathrm{D}}}^{\prime 01}} \end{aligned} \\ \begin{aligned} & R_{\mathrm{L}}^{\prime L_u}=\frac{C_{M_{\mathrm{L}}}^{\prime 01}}{C_{M_{\mathrm{L}}}^{\prime 02}}, R_{\mathrm{L}}^{\prime I_u}=\frac{C_{M_{\mathrm{L}}}^{\prime \mathrm{S} 1}}{C_{M_{\mathrm{L}}}^{\prime 01}} \\ & R_{\mathrm{T}}^{\prime L_u}=\frac{C_{M_{\mathrm{T}}}^{\prime 01}}{C_{M_{\mathrm{T}}}^{\prime 02}}, R_{\mathrm{T}}^{\prime I_u}=\frac{C_{M_{\mathrm{T}}}^{\prime \mathrm{S} 1}}{C_{M_{\mathrm{T}}}^{\prime 01}} \end{aligned} $ | (6) |
图 7给出了不同长宽比建筑湍流特性对基底力矩系数的影响。对于顺风向基底力矩系数平均值,无论长宽比大小,湍流积分尺度影响系数始终大于1,湍流强度影响系数始终小于1。顺风向基底力矩系数由迎风面和背风面风荷载共同决定。上述结果表明,湍流强度和湍流积分尺度对迎风面和背风面风压的影响规律基本不随建筑长宽比变化。当湍流强度增大时,迎风面和背风面平均风压都增大,且背风面负压比迎风面正压的增加量更大[22],因此顺风向平均风荷载反而减小;当湍流积分尺度增大时,迎风面正压增大,背风面负压减小[23],顺风向平均风荷载增大。对于顺风向基底力矩系数标准差,无论长宽比大小,湍流积分尺度影响系数和湍流强度影响系数都始终大于1。这是因为当湍流强度和湍流积分尺度增大时,迎风面和背风面风压脉动值都会增大[24],顺风向脉动风荷载增大。

|
图 7 湍流特性对基底力矩系数的影响 Fig. 7 Effect of turbulence characteristics on base moment coefficients |
对于横风向基底力矩系数标准差,湍流强度影响系数大致随长宽比先减小后增大。在D/B=1时,湍流强度影响系数小于1,其余长宽比大于1。这可能是因为不同长宽比的建筑横风向气动力由不同的流动特性主导。在小长宽比时,横风向气动力主要由尾流旋涡脱落控制,增大湍流强度会减弱旋涡脱落强度,横风向气动力减小;在大长宽比时,横风向气动力主要由剪切层再附控制,增大湍流强度使得剪切层平均曲率半径减小[18],再附现象提前发生,横风向气动力增大。在D/B=0.5时,湍流积分尺度影响系数小于1,其余长宽比大于1。因为湍流积分尺度较大的风场含有更多的大尺度湍流,更少的小尺度湍流。大尺度湍流使分离流下脉动风压值增大,而小尺度湍流促使分离流更早再附,且使分离流下的脉动风压值减小[23]。
对于扭转向基底力矩系数标准差,湍流强度影响系数大致随长宽比先减小再增大,最后减小。在D/B=2、3时,湍流强度影响系数小于1;其余长宽比大于1。除D/B=0.5时,湍流积分尺度影响系数都大于1。这是因为扭转向气动力除了受侧风面不平衡气动力的控制,还受到背风面脉动风压的分布不均影响。因此扭转向湍流特性影响系数变化规律与横风向相似,但是更趋复杂。
2.4 公式拟合根据上文结果可知,顺风向基底力矩系数平均值和标准差随长宽比增大都是先增大后减小,最后基本保持不变,曲线近似于Gamma分布,因此选取Gamma分布概率密度函数形式作为目标函数。采用非线性最小二乘法进行拟合,拟合公式为:
| $ C_{M_{\mathrm{D}}}=p_1(D / B)^{p_2} \mathrm{e}^{p_3(D / B)}+p_4 $ | (7) |
| $ C_{M_{\mathrm{D}}}^{\prime}=p_1^{\prime}(D / B)^{p_2^{\prime}} \mathrm{e}^{p_3^{\prime}(D / B)}+p_4^{\prime} $ | (8) |
式中:p1、p2、p3和p4为CMD的拟合参数,p′1、p′2、p′3和p′4为C′MD的拟合参数,参数拟合结果见表 2。
| 表 2 顺风向基底力矩系数平均值和标准差参数拟合结果 Tab. 2 Parameters fitting results of mean and standard deviation values of base moment coefficients in along-wind direction |
横风向和扭转向基底力矩标准差随长宽比增大都持续增大,曲线近似多项式形式,因此选取多项式作为目标函数。采用非线性最小二乘法进行拟合,拟合公式为:
| $ C_{M_{\mathrm{L}}}^{\prime}=p_0^{\mathrm{L}}+p_1^{\mathrm{L}}(D / B)+p_2^{\mathrm{L}}(D / B)^2 $ | (9) |
| $ C_{M_{\mathrm{T}}}^{\prime}=p_0^{\mathrm{T}}+p_1^{\mathrm{T}}(D / B)+p_2^{\mathrm{T}}(D / B)^2 $ | (10) |
式中:p0L、p1L和p2L为C′ML的拟合参数,p0T、p1T和p2T为C′MT的拟合参数,参数拟合结果见表 3。
| 表 3 横风向和扭转向基底力矩系数标准差参数拟合结果 Tab. 3 Parameters fitting results of standard deviation values of base moment coefficients in across-wind and torsional directions |
图 8给出了基底力矩系数拟合曲线,图 8(c)和(d)中分别给出了AIJ-2004[12]和GB 50009—2012[13]中公式对应曲线。AIJ-2004和GB 50009—2012中扭转向风力系数公式完全一致,故在图 8(d)不再重复。从图 8中可见拟合式与试验结果吻合良好,AIJ-2004经验公式低估了小长宽比建筑横风向和大长宽比建筑扭转向基底力矩系数,而且无法反映不同风场基底力矩系数的区别。GB 50009—2012中横风向风力系数公式严重偏离试验结果。本文提出的拟合公式可为建筑结构设计及荷载规范修订提供参考。

|
图 8 基底力矩系数拟合曲线 Fig. 8 Fitting curves of base moment coefficients |
对长宽比1/9~9的矩形高层建筑在4种风场下进行同步测压风洞试验,研究矩形高层建筑基底力矩系数后得到以下结论:
1) 当建筑长宽比不大于3时,顺风向基底力矩系数的平均值和标准差随长宽比先增大后减小;当建筑长宽比大于3时,尾流区旋涡的夹卷能力维持基本不变,平均值和标准差不再随长宽比变化。顺风向基底力矩系数平均值在长宽比等于0.67时取得最大值,标准差在长宽比等于1.0时取得最大值。
2) 横风向基底力矩系数标准差和扭转向基底力矩系数标准差均随长宽比单调增大。随着长宽比增大,尾流区旋涡脱落被抑制,横风向基底力矩系数标准差增长速度减小,由侧风面和尾流区域复杂流动引发的脉动风压的不均匀和不平衡性趋于增大,扭转向基底力矩系数增长速度增大。
3) 对于顺风向基底力矩系数,增大湍流积分尺度会使平均值和标准差增大;而增大湍流强度会使平均值减小,标准差增大。对于横风向和扭转向基底力矩系数标准差,湍流积分尺度和湍流强度的影响随长宽比的不同而不同。
4) 针对4种不同风场类型,给出了矩形高层建筑顺风向基底力矩系数平均值和标准差,横风向和扭转向基底力矩系数标准差的拟合公式。系列公式与试验结果吻合良好,可为建筑结构设计及荷载规范修订提供参考。
| [1] |
全涌, 曹会兰, 顾明. 高层建筑横风向风效应研究综述[J]. 同济大学学报(自然科学版), 2010, 38(6): 810. QUAN Yong, CAO Huilan, GU Ming. Cross-wind effect of high-rise buildings: state of art[J]. Journal of Tongji University (Natural Science), 2010, 38(6): 810. DOI:10.3969/j.issn.0253-374x.2010.06.006 |
| [2] |
CHENG C M, LU P C, TSAI M S. Acrosswind aerodynamic damping of isolated square-shaped buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 1743. DOI:10.1016/S0167-6105(02)00284-2 |
| [3] |
LIN Ning, LETCHFORD C, TAMURA Y, et al. Characteristics of wind forces acting on tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(3): 217. DOI:10.1016/j.jweia.2004.12.001 |
| [4] |
ZHOU Yin, KIJEWSKI T, KAREEM A. Aerodynamic loads on tall buildings: interactive database[J]. Journal of Structural Engineering, 2003, 129(3): 394. DOI:10.1061/(ASCE)0733-9445(2003)129:3(394) |
| [5] |
唐意. 高层建筑弯扭耦合风致振动及静力等效风荷载研究[D]. 上海: 同济大学, 2006 TANG Yi. Research on the wind-excited vibrations and static-equivalent wind loads of torsionally coupled high-rise buildings[D]. Shanghai: Tongjing University, 2006 |
| [6] |
熊勇, 全涌, 顾明. 矩形截面高层建筑顺风向平均风荷载的风洞试验研究[C]//第19届全国结构工程学术会议论文集(第Ⅰ册). 济南: 山东建筑大学, 2010: 390 XIONG Yong, QUAN Yong, GU Ming. Wind tunnel test study on mean values of alongwind loads of tall buildings with rectangular cross-sections[C]//Proceedings of the 19th National Conference on Structural Engineering (VolumeⅠ). Jinan: Shandong Jianzhu University, 2010: 390 |
| [7] |
顾明, 张正维, 全涌, 等. 矩形截面高层建筑气动基底扭矩系数均方根值研究[J]. 振动与冲击, 2011, 30(10): 1. GU Ming, ZHANG Zhengwei, QUAN Yong, et al. RMS values of base torsional moment coefficients of tall buildings with square and rectangular cross-sections[J]. Journal of Vibration and Shock, 2011, 30(10): 1. DOI:10.13465/j.cnki.jvs.2011.10.047 |
| [8] |
全涌, 张正维, 顾明, 等. 矩形截面高层建筑的横风向基底弯矩系数均方根值研究[J]. 土木工程学报, 2012, 45(4): 63. QUAN Yong, ZHANG Zhengwei, GU Ming, et al. Study of the RMS values of across-wind aerodynamic base moment coefficients of high-rise buildings with square or rectangular sections[J]. China Civil Engineering Journal, 2012, 45(4): 63. DOI:10.15951/j.tmgcxb.2012.04.015 |
| [9] |
李永贵, 李秋胜, 戴益民. 矩形截面高层建筑扭转向脉动风荷载数学模型[J]. 工程力学, 2015, 32(6): 177. LI Yonggui, LI Qiusheng, DAI Yimin. Mathematical models for torsional fluctuating wind loads on rectangular tall buildings[J]. Engineering Mechanics, 2015, 32(6): 177. DOI:10.6052/j.issn.1000-4750.2013.11.1105 |
| [10] |
张明月, 李永贵, 李毅, 等. 矩形高层建筑风力特性风洞试验研究[J]. 自然灾害学报, 2019, 28(1): 123. ZHANG Mingyue, LI Yonggui, LI Yi, et al. Experimental study on wind force characteristics of rectangular tall buildings[J]. Journal of Natural Disasters, 2019, 28(1): 123. DOI:10.13577/j.jnd.2019.0115 |
| [11] |
袁深根, 李永贵, 孟灿, 等. 矩形截面高层建筑横风向脉动风荷载特性[J]. 湖南城市学院学报(自然科学版), 2019, 28(3): 1. YUAN Shengen, LI Yonggui, MENG Can, et al. Characteristics of across-wind fluctuating loads on rectangular tall building[J]. Journal of Hunan City University (Natural Science), 2019, 28(3): 1. DOI:10.3969/j.issn.1672-7304.2019.03.0001 |
| [12] |
AIJ recommendations for loads on buildings: AIJ-2004[S]. Tokyo: Architectural Institute of Japan, 2004
|
| [13] |
建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012 Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Building Industry Press, 2012 |
| [14] |
LIU Yi, KOPP G A, CHEN Shuifu. Effects of plan dimensions on gust wind loads for high-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 194: 15. DOI:10.1016/j.jweia.2019.103980 |
| [15] |
Characteristics of atmospheric turbulence near the ground. Part Ⅱ: single point data for strong winds (neutral atmosphere): ESDU-74031[S]. London: Engineering Sciences Data Unit, 1974
|
| [16] |
Characteristics of atmospheric turbulence near the ground. Part Ⅱ: single point data for strong winds (neutral atmosphere): ESDU-85020[S]. London: Engineering Sciences Data Unit, 1985
|
| [17] |
Strong winds in the atmospheric boundary layer. Part I: hourly-mean wind speeds: ESDU-82026[S]. London: Engineering Sciences Data Unit, 1982
|
| [18] |
HOLMES J D. Wind loading of structures[M]. London: CRC Press, 2015: 92.
|
| [19] |
袁家辉, 陈水福, 刘奕. 不同长宽比矩形高层建筑的横风向风力特性[J]. 中南大学学报(自然科学版), 2021, 52(12): 4365. YUAN Jiahui, CHEN Shuifu, LIU Yi. Characteristics of across-wind force of rectangular high-rise buildings with different side ratios[J]. Journal of Central South University (Science and Technology), 2021, 52(12): 4365. DOI:10.11817/j.issn.1672-7207.2021.12.016 |
| [20] |
陈伏彬, 李秋胜, 胡尚瑜, 等. 开阔地貌台风风场现场实测与风洞试验应用研究[J]. 建筑结构, 2015, 45(2): 89. CHEN Fubin, LI Qiusheng, HU Shangyu, et al. Field measurement and wind tunnel test application research of typhoon wind field in open terrain[J]. Building Structure, 2015, 45(2): 89. DOI:10.19701/j.jzjg.2015.02.018 |
| [21] |
王怡静. 基于CAARC标准模型风洞试验的风场参数影响研究[D]. 哈尔滨: 哈尔滨工业大学, 2020 WANG Yijing. Research on the influence of wind field parameters based on CAARC standard model wind tunnel test[D]. Harbin: Harbin Institute of Technology, 2020 |
| [22] |
苏万林. 湍流对高层建筑风效应影响的风洞试验研究[D]. 长沙: 湖南大学, 2017 SU Wanlin. Wind tunnel tests research on turbulence effects of wind acting on tall buildings[D]. Changsha: Hunan University, 2017 |
| [23] |
刘奕, 陈水福. 湍流特性对矩形高层建筑风荷载影响的研究[J]. 空气动力学学报, 2021, 39(2): 145. LIU Yi, CHEN Shuifu. Effects of turbulence characteristics on wind loads on rectangular high-rise buildings[J]. Acta Aerodynamica Sinica, 2021, 39(2): 145. DOI:10.7638/kqdlxxb-2019.0091 |
| [24] |
卢占斌, 魏庆鼎. 网格湍流CAARC模型风洞试验[J]. 空气动力学学报, 2001, 19(1): 22. LU Zhanbin, WEI Qingding. An experiment on a CAARC model in grid turbulent flow[J]. Acta Aerodynamica Sinica, 2001, 19(1): 22. |
 2023, Vol. 55
2023, Vol. 55


