为提高桥梁的抗震能力,在过去30年里,纤维增强复合材料(fiber reinforced polymer, FRP)在桥梁加固领域得到了广泛应用[1-3]。常见的FRP材料如碳纤维(carbon FRP, CFRP),玻璃纤维(glass FRP, GFRP)等具有线性的拉伸应力-应变关系和较小的断裂应变(小于3%),一般被称为传统FRP[4-5]。近年来,一种新发展的断裂应变大于5%的大应变FRP(large rupture strain FRP, LRS FRP)[6]得到了越来越多的学者关注。LRS FRP是由废弃塑料中的聚萘二甲酸乙二醇酯(polyethylene naphthalate, PEN)和聚对苯二甲酸乙二醇酯(polyethylene terephthalate, PET)制成的,是一种绿色可再生环保材料。与传统FRP相比,LRS FRP表现出双线性的拉伸应力-应变关系和较大的断裂应变特点[4]。文献[7-9]表明LRS FRP约束混凝土表现出优越的延性行为和超高的耗能能力,因此LRS FRP更适合作为以增强延性为主要目标的抗震加固材料,有望为桥梁加固提供一种更经济、延性更好的解决方案。
准确地预测LRS FRP约束混凝土在往复轴压荷载下的应力-应变行为是LRS FRP加固桥墩抗震分析的基础。可是,目前大多数往复轴压模型[10-15]是基于传统FRP约束混凝土柱的试验结果提出的,关于LRS FRP约束混凝土往复轴压模型的研究较少。由于约束混凝土在往复轴压荷载下的应力-应变响应取决于其外部约束材料的特性,而LRS FRP的材料特性与传统FRP明显不同,所以文献[4, 9]指出如果将传统FRP约束混凝土模型直接应用于LRS FRP加固桥墩的抗震分析会低估其变形能力。最近作者课题组提出了考虑塑性损伤的简化LRS FRP约束混凝土往复轴压应力-应变模型[16]。该简化模型采用类似Karsan等[17]的线性加卸载准则来模拟LRS FRP约束混凝土在往复轴压下的加卸载曲线并可以对LRS FRP加固墩柱拟静力试验结果做出准确地预测。鉴于此,本文在作者课题组提出的简化LRS FRP约束混凝土往复轴压模型基础上,对一典型三跨连续梁桥在LRS FRP加固前后的地震易损性进行了分析,研究了LRS FRP加固桥梁地震损伤变化规律,以期为同类工程的抗震加固提供一定的技术支持。
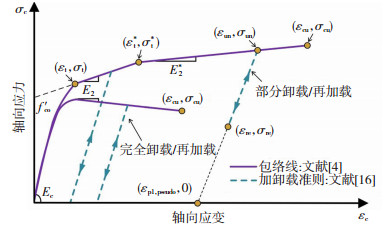
1 简化LRS FRP约束混凝土往复轴压模型 1.1 单调荷载下的应力-应变模型作者课题组发展的简化LRS FRP约束混凝土往复轴压模型[16]的包络线采用了文献[4]提出的基于刚度的单向轴压模型来表示。该模型是针对LRS FRP约束混凝土提出的,并且同样适用于传统FRP约束混凝土。此模型由三部分组成:第一部分抛物线阶段、第二部分线性阶段以及第三部分线性阶段,见图 1。第一部分和第二部分相交于点(εt, σt),第二部分与第三部分相交于点(εt*, σt*),模型详细信息参考文献[4]。
|
图 1 简化LRS FRP约束混凝土往复轴压模型 Fig. 1 Simplified LRS FRP-confined concrete model under axial cyclic compression |
包络线模型的数学表达式:
当第一段直线的斜率即刚度E2≥0时(强约束)
| $ \sigma_{\mathrm{c}}= \begin{cases}E_{\mathrm{c}} \varepsilon_{\mathrm{c}}-\frac{\left(E_{\mathrm{c}}-E_2\right)^2}{4 f_{\mathrm{co}}^{\prime}} \varepsilon_{\mathrm{c}}^2, & 0 \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{t}} \\ f_{\mathrm{co}}^{\prime}+E_2 \varepsilon_{\mathrm{c}}, & \varepsilon_{\mathrm{t}}<\varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{t}}^* \\ \sigma_{\mathrm{t}}^*+E_2^*\left(\varepsilon_{\mathrm{c}}-\varepsilon_{\mathrm{t}}^*\right), & \varepsilon_{\mathrm{t}}^*<\varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{cu}}\end{cases} $ | (1) |
当第一段直线的斜率即刚度E2 < 0时(弱约束)
| $ \sigma_{\mathrm{c}}= \begin{cases}E_{\mathrm{c}} \varepsilon_{\mathrm{c}}-\frac{E_{\mathrm{c}}^2}{4 f_{\mathrm{co}}^{\prime}} \varepsilon_{\mathrm{c}}^2, & 0 \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{t}} \\ \sigma_{\mathrm{t}}+E_2\left(\varepsilon_{\mathrm{c}}-\varepsilon_{\mathrm{t}}\right), & \varepsilon_{\mathrm{t}}<\varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{t}}^* \\ \sigma_{\mathrm{t}}^*+E_2^*\left(\varepsilon_{\mathrm{c}}-\varepsilon_{\mathrm{t}}^*\right), & \varepsilon_{\mathrm{t}}^*<\varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{cu}}\end{cases} $ | (2) |
式中:εc与σc分别为FRP约束混凝土的压应力和压应变;εcu为FRP约束混凝土的极限压应变,σcu为其对应的极限压应力;fco′为未约束混凝土的抗压强度,Ec为未约束混凝土的抗压弹性模量,E2和E2*分别为包络线模型的线性第二段和第三段的斜率。
1.2 加卸载准则和塑性应变卸载起点处的应变和应力分别称为卸载应变εun和卸载应力σun,再加载起点处的应变和应力分别称为再加载应变εre和再加载应力σre,见图 1。文献[16]提出的简化模型采用线性加卸载准则来模拟FRP约束混凝土往复轴压曲线的加卸载路径,为使预测的线性加卸载路径能准确代表整个试验加卸载曲线的位置,提出了伪塑性应变εpl, pseudo概念。该模型对应的线性加卸载准则为
| $ \sigma_{\mathrm{c}}=\frac{\sigma_{\mathrm{un}}}{\varepsilon_{\mathrm{un}}-\varepsilon_{\mathrm{pl}, \mathrm{pseudo}}}\left(\varepsilon_{\mathrm{c}}-\varepsilon_{\mathrm{pl}, \mathrm{pseudo}}\right) $ | (3) |
伪塑性应变为
| $ \varepsilon_{\mathrm{pl}, \mathrm{pseudo}}=\left\{\begin{array}{lr} 0, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad 0<\varepsilon_{\mathrm{un}}<0.001 \\ 0.47\left(\varepsilon_{\mathrm{un}}-0.001\right), 0.001 \leqslant \varepsilon_{\mathrm{un}} \leqslant 0.0035 \\ 0.82\left(\varepsilon_{\mathrm{un}}-0.002\right), \quad\quad\quad\quad \varepsilon_{\mathrm{un}}>0.0035 \end{array}\right. $ | (4) |
桥梁的地震易损性是指在任意给定的地震强度M下结构的需求D达到或超出其抗震能力C的条件概率P,可表示为
| $ P[D \geqslant C \mid M]=\Phi\left(\frac{\ln \frac{D}{C}}{\sqrt{\beta_{\mathrm{D}}^2+\beta_{\mathrm{C}}^2}}\right) $ | (5) |
式中Φ()为标准正态分布函数,βD2为桥梁地震需求对数标准差,βC2为桥梁抗震能力对数标准差。根据文献[18]建议,当易损性曲线以地震动峰值加速度Apg为自变量时,
参考文献[19],假设结构地震需求服从对数正态分布时,结构地震需求与地震动参数之间的关系为
| $ D=a \cdot M^b $ | (6) |
将上式两边同时取对数可得
| $ \ln (D)=a+b \ln M $ | (7) |
式中a与b为回归系数,可通过OpenSees计算提取桥梁结构响应数据进行统计回归得到。
将式(7)代入式(5)可得
| $ P[D>C \mid M]=\Phi\left(\frac{a+b \ln M-\ln C}{0.5}\right) $ | (8) |
地震易损性分析的核心是得出易损性曲线[20]。其主要分析过程可分为四部分:建立桥梁有限元模型;地震动记录选取和调幅;桥梁损伤状态等级划分;通过IDA法对桥梁模型进行地震反应分析得出易损性曲线。
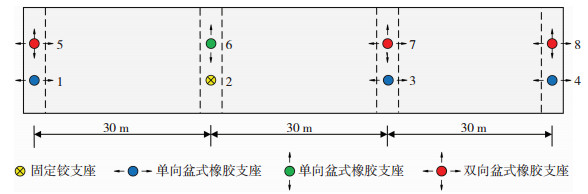
3 梁桥有限元分析模型 3.1 工程概况选取一座典型公路连续梁桥作为研究对象,桥梁总长为90 m,跨径布置为3×30 m,主梁为高1.8 m,宽13.25 m的单箱双室箱梁,桥墩采用无盖梁的单排圆形双柱墩,直径为1.4 m,墩身高度为8 m,两墩的中心距为5.5 m,桥址为Ⅱ类场地,桥梁示意见图 2。主梁和桥墩均采用C50混凝土,一期和二期恒载合计为68 kN/m,纵向钢筋和箍筋都采用HRB335钢筋,墩柱截面配有28根直径32 mm的纵筋,箍筋直径为12 mm,纵筋配筋率为1.46%,配箍率为0.51%。支座采用盆式橡胶支座,其平面布置方式和可移动方向见图 3。

|
图 2 桥梁示意(cm) Fig. 2 Diagram of the bridge (cm) |
|
图 3 支座平面布置 Fig. 3 Layout of bearing |
主梁在地震作用下通常不会发生损伤,因此采用弹性梁单元模拟,根据图 2(c)计算其截面几何特性见表 1。墩柱采用OpenSess中的ForceBeamColumn Element来模拟,每个墩柱被划分为8个单元,每个单元被分为6个积分点。钢筋采用Steel02模型,考虑箍筋对混凝土的约束作用,将截面划分为核心区混凝土、保护层混凝土及钢筋纤维截面,见图 4。此外,由于算例墩柱为悬臂墩,因此仅对其塑性铰区进行外包LRS FRP加固,LRS FRP材料特性见表 2。通过二次开发的方法将上述简化LRS FRP约束混凝土模型添加到OpenSees的单轴材料库中来模拟LRS FRP加固区混凝土的特性。对于未加固区混凝土,其保护层采用Concrete01模型,核心区采用Concrete02模型。
| 表 1 主梁截面几何特性 Tab. 1 Geometric characteristics of main beam |

|
图 4 墩柱纤维截面 Fig. 4 Fiber section of column |
| 表 2 LRS FRP材料参数 Tab. 2 Parameters of LRS FRP |
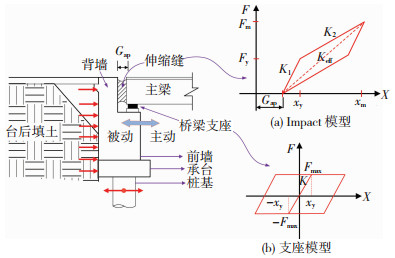
文献[20]指出主梁与桥台之间的碰撞对桥梁的动力响应有重要影响,在桥梁抗震分析中有必要准确模拟桥台与主梁的碰撞效应。本文采用接触单元方法模拟结构构件间碰撞效应,通过在梁体与桥台之间设置1个零长度单元并对零长度单元赋予OpenSees内置的Impact模型来实现。该材料是Muthukumar等[21]提出的双折线非线性碰撞模型,见图 5(a)。其中,K1为初始刚度,K2为屈服后刚度,Keff为有效刚度,Gap为伸缩缝宽度。算例Gap取50 mm,其他参数计算为K1=1 550 000 kN/m,K2=394 000 kN/m,Keff=509 000 kN/m。活动盆式支座的恢复力模型见图 5(b),Fmax为临界滑动摩擦力,xy为临界滑动位移。参考JTG/T 2231-01—2020《公路桥梁抗震设计规范》[22],算例支座的初始刚度K=50 000 kN/m。
|
图 5 桥台和支座模型 Fig. 5 Models of abutment and bearing |
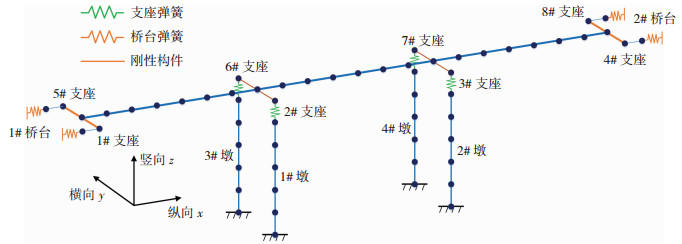
根据桥梁结构的整体构造布置,采用OpenSees建立三维非线性有限元分析模型。由于场地地质条件较好,不考虑基础弹性变形的影响,仅在墩底施加固定约束。主梁顺桥向为x轴,横桥向为y轴,竖向为z轴。为方便叙述,图 6给出了桥梁各个主要组成构件的编号。由图 3支座布置情况可知,2#支座为固定铰支座,其和6#支座共同约束了主梁x向自由度,1#、3#和4#支座约束了主梁y向自由度。因此,1#和3#桥墩在x向为固定墩,2#和4#桥墩为滑动墩。整个有限元模型包含130个框架单元及8个Link单元。
|
图 6 有限元模型 Fig. 6 Finite element model |
选择地震动输入是进行桥梁地震易损性分析的前提,文献[20]表明为了体现地震动的随机性,选择10~20条地震动记录能够达到一定精度。因此,根据“谱相容性原则”从美国太平洋地震研究中心(Pacific Earthquake Engineering Research Center, PEER)强震记录数据库选取震中距大于20 km的20条Ⅱ类场地地震波,以地震动峰值加速度Apg作为地震动参数,图 7给出了调幅后阻尼比为5%的各条地震波的平均谱加速度曲线与JTG/T 2231-01—2020《公路桥梁抗震设计规范》[22]中Ⅱ类场E1反应谱曲线的拟合情况。由图 7可看出,所选取地震记录的均值谱与Ⅱ类场的E1地震谱曲线吻合较好,可用于算例桥梁的地震时程分析。为简化起见,仅研究在纵向地震作用下的桥梁结构响应,因此只考虑纵向地震动输入。
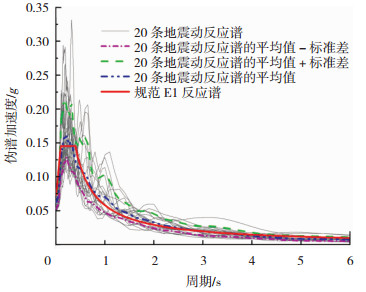
|
图 7 加速度反应谱 Fig. 7 Acceleration response spectrum |
在地震易损性分析中,文献[20]指出桥梁构件的抗震能力可定义为当桥梁构件丧失某一特定功能时桥梁所达到的破坏状态。采用OpenSees软件对墩底截面进行弯矩-曲率分析,采用文献[23]提出的划分极限状态值,得到桥墩4种不同损伤状态:轻微破坏、中等破坏、严重破坏、完全破坏所对应的曲率延性作为评判依据。虽然FRP加固可以明显地提高混凝土的变形能力[4-5],但其提供的是一种被动约束,即当混凝土膨胀时才会受到FRP的约束作用。因此,FRP加固对于墩柱轻微和中等破坏状态指标影响较小,而对于严重和完全破坏状态指标提高幅度较大。此外,参考文献[24-25],选择活动支座的相对位移作为其损伤指标。FRP加固前后桥墩和支座的各个极限状态值见表 3。
| 表 3 桥梁构件损伤指标取值 Tab. 3 Damage index values of bridge components |
基于OpenSees平台,将上述20条地震动记录分别输入到桥梁模型中进行IDA分析,每条地震动从0.1 g逐步调幅到1.2 g,提取各个地震动作用下各个桥墩的最大截面曲率和支座的最大相对位移,根据式(7)对这些散点进行线性回归分析,可得到其回归系数a值和b值,统计结果见表 4。
| 表 4 桥梁构件概率地震需求模型 Tab. 4 Probabilistic seismic demand model for bridge components |
值得注意的是,算例中的桥梁为规则桥梁,在考察桥梁系统的地震易损性分析时,主要是针对4个墩柱与8个支座进行各个极限状态的超越概率分析。算例桥梁主要由纵向地震动作用控制,主梁的纵向地震惯性力由固定墩承担,滑动墩处仅存在滑动摩擦力,该墩柱不会因活动支座传递的水平剪力而进入屈服,总在弹性阶段工作,因此,无需对柱顶设置活动支座的桥墩进行易损性分析。1#墩和3#墩由于刚度完全相同,其分担的地震作用水平剪力也一致,故其地震易损性结果也相同,仅需选择其一进行分析即可。考虑到纵向地震作用下可将主梁的运动视为刚体运动,活动支座的位移变形基本一致,其易损性分析结果相同,仅需选择1个活动支座进行分析。综上所述,对算例梁桥的地震易损性研究最终可转化为对1个固定墩和1个活动支座在纵向地震动作用下的易损性研究。因此,表 4仅给出了1#墩柱与3#支座的概率地震需求模型。
4 桥梁易损性分析 4.1 构件易损性曲线结合桥梁有限元模型分析结果(表 3和表 4),再利用式(8)即可求得1#桥墩和3#支座的地震易损性曲线,分别见图 8、9。图中横坐标表示地震动的大小,纵坐标表示地震作用下结构反应超越不同破坏状态的概率。

|
图 8 1#桥墩易损性曲线 Fig. 8 Fragility curves of 1# pier |

|
图 9 3#支座易损性曲线 Fig. 9 Fragility curves of 3# bearing |
由图 8可知,当Apg小于0.1 g时,桥墩轻微破坏概率小于15%,其他破坏等级概率趋于零,基本处于安全状态。当Apg为0.7 g时,未加固桥墩完全破坏即倒塌的概率达到了80%,存在倒塌的危险,经加固后,其倒塌概率降至了15%,加固效果较为明显。由图 9可知,LRS FRP加固结构的支座易损性概率降低在5%以内,表明采用LRS FRP加固对支座的破坏概率降低不明显。
4.2 系统易损性曲线桥梁整体中任何单个构件的失效都有可能导致全桥发生破坏,因此有必要从整体上评价桥梁的系统易损性。同时考虑桥墩、支座对桥梁系统易损性的影响,参考文献[20],采用一阶界限法计算桥梁系统失效概率的上界和下界,来逼近桥梁系统的易损性。
| $ \max\limits_{i=1}^n\left[P\left(F_i\right)\right] \leqslant P\left(F_{\mathrm{s}}\right) \leqslant 1-\prod\limits_{i=1}^n\left[1-P\left(F_i\right)\right] $ | (9) |
式中P(Fi)为第i个构件发生失效的概率,P(Fs)为桥梁系统失效概率,n为桥梁系统构件数量。
图 10分别给出了未加固和LRS FRP加固桥梁系统在各种破坏状态下易损性曲线的上界和下界。可看出对于“轻微破坏”与“中等破坏”,LRS FRP加固前后上下界基本接近,说明LRS FRP加固对这两种上下界影响不大;对于“严重破坏”及“完全破坏”,LRS FRP加固桥梁的上下界小于未加固桥梁,尤其当地震强度较大时,这种差距更为突出;LRS FRP加固得到的桥梁系统易损性曲线上下界与上述单个墩柱的影响规律基本一致。以上研究结果表明作者课题组提出的简化模型可有效评估算例桥梁的抗震性能。此外,该简化模型还适用于模拟其他各类LRS FRP加固圆形构件约束区混凝土材料的特性,可为LRS FRP加固结构的抗震分析提供一定的分析基础。
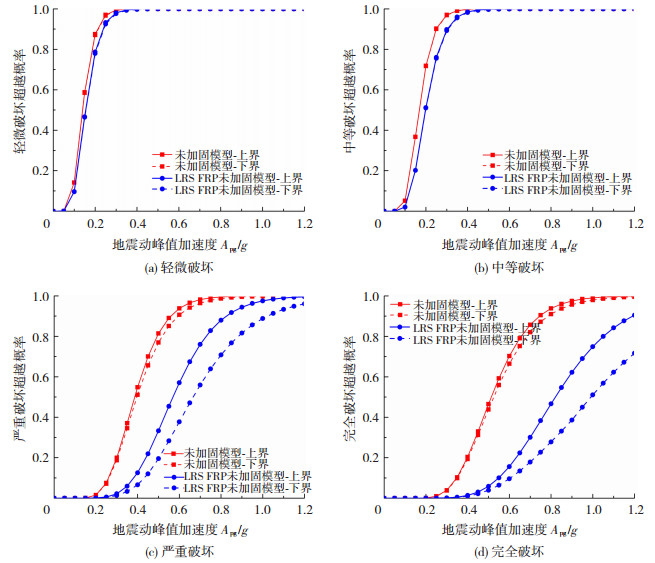
|
图 10 桥梁系统易损性曲线 Fig. 10 Fragility curves of bridge system |
根据作者课题组提出的简化LRS FRP约束混凝土往复轴压应力-应变模型,基于OpenSees平台,采用增量动力分析方法,对一典型三跨连续梁桥在LRS FRP加固前后的地震易损性进行了分析,研究了LRS FRP加固对桥梁抗震性能的影响,主要结论如下:
1) 轻微破坏和中等破坏状态下桥墩基本处于未受损伤的线弹性状态,比较LRS FRP加固前后两种状态桥墩的易损性曲线,二者基本吻合,说明LRS FRP加固对桥梁轻微破坏和中等破坏的地震易损性影响不大。
2) 严重破坏和完全破坏状态下,对比LRS FRP加固桥墩的易损性曲线,在同一损伤状态下,未加固桥梁的损伤超越概率明显大于LRS FRP加固的;当Apg为0.7 g时,未加固桥梁完全损伤即倒塌的概率达到了80%,存在倒塌的危险,经加固后,其倒塌概率降至了15%,加固效果较为明显。
3) 对于“轻微损伤”与“中等损伤”,LRS FRP加固前后上、下界基本接近,说明LRS FRP加固对这两种上、下界影响不大;对于“严重损伤”及“完全损伤”,FRP加固结构的上、下界小于未加固结构,尤其当地震强度较大时,这种差距更为突出。
4) 作者课题组提出的简化LRS FRP约束混凝土往复轴压模型可准确地评估LRS FRP加固桥梁的抗震性能,可为LRS FRP约束混凝土的工程实际应用提供参考。
| [1] |
HAROUN M A, MOSALLAM A S, FENG M Q, et al. Experimental investigation of seismic repair and retrofit of bridge columns by composite jackets[J]. Journal of Reinforced Plastics and Composites, 2003, 22(14): 1243. DOI:10.1177/0731684403035573 |
| [2] |
LEE C, SAM L. Development of FRP bridges in the UK—an overview[J]. Advances in Structural Engineering, 2010, 13(5): 823. DOI:10.1260/1369-4332.13.5.823 |
| [3] |
滕锦光. 新材料组合结构[J]. 土木工程学报, 2018, 51(12): 1. TENG Jinguang. New-material hybrid structures[J]. China Civil Engineering Journal, 2018, 51(12): 1. DOI:10.15951/j.tmgcxb.2018.12.001 |
| [4] |
BAI Y L, DAI J G, MOHAMMADI M, et al. Stiffness-based design-oriented compressive stress-strain model for large-rupture-strain (LRS) FRP-confined concrete[J]. Composite Structures, 2019, 223: 110953. DOI:10.1016/j.compstruct.2019.110953 |
| [5] |
SALEEM S, PIMANMAS A, QURESHI M I, et al. Axial behavior of PET FRP-confined reinforced concrete[J]. Journal of Composites for Construction, 2021, 25(1): 04020079. DOI:10.1061/(ASCE)CC.1943-5614.0001092 |
| [6] |
YE Y Y, LIANG S D, FENG P, et al. Recyclable LRS FRP composites for engineering structures: current status and future opportunities[J]. Composites Part B: Engineering, 2021, 212: 108689. DOI:10.1016/j.compositesb.2021.108689 |
| [7] |
DAI J G, LAM L, UEDA T. Seismic retrofit of square RC columns with polyethylene terephthalate (PET) fibre reinforced polymer composites[J]. Construction and Building Materials, 2012, 27(1): 206. DOI:10.1016/j.conbuildmat.2011.07.058 |
| [8] |
BAI Y L, DAI J G, TENG J G. Cyclic compressive behavior of concrete confined with large rupture strain FRP composites[J]. Journal of Composites for Construction, 2014, 18(1): 04013025. DOI:10.1061/(ASCE)CC.1943-5614.0000386 |
| [9] |
PIMANMAS A, SALEEM S. Evaluation of existing stress-strain models and modeling of PET FRP-confined concrete[J]. Journal of Materials in Civil Engineering, 2019, 31(12): 04019303. DOI:10.1061/(ASCE)MT.1943-5533.0002941 |
| [10] |
LAM L, TENG J G, CHEUNG C H, et al. FRP-confined concrete under axial cyclic compression[J]. Cement and Concrete Composites, 2006, 28(10): 949. DOI:10.1016/j.cemconcomp.2006.07.007 |
| [11] |
LAM L, TENG J G. Stress-strain model for FRP-confined concrete under cyclic axial compression[J]. Engineering Structures, 2009, 31(2): 308. DOI:10.1016/j.engstruct.2008.08.014 |
| [12] |
OZBAKKALOGLU T, AKIN E. Behavior of FRP-confined normal-and high-strength concrete under cyclic axial compression[J]. Journal of Composites for Construction, 2012, 16(4): 451. DOI:10.1061/(ASCE)CC.1943-5614.0000273 |
| [13] |
HANY N F, HANTOUCHE E G, HARAJLI M H. Axial stress-strain model of CFRP-confined concrete under monotonic and cyclic loading[J]. Journal of Composites for Construction, 2015, 19(6): 04015004. DOI:10.1061/(ASCE)CC.1943-5614.0000557 |
| [14] |
YU T, ZHANG B, TENG J G. Unified cyclic stress-strain model for normal and high strength concrete confined with FRP[J]. Engineering Structures, 2015, 102: 189. DOI:10.1016/j.engstruct.2015.08.014 |
| [15] |
LI P D, WU Y F, ZHOU Y W, et al. Cyclic stress-strain model for FRP-confined concrete considering post-peak softening[J]. Composite Structures, 2018, 201: 902. DOI:10.1016/j.compstruct.2018.06.088 |
| [16] |
BAI Y L, ZHANG Y F, JIA J F, et al. Simplified plasticity damage model for large rupture strain (LRS) FRP-confined concrete[J]. Composite Structures, 2022, 280: 114916. DOI:10.1016/j.compstruct.2021.114916 |
| [17] |
KARSAN I D, JIRSA J O. Behavior of concrete under compressive loadings[J]. Journal of the Structural Division, 1969, 95(12): 2543. DOI:10.1061/JSDEAG.0002424 |
| [18] |
HAZUS99. Earthquake loss estimation methodology: user's manual[M]. Washington: Federal Emergency Management Agency, 1999.
|
| [19] |
CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526. DOI:10.1061/(ASCE)0733-9445(2002)128:4(526) |
| [20] |
CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones[J]. Engineering Structures, 2004, 26(2): 187. DOI:10.1016/j.engstruct.2003.09.006 |
| [21] |
MUTHUKUMAR S, DESROCHES R. A Hertz contact model with non-linear damping for pounding simulation[J]. Earthquake Engineering and Structural Dynamics, 2006, 35: 811. DOI:10.1002/eqe.557 |
| [22] |
公路桥梁抗震设计规范: JTG/T 2231-01—2020[S]. 北京: 人民交通出版社, 2020 Specifications for seismic design of highway bridges: JTG/T 2231-01—2020[S]. Beijing: China Communications Press, 2020 |
| [23] |
HWANG H, LIU J B, CHIU Y H. Seismic fragility analysis of highway bridges[R]. [S. l. ]: Mid-America Earthquake Center, 2001
|
| [24] |
李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报, 2012, 45(10): 152. LI Lifeng, WU Wenpeng, HUANG Jiamei, et al. Study on system vulnerability of medium span reinforced concrete continuous girder bridge under earthquake excitation[J]. China Civil Engineering Journal, 2012, 45(10): 152. DOI:10.15951/j.tmgcxb.2012.10.005 |
| [25] |
吴文朋, 李立峰, 王连华, 等. 基于IDA的高墩大跨桥梁地震易损性分析[J]. 地震工程与工程振动, 2012, 32(3): 117. WU Wenpeng, LI Lifeng, WANG Lianhua, et al. Evaluation of seismic vulnerability of high-pier long-span bridge using incremental dynamic analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(3): 117. DOI:10.13197/j.eeev.2012.03.009 |
 2023, Vol. 55
2023, Vol. 55


