2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
重载、复杂建筑及基础设施随着国家发展不断涌现,钢管混凝土可有效利用混凝土和钢材的材料特性,具有一系列优越性能而广泛应用于重型承载结构[1-4]。然而在实际工程中,钢管混凝土柱逐渐暴露出不足之处。一方面,结构中常用的钢管混凝土柱在正常工作状态下都处于弹性工作范围[5],当所受的纵向荷载较小时,混凝土的横向变形小于钢管的横向变形,钢管不能很好地约束核心混凝土,对于采用高强混凝土的构件,两者脱离趋势更显著[6-7];当所受的纵向荷载较大时,核心混凝土产生弹塑性变形,虽然钢管相对而言能够较好地约束混凝土,但钢管处于轴向受压、环向及横向受拉的三轴异号受力状态,其承载力相对单轴受力时有所减弱。另一方面,随时间推移,核心混凝土会发生收缩徐变(收缩变形与徐变变形的总和即为长期变形),导致构件总变形增大,引起钢管和混凝土的内力重分布,使得结构体系各个组件的受力发生改变,将对结构产生不可忽略的影响[8-10]。此外,由于钢管混凝土柱直接暴露在空气中,其防火防腐问题需要特别注意。为提升和改善钢管混凝土柱的性能,可在钢管混凝土柱外套一层钢管,并在两层钢管间填充混凝土灌浆料(图 1),可加强对内部钢管混凝土的横向约束作用、提高构件承载力、增强塑性韧性和优化抗火性能,还可用于对结构中原有的钢管混凝土柱进行加固和修复[11]。本文主要研究核心混凝土应力比、内外层钢管总含钢率和内外层钢管含钢率比值对钢管约束的钢管混凝土轴压短柱长期变形的影响。

|
图 1 钢管约束的钢管混凝土柱示意 Fig. 1 Schematic of steel tube-confined concrete-filled steel tube column |
共设计了3个钢管混凝土短柱和22个钢管约束的钢管混凝土短柱(图 2),其中对9组共18个试件进行了持荷长达350 d的长期变形监测试验,另外1组共7个对比试件未施加荷载,只放置在相同环境中监测变形。设计的参数为内外层钢管含钢率比值、总含钢率和核心混凝土应力比。试件内层钢管的设计尺寸共有5种,分别为Φ165×1.0、Φ165×1.8、Φ165×2.5、Φ165×3.0、Φ165×4.0;外层钢管的名义截面尺寸共4种,分别为Φ219×1.0、Φ 219×1.5、Φ219×1.8、Φ219×2.5,试件开始加载时混凝土的龄期为28 d,各试件设计参数及实际尺寸见表 1,其中D1为内层钢管的外直径、t1为内层钢管的厚度、D2为外层钢管的外直径、t2为外层钢管厚度、L为试件长度、NL为长期施加在试件上的荷载设计值、α1为内层钢管含钢率、α2为外层钢管含钢率、α为总含钢率即内层钢管含钢率与外层钢管含钢率之和、n为内层钢管含钢率与外层钢管含钢率的比值。国外的混凝土收缩俆变模型在计算时一般采用混凝土圆柱体抗压强度,为了计算方便,用nc表示加载时刻核心混凝土应力与混凝土圆柱体抗压强度之比。选取试件长度L=500 mm,其长径比为3≤L/D1≤3.5。徐变试件需要在恒定荷载下长期持荷,为探究高应力状态下试件的长期性能,试件TCFST-0.35-2.5-1.5-a/b、TCFST-0.50-2.5-1.5-a/b和TCFST-0.65-2.5-1.5-a/b核心混凝土应力比nc分别取为0.35、0.50和0.65,其余试件核心混凝土的应力比nc取为0.35以保证核心区混凝土发生线性徐变。以TCFST-0.35-2.5-1.5-a为例说明试件编号规则:TCFST表示试件类型为钢管约束的钢管混凝土柱(steel tube-confined concrete-filled steel tube),CFST表示钢管混凝土柱(concrete-filled steel tube);0.35表示试件加载时混凝土截面的应力比为0.35;2.5表示内层钢管厚度为2.5 mm;1.5表示外层钢管厚度为2.5 mm;a、b和c表示同组具有相同参数的不同试件编号,a和b为长期持荷试验的2个试件,c为未加载的对比试件。表 2、3为材料力学性能,混凝土和钢材的材料性能根据标准试验方法[12-13]测得,其中Ec为混凝土弹性模量、μc为混凝土泊松比、fcu, 100为在开始对试件施加荷载的当天测得的混凝土立方体试块(边长100 mm)抗压强度平均值,fcu, 100经过换算可得到混凝土标准立方体试块抗压强度即fcu,同样经过换算可得到混凝土标准圆柱体抗压强度即fcm,换算系数[14]见表 4。

|
图 2 试件示意 Fig. 2 Schematic of specimens |
| 表 1 试件实际尺寸及详细参数表 Tab. 1 Actual size and detailed parameters of specimens |
| 表 2 钢材主要力学性能 Tab. 2 Main mechanical properties of steel |
| 表 3 混凝土主要力学性能 Tab. 3 Main mechanical performance of concrete |
| 表 4 不同形状和尺寸试件的混凝土单轴抗压强度换算系数 Tab. 4 Conversion coefficient of uniaxial compression strength of concrete of specimens with different shapes and sizes |
加载设备弹簧式压缩徐变仪见图 3,1台徐变仪可放置同一组的2个试件,放置时应保证上下试件同心以避免由于偏移对试验结果产生不良影响。油压千斤顶放置于徐变仪的上部和中部2个钢垫板之间,通过油泵施加和控制荷载,1台油泵通过3个阀门分别控制3台徐变仪。放置在中部钢垫板和压力板之间的压力传感器可监测荷载变化。在试件两边中部位置各布置一个纵向位移计,在试件中部三等分位置各布置一组应变片(图 4)。位移计型号为LVDT-V1-5MM,量程为0~5 mm,精度为0.01 mm。试验过程中数据由采集装置记录(图 5)。数据的采集频率为:在加载前100 d,每10 min采集一次,100 d之后,每30 min采集一次。另外,实验室采用了UPS备用电池可保证不间断供电。

|
图 3 弹簧式压缩徐变仪 Fig. 3 Spring-type compression creep tester |

|
图 4 位移计及应变片布置形式 Fig. 4 Arrangement form of displacement gauge and strain gauge |

|
图 5 数据采集系统XBY-2000 Fig. 5 Data acquisition system XBY-2000 |
混凝土养护到第28 d时对试件进行加载,在正式加载前分四级进行预加载,每级施加设计荷载的1/8,同一试件的2个位移计读数相差在10%以内即视为物理对中。预加载后分三级进行正式加载,每级施加设计荷载的1/3,同时记录位移传感器的数据以保证荷载施加位置为试件处于轴线,力传感器读数达到NL后拧紧中部钢垫板上排螺母。长期荷载持荷时间为350 d,季节跨度大、温湿度变化频繁,对试验数据的准确性有一定影响,采用空调及除湿机控制实验室温度为(20±5) ℃、湿度为60%±10%。同时由于混凝土发生收缩徐变使得反力杆提供的力有所下降,试件所受荷载也会随之降低,而温度变化引起油压千斤顶中的液压油热胀冷缩也会影响荷载,应实时监测力传感器读数,并允许荷载在(1±2%)NL范围内波动。若荷载降低超过2%,进行补载使荷载重新位于范围内。若补载后荷载提高超过2%,保持对应徐变仪的分流阀门打开以及其他分流阀门关闭,轻轻拧开总阀门卸掉部分油压并迅速拧紧总阀门。若油压卸载过多,可重复前述步骤进行加载,反复调整直至荷载达到规定范围,最后拧紧分阀门、松开总阀门。
1.3 试验结果经过350 d的持荷试验,得到试件的长期变形随时间变化的曲线。对比各组试验结果可知:在加载初期试件长期变形增长速率较快,后随时间增长而降低,前100 d时试件的长期变形能达到350 d时长期变形的60%~70%左右;试件的长期变形随应力比的提高而增大,且应力比越大其增长速率也越快(图 6);当总含钢率不变时,钢管约束的钢管混凝土柱试件的长期变形随内外层钢管含钢率比值的增大而减小,当内外层钢管含钢率比值从0.30增大到1.25和2.23时,试件在350 d的长期变形分别减小了约25%和40%(图 7)。

|
图 6 核心混凝土应力比的影响 Fig. 6 Influence of stress ratio of core concrete |

|
图 7 内外层钢管含钢率比值的影响 Fig. 7 Influence of steel ratio between inner and outer steel tubes |
当内外层钢管含钢率比值不变时,钢管约束的钢管混凝土柱试件的长期变形随总含钢率的增大而减小,当总含钢率从5.8%增大到10.5%和15.0%时,试件在350 d的长期变形分别减小了约15%和30%(图 8)。

|
图 8 总含钢率的影响 Fig. 8 Influence of total steel ratio |
收缩和徐变在结构施工和使用期间持续存在,若能正确预测收缩徐变,对优化设计、指导施工以及进行维护具有重要意义。本节基于素混凝土的长期变形理论计算模型,根据钢管约束的钢管混凝土柱在纵向荷载作用下的受力机理及各材料的相互作用推导了适用于钢管约束的钢管混凝土长期变形的理论计算方法:根据内层钢管与核心混凝土纵向变形协调条件、各层材料横向及环向变形协调条件、各材料的本构关系和平衡条件列出方程式,联立方程式求解,得到加载初期t0时刻核心混凝土、内外层钢管和夹层灌浆料截面的应力应变值;在素混凝土长期变形计算模型的基础上,考虑了内层钢管和核心混凝土的应力重分布作用,并结合截面平衡条件、变形协调条件和各材料的本构关系,联立求得ti-ti-1时间段内各材料的截面应力应变增量,进而可求得任意ti时刻核心混凝土、内外层钢管和夹层灌浆料截面的应力应变值。
在纵向荷载作用下,钢管约束的钢管混凝土柱主要由核心混凝土和内层钢管共同承担纵向荷载,外层钢管主要提供横向约束作用。在推导计算方法之前,先做以下假设:应力较小时徐变为线性徐变且多轴徐变符合叠加原理;内层钢管、外层钢管的长期变形较小,可忽略不计;夹层灌浆料的横向长期变形较小且对其能够提供的约束力影响不大,可以不考虑夹层灌浆料的长期变形,且在低应力状态下夹层灌浆料能保持弹性工作状态;内层钢管与核心混凝土、外层钢管与夹层灌浆料不产生相对滑移,能够共同工作,且内层钢管、外层钢管和夹层灌浆料横向变形协调;纵向力主要由内层钢管和核心混凝土共同承担,外层钢管及夹层灌浆料所受的纵向力很小,可以忽略不计。公式推导过程中的符号规定为:压应力为正,拉应力为负。
2.1.1 加载时刻t0的变形分析在钢管约束的钢管混凝土柱上施加恒定荷载N时,内层钢管和核心混凝土为三向受力(图 9、10),内层钢管截面的横向应力很大程度上小于环向应力,可视为双向受力状态,且构件纵向应变协调,则有
| $ \boldsymbol{\varepsilon}_{\mathrm{bv}, 0}=\boldsymbol{\varepsilon}_{\mathrm{cv}, 0} $ | (1) |

|
图 9 内层钢管受力示意 Fig. 9 Stress of inner steel tube |

|
图 10 核心混凝土受力示意 Fig. 10 Stress of core concrete |
式中:εbv, 0为t0时刻内层钢管发生的纵向应变,εcv, 0为t0时刻核心混凝土发生的纵向应变。
核心混凝土和内层钢管以各自刚度共同承受纵向力,根据受力平衡
| $ N=\sigma_{\mathrm{bv}, 0} A_{\mathrm{b}}+\sigma_{\mathrm{cv}, 0} A_{\mathrm{c}} $ | (2) |
式中:N为施加在试件上的恒定荷载,σbv, 0为t0时刻内层钢管纵向的应力,σcv, 0为t0时刻核心混凝土的纵向应力,Ab为内层钢管横截面面积,Ac为混凝土横截面面积。
核心混凝土处于三向受力状态,其本构关系满足:
| $ \varepsilon_{\mathrm{cv}, 0}=\frac{1}{E_{\mathrm{c}, 0}}\left(\sigma_{\mathrm{cv}, 0}-2 \mu_{\mathrm{c}} \sigma_{\mathrm{ch}, 0}\right) $ | (3) |
| $ \boldsymbol{\varepsilon}_{\mathrm{ch}, 0}=\frac{1}{E_{\mathrm{c}, 0}}\left[\left(1-\mu_{\mathrm{c}}\right) \sigma_{\mathrm{ch}, 0}-\mu_{\mathrm{c}} \sigma_{\mathrm{cv}, 0}\right] $ | (4) |
式中:εcv, 0为t0时刻混凝土纵向应变,Ec, 0为t0时刻混凝土弹性模量,μc为t0时刻混凝土泊松比,σch, 0为t0时刻混凝土横向应力,εch, 0为t0时刻混凝土横向应变。
核心混凝土的横向应变与内层钢管相互协调,则
| $ \boldsymbol{\varepsilon}_{\mathrm{ch}, 0}=\boldsymbol{\varepsilon}_{\mathrm{bs}, 0}=\boldsymbol{\varepsilon}_{\mathrm{bh}, 0} $ | (5) |
式中:εch, 0为t0时刻核心混凝土横向应变,εbs, 0为t0时刻内层钢管横向应变,εbh, 0为t0时刻内层钢管环向应变。
内层钢管处于平面应力状态,其本构关系为:
| $ \varepsilon_{\mathrm{bh}, 0}=\frac{1}{E_{\mathrm{s} 1}}\left(\sigma_{\mathrm{bh}, 0}-\mu_{\mathrm{s1}} \sigma_{\mathrm{bv}, 0}\right) $ | (6) |
| $ \varepsilon_{\mathrm{bv}, 0}=\frac{1}{E_{\mathrm{s} 1}}\left(\sigma_{\mathrm{bv}, 0}-\mu_{\mathrm{s} 1} \sigma_{\mathrm{bh}, 0}\right) $ | (7) |
式中:Es1为内层钢管弹性模量,μs1为内层钢管泊松比,σbh, 0为t0时刻内层钢管受到的环向应力。
根据横向力平衡
| $ 2 t_1 \sigma_{\mathrm{bh}, 0}=-\sigma_{\mathrm{ch}, 0}\left(D_1-2 t_1\right)+\sigma_{\text {chs} 1,0} D_1 $ | (8) |
式中:t1为内层钢管壁厚,D1为内层钢管外直径,σchs1, 0为t0时刻夹层灌浆料对内层钢管的横向约束应力。
夹层灌浆料受力情况见图 11,横向应力较远小于环向应力,可认为处于单轴应力状态,根据夹层灌浆料的本构关系以及横向力平衡:
| $ \boldsymbol{\varepsilon}_{\text {chslh}, 0}=\frac{\sigma_{\text {chslh}, 0}}{E_{\mathrm{c}}} $ | (9) |
| $ \sigma_{\text {chsll}, 0}\left(D_2-D_1-2 t_2\right)=\sigma_{\text {shs}, 0}\left(D_2-2 t_2\right)-\sigma_{\text {chsl}, 0} D_1 $ | (10) |

|
图 11 夹层灌浆料受力情况 Fig. 11 Stress of interlayer grouting material |
式中:t2为外层钢管壁厚,D2为外层钢管外直径,Ec为夹层灌浆料的弹性模量,σshsl, 0为t0时刻外层钢管对夹层灌浆料的横向约束应力,σchslh, 0为t0时刻夹层灌浆料受到的环向应力,εchslh, 0为t0时刻夹层灌浆料受到的环向应变。
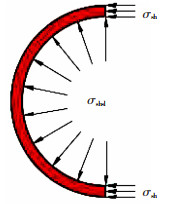
外层钢管受力情况见图 12,同时夹层灌浆料与外层钢管及核心混凝土横向、环向变形协调,则有:
| $ \boldsymbol{\varepsilon}_{\mathrm{bh}, 0}=\boldsymbol{\varepsilon}_{\text {chslh}, 0} $ | (11) |
| $ \boldsymbol{\varepsilon}_{\mathrm{sh}, 0}=\boldsymbol{\varepsilon}_{\mathrm{chslh}, 0} $ | (12) |
|
图 12 外层钢管受力情况 Fig. 12 Stress of outer steel tube |
式中:εbh, 0为t0时刻外层钢管横向应变,εchslh, 0为t0时刻核心混凝土横向应变。
外层钢管处于单轴应力状态,根据外层钢管的本构关系以及横向力平衡条件,则有:
| $ \varepsilon_{\mathrm{sh}, 0}=\frac{1}{E_{\mathrm{s} 2}} \sigma_{\mathrm{sh}, 0} $ | (13) |
| $ \sigma_{\text {sh}, 0}=-\frac{D_2-2 t_2}{2 t_2} \sigma_{\text {shsl}, 0} $ | (14) |
式中:σsh, 0为t0时刻外层钢管环向应力,εsh, 0为t0时刻外层钢管环向应变,Es2为外层钢管弹性模量。
t0时刻混凝土、内层钢管、外层钢管和夹层灌浆料的应力和应变值可联立式(1)~式(14)解得。
2.1.2 任意时刻构件的变形分析由文献[15]可知,混凝土在任意(ti-ti-1)时间段内受三向变应力时,理论纵向长期变形增量Δεcv, i和理论横向长期变形增量Δεch, i的计算公式为:
| $ \begin{gathered} \Delta \varepsilon_{\mathrm{cv}, i}=\left(\sigma_{\mathrm{cv}, 0}-2 \mu_{\mathrm{cp}, \mathrm{u}} \sigma_{\mathrm{ch}, 0}\right) \frac{\varphi\left(\tau_i, \tau_0\right)-\varphi\left(\tau_{i-1}, \tau_0\right)}{E_{\mathrm{c}, 0}}-\sum\limits_{j=1}^{i-2}\left(\Delta \sigma_{\mathrm{cv}, j}-2 \mu_{\mathrm{cp}, \mathrm{u}} \Delta \sigma_{\mathrm{ch}, j}\right) \times \\ \frac{\varphi\left(\tau_i, \tau_j\right)-\varphi\left(\tau_{i-1}, \tau_j\right)}{E_{\mathrm{c}, j}}-\left(\Delta \sigma_{\mathrm{cv}, i-1}-2 \mu_{\mathrm{cp}, \mathrm{u}} \Delta \sigma_{\mathrm{ch}, i-1}\right) \frac{\varphi\left(\tau_i, \tau_{i-1}\right)}{E_{\mathrm{c}, i-1}}+\varepsilon_{\mathrm{sh}, \mathrm{v}}\left(\tau_i, \tau_{i-1}\right) \end{gathered} $ | (15) |
| $ \begin{aligned} \Delta \varepsilon_{\mathrm{ch}, i}= & {\left[\left(1-\mu_{\mathrm{cp}, \mathrm{u}}\right) \sigma_{\mathrm{ch}, 0}-\mu_{\mathrm{cp}, \mathrm{u}} \sigma_{\mathrm{cv}, 0}\right] \frac{\varphi\left(\tau_i, t_0\right)-\varphi\left(\tau_{i-1}, t_0\right)}{E_{\mathrm{c}, 0}}-\\ \sum\limits_{j=1}^{i-2}\left[\left(1-\mu_{\mathrm{cp}, \mathrm{u}}\right) \Delta \sigma_{\mathrm{ch}, j}-\mu_{\mathrm{cp}, \mathrm{u}} \Delta \sigma_{\mathrm{cv}, j}\right] \times} \\ & \frac{\varphi\left(\tau_i, \tau_j\right)-\varphi\left(\tau_{i-1}, \tau_j\right)}{E_{\mathrm{c}, j}}-\left[\left(1-\mu_{\mathrm{cp}, \mathrm{u}}\right) \Delta \sigma_{\mathrm{ch}, i-1}-\\\mu_{\mathrm{cp}, \mathrm{u}} \Delta \sigma_{\mathrm{cv}, i-1}\right] \frac{\varphi\left(\tau_i, \tau_{i-1}\right)}{E_{\mathrm{c}, i-1}}+\varepsilon_{\mathrm{sh}, \mathrm{h}}\left(\tau_i, \tau_{i-1}\right) \end{aligned} $ | (16) |
式中:Δεcv, i为(τi-τi-1)时间段内混凝土的纵向收缩徐变,Δεch, i为(τi-τi-1)时间段内混凝土的横向收缩徐变,Ec, j为τj时刻混凝土弹性模量,μcp, u为单轴受压时核心混凝徐变泊松比,Δσcv, i为(τi-τi-1)时间段内混凝土所产生的纵向应力增量,Δσch, i为(τi-τi-1)时间段内混凝土的横向应力增量,φ(τi, τi-1)为(τi-1-τi)时间段内混凝土的徐变系数,εsh, v(τi,τi-1)为(τi-τi-1)时间段内混凝土的纵向收缩变形,εsh, h(τi,τi-1)为(τi-τi-1)时间段内混凝土的横向收缩变形。
内层钢管横截面与核心混凝土横截面之间由于产生了应力重分布,所以实际的混凝土的纵向和横向长期变形增量会小于理论值。内层钢管与混凝土的真实纵向、横向变形之间相互协调,则有:
| $ \Delta \varepsilon_{\mathrm{cl}, i}=\Delta \varepsilon_{\mathrm{bv}, i} $ | (17) |
| $ \Delta \varepsilon_{\mathrm{c} 2, i}=\Delta \varepsilon_{\mathrm{bs}, i}=\Delta \varepsilon_{\mathrm{bh}, i} $ | (18) |
式中:Δεc1, i为(ti-ti-1)时间段内混凝土发生的纵向应变实际增量,Δεbv, i为(ti-ti-1)时间段内内层钢管发生的纵向应变实际增量,Δεc2, i为(ti-ti-1)时间段内混凝土发生的横向应变实际增量,Δεbs, i为(ti-ti-1)时间段内内层钢管发生的横向应变实际增量,Δεbh, i为(ti-ti-1)时间段内外层钢管发生的环向应变实际增量。
混凝土在(ti-ti-1)时间段内发生收缩徐变使得内层钢管被压缩Δεc1, i,而混凝土被拉伸(Δεcv, i-Δεc1, i),则混凝土及内层钢管的受力关系:
| $ \Delta \varepsilon_{\mathrm{cv}, i}-\Delta \varepsilon_{\mathrm{cl}, i}=-\frac{1}{E_{\mathrm{c}, i}}\left(\Delta \sigma_{\mathrm{cv}, i}-2 \mu_{\mathrm{cpv}} \Delta \sigma_{\mathrm{ch}, i}\right) $ | (19) |
| $ \Delta \varepsilon_{\mathrm{ch}, i}-\Delta \varepsilon_{\mathrm{c} 2, i}=-\frac{1}{E_{\mathrm{c}, i}}\left[\left(1-\mu_{\mathrm{cph}}\right) \Delta \sigma_{\mathrm{ch}, i}-\mu_{\mathrm{cph}} \Delta \sigma_{\mathrm{cv}, i}\right] $ | (20) |
| $ \Delta \varepsilon_{\mathrm{bh}, i}=\frac{1}{E_{\mathrm{s} 1}}\left(\Delta \sigma_{\mathrm{bh}, i}-\mu_{\mathrm{s} 1} \Delta \sigma_{\mathrm{bv}, i}\right) $ | (21) |
| $ \Delta \varepsilon_{\mathrm{bv}, i}=\frac{1}{E_{\mathrm{sl}}}\left[\Delta \sigma_{\mathrm{bv}, i}-\mu_{\mathrm{sl}} \Delta \sigma_{\mathrm{bh}, i}\right] $ | (22) |
式中:Δσbh, i为(ti-ti-1)时间段内内层钢管环向应力增量,Δσbv, i为(ti-ti-1)时间段内内层钢管纵向应力增量,Δσch, i为(ti-ti-1) 时间段内核心混凝土横向应力增量,Δσcv, i为(ti-ti-1)时间段内核心混凝土纵向应力增量,Ec, i为ti时刻核心混凝土弹性模量,μcpv、μcph分别为核心混凝土的纵向和横向泊松比。
混凝土和内层钢管在收缩徐变的过程中发生了应力重分布,混凝土减小的纵向力和内层钢管增大的力大小相等,根据平衡条件则有:
| $ A_{\mathrm{c}} \Delta \sigma_{\mathrm{cv}, i}+A_{\mathrm{b}} \Delta \sigma_{\mathrm{bv}, i}=0 $ | (23) |
| $ 2 t_1 \Delta \sigma_{\mathrm{bh}, i}=-\Delta \sigma_{\mathrm{ch}, i}\left(D_1-2 t_1\right)+\Delta \sigma_{\text {chsl}, i} D_1 $ | (24) |
式中Δσchsl, i为(ti-ti-1)时间段内夹层灌浆料对内层钢管环向约束应力增量。
内层钢管和夹层灌浆料横向变形协调,同时考虑夹层灌浆料本构关系以及横向力平衡条件:
| $ \Delta \varepsilon_{\text {chslh}, i}=\Delta \varepsilon_{\mathrm{bh}, i} $ | (25) |
| $ \Delta \varepsilon_{\text {chslh}, i}=\frac{\Delta \sigma_{\text {chslh}, i}}{E_{\mathrm{c}}} $ | (26) |
| $ \Delta \sigma_{\text {shs}, i}\left(D_2-2 t_2\right)-\Delta \sigma_{\text {chsl}, i} D_1 $ | (27) |
式中:Δεchslh, i为(ti-ti-1)时间段内夹层灌浆料环向应变实际增量,Δεbh, i为(ti-ti-1)时间段内层钢管横向应变实际增量,Δσchslh, i为(ti-ti-1)时间段内夹层灌浆料环向应力实际增量,Δσchsl, i为(ti-ti-1)时间段内夹层灌浆料对内层钢管横向约束应力增量,Δσshsl, i为(ti-ti-1)时间段内夹层灌浆料对外层钢管横向约束应力增量。
外层钢管和夹层灌浆料横向变形协调,同时考虑外层钢管本构关系以及横向力平衡条件,则有:
| $ \Delta \varepsilon_{\text {chslh}, i}=\Delta \varepsilon_{\mathrm{sh}, i} $ | (28) |
| $ \Delta \varepsilon_{\mathrm{sh}, i}=\frac{\Delta \sigma_{\mathrm{sh}, i}}{E_{\mathrm{s} 2}} $ | (29) |
| $ \Delta \sigma_{\text {sh}, i} 2 t_2=-\Delta \sigma_{\text {shsl}, i}\left(D_2-2 t_2\right) $ | (30) |
式中:Δεsh, i为(ti-ti-1)时间段内外层钢管发生的环向应变实际增量,Δσsh, i为(ti-ti-1)时间段内外层钢管发生的环向应力实际增量。
联立式(15)~式(30) 可解得任意ti-1时刻到ti时刻各层截面的应力及和应变变化值,进一步可以求得任意时刻各层截面的应力和应变值。本文计算收缩徐变变形的总时长为350 d,时间步长按如下划分[16]:
| $ \tau_1=\tau_0+\frac{\left(\tau_k-\tau_0\right)}{k \tau_k} $ | (31) |
| $ \boldsymbol{\tau}_j=\tau_0+\left(k \tau_k\right)^{1 /(k-1)}\left(\boldsymbol{\tau}_{j-1}-\tau_0\right) $ | (32) |
式中:τ0为开始发生徐变的时间,τk为徐变结束的时间,k为划分点数,τj为在τ0与τk之间的任意时间,j=2, 3, 4, …, k-1, k。
2.2 理论计算结果与试验结果对比分析计算理论曲线时,为确定素混凝土收缩徐变计算模型,对目前可收集到的CEB-FIP 2010、ACI和EC模型[17-19]都进行了试算,试算时取钢管内混凝土相对湿度HR=100%[20]。各模型计算结果与实测结果总体吻合较好(图 13),由于CEB-FIP 2010模型应用范围更广,下面分析中选取CEB-FIP 2010模型进行计算。另外,相对湿度对混凝土收缩徐变变形的影响较大,有研究者认为钢管内核心混凝土处于密闭环境中,初期100%的相对湿度会随着混凝土水化消耗水分而降低[21]。

|
图 13 采用不同收缩徐变模型计算结果对比 Fig. 13 Comparison of calculation results between different shrinkage and creep models |
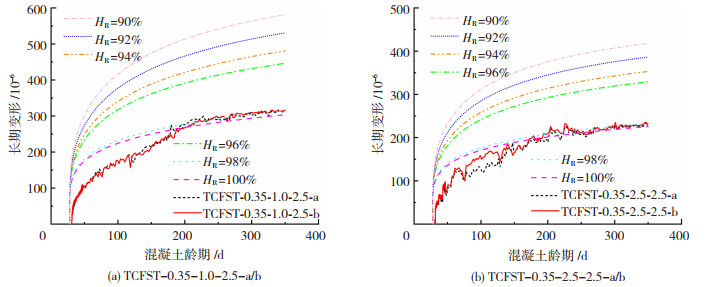
目前在钢管混凝土长期变形的研究中,常将钢管内混凝土的对湿度设为90%~100%[22-26]。为探究CEB-FIP 2010模型采用不同相对湿度值对理论计算结果的影响,相对湿度分别选取为90%、92%、94%、96%、98 %、100%进行计算,并与试验值进行对比(图 14),可以看出当相对湿度取98%~ 100%时,模拟结果与试验值吻合较好。建议计算钢管约束的钢管混凝土柱长期变形时采用CEB-FIP 2010模型,并取相对湿度为100%。按照此建议对钢管约束的钢管混凝土试件进行了分析计算,部分计算结果见图 15。可以看出理论分析结果和实测结果整体发展趋势基本吻合,但在前期长期变形发展较快阶段,二者吻合程度不如后期长期变形逐步趋于稳步增长阶段。所提出的计算方法可以较经济和方便的获得钢管约束的钢管混凝土柱长期变形预测结果,免除耗时长、场地占用大、长期空间温湿度控制和监测的人力和经济投入,具有重要的理论和工程实用价值。
|
图 14 相对湿度变化对计算结果的影响 Fig. 14 Influence of relative humidity changes on calculation results |

|
图 15 理论分析结果与试验结果对比 Fig. 15 Comparison between theoretical analysis results and test results |
通过16个钢管约束的钢管混凝土短柱和2个钢管混凝土短柱的长达350 d持荷试验的结果分析和理论计算,对钢管约束的钢管混凝土短柱长期变形性能得到以下结论:
1) 钢管约束的钢管混凝土柱的长期变形在加载初期发展较快,增长速率随时间增长而逐渐降低;应力比增大则长期变形随之增大;总含钢率或内层与外层钢管含钢率比值的增大均表现为长期变形的减小。
2) 采用不同混凝土收缩徐变模型计算长期变形时,相对湿度的影响程度不同,建议采用CEB-FIP 2010模型来计算钢管约束的钢管混凝土柱的长期变形,相对湿度取100%。
3) 本文提出的长期变形分析计算方法可以方便地预测钢管约束的钢管混凝土柱在长期荷载作用下的变形性能,替代占用空间和时间和环境温湿度控制的投入,具有重要的参考价值。
| [1] |
韩林海, 牟廷敏, 王法承, 等. 钢管混凝土混合结构设计原理及其在桥梁工程中的应用[J]. 土木工程学报, 2020, 53(5): 4. HAN Linhai, MU Tingmin, WANG Facheng, et al. Design theory of CFST (concrete-filled steel tubular) mixed structures and its applications in bridge engineering[J]. China Civil Engineering Journal, 2020, 53(5): 4. |
| [2] |
GUO J J. A review of research on seismic behavior of concrete filled steel tubular columns[J]. International Core Journal of Engineering, 2019, 5(7): 33. |
| [3] |
席龙辉. 钢管混凝土结构在桥梁建设中的应用分析[J]. 住宅与房地产, 2020(24): 195. XI Longhui. Application analysis of concrete filled steel tubular structure in bridge construction[J]. Housing and Real Estate, 2020(24): 195. |
| [4] |
WANG Haolei, SUN Tao, TANG Chen, et al. Experimental and numerical investigation of steel-ultra-high-performance concrete continuous composite beam behavior[J]. Advances in Structural Engineering, 2020, 23(10): 2220. DOI:10.1177/1369433220911140 |
| [5] |
KWAN A K H, DONG C X, HO J C M. Axial and lateral stress-strain model for circular concrete-filled steel tubes with external steel confinement[J]. Engineering Structures, 2016, 117: 528. DOI:10.1016/j.engstruct.2016.03.026 |
| [6] |
XIONG M X, XIONG D X, LIEW J Y R. Axial performance of short concrete filled steel tubes with high and ultra-high-strength materials[J]. Engineering Structures, 2017, 136: 494. DOI:10.1016/j.engstruct.2017.01.037 |
| [7] |
李健. 圆钢管约束的钢管混凝土短柱基本力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 LI Jian. Study on axial compression behavior of concrete filled steel tubular short columns restrained by steel tubes[D]. Harbin: Harbin Institute of Technology, 2018 |
| [8] |
HAVLASEK P, SMILAUER V, DOHNALOVA L, et al. Shrinkage-induced deformations and creep of structural concrete: 1-year measurements and numerical prediction[J]. Cement and Concrete Research, 2021, 144: 106402. DOI:10.1016/j.cemconres.2021.106402 |
| [9] |
AN G H, KIM J K. Relationship between the wide-flange steel and the long-term deformation of steel-reinforced concrete columns[C]// International Conference on Construction Materials and Structures. [S. l. ]: University of Johannesburg, 2014: 378
|
| [10] |
ZHENG Zhihui, HU Di, LIU Peng, et al. Considering the effect of the randomness of concrete strength and relative humidity on concrete creep[J]. Structural Concrete, 2021, 22(S1). |
| [11] |
卢炜. 钢管约束的钢管混凝土短柱轴压性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 LU Wei. Mechanical behavior of steel-tube-confined concrete-filled steel tubular stubs under axial compression[D]. Harbin: Harbin Institute of Technology, 2018 |
| [12] |
普通混凝土力学性能试验方法标准: GB/T 50081—2016[S]. 北京: 中国建筑工业出版社, 2016 Standard for test methods of mechanical properties of ordinary concrete: GB/T 50081—2016[S]. Beijing: China Architecture & Building Press, 2016 |
| [13] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1-2010[S]. 北京: 中国建筑工业出版社, 2010 Metallic materials—tensile testing—part 1: method of test at room temperature: GB/T 228.1—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [14] |
过镇海. 混凝土的强度和本构关系[M]. 北京: 中国建筑工业出版社, 2004: 145. GUO Zhenhai. Strength and constitutive relationship of concrete[M]. Beijing: China Architecture & Building Press, 2004: 145. |
| [15] |
李翔. 长期荷载作用下钢管约束钢筋混凝土轴压短柱徐变性能[D]. 哈尔滨: 哈尔滨工业大学, 2019 LI Xiang. Creep behavior of axially loaded reinforced-concrete stub columns constrained by steel tubes under sustained loading[D]. Harbin: Harbin Institute of Technology, 2019 |
| [16] |
GILBERT R I, RANZI G. Time-dependent behaviour of concrete structures[M]. London: CRC Press, 2011: 99.
|
| [17] |
CEB-FIP model code for concrete structures 2010[S]. Lausanne: International Federation for Structural Concrete, 2010
|
| [18] |
Prediction of creep, shrinkage and temperature effects in concrete structures: 209R-92[S]. Farmington Hills: ACI Committee, 1992
|
| [19] |
Eurocode 2: design of concrete structures[S]. Brussels: European Committee for Standardization, 2004
|
| [20] |
马迪. 考虑温度影响的钢管混凝土长期静力性能分析[D]. 哈尔滨: 哈尔滨工业大学, 2015 MA Di. Long-term static behaviour of concrete-filled steel tubes influenced by temperatures[D]. Harbin: Harbin Institute of Technology, 2015 |
| [21] |
高原. 干湿环境下混凝土收缩与收缩应力研究[D]. 北京: 清华大学, 2013 GAO Yuan. Studies on shrinkage and shrinkage stresses of concrete under dry-wet environment[D]. Beijing: Tsinghua University, 2013 |
| [22] |
赵哲. 钢管混凝土收缩徐变性能研究[D]. 成都: 西南交通大学, 2016 ZHAO Zhe. Study on shrinkage and creep of concrete filled steel tube[D]. Chengdu: Southwest Jiaotong University, 2016 |
| [23] |
赵金钢, 赵人达, 占玉林. 钢管混凝土轴心受压构件徐变计算方法及徐变模型对比分析[J]. 公路交通科技, 2013, 30(4): 46. ZHAO Jingang, ZHAO Renda, ZHAN Yulin. Comparative analysis of creep calculation methods and creep models for axially compressed CFST members[J]. Journal of Highway and Transportation Research and Development, 2013, 30(4): 46. |
| [24] |
王永宝, 赵人达, 徐腾飞, 等. 钢管混凝土轴压构件徐变简化计算方法研究[J]. 公路交通科技, 2016, 33(1): 57. WANG Yongbao, ZHAO Renda, XU Tengfei, et al. Study on simplified creep calculation method of CFST members under axial loading[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 57. |
| [25] |
韩林海, 刘威. 长期荷载作用对圆钢管混凝土压弯构件力学性能影响的研究[J]. 土木工程学报, 2002, 35(2): 8. HAN Linhai, LIU Wei. The effects of long-time loading on the behavior of concrete-filled steel tubular member[J]. China Civil Engineering Journal, 2002, 35(2): 8. |
| [26] |
陈松林. 钢管混凝土收缩徐变试验研究[D]. 广州: 广州大学, 2018 CHEN Songlin. Experimental study on shrinkage and creep of concrete filled steel tube[D]. Guangzhou: Guangzhou University, 2018 |
 2023, Vol. 55
2023, Vol. 55


