2. 北京交通大学 土木建筑工程学院,北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044
管涌、泥石流、翻浆冒泥均是由孔隙流体流动驱动土体颗粒运移诱发的工程病害,其根源在于孔隙流体与土体颗粒之间的相互作用。因此,深入研究流体流动和固体变形之间的耦合机制,以及合理预测土颗粒运移过程对于岩土工程建设与安全运营至关重要[1-5]。1943年Terzaghi[6]基于连续介质力学的基本假设提出了有效应力原理,为探究多孔介质中有效应力与孔隙水压力之间的关系提供了理论基础。有效应力原理的提出标志着岩土力学流-固耦合研究的开始。Biot[7-8]进一步研究了土体材料与孔隙压力的相互作用,并通过假设流体在土体孔隙中的流动遵循达西定律,建立了固结理论。随后,学者们分别基于不同孔隙材料的假设展开了理论研究,取得了大量有益的研究成果[9-17]。然而,由于流-固耦合问题涉及众多非线性因素,难以通过理论推导获得解析解,因此将流-固耦合理论与数值模拟方法相结合成为分析流-固耦合问题的常用途径。
近年来,学者们[18-21]将基于连续介质力学的耦合本构模型与有限单元法(FEM)相结合,用于流-固耦合问题的数值计算,已经取得了大量有益的研究成果。雷小芹等[18]采用FEM程序,模拟了降雨作用下一维非饱和堆积土内部的渗流潜蚀耦合响应过程。Mekonnen[20]则利用FEM分析了完全饱和的铁路路基在列车循环荷载作用下的孔隙水压力响应过程。FEM在模拟连续介质的变形方面具有独特的优势。然而,由于土体是颗粒状的离散介质,FEM基于连续介质的假设无法准确模拟土体中单个颗粒的细观行为。为更深入理解和更准确地预测颗粒-流体的相互作用,需要采用非连续数值方法来解释和预测土体的非连续变形。离散单元法(DEM)[22]不依赖于连续介质假设与宏观本构关系,在模拟土体非连续变形和大变形流动方面具有显著优势,已逐渐成为研究颗粒材料细观行为和宏观特性之间关系的强大工具[23-26]。
基于DEM,学者们开发了多种耦合计算模型[27-31],如晶格玻尔兹曼-离散元单元模型(LB-DEM)[27]、计算流体力学-离散单元模型(CFD-DEM)[28]、连续-离散耦合模型(Combined FDEM)[29]以及比例边界有限元-离散元模型(SBFEM-DEM)[30]等。在CFD-DEM耦合模型中,流体与土颗粒之间的相互作用不再依赖于有效应力原理,而是基于CFD控制方程模拟流体的宏观特性(如流动速度、水压力等),同时基于DEM表征颗粒的非连续变形。该模型将连续介质(流体)和离散介质(颗粒)相结合,能够同时从宏观和细观角度深入理解颗粒-流体系统的行为。此外,CFD-DEM模型能够表征渗流过程中土颗粒随时间变化的不连续空间分布特征,从而更精确地模拟渗流现象,为从细观尺度研究颗粒迁移及流-固耦合的力学响应与机理提供了有效的途径[32-36]。
基于CFD-DEM的流-固耦合方法已广泛应用于岩土工程中渗流引起的颗粒尺寸分布变化、理想颗粒堆积体内的渗流,以及颗粒在流体中的沉降等经典问题。Mondal等[37]使用CFD-DEM方法对颗粒在变截面槽道内的运移过程进行了模拟,合理预测了颗粒堵塞后形成的颗粒堆积体中的压降。Xiong等[38]通过考虑粒径分布、流速以及入流颗粒浓度,研究了渗流作用下细颗粒在多孔骨架中渗透迁移和滞留的宏观现象和细观成因。Mu等[39]研究了不同水力梯度与细颗粒含量影响下,双峰土壤内部侵蚀过程。Zou等[40]基于CFD-DEM方法,旨在分析渗流过程中土体内部的间隙级配、孔隙比及颗粒的分布随时间的分布变化规律,以研究土体级配与水力梯度对渗流侵蚀的影响。
CFD-DEM耦合方法在岩土工程中具有广泛的应用前景,特别是在理想堆积体孔隙渗流、间隙级配土体侵蚀变形等问题的分析方面显示出显著优势。然而,目前尚缺乏对CFD-DEM流-固耦合数值方法的系统总结以及未来研究趋势的深入了解。本文基于对CFD-DEM流-固耦合数值模型研究现状的回顾,系统概括了现有流-固耦合计算方法的优缺点,重点论述了CFD-DEM耦合方法的建模策略,包括固相颗粒形状建模与粒间接触模型、流体相控制方程及参数计算方法以及CFD-DEM耦合计算,并就相关问题进行了深入探讨,提出了CFD-DEM耦合方法未来的研究方向。
1 流-固耦合计算方法流-固耦合计算方法是模拟和分析流体与固体之间相互作用和力学响应规律的数值方法。在岩土工程中,存在数量庞大且形状各异的土颗粒,土体孔隙结构极其复杂[41-42],流体通过土体孔隙导致土颗粒发生运移,进而引发渗蚀、渗滤和冲刷等问题。采用流-固耦合方法揭示水土相互作用引起的土体灾害发生机制、预测灾害发展过程,为岩土工程问题提供新的研究视角和手段[43-45]。目前,流-固耦合计算方法主要有:Euler-Euler法[46];Lagrange-Lagrange法[47];Euler-Lagrange法[48]。
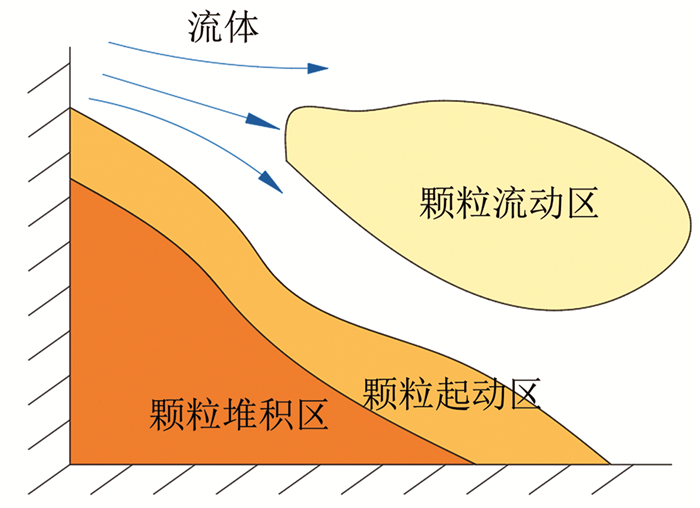
1.1 Euler-Euler法Euler-Euler法基于Darcy渗流定律或Biot固结理论将流体和固体视为两种不同的连续介质[49]。该方法采用双流体模型,通过平衡方程描述颗粒相与流体流动的宏观力学行为(图 1)。然而,Euler-Euler法的求解精度受到颗粒流动模型本构关系的制约。近年来,学者们根据经验公式针对不同材料和不同流动模式提出了各种理论模型,但至今尚未形成适用于所有连续流动情形的共识性理论模型。此外,部分工况下的数值模拟结果偏离实际情况,使得土体颗粒的应力计算存在一定偏差[50]。因此,Euler-Euler法在适用范围上存在显著的局限性。
|
图 1 基于Euler-Euler法的双流体模型 Fig. 1 Two-fluid model based on Euler-Euler method |
Lagrange-Lagrange法从细观角度出发,将流体相视为由颗粒集合组成的框架,能够求解流体界面的平流、变形以及拓扑变化等问题(图 2)。同时,该方法可以自然地描述流体中的颗粒运动。尤其在处理自由液面与移动边界的流-固流动问题时,Lagrange-Lagrange法具有明显的优势。此外,该方法允许在较低的分辨率下对整个计算域进行离散化,因此在研究多相流问题时广泛应用[51-52]。然而,与Euler-Euler法在固定计算域的网格节点或单元上对流体建模不同,Lagrange法在严格意义上非连续,因此与实际土体中流固两相的分布和存在形式不完全一致。由于Lagrange-Lagrange法中引入了大量流体与颗粒之间的临近检索与接触计算,导致计算成本显著提高。同时,该方法忽略了土颗粒迁移过程中孔隙变化对流体流动的影响,因此在应用中存在一定的局限性。
|
图 2 基于Lagrange-Lagrange法的流-固模型示意 Fig. 2 Schematic diagram of fluid-solid model based on Lagrange-Lagrange method |
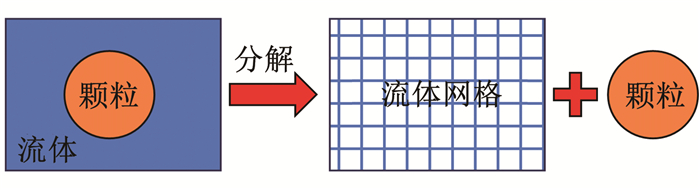
Euler-Lagrange法(图 3)综合上述两种方法的优势,将流体视为连续介质,采用欧拉坐标系描述流体相,同时将土体视为离散介质[53-55],并运用牛顿运动方程计算有限数量的离散颗粒在接触作用和非接触作用下的力学响应。Euler-Lagrange法计算结果更符合实际情况,并且解决了在考虑土颗粒间孔隙水运动特性时低效率的计算问题,从而使该方法具有广泛的应用价值。然而,Euler-Lagrange法计算精度受到计算机性能和流体网格分辨率的限制,而且其中部分模型缺乏完整的理论依据,因此需要依赖基于试验的半经验公式。CFD-DEM耦合方法属于Euler-Lagrange法。
|
图 3 基于Euler-Lagrange法的流-固模型示意 Fig. 3 Schematic diagram of fluid-solid model based on Euler-Lagrange method |
DEM将研究的物体离散为一系列独立运动的颗粒,利用牛顿第二定律建立每个颗粒的运动方程。同时,结合颗粒间接触模型,进行颗粒运动状态的模拟分析,揭示颗粒材料复杂宏观特性的细观机制[56-58]。
2.1 DEM控制方程在DEM模拟中颗粒运动通过常微分方程随时间的推移进行求解,颗粒运动控制方程由运动方程和转动方程组成。其中,运动方程用于描述颗粒受到的体力(如颗粒的重力)以及作用在颗粒上的总外力对颗粒的加速度与速度变化的影响。根据牛顿第二运动定律,颗粒i的运动方程为
| $m_i \frac{\mathrm{d} \boldsymbol{u}_i^{\mathrm{p}}}{\mathrm{d} t}=\boldsymbol{F}_i^{\mathrm{g}}+\boldsymbol{F}_i^{\mathrm{f}}+\sum\nolimits_{\mathrm{C}} \boldsymbol{F}_{i j}^{\mathrm{C}}$ | (1) |
式中:mi为颗粒i的质量,uip为颗粒i的速度,t为时间,Fig为作用在颗粒上的重力,FijC为颗粒i和颗粒j间的作用力,Fif为流体作用于土颗粒的力,具体计算方法将在第4节进行介绍。
转动方程描述了颗粒在外力矩作用下发生的转动:
| $I_i \frac{\mathrm{d} \boldsymbol{\omega}_i}{\mathrm{~d} t}=\sum\nolimits_{j=1}^{n_i^{\mathrm{c}}}\left(\boldsymbol{M}_{\mathrm{t} i j}^{\mathrm{C}}+\boldsymbol{M}_{\mathrm{r} i j}^{\mathrm{C}}\right)$ | (2) |
式中:Ii为颗粒i的转动惯量,ωi为颗粒i角速度,nic为与颗粒i接触的其他颗粒的总数量,MtijC为切向力(包含颗粒间作用力以及流体作用力)产生的力矩,MrijC为滚动摩擦产生的滚动力矩。MtijC和MrijC应基于接触模型计算,将在第2.3节进行详细的介绍。
2.2 DEM颗粒形状模型颗粒模型对颗粒间的相互作用以及颗粒与流体之间的力学响应有着显著影响[59-60]。早期简单的球形(3D)或者圆盘形(2D)颗粒模型无法满足现实工程的需求。近年来,颗粒模型逐渐演化为更贴近实际不规则土颗粒形状的形式。目前,构建不规则颗粒形状的常用方法包括:
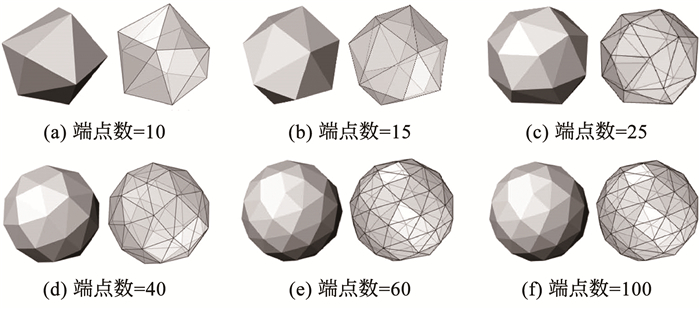
1) 多边形或多面体法。多边形或多面体法将颗粒定义为由一系列边缘或角点构成的集合,以更精确地描述颗粒形状。该方法因其对颗粒表面粗糙度及角度的准确刻画而在岩石和土壤颗粒材料建模中得到广泛应用。Zhao等[61]首次提出了一种反映颗粒角度变化的准球形多面体模型(图 4)。Qian等[62]利用该颗粒模型研究了颗粒角度对间隙级配土中渗流的影响。颗粒形状简化为多面体,虽然有益于提高计算效率,但是无法完全准确地刻画真实土颗粒的形状特征。
|
图 4 考虑颗粒角度变化的准球形多面体[61] Fig. 4 A quasi-spherical polyhedron considering the angle change of particles[61] |
2) 数学函数表示法。数学函数表示法通过数学函数描述粒子形状,可以精确地控制粒子的几何特征,有助于更准确地模拟粒子在流体中的行为以及颗粒之间的相互作用。Williams等[63]指出,80%具有对称性的粒子形状可以通过二次曲面或者更高维的连续函数进行描述。此外,针对特定形状的粒子,Clear[64]、Mustoe等[65]提出了在笛卡尔坐标中使用数学函数关系式描述颗粒的形状。然而,对于高度复杂或不规则的粒子形状,难以确定适当的数学函数。
3) 虚拟空间法。虚拟空间法将实际颗粒的几何形状转化为数字模型,通过像素或者体素等离散单元对颗粒形状进行数字化建模[66]。该方法具有高分辨率的特点,可以精确地捕捉颗粒的复杂几何形状和结构。Lu等[67]、Williams等[68]、Fagbemi等[69]通过3D光学和X射线扫描获取真实颗粒的形状数据。然而,获取准确的物体几何数据通常需要昂贵的扫描或成像设备,试验成本高昂无法在实际工程中广泛推广应用。
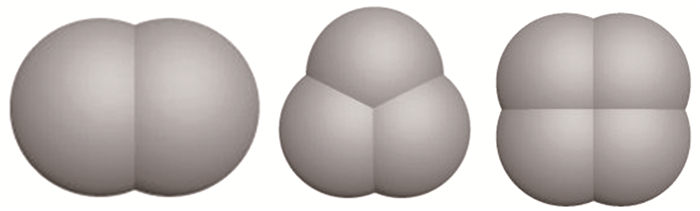
4) 组合基本元素法。组合基本元素法通过一系列基本元素(如圆盘或者球体)对颗粒形状进行近似建模[70-71]。该方法基于“面积等效原则”和“质量等效原则”,如图 5所示,通过多个基本元素模拟任意颗粒形状。Berkinova等[71]通过多个球体构建非球体粒子的重叠位置和半径,研究了不同形状颗粒的流动特性。该方法的模拟效果取决于构建颗粒的基本元素数量,然而,过多的基本元素势必降低计算效率。组合基本元素法无法准确反映真实颗粒角度。
|
图 5 基本元素模拟的简单粒子形状 Fig. 5 Basic elements simulate simple particle shapes |
接触模型是DEM研究和应用的重要基础,描述了颗粒在相互接触时的行为和力学响应。目前常用于模拟土颗粒相互作用的接触模型有刚度接触模型与黏结模型。
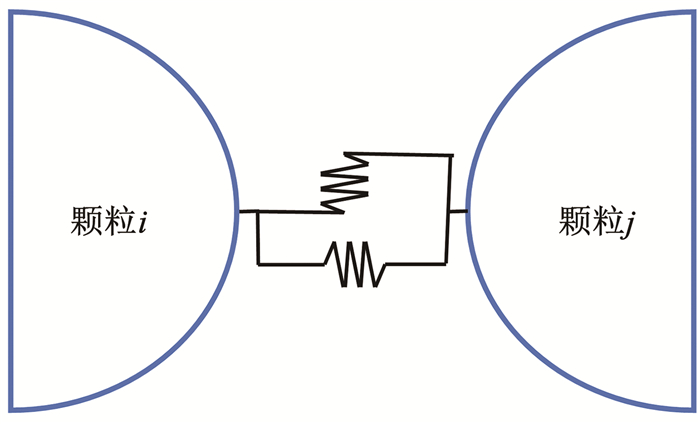
2.3.1 刚度接触模型刚度接触模型用于描述接触力与相对位移之间的关系,该模型基于弹簧-弹簧系统原理,将每一对相互接触的颗粒视为一个弹簧系统。当两个颗粒接触并受到外部力作用时,颗粒间的弹性行为通过弹簧的弹性刚度来描述,如图 6所示。则式(1)中颗粒间的相互作用力可表示为
| $\boldsymbol{F}_{i j}^{\mathrm{C}}=\boldsymbol{F}_{i j}^{\mathrm{n}}+\Delta \boldsymbol{F}_{i j}^{\mathrm{s}}=K^{\mathrm{n}} \boldsymbol{\delta}_{i j}^{\mathrm{n}}+K^{\mathrm{s}} \Delta \boldsymbol{\delta}_{i j}^{\mathrm{s}}$ | (3) |
|
图 6 线性接触模型 Fig. 6 Linear contact model |
式中:Fijn为法向接触力,采用全量表示;ΔFijs为切向接触力,采用增量表示;δijn表示法向重叠位移;Δδijs表示切向重叠位移增量,均为DEM模拟交互过程中迭代更新的变量。
两个颗粒通过串联接触的方式相互作用,则法向刚度Kn和切向刚度Ks表示为:
| $K^{\mathrm{n}} =\frac{k_i^{\mathrm{n}}+k_j^{\mathrm{n}}}{k_i^{\mathrm{n}} k_j^{\mathrm{n}}} $ | (4) |
| $K^{\mathrm{s}} =\frac{k_i^{\mathrm{s}}+k_j^{\mathrm{s}}}{k_i^{\mathrm{s}} k_j^{\mathrm{s}}}$ | (5) |
式中:kin、kis分别为颗粒i的法向刚度与切向刚度;kjn、kjs分别为颗粒j的法向刚度与切向刚度。
线性接触模型对颗粒间接触力的计算效率高,适用于大规模的颗粒-流体系统的计算。但是,在颗粒间的相互作用力影响下,颗粒会出现非线性变形,线性接触模型无法真实反映颗粒间的非线性行为。
最常用的非线性接触模型为经典的Hertz接触模型[35],见图 7。通过引入等效弹性模量E*、等效剪切模量G*和泊松比v三个参数,将法向与切向接触刚度定义为:
| $K^{\mathrm{n}}=\frac{4}{3} E^* \sqrt{R^* \boldsymbol{\delta}_{i j}^{\mathrm{n}}}$ | (6) |
| $K^{\mathrm{s}}=8 G^* \sqrt{R^* \boldsymbol{\delta}_{i j}^{\mathrm{s}}}$ | (7) |
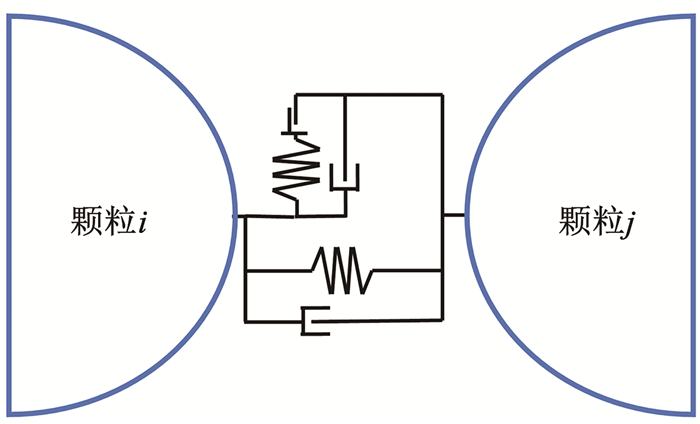
|
图 7 Hertzian接触模型 Fig. 7 Hertzian contact model |
如式(6)、(7)所示,法向与切向接触刚度是关于颗粒半径R*、弹性模量E*、等效剪切模量G*与重叠距离δij的函数,而R*、E*、G*可进一步表示为:
| $\frac{1}{R^*}=\frac{1}{r_i}+\frac{1}{r_j} $ | (8) |
| $\frac{1}{E^*}=\frac{1-v_i^2}{E_i}+\frac{1-v_j^2}{E_j} $ | (9) |
| $\frac{1}{G^*}=\frac{2\left(1-v_i\right)\left(1+v_i\right)}{E_i}+\frac{2\left(1-v_j\right)\left(1+v_j\right)}{E_j}$ | (10) |
式中:ri、rj为相互接触粒子i、j的半径,Ei、Ej为粒子i、j的弹性模量,可通过基于试验的直接测量法[72]或者参数标定方法[73]确定;vi、vj为粒子i、j的泊松比,可采用参数标定法[74]确定。
在实际工程中,土颗粒之间的接触并非完全弹性,因此无法忽略颗粒间的摩擦效应以及接触后的回弹性。Hertz-Mindlin接触模型基于Hertz[75]与Mindlin[76]理论,考虑颗粒黏滞性与回弹性的非线性关系(图 8),更准确地描述了土体的弹塑性力学响应。该方法将式(3)定义的法向接触力及切向接触力变为:
| $\boldsymbol{F}_{i j}^{\mathrm{n}}=K^{\mathrm{n}} \boldsymbol{\delta}_{i j}^{\mathrm{n}}-\gamma^{\mathrm{n}} \boldsymbol{u}_{i j}^{\mathrm{n}} $ | (11) |
| $\boldsymbol{F}_{i j}^{\mathrm{s}}=\min \left\{\left|K^{\mathrm{s}} \int_{t_{\mathrm{c}, 0}}^t \boldsymbol{u}_{i j}^{\mathrm{s}} \mathrm{d} t+\gamma^{\mathrm{s}} \boldsymbol{u}_{i j}^{\mathrm{s}}\right|, \mu_{\mathrm{c}} \boldsymbol{F}_{i j}^{\mathrm{n}}\right\}$ | (12) |
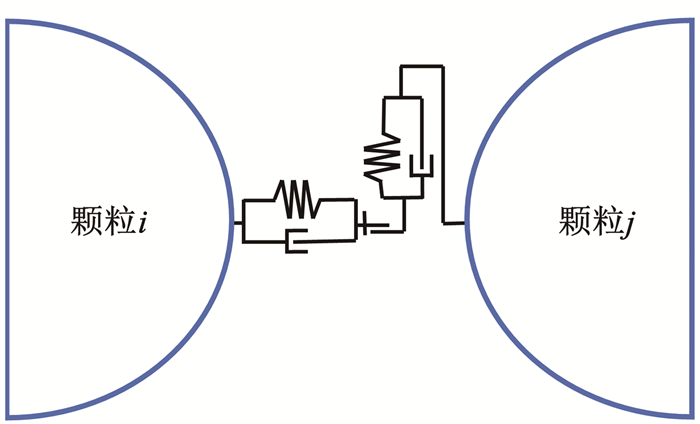
|
图 8 Hertz-Mindlin接触模型示意 Fig. 8 Diagram of the Hertz-Mindlin contact model |
式中:Kn表示法向刚度,Ks表示切向刚度,采用式(6)~(10)进行计算;δijn表示法向重叠位移;uijn、uijs为接触颗粒的相对法向、切向速度;积分项表示储存相对切向运动能量的增量弹簧,表示自t=tc, 0时发生的弹性切向变形[77];μc为颗粒间摩擦系数,可采用参数标定方法确定[78];γn、γs为法向、切向接触的黏弹性阻尼系数,计算方法为:
| $ \gamma^{\mathrm{n}}=-2 \sqrt{\frac{5}{6}} \beta \sqrt{S_{\mathrm{n}} m^*} \geqslant 0 $ | (13) |
| $ \gamma^{\mathrm{n}}=-2 \sqrt{\frac{5}{6}} \beta \sqrt{S_{\mathrm{n}} m^*} \geqslant 0 $ | (14) |
式中:
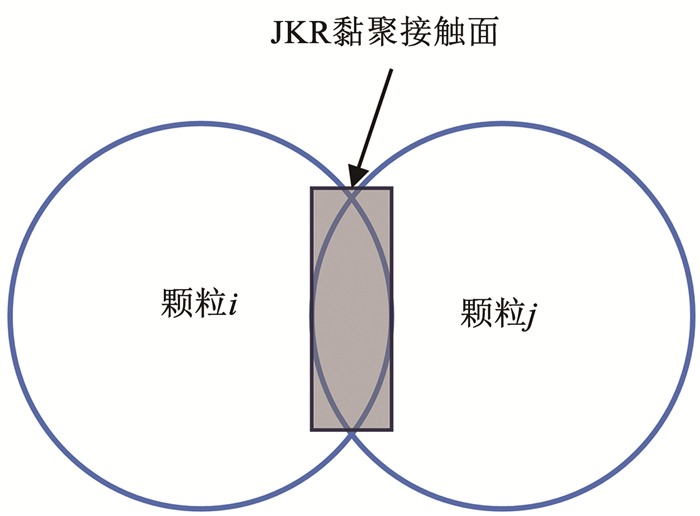
虽然Hertz-Mindlin接触模型能够反映颗粒接触的非线性特征,但是无法考虑土颗粒间的黏结作用[79-81],Johnson等[82]在1971年将表面能模型引入颗粒间的相互作用,建立了如图 9所示的JKR模型。将Hertz-Mindlin模型与JKR模型相结合,可以解决颗粒间因水分等原因产生的显著黏结和聚集问题[83]。Hertz-Mindlin与JKR结合的接触模型将两颗粒之间的黏结力定义为与液体表面张力及湿润角相关的量
| $\boldsymbol{F}_{i j}^{\mathrm{co}}=-2 \pi \alpha_{\mathrm{s}} \cos (\varphi) \sqrt{r_i r_j}$ | (15) |
|
图 9 JKR模型示意 Fig. 9 Schematic of the JKR model |
式中:αs为液体表面张力,φ为接触角。
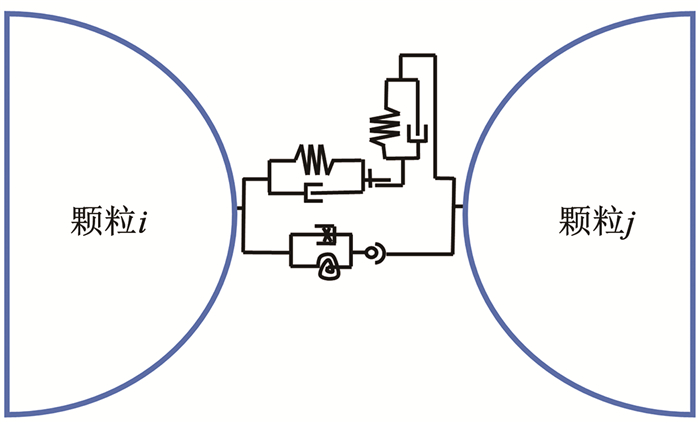
颗粒由于形状不规则产生的力学效应不可忽视,直接构建不规则颗粒往往会增加计算负担。因此,部分学者开发了滚动阻力模型,以模拟不规则形状产生的力学效应。该模型采用基础单颗粒形状,并在Hertz-Mindlin接触模型的基础上引入粒间滚动阻力,通过滚动摩擦系数μr解释颗粒的宏观力学特性[84],如图 10所示。此外,Ai等[85]考虑了粒子间的相对旋转滚动阻力矩作用,建立了2D滚动阻力模型。Kondic[86]将滚动阻力模型扩展到三维,建立了Matter模型,但是该模型需通过反复实验确定计算参数,结果存在不确定性。大多数3D滚动阻力模型只在切线平面上考虑滚动阻力矩的作用,忽略了接触法向的扭转阻力矩,无法准确描述粒子运动规律。为了克服上述挑战,Jiang等[87]提出了考虑滚动阻力和扭转阻力共同作用的3D模型。但是为了简化计算,该模型在法向方向基于弹性假设,在高压力和大位移情况下无法模拟颗粒的局部塑性变形。滚动阻力模型的选择通常取决于颗粒的几何特性和对模拟精度的要求。表 1汇总了上述文献中所采用的部分滚动摩擦阻力模型,公式中的符号意义参见各参考文献。
|
图 10 基于Hertz-Mindlin接触的滚转动阻力模型示意[84] Fig. 10 Schematic diagram of roll resistance model based on Hertz-Mindlin contact[84] |
| 表 1 滚动阻力模型汇总 Tab. 1 Summary of rolling resistance models |
黏结模型允许互相接触的颗粒通过连接黏结为一体,主要的黏结模型包括接触黏结模型与平行黏结模型。两者的主要区别在于:接触面的几何形状,接触黏结模型接触面为一点,而平行黏结模型的接触面为一个面,后者的黏结强度与稳定性高于前者;传递的力学特征不同,接触模型只能传递力,而平行黏结模型可以传递力与弯矩。
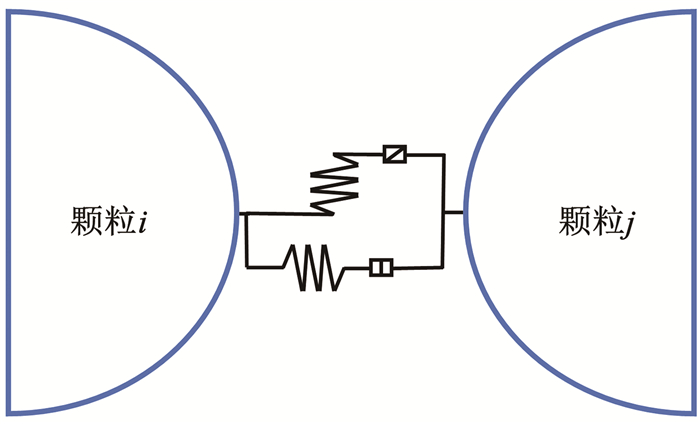
1) 接触黏结模型。接触黏结模型法向与切向方向都包含了一对作用在颗粒连接处的恒定刚度的弹簧,并具有一定的抗拉与抗剪强度。因此,接触黏结模型可以抑制模型的相对滑动[88]。图 11为接触黏结示意图,当相邻颗粒的重叠量小于0时,颗粒之间产生拉力,如果拉力超过抗拉强度,则发生拉伸破坏,此时法向与切向接触力变为0。如果切向力大于抗剪强度,则产生剪切破坏,此时法向接触力不一定为0。
|
图 11 接触黏结模型 Fig. 11 Contact bonding model |
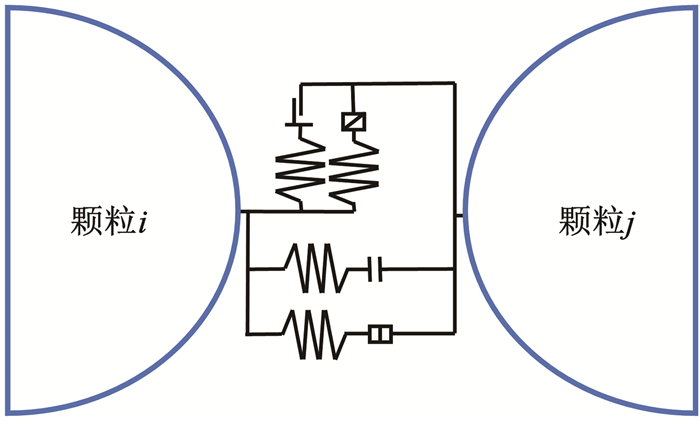
2) 平行黏结模型。如图 12所示,平行黏结假设接触面上均匀分布具有恒定法向与切向刚度的弹簧,同时也具有一定的抗拉强度与抗剪强度。其接触面积为A,平行黏结上受力状态主要为合力Fijc与合力矩Mijc,按法向与切向方向分解可表示为:
| $\boldsymbol{F}_{i j}^{\mathrm{c}}=\boldsymbol{F}_{i j}^{\mathrm{n}}+\boldsymbol{F}_{i j}^{\mathrm{s}}=K^{\mathrm{n}} A \boldsymbol{\delta}_{i j}^{\mathrm{n}}+K^{\mathrm{s}} A \boldsymbol{\delta}_{i j}^{\mathrm{s}} $ | (16) |
| $ \boldsymbol{M}_{i j}^{\mathrm{c}}=\boldsymbol{M}_i^{\mathrm{n}}+\boldsymbol{M}_i^{\mathrm{s}}=K^{\mathrm{s}} J \boldsymbol{\theta}_{i j}^{\mathrm{n}}+K^{\mathrm{n}} I_{\mathrm{p}} \Delta \boldsymbol{\theta}_{i j}^{\mathrm{s}}$ | (17) |
|
图 12 平行黏结模型 Fig. 12 Parallel bonding model |
式中:θ为转动增量,J为截面的极惯性矩, Ip为沿接触点对转动方向的转动惯量。根据梁截面理论,作用于平行截面上的最大拉应力与剪应力分别为:
| $\sigma_{\text {max }}=\frac{-\boldsymbol{F}_i^{\mathrm{n}}}{A}+\frac{\left|\boldsymbol{M}_i^{\mathrm{s}}\right|}{I_{\mathrm{p}}} \bar{R} $ | (18) |
| $\tau_{\text {max }}=\frac{\left|\boldsymbol{F}_i^{\mathrm{s}}\right|}{A}+\frac{\left|\boldsymbol{M}_i^{\mathrm{n}}\right|}{J} \bar{R}$ | (19) |
式中:R=λmin[ri, rj],λ为半径扩大系数。颗粒间作用力与力矩大于平行黏结上的最大法向力、切向力与弯矩强度值时,平行黏结将会发生破坏。平行黏结模型可以较好表现颗粒集合体的复杂力学响应,但由于每个颗粒团聚体需要包含一定数目的子颗粒,采用该方法模拟的计算成本也比较高。
接触模型中常用的力学器件见表 2。现有接触模型的建立较为主观,且部分模型的参数仍需要复杂的试验方法获取。此外,复杂接触模型在处理问题时进行了简化,特别是在涉及复杂颗粒形状的接触模型研究。这些局限性需要进一步研究来解决,尤其是在构建更适用于描述现实颗粒材料力学行为响应的完整理论体系方面。
| 表 2 力学元器件汇总 Tab. 2 Mechanical components summary |
CFD流体模型基于流体动力学原理,通过求解控制流体运动的控制方程,分析流体的流动规律。目前,常用的控制方程为基于达西定律的控制方程以及Navier-Stokes(N-S)方程。
3.1 基于达西定律的控制方程达西定律是描述多孔介质中渗流行为的基本方程之一,通常用于分析流体通过多孔介质(如土壤、岩石等)的渗透与渗流过程。该定律表明渗流速度与渗透率、压力梯度和介质性质之间存在关系,并进一步解释了液体在多孔介质孔隙中的传递机理和液体对多孔介质渗透性的影响规律。基于达西定律的流体控制方程满足达西定律以及质量守恒定律,且假设流体为不可压缩的牛顿流体,其表达式为
| $\begin{aligned} & \frac{\partial}{\partial x}\left(k_x \frac{\partial H}{\partial x}\right)+\frac{\partial}{\partial y}\left(k_y \frac{\partial H}{\partial y}\right)+ \\ & \frac{\partial}{\partial z}\left(k_z \frac{\partial H}{\partial z}\right)+Q=C_{\mathrm{w}} \varepsilon \gamma_{\mathrm{w}} \frac{\partial H}{\partial t}\end{aligned}$ | (20) |
式中:H为总水头,kx、ky、kz分别为笛卡尔坐标系中三个主轴方向上的渗透系数,Q为流体的输移量,ε为孔隙介质的孔隙率,Cw为水的可压缩系数,γw为水的重度。其中,水头边界条件为
| $H=H_t(t)$ | (21) |
流动边界条件为
| $\left(k_x \frac{\partial H}{\partial x}\right) l_x+\left(k_y \frac{\partial H}{\partial y}\right) l_y+\frac{\partial}{\partial z}\left(k_z \frac{\partial H}{\partial z}\right) l_z+q(t)=0$ | (22) |
式中:q(t)为流动边界上规定的流量,lx、ly、lz为垂直于流动边界上的单位向量余弦值。
基于达西定律的控制方程能准确描述土体渗透性的变化规律,同时具有计算简单和计算效率高的优势,因此在研究低流速多孔介质渗流问题中得到广泛运用[53]。然而,在高速流动条件下,由于颗粒与流体之间的相互作用具有显著的非线性特征,同时多孔介质的结构和渗透性会发生变化,达西定律中的线性假设和均匀多孔介质假设不再成立。因此基于达西定律的控制方程不适用于高速流动的流场模拟。
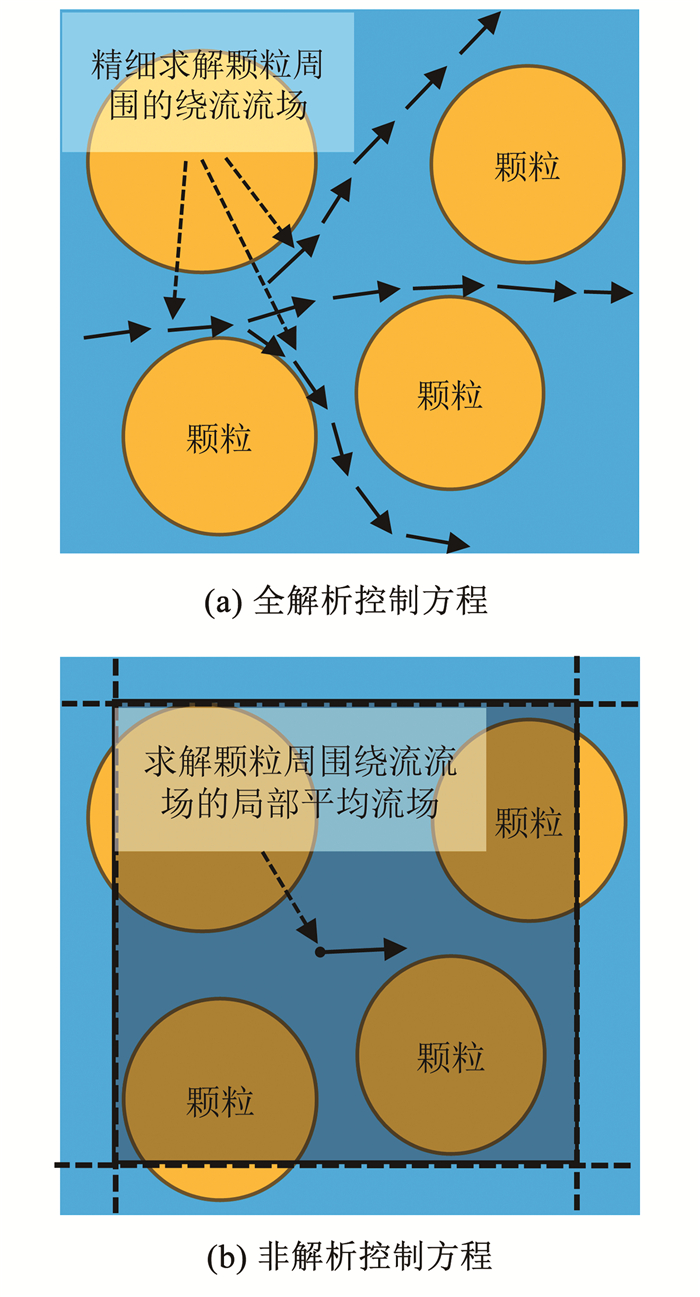
3.2 Navier-Stokes控制方程N-S控制方程通过引入孔隙率以反映多孔介质中流体与固体颗粒之间的相互作用。该方程基于连续假设,通过非线性偏微分方程(组)描述流体,具有物理意义明确和计算精度高的优势。虽然方程中涉及多个非线性物理量,但是当渗流速度较小时,流体状态满足连续性假设,方程中的非线性性质可以忽略。如图 13所示,根据对颗粒周围绕流流场是否进行全面求解,N-S控制方程分为全解析控制方程与非解析控制方程。
|
图 13 N-S控制方程 Fig. 13 N-S governing equation |
全解析N-S控制方程可以准确地描述岩土体等颗粒材料中的孔隙流动问题。根据质量守恒与动量守恒定律,全解析N-S控制方程为:
| $\nabla \boldsymbol{u}_{\mathrm{w}}=0 $ | (23) |
| $\rho_{\mathrm{w}}\left(\frac{\partial \boldsymbol{u}_{\mathrm{w}}}{\partial t}+\boldsymbol{u}_{\mathrm{w}} \cdot \nabla \boldsymbol{u}_{\mathrm{w}}\right)=\nabla \cdot \boldsymbol{\sigma}+\rho_{\mathrm{w}} \boldsymbol{g}$ | (24) |
式中:ρw为流体密度;uw为流体速度;σ=-pK+τ为流体应力,包括压力张量-pK与流体黏性应力张量τ,K为二阶单位张量;g为重力加速度。同时,流体作用于颗粒的力与流体应力之间应满足
| $\boldsymbol{F}_i^{\mathrm{f}}=\oint\limits_{\partial \varOmega_{\mathrm{p}}} \boldsymbol{n} \cdot \boldsymbol{\sigma} \mathrm{d} S$ | (25) |
式中:∂Ωp为颗粒与流体的边界面,S为边界面的面积,n为粒子表面的单位外法线向量。全解析N-S控制方程的精确求解要求流体网格尺寸至少小于颗粒直径的1/8~1/10。然而,当颗粒数量较多时,网格数量较大,将消耗大量的计算资源。因此,全解析N-S控制方程主要适用于模拟小规模颗粒数量的流固耦合,如小数量颗粒在流体内的沉降、理想颗粒堆积体内的渗流等小尺度的耦合模拟[89]。
如图 13(b)所示,非解析CFD-DEM方法不精确求解每个颗粒的流场,而基于局部平均化理论[34],采用局部平均化N-S方程来求解在局部区域内的流场。根据质量守恒条件,流体的运动应满足
| $\frac{\partial \varepsilon \rho_{\mathrm{w}}}{\partial t}+\nabla\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)=0$ | (26) |
基于不同的压降承担相假设,非解析N-S控制方程中的动量方程表现为三种形式:
| $\frac{\partial\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)}{\partial t}+\nabla \cdot\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)=-\varepsilon \nabla \boldsymbol{p}+\varepsilon \nabla \cdot \boldsymbol{\tau}+\varepsilon \rho_{\mathrm{w}} \boldsymbol{g}+\boldsymbol{F}_{\mathrm{p}}$ | (27a) |
| $\frac{\partial\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)}{\partial t}+\nabla \cdot\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)=-\varepsilon \nabla \boldsymbol{p}+\nabla \cdot \varepsilon \boldsymbol{\tau}+\varepsilon \rho_{\mathrm{w}} \boldsymbol{g}+\boldsymbol{F}_{\mathrm{p}}$ | (27b) |
| $\frac{\partial\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)}{\partial t}+\nabla \cdot\left(\varepsilon \rho_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)=-\nabla \boldsymbol{p}+\nabla \cdot \varepsilon \boldsymbol{\tau}+\varepsilon \rho_{\mathrm{w}} \boldsymbol{g}+\boldsymbol{F}_{\mathrm{p}}$ | (27c) |
式中:Fp为颗粒施加于所在流体网格内的平均体积作用力,其中
非解析控制方程要求流体网格尺寸大于颗粒直径的3~5倍,相较于全解析方法,非解析方法具有网格分辨率较低和计算成本低的优势,因此,该方法能够有效地模拟大规模颗粒迁移问题,在间隙级配土体渗流侵蚀等岩土工程问题中已被广泛应用。但是,非全解析方法仍无法合理模拟颗粒运移引起的粗骨架孔隙渗流发展问题,因此难以深入了解渗流作用下间隙级配土中细颗粒运移的细观机理[90]。
此外,近年来Cheng等[91]结合全解析与非全解析方法的优点提出了一种半解析控制方程,王胤等[92]在其基础上使用基于高斯的加权函数和新的阻力模型进一步改进了简化半解析模型的控制方程。其控制方程为:
| $\frac{\partial \varepsilon}{\partial t}+\nabla \cdot\left(\varepsilon \boldsymbol{u}_{\mathrm{w}}\right)=0$ | (28) |
| $\rho_{\mathrm{w}}\left[\frac{\partial \varepsilon \boldsymbol{u}_{\mathrm{w}}}{\partial t}+\nabla \cdot\left(\varepsilon \boldsymbol{u}_{\mathrm{w}} \boldsymbol{u}_{\mathrm{w}}\right)\right]=-\varepsilon \nabla \boldsymbol{p}+\varepsilon \nabla \boldsymbol{\tau}+\boldsymbol{F}_{\mathrm{fp}}+\varepsilon \boldsymbol{F}_{\mathrm{FD}}$ | (29) |
式中:Ffp为施加于所在流体网格内的作用力;FFD为粗颗粒附加相间作用力。半解析CFD-DEM方法克服了在对粗颗粒周围流场进行精细化模拟时可能产生的巨大计算负担,同时解决了在流体网格内细颗粒较多时无法获得局部平均化变量的问题。
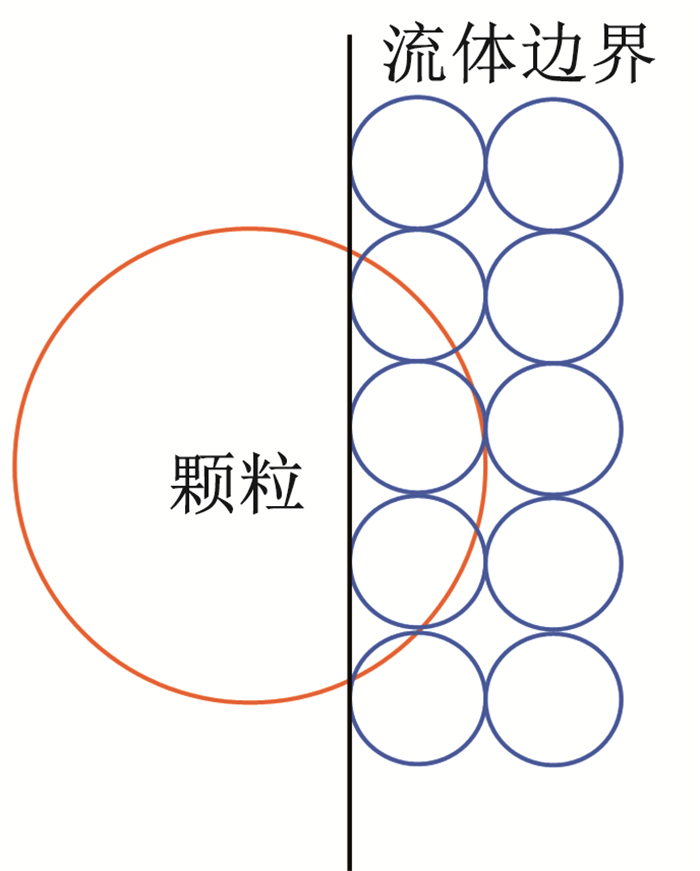
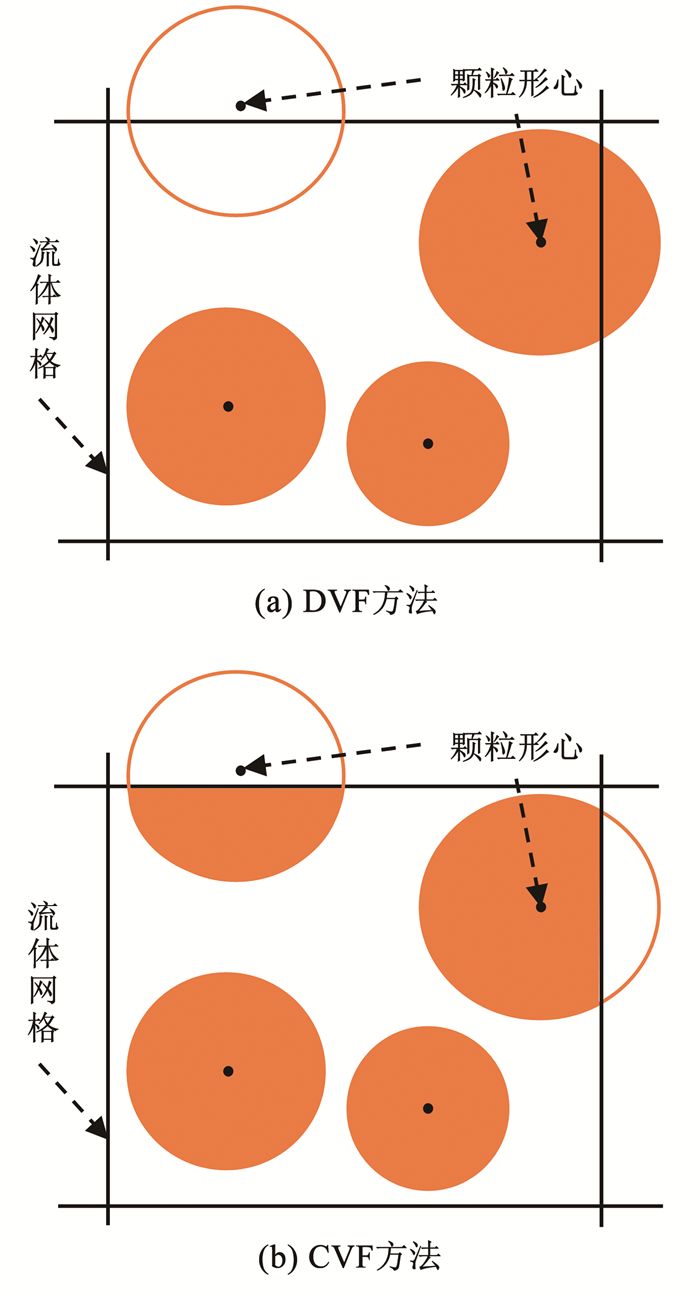
3.3 孔隙率计算方法及对流体控制方程的影响孔隙率ε直接影响多孔介质内部的流动性质和流体控制方程的表现,常用的孔隙率计算方法有分割孔隙分法(DVF)与中心孔隙分数法(CVF)[95],如图 14所示。CVF方法假设当颗粒的形心位于流体网格内,颗粒的总体积被视为填充孔隙度,无需分割颗粒体积。CVF计算效率高,适用于大规模颗粒的数值模拟。然而,在处理颗粒的质心接近流体网格边界的情况时,CVF方法孔隙率计算结果可能会出现较大误差,尤其是当流体网格尺寸与颗粒尺寸比值较小时,误差将更加显著,最高可达50%[93]。只有当流体网格尺寸达到颗粒粒径的3~5倍时,CVF方法的计算精度才能得到保证[94]。DVF假设当颗粒的形心位于流体网格边界上时,颗粒体积将被分割并以体积分数的形式分配给相邻的网格,然后计算孔隙率。因此,DVF方法在网格尺寸与颗粒尺寸比值较小的情况下,能够更准确地描述颗粒与流体网格的交互。然而,DVF方法需要对颗粒与流体网格是否发生重叠进行判断,并进行颗粒分割处理,这增加了计算的复杂性,因此不适用于大规模颗粒系统的模拟计算。
|
图 14 DVF方法与CVF方法示意 Fig. 14 Diagram of DVF method and CVF method |
在基于达西定律的控制方程中,渗透系数描述了多孔介质内部流体的渗透性,而ε则是计算渗透率所需的基础参数。因此,准确计算ε是确保渗透率模型精确性的关键因素。Kozeny[96]和Carman[97]基于多孔介质流动的实验数据,建立了Kozeny-Carman经验模型,用于求解渗透系数。然而,该模型仅适合于均匀的圆管状孔隙结构,对于非均匀孔隙中的流体渗透系数计算精度较低。为了解决这一问题,学者们考虑了流体黏性和颗粒形状等因素对Kozeny-Carman模型进行了修正[31, 53, 98, 99]。此外,Ergun公式[100]常被用于计算渗透系数,该公式在低速流动情况下描述了流体的黏性阻力,而在高流速下则表达了流体的惯性阻力。表 3汇总了常用的渗透系数计算公式,各参数的含义见各参考文献。
| 表 3 渗透系数计算公式汇总 Tab. 3 Summary of calculation formula of permeability coefficient |
ε直接影响非解析N-S控制方程模拟性能。当ε为常数时式(27b)可以简化为与式(27a)相同的形式。然而,随着ε空间梯度的增大,受颗粒形状和孔径分布等因素的影响两式会表现出显著的差异。Zhu等[101]发现对于单一几何尺寸颗粒的流场问题,式(27b)和(27c)的模拟结果相似,但在模拟由不同几何尺寸组成的流-固系统时,式(27b)和(27c)计
算结果存在一定差异。Guo等[102]对三种不同形式的动量方程在稀疏和稠密颗粒流体系统中的模拟结果进行了对比,发现对于相对稀疏的颗粒-流体系统,三种方程之间的差异可以忽略不计。但是,在处理致密颗粒流体系统时,不同动量方程模拟结果出现较大的差异。因此,动量方程的选择将取决于多孔介质的孔隙率。
4 CFD-DEM耦合计算 4.1 流-固耦合相互作用力CFD-DEM耦合的关键在于求解颗粒和流体间的相互作用力。学者们考虑了多种典型的颗粒-流体相互作用力,其中包括压力梯度力、浮力、黏滞力、颗粒在流体中运动受阻而产生的拖曳力以及非定常力。尽管流体作用在颗粒上的力相当复杂,但一般情况下并非所有力都同样重要。岩土工程问题中,由于流体处于低流速状态,与其他力相比,非定常力相对较小,可以忽略不计。因此,流体作用于单个颗粒的力Fif可表示为
| $\boldsymbol{F}_i^{\mathrm{f}}=\boldsymbol{F}_{\mathrm{d}}+\boldsymbol{F}_{\mathrm{g}}+\boldsymbol{F}_{\mathrm{v}}+\boldsymbol{F}_{\mathrm{m}}+\boldsymbol{F}_{\mathrm{f}}$ | (30) |
在流体网格中,颗粒受到的压力梯度力Fg、黏滞力Fv、浮力Ff表示为:
| $\boldsymbol{F}_{\mathrm{g}}=-V_{\mathrm{p} i} \nabla \boldsymbol{p}$ | (31) |
| $\boldsymbol{F}_{\mathrm{v}}=V_{\mathrm{p} i} \nabla \cdot \boldsymbol{\tau} $ | (32) |
| $\boldsymbol{F}_{\mathrm{f}}=\pi \rho_{\mathrm{w}} d_{\mathrm{pi}}^3 \boldsymbol{g} / 6$ | (33) |
式中:Vpi为颗粒i的体积, dpi为颗粒i的直径。压力梯度力、黏滞力以及浮力的物理意义明确,有准确的理论公式。单个颗粒在流场中所受拖曳力Fd的求解涉及复杂的流固相互作用,目前没有准确的理论公式[103]。学者们[100, 104-108]基于实验数据,提出了大量经验模型,将拖曳力的计算归结为求解拖曳力系数和颗粒雷诺数。
Ergun[100]基于堆积体渗透试验数据,提出了当ε < 0.8时拖曳力的半经验公式。Wen等[104]引入动量交换系数β对Ergun模型进行了补充,得到了适用于ε>0.8时的颗粒堆积体内拖曳力计算模型。但是Wen & Yu模型[104]存在间断点,导致流体计算不连续。为了解决计算的不连续性,Di Felice[105]通过整理和拟合颗粒堆积体内渗流试验数据,推导了连续函数形式的拖曳力计算公式。此外,Wang等[107]提出了考虑不规则颗粒形状等影响颗粒集合力学行为因素的拖曳力计算方法。Koch等[108]则认为拖曳力的变化与固体分数ϕ有关,提出了基于颗粒堆积体的完全求解方法。但是,Koch & Hill模型[108]计算复杂,且存在不连续的间断点,因此在岩土工程问题的模拟中并不常见。
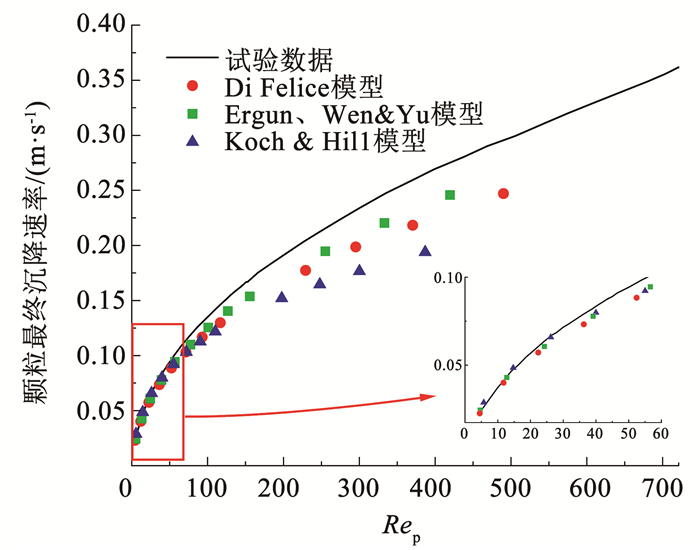
拖曳力模型的计算精度很大程度上决定了CFD-DEM耦合模拟的准确性。学者们[53, 77, 109-112]将单颗粒沉降基准算例的试验结果与经验模型的模拟计算结果进行对比,验证了Ergun、Wen & Yu、Di Felice以及Hill & Koch模型的合理性。彭恺然等[113]基于Brown等[114]的单颗粒沉降试验结果,研究了4种模型在解决颗粒沉降问题时的计算精度, 研究结果表明不同的雷诺数,4种模型的精度会发生变化, 如图 15所示。当Rep < 40时,Hill & Koch模型精度较高,Rep>40时, Ergun、Wen & Yu模型精度较高,两种情况下, Di Felice模型精度最低。但是随着雷诺数的增大,4种模型的误差逐渐增大,因此4种模型适用于低雷诺数的情况以保证计算精度。本文对拖曳力模型进行了总结,见表 4,其相关参数意义见各参考文献。
| 表 4 拖曳力模型汇总 Tab. 4 Summary of drag force models |
|
图 15 各拖曳力作用下颗粒最终沉降速率随雷诺数变化曲线[113] Fig. 15 The final settling rate of particles varies with Reynolds number under different dragging forces[113] |
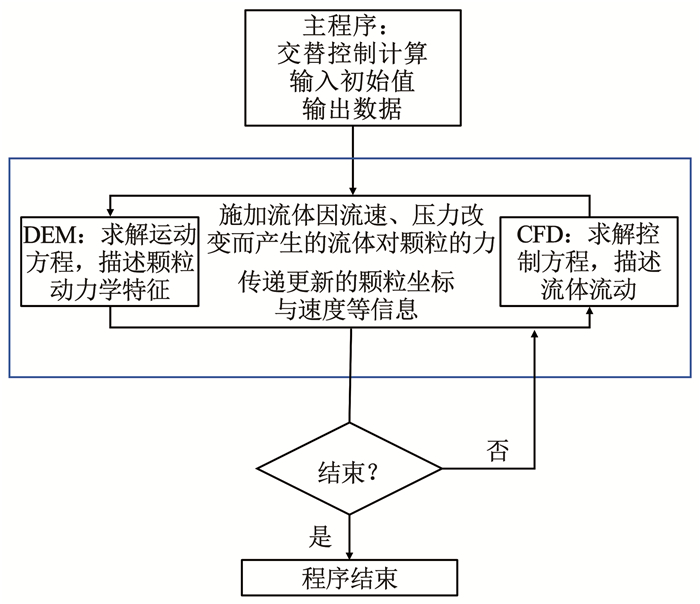
CFD-DEM耦合模型将流体和颗粒视为两个相互作用的子系统(CFD和DEM),并在时间上进行交替迭代,以模拟颗粒在流体中的运动和相互作用。图 16为CFD-DEM耦合算法的基本求解流程。计算开始前首先设置初始条件,包括流速、压力、颗粒的位置和速度等。模型参数初始化后,流体的流动状态通过控制方程求解,得到每个流体单元中的流体-颗粒相互作用力。然后,将流体-颗粒相互作用力传递给DEM循环计算模块,通过DEM模块循环计算后得到下一个流体时间步长中所有粒子的新位置、平动速度和转动速度;最后,将DEM计算更新的颗粒坐标与速度传递给CFD计算模块,求解流体控制方程。判断是否达到规定的计算时间,若未完成则将计算所得流体及颗粒数据传递进行下一循环计算;若完成计算,则输出最终计算结果。
|
图 16 CFD-DEM耦合流程图 Fig. 16 CFD-DEM coupling flow chart |
目前,CFD-DEM耦合计算方法尚难以实现对所有流固相互作用力进行全面计算,其中部分高度非线性的作用力在计算过程中进行了简化甚至忽略。流-固相互作用力计算模型应基于模拟研究目的及假设条件进行选择,从而实现对流固相互作用引起的渗透性、流体性质及颗粒运动转变过程的模拟。
5 结论与展望CFD-DEM耦合方法在岩土工程中具有广泛的应用前景。本文针对CFD-DEM耦合建模方法的研究现状进行了总结,提出了系统评述现有CFD-DEM耦合模型的体系。围绕CFD-DEM耦合方法及其在岩土工程上的应用,指出了当前建模方法中存在的不足,并提出了未来发展方向。现有耦合模型的研究中存在诸多局限性主要体现在以下三个方面:
1) 考虑颗粒形状的DEM建模方法需要进一步深入研究。目前,基本的颗粒形状模型,如多面体、椭球体、多球组合体等,已经在DEM中得到广泛应用。然而,对于更符合实际情况的、具有更加复杂几何形状的DEM颗粒模型,如不规则形状、多孔颗粒等,其建模过程复杂繁琐,计算成本高,从而限制了基于DEM的形状建模方法在大规模颗粒-流体系统耦合计算中的应用。
2) 颗粒接触模型理论有待完善。现有颗粒接触模型基于主观经验或简化假设构建,模型中部分参数需要依赖试验数据拟合确定,接触模型的选择缺乏相关理论依据,使得接触模型无法准确地捕捉真实颗粒接触的复杂物理现象。此外,使用经验公式或可调参数与实验数据进行拟合,虽然能够实现数值上的匹配,但模型参数却难以用物理概念合理解释,从而降低了接触模型的物理可解释性。
3) CFD-DEM耦合模拟效率仍需提升。尽管模拟更符合实际的土体孔隙结构流场变化可以支持精细的数值研究,但势必会导致网格数量的增加,不可避免地面临计算效率差的现象。现有耦合模型的计算效率制约了流-固耦合模型的精细化模拟。
针对上述研究中存在的问题与挑战,下一步的研究重点主要有:
1) 优化土体颗粒模型。基于DEM的颗粒形状建模方法具备还原真实土体形状的潜力,充分利用先进的计算几何学方法或数字扫描技术为模拟实际颗粒形状提供依据,并将其转化为DEM可用的模型,以更准确地捕捉颗粒的实际几何形状。
2) 完善颗粒接触模型理论体系。颗粒接触理论体系的完善将有助于提高DEM在岩土工程领域应用中的可靠性和适用性。深入研究颗粒间的相互作用,基于明确的物理原理构建适用于土体颗粒力学行为响应的接触模型。此外,建立接触模型选择客观标准,探索模型参数的确定方法,进一步提高参数确定的准确性和可重复性。
3) 建立协调计算精度和计算效率的耦合模型。研发网格依赖性低、计算效率高的流体计算方法,在大规模颗粒-流体系统的耦合计算中实现高效的模拟。此外,充分利用自适应网格技术,根据模拟中不同计算精度的要求来动态调整网格数量,减少计算资源的浪费。
| [1] |
HAN Bowen, CAI Guoqing, LI Jian, et al. Investigating particles migration caused by mud pumping in ballasted track subgrade under cyclic loading-wetting coupling[J]. Transportation Geotechnics, 2022, 37: 100830. DOI:10.1016/j.trgeo.2022.100830 |
| [2] |
王飞, 王常明, 徐佩华, 等. 一次洪水过程的泥石流物源体侵蚀机制试验[J]. 哈尔滨工业大学学报, 2017, 49(12): 131. WANG Fei, WANG Changming, XU Peihua, et al. Experimental study on debris flow erosion mechanism based on a flood process[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 131. DOI:10.11918/j.issn.0367-6234.201703034 |
| [3] |
吴帅峰, 严俊, 蔡红, 等. 尾矿管涌溃坝模式及下泄冲击特性试验研究[J]. 岩土工程学报, 2021, 43(11): 2134. WU Shuaifeng, YAN Jun, CAI Hong, et al. Experimental study on dam break mode of tailing piping and discharge impact characteristics[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 21341. DOI:10.11779/CJGE202111021 |
| [4] |
CAI Guoqing, HAN Bowen, ASREAZAD S, et al. Experimental study on hydro-mechanical and critical state behavior of unsaturated silty sands under constant matric suction[J]. Géotechnique, 2022, 1. DOI:10.1680/jgeot.21.00264 |
| [5] |
CAI Guoqing, LIU Qianqian, YANG Yu, et al. Hydro-mechanical coupling effect on water permeability of strongly weathered sandstones[J]. Canadian Geotechnical Journal, 2023, 60(5): 687. DOI:10.1139/cgj-2022-0113 |
| [6] |
TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley & Sons, Inc., 1943.
|
| [7] |
BIOT M A. General theory of three dimensional consolidation[J]. Journal of Applied Physics, 1941, 12: 155. DOI:10.1063/1.1712886 |
| [8] |
BIOT M A. Theory of elasticity and consolidation for a porous anisotropic solid[J]. Journal of Applied Physics, 1955, 26(2): 182. DOI:10.1063/1.1721956 |
| [9] |
CAI Guoqing, LIU Yi, LI Jian, et al. Water retention curve with different initial void ratios over a wide suction range and its application on shear strength[J]. International Journal of Geomechnics, 2022, 22(8): 04022120. DOI:10.1061/(ASCE)GM.1943-5622.0002484 |
| [10] |
杨光昌, 白冰, 刘洋, 等. 描述饱和砂土剪切特性的一个热力学本构模型[J]. 哈尔滨工业大学学报, 2021, 53(11): 93. YANG Guangchang, BAI Bing, Liu Yang, et al. A thermodynamic constitutive model for describing shear behavior of saturated sand[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 93. DOI:10.11918/202006073 |
| [11] |
苏彦林, 蔡国庆, 刘祎, 等. 考虑时间效应的超固结非饱和土弹黏塑性本构模型及其验证[J]. 岩土工程学报, 2023, 45(6): 1250. SU Yanlin, CAI Guoqing, LIU Yi, et al. Elastic-viscoplastic constitutive model for overconsolidated unsaturated soils considering time effects and its verification[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(6): 1250. DOI:10.11779/CJGE20220292 |
| [12] |
LI Mengzi, CAI Guoqing, ZHOU Annan, et al. An elastoplastic model for anisotropic clays with improved yield surfaces and rotational hardening rule[J]. Computers and Geotechnics, 2022, 148: 104821. DOI:10.1016/j.compgeo.2022.104821 |
| [13] |
WU Tianchi, CAI Guoqing, CLEALL P, et al. Microstructurally related model for predicting behavior of unsaturated soils with double porosity in triaxial space[J]. International Journal of Geomechanics, 2022, 22(12): 04022216. DOI:10.1061/(ASCE)GM.1943-5622.0002569 |
| [14] |
CAI Guoqing, ZHOU Annan, LIU Yi, et al. Soil water retention behavior and microstructure evolution of lateritic soil in the suction range of 0-286.7 MPa[J]. Acta Geotechnica, 2020, 15(12): 3327. DOI:10.1007/s11440-020-01011-w |
| [15] |
CAI Guoqing, HAN Bowen, WEI Jingwei, et al. Wetting-induced deformation characteristics of unsaturated compacted sandy loess[J/OL]. Acta Geotechnica[2023-08-20]. http://dx.doi.org/10.1007/s11440-023-01891-8
|
| [16] |
贾羽, 丁瑜, 王晅, 等. 循环加载下碎石层细观孔隙结构演化分析[J/OL]. 哈尔滨工业大学学报[2023-08-20]. http://dx.doi.org/10.11918/202212084 JIA Yu, DING Yu, WANG Xuan, et al. Evolution analysis of mesoscopic pore structure in gravel layer under cyclic loading[J/OL]. Journal of Harbin Institute of Technology[2023-08-20]. http://dx.doi.org/10.11918/202212084 |
| [17] |
RAVICHANDRAN N, MACHMER B, KRISHNAPILLAIH K, et al. Micro-scale modeling of saturated sandy soil behavior subjected to cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(11): 1212. DOI:10.1016/j.soildyn.2010.05.002 |
| [18] |
雷小芹, 刘恩龙, 何思明, 等. 非饱和堆积土边坡降雨-渗流潜蚀耦合过程模拟[J]. 工程科学与技术, 2021, 53(2): 28. LEI Xiaoqin, LIU Enlong, HE Siming, et al. Modelling of coupled process of rainfall infiltration and internal erosion within unsaturated deposited soil slopes[J]. Engineering Science and Technology, 2021, 53(2): 28. DOI:10.15961/j.jsuese.202000001 |
| [19] |
周洁, 李泽垚, 唐益群, 等. 软黏土三维水-热-力耦合冻融模型及应用[J]. 哈尔滨工业大学学报, 2022, 54(2): 117. ZHOU Jie, LI Zeyao, TANG Yiqun, et al. Three-dimensional thermal-hyrdraulic-mechanical coupling frost thaw model of soft clay and its application[J]. Journal of Harbin Institute of Technology, 2022, 54(2): 117. DOI:10.11918/202011033 |
| [20] |
MEKONNEN A. Train induced pore water pressure generation model: numerical comparison[J]. Journal of Vibroengineering, 2019, 21(4): 952. DOI:10.21595/jve.2018.20253 |
| [21] |
高广运, 张继严, 谢伟, 等. 高铁弹塑性地基振动与变形的2.5维有限元算法[J]. 哈尔滨工业大学学报, 2021, 53(11): 37. GAO Guangyun, ZHANG Jiyan, XIE Wei, et al. Improved 2.5D finite element method for vibration and deformation of elastoplastic subgrade under high-speed train load[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 37. DOI:10.11918/201912079 |
| [22] |
CUNDALl P A. A computer model for simulating progressive large-scale movements in blocky rock systems[J]. Proceedings of symposium for International Society of Rock Mechanics, 1971, 1(ii-b): 11. |
| [23] |
CAI Guoqing, LI Jian, LIU Shaopeng, et al. Liquid-bridge contact model of unsaturated granular materials and its application in discrete-element method[J]. International Journal of Geomechanics, 2021, 21(9): 04021176. DOI:10.1061/(ASCE)GM.1943-5622.0002122 |
| [24] |
CAI Guoqing, HE Xuzhen, DONG Liang, et al. The shear and tensile strength of unsaturated soils by a grain-scale investigation[J]. Granular Matter, 2020, 22(1): 1. DOI:10.1007/s10035-019-0969-4 |
| [25] |
金磊, 曾亚武, 程涛, 等. 土石混合体边坡稳定性的三维颗粒离散元分析[J]. 哈尔滨工业大学学报, 2020, 52(2): 41. JIN Lei, ZENG Yawu, CHENG Tao, et al. Stability analysis of soil-rock mixture slope based on 3-D DEM[J]. Journal of Harbin Institute of Technology, 2020, 52(2): 41. DOI:10.11918/201811110 |
| [26] |
蔡国庆, 王春莹, 李继光, 等. 非饱和土拉伸特性的三维离散元分析[J]. 应用基础与工程科学学报, 2022, 30(5): 1228. CAI Guoqing, Wang Chunying, Li Jiguang, et al. Study on tensile properties of unsaturated soil based on three dimensional discrete element method[J]. Journal of Applied Basic and Engineering Sciences, 2022, 30(5): 1228. DOI:10.16058/j.issn.1005-0930.2022.05.014 |
| [27] |
NGUYEN T T, BUDDHIMA I. The energy transformation of internal erosion based on fluid-particle coupling[J]. Computers and Geotechnics, 2020, 121(5): 103475. DOI:10.1016/j.compgeo.2020.103475 |
| [28] |
ZHANG Peiyun, MU Linlong, HUANG Maosong. A coupled CFD-DEM investigation into hydro-mechanical behaviour of gap-graded soil experiencing seepage erosion considering cyclic hydraulic loading[J]. Journal of Hydrology, 2023, 624. DOI:10.1016/j.jhydrol.2023.129908 |
| [29] |
CAI Weibing, GAO Ke, WU Shan, et al. Momenttensor-based approach for acoustic emission simulation in brittle rocks using combined finite-discrete element method (FDEM)[J]. Rock Mechanics and Rock Engineering, 2023, 56(6): 3903. DOI:10.1007/S00603-023-03261-Y |
| [30] |
罗滔, OOIE T, CHANA H C, 等. 一种模拟堆石料颗粒破碎的离散元-比例边界有限元结合法[J]. 岩土力学, 2017(5): 883. LUO Tao, OOI E T, CHAN A H C, et al. A combined DEM-SBFEM for modelling particle breakage of rock-fill materials[J]. Rock and Soil Mechanics, 2017(5): 883. DOI:10.16285/j.rsm.2017.05.029 |
| [31] |
WANG Tuo, WANG Pei, YIN Zhenyu, et al. DEM-DFM modeling of suffusion in calcareous sands considering the effect of double-porosity[J]. Computers and Geotechnics, 2022, 151: 1. DOI:10.1016/j.compgeo.2022.104965 |
| [32] |
YANG Yefeng, BAO Junji, YANG Han, et al. Microscopic analysis of the influence of soil properties on the suction bucket installation in sand based on the CFD-DEM model[J]. Computers and Geotechnics, 2023, 156: 105249. DOI:10.1016/j.compgeo.2023.105249 |
| [33] |
BAO Xiaohua, WU Han, XIONG Hao, et al. Particle shape effects on submarine landslides via CFD-DEM[J]. Ocean Engineering, 2023, 284: 115140. DOI:10.1016/J.OCEANENG.2023.115140 |
| [34] |
HU Zheng, ZHANG Yida, YANG Zhongxuan, et al. Suffusion-induced evolution of mechanical and microstructural properties of gap-graded soils using CFD-DEM[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(5): 04020024. DOI:10.1061/(ASCE)GT.1943-5606.0002245 |
| [35] |
LIU Yajing, WANG Lizhong, HONG Yi, et al. A coupled CFD-DEM investigation of suffusion of gap graded soil: coupling effect of confining pressure and fines content[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(18): 2473. DOI:10.1002/nag.3151 |
| [36] |
XIE Liangfu, ZHU Qingyang, GE Ying, et al. Instability simulation of the submerged anti-dip slope based on the CFD-DEM coupling method[J]. Frontiers in Earth Science, 2023, 10: 1013909. DOI:10.3389/FEART.2022.1013909 |
| [37] |
MONDAL S, WU C H, SHARMA M M. Coupled CFD-DEM simulation of hydrodynamic bridging at constrictions[J]. International Journal of Multiphase Flow, 2016, 84: 245. DOI:10.1016/j.ijmultiphaseflow.2016.05.001 |
| [38] |
XIONG Hao, ZHANG Zhimin, YANG Jie, et al. Role of inherent anisotropy in infiltration mechanism of suffusion with irregular granular skeletons[J]. Computers and Geotechnics, 2023, 162: 105692. DOI:10.1016/j.compgeo.2023.105692 |
| [39] |
MU Linlong, ZHANG Peiyun, SHI Zhenhao, et al. Coupled CFD-DEM investigation of erosion accompanied by clogging mechanism under different hydraulic gradients[J]. Computers and Geotechnics, 2023, 153: 105058. DOI:10.1016/j.compgeo.2022.105058 |
| [40] |
ZOU Yuhua, CHEN Qun, CHEN Xiaoqing, et al. Discrete numerical modeling of particle transport in granular filters[J]. Computers and Geotechnics, 2013, 47: 48. DOI:10.1016/j.compgeo.2012.06.002 |
| [41] |
蔡国庆, 刘祎, 徐润泽, 等. 干化-湿化路径下红黏土微观结构演化规律研究[J]. 中国科学: 技术科学, 2021, 51(2): 221. CAI Guoqing, LIU Yi, XU Runze, et al. Microstructural changes in red clay on drying-wetting paths[J]. Science in China: Technical Sciences, 2021, 51(2): 221. DOI:10.1360/SST-2020-0203 |
| [42] |
黄启迪, 蔡国庆, 赵成刚. 非饱和土干化过程微观结构演化规律研究[J]. 岩土力学, 2017, 38(1): 165. HUANG Qidi, CAI Guoqing, ZHAO Chenggang. Microstructure evolution of unsaturated soil during drying process[J]. Rock and Soil Mechanics, 2017, 38(1): 165. DOI:10.16285/j.rsm.2017.01.021 |
| [43] |
WU Tianchi, CAI Guoqing, CLEALL P, et al. Microstructurally informed model for unsaturated soils with double porosity[J]. International Journal of Geomechanics, 2022, 22(12): 33. DOI:10.1061/(ASCE)GM.1943-5622.0002569 |
| [44] |
HAN Bowen, CAI Guoqing, ZHOU Annan, et al. A bounding surface model for unsaturated soils considering the microscopic pore structure and interparticle bonding effect due to water menisci[J]. Acta Geotechnica, 2021, 16(5): 1331. DOI:10.1007/s11440-020-01120-6 |
| [45] |
蔡国庆, 王亚南, 周安楠, 等. 考虑微观孔隙结构的非饱和土水-力耦合本构模型[J]. 岩土工程学报, 2018, 40(4): 618. CAI Guoqing, WANG Yanan, ZHOU Anan, et al. A microstructure-dependent hydro-mechanical coupled constitutive model for unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 618. DOI:10.11779/CJGE201804005 |
| [46] |
LI Jinhui, XU Zhiming, HAN Zhimin. A particle deposition model considering particle size distribution based on the Eulerian approach[J]. Powder Technology, 2023, 427: 118759. DOI:10.1016/j.powtec.2023.118759 |
| [47] |
SUN Xiaosong, SAKAI M, SAKAI M T, et al. A lagrangian-lagrangian coupled method for three-dimensional solid-liquid flows involving free surfaces in a rotating cylindrical tank[J]. Chemical Engineering Journal, 2014, 246: 122. DOI:10.1016/j.cej.2014.02.049 |
| [48] |
WU Haiwen, XU Dabo. Trajectory tracking control of euler-lagrange systems with iss-like robustness to actuator noises[J]. Journal of Systems Science & Complexity, 2022, 35(5): 1719. DOI:10.1007/S11424-022-0219-4 |
| [49] |
郑颖人, 赵尚毅, 邓楚键, 等. 有限元极限分析法发展及其在岩土工程中的应用[J]. 中国工程科学, 2006, 8(12): 9. ZHENG Yingren, ZHAO Shangyi, DENG Chujian, et al. Development of finite element limit analysis method and its applications in geotechnical engineering[J]. Engineering Science, 2006, 8(12): 9. DOI:10.3969/j.issn.1009-1742.2006.12.005 |
| [50] |
ANDERSON T B, JACKSON R. Fluid mechanical description of fluidized beds equation of motion[J]. Industrial & Engineering Fundamentals, 1967, 6: 527. DOI:10.1021/I160024A007 |
| [51] |
YANADA Y, SAKAI M. Lagrangian-lagrangian simulations of solid-liquid flows in a bead mill[J]. Powder Technology, 2013, 239: 105. DOI:10.1016/j.powtec.2013.01.030 |
| [52] |
KOSHIZUKA S, OKA Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid[J]. Nuclear Science and Engineering, 1996, 123(3): 421. DOI:10.13182/NSE96-A24205 |
| [53] |
YIN Yanzhou, CUI Yifei, TANG Yao, et al. Solid-fluid sequentially coupled simulation of internal erosion of soils due to seepage[J]. Granular Matter, 2021, 23(2): 1. DOI:10.1007/S10035-020-01076-0 |
| [54] |
王胤, 艾军, 杨庆. 考虑粒间滚动阻力的CFD-DEM流-固耦合数值模拟方法[J]. 岩土力学, 2017, 38(6): 1771. WANG Yin, AI Jun, YANG Qing. A CFD-DEM coupled method incorporating soil inter-particle rolling resistance[J]. Rock and Soil Mechanics, 2017, 38(6): 1771. DOI:10.16285/j.rsm.2017.06.027 |
| [55] |
刘顺, 唐小微, 赵祥. 沉箱码头地震液化任意拉格朗日欧拉方法大变形分析[J]. 哈尔滨工业大学学报, 2022, 54(8): 117. LIU Shun, TANG Xiaowei, ZHAO Xiang. Large deformation analysis of ALE method for seismic liquefaction of caisson wharf[J]. Journal of Harbin Institute of Technology, 2022, 54(8): 117. DOI:10.11918/202103050 |
| [56] |
HE Xuzhen, CAI Guoqing, ZHAO Chenggang, et al. On the stress-force-fabric equation in triaxial compressions: some insights into the triaxial strength[J]. Computers and Geotechnics, 2017, 85(2): 71. DOI:10.1016/j.compgeo.2015.12.011 |
| [57] |
蔡国庆, 李继光, 许自立, 等. 非饱和土剪切特性的三维离散元分析[J]. 应用基础与工程科学学报, 2020, 28(6): 1447. CAI Guoqing, LI Jiguang, XU Zili, et al. Three-dimensional discrete element analysis of shear properties of unsaturated soils[J]. Journal of Applied Basic and Engineering Sciences, 2020, 28(6): 1447. DOI:10.16058/j.issn.1005-0930.2020.06.016 |
| [58] |
蔡国庆, 刘少鹏, 宋建正, 等. 非饱和土三维离散元计算中宏-细观参数关系探究[J]. 湖南大学学报, 2018, 45(增刊0): 110. CAI Guoqing, LIU Shaopeng, SONG Jianzheng, et al. Insight into relationships between macroscopic and grain-scale parameters in calculating three-dimensional discrete element of unsaturated soils[J]. Journal of Hunan University, 2018, 45(Sup.0): 110. DOI:10.16339/j.cnki.hdxbzkb.2018.S0.020 |
| [59] |
李涛, 赵洪扬, 翁勃航, 等. 细颗粒形状和含量对钙质混合砂强度的影响试验研究[J]. 岩土工程学报, 2023, 45(7): 1517. LI Tao, ZHAO Hongyang, WENG Bohang, et al. Experimental study on effects of shape and content of fine particles on strength of calcareous mixed sand[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(7): 1517. DOI:10.11779/CJGE20220535 |
| [60] |
MA Huaqing, ZHOU Lianyong, LIU Zihan, et al. A review of recent development for the CFD-DEM investigations of non-spherical particles[J]. Powder Technology, 2022, 412: 117972. DOI:10.1016/j.powtec.2022.117972 |
| [61] |
ZHAO Shiwei, ZHOU Xiaowen, LIU Wenhui, et al. Discrete element simulations of direct shear tests with particle angularity effect[J]. Granular Matter, 2015, 17(6): 793. DOI:10.1007/s10035-015-0593-x |
| [62] |
QIAN Jiangu, ZHOU Chuang, YIN Zhenyu, et al. Investigating the effect of particle angularity on suffusion of gap-graded soil using coupled CFD-DEM[J]. Computers and Geotechnics, 2021, 139: 104383. DOI:10.1016/j.compgeo.2021.104383 |
| [63] |
WILLIAMS J R, PENTLAND A P. Superquadric object representation for dynamics of multi-body structures[C]//In Proceedings of ASCE Structures. San Francisco: ASCE, 1989: 448
|
| [64] |
CLEARY P W. The effect of particle shape on simple shear flows[J]. Powder Technol, 2008, 179(3): 144. DOI:10.1016/j.powtec.2007.06.018 |
| [65] |
MUSTOE G G W, MIYATA M. Material flow analyses of noncircular-shaped granular media using discrete element methods[J]. Journal of Engineering Mechanics-asce, 2001, 127(10): 1017. DOI:10.1061/(ASCE)0733-9399(2001)127:10(1017) |
| [66] |
CAROLINE H. Shape representation and contact detection for discrete element simulations of arbitrary geometries[J]. Engineering Computations, 1998, 15(3): 374. DOI:10.1108/02644409810208525 |
| [67] |
LU Guangwu, THIRD J R, MVLLER C R, et al. Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in DEM simulations[J]. Chemical Engineering Science, 2012, 78: 226. DOI:10.1016/j.ces.2012.05.041 |
| [68] |
WILLIAMS J R, O'CONNOR R. A linear complexity intersection algorithm for discrete element simulation of arbitrary geometries[J]. Engineering Computations, 1995, 12(2): 185. DOI:10.1108/02644409510799550 |
| [69] |
FAGBEMI S, TAHMASEBI P, PIRI M, et al. Pore-scale modeling of multiphase flow through porous media under triaxial stress[J]. Advances in Water Resources, 2018, 122: 206. DOI:10.1016/j.advwatres.2018.10.018 |
| [70] |
DONG Kejun, WANG Chuncheng, YU Aibing, et al. A novel method based on orientation discretization for discrete element modeling of non-spherical particles[J]. Chemical Engineering Science, 2015, 126: 500. DOI:10.1016/j.ces.2014.12.059 |
| [71] |
BERKINOVA Z, YERMUKHAMBETOVA A, GOLMAN B. Simulation of flow properties of differently shaped particles using the discrete element method[J]. Computer Applications in Engineering Education, 2020, 29(5): 1061. DOI:10.1002/CAE.22359 |
| [72] |
WANG F, FU Boshen, LUO Huiyang, et al. Characterization of the grain-level mechanical behavior of Eglin sand by nanoindentation[J]. Experimental Mechanics, 2014, 54(5): 871. DOI:10.1007/s11340-013-9845-z |
| [73] |
BELHEINE N, PLASSIARD J P, DONZÉ F V, et al. Numerical simulation of drained triaxial test using 3D discrete element modeling[J]. Computers and Geotechnics, 2009, 36(1/2): 320. DOI:10.1016/j.compgeo.2008.02.003 |
| [74] |
CHENG Kuang, WANG Yin, YANG Qing, et al. Determination of microscopic parameters of quartz sand through tri-axial test using the discrete element method[J]. Computers and Geotechnics, 2017, 92: 22. DOI:10.1016/j.compgeo.2017.07.017 |
| [75] |
HERTZ H R. Uber die beruhrung fester elastischer korper und uber die harte[J]. Verhandlung des Vereins zur Beforderung des GewerbefleiBes, Berlin, 1882, 449. DOI:10.1515/crll.1882.92.156 |
| [76] |
MINDLIN R D. Elastic spheres in contact under varying oblique forces[J]. Journal of Applied Mechanics, 1953, 20: 327. DOI:10.1007/978-1-4613-8865-4_35 |
| [77] |
GONIVA C, KLOSS C, DEEN N G, et al. Influence of rolling friction on single spout fluidized bed simulation[J]. Particuology, 2012, 10(5): 582. DOI:10.1016/j.partic.2012.05.002 |
| [78] |
SALAZAR A, SÁEZ E, PARDO G. Modeling the direct shear test of a coarse sand using the 3D discrete element method with a rolling friction model[J]. Computers and Geotechnics, 2015, 67: 83. DOI:10.1016/j.compgeo.2015.02.017 |
| [79] |
THOMAS R, ANDRE K. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test[J]. Particuology, 2019, 45: 105. DOI:10.1016/j.partic.2018.08.005 |
| [80] |
LU Runrun, ZHANG Lin, RICOUX P, et al. Experiments and CFD-DEM simulations of cohesive particles sedimentation in stilled fluid[J]. Powder Technology, 2019, 356: 222. DOI:10.1016/j.powtec.2019.05.018 |
| [81] |
RABINOVICH Y I, ADLER J J, ATA A, et al. Adhesion between nanoscale rough surfaces[J]. Colloid Interface, 2000, 232: 10. DOI:10.1006/jcis.2000.7167 |
| [82] |
JOHNSON K L, KENDALL K, ROBERTS A D. Surface energy and the contact of elastic solids[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1971, 324(1558): 301. DOI:10.1098/rspa.1971.0141 |
| [83] |
李俊伟, 佟金, 胡斌, 等. 不同含水率黏重黑土与触土部件互作的离散元仿真参数标定[J]. 农业工程学报, 2019, 35(6): 130. LI Junwei, TONG Jin, HU Bin, et al. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(6): 130. DOI:10.11975/j.issn.1002-6819.2019.06.016 |
| [84] |
JIANG Mingjing, YU H S, HARRIS D. A novel discrete model for granular material incorporating rolling resistance[J]. Computers and Geotechnics, 2005, 32: 340. DOI:10.1016/j.compgeo.2005.05.001 |
| [85] |
AI Jun, CHEN Jianfei, ROTTER J M, et al. Assessment of rolling resistance models in discrete element simulations[J]. Powder Technology, 2011, 206: 269. DOI:10.1016/j.powtec.2010.09.030 |
| [86] |
KONDIC L. Dynamics of spherical particles on a surface: collision-induced sliding and other effects[J]. Physical Review. E, 1999, 60(1): 751. DOI:10.1103/PHYSREVE.60.751 |
| [87] |
JIANG Mingjing, SHEN Zhifu, WANG Jianfeng, et al. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147. DOI:10.1016/j.compgeo.2014.12.011 |
| [88] |
王涛, 韩彦辉, 朱永生, 等. PFC2D/3D颗粒离散元计算方法及应用[M]. 北京: 中国建筑工业出版社, 2020. WANG Tao, HAN YanHui, ZHU Yongsheng, et al. PFC2D/3D particle discrete element calculation method and application[M]. Beijing: China Building and Construction Press, 2020. |
| [89] |
ZHU Guangpei, ZHAO Yixin, WANG Zekun, et al. Semi-resolved CFD-DEM simulation of fine particle migration with heat transfer in heterogeneous porous media[J]. International Journal of Heat and Mass Transfer, 2022, 197: 123349. DOI:10.1016/J.IJHEATMASSTRANSFER.2022.123349 |
| [90] |
KAWANO K, SHIRE T, O'SULLIVAN C. Coupled particle-fluid simulations of the initiation of suffusion[J]. Soils and Foundations, 2018, 58(4): 972. DOI:10.1016/j.sandf.2018.05.008 |
| [91] |
CHENG Kuang, WANG Yin, YANG Qing, et al. A semi-resolved CFD-DEM model for seepage-induced fine particle migration in gap-graded soils[J]. Computers and Geotechnics, 2018, 100: 30. DOI:10.1016/j.compgeo.2018.04.004 |
| [92] |
王胤, 陶奕辰, 程旷, 等. 任意解流流固耦合数值方法及在砂土渗流分析中应用[J]. 岩土工程学报, 2021, 43(11): 2084. WANG Yin, TAO Yichen, CHENG Kuang, et al. Arbitrary resolved-unresolved CFD-DEM coupling method and its application to seepage flow analysis in sandy soil[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2084. DOI:10.11779/CJGE202111015 |
| [93] |
PENG Zhengbiao, MOGHTADERI B, DOROODCHI E. A modified direct method for void fraction calculation in CFD-DEM simulations[J]. Advanced Powder Technology, 2016, 27(1): 19. DOI:10.1016/j.apt.2015.10.021 |
| [94] |
TSUJI Y, KAWAGUCHI T, TANAKA T. Discrete particle simulation of two-dimensional fluidized bed[J]. Powder Technology, 1993, 77(1): 79. DOI:10.1016/0032-5910(93)85010-7 |
| [95] |
ZHAO Jidong, SHAN Tong. Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics[J]. Powder Technology, 2013, 239: 248. DOI:10.1016/j.powtec.2013.02.003 |
| [96] |
KOZENY J. Eber kapillare leitung des wassers im boden[J]. Sitzungsber Akad. Wiss, Wien, 1927, 136(2a): 271. |
| [97] |
CARMAN P C. Flow of gases through porous media[M]. London: Butterworths Scientific Publications, 1956.
|
| [98] |
TANG Yao, CHAN D H, ZHU D Z, et al. A coupled discrete element model for the simulation of soil and water flow through an orifice[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(14): 1477. DOI:10.1002/nag.2677 |
| [99] |
DING Yu, ZHANG Jiasheng, JIA Yu, et al. Study on two-phase fluid-solid coupling characteristics in saturated zone of subgrade considering the effects of fine particles migration[J]. Applied Sciences, 2020, 10(21): 7539. DOI:10.3390/APP10217539 |
| [100] |
ERGUN S. Fluid flow through packed columns[J]. Journal of Chemical Engineering Progress, 1952, 48(2): 89. DOI:10.1021/ie50474a011 |
| [101] |
ZHU H P, ZHOU Zongyan, YANG Ruizhen, et al. Discrete particle simulation of particulate systems: Theoretical developments[J]. Chemical Engineering Science, 2006, 62(13): 3378. DOI:10.1016/j.ces.2008.08.006 |
| [102] |
GUO Yuan, YU Xiong (Bill). Comparison of the implementation of three common types of coupled CFD-DEM model for simulating soil surface erosion[J]. International Journal of Multiphase Flow, 2017, 91: 89. DOI:10.1016/j.ijmultiphaseflow.2017.01.006 |
| [103] |
周宗青, 李利平, 石少帅, 等. 隧道突涌水机制与渗透破坏灾变过程模拟研究[J]. 岩土力学, 2020, 41(11): 3621. ZHOU Zongqing, LI Liping, SHI Shaoshuai, et al. Study on tunnel water inrush mechanism and simulation of seepage failure process[J]. Rock and Soil Mechanics, 2020, 41(11): 3621. DOI:10.16285/j.rsm.2020.0131 |
| [104] |
WEN C Y, YU Y H. Mechanics of fluidization[J]. Chemical Engineering Progress Symposium Series, 1966, 62: 100. |
| [105] |
DI FELICE R. The voidage function for fluid-particle interaction systems[J]. International Journal of Multiphase Flow, 1994, 20: 153. DOI:10.1016/0301-9322(94)90011-6 |
| [106] |
SCHILLER L, NAUMANN A. A drag coefficient correlation[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1935, 77: 318. |
| [107] |
WANG Yin, ZHOU Lingxin, YANG Qing. Hydro-mechanical analysis of calcareous sand with a new shape-dependent fluid-particle drag model integrated into CFD-DEM coupling program[J]. Powder Technology, 2019, 344: 108. DOI:10.1016/j.powtec.2018.12.008 |
| [108] |
KOCH D L, HILL R J. Inertial effects in suspension and porous-media flows[J]. Annual Rev Fluid Mech, 2001, 33(1): 619. DOI:10.1146/annurev.fluid.33.1.619 |
| [109] |
ZOU Yuhua, CHEN Chen, ZHANG Limin, et al. Simulating progression of internal erosion in gap-graded sandy gravels using coupled CFD-DEM[J]. International Journal of Geomechanics, 2020, 20(1): 04019135. DOI:10.1061/(ASCE)GM.1943-5622.0001520 |
| [110] |
KANITZ M, GRABE J. The influence of the void fraction on the particle migration: A coupled computational fluid dynamics-discrete element method study about drag force correlations[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 45(1): 45. DOI:10.1002/nag.3131 |
| [111] |
IVAN M, JOHAN P T. Fluidization of elongated particles—effect of multi-particle correlations for drag, lift, and torque in CFD-DEM[J]. AIChE Journal, 2021, 65(4): 17157. DOI:10.1002/AIC.17157 |
| [112] |
AGRAWAL V, SHINDE Y, SHAH M T, et al. Effect of drag models on CFD-DEM predictions of bubbling fluidized beds with Geldart D particles[J]. Advanced Powder Technology, 2018, 29(11): 2658. DOI:10.1016/j.apt.2018.07.014 |
| [113] |
彭恺然, 刘红帅, 平新雨, 等. CFD-DEM耦合模拟中拖曳力模型精度[J]. 吉林大学学报(地球科学版), 2021, 51(5): 1400. PENG Kairan, LIU Hongshuai, PING Xinyu, et al. Accuracy of drag force models in the CFD-DEM method[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(5): 1400. DOI:10.13278/j.cnki.jjuese.20210017 |
| [114] |
BROWN P P, LAWLER D F. Sphere drag and settling velocity revisited[J]. Journal of Environmental Engineering, 2003, 129(3): 222. DOI:10.1061/(ASCE)0733-9372(2003)129:3(222) |
 2024, Vol. 56
2024, Vol. 56