2. 浙江大学建筑设计研究院有限公司, 杭州 310027;
3. 浙江大学 平衡建筑研究中心, 杭州 310027
2. The Architectural Design and Research Institute of Zhejiang University Co. Ltd., Hangzhou 310027, China;
3. Center for Balance Architecture, Zhejiang University, Hangzhou 310027, China
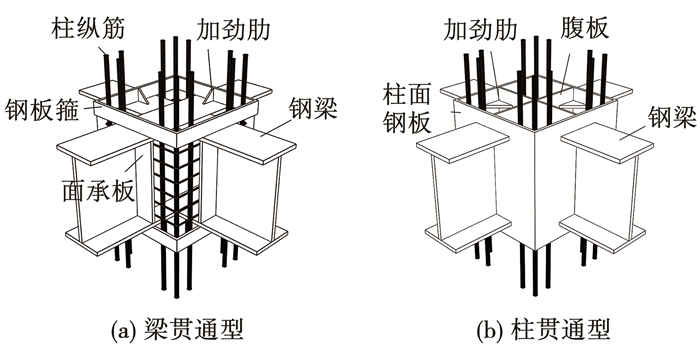
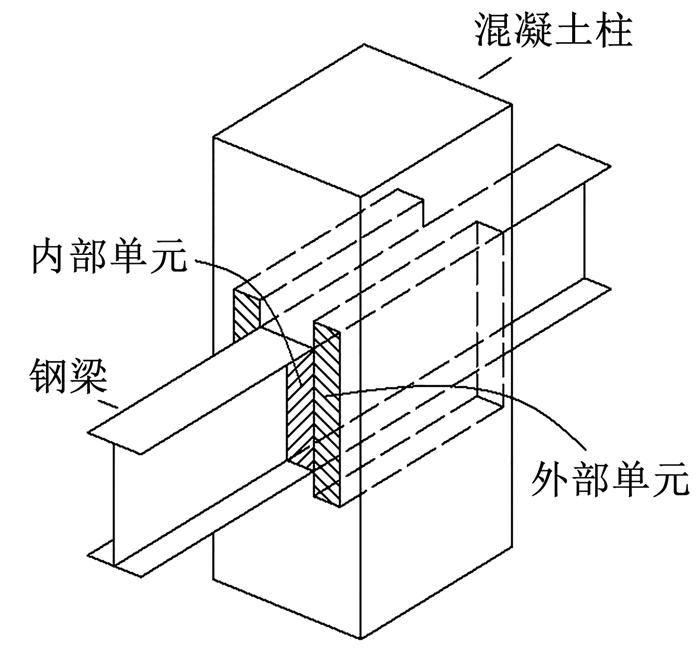
钢筋混凝土柱-钢梁(reinforcement concrete column-steel beam,简称RCS)框架结构兼具了钢筋混凝土柱和钢梁的优点,与钢筋混凝土结构和钢结构相比,既能保证一定的侧向刚度,又能获得较大的结构跨度。美国最早在20世纪80年代将RCS混合框架应用于中高层建筑,而日本更多将其应用于低层商业中心建筑中,以实现大跨度空间。中国早期多将RCS结构应用于工业厂房,近年来也逐渐用于民用建筑中[1-2]。但由于钢与混凝土材料性能之间的差异,使得RCS梁柱节点核心区的受力机理较普通钢筋混凝土节点和钢节点更为复杂, 典型的RCS节点见图 1。自20世纪90年代以来,国内外学者对各类RCS节点进行了大量试验研究,提出了多种节点构造,并研究了不同设计参数对节点性能的影响。基于试验结果和理论分析,各国学者曾提出多种节点承载力计算方法,计算思路分为两种: 一是将节点内各部分如混凝土、箍筋、腹板等各分项强度分别计算后叠加得到总承载力;第二种是以节点内钢梁翼缘内外为分界,将混凝土分为内部单元和外部单元(见图 2),节点承载力由内外混凝土单元和腹板提供。目前两种计算思路均有广泛应用。
|
图 1 典型RCS节点形式 Fig. 1 Typical RCS connection types |
|
图 2 内外混凝土单元 Fig. 2 Inner concrete element and outer concrete element |
美国土木工程协会(ASCE)在1994年最早发布了RCS节点的设计指南[4]。该指南适用于低中地震烈度区的钢梁贯通型节点设计,指南规定节点承载力由腹板、内部混凝土斜压杆和外部混凝土斜压场贡献。ASCE方法计算结果对应1/100位移角时的节点剪力,而此时大部分节点并未达到极限承载力,因此预测偏于保守。Kanno等[5]在ASCE方法的基础上考虑了节点设置直交梁的情况,并且认为ASCE规定的最小配箍率可以适当放宽。Choi等[6]同样额外引入参数,考虑了直交梁和延伸面承板的影响。可以看出,后续研究工作多通过引入不同参数对ASCE方法进行改进,扩大其适用范围,但多数公式计算较为繁琐,不利于工程应用。
Parra等[7]试验研究了一批不同构造的梁贯通边节点抗震性能,在此基础上提出了新的梁贯通式节点承载力计算方法。该方法假设抗剪承载力由三部分组成: 钢腹板、内部混凝土斜压杆和外部混凝土斜压杆。相比于ASCE方法,Parra方法结果与已有试验吻合较好,但公式中各系数取值需查表得到,计算复杂。Fargier等[8]认为Parra方法低估了外部单元的承载力,因此增大了原公式中外部单元的宽度取值,对于特定节点计算准确度有一定提升。
日本学者Nishiyama等[9]于2004年发布了RCS结构抗震设计指南,提出节点受力由混凝土、箍筋、腹板和柱面钢板共同承担,该方法对梁贯通与柱贯通节点均适用。试验数据验证表明该公式偏于保守。
中国对RCS结构的研究和应用自21世纪才逐渐展开。CECS 347:2013《约束混凝土柱组合梁框架结构技术规程》[10]给出了节点承载力的计算公式,规定节点承载力由混凝土、箍筋和钢板的抗剪强度叠加得到。门进杰等[11]统计了RCS节点试验结果,通过分析混凝土、腹板和箍筋等对节点承载力的贡献,提出了改进的抗剪承载力公式,适用性较好。
综上所述,虽已有多位学者研究了RCS节点承载力计算方法,但由于节点构造形式复杂多样,公式计算结果离散性较大,各方法的参数适用范围也未深入研究。因此,本文对近年来国内外RCS节点剪切破坏试验进行统计,采用目前常用的几种理论方法逐一计算,对方法的精度及参数适用性进行分析,并对中国规程方法提出改进建议,供RCS节点抗震设计参考。
1 节点核心区受剪计算方法由于RCS节点构造形式的多样性,部分学者提出的抗剪承载力计算方法存在适用性不强或计算繁琐等缺点。本文选取4种具有代表性,可用于工程设计的计算方法进行分析。
1.1 ASCE计算方法基于文献[12]的研究基础,ASCE最早于1994年发布了RCS节点设计指南。该指南面向有面承板且节点内钢板翼缘外侧设有抗剪键的梁贯通型节点。ASCE规定该指南不适用于高地震烈度区,并给出了材料强度的限值,如节点混凝土强度不超过40 MPa,钢板屈服强度不超过345 MPa,钢筋强度不超过410 MPa等。
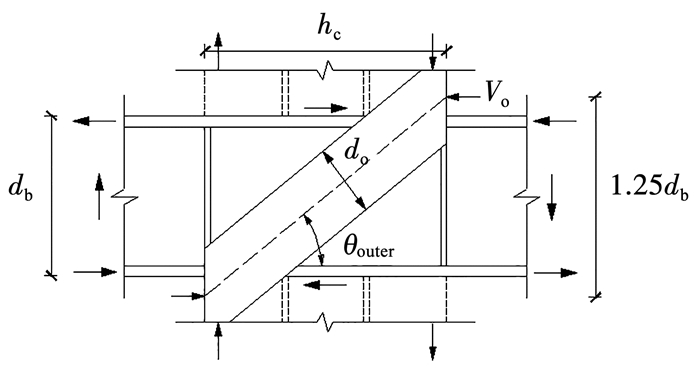
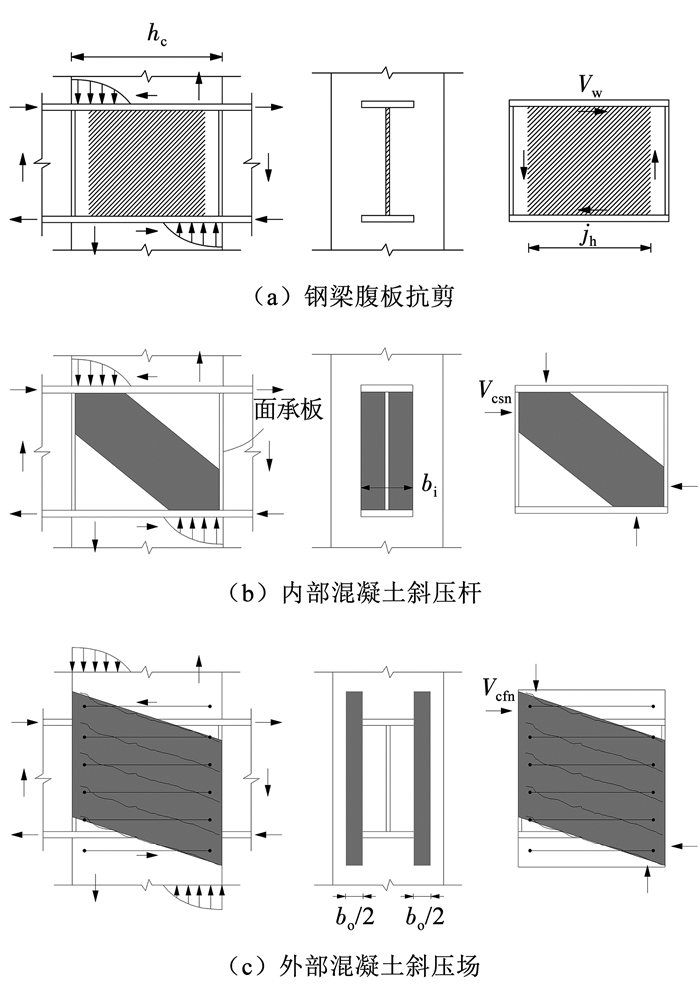
ASCE指南认为RCS节点承载力包含图 3所示的3种传力模型:钢梁腹板Vw,内部混凝土斜压杆Vcsn,外部混凝土斜压场Vcfn。其中混凝土强度计算参考了ACI规范[13]中钢筋混凝土节点的计算思想,具体计算公式为:
|
图 3 ASCE指南提出的RCS节点抗剪机制[4] Fig. 3 Strength mechanisms in RCS connections proposed by ASCE guideline[4] |
1) 钢梁腹板抗剪:
| $V_{\mathrm{w}}=0.6 f_{\mathrm{wy}} t_{\mathrm{w}} j_{\mathrm{h}}$ | (1a) |
式中: fwy为腹板屈服强度;tw为腹板厚度;jh为腹板有效计算宽度,保守起见通常取0.7hc;hc为柱截面高度。
2) 内部混凝土斜压杆抗剪:
| $V_{\mathrm{csn}}=1.7 \sqrt{f_{\mathrm{c}}^{\prime}} b_{\mathrm{i}} h_{\mathrm{c}}$ | (1b) |
式中: f′c为混凝土圆柱体抗压强度;hc为混凝土柱截面高度;bi为内部单元宽度,通常取面承板与翼缘宽度的较大值。
3) 外部混凝土斜压场抗剪:
| $V_{\mathrm{cfn}}=0.4 \sqrt{f_{\mathrm{c}}^{\prime}} b_{\mathrm{o}} h_{\mathrm{c}}+\frac{0.9 A_{\mathrm{sh}} f_{\mathrm{y}} h_{\mathrm{c}}}{s_{\mathrm{h}}} \leqslant 1.7 \sqrt{f_{\mathrm{c}}^{\prime}} b_{\mathrm{o}} h_{\mathrm{c}}$ | (1c) |
式中: bo为外部单元宽度,根据节点内不同剪力键构造计算得到。当节点内钢梁翼缘上不设置剪力键时,外部单元宽度为0,即不考虑外部混凝土的贡献;Ash为一个间距内各肢箍筋总面积;fy为箍筋屈服强度;sh为箍筋间距。此公式规定了外部单元强度的上限,为了避免高估箍筋对承载力的贡献。
1.2 Parra计算方法为弥补ASCE方法的缺陷,Parra等[7]提出了可用于高地震烈度区设计的计算方法。Parra公式未给出钢材强度限制,但规定适用的混凝土强度范围为21~70 MPa。
与ASCE方法类似,Parra方法将抗剪承载力分为3部分:钢梁腹板抗剪Vw,内部混凝土斜压杆Vi,外部混凝土斜压杆Vo,其中前两种抗剪机理与ASCE方法相同(图 3(a)、(b))。不同的是,该方法在计算外混凝土单元强度时也采用斜压杆机制(图 4),并且外部混凝土压杆中忽略了箍筋强度的贡献,仅考虑其对混凝土的约束作用。具体公式为
| $V_{\mathrm{j}}=0.9 \frac{f_{\mathrm{wy}}}{\sqrt{3}} t_{\mathrm{w}} h_{\mathrm{c}}+0.3 f_{\mathrm{ci}}^{\prime} b_{\mathrm{i}} h_{\mathrm{c}}+0.3 f_{\mathrm{co}}^{\prime} b_{\mathrm{o}} h_{\mathrm{c}}$ | (2) |
式中从左到右3项分别为腹板、内部单元、外部单元的强度贡献。f′ci和f′co分别为内部与外部单元的混凝土强度,表达式分别为:
| $f_{\mathrm{ci}}^{\prime}=\nu_{\text {ibase }}\left(-0.0048 f_{\mathrm{c}}^{\prime}+1.13\right) k_1 k_2$ | (3a) |
| $f_{\mathrm{co}}^{\prime}=\nu_{\text {obase }}\left(-0.0048 f_{\mathrm{c}}^{\prime}+1.13\right) k_1 k_2 k_3$ | (3b) |
式中:νibase和νobase为基本强度因子,RCS中节点的基本强度因子约为边节点的两倍;k1~k3为混凝土约束系数,目的是为考虑箍筋、钢板箍、柱面钢板和直交梁等构造对混凝土的约束带来的强度提升,计算时需根据不同构造选取相应数值,具体详见文献[7]表 1。
| 表 1 试件参数范围与类型数量 Tab. 1 Range of parameters of specimens and quantity of different types of specimens |
Nishiyama等[9]在RCS结构抗震设计指南中给出了节点设计方法,规定了该方法适用于设计混凝土强度在21~60 MPa间的RCS节点。与前述两种方法不同,Nishiyama方法不再将混凝土分为内外单元,而是将混凝土、腹板、箍筋和柱面钢板的抗剪强度直接叠加,得到节点承载力。计算公式为:
| $V_{\mathrm{j}}=V_{\mathrm{w}}+V_{\mathrm{f}}+V_{\mathrm{h}}+V_{\mathrm{c}}$ | (4a) |
| $V_{\mathrm{w}}=C_1 A_{\mathrm{w}} f_{\mathrm{wy}} / \sqrt{3}$ | (4b) |
| $V_{\mathrm{f}}=0.5 A_{\mathrm{f}} f_{\mathrm{fy}} / \sqrt{3}$ | (4c) |
| $V_{\mathrm{h}}=0.25 p_{\mathrm{w}} f_{\mathrm{y}} b_{\mathrm{c}} d$ | (4d) |
| $V_{\mathrm{c}}=0.04 C_2 C_3 b_{\mathrm{c}} h_{\mathrm{c}} f_{\mathrm{c}}^{\prime} \delta$ | (4e) |
式中: Vw、Vf、Vh、Vc分别为腹板、柱面钢板、箍筋、混凝土的承载力贡献;Aw和Af分别为腹板与柱面钢板截面积;ffy为柱面钢板屈服强度;pw为节点配箍率;bc为柱截面宽度;d为受拉与受压纵筋的间距;δ为节点位置影响系数,对中柱节点取3,边柱节点取2,顶柱角节点取1;C1与为面承板对腹板抗剪强度的影响,有面承板时取0.9,反之取0.8;C2、C3为与节点构造相关的系数,具体考虑了延伸面承板、钢板箍,直交梁等对混凝土强度的提高,具体数值详见文献[9]中表 2。
| 表 2 试件参数及计算结果对比 Tab. 2 Parameters of specimens and comparison of experimental and calculation results |
中国规程CECS 347:2013《约束混凝土柱组合梁框架结构技术规程》[10]建议了梁贯通型和柱贯通型节点形式,并给出了相应承载力计算公式。公式计算思路与Nishiyama方法类似,即将各部分的抗剪强度直接叠加即得到节点承载力。梁贯通型节点强度由混凝土、腹板和柱面钢板组成:
| $V_{\mathrm{i}}=0.14 \alpha b_{\mathrm{c}} h_{\mathrm{c}} f_{\mathrm{c}}+0.58 A_{\mathrm{w}} f_{\mathrm{wy}}+0.4 \sum A_{\mathrm{f}} f_{\mathrm{fy}}$ | (5) |
式中:从左到右3项分别为混凝土、腹板、柱面钢板的强度贡献;fc为混凝土轴心抗压强度;α为节点位置影响系数,对中柱节点取1,边柱节点取0.7,顶柱角节点取0.4。
柱贯通节点强度由混凝土、箍筋和柱面钢板组成:
| $V_{\mathrm{i}}=0.15 \alpha b_{\mathrm{c}} h_{\mathrm{c}} f_{\mathrm{c}}+p_{\mathrm{w}} f_{\mathrm{y}} b_{\mathrm{c}} h_{\mathrm{c}}+0.4 \sum A_{\mathrm{f}} f_{\mathrm{fy}}$ | (6) |
相比以上3种方法,中国规程公式无需根据构造措施查表选取系数,计算简便。值得注意的是,中国规程中并没有同时将腹板和箍筋的强度纳入公式。考虑到腹板的强度贡献较大,当二者同时存在时,本文计算仅考虑腹板。
2 计算精度对比为比较与分析各方法的精确度与适用性,本文统计了1987—2020年间的RCS节点剪切破坏试验,共收集了15篇文献中的66个试件。试件的主要参数范围及试件类型数量详见表 1,其中约83%的试件(55个)混凝土强度低于50 MPa,采用60 MPa以上高强混凝土的试件有11个;约92%的试件的轴压比低于0.2(61个),其中轴压比为0和0.2的试件均为24个,轴压比高于0.3的试件有5个;试件的节点配箍率范围在0%~1.4%,配箍率低于1%的试件约为89%(59个),其中28个试件节点区没有配置箍筋;试件柱梁宽度比的范围为1.88~4.00,其中约78%的试件(52个)集中于2.25~ 3.25。此外,各节点位置,节点形式和有无直交梁构造的试件数量也在表 1中给出。
本文采用前述4种计算方法对各试件逐一计算,基于试验结果对各方法的精度进行了比较,计算结果见表 2,其中结果为试验梁端荷载Vexp与计算梁端荷载Vcal的比值。计算时混凝土与钢材强度均为实测值。需要说明的是,各文献中混凝土抗压强度的试验方法存在差异,为使结果具有可比性,各混凝土试验强度均换算为公式指定强度后代入计算。表 2可见部分计算结果偏于不安全,文献[20]的3号试件未设置面承板,混凝土内部单元的约束较低,从而试验结果远远小于计算值,在引入面承板后,节点承载力才逐渐上升;文献[24]提出的一种翼缘部分切除式节点,由于翼缘削弱造成对混凝土的约束不足,从而采用现有公式会高估混凝土部分的承载力。对于存在简化构造的节点,计算时应考虑足够安全储备。4种方法对同一试件的计算也会存在较大差异,如文献[21],中国规程与Nishiyama方法计算值明显高于另外两种方法。这是由于试件中的柱面钢板在节点破坏时并未发挥全部抗剪强度,中国规程与Nishiyama公式中存在的柱面钢板项导致节点承载力被高估。
图 5为4种方法的计算结果散点图。可以看出,各公式均具有一定的计算精度,具备工程实用性,其中Parra方法结果离散程度最小。ASCE方法计算结果偏于保守,原因是该方法预测的是1/100位移角时的节点荷载,并未达到节点极限承载力,并且ASCE指南中未全面考虑各类节点构造,因此计算离散性较大。比较图 5(c)和(d),可以看出中国规程和Nishiyama方法计算结果接近,这是因为二者公式计算思路类似且公式中各项系数也较为接近。
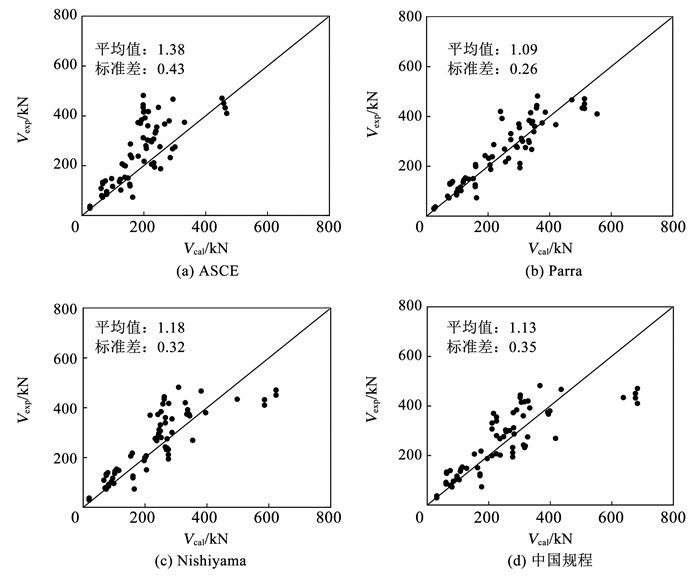
|
图 5 4种方法的试验值与计算值比较 Fig. 5 Experimental results versus calculation results of four methods |
为了解各部分材料强度对RCS节点承载力的贡献,表 3给出了4种方法中各分项对承载力贡献的平均值,可以看出,混凝土和腹板对节点承载力贡献平均超过90%,因此提高混凝土和腹板的强度是提升RCS节点承载力最有效的方法。相比之下,箍筋的强度贡献较小,平均低于10%。这是由于箍筋的作用主要是约束节点区混凝土,限制节点变形。当节点内腹板屈服并发生较大变形后,箍筋才能充分发挥强度作用。虽然中国规程中考虑了箍筋的承载力,但计算时仅有4例试件考虑了箍筋,结果不具代表性。ASCE和Parra都将箍筋的作用考虑进混凝土外部单元,表明箍筋对节点承载力的直接强度贡献并不重要。
| 表 3 各部分对抗剪承载力的贡献比例 Tab. 3 Contribution ratio of strength of each component to shear capacity |
为体现Nishiyama方法和中国规程方法中柱面钢板的贡献,表 3将有柱面钢板的试件数据单独列出。由于有柱面钢板的试件都未设置箍筋,因此Nishiyama方法中的箍筋贡献降为0。当节点设置柱面钢板时,中国规程方法中的混凝土项贡献均下降接近10%,腹板项下降了约15%。Nishiyama方法中混凝土项下降约8.5%,腹板项贡献几乎不变,原因推测是Nishiyama方法中柱面钢板强度计算值约为中国规程计算值的70%,并且柱面钢板分担了箍筋原来的贡献比例,导致混凝土和腹板的贡献比例下降较少。
3 参数分析本节对混凝土强度、轴压比、节点配箍率、几何参数、节点位置、节点形式、有无直交梁等参数对计算结果的影响进行了分析,总结了各方法的参数适用性,供RCS节点设计参考。
3.1 混凝土强度图 6为混凝土强度对计算结果的影响。可以看出,ASCE的计算离散性较大,混凝土强度对结果无明显影响。Parra方法在混凝土分项中引入了强度影响系数,该系数随着混凝土强度的提高而线性下降,因此混凝土强度对Parra方法计算精度无影响。引入强度系数的原因是混凝土峰值压应变随着混凝土等级的提高而增大,而当节点发生相同的剪切变形时,高强混凝土并未达到极限抗压强度,若将抗压强度直接代入公式计算,则会高估混凝土的承载力。对于中国规程,随着混凝土强度的提高,试验与计算比值有明显下降的趋势。当混凝土强度高于60 MPa时,计算结果偏于危险,表明公式在计算高强混凝土RCS节点时存在局限。相同的规律也存在于Nishiyama方法中,不同的是文献[9]中曾建议Nishiyama方法不适用于混凝土强度60 MPa以上的结构,而中国规程并未给出限定,应予以改进。
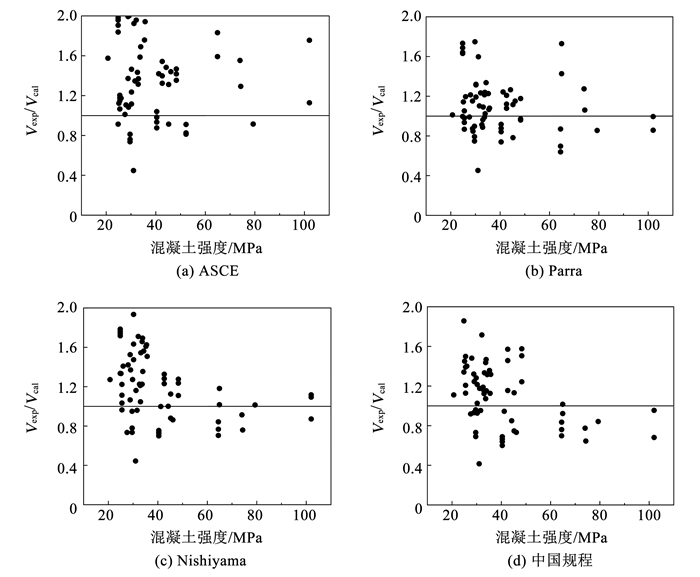
|
图 6 混凝土强度对结果的影响 Fig. 6 Relationship of concrete strength and calculation results |
图 7为试验与计算比值和轴压比的关系。由于各计算方法均未考虑轴力,因此可直接得到轴力对各方法结果的影响。可以看出,当轴压比在0~0.2时,4种方法计算值总体均小于试验值,这表明增大轴力能够提高抗剪承载力,公式中不考虑轴力影响是偏于安全的。这是由于轴向压力使得柱截面受压区面积加大,混凝土斜压杆宽度增大,因此节点承载力提高。但当轴压比大于0.3时,试验与计算比值逐渐下降,说明轴力超过一定限值时对抗剪承载力是不利的,因为此时混凝土被压碎,斜压杆未发挥全部的强度。文献[24]的试验结果表明,0.35轴压比时的节点承载力比0.05轴压比时低5%,延性也较差。
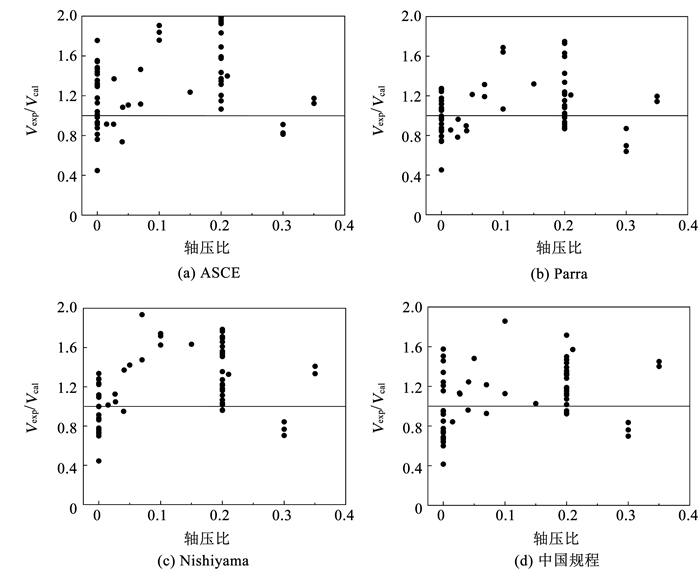
|
图 7 轴压比对结果的影响 Fig. 7 Relationship of axial load ratio and calculation results |
图 8给出了节点配箍率对计算结果的影响。现有文献RCS节点配箍率大部分在1%以下。当节点存在柱面钢板或采用高强材料时,配置箍筋的效果不明显,可降低配箍率。通常认为增大节点配箍率能够加强节点约束,增大承载力,但由图 8可以看出,配箍率对各方法结果并无明显影响,因此可以认为设计时满足最小配箍率即可,在保证节点混凝土整体性的同时方便节点施工。
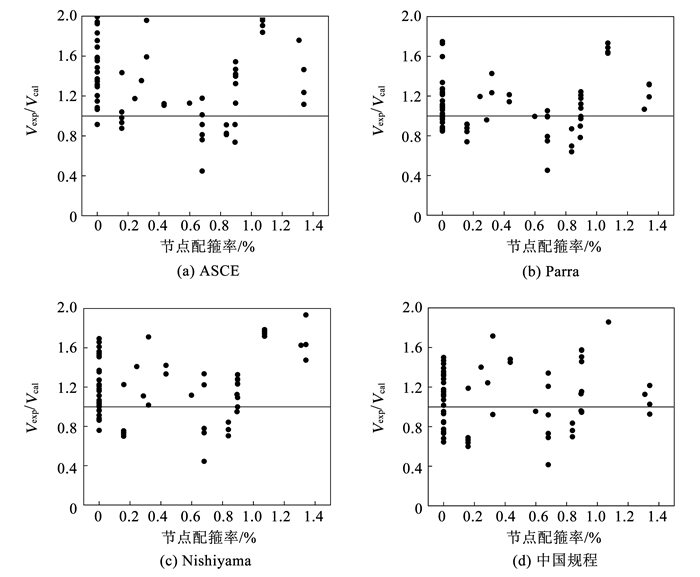
|
图 8 节点配箍率对结果的影响 Fig. 8 Relationship of stirrup ratio in connections and calculation results |
图 9为承载力比值和柱梁宽度比的关系。可以看出,随着柱梁宽度比增大,各方法结果均略有下降,特别是比值大于3时,中国规程和Nishiyama方法略偏于不安全。通过分析文献的试验结果,分析原因推测是梁宽相对柱宽较小时,钢梁翼缘外侧混凝土压碎更加严重,外部混凝土单元更早失效,从而降低了节点的抗剪承载力[20]。
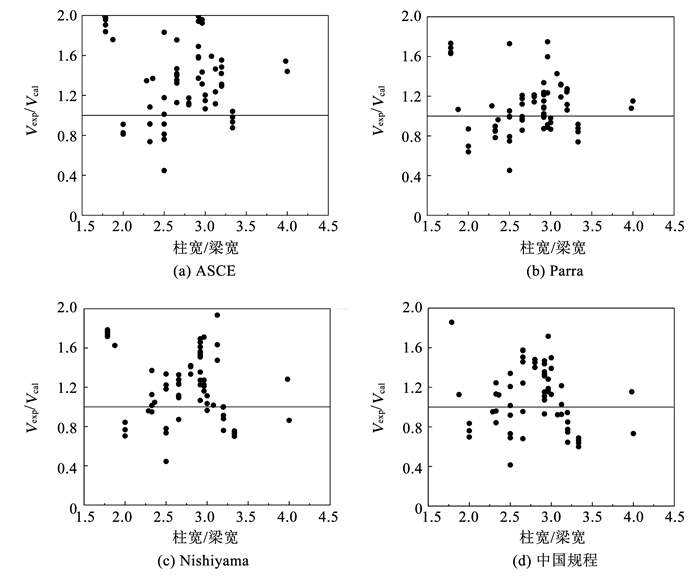
|
图 9 柱梁宽度比对结果的影响 Fig. 9 Relationship of ratio of column width to beam width and calculation results |
本文选取的试件按位置分为61个中节点和5个边节点。本文所述4种计算公式中,都考虑了节点位置对结果的影响。由图 10可看出,4种方法对边节点的计算结果均较为准确,但Parra公式对边节点的计算结果略偏于不安全,建议按此式设计时考虑安全储备。目前尚未收集到角节点的剪切破坏试验,因此公式对于该类节点的适用性有待进一步确认。
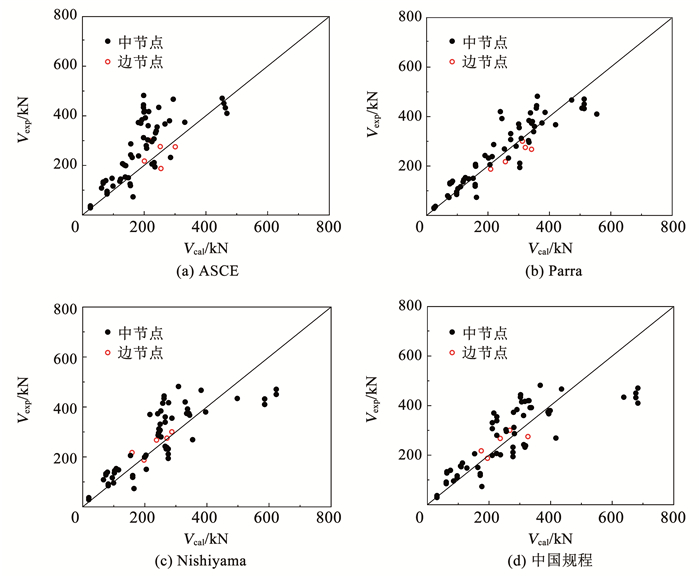
|
图 10 节点位置对结果的影响 Fig. 10 Relationship of connection positions and calculation results |
RCS节点可根据梁柱是否连续分为梁贯通和柱贯通形式。本文选取的66个试件中44个为梁贯通,22个为柱贯通。中国规程和Nishiyama方法都分别给出了梁贯通和柱贯通节点的计算方法,而Parra和ASCE方法是基于梁贯通节点提出的,适用性有待确认。由图 11可看出,各方法都能较准确地预测梁贯通节点承载力。对于柱贯通节点,各方法的预测结果均偏于安全。这是由于文献中柱贯通节点多采用柱面钢板或加宽面承板等构造,节点区混凝土受较强约束,从而导致承载力偏大。
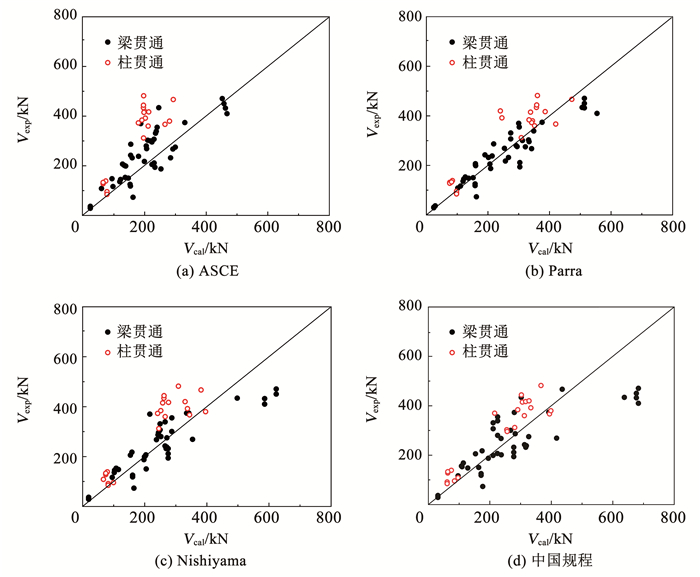
|
图 11 梁柱贯通形式对结果的影响 Fig. 11 Relationship of connection types and calculation results |
直交梁是增大节点承载力的有效措施。当有直交梁时,Nishiyama和Parra计算公式中引入系数提高了混凝土的强度,而中国规程和ASCE指南中并未考虑直交梁的影响。本文选取的66个试件中有27个设置了直交梁。图 12中区分出了有直交梁节点的计算结果。可以看出,Parra方法对有直交梁试件计算较为准确且离散性较小。中国规程与Nishiyama方法预测结果偏于保守且离散性稍大。ASCE指南对于有直交梁的试件计算过于保守,应予以改进。综上所述,各公式的参数适用性总结如下:
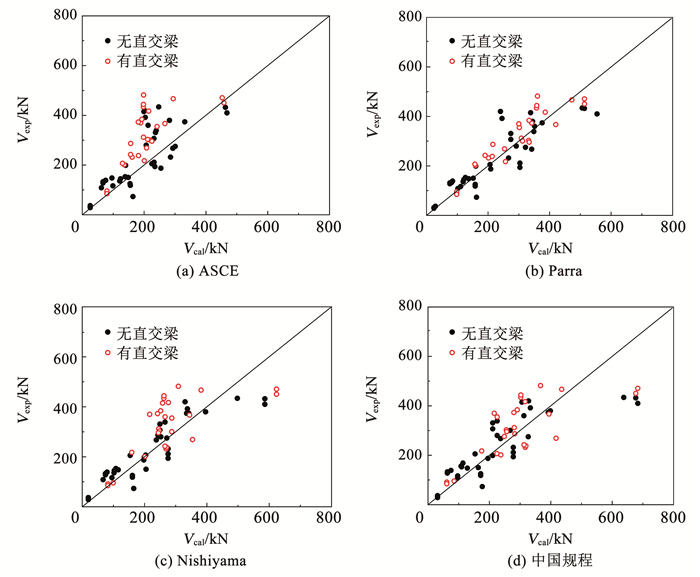
|
图 12 直交梁对结果的影响 Fig. 12 Relationship of transverse beam and calculation results |
1) Parra方法能准确考虑混凝土强度对承载力的影响,中国规程与Nishiyama方法对混凝土强度超过60 MPa的节点承载力预测偏于危险;
2) 各方法对不同配箍率与不同位置的节点均有较好适用性;
3) 各方法对小轴压比节点(轴压比0~0.2)与柱贯通节点预测均偏于保守;
4) 柱梁宽度比增大会使各方法试验与计算结果比值降低,当宽度比大于3时,中国规程和Nishiyama方法略偏于不安全;
5) Parra方法对有直交梁试件计算较为准确,ASCE指南方法对于有直交梁的试件计算过于保守。
4 中国规程方法的改进建议基于与试验对比及参数分析的结果,作者认为中国规程方法对混凝土强度与直交梁的影响考虑不足,据此对公式中的混凝土分项提出改进建议。
4.1 高强混凝土的影响由3.1节可知,当混凝土强度高于60 MPa时,中国规程方法对于节点承载力的预测均偏于危险,此时若将实际抗压强度代入公式会高估节点承载力。本文建议当混凝土强度大于60 MPa时,引入混凝土强度系数来降低混凝土项的贡献。
4.2 直交梁的影响中国规程方法没有考虑直交梁对节点承载力的影响,但从以往试验结果来看,引入直交梁会使节点承载力提升约15%[14, 16, 20]。本文建议当节点有直交梁时,在混凝土项引入1.15的强度系数,提高混凝土的强度贡献。
综上,作者建议改进后的混凝土分项计算式为
| $V_{\mathrm{c}}=0.14 \phi_{\mathrm{c}} \eta_{\mathrm{j}} \alpha b_{\mathrm{c}} h_{\mathrm{c}} f_{\mathrm{c}}$ | (7) |
式中:ϕc为混凝土强度系数,通过数据拟合得到,当fc≥60 MPa时,取(1.57-0.009 5fc),当fc < 60 MPa时,取1;ηj为直交梁约束系数,对节点有直交梁的情况取1.15,其他情况取1。
采用改进后的公式对部分节点进行验算,得到结果见表 4、5。可以看出,改进方法对高强混凝土节点和有直交梁试件的预测精度有明显提升。
| 表 4 高强混凝土节点采用改进方法的计算结果 Tab. 4 Calculation results of modified equation for high strength concrete connections |
| 表 5 有直交梁节点采用改进方法的计算结果 Tab. 5 Calculation results of modified method for connections with transverse beams |
1) ASCE指南、Parra、Nishiyama和中国规程4种钢筋混凝土柱-钢梁节点抗剪承载力计算方法均具备工程实用价值,其中Parra方法结果离散性最小,中国规程计算最为简便;ASCE方法适用于低中地震烈度区,结果偏于保守且离散性最大,尤其对于有直交梁试件ASCE方法预测值过于保守;中国规程和Nishiyama方法计算结果相近,二者对于混凝土强度超过60 MPa的节点预测均偏于危险。
2) 各方法对不同的配箍率与节点位置试件均有较好适用性。
3) 各方法中不考虑柱轴力是偏于安全的,但当轴压比大于0.3时会对节点承载力和延性有不利影响,设计时应避免。
4) 柱梁宽度比增大会使计算与试验值之比增大,推测原因是钢梁翼缘外侧混凝土压碎导致外部混凝土单元抗剪强度下降。
5) 各方法对于柱贯通节点预测均偏于保守,原因是柱贯通节点中柱面钢板或加宽面承板等构造对节点混凝土有较强的约束,使节点承载力提高。
6) 建议在中国规程公式中引入混凝土强度系数和直交梁约束系数,考虑二者对节点承载力的影响。
| [1] |
DEIERLEIN G G, NOGUCHI H. Overview of U.S.-Japan research on the seismic design of composite reinforced concrete and steel moment frame structures[J]. Journal of Structural Engineering, 2004, 130(2): 361. DOI:10.1061/(ASCE)0733-9445(2004)130:2(361) |
| [2] |
门进杰, 史庆轩, 周琦. 钢筋混凝土柱-钢梁组合框架节点研究进展[J]. 结构工程师, 2012, 28(1): 153. |
| [3] |
TAO Yuchen, ZHAO Weijian, SHU Jiangpeng, et al. Nonlinear finite-element analysis of the seismic behavior of RC column-steel beam connections with shear failure mode[J]. Journal of structural engineering, 2021, 147(10): 4021160. DOI:10.1061/(ASCE)0733-9445(2004)130:2(361) |
| [4] |
ASCE Task Committee on Design Criteria for Composite Structures in Steel and Concrete. Guidelines for design of joints between steel beams and reinforced concrete columns[J]. Journal of Structural Engineering, 1994, 120(8): 2330. DOI:10.1061/(ASCE)0733-9445(1994)120:8(2330) |
| [5] |
KANNO R, DEIERLEIN G G. Design model of joints for RCS frames[C]//Composite Construction in Steel and Concrete Ⅳ Conference. Banff: ASCE, 2000: 947
|
| [6] |
CHOI Y C, MOON J H, LEE E J, et al. Development of a shear strength equation for beam-column connections in reinforced concrete and steel composite systems[J]. International Journal of Concrete Structures and Materials, 2017, 11(2): 185. DOI:10.1007/s40069-017-0199-2 |
| [7] |
PARRA-MONTESINOS G, WIGHT J K. Modeling shear behavior of hybrid RCS beam-column connections[J]. Journal of Structural Engineering, 2001, 127(1): 3. DOI:10.1061/(ASCE)0733-9445(2001)127:1(3) |
| [8] |
FARGIER-GABALDON L B, PARRA-MONTESINOS G J, WIGHT J K. Seismic behavior of exterior reinforced concrete wide-column-to-steel beam joints[J]. ACI Structural Journal, 2020, 117(2): 117. |
| [9] |
NISHIYAMA I, KURAMOTO H, NOGUCHI H. Guidelines: seismic design of composite reinforced concrete and steel buildings[J]. Journal of Structural Engineering, 2004, 130(2): 336. DOI:10.1061/(ASCE)0733-9445(2004)130:2(336) |
| [10] |
约束混凝土柱组合梁框架结构技术规程: CECS 347: 2013[S]. 保定: 河北合创建筑节能科技有限公司, 2013
|
| [11] |
门进杰, 李慧娟, 王晓丹, 等. 钢筋混凝土柱-钢梁组合节点抗剪承载力研究[J]. 建筑结构, 2014, 44(6): 74. |
| [12] |
DEIERLEIN G G, SHEIKH T M, YURA J A, et al. Beam-column moment connections for composite frames: part 2[J]. Journal of Structural Engineering, 1987, 115(11): 2858. DOI:10.1061/(ASCE)0733-9445(1989)115:11(2858) |
| [13] |
ACI-ASCE Committee 352. Recommendations for design of beam-column joints in monolithic reinforced concrete structures[J]. Journal of American Concrete Institute, 1985, 82(3): 266. |
| [14] |
PARRA-MONTESINOS G, WIGHT J K. Seismic response of exterior RC column-to-steel beam connections[J]. Journal of Structural Engineering, 2000, 126(10): 1113. DOI:10.1061/(ASCE)0733-9445(2000)126:10(1113) |
| [15] |
KHALOO A, BAKHTIARI D R. Seismic performance of precast RC column to steel beam connections with variable joint configurations[J]. Engineering Structures, 2018, 160: 408. DOI:10.1016/j.engstruct.2018.01.039 |
| [16] |
LEE H J, PARK H G, HWANG H J, et al. Cyclic lateral load test for RC column-steel beam joints with simplified connection details[J]. Journal of Structural Engineering, 2019, 145(8): 325. DOI:10.1061/(ASCE)ST.1943-541X.0002369 |
| [17] |
KURAMOTO H, NISHIYAMA I. Seismic performance and stress transferring mechanism of through-column-type joints for composite reinforced concrete and steel frames[J]. Journal of Structural Engineering, 2004, 130(2): 352. DOI:10.1061/(ASCE)0733-9445(2004)130:2(352) |
| [18] |
刘阳, 郭子雄, 戴镜洲, 等. 不同破坏机制的装配式RCS框架节点抗震性能试验研究[J]. 土木工程学报, 2013, 46(3): 18. |
| [19] |
李升才, 颜军, 王会丽. 混凝土柱-蜂窝钢梁组合节点拟静力试验研究[J]. 建筑结构学报, 2009, 30(2): 30. |
| [20] |
KANNO R. Strength, deformation, and seismic resistance of joints between steel beams and reinforced concrete columns[D]. Ithaca: Cornell University, 1993
|
| [21] |
SHEIKH T M. Moment connections between steel beams and concrete columns[D]. Austin: The University of Texas at Austin, 1987
|
| [22] |
中田寛二, 小澤潤治, 佐藤良介, 等. 柱鉄筋コンクリート造· 梁鉄骨造で構成される十字形接合部に関する解析的研究: No. 44[R]. 东京: 東急建設技術研究所, 2018
|
| [23] |
波田雅也, 竹内健一, 海野敦成. 「柱RC梁S ハイブリッド構法」の開発および適用事例: No. 2[R]. 东京: 青木あすなろ建設, 2017
|
| [24] |
易勇. 钢梁—钢筋混凝土柱组合框架中间层中节点抗震性能试验研究[D]. 重庆: 重庆大学, 2005
|
| [25] |
门进杰, 郭智峰, 史庆轩, 等. 钢筋混凝土柱-腹板贯通型钢梁混合框架中节点抗震性能试验研究[J]. 建筑结构学报, 2014, 35(8): 72. |
| [26] |
森本仁, 古川淳, 市川昌和, 等. 柱貫通型·柱鉄筋コンクリート-梁鉄骨造柱·変形能に関する実験的研究[J]. 日本建築学会構造系論文集, 1998, 513: 181. |
| [27] |
藤本利昭, 八ツ繁公一, 宮野洋一, 等. 柱RC·梁Sで構成される柱梁接合部の開発[J]. 鋼構造論文集, 1994, 1(2): 91. |
 2024, Vol. 56
2024, Vol. 56