2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 金风科技股份有限公司, 北京 100167
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. Goldwind Science & Technology Co. Ltd., Beijing 100167, China
高层建筑经过长期服役,由于材料老化、环境侵蚀等因素,结构力学性能(承载力和刚度)会不可避免地出现退化现象。服役多年后的建筑结构在地震、台风等动荷载作用下是否还能满足结构初始设计时的安全性与舒适性标准是住建管理部门和大众极为关心的问题。而解答这一关切的核心是如何利用监测或检测数据建立一个可以准确地反映既有建筑结构在地震、台风等动荷载作用下动力响应的结构模型。
利用监测系统测量的结构动力响应数据来识别并更新结构模型参数,是属于结构健康监测领域结构模型修正的研究范畴。早在20世纪70年代,Baruch等[1-2]就提出了直接利用监测数据来修正结构刚度矩阵的方法,然而这些方法中刚度矩阵更新并不具有物理意义,无法反映结构具体构件的力学性能退化。为此,Kabe[3]、Jafarkhani等[4]、Sipple等[5]在模型修正中考虑了刚度矩阵对称性以及各单元拓扑连接关系,使得模型修正结果可与实际结构构件的损伤情况相对应。Mottershead等[6]讨论了基于灵敏度和迭代优化的模型修正方法,Yuan等[7]、Jafari等[8]给出了该方法参数选择的一般原则。该方法需要结构参数在模型更新优化过程中不断迭代,当结构较为简单时,能较快收敛[9-10],但随着结构复杂度的提升,不仅计算成本大幅增高同时也难以保障识别参数收敛到全局最优解[11]。此外,模型修正往往是病态的优化问题,为了提高结构参数识别精度,求解模型修正问题时常需要引入正则化项,常用正则化方法包括:L2 Tikhonov正则化[12],L1正则化[13],min-max规则[14],L-curve规则[15]等。
针对建筑结构,杨朋超等[16]对各种矩阵型有限元模型修正方法进行了总结,考虑模态参与因子约束,以一栋高层钢结构为对象进行初始有限元模型修正。王小娟等[17]融合加速度与应变数据以频率、振型构建目标函数对二维框架结构进行了修正。由于建筑结构模型复杂、模型参数众多且监测系统传感器数量有限,模型修正方法往往难以得到较为准确的结构参数。因此,上述方法都是针对结构特点,选取一些模型参数较少的简化模型开展模型修正。以本文所研究的框架结构为例,因为框架结构具有主要质量集中在楼层位置且楼层平面内刚度很大的特点,人们常采用层集中质量简化模型[16](如层剪切模型等)来模拟实际建筑结构动力响应。但这些简化模型因直接或间接地忽略结构转动自由度影响而引入模型误差,导致难以准确模拟实际结构的动力响应;而上述简化模型模型误差如何影响预测实际结构动力响应的准确性,在理论层面还没有很好的分析方法。由此可见,寻找一种新方法来量化评价简化模型误差,并以此为基础构建能够准确模拟实际建筑动力响应的新型简化模型,成为破解现有研究瓶颈的关键。
本文将提出一种以简化模型层间剪力与实际建筑结构相等效为目标的建筑结构简化模型构建方法,并从理论分析角度证明了以该方法构建的简化模型具备准确模拟实际建筑结构动力响应的潜力。将该简化模型构建方法应用于框架结构,推导了框架结构简化模型的具体形式。根据框架结构简化模型参数的特点,提出了一种仅使用少量无线移动传感器,识别简化模型全部参数的方法。最后,通过一个12层3跨的钢框架结构数值模拟算例,验证本文提出的简化模型准确模拟框架结构在不同位置水平激励作用下动力响应的能力。
1 建筑结构简化模型构建的层间剪力等效原理本节提出建筑结构简化模型建模的层间剪力等效原理,并从理论上证明了以此等效原理为基础建立的简化模型具备准确模拟建筑结构在地震、风等水平荷载作用下动力响应的能力,为后续构建框架结构等效简化模型提供了理论基础。
图 1给出了一个框架建筑结构和对应的层集中质量简化模型。根据达朗伯特动力平衡原理,建筑结构与简化模型第i层水平向加速度响应可简单地由其相邻两层结构层间剪力计算求得:
| $m_i \ddot{x}_i(t)=v_i(t)-v_{i-1}(t)+f_i(t)$ | (1) |
| $m_i \bar{\ddot{x}}_i(t)=\bar{v}_i(t)-\bar{v}_{i-1}(t)+f_i(t)$ | (2) |
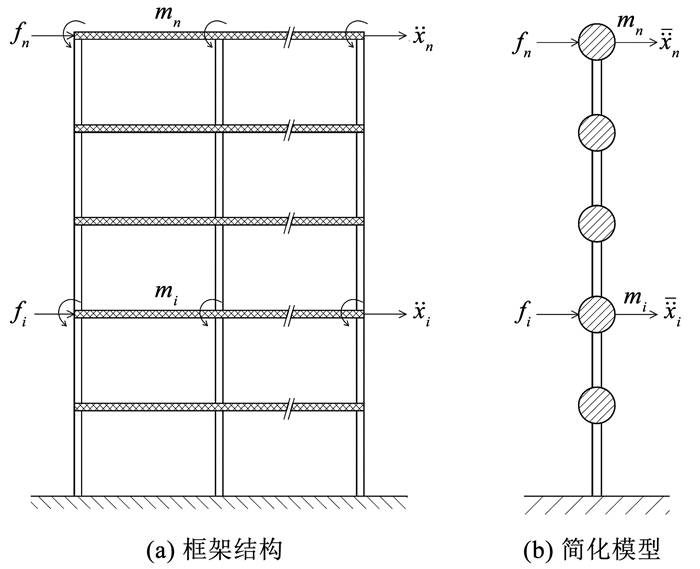
|
图 1 框架结构与简化模型对比 Fig. 1 Comparison between frame structure and simplified model |
式中:
| $\begin{gathered} \frac{1}{t_{\mathrm{f}}} \int_0^{t_{\mathrm{f}}}\left[\ddot{x}_i(t)-\bar{\ddot{x}}_i(t)\right]^2 \mathrm{~d} t=\frac{1}{t_{\mathrm{f}} m_i^2} \int_0^{t_{\mathrm{f}}}\left\{\left[v_i(t)-\bar{v}_i(t)\right]-\right.\\ \left.\left[v_{i-1}(t)-\bar{v}_{i-1}(t)\right]\right\}^2 \mathrm{~d} t \leqslant \frac{2}{t_{\mathrm{f}} m_i^2} \int_0^{t_{\mathrm{f}}}\left[v_i(t)-\bar{v}_i(t)\right]^2 \mathrm{~d} t+ \\ \frac{2}{t_{\mathrm{f}} m_i^2} \int_0^{t_{\mathrm{f}}}\left[v_{i-1}(t)-\bar{v}_{i-1}(t)\right]^2 \mathrm{~d} t\end{gathered}$ | (3) |
式中tf为结构响应总时长。式(3)分析结果表明:对于简化模型第i层集中质量,当与其相邻的2层层间剪力与实际建筑结构层间剪力完全等效时(即vi(t)=vi(t)和vi-1(t)=vi-1(t)),简化模型集中质量将与实际建筑结构对应楼层具有完全相同水平向动力响应(即
上述结论被命名为建筑结构简化模型的层间剪力等效原理。这一原理为构造建筑结构等效简化模型提供了一条新思路,即尽可能使构造的简化模型层间剪力接近实际建筑结构层间剪力,而由此原理构造的简化模型将具备准确模拟实际结构在水平荷载作用下动力响应的能力。
2 框架结构简化模型建模方法 2.1 框架结构简化模型构建基于上述建筑结构层间剪力等效原理,本节将研究框架结构等效简化模型构建方法。通过力学分析可知,框架结构第i层层间剪力vi包含两个部分:由结构构件弹性变形贡献的弹性层间剪力vi, e和由结构阻尼贡献的阻尼层间剪力vi, d。
| $v_i=v_{i, \mathrm{e}}+v_{i, \mathrm{~d}}$ | (4) |
本文采用欧拉伯努利梁单元来模拟框架柱变形提供的弹性层间剪力vi, e:
| $v_{i, \mathrm{e}}=\sum\nolimits_{j=0}^m\left[-\frac{12 E I_{i j}}{H_i^3}\left(x_i-x_{i-1}\right)-\frac{6 E I_{i j}}{H_i^2}\left(\theta_{i j}^{\mathrm{b}}+\theta_{i j}^{\mathrm{t}}\right)\right]$ | (5) |
式中:EIij(i=1, …, n; j=0, …, m)表示第i层第j个柱子的抗弯刚度,θijb和θijt分别表示第i层结构第j个柱的底部和顶部转角,Hi表示第i层结构高度。为了简化式(5),引入下列参数:
| $k_i=\frac{12}{H_i^3} E I_i ; \theta_i^{\mathrm{b}}=\sum\nolimits_{j=0}^m \theta_{i j}^{\mathrm{b}}\left[\frac{E I_{i j}}{E I_i}\right] ; \theta_i^{\mathrm{t}}=\sum\nolimits_{j=0}^m \theta_{i j}^{\mathrm{t}}\left[\frac{E I_{i j}}{E I_i}\right]$ | (6) |
式中:
| $\begin{aligned} v_{i, \mathrm{e}}= & \left.-k_i\left[x_i-x_{i-1}+\left(\theta_i^{\mathrm{b}}+\theta_i^{\mathrm{t}}\right) H_i / 2\right)\right]= \\ & -k_i\left(x_i-x_{i-1}+\delta_i\right)\end{aligned}$ | (7) |
式中δi是框架柱转角响应对第i层层间剪力修正项。
为了便于简化模型参数识别,假设结构阻尼层间剪力vi, d为
| $v_{i, \mathrm{~d}}=-c_i\left(\dot{x}_i-\dot{x}_{i-1}+\dot{\delta}_i\right)$ | (8) |
式中ci是第i层等效阻尼系数。张东昱[18]指出尽管式(8)不一定能够非常准确地反映框架结构实际阻尼层间剪力,但由于一般情况下结构阻尼力贡献的层间剪力远小于弹性层间剪力,因此采用式(8)中层间阻尼力模型不会对结构总层间剪力模拟引入很大误差。
将式(7)和式(8)结果代入式(4),可得
| $v_i=-k_i\left(x_i-x_{i-1}+\delta_i\right)-c_i\left(\dot{x}_i-\dot{x}_{i-1}+\dot{\delta}_i\right)$ | (9) |
式(9)表明,简化模型若要准确模拟实际结构层间剪力,必须要考虑层间剪力修正项δi的影响。然而根据式(6)和式(7)中定义,δi的计算需要框架结构所有转角响应,而这些转角响应在实际结构中难以直接测量得到。一般建筑结构监测系统仅测量楼层水平向响应,因此如何利用结构水平位移响应来间接计算δi,成为一个必须解决的问题。
在忽略结构阻尼影响条件下,将结构动力方程按照平动与转动自由度进行重新排序可得
| $\left[\begin{array}{ll}\boldsymbol{M}_{\mathrm{tt}} & \boldsymbol{M}_{\mathrm{tr}} \\ \boldsymbol{M}_{\mathrm{rt}} & \boldsymbol{M}_{\mathrm{rr}}\end{array}\right]\left[\begin{array}{l}\ddot{\boldsymbol{X}}_{\mathrm{t}} \\ \ddot{\boldsymbol{X}}_{\mathrm{r}}\end{array}\right]+\left[\begin{array}{ll}\boldsymbol{K}_{\mathrm{tt}} & \boldsymbol{K}_{\mathrm{tr}} \\ \boldsymbol{K}_{\mathrm{rt}} & \boldsymbol{K}_{\mathrm{rr}}\end{array}\right]\left[\begin{array}{l}\boldsymbol{X}_{\mathrm{t}} \\ \boldsymbol{X}_{\mathrm{r}}\end{array}\right]=\left[\begin{array}{l}\boldsymbol{F}_{\mathrm{t}} \\ \boldsymbol{F}_{\mathrm{r}}\end{array}\right]$ | (10) |
式中结构参数、响应以及激励项下标t、r分别表示结构的平动与转动自由度。因为一般情况下框架结构转动质量远小于平动质量,通过静力凝聚方法可利用结构楼层水平响应线性组合计算修正项δi:
| $\delta_i=\boldsymbol{T} \boldsymbol{X}_{\mathrm{r}} \approx-\boldsymbol{T} \boldsymbol{K}_{\mathrm{rr}}^{-1} \boldsymbol{K}_{\mathrm{rt}} \boldsymbol{X}_{\mathrm{t}} \approx \boldsymbol{h}_i \boldsymbol{X}_{\mathrm{t}}$ | (11) |
式中:Xt表示楼层水平位移响应向量,T是转角向量向修正项δi转换的线性变换矩阵,hi表示由楼层水平位移响应计算修正项δi的线性组合系数向量。
2.2 框架结构简化模型及其参数特点结合式(9)和式(11)结果,框架结构可转换为图 2所示的一个层集中质量简化模型。该模型集中质量对应框架结构楼层质量,相邻楼层质量之间采用一个梁单元链接。这里需要指出,图 2中简化模型并非一般意义上的悬臂梁模型;因为悬臂梁模型中结构节点水平运动与转动是相互独立的,而根据式(11)所示,本文提出的简化模型转角响应完全依赖于结构水平响应。本文提出的简化模型每一层结构包含3个参数(即[ki ci hi]),ki和ci反映了简化模型层刚度和阻尼参数,而向量hi反映了不同楼层水平方向响应对于第i层层间剪力修正项δi的贡献(向量hi中单元数值绝对值越大,则对应楼层水平响应对修正项δi影响越大)。
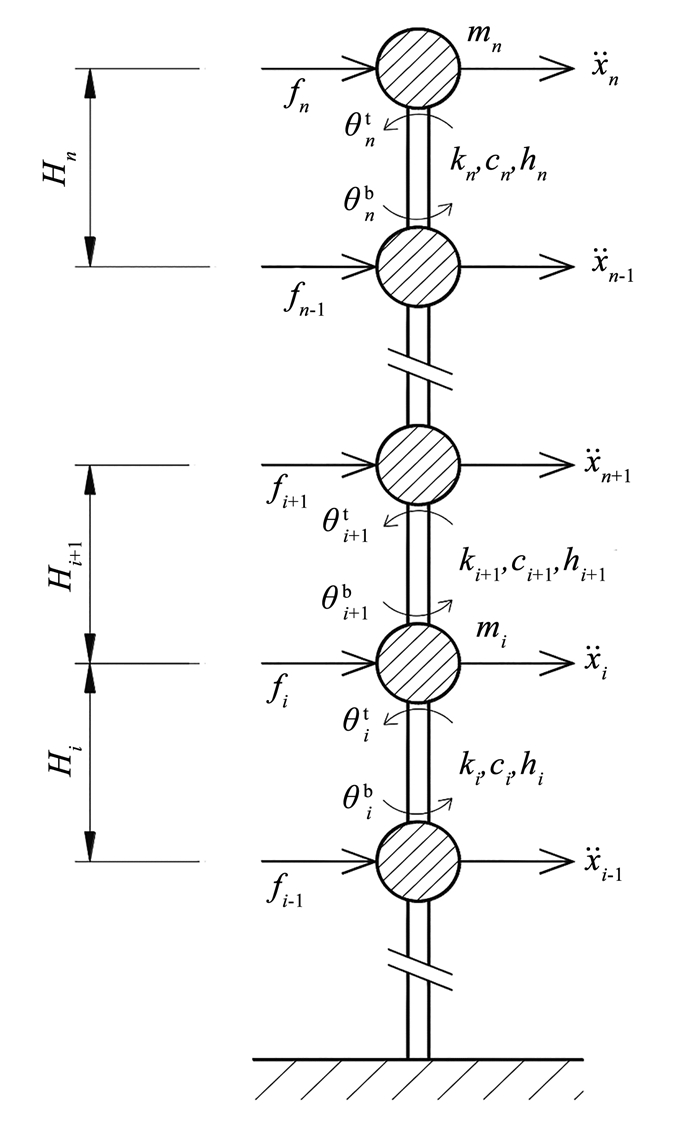
|
图 2 框架结构的新型简化模型 Fig. 2 Novel simplified model of frame structure |
结构刚度矩阵已知条件下,向量hi可以直接由式(11)计算得到。通过对向量hi的特点进行系统研究,发现向量hi中仅与第i层结构临近的元素具有较大数值,而远离第i层结构的元素数值非常小。这意味着:仅采用第i层临近的几层结构水平响应来近似估计修正项δi不会引入较大的计算误差。为了更直观展示上述向量hi特征,图 3给出了第5节中12层3跨框架结构所有层的向量hi元素绝对值,其中hij代表向量hi中第j个元素。
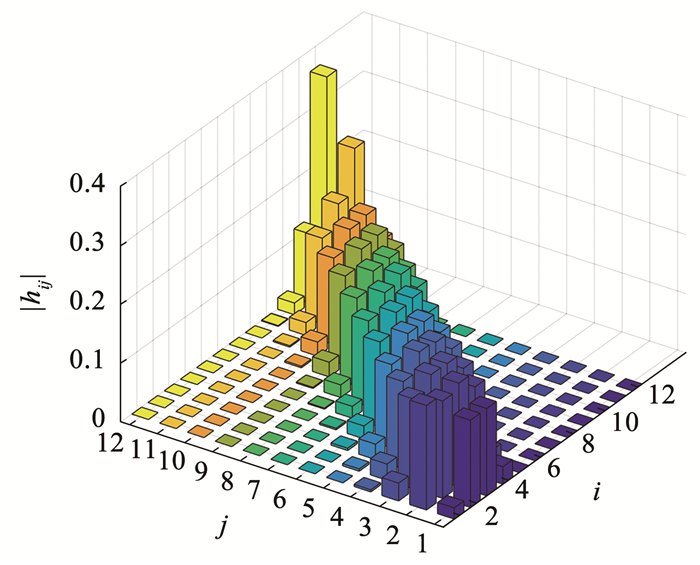
|
图 3 参数hij绝对值 Fig. 3 Absolute value of parameters hij |
为了进一步研究仅采用第i层附近的少量结构响应近似计算层间剪力修正项δi所带来的误差,本文提出衡量δi估计精度的近似指标γi(k):
| $\gamma_i(k)=\frac{\sum\nolimits_{j=\max [1, i-k-1]}^{\min [n, i+k]}\left|\boldsymbol{h}_{i j}\right|}{\sum\nolimits_{j=1}^n\left|\boldsymbol{h}_{i j}\right|}$ | (12) |
该指标反映了仅采用第i-k-1层到i+k层之间所有楼层水平响应来计算δi时所带来的近似误差:指标γi(k)越接近1,则表明近似误差越小。对于第5节中的12层钢框架结构,当k=2时,所有楼层的近似指标γi(k)均大于0.98(非常接近1),因此可以认为仅采用i-3层到i+2层之间6层楼层水平响应就可以很准确地估计修正项δi数值。此外,通过改变框架结构的层数、梁柱刚度比等参数,研究了不同类型框架结构的δi估计近似指标γi(k),发现上述仅使用连续6层结构水平响应即可准确计算修正项δi的结论对所有的框架结构都依然适用。本节的上述分析结果为第3节中仅使用少量移动无线传感器实现框架结构简化模型所有参数识别的方法提供了重要理论支撑。
3 基于少量移动无线传感器的框架结构简化模型参数识别方法对于退化后的既有实际框架结构,往往仅能得到结构质量信息,而结构刚度与阻尼矩阵信息难以准确获得。因而,无法根据式(11)直接计算获得向量hi以及简化模型层刚度与阻尼参数[ki ci]。为此,本节提出了一种利用测量的框架结构楼层水平加速度响应对简化模型参数[ki ci hi]进行识别的方法。将式(4)和式(11)代入式(2),可得简化模型第i层动力平衡方程:
| $\begin{aligned} & m_i \ddot{x}_i(t)+c_i\left(\dot{x}_i-\dot{x}_{i-1}+\boldsymbol{h}_i \dot{\boldsymbol{X}}_{\mathrm{t}}\right)+k_i\left(x_i-x_{i-1}+\boldsymbol{h}_i \boldsymbol{X}_{\mathrm{t}}\right)- \\ & c_{i+1}\left(\dot{x}_{i+1}-\dot{x}_i+\boldsymbol{h}_{i+1} \dot{\boldsymbol{X}}_{\mathrm{t}}\right)-k_{i+1}\left(x_{i+1}-x_i+\boldsymbol{h}_{i+1} \boldsymbol{X}_{\mathrm{t}}\right)=f_i(t)\end{aligned}$ | (13) |
为了减小测量结构响应噪声对于参数识别精度的不利影响,将式(13)两侧同时乘以一个参考响应y(t-τ),并对结构响应关于时间t取数学期望,再进行傅里叶变换。假定结构响应满足广义平稳条件,则式(13)可改写为
| $\begin{aligned} & m_i S_{\ddot{x}_i y}(\mathrm{j} \omega)+\left[\frac{c_i}{\mathrm{j} \omega}+\frac{k_i}{(\mathrm{j} \omega)^2}\right]\left[S_{\ddot{x}_i y}(\mathrm{j} \omega)-S_{\ddot{x}_{i-1} y}(\mathrm{j} \omega)+\right. \\ & \left.\boldsymbol{h}_i S_{\ddot{\boldsymbol{X}}_{\rm t}y}(\mathrm{j} \omega)\right]-\left[\frac{c_{i+1}}{\mathrm{j} \omega}+\frac{k_{i+1}}{(\mathrm{j} \omega)^2}\right]\left[S_{\ddot{x}_{i+1}y}(\mathrm{j} \omega)-S_{\ddot{x}_{i^y}}(\mathrm{j} \omega)+\right. \\ & \left.\boldsymbol{h}_{i+1} S_{\tilde{\boldsymbol{X}}_{\rm t}y}(\mathrm{j} \omega)\right]=S_{f_i y}(\mathrm{j} \omega) \\ & \end{aligned}$ | (14) |
式中:
| $\begin{aligned} & \underset{k_i, c_i, \boldsymbol{h}_i}{\operatorname{argmin}} J\left(k_i, c_i, \boldsymbol{h}_i\right)= \\ & \sum\nolimits_{\omega_l }\left|\begin{array}{l}m_i S_{\ddot{x}_i y, l}-S_{f_i y, l}+ \\ {\left[c_i /\left(\mathrm{j} \omega_l\right)+k_i /\left(\mathrm{j} \omega_l\right)^2\right]\left[S_{\ddot{x}_i y, l}-S_{\ddot{x}_{i-1}y, l}+\boldsymbol{h}_i S_{\ddot{X}_{\rm t}y, l}\right]-} \\ {\left[c_{i+1} /\left(\mathrm{j} \omega_l\right)+k_{i+1} /\left(\mathrm{j} \omega_l\right)^2\right]\left[S_{\ddot{x}_{i+1}y, l}-S_{\ddot{x}_i y, l}+\boldsymbol{h}_{i+1} S_{\dot{X}_{\rm t}y, l}\right]}\end{array}\right|^2\end{aligned}$ | (15) |
对于顶层结构(第n层),由于不存在n+1层结构,式(15)可简化为
| $\begin{aligned} & \underset{k_n, c_n, \boldsymbol{h}_n}{\operatorname{argmin}} J\left(k_n, c_n, \boldsymbol{h}_n\right)= \\ & \sum\nolimits_{\omega_l}\left|\begin{array}{l}m_n S_{\ddot{x}_n y, l}-S_{f_n y, l}+ \\ {\left[c_n /\left(\mathrm{j} \omega_l\right)+k_n /\left(\mathrm{j} \omega_l\right)^2\right]\left[S_{\ddot{x}_n y, l}-S_{\ddot{x}_{n-1} y, l}+\boldsymbol{h}_n S_{\ddot{X}_{\rm t}y, l}\right]}\end{array}\right|^2 \\ & \end{aligned}$ | (16) |
由式(16)识别简化模型顶层参数[kn cn hn],再结合式(15)形成一个迭代识别方法,从而实现简化模型所有层参数自上而下的依次识别。
这里还需要指出,根据2.2节中关于向量hi特点的分析结果,进行式(15)中参数识别时,仅需测量结构第i-3层到i+3层之间连续7个楼层水平响应,无需测量其他楼层响应。此外,由于简化模型不同层参数无需同时进行识别,因此无需同时测量结构所有层加速度响应,可采用一个由7个无线移动传感器组成的监测网络,随着参数识别楼层(第i层)的变化,不断调整这个监测网络传感器的监测楼层位置(仅测量第i-3层到i+3层之间连续7层结构响应),从而实现在仅使用少量移动无线传感器的条件下,对简化模型所有层参数自上而下的迭代识别。
4 基于简化模型的框架结构动力响应预测本节利用第2节和第3节中获得的框架简化模型及其模型参数识别结果,构建简化模型整体动力方程,并将其转化为状态空间模型,用于框架结构在各种不同激励下的动力响应预测。结合式(2)、式(9) 和式(11),简化模型第i层(非顶层)动力方程为
| $m_i \ddot{x}_i+\left(\overline{\boldsymbol{c}}_i+\overline{\boldsymbol{c}}_{i+1}\right) \dot{\boldsymbol{X}}_{\mathrm{t}}+\left(\overline{\boldsymbol{k}}_i+\overline{\boldsymbol{k}}_{i+1}\right) \boldsymbol{X}_{\mathrm{t}}=0$ | (17) |
式中:
| $\begin{aligned} & \overline{\boldsymbol{k}}_i=-k_i\left[h_{i 1} \cdots h_{i(i-1)}-1 \quad h_{i i}+1 \quad \cdots \quad h_{i n}\right] \\ & \overline{\boldsymbol{c}}_i=-c_i\left[h_{i 1} \cdots h_{i(i-1)}-1 \quad h_{i i}+1 \quad \cdots \quad h_{i n}\right]\\ & \overline{\boldsymbol{k}}_{i+1}=-k_{i+1}\left[h_{(i+1) 1} \cdots h_{(i+1) i}-1 \quad h_{(i+1)(i+1)}+1 \quad \cdots \quad h_{(i+1) n}\right] \\ & \overline{\boldsymbol{c}}_{i+1}=-c_{i+1}\left[h_{(i+1) 1} \cdots h_{(i+1) i}-1 \quad h_{(i+1)(i+1)}+1 \quad \cdots \quad h_{(i+1) n}\right] \end{aligned}$ | (18) |
则简化模型整体动力方程为
| $\boldsymbol{M}_{\mathrm{eq}} \ddot{\boldsymbol{X}}_{\mathrm{t}}(t)+\boldsymbol{C}_{\mathrm{eq}} \dot{\boldsymbol{X}}_{\mathrm{t}}(t)+\boldsymbol{K}_{\mathrm{eq}} \boldsymbol{X}_{\mathrm{t}}(t)=\boldsymbol{F}_{\mathrm{t}}(t)$ | (19) |
式中:Meq、Keq、Ceq是框架结构等效质量矩阵、等效刚度矩阵和等效阻尼矩阵,具有如下形式:
| $\boldsymbol{M}_{\mathrm{eq}}=\left[\begin{array}{ccc}m_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & m_n\end{array}\right] ; \boldsymbol{C}_{\mathrm{eq}}=\left[\begin{array}{c}\overline{\boldsymbol{c}}_1-\overline{\boldsymbol{c}}_2 \\ \overline{\boldsymbol{c}}_2-\overline{\boldsymbol{c}}_3 \\ \vdots \\ \overline{\boldsymbol{c}}_n\end{array}\right] ; \boldsymbol{K}_{\mathrm{eq}}=\left[\begin{array}{c}\overline{\boldsymbol{k}}_1-\overline{\boldsymbol{k}}_2 \\ \overline{\boldsymbol{k}}_2-\overline{\boldsymbol{k}}_3 \\ \vdots \\ \overline{\boldsymbol{k}}_n\end{array}\right]$ | (20) |
这里需要指出,式(19)中简化模型等效刚度矩阵和等效阻尼矩阵是利用第3节中识别的简化模型参数构建得到的,因此无法保证构建的刚度与阻尼矩阵具有对称性。为方便简化模型动力方程求解,将式(19)中简化模型二阶动力方程转化为一阶状态空间模型进行求解。定义简化模型状态向量
| $\dot{\boldsymbol{Z}}=\boldsymbol{A} \boldsymbol{Z}+\boldsymbol{B F}_{\mathrm{t}}=\left[\begin{array}{cc}\boldsymbol{0}_n & \boldsymbol{I}_n \\ -\boldsymbol{M}_{\mathrm{eq}}^{-1} \boldsymbol{K}_{\mathrm{eq}} & -\boldsymbol{M}_{\mathrm{eq}}^{-1} \boldsymbol{C}_{\mathrm{eq}}\end{array}\right]\left[\begin{array}{c}\boldsymbol{X}_{\mathrm{t}} \\ \dot{\boldsymbol{X}}_{\mathrm{t}}\end{array}\right]+\left[\begin{array}{c}\mathbf{0}_n \\ \boldsymbol{M}_{\mathrm{eq}}^{-1}\end{array}\right] \boldsymbol{F}_{\mathrm{t}}$ | (21) |
当考虑状态空间模型输出为结构位移和加速度时,系统输出方程分别为:
| $\boldsymbol{X}_{\mathrm{t}}=\left[\begin{array}{ll}\boldsymbol{I}_n & \mathbf{0}_n\end{array}\right]\left[\begin{array}{ll}\boldsymbol{X}_{\mathrm{t}} & \dot{\boldsymbol{X}}_{\mathrm{t}}\end{array}\right]^{\mathrm{T}}=\boldsymbol{C}_1 \boldsymbol{Z}$ | (22) |
| $\begin{aligned} \ddot{\boldsymbol{X}}_{\mathrm{t}}= & {\left[\begin{array}{ll}-\boldsymbol{M}_{\mathrm{eq}}^{-1} \boldsymbol{K}_{\mathrm{eq}} & -\boldsymbol{M}_{\mathrm{eq}}^{-1} \boldsymbol{C}_{\mathrm{eq}}\end{array}\right]\left[\begin{array}{ll}\boldsymbol{X}_{\mathrm{t}} & \dot{\boldsymbol{X}}_{\mathrm{t}}\end{array}\right]^{\mathrm{T}}+} \\ & {\left[\boldsymbol{M}_{\mathrm{eq}}^{-1}\right] \boldsymbol{F}_{\mathrm{t}}=\boldsymbol{C}_2 \boldsymbol{Z}+\boldsymbol{D}_2 \boldsymbol{F}_{\mathrm{t}} }\end{aligned}$ | (23) |
本节通过一个12层3跨平面钢框架模型数值算例,来验证本文提出的简化模型准确模拟框架结构在不同动力荷载作用下结构响应的能力。钢框架结构模型参数如下:层高Hi=3 m,跨度Lj=3 m,各层楼板集中质量mi=1×105 kg,梁和柱的单位长度质量200 kg/m,梁和柱的抗弯刚度分别为4.5×107 N·m2和9×107 N·m2。为了模拟既有结构的刚度退化,随机选取3个构件(第一层边柱,第五层和第八层中间跨梁),使构件抗弯刚度分别下降10%、20%和30%。对于结构阻尼,这里假设结构阻尼矩阵与刚度矩阵成正比例,比例系数由结构第一阶振型阻尼比0.02反算求得。
为了识别框架结构简化模型参数,使结构基底受到一个截止频率为10 Hz的低通高斯过滤白噪声加速度激励,计算框架结构各层加速度响应,共生成60 min结构动力响应(采样频率为200 Hz)。为了模拟测量噪声作用,在计算得到的结构加速度响应中增加10%高斯白噪声干扰。采用第3节中提出的方法对简化模型参数进行识别。上述识别过程共执行10次,10次识别结果的平均值作为简化模型参数名义值,用来构建简化模型状态空间模型,预测框架结构动力响应。
5.1 简化模型误差评价根据第1节中层间剪力等效原理,可采用简化模型与框架结构层间剪力差异来表征简化模型的误差大小。为此,本文提出了简化模型的误差评价指标Ei:
| $E_i=\sqrt{\frac{\int_{\omega_l}\left|V_i(\mathrm{j} \omega)-\bar{V}_i(\mathrm{j} \omega)\right|^2 \mathrm{~d} \omega}{\int_{\omega_l}\left|V_i(\mathrm{j} \omega)\right|^2 \mathrm{~d} \omega}}$ | (24) |
式中:Vi(jω)、Vi(jω)分别表示框架模型与简化模型第i层层间剪力的频域响应。表 1给出本文提出的简化模型各层误差评价指标Ei。作为对比,由层间剪力等效准则构建的剪切模型的模型误差评价指标也同时在表 1中列出。可以看出,本文提出的简化模型误差指标非常小(最大值仅为1.62%),且远远小于剪切模型误差指标(最小值为15.70%)。根据层间剪力等效原理,识别得到的简化模型应能够准确模拟框架结构动力响应;相反的,由于剪切模型没有考虑框架柱节点转动对层间剪力的影响,导致其模型误差较大,将严重影响剪切模型对框架结构动力响应的预测精度。
| 表 1 简化模型和剪切模型的模型误差指标Ei Tab. 1 Modelling error index Ei of simplified model and shear model |
为了验证上述分析结果,本文计算了在相同基底激励作用下框架结构、简化模型和剪切模型楼层加速度响应。表 2中给出了与框架结构响应相比,简化模型和剪切模型各层加速度响应的相对均方根误差。计算结果完全符合上述分析:由于简化模型可以准确地模拟框架结构的层间剪力,因此简化模型可以很准确地模拟框架结构楼层加速度响应(平均相对均方根误差为2.30%,最大相对均方根误差仅为3.13%);而剪切模型由于难以准确模拟框架结构层间剪力,造成计算得到的加速度响应具有较大误差(平均相对均方根误差为63.43%)。
| 表 2 简化模型和剪切模型在基底激励作用下框架结构动力响应预测的相对均方根误差 Tab. 2 Relative root mean square error of predicted frame structural accelerations for simplified model and shear model under ground excitation |
在第2~4节简化模型构建过程中,并未对框架结构外激励位置进行约束,这就意味着由一种外荷载作用工况下结构响应识别并构建的框架结构简化模型,也应该同样可以用来准确预测在其他外荷载工况下的结构动力响应。为了验证上述推论,本文计算了框架结构分别在2、4、6、8、10、12楼层单一水平外荷载激励下的结构加速度和位移响应,并与5.1节中构建的简化模型在相同激励下模拟的结构响应进行对比。图 4给出了简化模型在上述外激励条件下预测框架结构各楼层加速度和位移响应的相对均方根误差,从中可见由框架结构在基底振动条件下结构响应识别并构建的简化模型同样可以准确地预测在其他外荷载工况下框架结构的加速度和位移响应,预测误差水平基本保持不变。
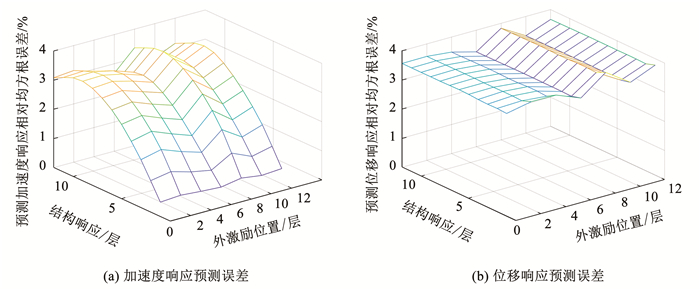
|
图 4 在不同外激励条件下简化模型加速度和位移响应预测的相对均方根误差 Fig. 4 Relative root mean square error of predicted frame acceleration and displacement of simplified model subjected to different conditions of excitation |
本文提出的简化模型可以准确预测实际框架结构楼层动力响应的原因,主要是因为在简化模型构造以及模型参数识别过程中遵循了层间剪力等效原理,通过在模型中引入层间剪力修正项δi,使简化模型层间剪力尽可能地接近实际框架结构层间剪力,从而实现了简化模型准确模拟框架结构动力响应的目标。此外,在简化模型构造过程中没有对施加在结构上的水平荷载形式有任何约束,即构造的简化模型可以用来预测任何形式水平荷载作用下的框架结构动力响应。这就解释了为什么利用框架结构在基底激励作用下结构响应构建的简化模型可以同样准确预测框架结构在其他类型水平荷载作用下结构动力响应。
6 结论1) 提出了建筑结构简化模型构建的层间剪力等效原理,从理论上论证了以该原理构建的简化模型具有准确模拟原建筑结构楼层处动力响应的能力。
2) 基于层间剪力等效原理,提出了一种框架结构的新型简化模型,并实现了在仅使用少量移动加速度传感器条件下对简化模型所有参数的准确识别。
3) 通过一个12层3跨框架结构数值算例,验证了本文构建的等效简化模型准确模拟不同荷载工况下框架结构加速度和位移响应的能力。该模型将在评估既有框架建筑结构在风、地震等动荷载作用下的结构安全性和舒适性方面具有重要应用前景。
| [1] |
BARUCH M. Optimization procedure to correct stiffness and flexibility matrices using vibration tests[J]. AIAA Journal, 1978, 16(11): 1208. DOI:10.2514/3.61032 |
| [2] |
BARUCH M, BAR ITZHACK I Y. Optimal weighted orttiogonalization of measured modes[J]. AIAA Journal, 1978, 16(4): 346. DOI:10.2514/3.60896 |
| [3] |
KABE A M. Stiffness matrix adjustment using mode data[J]. AIAA Journal, 1985, 23(9): 1431. DOI:10.2514/3.9103 |
| [4] |
JAFARKHANI R, MASRI S F. Finite element model updating using evolutionary strategy for damage detection[J]. Computer-Aided Civil and Infrastructure Engineering, 2011, 26(3): 207. DOI:10.1111/j.1467-8667.2010.00687.x |
| [5] |
SIPPLE J D, SANAYEI M. Finite element model updating using frequency response functions and numerical sensitivities[J]. Structural Control and Health Monitoring, 2014, 21(5): 784. DOI:10.1002/stc.1601 |
| [6] |
MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275. DOI:10.1016/j.ymssp.2010.10.012 |
| [7] |
YUAN Z, LIANG P, SILVA T, et al. Parameter selection for model updating with global sensitivity analysis[J]. Mechanical Systems and Signal Processing, 2019, 115(15): 483. DOI:10.1016/j.ymssp.2018.05.048 |
| [8] |
JAFARI M, AKBARI K. Global sensitivity analysis approaches applied to parameter selection for numerical model-updating of structures[J]. Engineering Computations, 2019, 36(4): 1282. DOI:10.1108/EC-08-2018-0336 |
| [9] |
闫桂荣, 段忠东, 欧进萍. 遗传算法在结构有限元模型修正中的应用[J]. 哈尔滨工业大学学报, 2007, 39(2): 181. YAN Guirong, DUAN Zhongdong, OU Jinping. Application of genetic algorithm on structural finite element model updating[J]. Journal of Harbin Institute of Technology, 2007, 39(2): 181. DOI:10.3321/j.issn:0367-6234.2007.02.004 |
| [10] |
张连振, 黄侨. 基于优化设计理论的桥梁有限元模型修正[J]. 哈尔滨工业大学学报, 2008, 40(2): 246. ZHANG Lianzhen, HUANG Qiao. Updating of bridge finite element model based on optimization design theory[J]. Journal of Harbin Institute of Technology, 2008, 40(2): 246. DOI:10.3321/j.issn:0367-6234.2008.02.018 |
| [11] |
张皓, 李东升, 李宏男. 有限元模型修正研究进展: 从线性到非线性[J]. 力学进展, 2019, 49(1): 542. ZHANG Hao, LI Dongsheng, LI Hongnan. Recent progress on finite element model updating: from linearity to nonlinearity[J]. Advances in Mechanics, 2019, 49(1): 542. DOI:10.6052/1000-0992-18-004 |
| [12] |
LI X Y, LAW S S. Adaptive Tikhonov regularization for damage detection based on nonlinear model updating[J]. Mechanical Systems and Signal Processing, 2010, 24(6): 1646. DOI:10.1016/j.ymssp.2010.02.006 |
| [13] |
BAO Y, LI H, OU J. Emerging data technology in structural health monitoring: compressive sensing technology[J]. Journal of Civil Structural Health Monitoring, 2014, 4(2): 77. DOI:10.1007/s13349-013-0064-1 |
| [14] |
JOHNSTONE I M. On minimax estimation of a sparse normal mean vector[J]. The Annals of Statistics, 1994, 22(1): 271. DOI:10.1214/aos/1176325368 |
| [15] |
HANSEN P C. Analysis of discrete Ill-Posed problems by means of the L-Curve[J]. SIAM Review, 1992, 34(4): 561. DOI:10.1137/1034115 |
| [16] |
杨朋超, 薛松涛, 谢丽宇. 结构动力模型的改进直接修正方法及工程应用[J]. 建筑结构学报, 2021, 42(3): 34. YANG Pengchao, XUE Songtao, XIE Liyu. An improved direct method for dynamic model updating and its practical engineering applications[J]. Journal of Building Structures, 2021, 42(3): 34. DOI:10.14006/j.jzjgxb.2019.0878 |
| [17] |
王小娟, 陈峰, 周宏元, 等. 基于混合模态数据融合的模型修正损伤识别方法[J]. 地震工程与工程振动, 2022, 42(5): 83. WANG Xiaojuan, CHEN Feng, ZHOU Hongyuan, et al. Model updating method with hybrid modal shape for damage detection[J]. Earthquake Engineering and Engineering Dynamics, 2022, 42(5): 83. DOI:10.13197/j.eeed.2022.0509 |
| [18] |
张东昱. 建筑结构健康监测的子结构方法研究: 11-1145[R]. 哈尔滨: 哈尔滨工业大学, 2015 ZHANG Dongyu. Research on substructure methods for structural health monitoring of building structures: 11-1145[R]. Harbin: Harbin Institute of Technology, 2015 |
 2024, Vol. 56
2024, Vol. 56


