2. 中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration (Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
自从1933年记录到世界上第一条地震动加速度记录以来,各国学者提出的地震动参数达数十个,能表征地震动破坏强度的地震动参数往往只有有限几个。如何从大量地震动参数中识别出能综合反映地震动破坏强度的少量地震动参数,即地震动特征参数选择,是地震工程研究面临的难点。合理选择地震动参数不仅有助于准确评估地震动破坏势,也有助于减小结构地震风险评估的不确定性。
作为表征地震动破坏势的参数以及联系地震危险性和结构地震响应的桥梁,地震动参数的提出经历了三种形式。第一种形式,以地震动峰值加速度Apg为代表的幅值参数。由于幅值参数与结构的峰值响应高度相关,通常被广泛用于表征给定场地的地震危险性。这一类地震动参数虽然能表征地震动的破坏强度,但是其无法与地震作用下结构的最大内力相关联。第二种形式,基于反应谱Sa(T1, ξ)-based的参数,包括Sa(T1, ξ)、Sa(T1, ξ)+ ε[1-2]、Sa(T1, ξ)+η[3]、Sa, avg[4]以及IMcomb[5]等,其中ε和η为谱形系数。这一类地震动参数的缺点是不能考虑持时和累积能量的影响。第三种形式,地震动全时程特征参数,包括Vfi[6]、Ip(T1)[7]等。这一类地震动参数虽然能够反映地震动全时程特征,但由于其表达式过于复杂,难以被广泛使用。如何从数十个地震动参数中选取少量参数以定量评估地震动破坏势是长期存在的问题。基于地震动参数与结构响应的相关性评价方法是筛选合适地震动参数的主要思路[8-9],这种方法主要用来评价地震动参数与结构响应线性相关性[10]。地震动的随机性以及结构系统的复杂特性使得地震作用下结构响应与地震动参数之间呈现复杂的非线性关系[11],故而基于相关性评价方法筛选地震动参数存在一定的局限性。
作为数据分析和挖掘的有效工具之一,机器学习算法近年来在各领域得到了广泛应用。建立输入变量(地震动参数)和输出变量(结构响应)的映射关系,实现单体建筑与区域建筑群体的地震损失预测与评估,是机器学习在地震工程与土木工程领域应用的动力。近年来,基于机器学习的地震动参数筛选逐渐得到研究人员的关注。Xu等[12]基于支持向量机、逻辑回归以及决策树三种机器学习算法对多个地震动参数进行了比选。吴梓楠等[13]使用极端随机森林算法开展敏感性研究评估了地震动参数对结构损伤的影响程度。王晓岳[14]基于人工神经网络算法提出了地震动参数的筛选方法,并通过工程算例验证了所提方法的有效性。值得指出的是,上述关于机器学习的地震动参数筛选方法都是有监督的机器学习算法,地震动的数量须满足训练需求,同时模型的可解释性和泛化能力都值得进一步研究。
地震动参数(特征)选择既是地震工程研究面临的难点,也是模式识别的关键问题。基于惩罚函数的线性回归是最有力的手段,这类方法是在目标函数基础上增加惩罚项(正则化项),将回归系数压缩至零从而达到变量选择(地震动参数)的目的。弹性网络回归[15]可以较好地解决线性回归中出现的非满秩矩阵求解出错问题以及过拟合问题,可以通过在损失函数中加入正则项来实现。弹性网络回归的惩罚函数为Ridge回归[16]和Lasso回归[17]惩罚函数的凸线性组合,既具有良好的群组效应又能实现变量筛选。
本文旨在提出基于无监督机器学习算法的地震动参数比选方法,根据弹性网络回归参数敏感性和频数分析结果对地震动参数进行排序,筛选出排序结果受地震动集、结构恢复力模型和结构极限状态影响较小的地震动参数,以期为结构抗震能力预测用地震动参数的比选提供理论基础。
1 弹性网络回归模型介绍弹性网络回归[15]可以较好地解决线性回归中出现的非满秩矩阵求解出错问题以及过拟合问题,可以通过在损失函数中加入正则项来实现。对于一般的线性回归模型来说,假设预测变量的个数为p,样本容量为N,则
| {yi=β0+β1xi1+⋯+βpxip+εiεi∼N(0,σ2),i=1,2,⋯,N | (1) |
式中:β0为常数项,βp为回归系数,ε为误差项,通常假定是服从均值为0,方差为σ2的正态分布。线性回归模型用矩阵表示为
| {Y=Xβ+εε∼NN(0,σ2IN) | (2) |
故回归系数的最小二乘估计为
| ˆβLS=(XTX)(−1)XTY | (3) |
对于线性回归模型,弹性网络回归估计的定义为
| ˆβElastic-net =argmin{N∑i=1(yi−β0−p∑j=1xijβj)2+λ1p∑j=1|βj|+λ2p∑j=1β2j} | (4) |
式中λ1和λ2为惩罚参数。当λ1=0,λ2=0时,回归模型为最小二乘回归;当λ1=0,λ2>0时,回归模型为Ridge回归[16];当λ1>0,λ2=0时,回归模型为Lasso回归[17];当λ1>0,λ2>0时,回归模型为弹性网络回归。本文采用弹性网络回归进行地震动参数筛选。
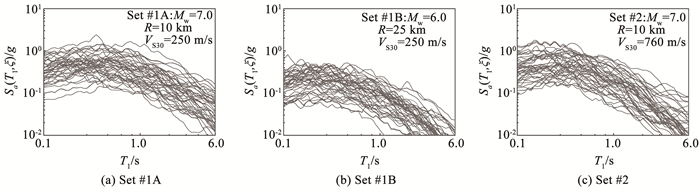
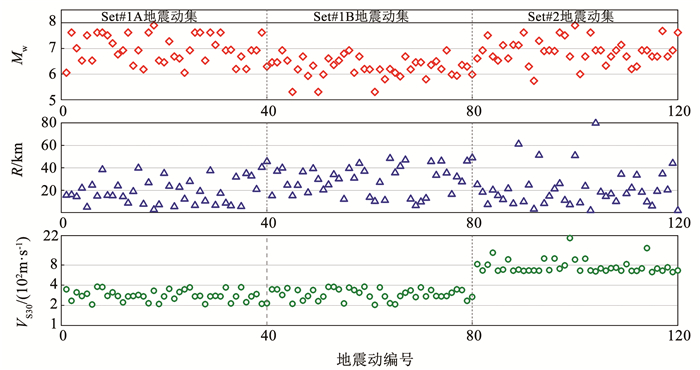
2 地震动记录选取采用Baker等[18]匹配目标谱从PEER NGA-West2地震动数据库中挑选出的三个地震动集,分别为Set #1A、Set #1B、Set #2地震动集。Set #1A地震动集由40组水平双向地震动分量组成,其加速度反应谱与设定地震事件(矩震级Mw为7.0、走滑断层、断层距R为10 km,地表以下30 m范围内的土层平均剪切波速VS30为250 m/s)的目标加速度反应谱相匹配;Set #1B地震动集由40组水平双向地震动分量组成,其加速度反应谱与设定地震事件(Mw为6.0、走滑断层、R为25 km、VS30为250 m/s)的目标加速度反应谱相匹配;Set #2地震动集由40组水平双向地震动分量组成,其加速度反应谱与设定地震事件(Mw为7.0、走滑断层、R为10 km、VS30为760 m/s)的目标加速度反应谱相匹配。三个地震动集的水平加速度反应谱见图 1,其中Sa(T1, ξ)为加速度反应谱值,T1为结构自振周期,ξ为阻尼比,取值为0.05。三个地震动集的Mw、R和VS30分布情况见图 2。
|
图 1 三个地震动集加速度反应谱 Fig. 1 Acceleration response spectra of three ground motion sets |
|
图 2 三个地震动集Mw、R、VS30分布 Fig. 2 Distribution of Mw, R and VS30 of three ground motion sets |
本文初步选取了31个地震动参数作为原始地震动参数集,将这31个地震动参数分为幅值参数、频谱参数以及能量和持时参数三大类,见表 1。其中,幅值参数计算式中a(t)、v(t)和d(t)分别表示地震动加速度时程、地震动速度时程和地震动位移时程;频谱参数计算式中Sv(T1, ξ)和Sd(T1, ξ)分别为速度反应谱值和位移反应谱值,N为周期点的个数,ci的取值范围为0.2~3.0,Ti和Tj分别表示自振周期T1的上限值和下限值;能量和持时参数计算式中t5、t95、tf、Td分别表示5%Arias强度对应的时间点、95%Arias强度对应的时间点、地震动总的持续时间以及90%能量持时,vo表示地震动加速度时程单位时间穿越零线的次数,β取值为0.7。
| 表 1 初选的地震动参数 Tab. 1 Preliminary selection of ground motion parameters |
由于初选的地震动参数之间的表达式相近,需要对这些地震动参数进行筛选。初步筛选的原则:1)两个地震动参数在表达式上相差一个指数时只留其中之一。2)某个地震动参数的表达式在对数坐标系下是另一个或者几个地震动参数的线性组合,选择表达式较为简单的。Ams、Vms、Dms、Asq、Vsq、Dsq分别与Arms、Vrms、Drms、Ars、Vrs、Drs在表达式上相差一个指数。Asq和Ia在表达式上相差一个常数。幅值、频谱以及能量和持时三类参数经过筛选后得到的24个地震动参数。筛选出的幅值参数包含Apg、Vpg和Dpg,筛选出的频谱参数包含Asi、Vsi、Dsi、Aep、Vep、Dep、Sa, avg、Rva、Rdv,筛选出的能量和持时参数包含Ams、Asq、Vca、Vms、Dca、Vsq、Iam、Dms、Ica、Dsq、Td、Vfi。
4 结构建模与地震需求分析单自由度(single-degree of freedom, SDOF)体系恢复力模型选择双折线塑性(bilinear plastic, BP)模型和修正的Clough(modified Clough, MC)模型[19]。BP模型和MC模型的恢复力模型曲线,即力- 位移(F - d)曲线见图 3。SDOF体系自振周期取值范围为0.1~2.0 s,周期间隔为0.1 s;屈服后刚度系数α取值范围为0~0.2,间隔为0.05;屈服强度系数Cy取值范围为0.1~0.8,间隔为0.1。此时,BP模型和MC模型的SDOF体系的数量都为800个。本文采用文献[20]中的8层钢框架模型,平面尺寸为42.7 m×30.5 m,水平双向各三跨,首层层高4.6 m,标准层高4.0 m,见图 4。采用OpenSees建立8层钢框架结构模型,结构基本周期T1为1.64 s。梁和柱单元塑性铰为集中塑性铰模型。

|
图 3 SDOF体系恢复力模型 Fig. 3 Hysteretic models of SDOF systems |

|
图 4 8层钢框架模型 Fig. 4 8-story steel frame model |
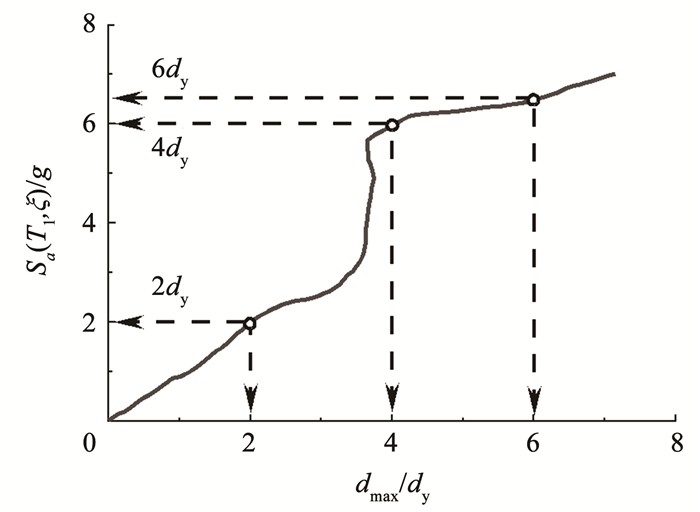
本文采用增量动力分析(incremental dynamic analysis, IDA)[21]进行结构地震需求分析,IDA方法的核心思想是将地震动调幅至不同强度水平后对结构进行时程分析从而获得不同强度水平下结构的响应。IDA方法的优点在于能建立性态反应量与地震动参数的联系,捕捉非线性分析中结构从轻微破坏到倒塌以及固有特性变化的全过程,同时通过多条IDA曲线可以从概率意义上定量评估地震作用下结构的抗震能力。IDA分析时地震动强度指标选取Sa(T1, ξ),结构极限状态:轻微破坏、中等破坏和严重破坏对应的结构位移分别取2dy、4dy以及6dy,其中dy为结构的屈服位移。IDA分析中结构极限状态对应的强度水平为结构的抗震能力值,见图 5。
|
图 5 单条地震动记录的IDA曲线 Fig. 5 A single-record IDA curve |
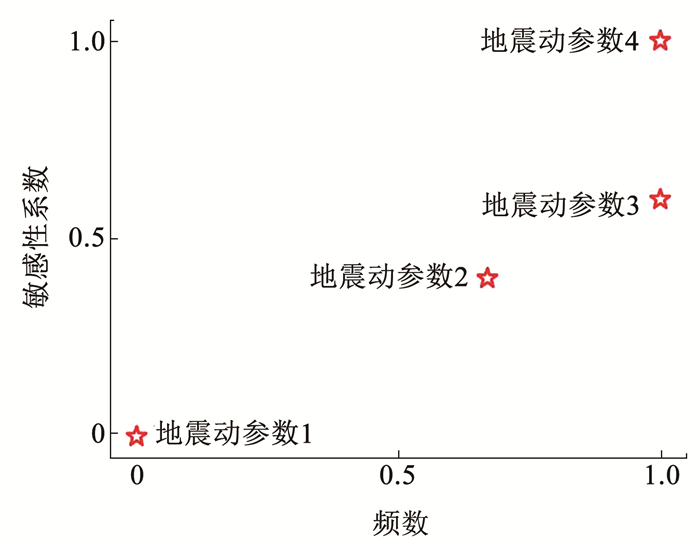
本文基于大量SDOF体系IDA分析结果建立弹性网络回归模型来实现地震动参数比选,弹性网络回归模型中因变量(响应变量)为结构抗震能力,自变量(解释变量)为地震动参数。敏感性系数定义为800个回归模型中地震动参数的回归系数值平方的总和,频数定义为800个回归模型中地震动参数回归系数值为非零值的个数。通过敏感性系数和频数将地震动参数表示为二维空间中的点,按照其与点(0, 0)之间的欧氏距离的大小进行排序,欧氏距离越大,则排名越靠前;欧氏距离越小,则排名越靠后,见图 6。为了方便计算地震动参数与点(0, 0)之间的欧氏距离,先分别对地震动参数的敏感性系数和频数进行归一化,归一化的方法为某一地震动参数的敏感性系数和频数与加入到回归模型中的地震动参数敏感性系数最大值和频数最大值之间的比值。
|
图 6 使用弹性网络回归结果评估地震动参数的敏感性和频数示例 Fig. 6 Example evaluation of sensitivity and frequency of ground motion parameters using the results of elastic net regression |
本节讨论地震动集、结构恢复力模型以及结构极限状态,即地震动频谱特性、结构特性以及地震作用下结构非线性反应的深度三个因素对地震动参数排序结果的影响。值得注意的是,地震动参数敏感性系数和频数的统计特性在加速度敏感区、速度敏感区和位移敏感区三个周期区间内可能会略有差别,本文基于大量SDOF体系的分析结果进行统计分析时,不再考虑结构周期的影响。
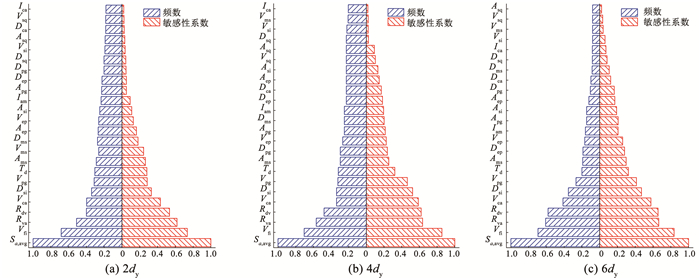
图 7给出了2dy、4dy和6dy三种极限状态下地震动参数敏感性系数和频数的统计结果,其中所采用的地震动集为Set #1A地震动集,SDOF体系的恢复力模型为BP模型。由图 7可知,2dy、4dy和6dy三种极限状态下排名为1至9的地震动参数分别为Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams。这说明基于弹性网络回归的地震动参数排名受结构极限状态的影响较小,尤其是排名为1至9的地震动参数。为了筛选关键的地震动参数,在最小二乘回归模型中加入地震动参数作为解释变量,将这些地震动参数按照距离坐标原点距离由远到近的顺序依次加入到最小二乘回归模型中。对每个SDOF体系的IDA分析结果,求出残差的标准差。
|
图 7 不同极限状态下地震动参数敏感性系数和频数统计结果(Set #1A地震动集,BP模型) Fig. 7 Statistics of sensitivity and frequency of ground motion parameters under different limit-states (Set #1A set, BP system) |
图 8给出了800个SDOF结构残差标准差的平均值,其中地震动参数的个数从0增加到24,采用的地震动记录为Set #1A地震动集,SDOF恢复力模型为BP模型。由图 8可知,2dy、4dy和6dy三种极限状态下排名前9的地震动参数作为解释变量加入最小二乘回归模型时,回归分析中残差的标准差能分别减少31%、44%以及51%。当没有地震动参数加入到最小二乘回归模型中时,2dy、4dy和6dy三种极限状态下800个SDOF结构残差标准差的均值都为1。在地震动参数依次加入到最小二乘回归模型中的过程中,残差标准差的下降幅值在地震动参数依次加入的早期较大,在后期残差标准差的下降幅值较小,这是因为在最后阶段加入的地震动参数贡献相对较弱。说明根据敏感性和频次分析有助于筛选关键的地震动参数。需要注意的是,即使所有的地震动参数都加入到最小二乘回归模型中,采用所有地震动参数预测结构抗震能力仍然存在误差,说明采用所选的地震动参数预测抗震能力的局限性。随着极限状态水平的提高,采用所有地震动参数进行回归分析得到的残差标准差逐渐减小,这说明随着极限状态水平的提高,采用所选地震动参数预测结构的抗震能力更加准确。

|
图 8 不同极限状态下回归分析中残差标准差与地震动参数之间的关系(Set #1A地震动集,BP模型) Fig. 8 Relationship between standard deviations of the residuals by the least square regressions and ground motion parameters under different limit-state (Set #1A set, BP system) |
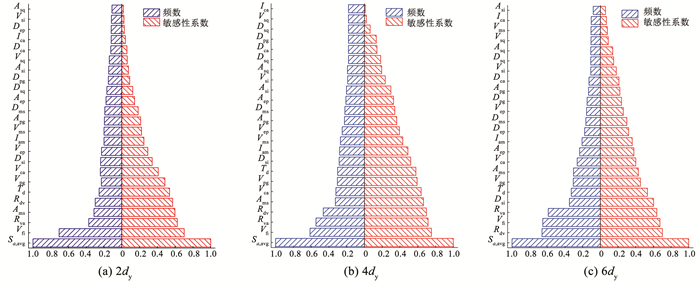
图 9给出了2dy、4dy和6dy三种极限状态地震动参数敏感性系数和频数的统计结果,其中所采用的地震动集为Set #1A地震动集,SDOF体系的恢复力模型为MC模型。由图 9可知,2dy极限状态排名为1至9的地震动参数分别为Sa, avg、Vfi、Rva、Ams、Rdv、Td、Vpg、Vca、Dsi;4dy极限状态排名为1至9的地震动参数分别为Sa, avg、Vfi、Rva、Rdv、Ams、Vca、Vpg、Td、Dsi;6dy极限状态排名为1至9的地震动参数分别为Sa, avg、Rdv、Vfi、Rva、Dsi、Td、Vpg、Ams、Vca。可以发现,基于MC模型SDOF体系的IDA分析结果进行地震动参数排名的前9名与基于BP模型SDOF体系的IDA分析结果进行地震动参数排名的前9名一致,都为Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams。这说明基于弹性网络回归的地震动参数排名受恢复力模型的影响较小,尤其是排名为1到9的地震动参数。
|
图 9 不同极限状态下地震动参数敏感性系数和频数统计结果(Set #1A地震动集,MC模型) Fig. 9 Statistics of sensitivity and frequency of ground motion parameters under different limit-states (Set #1A set, MC system) |
图 10给出了不同地震动集作用下6dy极限状态的地震动参数敏感性系数和频数的统计结果,其中SDOF体系的恢复力模型为BP模型。Set #1A、Set #1B和Set #2地震动集作用下排名为1至9的地震动参数都为Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams,这说明基于弹性网络回归的地震动参数排名受地震动集的影响较小,尤其是排名为1至9的地震动参数。

|
图 10 不同地震动集作用下地震动参数敏感性系数和频数统计结果(BP模型) Fig. 10 Statistics of sensitivity and frequency of ground motion parameters under different ground motion sets (BP system) |
由上述的大量SDOF体系敏感性和频数分析结果可知基于弹性网络回归分析的地震动参数排名受恢复力模型、地震动集以及极限状态的影响较小,尤其是排名为1至9的地震动参数受恢复力模型、地震动集以及极限状态的影响较小,最终选取排名前9的地震动参数,Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams为代表性的地震动参数。
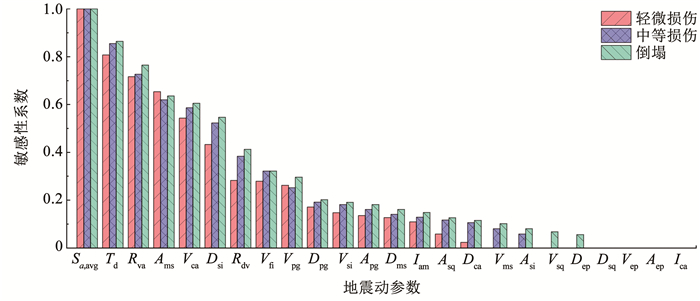
5.4 基于多自由度结构的地震动参数比选有效性验证5.3节给出了大量SDOF体系基于弹性网络回归分析的地震动参数比选结果,为了验证基于弹性网络回归分析比选出的地震动参数能够有效减小结构损伤预测的不确定性,本节对一座8层钢框架结构进行分析。其中所采用的地震动集为Set #1A地震动集,以最大层间位移角θmax作为结构损伤指标,轻微破坏、中等破坏以及倒塌三个结构极限状态对应的θmax限值分别为0.7%、2%以及10%。基于8层钢框架分析结果建立弹性网络回归模型时,不同极限状态下某一地震动参数的频数为0或者1,因此基于8层钢框架分析结果验证地震动参数比选的有效性时不再给出地震动参数频数的统计结果。图 11给出了8层钢框架结构的地震动参数敏感性系数的统计结果。由图 11可知,轻微破坏、中等破坏以及倒塌三个结构极限状态下排名为1至9的地震动参数分别为Sa, avg、Td、Rva、Ams、Vca、Dsi、Rdv、Vfi、Vpg。尽管基于8层钢框架结构分析结果比选出的前9个地震动参数的排名与基于大量SDOF体系统计结果比选出的前9个地震动参数的排名略有差别,但是两者比选出的前9个地震动参数都为Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams。
|
图 11 8层钢框架地震动参数敏感性系数统计结果(Set #1A地震动集) Fig. 11 Statistics of sensitivity of ground motion parameters of 8-story steel frame (Set #1A set) |
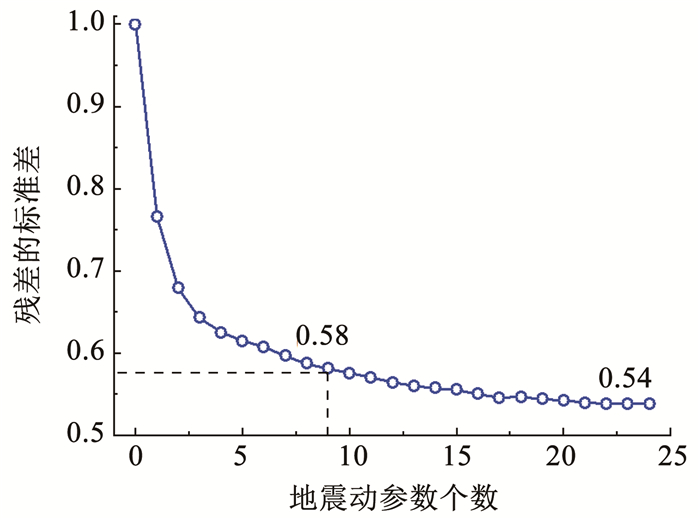
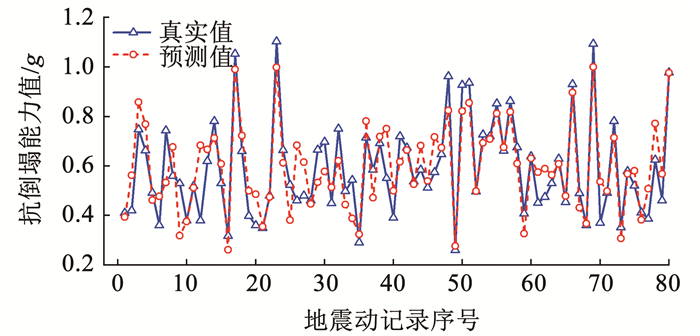
图 12给出了8层钢框架结构倒塌状态下地震动参数的个数从0增加到24时残差的标准差。由图可知,倒塌状态下排名前9的地震动参数作为解释变量加入最小二乘回归模型时,回归分析中残差的标准差减少42%。图 13给出了将排名前9的地震动参数作为解释变量加入最小二乘回归模型时,8层钢框架结构抗倒塌能力预测值与真实值的对比。由图 13可知,选取代表性的地震动参数作为解释变量构建回归模型能够有效预测结构的抗倒塌能力值。综上所述,基于弹性网络回归分析比选出的地震动参数能够有效减小结构损伤预测的不确定性。
|
图 12 8层钢框架倒塌状态下回归分析中残差标准差与地震动参数之间的关系 Fig. 12 Relationship between standard deviations of the residuals by the least square regressions and ground motion parameters of 8-story steel frame under collapsing state |
|
图 13 8层钢框架抗倒塌能力预测值与真实值对比 Fig. 13 Comparison of prediction and observation of collapsing capacity of 8-story steel frame |
本文基于多种地震动参数以及大量SDOF模型IDA结果建立弹性网络回归模型,统计分析弹性网络回归模型中地震动参数的敏感性系数和频数,基于地震动参数敏感性和频数统计结果对地震动参数进行排序,筛选出了受地震动集、结构恢复力模型和结构极限状态影响较小的地震动参数,主要结论:
1) 选取基于弹性网络回归分析筛选的代表性地震动参数加入最小二乘回归模型时,2dy、4dy和6dy三种结构极限状态下回归分析中残差的标准差能分别减少31%、44%和51%。说明基于弹性网络回归分析有助于筛选代表性的地震动参数。随着结构极限状态水平的提高,采用所有地震动参数加入最小二乘回归模型得到的残差标准差逐渐减小。说明随着结构极限状态水平的提高,采用所选地震动参数预测结构的抗震能力更加准确。
2) 基于大量SDOF体系的敏感性系数和频数统计结果可知基于弹性网络回归分析的地震动参数排名受恢复力模型、地震动集以及极限状态的影响较小,尤其是排名前9的地震动参数受恢复力模型、地震动集以及极限状态的影响较小。
3) 根据地震动参数排序结果筛选出了受结构恢复力模型、地震动集和极限状态影响较小的代表性参数,Sa, avg、Vfi、Rva、Rdv、Vca、Dsi、Vpg、Td、Ams。
4) 基于弹性网络回归分析以及地震动参数敏感性和频数分析的地震动参数排序及筛选方法可为结构抗震能力预测用地震动参数的比选提供理论基础。
| [1] |
BAKER J W, CORNELL C A. Spectral shape, epsilon, and record selection[J]. Earthquake Engineering and Structural Dynamics, 2006, 35: 1077. DOI:10.1002/eqe.571 |
| [2] |
HASELTON C B, BAKER J W, LIEL A B, et al. Accounting for ground-motion spectral shape characteristics in structural collapse assessment through an adjustment for epsilon[J]. Journal of Structural Engineering, 2011, 137(3): 332. DOI:10.1061/(ASCE)ST.1943-541X.0000103 |
| [3] |
MOUSAVI M, GHAFORY-ASHTIANY M, AZARBAKHT A. A new indicator of elastic spectral shape for the reliable selection of ground motion records[J]. Earthquake Engineering and Structural Dynamics, 2011, 40(12): 1403. DOI:10.1002/eqe.1096 |
| [4] |
EADS L, MIRANDA E, LIGNOS D G. Average spectral acceleration as an intensity measure for collapse risk assessment[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(12): 2057. DOI:10.1002/eqe.2575 |
| [5] |
MARAFI N A, BERMAN J W, EBERHARD M O. Ductility-dependent intensity measure that accounts for ground-motion spectral shape and duration[J]. Earthquake Engineering and Structural Dynamics, 2016, 45(4): 653. DOI:10.1002/eqe.2678 |
| [6] |
DÁVALOS H, MIRANDA E. Filtered incremental velocity: a novel approach in intensity measures for seismic collapse estimation[J]. Earthquake Engineering and Structural Dynamics, 2019, 48(12): 1384. DOI:10.1002/eqe.3205 |
| [7] |
ZENGIN E, ABRAHAMSON N A. A vector-valued intensity measure for near-fault ground motions[J]. Earthquake Engineering and Structural Dynamics, 2020, 49(7): 716. DOI:10.1002/eqe.3261 |
| [8] |
李爽, 谢礼立, 郝敏. 地震动参数及结构整体破坏相关性研究[J]. 哈尔滨工业大学学报, 2007, 39(4): 505. |
| [9] |
邱意坤, 甄伟, 周长东. 近断层脉冲型地震动强度指标与高耸结构损伤关联性[J]. 哈尔滨工业大学学报, 2023, 55(5): 139. |
| [10] |
PEARSON K. Notes on the history of correlation[J]. Biometrika, 1920, 13(1): 25. DOI:10.2307/2331722 |
| [11] |
TEZCAN J, CHENG Q. Support vector regression for estimating earthquake response spectra[J]. Bulletin of Earthquake Engineering, 2012, 10: 1205. DOI:10.1007/S10518-012-9350-2 |
| [12] |
XU Y, LU X, TIAN Y, et al. Real-time seismic damage prediction and comparison of various ground motion intensity measures based on machine learning[J]. Journal of Earthquake Engineering, 2022, 26(8): 4259. DOI:10.1080/13632469.2020.1826371 |
| [13] |
吴梓楠, 韩小雷, 马建峰, 等. 基于机器学习的地震动强度指标敏感性分析与破坏势评估[J]. 建筑结构学报, 2023, 44(11): 216. |
| [14] |
王晓岳. 基于人工神经网络的地震动强度指标比选方法[D]. 哈尔滨: 中国地震局工程力学研究所, 2022
|
| [15] |
ZOU H, HASTIE T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2005, 67(2): 301. DOI:10.1111/J.1467-9868.2005.00527.x |
| [16] |
HOERL A E, KENNARD R W. Ridge regression: biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1): 55. DOI:10.2307/1267351 |
| [17] |
TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1996, 58(1): 267. DOI:10.1111/J.2517-6161.1996.tb02080.x |
| [18] |
BAKER J W, LIN T, SHAHI S K, et al. New ground motion selection procedures and selected motions for the peer transportation research program: peer report 2011/3[R]. california: Pacific Earthquake Engineering Research Center, College of Engineering, University of California, 2011
|
| [19] |
MAHIN S A, BERTERO V V. Nonlinear seismic response of a coupled wall system[J]. Journal of the Structural Division, 1976, 102(9): 1759. DOI:10.1061/JSDEAG.0004428 |
| [20] |
ELKADY A, LIGNOS D G. Modeling of the composite action in fully restrained beam-to-column connections: implications in the seismic design and collapse capacity of steel special moment frames[J]. Earthquake Engineering and Structural Dynamics, 2014, 43(13): 1935. DOI:10.1002/EQE.2430 |
| [21] |
VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491. DOI:10.1002/eqe.141 |
 2024, Vol. 56
2024, Vol. 56



