2. 河南工业大学 土木建筑学院,郑州 450001;
3. 浙江数智交院科技股份有限公司,杭州 310030
2. College of Civil Engineering and Architecture, Henan University of Technology, Zhengzhou 450001, China;
3. Zhejiang Institute of Communications Co. Ltd., Hangzhou 310030, China
超高性能混凝土(ultra-high performance concrete, UHPC)凭借优异的力学和耐久性能,在桥梁工程中得到了广泛应用[1-3]。钢-UHPC轻型组合桥面结构是UHPC目前在桥梁工程中应用最广泛的结构形式之一,已应用于涵盖梁桥、拱桥、斜拉桥和悬索桥等各类基本桥型[4]。UHPC的应用可同时解决钢桥面结构疲劳破坏及传统铺装易开裂的难题,还兼具轻量化和高耐久的特点[4]。
钢与UHPC两种材料之所以能够组合在一起,发挥各自的长处,其关键在于抗剪件的连接作用。目前最常用的是焊接栓钉连接件[5]。文献[6-8]研究了UHPC板中焊接栓钉的抗剪性能以及钢-UHPC组合板的抗弯性能。然而,现有钢-UHPC推出实验结果表明[9],采用焊接栓钉的钢-UHPC组合结构较普通钢-混凝土组合结构的延性差,且不能满足Eurocode 4中对钢与混凝土在推出试验中相对位移要大于6 mm的延性设计要求。
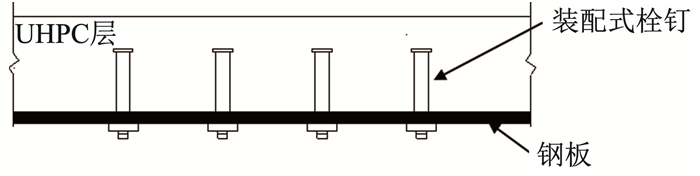
为提高钢-UHPC组合结构的延性,作者采用装配式栓钉对钢-UHPC组合构件进行连接,见图 1。其中装配式栓钉文献[10]在2015年提出的,由普通栓钉加工而成。文献[11]对采用装配式栓钉连接的钢-混凝土组合结构的抗剪和抗弯性能进行了试验研究,但目前国内外对采用装配式栓钉连接的钢-UHPC组合构件的相关研究很少,且尚未有对其抗弯性能的研究。2017年,文献[12]通过推出试验研究了装配式栓钉在钢-UHPC中的抗剪性能,试验结果表明采用装配式栓钉抗剪连接件的钢-UHPC组合构件的延性要优于采用焊接栓钉的组合构件。
|
图 1 装配式栓钉连接的钢-UHPC组合构件 Fig. 1 Demountable steel-UHPC composite structures |
此外,采用装配式栓钉的钢-UHPC组合结构还具有以下优点:1)高静、动态延性[12],与焊接抗剪连接件不同,装配式栓钉、孔壁以及UHPC均可变形,且通过适当设计栓钉孔的尺寸和形状,可以进一步提高组合构件的变形能力;2)高疲劳寿命,装配式栓钉可消除传统焊接栓钉的焊接残余应力,在疲劳荷载下具有更高的疲劳寿命;3)环境友好[11],组合结构易于拆卸更换,便于后期的使用和维护,且拆卸后未损坏构件可循环使用,符合绿色和可持续发展的理念。
本文通过四点弯曲试验,对具有不同抗剪连接程度的采用装配式栓钉钢-UHPC组合板的抗弯性能进行了试验研究,并与采用焊接栓钉的组合板进行了对比分析,并讨论了组合板的可拆卸性,建立了采用装配式的钢-UHPC组合板抗弯承载力和刚度的理论计算公式,为该组合板的设计和应用提供理论依据。
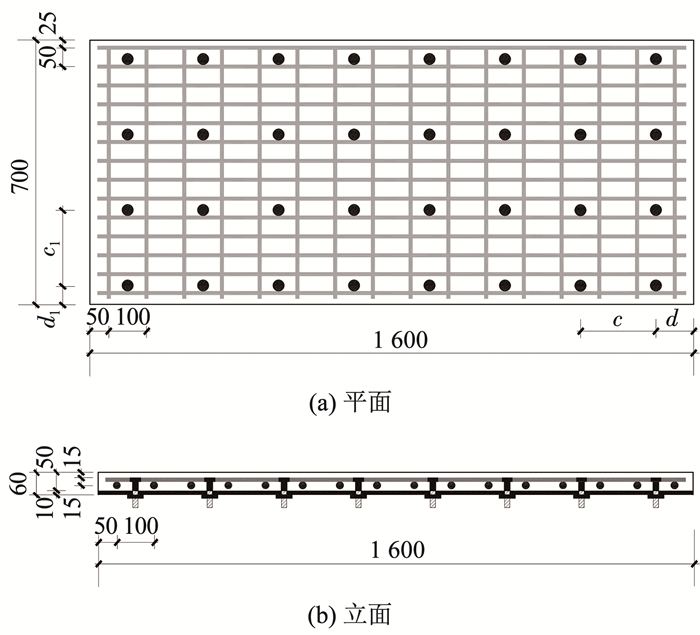
1 试验概况 1.1 试件设计及制作采用装配式栓钉的钢-UHPC组合板试件的具体构造及尺寸见图 2。组合板长1 600 mm,宽700 mm。UHPC保护层厚度参考SIA 2052瑞士UHPC规范[13]中对配筋UHPC结构的规定,设置为15 mm。组合板的总厚度为60 mm。
|
图 2 采用装配式栓钉的钢-UHPC组合板几何尺寸及构造(mm) Fig. 2 Dimensions and configurations of demountable steel-UHPC composite slabs(mm) |
UHPC板和钢板之间通过装配式栓钉连接。见图 3,装配式栓钉由传统圆柱头栓钉加工而成,根据文献[12]中推出试验的结果,当栓钉长径比>1.5时,破坏模式为栓钉剪断,因此栓钉正面露出的长度和直径的比值要>1.5,剩余部分为背面露出长度,即阴影车制螺纹部分。本文装配式栓钉的原始栓杆直径为16 mm,车完螺纹后螺径为14 mm,埋入UHPC层中的高度为35 mm,钢板上的孔径比装配式栓钉螺纹直径大1 mm。

|
图 3 装配式栓钉尺寸设计(mm) Fig. 3 Size design of demountable studs(mm) |
本文主要研究不同抗剪连接程度下采用装配式栓钉的钢-UHPC组合板的抗弯性能,因此试验参数为栓钉间距,分别设置为150、200和250 mm。组合板的配筋率为3.1%。试件编号及详细构造尺寸见图 2和表 1。试验同时设计了一块栓钉间距为250 mm的采用焊接栓钉的组合板进行对比。
| 表 1 试件编号及构造参数 Tab. 1 Test specimens and parameters |
图 4为采用装配式栓钉的钢-UHPC组合板的制作细节。将装配式栓钉通过螺帽固定在钢板上后,根据试验设计方案布置钢筋,制作模具。然后将搅拌好的UHPC倒入模具中,组合板浇筑完成后进行抹面,常温养护28 d后拆模。

|
图 4 钢-UHPC组合板制作细节 Fig. 4 Fabrication details of steel-UHPC composite slabs |
按厂家出厂检测报告,装配式栓钉的极限抗拉强度为428 MPa。钢板采用Q345B级,10 mm厚的钢材。钢板留样进行材性试验,其屈服强度和抗拉强度的平均值分别为375 MPa和421 MPa。
组合板中的横向和纵向钢筋均采用直径为10 mm的HRB400钢筋。钢筋留样进行材性试验,试验得其屈服强度、极限强度和弹性模量的平均值分别为417 MPa、552 MPa和198 GPa。
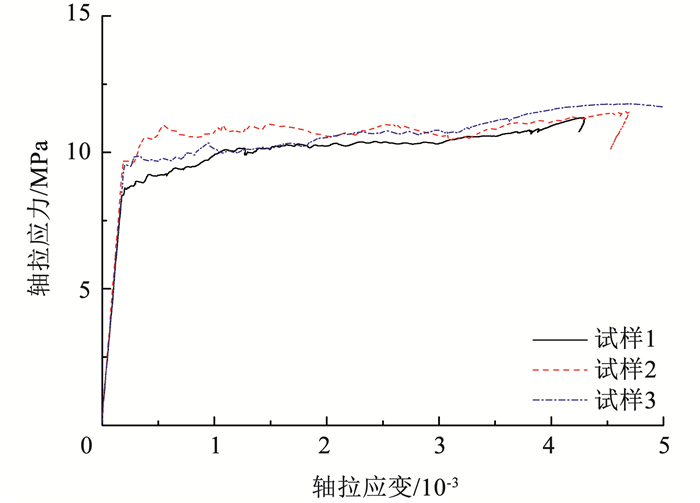
1.2.2 应变强化UHPC的轴拉力学性能本文采用应变强化UHPC,基体配合比见表 2,纤维采用长度16 mm,直径200 μm的平直形钢纤维,体积掺量2.5%。按规范GB/T 31387—2015《活性粉末混凝土》[14]和文献[2]中对材料28 d抗压和轴拉测试的要求,在浇筑组合板的同时成型、养护并测试了6个100 mm立方体抗压试件和3根轴拉试件(50 mm×100 mm)。应变强化UHPC的28 d抗压强度平均值为146 MPa。图 5为应变强化UHPC的轴拉应力-应变曲线,其极限抗拉强度平均值为11.5 MPa,强化极限应变平均值为0.455%。按照规范GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法》[15]采用非接触式混凝土收缩变形测定仪测定应变强化UHPC从搅拌后到28 d的自收缩变形,终凝到28 d的收缩值为0.066%应变。
| 表 2 UHPC基体配合比 Tab. 2 Mix proportion of UHPC matrix |
|
图 5 应变强化UHPC轴拉应力-应变曲线 Fig. 5 Tensile stress-strain curves of strain-hardening UHPC |
为消除不同扭矩对钢-UHPC组合板工作性能的影响,防止预应力损失,在各组合板加载前用数显扭矩扳手将各装配式栓钉拧紧至统一的扭矩。扭矩同文献[12]中抗剪试验时所设置的扭矩计算,即按栓钉可承受最大扭矩的20%计算,最大扭矩按式(1)计算,以便于推导组合板的抗弯承载力计算公式时可直接采用文献[12]中装配式栓钉的抗剪承载力计算公式。
| $ T_{\max }=\tau_{\max } \times W_{\mathrm{t}} $ | (1) |
式中:τmax是栓钉材料能承受的最大切应力,Wt是栓钉扭转截面系数。计算得装配式栓钉预设扭矩为23.14 N·m。
加载试验设备为FORMTEST的LFV-SP600型四柱压力试验机,加载装置见图 6。组合板采用两点对称的集中加载方式,支座一端为固定铰支座,另一端为滚动铰支座。组合板试件整体跨度为1 400 mm,纯弯段长度为400 mm,两边剪跨段长度为500 mm。组合板在达到屈服前按力控制,加载速率为5 kN/min,每级荷载增量为10 kN。在达到屈服之后按位移控制,加载速率5 mm/min,每级位移增量为5 mm,直至试件破坏。

|
图 6 加载装置 Fig. 6 Test setup |
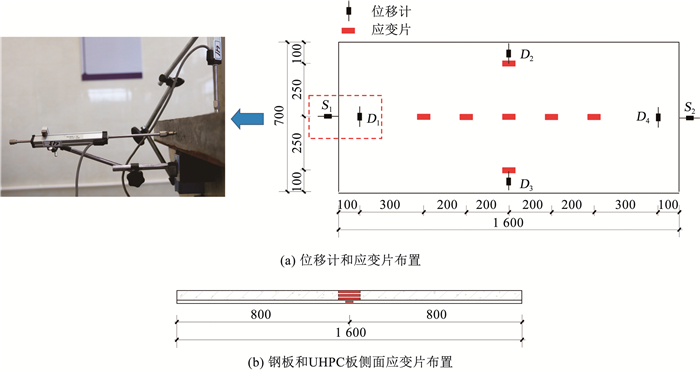
试验中主要量测了组合板试件的跨中、加载点、剪跨段和支座处的竖向位移,钢板与UHPC板之间的相对滑移,位移计的详细布置见图 7(a)。钢板和UHPC板上应变测点位置见图 7。试验中同时对UHPC板侧面的裂缝进行观察,使用精度为0.01 mm的裂缝测宽仪观测UHPC板裂缝的开展情况,并量测出当前荷载等级下的最大缝宽,同时用记号笔对裂缝的分布情况进行标记。
|
图 7 测点布置(mm) Fig. 7 Arrangement of measuring points(mm) |
图 8是3块采用装配式栓钉连接的钢-UHPC组合板试件的破坏形态。3块组合板试件均为纵向水平剪切黏结破坏,剪跨段内装配式栓钉剪断造成钢板与UHPC板脱开,导致两者无法共同工作,破坏时板端相对滑移值可达5~10 mm,数值较大。这是因为3块组合板的抗剪连接程度均为部分抗剪连接。即使是栓钉间距为250 mm的组合板,也未观察到钢板的局部屈曲变形,说明10 mm的厚度即可保证钢板的稳定性。

|
图 8 装配栓钉连接的钢-UHPC组合板的破坏形态 Fig. 8 Failure modes of demountable steel-UHPC composite slabs |
图 8中加载后装配式栓钉与UHPC板连接处的典型照片可见,剪跨段最外侧剪断的装配式栓钉断面呈现光滑的剪切破坏面,剪跨段未发生剪断的栓钉根部也出现了明显的纵向滑移,纯弯段的装配式栓钉根部未出现滑移现象。
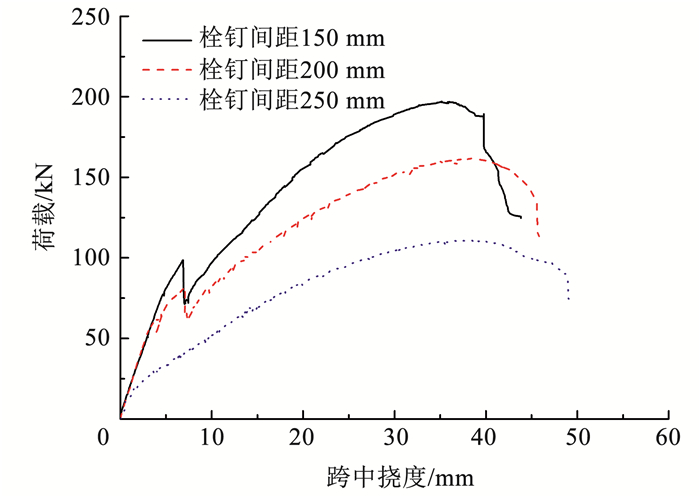
2.2 荷载-挠度曲线图 9为荷载作用下组合板试件的荷载-挠度曲线。曲线可分为弹性段、弹塑性段和下降段。在弹性段内,组合板试件未出现裂缝,该阶段结束的标志为UHPC板与钢板脱黏,反映在荷载-挠度曲线上为荷载突然下降。弹塑性段,组合板刚度下降,UHPC板侧面的裂缝首先出现在加载点附近,为剪跨段内的斜裂缝;随着荷载增大,纯弯段也开始出现竖向裂缝,并由UHPC板和钢板的交界面处向上延伸;在接近荷载峰值点附近,剪跨段的一条斜裂缝斜向往加载点延伸贯穿UHPC板厚方向;此阶段内UHPC板和钢板之间产生较大相对滑移,UHPC处于塑性状态,钢板仍在弹性阶段。当荷载达到极限荷载,最外侧的部分装配式栓钉被剪断并发出脆响,组合板承载力迅速下降,荷载-挠度曲线进入下降段,破坏时钢板未达到屈服强度。
|
图 9 荷载-挠度曲线 Fig. 9 Load-deflection curves |
见图 9,栓钉间距为250、200和150 mm的组合板试件的极限承载力分别为110.9、161.7和197.14 kN,降低栓钉间距能有效提高钢板和UHPC板的协同工作能力,从而提高结构的极限承载力。对比不同栓钉间距的组合板试件的刚度可知,栓钉间距为250、200和150 mm的组合板试件在弹性段的刚度分别为17.53、17.40和16.24 GPa,栓钉间距的变化对结构弹性段的刚度基本没有影响,这主要是因为在弹性段内,钢板和UHPC层之间的黏结力以及栓钉的静摩擦力平衡了钢板和UHPC层之间的剪力,保证了栓钉未出现滑移。栓钉间距为250、200和150 mm的组合板在弹塑性阶段的刚度分别为2.8、3.29和4.67 GPa,降低栓钉间距能有效提高结构弹塑性段的刚度。上述数据说明降低栓钉间距能提高组合板结构的极限承载力以及弹塑性阶段的刚度,这有助于提高结构的极限承载力并控制其在正常使用阶段的变形。
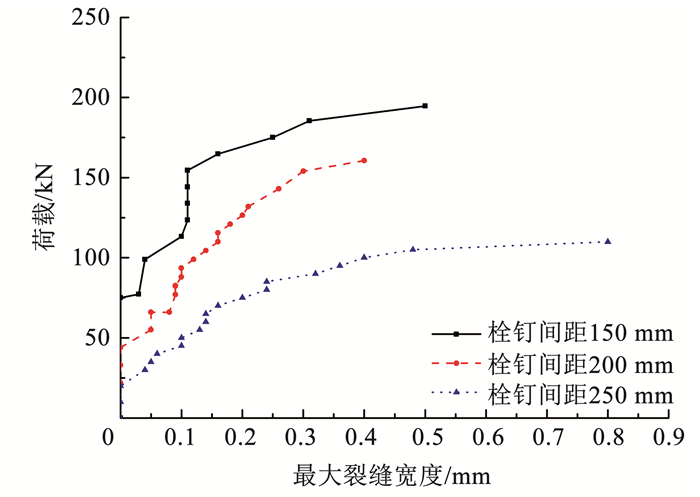
2.3 荷载-最大裂缝宽度曲线由于组合板的抗剪连接程度为部分抗剪连接,因此钢板和组合板中各有一个塑性中和轴,导致UHPC板的受拉层出现裂缝。图 10为UHPC板侧面最大裂缝宽度曲线。见图 10,对比不同栓钉间距的组合板试件裂缝宽度的发展规律可知,降低栓钉间距可以有效提高UHPC板开始出现裂缝时对应的荷载,还能控制UHPC板裂缝宽度的增长速率,尤其是在弹塑性阶段的前期。这是因为提高组合板结构的抗剪连接程度,可以提高UHPC板和钢板的协同工作能力,当两者协调变形时,钢板可以作为UHPC板的保护层有效抑制UHPC板裂缝的萌芽以及裂缝宽度的增长。因此提高组合板的抗剪连接程度可有效提升结构在正常使用阶段的耐久性能。
|
图 10 荷载-最大裂缝宽度曲线 Fig. 10 Load-maximum crack width curves |
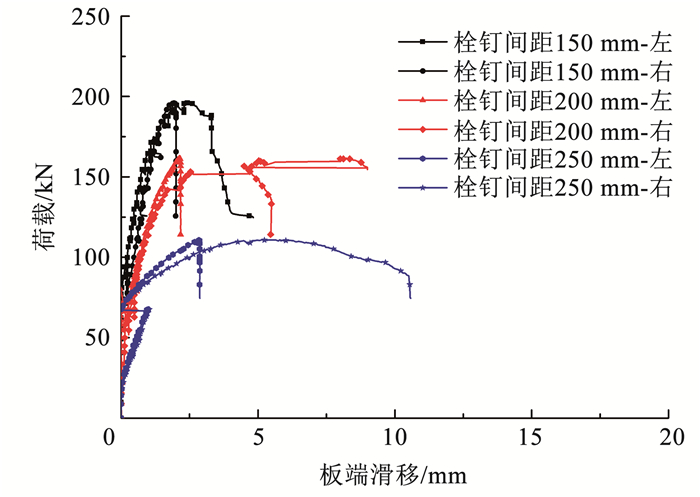
图 11为荷载作用下组合板试件的荷载-板端滑移曲线。组合板板端滑移的发展过程如下:1)当栓钉的摩擦力和钢板与UHPC板之间的黏结力之和大于界面剪力时,组合板未发生相对滑移,此阶段的终点,即组合板开始滑移时对应的荷载随着栓钉间距的降低而提高,这是因为更多的栓钉提供给了更多的静摩擦力;2)当界面剪力大于栓钉的摩擦力和钢板与UHPC板之间的黏结力之和时,由于钢板上的开孔的孔径大于装配式栓钉栓杆的直径,装配式栓钉开始滑动,板端滑移开始增长;3)当钢板与UHPC板之间的黏结力消失时,曲线中观察到板端滑移瞬时的波动,且在栓钉间距越小的组合板中越剧烈,随后装配式栓钉开始快速滑动,在此阶段,栓钉与钢板的孔壁接触,界面剪力仅由栓杆承受;4)当钢板和UHPC板界面的剪力超过栓钉的抗剪承载力时,有一端最外侧的栓钉剪断,一端滑移值突然增大,另一端的滑移值基本保持不变。对比不同栓钉间距的组合板试件的板端滑移值的发展规律可发现,随着栓钉间距的降低,钢板与UHPC板协同变形的能力提升。
|
图 11 荷载-板端滑移曲线 Fig. 11 Load-relative slip curves |
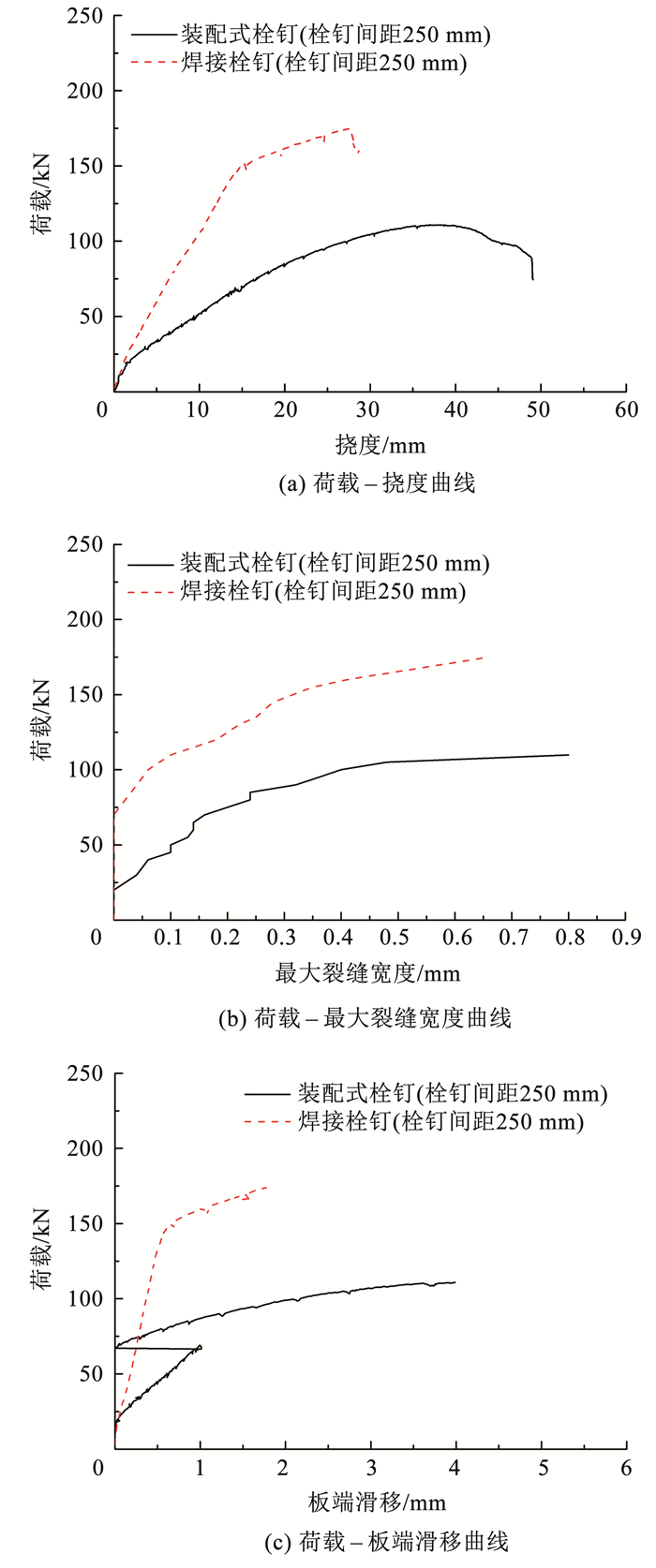
采用焊接栓钉的钢-UHPC组合板的破坏模式与采用装配式栓钉的组合板相同,均为剪跨段的栓钉剪断。图 12对比了两种组合板的试验结果。见图 12(a),在装配式栓钉滑移之前,装配式栓钉连接的钢-UHPC组合板的刚度与采用焊接栓钉的基本相同。在装配式栓钉开始滑移后,采用装配式栓钉的钢-UHPC组合板的刚度远小于采用焊接栓钉的。与采用焊接栓钉的组合板相比,采用装配式栓钉的组合板的极限承载力降低了36%,这主要是因为栓钉车制螺纹后,栓杆的有效直径变小,降低了采用装配式栓钉的组合板的抗剪连接程度,导致钢板和UHPC板之间的组合作用减弱。
|
图 12 装配式栓钉与焊接栓钉的钢-UHPC组合板对比 Fig. 12 Comparison of test results of steel-UHPC composite slabs with demountable shear connectors and welded shear connectors |
采用装配式栓钉的组合板在极限荷载时的挠度为38.69 mm,是采用焊接栓钉的组合板的1.4倍。上述数据表明采用装配式栓钉的组合板可以比焊接栓钉实现更高的变形能力。这是因为装配式栓钉和钢板孔壁之间的间隙允栓钉发生较大滑动。总体而言,采用装配式栓钉的钢-UHPC组合板的抗弯承载力和刚度低于采用焊接栓钉的组合板,但变形能力更好。
见图 12(b),UHPC开裂后,采用装配式栓钉的组合板的最大裂缝宽度比采用焊接栓钉的发展快。当最大裂缝宽度达到0.05 mm时,采用装配式栓钉组合板的荷载比采用焊接栓钉的组合板低63%。这是因为装配式栓钉车完螺纹后有效直径的减小导致了组合板的抗剪连接程度的降低,钢板对UHPC板变形的约束和保护作用降低,UHPC组合板和钢板各自受弯,UHPC板的变形增大。
见图 12(c),与采用焊接栓钉的组合板相比,采用装配式栓钉的组合板在初始阶段表现出几乎相同的相对滑移,这是因为钢板和UHPC板的界面剪切力由栓钉的摩擦力和钢板与UHPC板之间的黏结力来共同抵抗。当装配式栓钉滑移后,组合板的板端滑移发展速度远快于采用焊接栓钉的组合板试件。当钢板和UHPC板之间的黏结力消失时,组合板的板端滑移有剧烈的波动,这是因为设计时装配式栓钉和钢板孔壁有间隙。采用装配式栓钉的组合板和采用焊接栓钉的组合板在极限载荷下的未剪断一端的板端滑移分别为2.8和1.9 mm。这主要是因为钢板的孔径比装配式栓钉的直径大1 mm,因此理论上装配式栓钉在接触孔壁之前可能会发生1 mm的滑动。
2.6 可拆卸性讨论图 13评估了装配式栓钉连接的钢-UHPC组合板的拆卸性。加载后选取US-D-200-3.1%试件进行拆卸,尽管组合板在加载中产生了较大的变形,但将所有装配式栓钉的螺帽松开后,钢板和UHPC板仍可较容易分离,这也说明在钢板开孔孔径仅比栓钉螺纹直径大1 mm的条件下即可保证组合板的可拆卸性。这为钢-UHPC组合板的日常维护提供了新方法:如在钢板需要更换或UHPC板需要维护时,可将组合板拆卸后更换钢板或对UHPC板进行高温蒸养以恢复其力学性能和耐久性能[16];采用装配式栓钉可在组合板构件设计寿命结束后,对钢板或UHPC板的力学性能进行检测评估,在满足力学性能规定的前提下可对其进行重复使用,从而提高材料的剩余价值,减少与材料生产相关的碳排放。

|
图 13 装配式栓钉连接的钢-UHPC组合板破坏后拆卸 Fig. 13 Disassembly of a demountable steel-UHPC composite slab after failure |
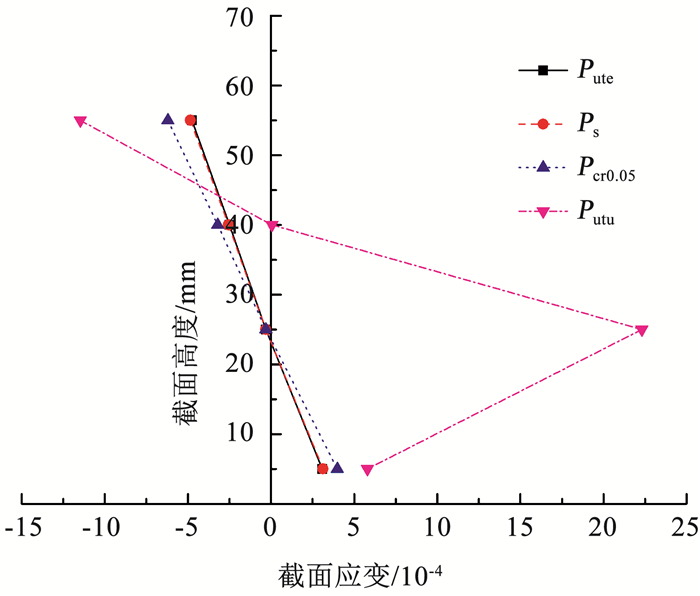
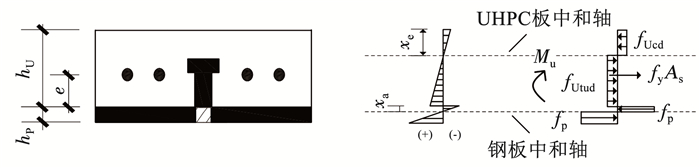
装配式栓钉连接的钢- UHPC组合板试件的抗剪连接程度为部分抗剪连接。图 14为US-D-150-3.1% 试件跨中截面应变分布图。钢板和UHPC板之间存在相对滑移,因此钢板和组合板中各有一个塑性中和轴。本文考虑组合板的界面滑移,采用塑性理论[17]来分析其极限承载力的计算方法,采用如下基本假定[18]:钢板的受拉区和受压区均达到屈服强度;位于UHPC板中和轴以上的UHPC受压区达到UHPC的抗压强度。基于上述假定,装配式栓钉连接的钢-UHPC组合板在达到承载力极限状态时的应变及应力分布模型见图 15。
|
图 14 US-D-150-3.1%试件跨中截面应变分布 Fig. 14 Midspan strain profiles of specimen US-D-150-3.1% |
|
图 15 装配式栓钉连接的钢-UHPC组合板承载力极限状态 Fig. 15 Demountable steel-UHPC composite slabs in ultimate capacity state |
见图 15,根据UHPC板的轴力平衡方程,UHPC板的受压区高度(xe)可按下式计算:
| $ x_{\mathrm{e}}=\frac{n N_{\mathrm{v}}^{\mathrm{c}}+f_{\mathrm{y}} A_{\mathrm{s}} f_{\mathrm{Utud}} b h_{\mathrm{u}}}{f_{\mathrm{Ucd}} b+f_{\mathrm{Utud}} b} $ | (2) |
根据钢板的轴力平衡方程,钢板的受压区高度(xa)可按下式计算:
| $ x_{\mathrm{a}}=\frac{n N_{\mathrm{v}}^{\mathrm{c}}+f_{\mathrm{p}} b h_{\mathrm{p}}}{2 f_{\mathrm{p}} b} $ | (3) |
式中:fy为钢筋的屈服强度设计值; fp为钢板的屈服强度设计值; n为剪跨段装配式栓钉的个数; Nvc为装配式栓钉极限抗剪承载力,按文献[12]中推导的计算公式确定; fUcd、fUtud分别为UHPC材料的抗压和抗拉强度设计值,按SIA 2052瑞士UHPC规范[13]中提出的计算方法确定(式(4)、(5))。
| $ f_{\mathrm{Ucd}}=\frac{\eta_{\mathrm{t}} \times f_{\mathrm{Utck}}}{\gamma_{\mathrm{U}}} $ | (4) |
| $ f_{\mathrm{Utud}}=\frac{\eta_{\mathrm{t}} \times \eta_{\mathrm{hU}} \times \eta_{\mathrm{k}} \times f_{\mathrm{Utuk}}}{\gamma_{\mathrm{U}}} $ | (5) |
式中:fUtck为UHPC的抗压强度特征值,本文中取UHPC抗压强度的平均值; ηt为荷载作用系数,持续性荷载时系数取1;γu为UHPC结构抵抗力系数,配筋UHPC结构取1.3;fUtuk为UHPC的抗拉强度特征值,本文中取UHPC抗拉强度的平均值; ηk为纤维方向系数,取1;ηhU考虑了纤维分布方向上构件厚度的影响,当构件厚度≤50 mm时,系数取1。装配式栓钉连接的钢-UHPC组合板试件的极限受弯承载力计算公式为
| $ \begin{aligned} M_{\mathrm{u}, \mathrm{P}}= & f_{\mathrm{y}} A_{\mathrm{s}}\left(h_{\mathrm{u}}-e-\frac{1}{2} x_{\mathrm{e}}\right)+f_{\mathrm{Utud}} b\left(h_{\mathrm{u}}-x_{\mathrm{e}}\right) \frac{1}{2} h_{\mathrm{u}}- \\ & f_{\mathrm{p}} x_{\mathrm{a}} b\left[h_{\mathrm{u}}+\frac{1}{2}\left(x_{\mathrm{a}}-x_{\mathrm{e}}\right)\right]+f_{\mathrm{p}} b\left(h_{\mathrm{p}}-x_{\mathrm{a}}\right) \times \\ & {\left[\frac{1}{2} h_{\mathrm{p}}+h_{\mathrm{u}}+\frac{1}{2}\left(x_{\mathrm{a}}-x_{\mathrm{e}}\right)\right] } \end{aligned} $ | (6) |
分别求得UHPC板和钢板的受压区高度后代入式(6),即可求得装配式栓钉连接的钢-UHPC组合板试件极限受弯承载力。表 3对比了组合板挠度的计算值(Mu, P)与试验值(Mu, t),试验值与计算值的比值在0.94~1.09,两者吻合较好。
| 表 3 组合板试件极限受弯承载力计算值与试验值比较 Tab. 3 Comparison between calculated and test values of ultimate flexural capacity of composite slabs |
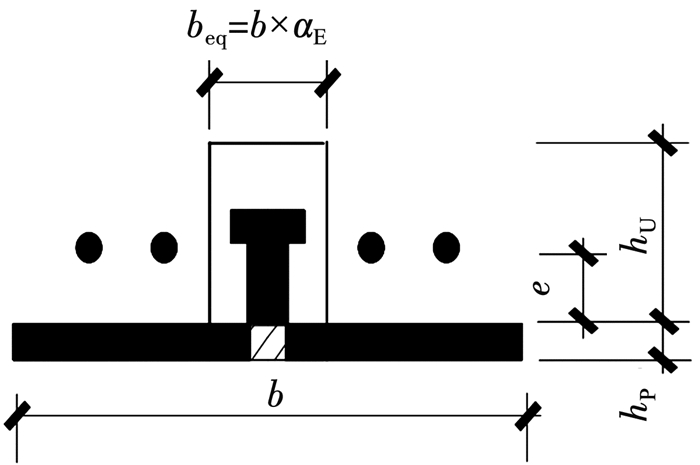
GB 50017—2017《钢结构设计标准》[19]和Eurocode 4[20]中钢-混凝土组合结构的抗弯刚度按截面换算法计算。见图 16,将UHPC层的截面转换为钢板的截面,则装配式栓钉连接的钢-UHPC组合板的有效截面的惯性矩(Ieq)可通过式(7)计算。
| $ \begin{aligned} I_{\mathrm{eq}}= & \frac{b h_{\mathrm{p}}^3}{12}+b h_{\mathrm{p}}\left(y_0-\frac{h_{\mathrm{p}}}{2}\right)^2+\frac{b_{\mathrm{eq}}\left(\beta_{\mathrm{U}} h_{\mathrm{U}}\right)^3}{12}+ \\ & b_{\mathrm{eq}} \beta_{\mathrm{U}} h_{\mathrm{U}}\left(\frac{\beta_{\mathrm{U}} h_{\mathrm{U}}}{2}+h_{\mathrm{p}}-y_0\right)^2+A_{\mathrm{s}}\left(e+h_{\mathrm{p}}-y_0\right)^2 \end{aligned} $ | (7) |
|
图 16 截面转换法 Fig. 16 Conversion of cross-sections |
式中:b是组合板的宽度,αE是钢板与UHPC材料的弹性模量比(αE=EP/EU)。现有规范计算组合结构的刚度时考虑了混凝土构件整个高度的贡献。由上述试验可知,装配式栓钉连接的钢-UHPC组合板在受荷时存在两个中性轴,钢板和UHPC板各自受弯,此时有部分UHPC已处于开裂阶段,因此在计算组合板的抗弯刚度时,应对UHPC板的高度进行折减,因此本文提出UHPC板高度的折减系数(βU)。y0是组合板中性轴到钢板底部的距离,可按式(8)计算:
| $ y_0=\frac{b h_{\mathrm{p}}^2 / 2+b_{\mathrm{eq}} \beta_{\mathrm{U}} h_{\mathrm{U}}\left(\beta_{\mathrm{U}} h_{\mathrm{U}}+h_{\mathrm{p}}\right) / 2+A_{\mathrm{s}}\left(e+h_{\mathrm{p}}\right)}{b_{\mathrm{eq}} \beta_{\mathrm{U}} h_{\mathrm{U}}+b h_{\mathrm{p}}+A_{\mathrm{s}}} $ | (8) |
则组合板的刚度可按式(9)计算:
| $ B=\frac{E_{\mathrm{s}} I_{\mathrm{eq}}}{1+\zeta} $ | (9) |
式中ζ是考虑UHPC板和钢板界面滑移的抗弯刚度折减系数,参考文献[21-22]计算。
为确定正常使用极限状态下UHPC板高度的折减系数(βU),将考虑不同折减系数的弯曲刚度计算的跨中挠度(D)与试验结果进行比较,挠度的计算公式:
| $ D=\frac{M}{24 B}\left(3 l^2-4 a^2\right) $ | (10) |
式中M为组合板正常使用阶段的弯矩,a是支座到加载点之间的距离。
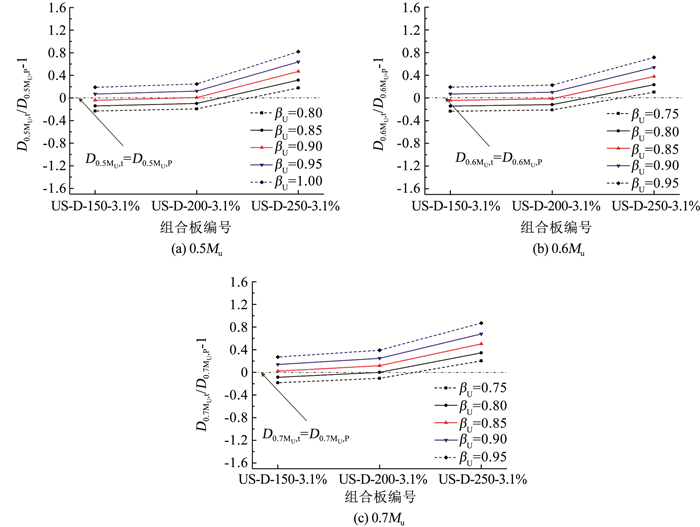
图 17比较了0.5Mu、0.6Mu和0.7Mu时组合板挠度的试验值(DMu,t)和计算值(DMu,p)。见图 17,在0.5Mu,βU取0.9时计算挠度和试验挠度相差最小;在0.6Mu和0.7Mu,βU取0.85时计算挠度最准确。为安全预测装配式栓钉连接的钢-UHPC组合板的抗弯刚度,建议将UHPC板高度的折减系数(βU)取为0.85。此时试验值和计算值之间的平均偏差值和对应的标准差分别为11.6%和9.4%。
|
图 17 对比挠度的试验值和计算值 Fig. 17 Comparison of test and calculated values of deflection |
试验研究了不同抗剪连接程度的装配式栓钉连接的钢-UHPC组合板的抗弯性能。分析了组合板试件的破坏形态、极限承载力、刚度、裂缝发展规律和板端滑移,并与采用焊接栓钉连接的钢-UHPC组合板进行了对比分析,讨论了组合板试件的可拆卸性,最后对其极限抗弯承载力和抗弯刚度进行了理论分析并推导了计算公式,得到以下结论:
1) 装配式栓钉连接的钢-UHPC组合板荷载-挠度曲线可分为弹性段、弹塑性段和下降段,破坏模式为纵向水平剪切黏结破坏。
2) 降低栓钉间距能提高装配式栓钉连接的钢-UHPC组合板的协同变形能力,从而提高组合板结构的极限承载力、弹塑性阶段的刚度和裂缝控制能力。
3) 装配式栓钉连接的钢-UHPC组合板在发生较大变形的情况下,钢板和UHPC板仍然可较容易地拆卸分离,因此在满足力学性能规定的前提下可对钢板或UHPC板进行重复利用,同时也为钢-UHPC组合板的日常维护提供了新思路。
4) 采用塑性理论并考虑滑移效应推导了装配式栓钉连接的钢-UHPC组合板的极限承载力计算方法。同时推导了其抗弯刚度计算公式,提出了UHPC板高度的折减系数(βU),建议取值为0.85,理论计算结果与试验结果吻合良好,可供设计参考。
| [1] |
陈宝春, 杨简, 吴香国, 等. UHPC力学性能的多指标分级[J]. 中国公路学报, 2021, 34(8): 23. CHEN Baochun, YANG Jian, WU Xiangguo, et al. Multi-indicators classification of UHPC mechanical properties[J]. China Journal of Highway and Transport, 2021, 34(8): 23. DOI:10.19721/j.cnki.1001-7372.2021.08.002 |
| [2] |
WANG Junyan, GUO Junyuan. Damage investigation of ultra high performance concrete under direct tensile test using acoustic emission techniques[J]. Cement and Concrete Composites, 2018, 88: 17. DOI:10.1016/j.cemconcomp.2018.01.007 |
| [3] |
KRUSZEWSKI D, WILLE K, ZAGHI A E. Design considerations for headed shear studs embedded in ultra-high performance concrete as part of a novel bridge repair method[J]. Journal of Constructional Steel Research, 2018, 149: 180. DOI:10.1016/j.jcsr.2018.07.015 |
| [4] |
邵旭东, 罗军, 曹君辉, 等. 钢-UHPC轻型组合桥面结构试验及裂缝宽度计算研究[J]. 土木工程学报, 2019, 52(3): 61. SHAO Xudong, LUO Jun, CAO Junhui, et al. Experimental study and crack width calculation of steel-UHPC lightweight composite deck structure[J]. China Civil Engineering Journal, 2019, 52(3): 61. DOI:10.15951/j.tmgcxb.2019.03.007 |
| [5] |
TONG Lewei, CHEN Luhua, WEN Ming, et al. Static behavior of stud shear connectors in high-strength-steel-UHPC composite beams[J]. Engineering Structures, 2020, 218: 110827. DOI:10.1016/j.engstruct.2020.110827 |
| [6] |
王皓磊, 孙韬, 刘晓阳, 等. 钢-UHPC连续组合梁抗弯性能试验[J]. 中国公路学报, 2021, 34(8): 218. WANG Haolei, SUN Tao, LIU Xiaoyang, et al. Experimental investigation on flexural capacity of steel-UHPC continuous composite girder[J]. China Journal of Highway and Transport, 2021, 34(8): 218. DOI:10.19721/j.cnki.1001-7372.2021.08.018 |
| [7] |
GAO Xiaolong, WANG Junyan, YAN Jiabao. Experimental studies of headed stud shear connectors in UHPC steel composite slabs[J]. Structural Engineering and Mechanics, 2020, 74(5): 657. DOI:10.12989/sem.2020.74.5.657 |
| [8] |
ZHANG Yang, CAI Shukun, ZHU Yanping, et al. Flexural responses of steel-UHPC composite beams under hogging moment[J]. Engineering Structures, 2020, 206: 110134. DOI:10.1016/j.engstruct.2019.110134 |
| [9] |
KIM J S, KWARK J, JOH C, et al. Headed stud shear connector for thin ultra high-performance concrete bridge deck[J]. Journal of Constructional Steel Research, 2015, 108: 23. DOI:10.1016/j.jcsr.2015.02.001 |
| [10] |
DAI X H, LAM D, SAVERI E. Effect of concrete strength and stud collar size to shear capacity of demountable shear connectors[J]. Journal of Structural Engineering, 2015, 141(11): 1. DOI:10.1061/(ASCE)ST.1943-541X.0001267 |
| [11] |
LAM D, DAI X H, ASHOUR A, et al. Recent research on composite beams with demountable shear connectors[J]. Steel Construction, 2017, 10(2): 125. DOI:10.1002/stco.201710016 |
| [12] |
WANG Junyan, GUO Junyuan, JIA Liangjiu, et al. Push-out tests of demountable headed stud shear connectors in steel-UHPC composite structures[J]. Composite Structures, 2017, 170: 69. DOI:10.1016/j.compstruct.2017.03.004 |
| [13] |
Recommendation: ultra-high performance fibre reinforced cement-based composites(UHPFRC): construction material, dimensioning and application: SIA 2052[S]. Lausanne: EPFL, 2016
|
| [14] |
活性粉末混凝土: GB/T 31387—2015[S]. 北京: 中国标准出版社, 2015 Reactivepowder concrete: GB/T 31387—2015[S]. Beijing: China Planning Press, 2015 |
| [15] |
普通混凝土长期性能和耐久性能试验方法: GB/T 50082—2009[S]. 北京: 中国建筑工业出版社, 2009 Standard for test methods of long-term performance and durability of ordinary concrete: GB/T 50082—2009[S]. Beijing: China Planning Press, 2009 |
| [16] |
GUO Junyuan, WANG Junyan, WU Kai. Effects of self-healing on tensile behavior and air permeability of high strain hardening UHPC[J]. Construction and Building Materials, 2019, 204: 342. DOI:10.1016/j.conbuildmat.2019.01.193 |
| [17] |
薛建阳. 钢与混凝土组合结构[M]. 2版. 武汉: 华中科技大学出版社, 2007: 51. XUE Jianyang. Steel-concrete composite structures[M]. 2nd ed. Wuhan: Huazhong University of Science and Technology Press, 2007: 51. |
| [18] |
王挺, 聂建国, 李炳益, 等. 钢-压型钢板混凝土组合梁极限抗弯承载力的研究[J]. 建筑结构学报, 2001, 22(2): 61. WANG Ting, NIE Jianguo, LI Bingyi, et al. Experimental study on moment redistribution of continuous composite steel-concrete beams with profiled sheeting[J]. Journal of Building Structures, 2001, 22(2): 61. DOI:10.3321/j.issn:1000-6869.2001.02.011 |
| [19] |
钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [20] |
European Committee for Standardization. Eurocode 4: design of composite steel and concrete structures: EN 1994-2: 2005[S]. Brussels: CEN, 2005
|
| [21] |
徐荣桥, 陈德权. 组合梁挠度计算的改进折减刚度法[J]. 工程力学, 2013, 30(2): 285. XU Rongqiao, CHEN Dequan. Modified reduced stiffness method forcalculating the deflection of composite beams[J]. Engineering Mechanics, 2013, 30(2): 285. DOI:10.6052/j.issn.1000-4750.2011.08.0557 |
| [22] |
GIRHAMMAR U A. A simplified analysis method for composite beams with interlayer slip[J]. International Journal of Mechanical Sciences, 2009, 51(7): 515. DOI:10.1016/j.ijmecsci.2009.05.003 |
 2024, Vol. 56
2024, Vol. 56


