2. 中南大学 高速铁路建造技术国家工程研究中心,长沙 410075;
3. 中建五局第三建设有限公司,长沙 410004
2. China National Engineering Laboratory of High-Speed Railway Construction Technology, Changsha 410075, China;
3. 3rd Construction Co. Ltd. of China Construction 5th Engineering Bureau, Changsha 410004, China
针对中国绿色建筑和建筑产业化的要求,开发具有足够安全性和耐久性的组合结构体系成为结构工程的核心发展趋势[1],而装配式建筑同时具有施工速度快、预制混凝土技术应用充分、工业化程度高和节能环保等优点[2]。
近年来,随着建筑技术的发展,国内外学者对组合楼板的研究不断深入,结构形式随之多样化,主要有:叠合楼板、压型钢板-混组合楼板、钢边框楼板、薄壁型钢-混组合楼板等[3-4]。在国内,王元清等[5-6]对一种拼装式混凝土双向叠合楼板进行了弹性范围的均布堆载和集中荷载破坏对比试验,研究了此拼装式叠合板的承载性能,结果表明该结构具有双向受力性能优势;刘学春等[7]研究了一种带C形钢边框的装配式钢筋混凝土预制楼板,板块间通过断续焊接,实现楼板双向受力,增大了楼板承载力,提高了刚度,基于这种结构提出了考虑带C形钢-钢筋混凝土的承载力计算方法;周绪红等[8-9]对冷弯薄壁型钢-混组合楼盖进行了研究,提出了复合作用下楼板抗弯承载力的简化设计方法,推导了部分抗剪连接T形截面组合梁的等效抗弯刚度;王新唐等[10-13]对薄壁型钢-混楼板结构展开了不同混凝土材料的研究,引入了考虑混凝土板和钢梁协同工作效应的组合系数,对组合楼板整体工作性能进行分析。在国外,Ferrante等[14]提出一种新型钢-混组合楼板结构,混凝土楼板包裹蜂窝梁的上翼缘形成组合结构,抗剪连接件由钢梁上翼缘、横向钢筋、角钢等组成,进行了相应的推出试验和组合梁抗弯试验,结果验证了该钢-混组合楼板结构协同工作性能良好; Grossi等[15]对加筋压型钢板-混组合楼板开展试验,结果表明附加钢筋提高了组合楼板的承载能力和纵向抗剪延性,可以更好地利用组合板截面的塑性弯曲能力; Hassan等[16]提出一种新型联锁预制钢-混组合楼板,可以实现水平力在不连续楼板间的传递,采用了后浇法将不连续的预制楼板与工字型钢、栓钉抗剪连接件、联锁钢筋填充构筑为整体,通过试验证明了其承载力比简支非组合楼板高40%,比连续组合楼板低10%。
学者们对装配式组合楼板的研究非常丰富,但已有的研究中仍存在以下不足:1)部分组合梁仍需现场湿作业,施工速度慢,养护周期长;2)常规组合梁梁高较大,占用较大的楼层结构高度;3)钢结构腹板无混凝土支承,有局部失稳风险。
本课题组根据国内外对装配式建筑的规定,提出了一种全装配式建筑预制梁板体系[17],将混凝土楼板布置在双排槽钢上翼缘下方,实现钢梁和混凝土融合,减小梁高。梁板安装后,混凝土扶持槽钢上翼缘和腹板受压区域,提高钢板件的稳定性能,相邻槽钢形成双排槽钢梁,作为楼板梁承担竖向荷载。可实现模块间完全干式连接,采用开孔钢板连接件[18]连接槽钢和混凝土,抗剪能力强,抗滑移刚度大,预制模块损坏后可快速拆卸更换,实现对建筑快速修复。为研究该组合楼板的受力性能,本文以抗剪连接件间距、螺栓间距为试验参数对1个楼板和2个双排楼板进行了静载试验,分析结构的破坏形态、平面外分离、应变等,并提出了双拼槽钢-混凝土组合楼板的极限抗弯承载力计算方法。
1 试验概况 1.1 试件设计预制模块由1个混凝土板,2个槽钢钢梁组成,钢梁通过纵向加劲肋、抗剪连接件、连接件锚筋与混凝土板组合,组合楼板结构见图 1。设计制作了5个组合梁板预制模块,编号为A~E,楼板内布置双层双向钢筋网,横向配筋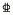
|
图 1 组合楼板示意 Fig. 1 Schematic of composite floor |
| 表 1 组合梁板试件参数 Tab. 1 Parameters of composite beam and plate specimen |
预制混凝土板内部钢筋和连接件锚筋采用HRB400级钢筋,垂直钢梁方向钢筋直径为12 mm,沿钢梁方向钢筋直径为10 mm,连接件锚筋直径选用20 mm。槽钢采用Q235B级钢,纵向加劲肋采用Q345级钢(板厚16 mm),每种规格的钢筋(板)均进行3个试样的抗拉强度试验,按照GB/T 228.1—2021《金属材料拉伸试验第1部分:室温试验方法》的规定[19],测得的钢材力学性能指标见表 2。
| 表 2 钢材材性 Tab. 2 Steel properties |
浇筑6个标准材性试块(150 mm×150 mm×150 mm),与楼板在同等条件下自然养护,根据GB/T 50081—2019《混凝土物理力学性能试验方法标准》[20]进行混凝土材性试验,实测混凝土立方体抗压强度均值为39.15 MPa,由式(1)[21]推算弹性模量为3.24×104 MPa。
| $ E_{\mathrm{c}}^{\mathrm{o}}=\frac{10^5}{2.2+\frac{34.7}{f_{\mathrm{cu}}^{\mathrm{o}}}} $ | (1) |
式中Eco为混凝土实际弹性模量的推算值,fcuo为混凝土的立方体抗压强度实测值。
1.3 加载制度根据GB/T 50152—2012《混凝土结构试验方法标准》[21]设定试验加载程序,对SP试件进行加载试验时,采用分配梁对试件做两级四点加载,加载点位于板跨三分点处,为了减小钢垫板对组合楼板沿梁长方向的转动的影响,辊轴沿梁长布置。钢梁两端简支于承台上。对DP1、DP2进行加载试验时,采用U型管同时控制两台油压千斤顶,其他装置与SP试件相同,加载装置见图 2。

|
图 2 加载装置示意 Fig. 2 Schematic of loading device |
以试件SP为例,首先在加载梁上放置千斤顶进行第一次采集,其次控制千斤顶逐级加载,加载步长为5 kN,每级停留5 min后采集数据并观察裂缝开展状况。正常使用阶段抗弯刚度试验时,加载到40 kN后持荷12 h。进行破坏试验时,楼板出现裂缝后,以2.5 kN的荷载级继续加载,钢梁达到屈服强度后,进行位移控制加载至试件破坏。
1.4 主要测试内容主要观测内容包括组合楼板的挠度、应变(混凝土、钢筋网、钢梁)、边梁扭转、主梁分离以及开裂模式等,测点编号及位置见图 3,具体内容如下:

|
图 3 组合楼板测点示意(mm) Fig. 3 Schematic of composite floor measuring point (mm) |
1) 在试验中使用了标距为100 mm和50 mm的位移计来测量组合楼板的挠度(SP:L1~L11;DP1、DP2:L1~L19)、边梁扭转(LT1~LT2)、主梁分离(LE1~LE3)。
2) 混凝土板主要的应变测量内容有:混凝土应变、钢筋应变。混凝土板应变测点以C+数字+方位表示,如C1X表示混凝土板板底X方向(沿梁长方向)应变测点;钢筋应变测点以R+数字+方位表示,如R1Y表示下侧钢筋网Y向(垂直梁长方向)应变测点;钢梁应变测点以S表示,测量钢梁跨中截面的应变。
3) 试验中采用观测和电测相结合的方法确定组合楼板的开裂荷载值。
2 试验现象以试件DP1为例,对各个试件在试验中所呈现的相同特征作如下说明:
1) 当荷载加载到55 kN后,在混凝土板板底中心Y方向1 000 mm范围内,沿X方向出现不同程度的纵向裂缝,并逐渐向两侧延伸,直至侧面(图 4(a))。

|
图 4 试件破坏特征 Fig. 4 Failure characteristics of specimens |
2) 荷载达到65 kN时,混凝土板顶部出现角部裂缝(图 4(b)),随着荷载进一步增大,混凝土板底部出现斜裂缝(图 4(c))。
3) 荷载达到80 kN板底中心区域沿Y方向出现横向裂缝,与纵向裂缝形成板底中心网状裂缝(图 4(d));在接近极限荷载时,板顶沿梁长方向两侧出现斜向约45°裂缝并逐渐贯通形成环形裂缝(图 4(e))。
4) 各试件边梁达到屈服荷载以后,出现不同程度的侧扭,最终产生明显变形。
5) 各试件在钢梁明显屈服和扭转、混凝土板多处明显开裂、整体变形较大(最大位移均大于Ly/100) 的情况下始终未见整体坍塌的趋势,说明该组合楼板具有良好的整体工作性能。
在试验中构件呈现的不同破坏特征主要有:
1) 试件SP、DP1、DP2混凝土板底部出现纵向裂缝的荷载水平分别为45、55和50 kN,说明试件SP受到的约束较弱,刚度低、变形较大,混凝土板底出现裂缝时的荷载水平明显较低。组合楼板拼装后整体刚度明显提升,梁板间协同工作有助于延迟竖向裂缝的发生,而抗剪连接件的间距同样对开裂荷载影响较大。
2) 在接近破坏荷载时,试件DP2的混凝土板与钢梁交界面分离裂缝较DP1更为明显(图 4(f)),说明抗剪连接件的设置使得钢梁和混凝土板的结合更为紧密。
3) 荷载达到120 kN后,DP1、DP2沿主梁负弯矩区出现纵向裂缝(图 4(g)),由主梁跨中向两侧延伸,直至与弧形裂缝贯通。
4) 对于试件DP1、DP2,混凝土板底部靠边梁一侧先出现斜裂缝,在构件破坏时试件底部混凝土板斜裂缝的开裂程度也明显不对称。加载后期在中梁附近出现冲切破坏,上部混凝土压溃,无法继续加载。
上述结果表明:试件的破坏形式主要为钢梁与混凝土板分离、混凝土板破坏呈现双向板特征,混凝土板破坏时均表现出板顶角部裂缝和弧形裂缝,板底中心区域为网状裂缝和向角部延伸的斜裂缝,楼板整体裂缝示意见图 5。

|
图 5 组合板破坏裂缝示意 Fig. 5 Damage crack indication of composite slab |
在加载过程中,双板构件荷载-位移曲线基本呈线性增长,说明组合楼板始终处于弹性范围,混凝土板底及侧面未出现任何裂缝,卸载后楼板残余变形均为0。
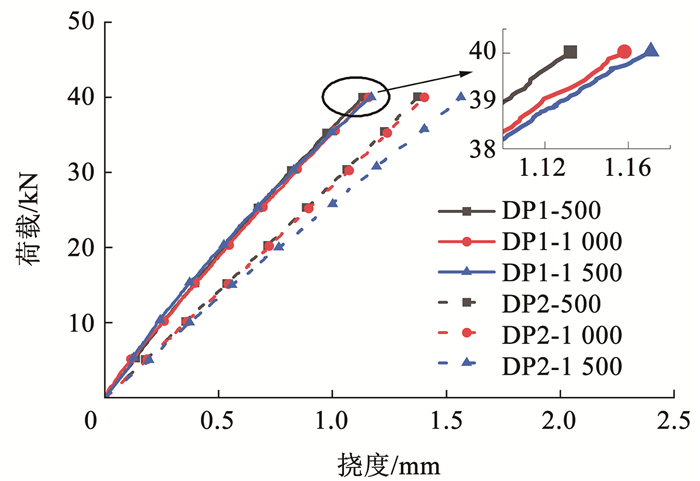
组合楼板试件在3种螺栓间距工况下主梁的荷载-位移曲线见图 6。在弹性阶段,对于两种不同抗剪连接件间距的试件,DP1楼板组合梁的抗弯刚度较大,与DP2相比提升了约22%,说明连接件间距较小情况下,结构的钢-混组合程度更高,协同工作性能更好。对于不同螺栓间距的楼板:随着螺栓间距的增加,抗弯刚度略微减小,在正常使用阶段,组合梁试件跨中挠度满足挠度容许值l/200(10 mm)要求[22]。试验证明:螺栓连接间距影响不显著,而在螺栓间距500 mm时主梁刚度略大于螺栓间距1 000 mm和1 500 mm时,采用500 mm螺栓间距工况对楼板试件进行抗弯承载力试验。
|
图 6 不同螺栓间距下主梁荷载-位移曲线 Fig. 6 Load-displacement curve of main beam with different bolt spacing |
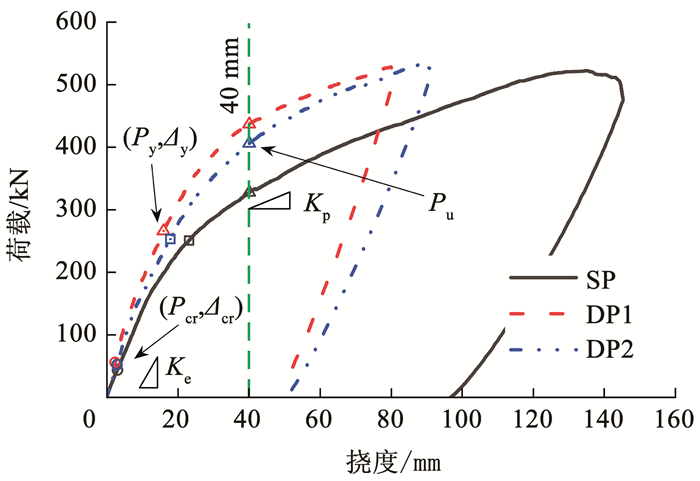
图 7为组合楼板混凝土板荷载-跨中挠度曲线,3组试件混凝土板的荷载-挠度曲线变化可分为4个阶段:
|
图 7 楼板荷载-挠度曲线 Fig. 7 Floor load-deflection curve |
1) 未开裂弹性阶段:荷载与挠度近似线性关系,荷载增长速度较快而挠度增长缓慢,曲线斜率较大。
2) 混凝土开裂阶段:混凝土板下部受拉出现纵向裂缝,裂缝处混凝土退出工作,荷载和挠度仍近似为线性关系,但曲线斜率略有减小,组合楼板处于带裂缝工作阶段。
3) 钢筋和槽钢梁屈服阶段:随着荷载的增大,楼板的裂缝不断延伸并扩展,裂缝数量迅速增加;横向钢筋首先屈服,由于此时边缘钢梁仍未屈服,所以组合楼板荷载-位移曲线依旧在增长;随着槽钢上下翼缘开始屈服,此时楼板荷载位移曲线斜率逐渐降低。
4) 破坏阶段:荷载增长缓慢,但跨中挠度急剧增大,在混凝土板顶部逐渐出现环形塑性铰裂缝,楼板上表面出现混凝土压碎的现象。此时混凝土板受拉区大部分退出工作,试件刚度迅速下降。
试件DP1、DP2的连接件间距由250 mm增大到1 000 mm,破坏荷载差距较小,说明开孔钢板抗剪连接件钢-混组合作用较强,具有较高的抗剪承载力,适当放宽抗剪连接件间距对抗弯承载力影响不大。
试验得到的各试件主要荷载-位移指标见表 3,其中:Pcr为混凝土开裂荷载;Py为钢筋屈服荷载,取沿钢梁方向楼板跨中截面钢筋达到塑性应变时荷载;Pu为极限荷载,采用了GB/T 50152—2012 《混凝土结构试验方法标准》[21]规定的楼板跨中挠度达到l0/50(40 mm)时的荷载;Δcr为开裂位移;Δy为屈服位移;Ke为整体弹性刚度,取为试件开裂时的荷载值与混凝土板跨中位移的比值,即Ke=Pcr/Δcr。
| 表 3 试件主要性能指标 Tab. 3 Main performance indexes of specimens |
各试件Py/Pu分布在0.61~0.76范围内,表明双拼槽钢-混凝土楼板从屈服到破坏具有一定的承载力安全储备;Δy分布在15.98~23.53 mm范围内,远小于40 mm的挠度要求,表明其完全满足正常使用极限状态的要求,可保证楼板在使用过程中处于安全状态。
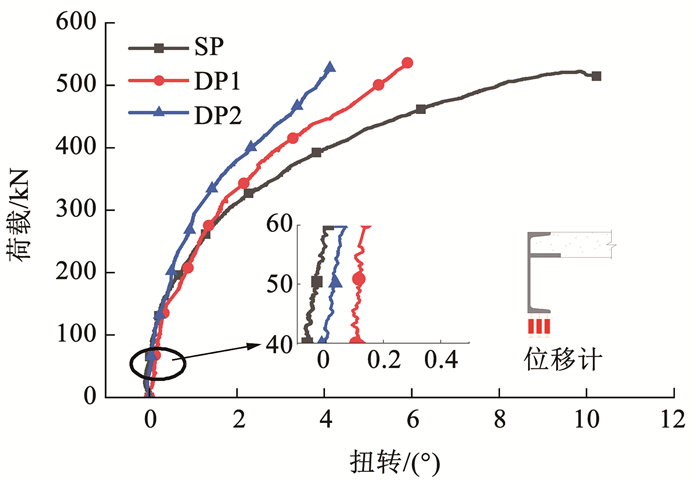
图 8所示为试件边缘的槽钢扭转角度-荷载的变化曲线,在弹性阶段,钢梁基本不发生扭转,随着荷载增加,混凝土板钢筋屈服,板件变形较大,槽钢扭转速率加快,随着钢梁的屈服,扭转速率进一步增加。加载到极限荷载Pu时,SP、DP1、DP2侧扭度数分别为:2.3°、3.2°、2.9°,单板试件扭转小于双板试件,原因是双拼构件的中梁因螺栓连结刚度增大,刚度较小的边梁更易侧扭,而单板构件两侧变形均匀,因此双拼构件侧扭度数较大。与DP1试件相比,DP2试件的侧扭度数较小,这是因为抗剪连接件间距较大时,随着荷载增大混凝土板与钢梁产生平面外分离,削弱了两者的协同工作能力。
|
图 8 边梁扭转响应曲线 Fig. 8 Torsion response curve of side beam |
图 9为荷载-横向分离曲线,即两拼装模块的槽钢梁上翼缘距离和荷载的变化规律曲线。在弹性阶段,两槽钢无明显分离,说明高强螺栓可有效连接两个预制模块,结构整体工作性能良好。随着荷载增加,在钢梁上下翼缘屈服后,两槽钢横向位移增长速率加快。达到钢筋屈服荷载时,DP1、DP2试件的横向位移分别为:1.43 mm、0.76 mm,约为单个板宽的0.07%、0.04%,说明钢梁分离的间隙很小,装配模块间协同工作性能良好。

|
图 9 荷载-主梁横向分离曲线 Fig. 9 Load-lateral separation curve of main beam |
试验的3个试件的应变发展趋势相似,以DP1为例说明试验过程中试件混凝土、钢筋网以及槽钢主要测点的应变变化。
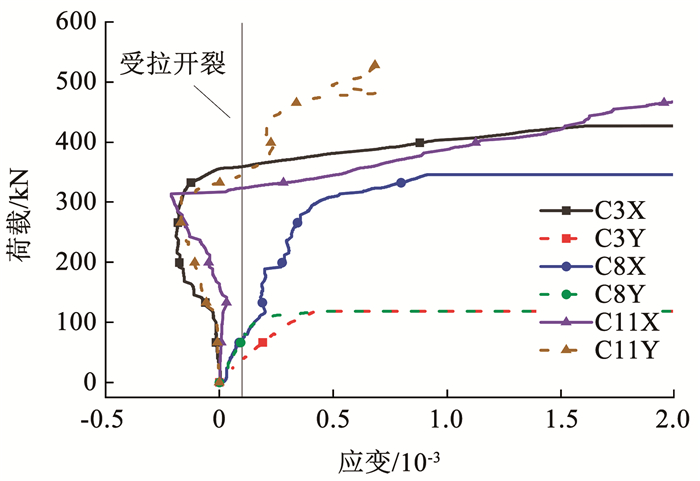
图 10所示为混凝土板下表面3个测点在两个垂直方向上的应变,对于测点3,X方向应变发展迅速,加载到50 kN左右时达到弹性极限,与裂缝发展规律相一致;测点8两个方向的应变曲线在未开裂前几乎完全重合,由此可间接证明组合板的双向受力性能;而测点11位于支座附近,受支座负弯矩的影响,应变发展不充分,在结构大变形破坏后,支座附近也出现混凝土裂缝,导致该处测点迅速破坏。
|
图 10 混凝土板下表面荷载-应变曲线 Fig. 10 Load-strain curves of lower surface of concrete slab |
图 11为组合楼板底部钢筋网在荷载作用下的荷载-应变曲线,总体上Y向的钢筋应变大于X向的钢筋应变,说明组合楼板在平行钢梁方向的刚度较大,这是由于短向板带相对于长向板带具有一定的支承作用,且钢梁抗弯刚度较大,在槽钢腹板屈服前承担了较多的弯矩。对于底部Y向钢筋,测点3即混凝土板跨中区域在荷载达到253.29 kN时达到屈服应变2.1×10-3,随后应变快速增加,达到4.3× 10-3后测点失效。随着荷载的增加和结构的变形,测点7、8的钢筋几乎同时进入屈服阶段。不同的是,测点8在进入塑性阶段后应变急剧增大,在荷载为455.64 kN时达到最大应变1.2×10-3后失效;而测点7应变发展缓慢,同时该点X方向应变逐渐发展,在达到屈服应变后,Y方向钢筋应变快速增大,说明该测点钢筋双向受力,位于塑性铰线区段上。

|
图 11 DP1钢筋网荷载-应变曲线 Fig. 11 Load-strain curve of DP1 steel mesh |
图 12为钢梁上下翼缘荷载应变曲线。由图 12可知:1)钢梁上下翼缘在弹性阶段呈线性发展,且双拼槽钢主梁两侧应变发展基本一致;2)荷载达到253 kN后,钢筋开始屈服,此时槽钢还没有屈服,这个阶段增加的荷载更多由槽钢承担,槽钢应变变化速率略有加快;3)荷载达到320 kN后,S2-6测点应变达到1.5×10-3后屈服,此时槽钢应变开始快速增长,随着荷载的增加,主梁两侧应变发展偏差逐渐增大,这是因为两预制模块间产生平面外变形,整体工作性能略有降低。

|
图 12 DP1钢梁上下翼缘荷载-应变曲线 Fig. 12 Load-strain curves of upper and lower flanges of DP1 steel beam |
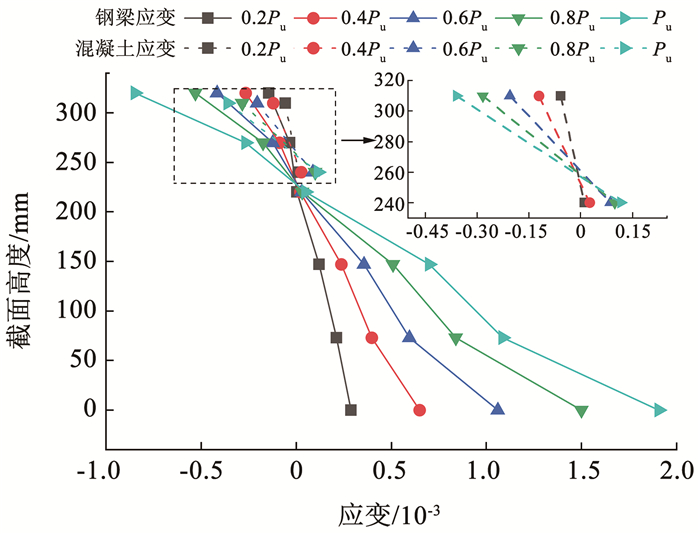
图 13所示为组合楼板试件主梁跨中截面位置的测点应变在不同荷载等级下沿截面高度的分布,同时给出靠近钢梁的混凝土板测点应变在上下表面的分布。在加载过程中主梁跨中截面正应变沿截面高度分布符合平截面假定,而该处混凝土板应变沿高度分布连线与钢梁基本平行,说明在加载全过程,混凝土板与钢梁的弯曲曲率相同,预制模块有较好的协同变形能力。
|
图 13 DP1试件沿截面高度应变分布 Fig. 13 Height strain distribution of DP1 specimen along section |
综上所述,由应变分析可得楼板试件协同工作性能良好,混凝土、钢筋及槽钢三者黏结良好,整体协同工作性能优良。
4 极限承载力计算双向板求解承载力常用板块平衡法,但计算结果通常小于试验结果,这是由于在板块变形较大时,塑性铰区域钢筋受拉伸长,产生受拉薄膜效应[22]。同时,对于双拼槽钢-混组合楼板,混凝土板和槽钢梁协同工作,楼板的钢梁边在极限加载阶段产生了不可忽略的弹性变形,可将楼板支承条件视为支承于钢梁上的弹性固支,采用抗弯刚度考虑钢梁对于结构抗弯的贡献。因此,对于双拼槽钢-混楼板大挠度情况下,分别有:荷载做功W、弹性支承势能Uk、板块转动做功Ue、钢筋薄膜效应做功D,根据能量原理可以得到:
| $ W=U_{\mathrm{e}}+U_{\mathrm{k}}+D $ | (2) |
楼板试件破坏形态呈现双向板特征,混凝土裂缝线将楼板分割成4个板块,可根据塑性铰理论求解楼板承载力。通过板块平衡法求解双向板问题[23],采用以下假定:1)结构在钢筋屈服后形成塑性铰,整个混凝土板沿着塑性铰线被分割成若干板块,形成几何可变体系;2)板的负塑性铰发生在楼板与槽钢梁的上表面交界处,板的正塑性铰线发生在板下部的正弯矩处;3)整个楼板的变形集中于塑性铰线上,各板块均绕塑性铰线转动;4)板的正弯矩塑性铰线处,扭矩和剪力很小,忽略不计。
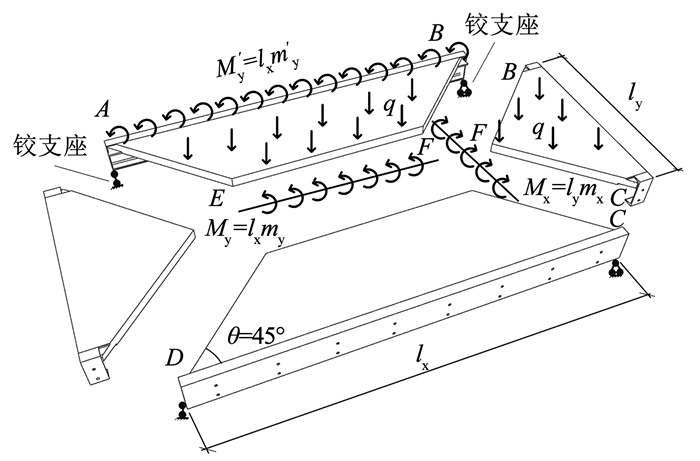
双向板产生塑性铰线后4个板块的极限平衡受力情况见图 14,以lx方向为例,塑性铰线上单位板宽内的极限弯矩mx为
| $ m_{\mathrm{x}}=A_{\mathrm{sx}} f_{\mathrm{y}} \gamma_{\mathrm{s}} h_{0 \mathrm{x}} $ | (3) |
|
图 14 双向板4个板块的极限平衡受力 Fig. 14 Limit equilibrium force diagram of four plates of bidirectional plate |
式中:Asx、fy、γs、h0x分别为板跨内截面沿lx方向单位板宽内的纵向受力钢筋截面面积、钢筋抗拉强度、内力偶臂系数、混凝土板有效厚度;γs=1-0.5fyAsx/(fch0x),fc为混凝土抗压强度。
取梯形ABEF板块为脱离体,荷载做功为
| $ W=q l_{\mathrm{y}}^2\left(\frac{l_{\mathrm{x}}}{8}-\frac{l_{\mathrm{y}}}{12}\right) $ | (4) |
板块转动做功为
| $ U_{\mathrm{e}}=l_{\mathrm{x}} m_{\mathrm{y}}+l_{\mathrm{x}} m_{\mathrm{y}}^{\prime} $ | (5) |
同理,对于BCF板块,可以得到:
| $ W=q \frac{l_{\mathrm{y}}^3}{24} $ | (6) |
| $ U_{\mathrm{e}}=l_{\mathrm{y}} m_{\mathrm{x}} $ | (7) |
板块下挠较大时,受拉钢筋承受水平拉力外,产生了竖向分力,正是这部分竖向分力使混凝土板承受的外荷载增加,即受拉薄膜效应的发生机理,以ABEF板块为例,钢筋受力情况见图 15。其中:F为塑性铰线截面上受压区混凝土的合力;N为塑性铰线截面上板底钢筋的合力;N1、N2分别为N的水平分力、竖直分量。如前所述,F和N1形成截面的抵抗弯矩,N2则为每个板块上受拉薄膜效应产生的直接原因。

|
图 15 钢筋受力 Fig. 15 Stress of steel bar |
以lx方向为例,该方向上单位宽度的钢筋合力为
| $ N=A_{\mathrm{sx}} f_{\mathrm{y}}=\frac{m_{\mathrm{x}}}{\gamma_{\mathrm{s}} h_{0 \mathrm{x}}} $ | (8) |
钢筋合力N和竖直分量N2的夹角,即板块绕板边的转角,可按照图 16考虑。图中θ为板块绕板边的转角,θ0为形成塑性绞线时的转角,v和v0为相对应的挠度。

|
图 16 板的挠度和转角 Fig. 16 Deflection and rotationangle of the plate |
则有
| $ \sin \theta=\frac{2 \nu}{\sqrt{4 \nu^2+l_{\mathrm{y}}^2}} $ | (9) |
薄膜效应一般发生于混凝土板变形较大时,因此可认为受拉薄膜效应在结构产生塑性铰线时发生,则ABEF板块钢筋薄膜效应做功为
| $ D=\frac{m_{\mathrm{y}}\left(\nu-\nu_0\right)\left(2 l_{\mathrm{x}} l_{\mathrm{y}}-l_{\mathrm{y}}^2\right)}{2 \gamma_{\mathrm{sy}} h_{0 \mathrm{y}} \sqrt{4 \nu^2+l_{\mathrm{y}}^2}} $ | (10) |
同理,BCF板块钢筋薄膜效应做功为
| $ D=\frac{m_{\mathrm{x}}\left(\nu-\nu_0\right) l_{\mathrm{y}}^2}{2 \gamma_{\mathrm{sx}} h_{0 \mathrm{x}} \sqrt{4 \nu^2+l_{\mathrm{y}}^2}} $ | (11) |
假定形成塑性铰时钢筋的平均应变为0.1fy,结构产生塑性铰线的挠度v0为[24]
| $ v_0=\sqrt{\left(\frac{0.1 f_{\mathrm{y}}}{E_{\mathrm{s}}}\right) \frac{3 L^2}{8}} $ | (12) |
组合槽钢梁的边界条件为w|x=0=0、w|x=l=0,l为板边长度,简支钢梁支承边位移函数选用简支梁经典挠曲线方程:
| $ w(x)=\frac{1}{k}\left(\frac{q l}{12} x^3-\frac{q}{24} x^4-\frac{q l^3}{24} x\right) $ | (13) |
式中:k为弹性支承刚度,采用试验测量值,取为2.6×103(N/mm2);x为支承边长度。
则弹性支承势能为
| $ U_{\mathrm{k}}=\int_0^l \frac{1}{2} k w^2(x) \mathrm{d} x $ | (14) |
分别联立式(2)、(4)、(5)、(10)、(14);式(2)、(6)、(7)、(11)得到:
| $ \begin{gathered} q l_{\mathrm{y}}^2\left(\frac{l_{\mathrm{x}}}{8}-\frac{l_{\mathrm{y}}}{12}\right)=l_{\mathrm{x}} m_{\mathrm{y}}+l_{\mathrm{x}} m_{\mathrm{y}}^{\prime}+ \\ \frac{N(\sin \theta)\left(2 l_{\mathrm{x}}-l_{\mathrm{y}}^2\right)}{4}+\int_0^l \frac{1}{2} k w^2(x) \mathrm{d} x \end{gathered} $ | (15) |
| $ q \frac{l_{\mathrm{y}}^3}{24}=l_{\mathrm{y}} m_{\mathrm{x}}+\frac{m_{\mathrm{x}}\left(\nu-\nu_0\right) l_{\mathrm{y}}^2}{2 \gamma_{\mathrm{sx}} h_{0 \mathrm{x}} \sqrt{4 \nu^2+l_{\mathrm{y}}^2}} $ | (16) |
不难发现,式(15)、(16)求解结果q1≠q2,组合楼板的承载力应取
| $ q=\min \left(q_1, q_2\right) $ | (17) |
按照上述方法计算得到的单板的极限承载力与试验值较为吻合,但对于双板试件的挠度预估偏大,产生这种现象的主要原因是:对于单板试件的槽钢梁,荷载处于槽钢一侧,楼板加载时主要绕钢梁转动,抗弯刚度贡献较小,而双板试件的主梁两侧受对称荷载,加载时产生垂直钢梁截面的转动较大,因此位于楼板高度范围的钢梁抗弯刚度贡献显著。
针对以上原因,笔者引入考虑混凝土板高度范围的主梁刚度强化系数:
| $ \phi=\left(I_1+I_0\right) / 2 I_0 $ | (18) |
式中:I0为板带截面的初始惯性矩,I1为板带截面在混凝土板高度上考虑钢梁的惯性矩。
修正后的双拼板承载力可取为
| $ q=\phi \min \left(q_1, q_2\right) $ | (19) |
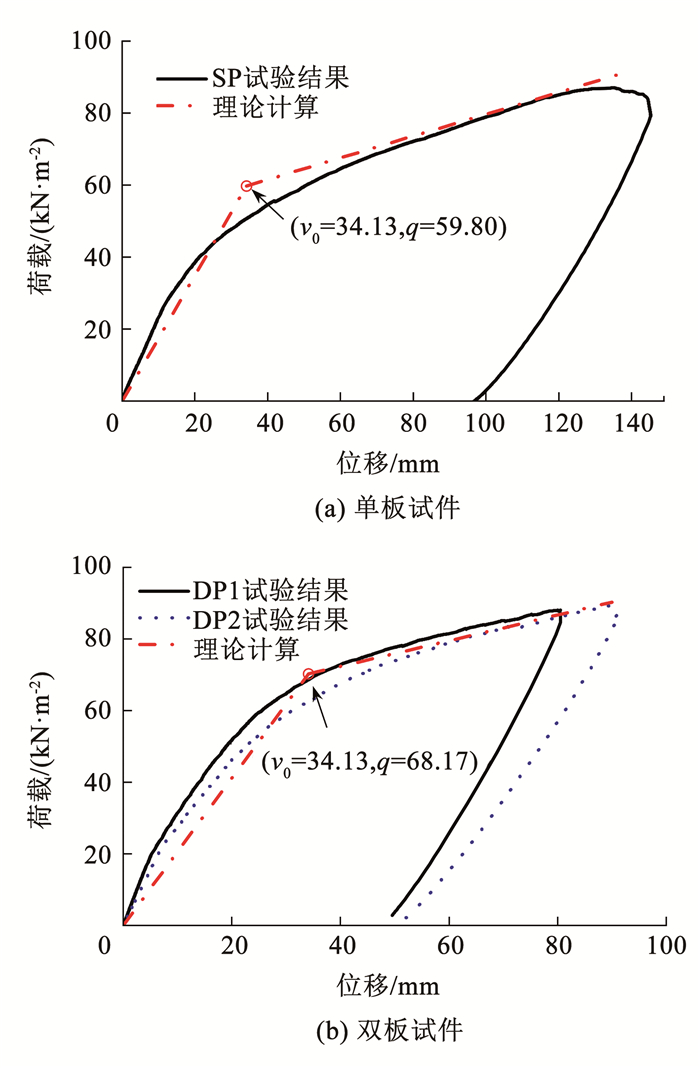
由式(12)计算得到v0为34.13 mm,楼板在形成塑性铰线后,考虑受拉薄膜效应的承载力随挠度变化的荷载-位移曲线见图 17,与试验得到的等效均布荷载-位移曲线对比,计算结果与试验结果吻合较好,双拼槽钢梁可有效提高板间连接强度,增加楼板刚度。
|
图 17 承载力计算与试验结果对比 Fig. 17 Comparisonbetween bearing capacity calculation and test results |
本文提出一种装配式双拼槽钢-混凝土组合楼板结构,对3组试件进行了不同工况下弹性刚度试验以及极限承载力试验,分析了组合梁双向板受力模式,并建立了相应的计算公式,得到如下结论:
1) 双拼槽钢-混凝土组合楼板板间连接简单,便于施工,可有效提高板间连接强度,增加楼板刚度。
2) 抗剪连接件间距对结构刚度影响较大,连接间距由250 mm增大到1 000 mm,刚度降低了约22%,螺栓连接间距影响不显著,而在螺栓间距500 mm时优于螺栓间距1 000 mm和1 500 mm时。
3) 组合梁产生的扭转和主梁横向分离均微乎其微,在钢筋屈服时,SP试件最大扭转为1.19°,DP1试件最大横向分离为1.43 mm,分析时可忽略对结构的影响。
4) 组合楼板在极限加载阶段未出现混凝土和槽钢、钢筋滑移或者脱离的现象,钢筋、槽钢和混凝土三者黏结性能良好,整体协同工作性能优秀。
5) 提出考虑受拉薄膜效应的组合楼板极限承载力计算方法,能够较准确地预测楼板荷载-挠度全过程曲线,然而,对双向板承载力的影响因素有很多,包括双向板的配筋率、宽跨比、钢梁腹板厚度等,有待进一步研究。
| [1] |
NIE Jianguo, WANG Jiaji, GOU Shuangke, et al. Technological development and engineering applications of novel steel-concrete composite structures[J]. Frontiers of Structural and Civil Engineering, 2019, 13(1): 1. DOI:10.1007/s11709-019-0514-x |
| [2] |
郝际平, 孙晓岭, 薛强, 等. 绿色装配式钢结构建筑体系研究与应用[J]. 工程力学, 2017, 34(1): 2. HAO Jiping, SUN Xiaoling, XUE Qiang, et al. Research and application of green prefabricated STEEL structure building system[J]. Engineering Mechanics, 2017, 34(1): 2. DOI:10.6052/j.issn.1000-4750.2016.08.ST14 |
| [3] |
American Concrete Institute. Building code requirements for structural concrete and commentary: ACI: 318-11[S]. Farmington Hills: ACI, 2011
|
| [4] |
组合结构设计规范: JGJ 138—2016[S]. 北京: 中国建筑工业出版社, 2016 Code for design of composite structures: JGJ 138—2016[S]. Beijing: China Building Industry Press, 2016 |
| [5] |
王元清, 袁霞, 张延年, 等. 拼装式混凝土双向叠合楼板承载性能试验研究[J]. 湖南大学学报(自然科学版), 2015, 42(9): 14. WANG Yuanqing, YUAN Xia, ZHANG Yannian, et al. Experimental study on bearing capacity of assembled concrete two-way composite floor[J]. Journal of Hunan University (Natural Science Edition), 2015, 42(9): 14. DOI:10.16339/j.cnki.hdxbzkb.2015.09.003 |
| [6] |
王元清, 袁霞, 张延年, 等. 钢筋桁架混凝土双向叠合楼板承载性能分析[J]. 沈阳建筑大学学报(自然科学版), 2014, 30(3): 385. WANG Yuanqing, YUAN Xia, ZHANG Yannian, et al. Bearing capacity analysis of reinforced truss concrete two-way composite floor[J]. Journal of Shenyang Jianzhu University (Natural Science Edition), 2014, 30(3): 385. DOI:10.11717/j.issn:2095-1922.2014.03.01 |
| [7] |
刘学春, 宋杰, 陈学森, 等. 带C形钢边框装配式钢筋混凝土预制楼板试验研究[J]. 工程力学, 2022, 39(增刊1): 312. LIU Xuechun, SONG Jie, CHEN Xuesen, et al. Experimental study on prefabricated reinforced concrete slabs with C-shaped steel frames[J]. Engineering Mechanics, 2022, 39(Sup.1): 312. DOI:10.6052/j.issn.1000-4750.2021.06.S055 |
| [8] |
ZHOU Xuhong, SHI Yu, XU Lei, et al. A simplified method to evaluate the flexural capacity of lightweight cold-formed steel floor system with oriented strand board subfloor[J]. Thin-Walled Structures, 2019, 134: 40. DOI:10.1016/j.tws.2018.09.006 |
| [9] |
管宇, 周绪红, 石宇, 等. 冷弯薄壁型钢组合楼盖面外和面内刚度试验研究及理论分析[J]. 工程力学, 2023, 40(10): 21. GUAN Yu, ZHOU Xuhong, SHI Yu, et al. Experimental study and theoretical analysis of out-of-plane and in-plane stiffness of cold-formed thin-walled steel composite floor[J]. Engineering Mechanics, 2023, 40(10): 21. DOI:10.6052/j.issn.1000-4750.2022.01.0079 |
| [10] |
王新堂, 杨景, 王万祯. 开孔薄壁钢梁-轻骨料混凝土装配式组合楼板受力性能试验研究[J]. 建筑结构学报, 2016, 37(5): 39. WANG Xintang, YANG Jing, WANG Wanzhen. Experimental study on the mechanical properties of perforated thin-walled steel beam-lightweight aggregate concrete assembled composite slabs[J]. Journal of Building Structures, 2016, 37(5): 39. DOI:10.14006/j.jzjgxb.2016.05.005 |
| [11] |
王新堂, 田兴兴, 任鹏飞. 陶粒混凝土-开孔薄壁钢梁组合楼板的受力性能研究[J]. 建筑结构学报, 2018, 39(增刊1): 237. WANG Xintang, TIAN Xingxing, REN Pengfei. Study on the mechanical properties of ceramsite concrete-thin-walled steel beam composite floor[J]. Journal of Building Structures, 2018, 39(Sup.1): 237. DOI:10.14006/j.jzjgxb.2018.S1.031 |
| [12] |
王新堂, 田兴兴, 任鹏飞. 帽型薄壁钢梁-轻骨料混凝土组合楼板受力性能试验研究[J]. 建筑结构学报, 2018, 39(增刊1): 246. WANG Xintang, TIAN Xingxing, REN Pengfei. Experimental study on mechanical properties of hat-shaped thin-walled steel beam-lightweight aggregate concrete composite slab[J]. Journal of Building Structures, 2018, 39(Sup.1): 246. DOI:10.14006/j.jzjgxb.2018.S1.032 |
| [13] |
王新堂, 窦华坤, 梧松. 冷弯薄壁钢-陶粒混凝土组合楼板静载性能研究[J]. 建筑结构学报, 2019, 40(增刊1): 54. WANG Xintang, DOU Huakun, WU Song. Research on static load performance of cold-formed thin-walled steel-ceramsite concrete composite floor[J]. Journal of Building Structures, 2019, 40(Sup.1): 54. DOI:10.14006/j.jzjgxb.2019.S1.007 |
| [14] |
DE O FERRANTE C A, DE ANDRADE S A L, DE LIMA L R O, et al. Analytical study and experimental tests on innovative steel-concrete composite floorings[J]. Journal of Constructional Steel Research, 2020, 168: 105868. DOI:10.1016/j.jcsr.2019.105868 |
| [15] |
GROSSI L G F, SANTOS C F R, MALITE M. Longitudinal shear strength prediction for steel-concrete composite slabs with additional reinforcement bars[J]. Journal of Constructional Steel Research, 2020, 166: 105908. DOI:10.1016/j.jcsr.2019.105908 |
| [16] |
HASSAN M K, SUBRAMANIAN K B, SAHA S, et al. Behaviour of prefabricated steel-concrete composite slabs with a novel interlocking system-numerical analysis[J]. Engineering Structures, 2021, 245: 112905. DOI:10.1016/j.engstruct.2021.112905 |
| [17] |
周凌宇, 朱医博, 廖飞, 等. 一种全装配式建筑的预制梁板体系及其梁板模块预制方法: CN114232783A[P]. 2022-03-25 ZHOU Lingyu, ZHU Yibo, LIAO Fei, et al. A prefabricated beam-slab system and its beam-slab module prefabrication method for fully assembled buildings: CN114232783A[P]. 2022-03-25 |
| [18] |
周凌宇, 范进凯, 方蛟鹏, 等. 装配式槽钢组合梁中开孔钢板连接件力学性能[J/OL]. 哈尔滨工业大学学报[2023-04-29]. http://dx.doi.org/10.11918/202211021 ZHOU Lingyu, FAN Jinkai, FANG Jiaopeng, et al. Mechanical properties of perforated steel plate connectors in prefabricated channel steel-concrete composite beams[J/OL]. Journal of Harbin Institute of Technology. [2023-04-29]. http://dx.doi.org/10.11918/202211021 |
| [19] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2021[S]. 北京: 中国建筑工业出版社, 2021 Metallic materials-tensile testing-part1: method of test at room temperature: GB/T 228.1—2021[S]. Beijing: China Architecure & Building Press, 2021 |
| [20] |
混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019 Standard for test methods of concrete physical and mechanical properties: GB/T 50081—2019[S]. Beijing: China Construction Industry Press, 2019 |
| [21] |
混凝土结构试验方法标准: GB/T 50152—2012[S]. 北京: 中国建筑工业出版社, 2012 Standard for test method of concrete structures: GB/T 50152—2012[S]. Beijing: China Architecure & Building Press, 2012 |
| [22] |
张大山, 董毓利, 房圆圆. 考虑受拉薄膜效应的板块平衡法修正及在混凝土双向板中的应用[J]. 工程力学, 2017, 34(3): 204. ZHANG Dashan, DONG Yuli, FANG Yuanyuan. Plate equilibrium method correction considering tensile membrane effect and its application in concrete two-way slabs[J]. Engineering Mechanics, 2017, 34(3): 204. DOI:10.6052/j.issn.1000-4750.2015.08.0664 |
| [23] |
沈蒲生. 混凝土结构设计[M]. 北京: 高等教育出版社, 2020: 54. SHEN Pusheng. Concrete structure design[M]. Beijing: Higher Education Press, 2020: 54. |
| [24] |
DONG Yuli, FANG Yuanyuan. Determination of tensile membrane effects by segment equilibrium[J]. Magazine of Concrete Research, 2010, 62(1): 17. DOI:10.1680/macr.2008.62.1.17 |
 2024, Vol. 56
2024, Vol. 56


