2. 西安建筑科技大学 土木工程学院,西安 710055;
3. 结构工程与抗震教育部重点实验室(西安建筑科技大学),西安 710055
2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. Key Lab of Structural Engineering and Earthquake Resistance (Xi'an University of Architecture and Technology), Ministry of Education, Xi'an 710055, China
免拆模板,又被称为永久性模板,将其用作现浇混凝土结构的模板后不用拆卸,模板与结构形成一体,共同受力,可有效节约施工时间,降低工程成本。超高性能混凝土(ultra-high performance concrete, UHPC)是一种具有超高强度、高韧性和高耐久性的水泥基材料[1-2],将其制成薄板作为免拆模板,无需在薄板中设置纤维编织网或钢丝网,UHPC免拆模板不仅能满足施工阶段施工模板的要求,而且在结构服役阶段其作为结构构件的保护层可以提高结构耐久性能,UHPC免拆模板与后续浇筑的混凝土结合形成整体受力构件,共同提供结构抗力,可充分发挥超高性能混凝土的优势。
目前,有关UHPC免拆模板的研究相对较少,且主要集中在UHPC免拆模板RC构件静力学性能研究上。由于UHPC本身力学性能优异,将其制成免拆模板用于RC梁后不仅可以提高梁的受弯承载力,还可以有效抑制裂缝的产生,减少裂缝的数量。此外,U型UHPC免拆梁模板还可以代替梁内箍筋起到抗剪作用,且其抗剪效果甚至优于箍筋[3-7]。杨医博等[8]对整体预制的UHPC免拆模板RC柱的轴压性能进行了研究,结果表明,试件破坏时,UHPC免拆模板整体性良好,表面混凝土剥落较少,且UHPC免拆模板RC柱的承载力远高于普通混凝土柱。单波等[9-10]和王均等[11]在研究活性粉末混凝土(reactive powder concrete, RPC)免拆模板RC柱时也得到了类似的结论。Lin等[12]在研究梁柱节点抗震性能时发现,采用UHPC模板浇筑的节点试件的延性和耗能能力均有显著提高。此外,为进一步了解UHPC免拆模板RC柱在水平往复荷载作用下的破坏模式与力学性能,梁兴文等[13]通过拟静力试验研究了拼接成型的UHPC免拆模板RC柱的抗震性能,结果表明,由于UHPC免拆柱模在设计时未考虑单块模板之间的连接,且未对模板表面做粗糙处理,因此,在加载至峰值荷载前,UHPC模板即与核心混凝土发生了剥离,此时荷载约为峰值荷载的70%,与普通RC柱相比,UHPC免拆模板RC柱的承载力和前期刚度有所降低。
综上所述,UHPC免拆模板混凝土结构是一种比较好的结构形式,但目前基于该类结构形式所进行的研究还非常有限,且已开展的工作多集中于整体式免拆模板构件及其静力性能的研究,而对其抗震性能研究甚为缺乏。整体预制模板占据空间大、不易运输,且在施工现场不易安装、灵活性差。因此,本文基于UHPC免拆模板平板拼接,研究了模板拼接方式及表面处理方式对该类柱抗震性能的影响。通过拟静力试验,分析了其破坏模式、滞回特性、刚度退化、延性和耗能能力等。最后,基于平截面假定提出了UHPC免拆模板RC柱的正截面偏压承载力计算式。
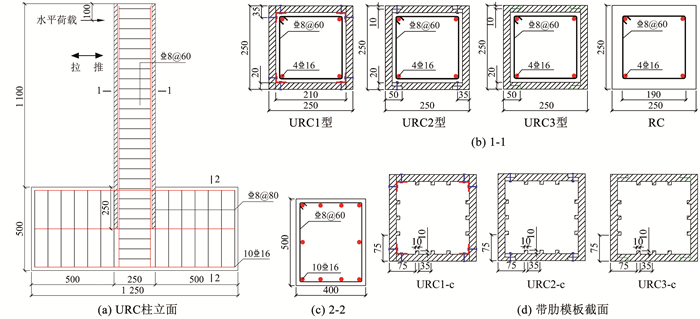
1 试验概况 1.1 试件设计本文以UHPC免拆模板的拼接方式和模板表面处理方式为参数,共设计了10个柱试件,包括1个RC对比柱、3个采用螺栓加角钢连接的URC柱、3个采用螺栓连接的URC柱以及3个采用环氧树脂砂浆连接的URC柱,试件的详细参数见表 1。所有试件的截面尺寸均为250 mm×250 mm,高为1 100 mm,UHPC模板厚度为20 mm,混凝土保护层厚度为30 mm(含模板厚度),纵筋和箍筋均为HRB400级钢筋,直径分别为16 mm和8 mm,设计普通混凝土强度为C40,设计轴压比为0.4(轴压力为530 kN)。各试件的详细尺寸和配筋见图 1。此外,用于连接模板的角钢强度为Q235级,其规格为30 mm×30 mm×3 mm,角钢每边开有直径10 mm,间距为100 mm的螺栓孔。用来处理模板表面的气泡膜直径为10 mm,厚度为5 mm,试验中用到的角钢和气泡膜见图 2。
| 表 1 试件详细参数 Tab. 1 Specimen details |
|
图 1 试件详细尺寸及配筋(mm) Fig. 1 Dimensions and reinforcements of specimens(mm) |

|
图 2 角钢和气泡膜 Fig. 2 Details of angle steel and bubble film |
UHPC免拆模板的制作过程如下:1)根据所需UHPC模板形式制作底模,对于有螺栓孔的模板,使用PVC管固定在底模上来成型所需螺栓孔;2)浇筑UHPC,浇筑完成后在混凝土表面铺上一层土工布,室温下养护一周后拆模,图 3为成型后的UHPC模板。

|
图 3 成型后的UHPC模板 Fig. 3 UHPC formwork after forming |
UHPC模板养护完成后,将其按照图 1所示的方式拼装在一起,拼装完成后的UHPC免拆柱模见图 4。将拼好的UHPC柱模套在绑扎好的钢筋骨架外面并固定,然后浇筑核心混凝土,浇筑过程中使用振动棒不停振捣,以保证URC柱内部混凝土充分密实。

|
图 4 拼接成型的UHPC柱模 Fig. 4 Assembly UHPC column formwork |
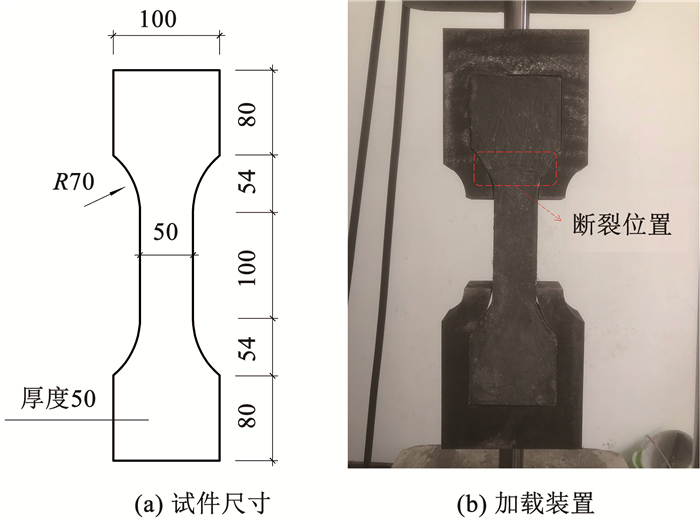
试验中用到的普通混凝土以及环氧树脂砂浆均为商品材料,UHPC的配合比见表 2。在浇筑UHPC模板和URC柱时,分别预留了100 mm×100 mm×100 mm的UHPC立方体试块和C40立方体试块,此外,还预留了UHPC轴心抗拉试件,试件尺寸和加载装置见图 5。所有试块与试件均在同条件下养护,按照GB/T 50081—2002《普通混凝土力学性能试验方法标准》[14]测试了其材料性能,结果见表 3。钢筋的力学性能测试根据GB/T 228.1—2010《金属材料拉伸试验第1部分:室温试验方法》[15]的要求进行,测试结果见表 4。
| 表 2 UHPC配合比 Tab. 2 Mix proportions of UHPC |
|
图 5 UHPC抗拉试验(mm) Fig. 5 Axial tension test of UHPC(mm) |
| 表 3 混凝土力学性能 Tab. 3 Mechanical properties of concrete |
| 表 4 钢材力学性能 Tab. 4 Mechanical properties of steel |
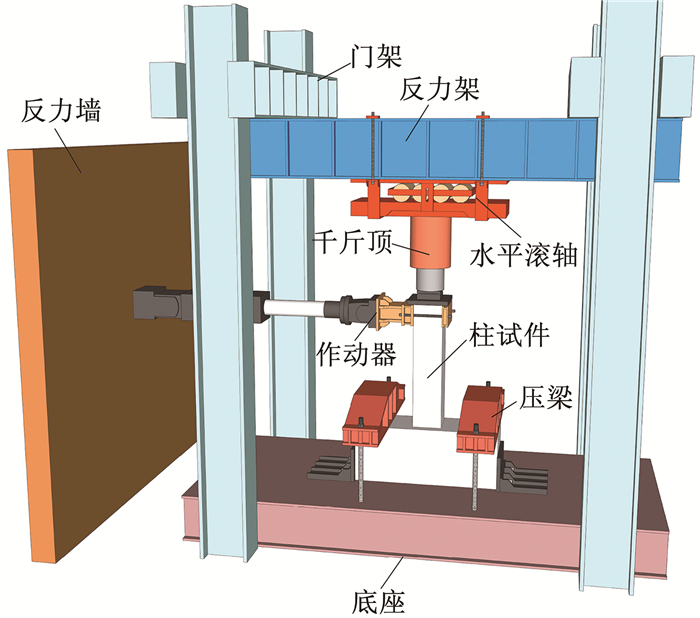
试验在西安建筑科技大学结构与抗震教育部重点实验室进行,加载装置见图 6,加载方案由恒定竖向荷载和水平往复荷载组成,其中,竖向荷载由1 000 kN的竖向油压千斤顶提供,水平往复荷载由500 kN水平作动器施加,通过MTS加载系统中的传感器来记录加载过程中的荷载和位移。加载开始前先施加竖向荷载至预定值,整个加载过程竖向荷载保持不变。水平加载时采用力和位移共同控制的方式,加载初期先用荷载控制,每级荷载增量为10 kN,循环1次,直到纵向钢筋屈服。纵筋屈服后采用位移控制,每级位移增量为3 mm,每级位移循环3次,当试件的水平承载力下降到极限承载力的70%以下或试件出现明显剥离破坏时停止加载。
|
图 6 加载装置 Fig. 6 Loading setup |
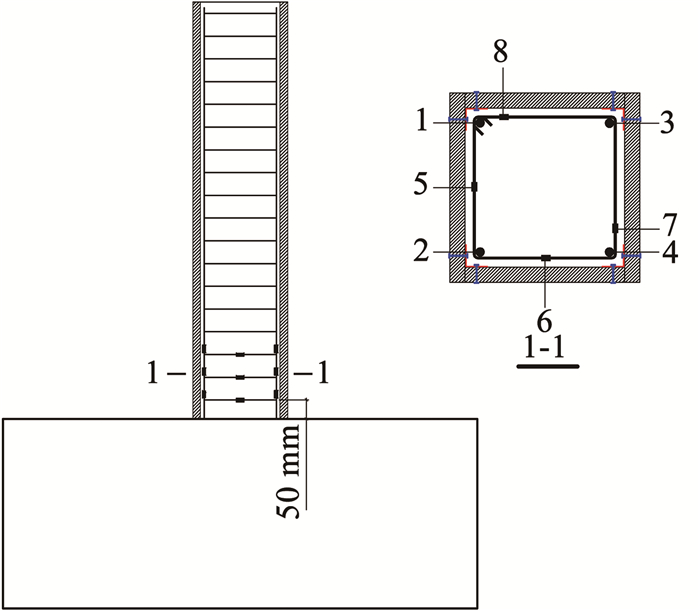
图 7为URC柱的钢筋应变片布置情况,沿柱高方向共设置了3个监测点,最下方测点距柱底高度为50 mm。对于每一个测点,试件的4根纵筋上均布置一个应变片,用来监测试件的纵筋应力变化情况;箍筋每边各布置一个应变片,用来监测箍筋不同部位的应力变化情况。
|
图 7 钢筋应变量测 Fig. 7 Layout of strain gauges |
所有试件均发生了弯曲破坏,最终的破坏形态见图 8,在水平往复荷载作用下,各试件的破坏过程如下:

|
图 8 试件破坏形态 Fig. 8 Failure modes of specimens |
对于RC试件,在加载初期,试件处于弹性阶段,表面无明显现象;当加载至50 kN时(侧移角1/333),距柱底170 mm处出现第一条水平裂缝,裂缝长约250 mm;当加载至77 kN时(侧移角1/143),试件屈服,此时沿柱高出现多条水平短裂缝;随着加载位移的持续增加,柱身不断有新的裂缝产生,部分原有裂缝开始斜向延长;当加载至94 kN时(侧移角1/63),荷载达到峰值,柱底混凝土表面开始起皮,部分混凝土被压碎脱落;当加载至侧移角为1/50时,水平裂缝明显变宽,柱底混凝土大量脱落;当加载至侧移角为1/42时,水平荷载迅速下降,柱底混凝土逐渐压溃剥落,当水平荷载降至峰值荷载的70%以下时,停止加载。
对于URC柱,其破坏特征主要有两种,一种是试件塑性铰区UHPC模板断裂破坏,另一种是试件UHPC模板剥离破坏,前者说明UHPC免拆模板与后浇混凝土界面黏结性能较好,试件具有良好的整体性。
1) 塑性铰区UHPC模板断裂破坏(试件URC1-a、URC1-b、URC1-c、URC2-a、URC2-c、URC3-b)
加载初期,各试件处于弹性阶段,表面无变化;当加载至80~90 kN时(侧移角约为1/250),各试件出现第一条水平裂缝,长度约为100 mm,分布在距柱底300 mm范围内,对于有螺栓孔的试件,裂缝主要出现在螺栓孔附近;当加载至90~110 kN时(侧移角1/200~1/143),各试件相继屈服,沿柱高出现多条细小水平裂缝和斜裂缝,原有裂缝不断延伸;当加载至112~135 kN时(侧移角1/77~1/63),荷载达到峰值,柱身中部以下位置出现多条新的水平裂缝,并沿柱高形成多条水平通长裂缝;当加载至侧移角1/40时,位于柱底部的水平通长裂缝不断变宽,逐渐形成一条主裂缝,裂缝四周的混凝土被压碎脱落;当加载至位移角为1/25时,柱底UHPC模板沿主裂缝处完全断裂,此时荷载下降到峰值荷载的70%以下,试件破坏明显,停止加载。
2) UHPC模板剥离破坏(试件URC2-b、URC3-a、URC3-c)
加载初期,各试件处于弹性阶段,表面无变化;当加载至85~93 kN时(侧移角约为1/250),各试件表面相继出现第一条裂缝;此后,继续加载,试件在峰值荷载前(侧移角1/77~1/63)的裂缝发展情况与发生塑性铰区UHPC模板断裂破坏的URC柱类似,表明在峰值荷载前,UHPC模板与后浇混凝土黏结较好;当加载至侧移角为1/53时,试件URC2-b的UHPC模板在拼接处的螺栓孔位置发生断裂,形成竖向断裂裂缝,试件URC3-a因环氧树脂砂浆连接失效而产生UHPC模板拼接处的竖向分离裂缝,而试件URC3-c的模板拼接处尚未出现裂缝;随着位移的增加,试件URC3-c也开始在模板拼接处出现竖向分离裂缝,而试件URC2-b和URC3-a在模板拼接处的竖向裂缝不断变宽,模板与核心混凝土出现明显剥离;当加载至侧移角为1/42和1/29时,伴随着一声巨响,试件URC2-b、URC3-a的模板在受压侧突然折断,荷载出现陡降,试件发生模板剥离破坏,加载结束。URC3-c在出现竖向分离裂缝后的破坏过程与前两个试件类似,当加载至侧移角为1/25时,模板剥离,停止加载。
对比各试件的破坏情况可知:与普通RC柱相比,URC柱的开裂荷载提高了60%~86%,同时URC柱塑性铰区域混凝土压碎程度相对较轻,这主要归因于UHPC超高的抗压强度和内部钢纤维的桥接作用。对于URC柱,当UHPC模板在拼接处出现明显破坏后,继续加载,模板之间的连接作用显著降低,模板弯曲变形加大,当变形增加到一定程度后,模板与核心混凝土的界面黏结失效,模板发生剥离破坏,由此可知,可靠的模板拼接方式是决定URC柱试件破坏形式的关键因素,在所有试件中,只有采用螺栓加角钢连接的URC柱没有在拼接处发生破坏,故相比之下,螺栓加角钢这种拼接方式更加可靠。
试验结束后,撬开UHPC模板,发现模板带肋的URC柱肋被拉断,嵌入到核心混凝土内部,气泡膜处理的URC柱的核心混凝土表层部分被撕裂,而光面处理的URC柱模板与核心混凝土结合面光滑平整(见图 9)。综上可知,对模板表面进行粗糙处理可以有效提高模板与核心混凝土的界面黏结力。

|
图 9 UHPC模板与核心混凝土界面破坏特征 Fig. 9 Failure characteristics of interface between UHPC formwork and core concrete |
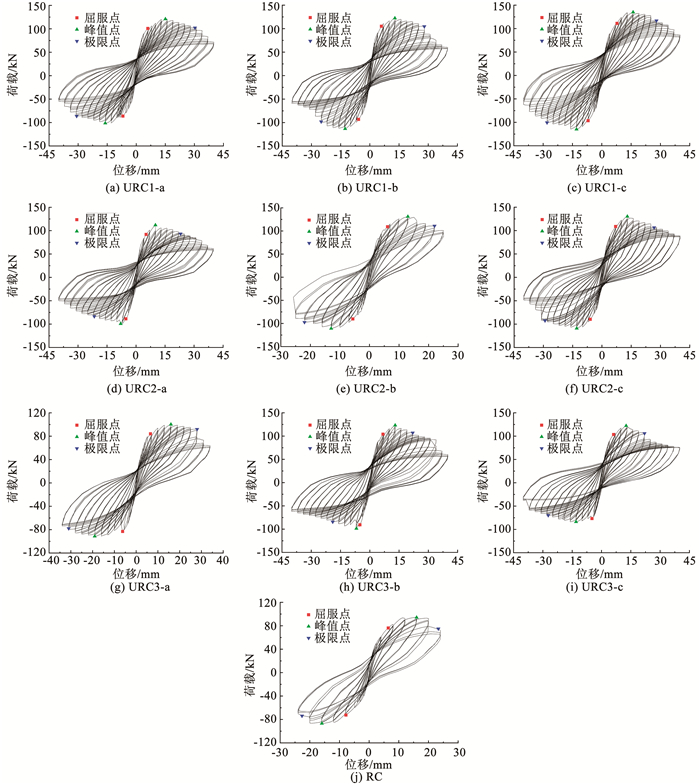
图 10为各试件在水平循环荷载作用下的荷载-位移曲线,对比不同试验参数下试件的滞回曲线可知:
|
图 10 试件滞回曲线 Fig. 10 Hysteretic curves of specimens |
1) 在整个加载过程中,各URC柱的滞回曲线存在一定差异,但总体均呈弓型,曲线的中部有明显的捏拢现象,且随着位移的增加,这种捏拢现象越明显。主要原因为URC柱身出现裂缝后,继续加载,裂缝不断变宽,在反向卸载过程中,施加的水平荷载需要让这些裂缝闭合,而在此期间产生了较大的位移,从而导致滞回曲线出现明显的捏缩现象。
2) 与RC柱相比,URC柱的峰值荷载更大。峰值荷载后,继续加载至极限位移的过程中(荷载下降到峰值荷载85%时所对应的位移),URC柱的承载力衰减相对缓慢,而RC柱的承载力下降明显,URC柱表现出更加稳定的承载性能,主要原因为UHPC模板内部钢纤维的桥接作用可以很好地抑制裂缝的发展,减轻URC柱塑性铰区混凝土的压碎程度,从而保持较好的承载力稳定性。
3) 模板拼接方式和表面处理方式对URC柱的滞回特性无明显影响,但对其承载力有一定影响。采用螺栓加角钢连接和螺栓连接的试件承载力大于环氧树脂砂浆连接的试件,且模板表面经过气泡膜印花处理和设肋处理的试件承载力大于光面处理试件。
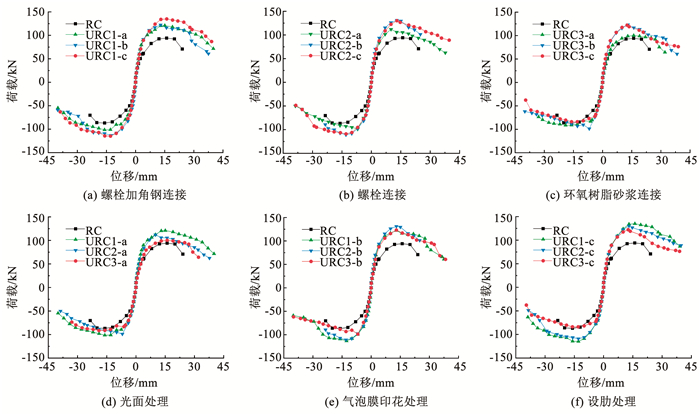
3.2 骨架曲线与特征值图 11为各试件的骨架曲线对比,表 5给出了各试件的特征点位移和荷载,其中,Δy、Py为屈服位移和屈服荷载,由能量等效法[16]计算得到;Δm、Pm为峰值位移和峰值荷载;Δu、Pu为极限位移和极限荷载,极限荷载Pu取0.85Pm;μ为试件的延性系数,μ=Δu /Δy。由图 11和表 5可知:
|
图 11 试件骨架曲线对比 Fig. 11 Skeleton curves of specimens |
| 表 5 试件各特征点荷载、位移及延性系数 Tab. 5 Loads, displacement, and ductility coefficients of specimens |
1) 相比RC柱,URC柱的屈服荷载和峰值荷载均有明显提高。其中,URC柱的屈服荷载提高了10.4%~44.5%,峰值荷载提高了6.4%~43.3%,说明使用UHPC作为免拆模板可提高RC柱的承载力。
2) 对于采用同一种拼接方式的URC柱,模板表面经过处理后的试件承载力高于未做处理的光面试件。如URC2-b和URC2-c的承载力分别比URC2-a提高了17.1%和16.3%,这主要是因为经过处理后的模板表面更加粗糙,提高了与核心混凝土的机械咬合力,进而增大了二者的界面黏结强度,使得URC柱的整体性更好,受力时能更好发挥UHPC材料强度高的优势,从而提高URC柱的承载能力。此外,从图 11还可以看出,气泡膜印花处理和设肋处理对URC柱的承载力提升效果基本相同,而气泡膜印花处理施工更加方便,实际运用时可优先考虑。
3) 对于采用同一种表面处理方式的URC柱,使用螺栓加角钢连接的URC柱承载力相对较高,如试件URC1-a的承载力分别比URC2-a和URC3-a提高了5.3%和20.7%,主要原因为URC柱在承受水平往复荷载作用时,模板拼接位置是一个薄弱点,容易发生破坏,从而影响URC柱的整体性,使其承载力降低。而对于采用螺栓加角钢连接的URC柱,由于在柱的四个角部位置设有角钢,因此,与另外两种拼接方式相比,单块UHPC模板之间的连接更牢固,在受到外力作用时能更好保证URC柱的整体性,同时角钢还能发挥纵筋的作用,因此,采用螺栓加角钢连接的URC柱承载力更高。
4) 由表 5可知,与RC柱相比,URC柱的屈服位移和峰值位移都有所降低,屈服位移降低了约15.8%,峰值位移降低了约21.4%。其主要原因为在加载过程中发现URC柱与RC柱的开裂位移基本相同,而URC柱的开裂荷载却明显高于RC柱,这使得URC柱开裂后内部纵筋很快就达到了屈服,从而导致其屈服位移和峰值位移都有所提前,柱的变形能力有所降低。然而,尽管URC柱的屈服位移和峰值位移有所降低,但URC柱的整体延性却有明显的提高,其延性较RC柱提高了11.4%~48.7%,且满足抗震设计要求的3.0~5.0[17],说明使用UHPC作免拆模板的钢筋混凝土柱具有足够的延性能力。
3.3 刚度退化结构的刚度指结构在荷载作用下抵抗变形的能力。本文采用割线刚度来表征试件的刚度退化[18],计算式为
| $ K_i=\frac{\left|+F_i\right|+\left|-F_i\right|}{\left|+X_i\right|+\left|-X_i\right|} $ | (1) |
式中:Ki为第i次循环时的割线刚度,+Fi、-Fi为第i次循环时正、反向峰值点的荷载,+Xi、-Xi为第i次循环时正、反向峰值点的位移。
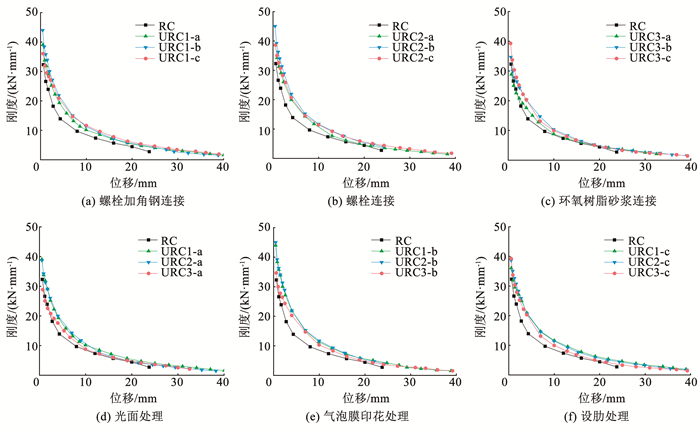
图 12为各试件的刚度退化曲线对比,可知:
|
图 12 刚度退化曲线对比 Fig. 12 Comparison of stiffness degradation curves |
1) 整体来看,URC柱的初始刚度大于RC柱,且随着位移的增加,RC柱的刚度退化速度更快。原因在于RC柱混凝土开裂后继续加载的过程中混凝土损伤更严重,部分混凝土被压碎剥落,使得其刚度降低明显,而URC柱由于UHPC模板的存在,对核心混凝土起到了一个保护作用,可有效减轻核心混凝土的破坏程度,此外,UHPC中钢纤维的桥接作用使得UHPC模板混凝土开裂后不会发生大面积的剥落,混凝土可继续发挥作用,因此,URC柱的刚度退化速度相对较慢。
2) 当模板拼接方式相同时,模板表面经过处理的URC柱初始刚度基本都大于光面模板URC柱,且随着位移的增加,光面模板URC柱的刚度退化更快,说明对模板表面进行粗糙处理,提高结合面的黏结强度可以延缓URC柱的刚度退化。
3) 当模板表面处理方式相同时,对比不同模板拼接方式的URC柱可知,采用环氧树脂砂浆连接的URC柱刚度退化更快,而采用螺栓连接和螺栓加角钢连接的URC柱刚度退化速率基本相同,说明采用环氧树脂砂浆连接的URC柱拼接效果相对较差。
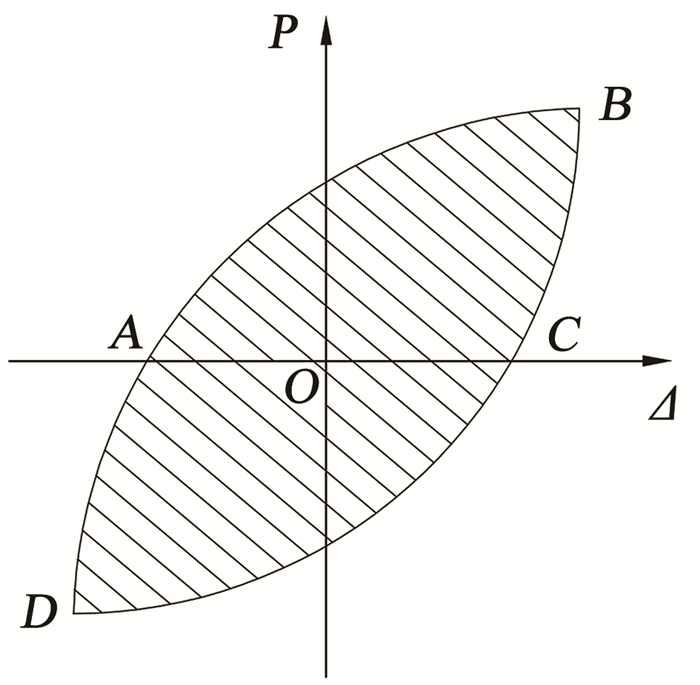
3.4 耗能能力试件的耗能能力,可以用滞回曲线所围成的面积来衡量(图 13)。本文采用每一级滞回环包围的面积相加得到的累积耗能来评估试件的耗能能力,每级滞回环的耗能能力计算式为
|
图 13 滞回耗能计算 Fig. 13 Energy consumption calculation |
| $ E=S_{A B C}+S_{A D C} $ | (2) |
式中SABC为曲线AB和BC与水平轴包围的面积,SADC为曲线AD和DC与水平轴包围的面积。
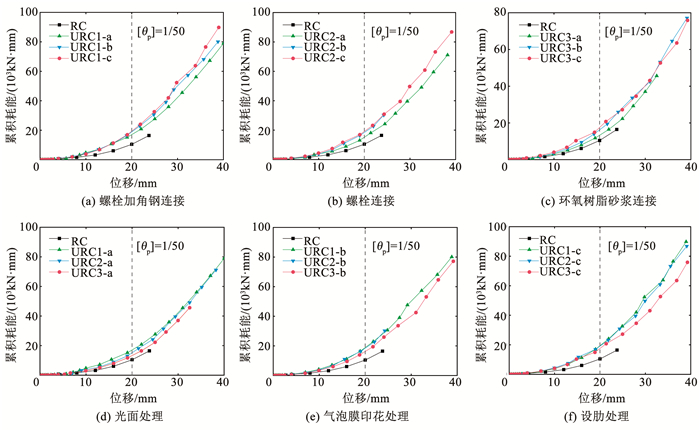
将试件每级滞回环的面积进行累加,得到了试件的累积耗能与水平位移的关系曲线(图 14)。由于试件URC2-b因模板提前剥离导致加载位移只有25 mm,因此,引入了弹塑性层间位移角限值[θp]=1/50[19]来更好地对比分析URC柱的累积耗能能力,由图 14可知:
|
图 14 累积耗能对比 Fig. 14 Comparison of cumulative energy consumption |
1) 加载初期,URC柱与RC柱的累积耗能基本相同,随着位移增加,两者之间的累积耗能差别逐渐增大,当加载至弹塑性层间位移角限值[θp]=1/50时,URC柱的累积耗能比RC柱提高了27.7%~85.3%。
2) 当模板拼接方式相同时,模板表面经过处理的URC柱在[θp]=1/50时的累积耗能基本相同,且大于光面处理的试件,说明对模板表面进行粗糙处理可以提高URC柱的累积耗能能力。
3) 当模板表面处理方式相同时,采用螺栓加角钢连接和螺栓连接的试件在[θp]=1/50时的累积耗能基本相同,且大于采用环氧树脂砂浆连接的试件,说明可靠的模板拼接方式是提高URC柱耗能能力的重要因素。
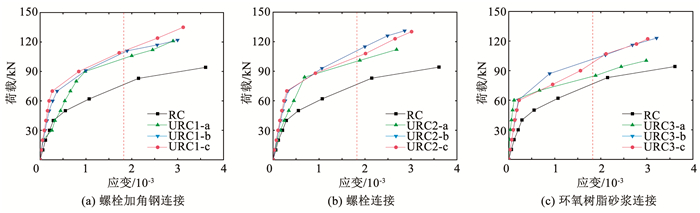
3.5 钢筋应变图 15给出了试件加载至峰值荷载推方向纵筋应变随荷载变化的关系曲线。可以看出,在试件加载至峰值荷载的过程中,各试件的纵筋应变规律具有一定的相似性。从加载开始至试件开裂期间,纵筋应变增长速率相对较慢,试件开裂后,拉力主要由纵筋承担,因此,纵筋应变开始快速增加,当试件达到峰值荷载时,纵筋完全屈服。
|
图 15 纵筋应变对比 Fig. 15 Comparison of longitudinal reinforcement strain |
从图 15还可看出,峰值荷载时,URC柱的纵筋应变小于RC柱的纵筋应变,相差范围为12.5%~34.4%,说明UHPC模板可以限制URC柱纵筋的变形能力。当模板拼接方式相同时,不同表面处理方式的URC柱在峰值荷载时的纵筋应变值有一定差异,但总体区别不大,其中,模板表面光面处理的URC柱纵筋应变最小,而气泡膜印花处理和设肋处理的URC柱纵筋应变基本相同。
4 偏压承载力计算为进一步推进UHPC免拆模板的应用,本文基于平截面假定,提出了UHPC免拆模板RC柱的正截面偏压承载力计算式,并结合试验数据对计算结果进行了验证。
4.1 基本假定1) 峰值荷载前,UHPC模板与核心混凝土之间不存在界面滑移,URC柱满足平截面假定,即整个截面应变按线性分布。
2) 峰值荷载前,UHPC模板与核心混凝土变形协调,可将两部分承载力叠加计算。
3) 不考虑钢筋、角钢与混凝土之间的滑移。
4) 截面受拉区的拉力由UHPC、受拉钢筋、受拉角钢承担,不考虑普通混凝土的抗拉作用。
4.2 偏压承载力分析以螺栓加角钢连接的URC柱为例,对其偏压承载力的计算过程进行分析,其他两种连接方式的URC柱承载力计算过程类似。
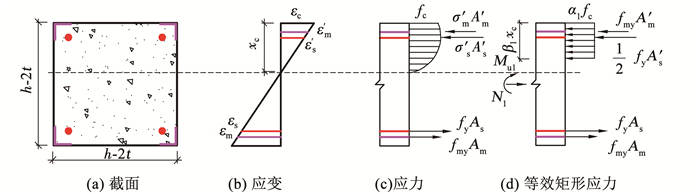
4.2.1 核心混凝土截面应变、应力分布核心混凝土截面简化模型及尺寸见图 16(a),其截面应变、应力分布见图 16(b)、(c)。当试件达到峰值荷载时,根据试验结果可知受拉侧纵筋和角钢已经屈服,受压侧角钢已经屈服,而受压侧纵筋应变约为屈服应变的一半。此外,为简化计算,将受压区混凝土的应力曲线图形等效为相应的矩形应力图形,并保持受压区合力点位置和大小不变,图 16(d)为简化后的应力分布,其中,α1、β1为核心混凝土等效矩形应力系数,其取值按照规范[20]选择。
|
图 16 核心混凝土截面应变、应力分布 Fig. 16 Strain and stress distributions for core concrete section |
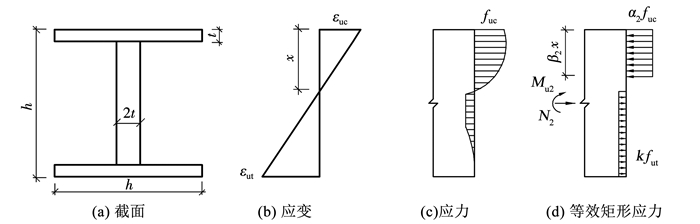
如图 17(a)所示,将UHPC模板简化为工字型截面,其截面应变、应力分布见图 17(b)、(c),为便于计算,将UHPC模板截面受拉区和受压区应力分布图形等效为矩形应力图形(图 17(d)),并保持合力点位置和大小不变。图 17中,k为UHPC模板受拉区应力折减系数,其主要由截面高度和钢纤维长度决定,根据文献[21]取k=0.8;α2、β2为UHPC等效矩形应力系数,根据文献[22]取α2=0.878,β2=0.74。
|
图 17 UHPC模板截面应变、应力分布 Fig. 17 Strain and stressdistributions for UHPC formwork section |
基于4.1节的基本假定,URC柱的截面内力可以由UHPC模板截面内力和核心混凝土截面内力叠加所得,因此,结合图 16和图 17,根据受力平衡可得:
| $ \begin{gathered} N+f_{\mathrm{y}} A_{\mathrm{s}}+f_{\mathrm{my}} A_{\mathrm{m}}+2 k f_{\mathrm{ut}} t(h-x)+k f_{\mathrm{ut}}(h-2 t) t= \\ \alpha_1 f_{\mathrm{c}}(h-2 t) \beta_1 x_{\mathrm{c}}+\frac{1}{2} f_{\mathrm{y}} A_{\mathrm{s}}^{\prime}+f_{\mathrm{my}} A_{\mathrm{m}}^{\prime}+ \\ \alpha_2 f_{\mathrm{uc}}(h-2 t) t+2 \alpha_2 f_{\mathrm{uc}} t \beta_2 x \end{gathered} $ | (3) |
| $ x=x_{\mathrm{c}}+t $ | (4) |
式中:N为试验中施加的竖向轴压力,fy为钢筋的屈服强度,As为受拉侧钢筋面积之和,fmy为角钢屈服强度,Am为受拉侧角钢面积之和,fut为UHPC抗拉强度,t为UHPC模板厚度,h为试件截面高度,x为等效工字型模板截面受压区高度,fc为核心混凝土抗压强度,xc为核心混凝土截面受压区高度,A′s为受压侧钢筋面积之和,A′m为受压侧角钢面积之和,fuc为UHPC抗压强度。
根据式(3)、(4),计算出URC柱截面受压区高度后,对截面形心轴取矩,可以得到URC柱的正截面偏压承载力计算式:
| $ \begin{aligned} M_{\mathrm{u}}= & \alpha_1 f_{\mathrm{c}}(h-2 t) \beta_1(x-t)\left[\frac{h}{2}-t-\frac{\beta_1(x-t)}{2}\right]+ \\ & \frac{1}{2} \alpha_2 f_{\mathrm{uc}}(h-2 t) t(h-t)+\alpha_2 f_{\mathrm{uc}} t \beta_2 x\left(t-\beta_2 x\right)+ \\ & \frac{1}{2} f_{\mathrm{y}}^{\prime} A_{\mathrm{s}}^{\prime}\left(\frac{h}{2}-a_{\mathrm{s}}^{\prime}\right)+f_{\mathrm{my}} A_{\mathrm{m}}^{\prime}\left(\frac{h}{2}-a_{\mathrm{m}}^{\prime}\right)+f_{\mathrm{y}} A_{\mathrm{s}}\left(\frac{h}{2}-a_{\mathrm{s}}\right)+ \\ & f_{\mathrm{my}} A_{\mathrm{m}}\left(\frac{h}{2}-a_{\mathrm{m}}\right)+\frac{1}{2} k f_{\mathrm{ut}}(h-2 t) t(h-t)+ \\ & \frac{1}{2} k f_{\mathrm{ut}} t h^2-\frac{1}{2} k f_{\mathrm{ut}} t\left(\frac{h}{2}-x\right)^2 \end{aligned} $ | (5) |
式中:a′s、a′m分别为受压侧纵筋、角钢合力点至URC柱截面边缘的距离,as、am分别为受拉侧纵筋、角钢合力点至URC柱截面边缘的距离。
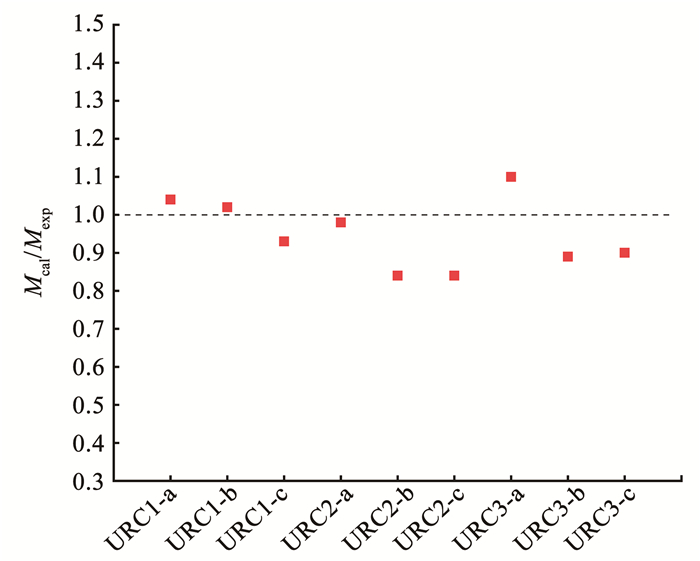
4.4 计算结果与试验结果对比根据式(5)计算得到的URC柱承载力见表 6,图 18给出了计算值与试验值的对比。由表 6和图 18可知,计算值与试验值的最大偏差为16%,对于模板表面经过处理的URC柱,采用式(5)计算的结果较为保守,低估了此类试件的承载能力。但总体来看,本文所提公式的计算结果与试验结果吻合较好,计算值与试验值的比值均值为0.95,变异系数为0.09。说明本文提出的UHPC免拆模板RC柱偏压承载力计算方法精度较好,可为理论设计提供参考。
| 表 6 URC柱承载力对比 Tab. 6 Comparison of bearing capacity of URC columns |
|
图 18 计算值与试验值对比 Fig. 18 Comparison of calculated and test results |
本文通过拟静力试验研究了URC柱的抗震性能,探讨了模板拼接方式和表面处理方式对URC柱破坏形态、承载力、延性、刚度退化和累积耗能能力等影响,同时提出了URC柱的偏压承载力计算式,结论如下:
1) 所有URC柱均发生了弯曲破坏,且UHPC模板拼接方式对URC柱破坏特征影响显著。峰值荷载前,各URC柱的模板连接处无明显破坏,均表现出良好的整体性;峰值荷载后,继续加载,采用螺栓连接和环氧树脂砂浆连接的URC柱相继在模板连接处发生了破坏,导致试件承载力出现突降。而采用螺栓加角钢连接的URC柱直到加载结束,其模板连接处依旧相对完整,说明采用螺栓加角钢这种拼接方式更加可靠。
2) 采用UHPC材料制成免拆模板用于钢筋混凝土柱可显著提升柱的抗震性能。与RC柱相比,URC柱的承载能力提高了6.4%~43.3%,延性提高了11.4%~48.7%,耗能能力提高了27.7%~85.3%。
3) UHPC模板表面处理方式和拼接方式对URC柱的承载力、刚度退化和累积耗能影响显著。相比于光面模板URC柱,模板表面经过气泡膜印花处理和设肋处理的URC柱承载能力和耗能能力显著提高,刚度退化也更缓慢。三种拼接方式中,螺栓加角钢连接和螺栓连接的URC柱承载力和耗能能力基本相同,且均优于环氧树脂砂浆连接的试件,综合试件的破坏模式、承载能力、延性等考虑,建议采用螺栓加角钢这种模板拼接方式。
4) 基于平截面假定提出了URC柱偏压承载力计算式,计算结果与试验结果吻合较好,可为实际应用提供参考。
| [1] |
李庆华, 黄博滔, 周宝民, 等. 超高韧性水泥基复合材料单轴压缩疲劳性能研究[J]. 建筑结构学报, 2016, 37(1): 141. LI Qinghua, HUANG Botao, ZHOU Baomin, et al. Study on compression fatigue properties of ultra high toughness cementitious composites[J]. Journal of Building Structures, 2016, 37(1): 141. DOI:10.14006/j.jzjgxb.2016.01.015 |
| [2] |
YOO D Y, YOON Y S. Structural performance of ultra-high-performance concrete beams with different steel fibers[J]. Engineering Structures, 2015, 102: 418. DOI:10.1016/j.engstruct.2015.08.029 |
| [3] |
梁兴文, 汪萍, 徐明雪, 等. 免拆超高性能混凝土模板钢筋混凝土梁的受力性能及短期刚度研究[J]. 建筑结构学报, 2020, 41(7): 161. LIANG Xingwen, WANG Ping, XU Mingxue, et al. Mechanical behavior and immediate stiffness of RC beams with UHPC permanent formwork[J]. Journal of Building Structures, 2020, 41(7): 161. DOI:10.14006/j.jzjgxb.2018.0204 |
| [4] |
梁兴文, 汪萍, 徐明雪, 等. 免拆UHPC模板RC梁受弯性能试验及承载力分析[J]. 工程力学, 2019, 36(9): 105. LIANG Xingwen, WANG Ping, XU Mingxue, et al. Flexural behavior and capacity analysis of RC beams with permanent UHPC formwork[J]. Engineering Mechanics, 2019, 36(9): 105. |
| [5] |
夏洋. 预制UHPC永久模板-GFRP筋混凝土组合梁抗弯性能研究[D]. 郑州: 郑州大学, 2020: 50 XIA Yang. Research on flexural performance of hybrid beams composed of prefabricated UHPC permanent formwork and cast-in-situ concrete core reinforced by GFRP bars[D]. Zhengzhou: Zhengzhou University, 2020: 50 |
| [6] |
韩京城. RUHPC-RC复合梁受弯机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2019: 46 HAN Jingcheng. Research on flexural mechanism of RUHPC-RC composite beam[D]. Harbin: Harbin Institute of Technology, 2019: 46 |
| [7] |
张锐, 胡棚, 李晰, 等. U形UHPC永久模板RC无腹筋组合梁抗剪性能试验[J]. 中国公路学报, 2021, 34(8): 154. ZHANG Rui, HU Peng, LI Xi, et al. Shear behavior of reinforced concrete composite beams without stirrups using U-shape UHPC permanent formwork[J]. China Journal of Highway and Transport, 2021, 34(8): 154. DOI:10.19721/j.cnki.1001-7372.2021.08.012 |
| [8] |
杨医博, 杨凯越, 吴志浩, 等. 配筋超高性能混凝土用作免拆模板对短柱力学性能影响的实验研究[J]. 材料导报, 2017, 31(23): 123. YANG Yibo, YANG Kaiyue, WU Zhihao, et al. An experimental study on the influence of reinforced ultra-high performance concrete permanent template to short column's mechanical property[J]. Material Reports, 2017, 31(23): 123. |
| [9] |
单波, 王志鸿, 肖岩, 等. RPC管-海水海砂混凝土组合柱抗压性能[J]. 湖南大学学报(自然科学版), 2020, 47(9): 110. SHAN Bo, WANG Zhihong, XIAO Yan, et al. Compression performance of seawater and sea sand concrete filled RPC tube composite columns under axial load[J]. Journal of Hunan University (Natural Sciences), 2020, 47(9): 110. DOI:10.16339/j.cnki.hdxbzkb.2020.09.012 |
| [10] |
单波, 罗校炳, 肖岩, 等. 大尺寸RPC管-混凝土组合短柱轴压性能研究[J]. 湘潭大学学报(自然科学版), 2019, 41(2): 92. SHAN Bo, LUO Xiaobing, XIAO Yan, et al. Experimental research on compressive performance of large-scale concrete-filled RPC tube columns[J]. Journal of Xiangtan University (Natural Sciences), 2019, 41(2): 92. DOI:10.13715/j.cnki.nsjxu.2019.02.011 |
| [11] |
王钧, 王志彬, 李论. 配有钢纤维RPC免拆柱模的钢筋混凝土短柱轴压力学性能[J]. 建筑科学与工程学报, 2016, 33(2): 104. WANG Jun, WANG Zhibin, LI Lun. Mechanical behavior of reinforced concrete short columns with steel fiber RPC column-permanent template subjected to axial compression[J]. Journal of Architecture and Civil Engineering, 2016, 33(2): 104. |
| [12] |
LIN Yu, CHEN Zixuan, GUAN Dongzhi, et al. Experimental study on interior precast concrete beam-column connections with UHPC core shells[J]. Structures, 2021, 32: 1112. DOI:10.1016/j.istruc.2021.03.087 |
| [13] |
梁兴文, 史纪从, 于婧, 等. 免拆超高性能混凝土模板钢筋混凝土柱抗震性能研究[J]. 地震工程学报, 2020, 42(3): 587. LIANG Xingwen, SHI Jicong, YU Jing, et al. Seismic behavior of reinforced concrete columns with permanent template of ultra-high-performance concrete[J]. China Earthquake Engineering Journal, 2020, 42(3): 587. |
| [14] |
普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2002 Standard for method of mechanical properties on ordinary concrete: GB/T 50081—2002[S]. Beijing: China Architecture & Building Press, 2002 |
| [15] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010 Metallic material—tensile testing—Part 1: method of test at room temperature: GB/T 228.1—2010[S]. Beijing: China Standard Press, 2010 |
| [16] |
MAHIN S A, BERTERO V V. Problems in establishing and predicting ductility in aseismic design[C]//Proceedings of the International Symposium on Earthquake Structural Engineering. Saint Louis: [s. n. ], 1976: 613
|
| [17] |
侯利军, 徐冉, 张秀芳, 等. 纤维网-超高韧性水泥基复合材料加固钢筋混凝土柱抗震性能研究[J]. 建筑结构学报, 2021, 13(5): 9. HOU Lijun, XU Ran, ZHANG Xiufang, et al. Study on seismic behavior of reinforced columns strengthened by textile-UHTCC[J]. Journal of Building Structures, 2021, 13(5): 9. DOI:10.14006/j.jzjgxb.2021.0513 |
| [18] |
建筑抗震试验规程: JGJ/T 101—2015[S]. 北京: 中国建筑工业出版社, 2015 Specification for seismic test of building: JGJ/T 101—2015[S]. Beijing: China Architecture & Building Press, 2015 |
| [19] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of building: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2015 |
| [20] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [21] |
彭飞, 方志. 钢筋UHPC梁正截面抗弯承载力计算方法[J]. 土木工程学报, 2021, 54(3): 90. PENG Fei, FANG Zhi. Calculation approach for flexural capacity of reinforced UHPC beams[J]. China Civil Engineering Journal, 2021, 54(3): 90. DOI:10.15951/j.tmgcxb.2021.03.008 |
| [22] |
徐明雪, 梁兴文, 汪萍, 等. 超高性能混凝土梁正截面受弯承载力理论研究[J]. 工程力学, 2019, 36(8): 76. XU Mingxue, LIANG Xingwen, WANG Ping, et al. Theoretical investigation on normal section flexural capacity of UHPC beams[J]. Engineering Mechanics, 2019, 36(8): 76. |
 2024, Vol. 56
2024, Vol. 56



 16
16