2. 中国地震局地震工程与工程振动重点试验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration (lnstitute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
双层钢管混凝土柱是指在钢管混凝土中内置圆钢管,浇筑混凝土后形成的一种钢管混凝土组合柱,具有承载力高、塑性和延性好等优势[1],常用于风力发电机支架、输电塔杆、桥墩等结构。目前的大量研究成果多集中在钢管混凝土柱的轴心受压、偏心受压、压弯等简单受力方面,而受扭和压扭荷载下钢管混凝土柱的力学性能研究较少。
徐积善等[2]对不同截面形式的钢管混凝土柱进行了非比例加载的双轴压扭试验研究,给出了简化理论计算公式; 韩林海等[3]进行了4个圆钢管混凝土柱的抗扭试验研究和有限分析,给出了钢管混凝土抗扭承载力指标的定义方法及其简化公式; 史艳莉等[4]对内置十字型钢骨钢管混凝土柱进行了有限元分析,分析了钢管强度、含钢率、长细比等因素对构件抗扭承载力的影响; 聂建国等[5]以几何方程、材料本构和平衡方程为基础,建立了钢管混凝土柱在轴力-扭矩复合作用下全过程分析的分层筒理论模型,弥补了现有关于钢管混凝土柱抗扭性能分析理论的缺陷; 黄宏等[6]对6根圆中空夹层钢管混凝土柱和一根双层空钢管柱进行了抗扭试验研究,研究表明钢管和混凝土协同工作性能良好; 聂影等[7]对内嵌H型钢的钢管混凝土柱进行了压扭试验,分析了扭转滞回性能,研究表明内嵌H型钢的钢管混凝土柱具有良好的扭转耗能能力。
上述研究,多以理论分析和数值模拟为主,试验研究尚少,且研究目标多为短柱,但随着高耸建筑和大跨建筑的发展,钢管混凝土长柱[8](λ>16,λ=4L/D)的应用也越来越多。基于此,本文采用课题组研制的Stewart三向六自由度加载装置,进行了两个圆钢管混凝土长柱和两个双层圆钢管混凝土长柱在纯扭、压扭作用下的拟静力试验研究,对比分析了圆钢管混凝土长柱的承载力、刚度、扭转变形能力、滞回特性和损伤演化规律等。建立了圆钢管混凝土长柱有限元模型,对压扭工况下的双层圆钢管混凝土长柱进行了考虑结构非线性的弹塑性分析,研究了轴压比、内层圆钢管径厚比等因素对双层圆钢管混凝土长柱压扭性能的影响。
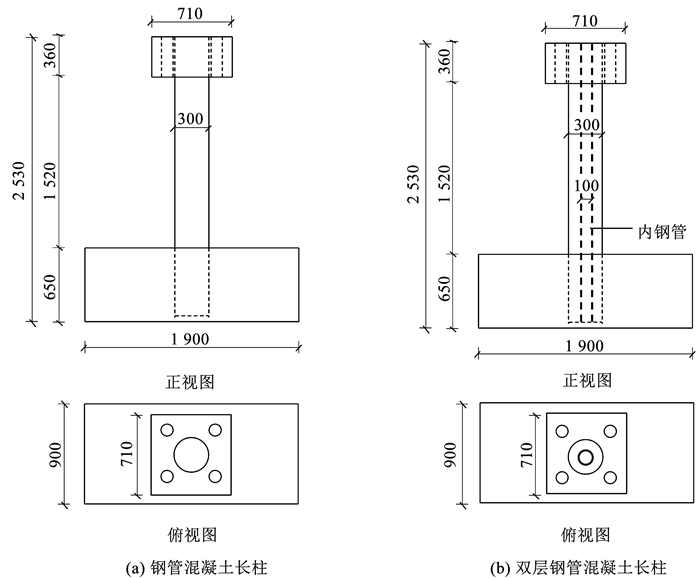
1 试验概况设计了两个圆钢管混凝土长柱和两个双层圆钢管混凝土长柱试件,试件截面形式和几何尺寸见图 1,具体参数及编号见表 2,其中试件编号中的1、2分别表示钢管混凝土长柱和双层圆钢管混凝土长柱两种截面形式,T、NT分别表示纯扭、压扭试件。钢管钢材等级为Q345B,实测力学性能指标见表 1;混凝土强度等级为C40,实测立方体抗压强度为42.6 MPa,轴心抗压强度32.3 MPa,弹性模量3.3×104 MPa。
|
图 1 试件几何尺寸(mm) Fig. 1 Specific size of specimens (mm) |
| 表 1 钢管材性试验结果 Tab. 1 Steel material properties |
| 表 2 试件参数 Tab. 2 Parameters of specimens |
Stewart三向六自由度加载装置[10]的上平台固定,下平台具有沿x、y、z方向平动和绕x、y、z方向转动等6个方向的自由度,加载平台通过侧挂框与试验室反力墙连接。该装置具有刚度大、承载力高、位置误差不累计等特点,可以在空间六维实现运动和力的输出,能够准确模拟构件的实际受力状态,已在航空、航天、海底作业、地下开采、制造装配等行业的运动模拟领域广泛应用。
本文试验的试件安装见图 2,试件顶部加载头通过锚固螺栓与下平台连接,侧限螺杆加强柱顶加载头的约束。试件与反力地板之间通过刚性底座连接,刚性底座与反力地板、试件基础与刚性底座之间均通过锚固螺栓连接。在刚性底座四周安装千斤顶,防止基础侧向滑动。

|
图 2 试件安装示意 Fig. 2 Connection between specimens and loading devices |
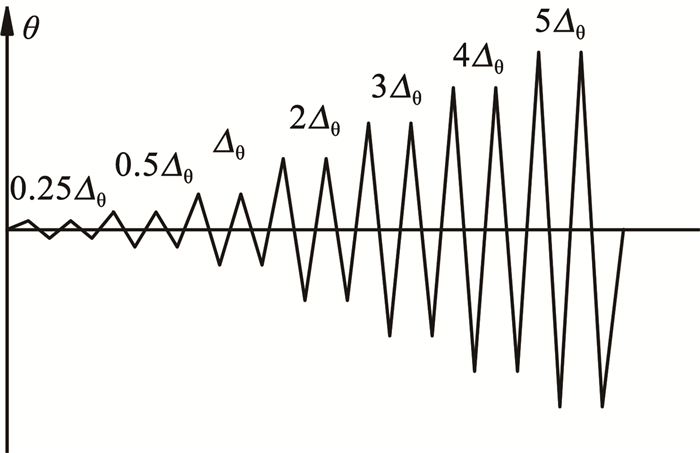
试验前先对钢管混凝土长柱扭转试验进行有限元试算,估算出钢管混凝土柱的屈服扭转角Δθ在4°左右。纯扭试验采用位移角控制加载,按照估算屈服扭转角的倍数分级加载,每级往复加载两次;压扭工况的试件先按照相应轴压比施加轴向荷载,然后再施加扭转位移角,扭转加载制度见图 3。
|
图 3 扭转试验加载制度 Fig. 3 Torsional test loading program |
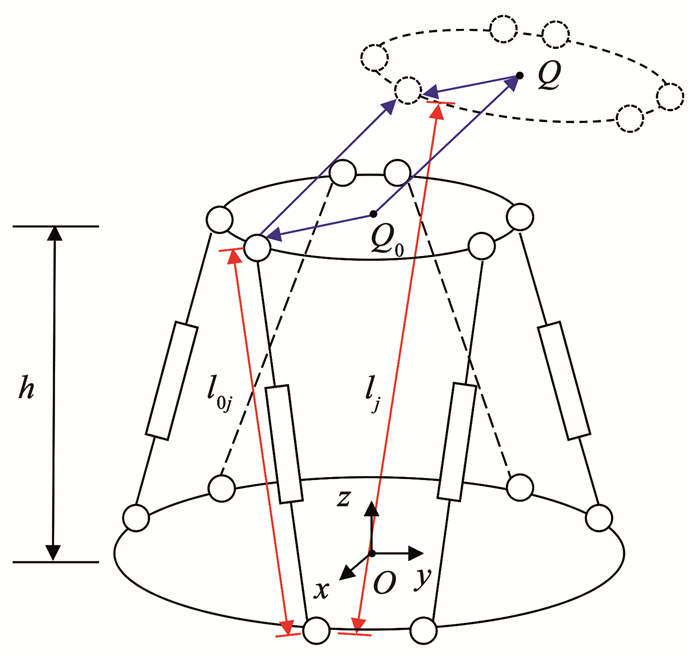
位移测量采用外环多自由度位移测量方法[11],具体测量原理见图 4,通过6个位移计从初始长度l0j到终止长度lj(j=1, …, 6)的伸长量反算测量点Q0移动到Q时,x、y、z方向的平动位移和3个方向的转角。本次试验中6个位移计的两端分别连接至基础和试件加载头的位移计支架,位移计支架两端分别与试件加载头和基础连接,可直接测量柱顶和基础之间的相对位移,避免了由于基础和加载头滑动带来的测量误差。
|
图 4 外环多自由度位移测量原理图 Fig. 4 Schematic diagram of the displacement measurement |
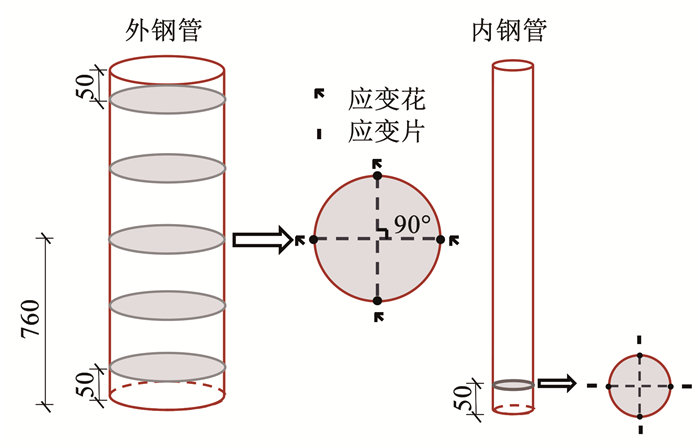
在外钢管布置应变片花,在内钢管底部布置应变片,具体位置见图 5。
|
图 5 应变测点布置(mm) Fig. 5 Arrangement of strain measurement points |
各试件的损伤发展过程见图 6。圆钢管混凝土长柱试件1T的扭转角加载至12°之前钢管壁无明显现象。当加载到扭转角至16°,反向卸载至14°时,钢管外壁撕裂,外钢管对核心混凝土的约束力减弱,核心混凝土裂缝发展迅速,反向加载至-16°时出现明显斜向扭剪裂缝,局部混凝土剥落,卸载至0°时,钢管外壁撕裂残余变形较大,见图 6(a)。

|
图 6 试件破坏过程 Fig. 6 Failure modes of specimens |
双层圆钢管混凝土长柱试件2T与普通圆钢管混凝土长柱试件1T相比,双层圆钢管混凝土长柱试件在试验过程中无明显现象,仅钢管外表面的网格发生明显的倾斜,见图 6(b);说明内层钢管提高了钢管混凝土长柱的抗扭能力。
3.1.2 压扭试验与纯扭试验相比,轴压比为0.3,扭转角加载至20°时,普通圆钢管混凝土长柱试件1NT和双层圆钢管混凝土长柱试件2NT均无明显现象,表明轴压的存一定程度上抑制了钢管拉应力的发展,提高了钢管混凝土长柱的抗扭能力,见图 6(c)和图 6(d)。
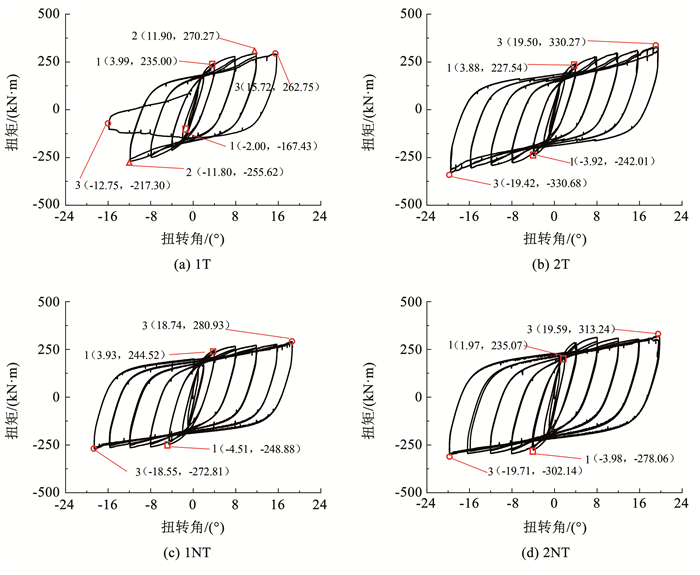
3.2 扭矩-扭转角关系扭矩-扭转角滞回曲线见图 7,曲线上的数字1、2、3分别表示等效屈服点、峰值点和极限点。等效屈服点通过最远点法[12]确定,峰值点定义为扭矩承载力最大点,极限点定义为试验结束时的最大位移点。
|
图 7 扭矩-扭转角滞回曲线 Fig. 7 Torsion moment-rotation angle hysteresis loops |
由图 7可见:1)所有的试件扭矩-扭转角曲线均表现出双折线特征。试件1NT、2T、2NT没有下降段,峰值点即为极限点;2)除了焊缝开裂的试件1T外,其余纯扭、压扭试件的滞回曲线都较饱满,纯扭试件1T、2T加载后期扭转角过大时滞回曲线轻微捏缩,卸载时的刚度近似等于初始刚度,强度和刚度的退化较少,表明其具有良好的变形能力;3)压扭试件的滞回曲线较纯扭试件饱满,且无捏缩现象,表明一定范围内轴压可提高钢管混凝土长柱的扭转耗能能力;4)双层钢管混凝土长柱中内部钢管的存在延缓了外钢管损伤,当外钢管损伤时,内部钢管进一步加强了外钢管对混凝土约束作用,截面内应力重分布,原外钢管损伤部分承担的内力由混凝土和内钢管共同承担。
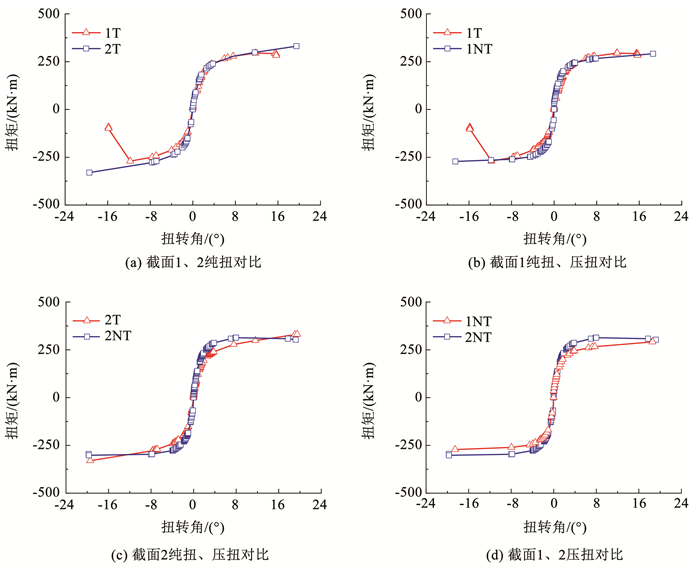
3.3 骨架曲线与刚度退化 3.3.1 骨架曲线实测扭矩-扭转角骨架曲线见图 8。由图 8可知:1)骨架曲线呈S形,由于加载设备扭转幅度的限制,骨架曲线并没有产生明显的下降段,单方向骨架曲线近似双折线;2)各试件的初始刚度比较接近,双层钢管混凝土长柱试件的承载力和屈服后刚度,均比普通钢管混凝土长柱试件大;施加轴向荷载后,钢管混凝土长柱的承载力和屈服后的刚度也有明显提升;3)双层钢管混凝土长柱试件和压扭试件的骨架曲线的水平段较长,表明内置钢管和增加轴压能够提高延性和弹塑性变形能力。
|
图 8 扭矩-扭转角骨架曲线 Fig. 8 Torsion moment-rotation angle skeleton curves |
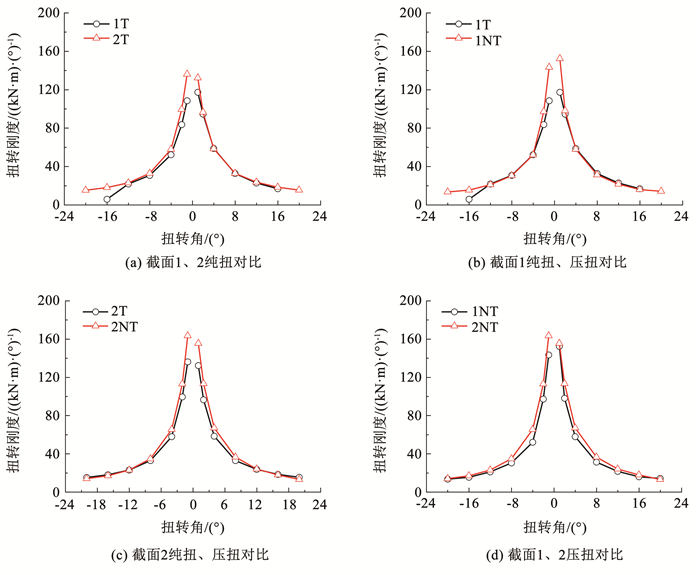
采用等效割线刚度方法计算各试件刚度,等效割线刚度为每级循环加载正负向峰值承载力绝对值之和与正负向连梁转角绝对值之和的比值,见式(1),各试件刚度退化曲线见图 9。
|
图 9 扭转刚度退化曲线 Fig. 9 Rigidity degradation versus displacement curves of specimens |
| $ K_i=\frac{\left|+P_i\right|+\left|-P_i\right|}{\left|+\theta_i\right|+\left|-\theta_i\right|} $ | (1) |
式中:+Pi和-Pi分别为第i级循环加载在正负向的峰值承载力,+θi和-θi分别为第i级循环加载正负向峰值承载所对应的扭转角。
由图 9可见:1)与普通圆钢管混凝土试件1T相比,双层圆钢管混凝土长柱试件2T初始扭转刚度提高了31%,试件2NT的初始刚度较1NT提高了8%,且双层钢管混凝土长柱2T、2NT后期刚度下降较缓慢,表明双层钢管混凝土长柱中的内层钢管对抗扭刚度有一定的贡献;2)试件1NT较1T而言,轴压的存在使得扭转刚度提高31%,试件2NT的初始扭转刚度较2T提高了19%,试件2NT的初始刚度较1NT提高了8%,屈服之后扭转刚度退化速度变慢。表明一定范围内轴压会提高钢管混凝土长柱的初始刚度,而对于后期刚度退化影响不大。
3.3.3 承载力与变形根据骨架曲线,采用最远点法[12]确定屈服扭转角,极限扭转角定义为承载力下降至峰值承载力的85%或试验终止时的扭转角度,将极限扭转角和等效屈服扭转角的比值定义为扭转延性系数。实测各试件的初始刚度、屈服扭矩、极限扭矩、屈服扭转角、极限扭转角以及扭转延性系数见表 3。表中相对值是对比件相对于标准件在各个不同指标下的比值。
| 表 3 试件关键点受力特征 Tab. 3 Mechanical characteristics of specimens |
由表 3可见:1)与钢管混凝土长柱试件1T相比,双层钢管混凝土长柱试件2T的初始刚度提高了19%,屈服扭矩提高了18%,极限扭矩提高了34%,屈服扭转角提高了3%,极限扭转角提高了26%,延性系数提升较大;2)与无轴压长柱试件1T相比,轴压比为0.3的试件1NT的初始刚度提高了31%,屈服扭矩提高了24%,极限扭矩提高了12%,屈服扭转角提高了11%,极限扭转角提高了18%,延性系数略有提升;与无轴压双层圆钢管混凝土长柱试件2T相比,轴压比为0.3的双层圆钢管混凝土长柱试件2NT的初始刚度提高了19%,屈服扭矩提高了9%,极限扭矩略有降低,屈服扭转角降低了24%,极限扭转角相差不大,延性系数大幅提升;3)与轴压比为0.3的普通圆钢管混凝土长柱试件1NT相比,轴压比为0.3的双层圆钢管混凝土长柱试件2NT的初始刚度提高了8%,屈服扭矩提高了9%,极限扭矩提高了11%,屈服扭转角降低了29%,极限扭转角提高了8%。延性系数大幅提升。
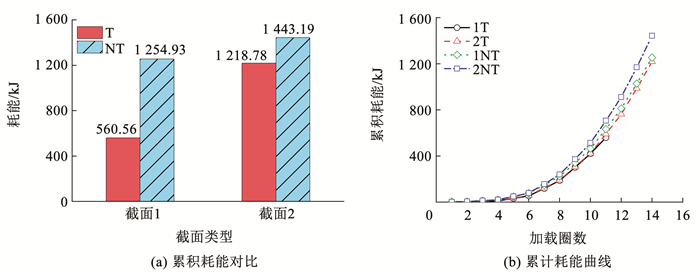
3.4 耗能能力结构的耗能能力是指结构在地震作用下发生塑性变形,吸收和耗散能量的能力。以每级循环加载的滞回曲线所包围的面积作为试件耗能能力的评价标准。各试件的扭转变形累积耗能随加载级别数的变化见图 10。
|
图 10 累积耗能 Fig. 10 Energy dissipation of specimens |
由图 10可见:1)各试件在第四级加载循坏(扭转角小于2°)前,扭转耗能与加载级数为线性关系,且各试件的耗能能力接近。第5次加载循坏(扭转角达到屈服点4°左右)时,各试件的累积耗能开始迅速增加;2)与普通圆钢管混凝土长柱试件1T相比,双层圆钢管混凝土长柱试件2T的扭转累积耗能提高了4%,表明纯扭工况下内层圆钢管对钢管混凝土长柱的耗能能力提升有限;3)与无轴压试件相比,轴压比为0.3的普通圆钢管混凝土长柱试件1NT的扭转累积耗能比无轴压普通圆钢管混凝土长柱试件1T提高了13%,轴压比为0.3的双层圆钢管混凝土长柱试件2NT的扭转累积耗能比无轴压双层圆钢管混凝土长柱试件2T提高21%,轴向荷载可显著提升圆钢管混凝土长柱的扭转耗能能力;4)轴压比均为0.3时,双层圆钢管混凝土长柱试件2NT的累积耗能比普通圆钢管混凝土长柱试件1NT提高了11%,施加轴压后,双层圆钢管混凝土长柱的扭转耗能能力较普通圆钢管混凝土长柱有一定幅度的提升。
综上,普通圆钢管混凝土长柱和双层圆钢管混凝土长柱的扭转耗能能力均较强,其中双层圆钢管混凝土长柱的扭转耗能能力优于普通圆钢管混凝土长柱;一定范围内轴向荷载可显著提高圆钢管混凝土长柱试件的扭转耗能能力。
3.5 应变分析选取各外钢管底层测点的应变进行分析。测点的剪应变根据应变花测量的数据,计算方法为
| $ \gamma=\varepsilon_{\mathrm{a}}+\varepsilon_{\mathrm{b}}-2 \varepsilon_{\mathrm{c}} $ | (2) |
式中:εa为测点的水平环向正应变,εb为测点的竖向正应变,εc为测点的斜向45°正应变。
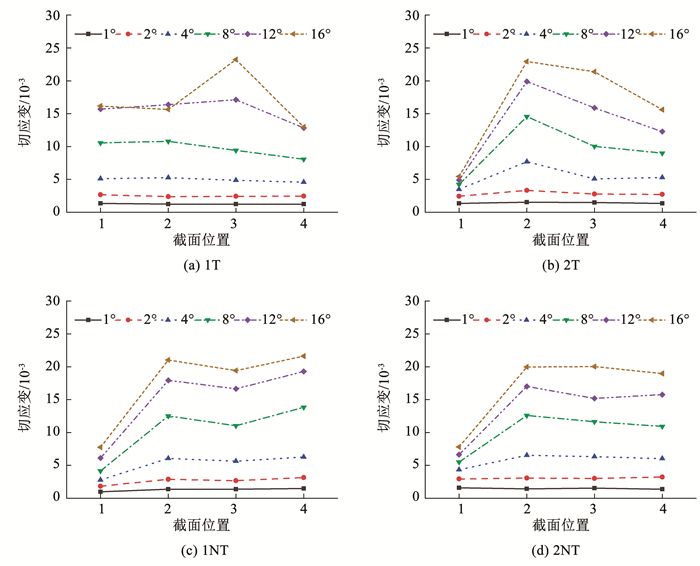
外钢管底层峰值剪应变在不同加载级下的分布见图 11。图中横坐标1至4分别表示外钢管圆周四等分点的位置。本文所有钢管混凝土试件的外钢管均为直缝焊接钢管,其中1号位置为钢管焊缝所在位置,钢材在焊接后内部存在残余应力,且塑性和韧性降低。故试件2T、1NT、2NT在1号位置的剪应变略低于同一截面其他位置的剪应变。试件1T钢管焊缝位置在4号位置,故试件1T的4号位置加载后期剪应变偏小。
|
图 11 峰值应变分布 Fig. 11 Peak strain distribution |
由图 11可见:1)各试件在加载达到屈服之前剪应变分布均匀,屈服之后由于截面焊缝的存在以及钢管本身的不均匀性和内部混凝土缺陷等原因导致同一截面的剪应变分布有所差别;2)普通圆钢管混凝土长柱试件1T扭转角加载至8°之前截面各位置剪应变相差不大,表明扭转角较小时截面受扭均匀;3)试件1T中4号位置、试件2T、1NT、2NT中1号位置为外钢管焊缝所在位置,各级加载的峰值应变均略小于截面平均剪应变水平;4)双层圆钢管混凝土长柱试件,内部钢管直径较小,对截面抗扭的贡献不大,致使剪应变变化不明显。
4 有限元分析 4.1 有限元模型采用有限元软件Abaqus建立了双层圆钢管混凝土长柱试件的弹塑性有限元模型。混凝土和外钢管采用实体单元,内部钢管采用壳单元。钢管与混凝土的法向接触采用硬接触,切向力传递时采用库仑摩擦模型;内部圆钢管在混凝土中定义为内置区域。将试件加载头表面耦合到参考点rp1,在rp1点施加轴向荷载和扭转位移。
4.1.1 材料参数钢管采用弹塑性本构,依据材性试验实测屈服强度以及应力-应变关系。韩林海[1]研究了大量国内外钢管混凝土轴压试验后,对试验结果进行分析整理后基于约束效应系数ξ提出了韩林海本构。
| $ \xi=\left(A_{\mathrm{s}} f_{\mathrm{y}}\right) /\left(A_{\mathrm{c}} f_{\mathrm{c}}\right) $ | (3) |
式中:As、Ac分别为钢管面积和核心混凝土面积,fc、fy分别为核心混凝土抗压强度和钢材屈服强度。
刘威[13]对韩林海本构进行修正后,提出了下列本构关系:
| $ y=\left\{\begin{array}{cc} 2 x-x^2, & x \leqslant 1 \\ \frac{x}{\beta(x-1)^\eta+x}, & x>1 \end{array}\right. $ | (4) |
式中:x=ε/ε0;y=σ/σ0;σ0=fc(N/mm2);ε0=εc+0.000 8ξ0.2;εc=(1 300+12.5fc)×10-6(N/mm2);
| $ \eta=\left\{\begin{array}{cc} 2, & \text { 圆钢管混凝土 } \\ 1.6+1.5 / x, & \text { 方钢管混凝土 } \end{array}\right. $ |
| $ \beta= \begin{cases}\left(2.36 \times 10^{-5}\right)^{\left[0.25+(\xi-0.5)^7\right]} \times f_{\mathrm{c}}^{0.5} \times 0.5 \geqslant 0.12, & \text { 圆钢管 } \\ \frac{f_{\mathrm{c}}^{0.1}}{1.2 \sqrt{1+\xi}}, & \text { 方钢管 }\end{cases} $ |
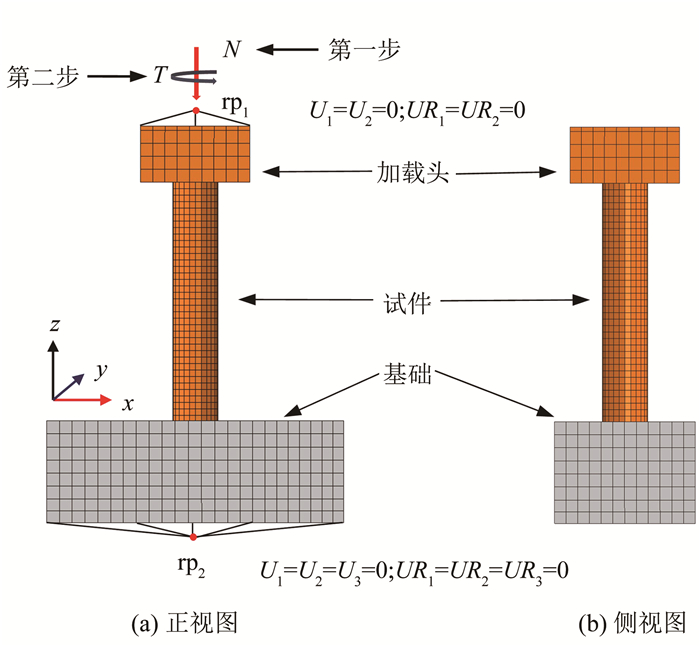
在柱端参考点rp1输入扭转位移进行加载,并约束x、y方向的平动和转动自由度,模型底部为固结。纯扭工况下在参考点rp1输入转角,压扭工况分两个荷载步,首先在参考点rp1施加竖向轴力,然后施加扭转位移,模型示意见图 12。
|
图 12 有限元模型示意 Fig. 12 Numerical models |
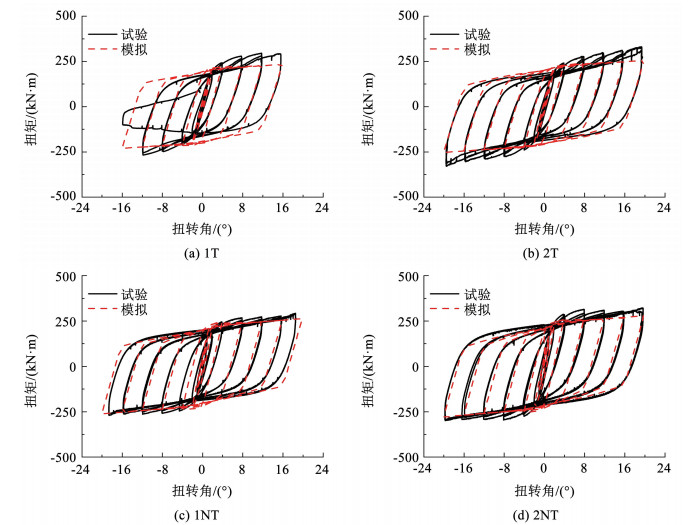
采用与试验相同的加载制度,试验与数值模拟结果对比见图 13。由图 13可见:1)普通圆钢管混凝土长柱试件1T的数值模拟与试验结果差异较大,这是由于该试件的破坏发生在正向16°,外钢管焊缝撕裂严重导致承载力突降;2)试件1NT、2T、2NT在整个加载过程中钢管焊缝未开裂,钢管整体工作性能良好,数值模拟结果与试验实测结果吻合较好,表明本文采用的建模方式可以较好地模拟钢管混凝土构件扭转试验中的扭矩-扭转角关系。
|
图 13 有限元模拟验证 Fig. 13 Validation of finite element model |
采用有限元模型,对双层圆钢管混凝土长柱进行了参数分析,研究了内钢管径厚比和轴压比对抗扭性能的影响。
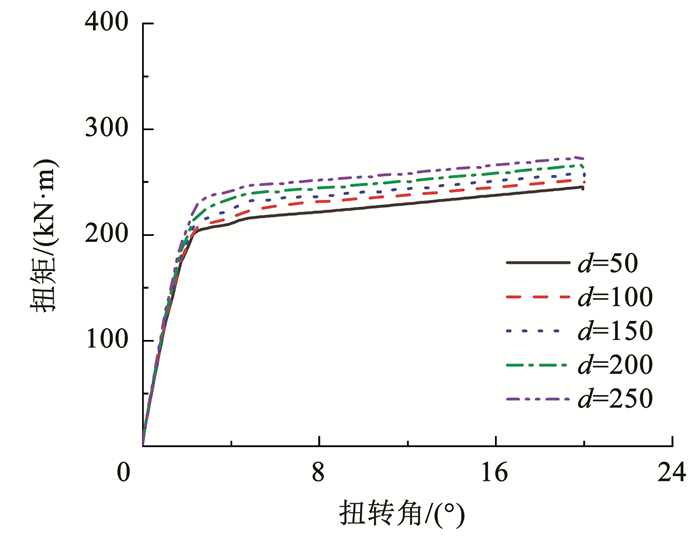
4.3.1 内钢管径厚比影响试验结果表明双层圆钢管混凝土长柱的抗扭刚度高于普通圆钢管混凝土长柱,内层钢管对承载力的影响并不明显。考虑是由于内钢管径厚比较小,内钢管对整体扭转承载力的贡献较小。因此,通过有限元分析了内层钢管面积一定,直径分别为50、100、150、200、250 mm,对应的径厚比分别为8、35、80、144、220时,双层圆钢管混凝土长柱试件在纯扭和压扭工况下的承载力,分析结果见图 14。
|
图 14 内钢管径厚比的影响 Fig. 14 The influence of diameter-to-thickness ratio of theinner steel tube |
由图 14可见:1)内层钢管径厚比不同时,圆钢管混凝土长柱试件屈服前,各试件的刚度基本相同;2)双层圆钢管混凝土长柱的承载力和延性,均随径厚比的增大而增大,表明考虑扭转影响时,应尽量增大双层钢管混凝土长柱内层钢管的径厚比。
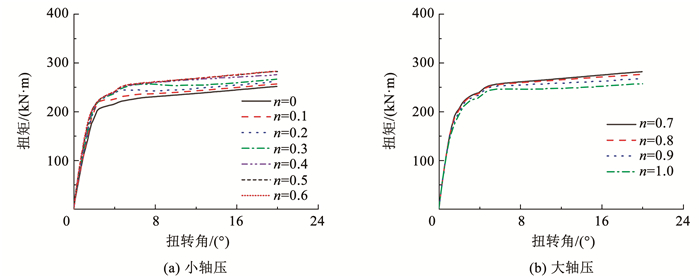
4.3.2 轴压比影响由于试件数量的限制,双层钢管混凝土长柱扭转试验仅对压扭工况下轴压比n=0(纯扭)和n=0.3(压扭)两种工况进行了试验研究。为进一步研究轴压大小对压扭试件的影响,分别进行了轴压比从0至1等不同轴压水平下的数值模拟,数值模拟结果见图 15。
|
图 15 轴压的影响 Fig. 15 The influence of axial pressure |
由图 15可见:1)轴压比从0增加至0.6时,随着轴压的增大,双层钢管混凝土的抗扭承载力逐渐增大;当轴压比从0.7增加至1时,随着轴压的增大,双层圆钢管混凝土长柱的抗扭承载力逐渐减小;2)轴压比从0增加至0.6时,随着轴压的增大,双层圆钢管混凝土长柱的抗扭刚度逐渐增大,当轴压比从0.7增加至1时,双层圆钢管混凝土长柱试件的初始刚度逐渐增大,但屈服后刚度逐渐减小。
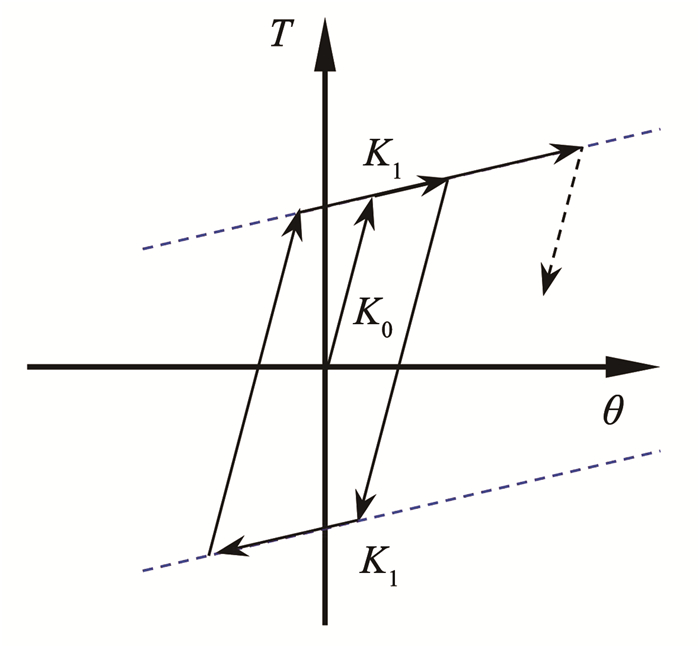
5 扭转恢复力简化模型试验数据和数值模拟的结果表明纯扭和压扭受力状态下,往复扭转的扭矩-扭转角关系可以近似划分为弹性阶段和强化阶段,曲线呈双折线状,故考虑采用双折线模型建立扭转恢复力模型, 见图 16。
|
图 16 扭矩-扭转角恢复力模型 Fig. 16 Simplified formula model of torque-torsion angle curve |
弹性阶段钢管混凝土的扭转刚度K′T[14]为
| $ K_{\mathrm{T}}^{\prime}=(2 \alpha+0.42) G_{\mathrm{sc}} I_{\mathrm{p}} $ | (5) |
式中:α为截面含钢率,Gsc为钢管混凝土的组合剪切模量,Ip为钢管混凝土的极惯性矩。
本文在式(5)基础上引进轴压影响系数m和内钢管影响系数n, 得到弹性阶段扭转刚度K0的计算公式为
| $ K_0=m n(2 \alpha+0.42) G_{\mathrm{sc}} I_{\mathrm{p}} $ | (6) |
式中m和n通过试验数据以及有限元模型拟合后分别取1.12和1.08。
对实验结果和有限元结果拟合后,取强化段刚度K1=0.1m1n1K0,其中m1、n1分别表示强化阶段二次刚度的轴压衰减系数和内钢管衰减系数。试验结果表明内部钢管对于二次刚度的影响不明显,而轴压会明显降低二次刚度,故对试验数据拟合后m1取为0.7,n1取为1;卸载刚度近似等于初始刚度,故将卸载刚度定义为弹性阶段的刚度;往复扭转时扭矩-扭转角曲线呈对称分布,故反向加载时的刚度也取为K1。
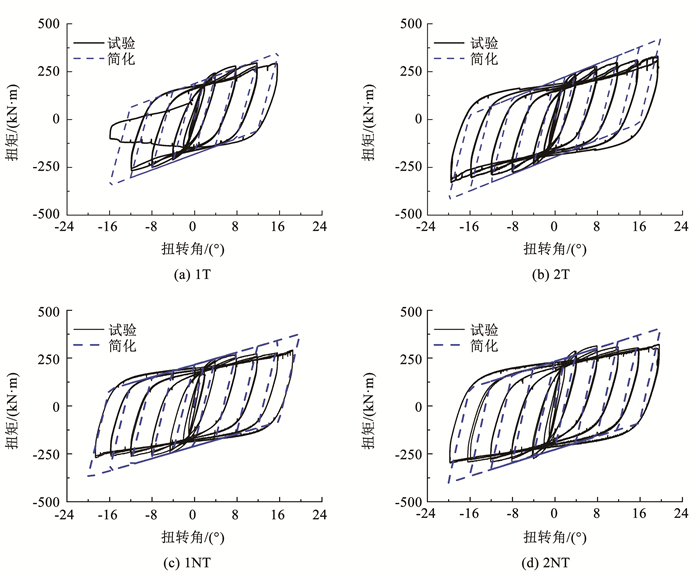
利用上述简化模型对试验结果进行验证,对比结果见图 17。
|
图 17 恢复力模型验证 Fig. 17 Comparison between test results and simplified formula results |
构件的承载力一般定义为峰值荷载点,已有大量文献表明钢管混凝土的扭矩-扭转角曲线没有下降段,进入塑性阶段后,随着扭转角的增大,扭矩值仍缓慢上升。本次试验结果也验证了这一现象。因此,在对钢管混凝土的抗扭承载力计算公式进行研究时,首先需要对其进行定义。韩林海等[3]考虑了受力和变形的特点,将钢管混凝土扭转试件边缘剪应变达到0.01时对应的扭矩值作为钢管混凝土抗转承载力。本文将利用试验中的1T试件对已有的抗扭承载力计算公式进行验证。由于试验数据有限,对于双层钢管混凝土的抗扭承载力以及压扭相关方程的研究将在后续研究中进行。
1) 尧国皇[15]通过大量参数分析对韩林海等[3]提出的抗扭承载力公式的抗扭强度计算系数进行修正,得到了抗扭承载力计算公式(7),其中γt为抗扭强度计算系数,WscT为截面抗扭惯性矩,τscy为抗扭屈服极限指标。
| $ T_{\mathrm{u}}=\gamma^{\mathrm{t}} W_{\mathrm{sc}}^{\mathrm{T}} \tau_{\mathrm{sc}}^{\mathrm{y}} $ | (7) |
2) 王宇航等[16]基于分层筒模型分析了大量算例,并通过回归分析,将钢管混凝土的抗扭承载力分解为钢管抗扭承载力和混凝土抗扭承载力的叠加,提出了公式(8),其中α为含钢率,ξ为套箍系数,fc为混凝土轴心抗压强度,D为钢管外直径。
| $ \begin{gathered} T_{\mathrm{u}}=T_{\mathrm{cu}}+T_{\mathrm{su}}=\left(\frac{1}{0.216 \mathrm{e}^{8.7 \alpha}+0.235 \alpha+12.25}+\right. \\ \left.\frac{\xi}{16.47 \alpha^2+2.94 \alpha+4.9}\right) f_{\mathrm{c}} D^3 \end{gathered} $ | (8) |
3) 谢先义等[17]通过理论推导,得到了钢管混凝土柱的抗扭承载力理论计算公式(9),其中As为钢管面积,fy为钢材屈服强度,r为钢管混凝土的外半径。
| $ T_{\mathrm{u}}=0.7 A_{\mathrm{s}} f_{\mathrm{y}} r $ | (9) |
表 4为钢管混凝土抗扭承载力计算值验证,3种钢管混凝土柱的抗扭承载力计算值与1T的试验值相比均偏于安全,其中文献[16-17]的计算方法与试验值更接近,文献[15]的计算方法与试验值有一定偏差。
| 表 4 钢管混凝土抗扭承载力计算值验证 Tab. 4 Comparing calculated and experimental values of torsional capacity |
1) 普通圆钢管混凝土长柱和双层圆钢管混凝土长柱均具有较好的抗扭能力,一定范围内的轴向荷载会减小钢管产生的拉应力,从而提高钢管混凝土长柱的抗扭能力。
2) 与普通圆钢管混凝土长柱相比,双层钢管混凝土长柱的初始刚度和承载力略有提升,滞回曲线更饱满,耗能能力提升明显。
3) 含钢率一定时,随着内层钢管径厚比的增大,双层圆钢管混凝土长柱抗扭能力逐渐增强。
4) 轴压比小于0.6时,随着轴压比增大,圆钢管混凝土长柱的抗扭能力逐渐增强;轴压比大于0.7时,随着轴压比增大,圆钢管混凝土长柱的抗扭能力逐渐降低。
5) 利用双折线恢复力模型可以较好地拟合钢管混凝土扭矩-扭转角关系。
6) 利用已有的抗扭承载力计算公式计算了本文扭转试件的抗扭承载力,并与试验结果进行对比,验证了已有计算公式的正确性。
| [1] |
韩林海. 钢管混凝土结构—理论与实践[M]. 3版. 北京: 科学出版社, 2007: 5. HAN Linhai. Concrete filled steel tubular structures—theory and practice[M]. 3rd ed. Beijin: Science Press, 2007: 5. |
| [2] |
徐积善, LEEG, CHANGK C, 等. 钢管混凝土短柱在压扭共同作用下的试验研究[J]. 北京建筑工程学院学报, 1991(2): 1. XU Jishan, LEE G, CHANG K C, et al. Experimental studies on steel tube cored concreteand concrete filled steel tube short column under compression and torsion[J]. Journal of Beijing Institute of Civil Engineering and Architecture, 1991(2): 1. |
| [3] |
韩林海, 钟善桐. 钢管混凝土纯扭转问题研究[J]. 工业建筑, 1995(1): 7. HAN Linhai, ZHONG Shantong. The studies of pure torsion problem for concrete filled steel tube[J]. Industrial Construction, 1995(1): 7. DOI:10.13204/j.gyjz199501002 |
| [4] |
史艳莉, 张海龙, 王文达. 内置钢骨圆钢管混凝土纯扭构件力学性能研究[J]. 建筑结构学报, 2013, 34(增刊1): 327. SHI Yanli, ZHANG Hailong, WANG Wenda. Research on mechanical behavior of concrete-filled steel tubular member with encased profiled steel under pure torsion[J]. Journal of Building Structures, 2013, 34(Sup.1): 327. DOI:10.14006/j.jzjgxb.2013.s1.049 |
| [5] |
聂建国, 王宇航, 樊健生. 用于分析钢管混凝土柱在轴力-扭矩复合作用下非线性反应的"分层筒"模型[J]. 土木工程学报, 2013, 46(1): 16. NIE Jianguo, WANG Yuhang, FAN Jiansheng. Laminated tubes model for non-linear analysis on concrete filled steel tubes under combined action of axial force and torsion[J]. China Civil Engineering Journal, 2013, 46(1): 16. DOI:10.15951/j.tmgcxb.2013.01.011 |
| [6] |
黄宏, 陈梦成, 黄斌洁. 圆中空夹层钢管混凝土柱扭转试验研究[J]. 试验力学, 2012, 27(3): 288. HUANG Hong, CHEN Mengcheng, HUANG Binjie. Experimental study of concrete-filled double-skin circular steel tube subjected to pure torsion[J]. Journal of Experimental Mechanics, 2012, 27(3): 288. |
| [7] |
聂影, 皮正波, 陶修, 等. 轴压、压扭荷载作用下内嵌H型钢钢管混凝土柱的受力性能研究[J]. 特种结构, 2022, 39(3): 15. NIE Ying, PI Zhengbo, TAO Xiu, et al. Mechanical behaviors of h-shaped steel encased in concrete-filled steel tube columns under axial loads and torsion loads[J]. Special Structures, 2022, 39(3): 15. |
| [8] |
蔡绍怀, 焦占拴. 钢管混凝土短柱的基本性能和强度计算[J]. 建筑结构学报, 1984, 5(6): 13. CAI Shaohuai, JIAO Zhanquan. Behavior and ultimate strength of short concrete-filled steel tubular columns[J]. Journal of Building Structures, 1984, 5(6): 13. DOI:10.14006/j.jzjgxb.1984.06.002 |
| [9] |
赵大洲. 钢骨-钢管高强混凝土组合柱力学性能的研究[D]. 大连: 大连理工大学, 2003 ZHAO Dazhou. Study on the mechanical properties of steel tubular columns filled with steel-reinforced high-strength concrete[D]. Dalian: Dalian University of Technology, 2003 |
| [10] |
STEWART D. A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineers, 1965, 180(15): 371. DOI:10.1243/PIME_PROC_1965_180_029_02 |
| [11] |
DU C, WANG T, ZHOU H, et al. Development of an integrated load testing device for a substructure hybrid test of a curved bridge[J]. Experimental Techniques, 2022(46): 398. DOI:10.1007/s40799-021-00492-y |
| [12] |
冯鹏, 强翰霖, 叶列平. 材料、构件、结构的"屈服点"定义与讨论[J]. 工程力学, 2017, 34(3): 36. FENG Peng, QIANG Hanlin, YE Lieping. Discussion and definition on yield points of materials, members and structures[J]. Engineering Mechanics, 2017, 34(3): 36. DOI:10.6052/j.issn.1000-4750.2016.03.0192 |
| [13] |
刘威. 钢管混凝土局部受压时的工作机理研究[D]. 福州: 福州大学, 2005 LIU Wei. Research on mechanism of concrete filled steel tubes subjected to local compression[D]. Fuzhou: Fuzhou University, 2005 |
| [14] |
谢先义. 钢管混凝土构件抗剪抗扭性能和标准的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011 XIE Xianyi. Research on shear and torsion behavior of concrete filled steel tubular members and the application in national standard[D]. Harbin: Harbin Institute of Technology, 2011 |
| [15] |
尧国皇. 钢管混凝土构件在复杂受力状态下的工作机理研究[D]. 福州: 福州大学, 2006 YAO Guohuang. Research on behaviour of concrete filled steel tubes subjected to complicated loading states[D]. Fuzhou: Fuzhou University, 2006 |
| [16] |
王宇航, 聂建国, 樊健生. 圆钢管混凝土柱的受扭性能研究[J]. 工程力学, 2014, 31(3): 222. WANG Yuhang, NIE Jianguo, FAN Jiansheng. Study on the torsion behavior of concrete filled steel tube column with circular section[J]. Engineering Mechanics, 2014, 31(3): 222. |
| [17] |
谢先义, 查晓雄. 空、实心钢管混凝土构件抗扭抗剪性能的研究Ⅱ: 强度的理论研究[J]. 建筑钢结构进展, 2012, 14(3): 8. XIE Xianyi, ZHA Xiaoxiong. Torsion and shear behavior study of hollow and solid concrete filled steel tubular (CFST) membersⅡ: Theoretical research on strength[J]. Progress in Steel Building Structures, 2012, 14(3): 8. |
 2024, Vol. 56
2024, Vol. 56


