2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
据统计,建筑能耗约占社会总能耗的40%,而用于给建筑物内部创造舒适工作和生活条件的制冷和供暖设备是造成建筑高能耗的主要来源[1-2]。因此,可通过增强建筑外墙的保温隔热性能来降低建筑能耗[3-4]。从建筑外墙保温形式来看,目前约有70%的建筑物采用外保温形式,而内保温形式和夹芯保温形式分别仅占26%和4%[5]。然而,传统的建筑外保温系统因长期存在的施工工艺复杂[6]、使用寿命短[7]以及保温层易脱落[8]等缺陷,已难以满足当前形势下建筑行业的发展需求。
近年来,免拆复合保温外模板作为保温领域先进技术代表,因其显著的节能和经济效益引起了工程界的广泛关注。苏冬媛[9]的研究指出,与传统的外贴EPS板复合剪力墙体系相比,免拆墙模复合剪力墙体系可节约大量的能源和资源,是有前途的设计方案。黄婕[10]通过研究以EPS板为保温芯材的新型保温免拆模板的抗折性能,发现开槽处理能极大提高新型保温免拆模板的抗折性能,且斜向交叉矩形槽对提高保温模板性能的效果最为显著。为了解锚固钉对保温免拆模板与混凝土界面黏结特性的影响,潘鸿健[11]对其进行了多组推出试验,结果表明保温免拆模板与混凝土之间需添加锚固钉,且建议采取四周布置的方式。此外,一些学者还对免拆复合保温外模板的热工性能[12]、抗风承载力[13]以及抗震性能[14]进行了研究。但从现有研究来看,目前关于岩棉保温芯材开发的免拆复合保温外模板的报道较少,尤其是有限元分析方面的有用信息更为有限。
鉴于此,本文研究了一种集保温和建筑模板于一体的岩棉复合保温外模板(RW-CIEF)体系,并验证了其可行性。基于全寿命周期成本(Clc)确定了岩棉芯材的最佳厚度。采用有限元模拟和理论分析相结合的方法研究了RW-CIEF的抗弯性能,并探讨了开槽处理对RW-CIEF抗弯性能的影响。基于有限元分析方法讨论了RW-CIEF的施工承载力以及温度效应下的应力和变形。
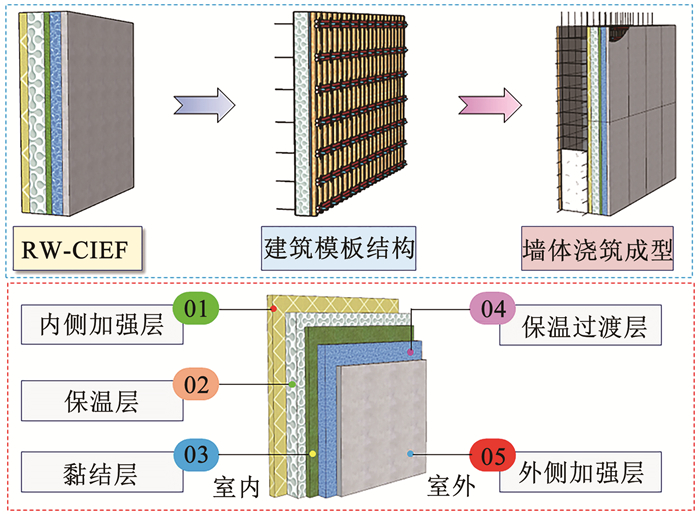
1 RW-CIEF设计 1.1 构造层设计基于综合考虑,本文所设计的RW-CIEF共包含5层,由内到外依次为内侧加强层、保温层、黏结层、保温过渡层以及外侧加强层,见图 1。其中,内侧加强层和外侧加强层由M15聚合物砂浆和耐碱玻璃纤维网制成。保温层采用保温隔热性能和防火性能兼优的岩棉材料。为了避免外侧加强层因温度效应引起的空鼓、开裂现象,在保温层和外侧加强层之间设置了保温过渡层,为无机保温砂浆。保温层与保温过渡层之间通过设置黏结层将其有效结合。
|
图 1 RW-CIEF的构造示意 Fig. 1 Structure diagram of RW-CIEF |
表 1为RW-CIEF各构造层的特性指标。由GB 50176—2016 《民用建筑热工设计规范》[15]可知,当岩棉保温材料应用于严寒地区的室外部件时,其导热系数需乘以1.1的修正系数。因此,后续计算中,岩棉保温芯材修正后的导热系数采用0.050 6 W/(m·K)。
| 表 1 RW-CIEF各构造层的特性指标 Tab. 1 Characteristic indexes of each structural layer of RW-CIEF |
经济合理性是节能建筑设计中必须考虑的因素之一,全寿命周期成本(Clc)可被应用于确定隔热材料的最佳厚度[16]。在Clc分析中,具有最小Clc的参数组合通常用作最优设计方案[17]。组合参数通常包括投资成本、运营成本(采暖期和制冷期)、维护更新成本以及处置成本。基于上述分析,Clc可表示为[18]:
| $ C_{\mathrm{lc}}=C_{\mathrm{c}}+\left(C_{\mathrm{o}}+C_{\mathrm{m}}\right) F_{\mathrm{pv}}-C_{\mathrm{r}} $ | (1) |
| $ F_{\mathrm{pv}}=\frac{(1+r)^N-1}{r \times(1+r)^N} $ | (2) |
| $ C_{\mathrm{m}}=\eta C_{\mathrm{c}} $ | (3) |
式中:Cc为保温材料成本;Co为运营成本,主要包括采暖期和制冷期两部分;Cm为维修更新成本; η为年度维修费用系数, η=1.8%;Cr为残值,Cr=0[19];Fpv为现值函数; r为折现率, r=5%[20]; N为房屋使用年限, N=50 a。
哈尔滨位于中国东北部,该地区是中国采暖期最长、采暖需求最高的地区之一,对该地区的外保温系统进行研究具有代表性, 本文以哈尔滨市为例进行分析, 采暖期和制冷期的成本参照作者先前的一项研究来确定[18]。全寿命周期成本最终可表示为
| $ C_{\mathrm{lc}}=R_{\mathrm{c}} t_{\mathrm{rw}}\left(1+0.018 F_{\mathrm{pv}}\right)+\frac{29.403 F_{\mathrm{pv}}}{0.375+t_{\mathrm{rw}} / \lambda_{\mathrm{rw}}} $ | (4) |
由式(4)可知,当
| $ t_{\mathrm{op}}=\sqrt{\frac{29.403 F_{\mathrm{pv}} \lambda_{\mathrm{rw}}}{\left(1+0.018 F_{\mathrm{pv}}\right) R_{\mathrm{c}}}}-0.375 \lambda_{\mathrm{rw}} $ | (5) |
式中:Rc为单位体积岩棉保温芯材的成本,由于各地岩棉保温芯材价格差异较大,基于已有研究[18, 21],取其平均值作为本研究中岩棉保温芯材的价格,即618.5元/m3;trw为岩棉保温芯材的厚度;λrw为岩棉保温芯材的导热系数;top为岩棉保温芯材的最佳厚度。
为了满足节能设计要求,本文基于传热系数对岩棉保温芯材的厚度进行了验证。建筑物墙体传热系数由式(6)、(7)来确定。由DB 23/1270—2019《黑龙江省居住建筑节能设计标准》[22]中对传热系数限值的规定可知,哈尔滨市属于严寒B区。表 2为严寒B区不同楼层外墙部位传热系数限值。由表 2可知,当楼层≤3层时,岩棉保温芯材的厚度限值最大。假定本文中的建筑物复合墙体由钢筋混凝土墙和RW-CIEF两部分组成,其中钢筋混凝土墙体厚度设计为200 mm,导热系数为1.74 W/(m·K)。结合表 1中的相关参数,得知岩棉保温芯材的厚度为150 mm时,即可满足传热系数限值要求。因此,基于经济效益确定的最佳厚度163 mm满足节能设计要求。
| 表 2 严寒B区不同楼层外墙部位传热系数限制 Tab. 2 Limit value of heat transfer coefficient of external walls of different floors in severe cold area B |
| $ K=\frac{1}{R_{\mathrm{t}}} $ | (6) |
| $ R_{\mathrm{t}}=R_{\mathrm{i}}+\sum\limits_{j=1}^n \frac{\delta_j}{\lambda_j}+R_{\mathrm{e}} $ | (7) |
式中:K为传热系数,W/(m2·K);Rt为围护结构总热阻,(m2·K)/W;Ri为内表面换热阻,Ri=0.11 (m2·K)/W;Re为外表面换热阻,Re=0.04 (m2·K)/W;δj为j结构层的厚度,m;λj为j结构层的导热系数,W/(m·K)。
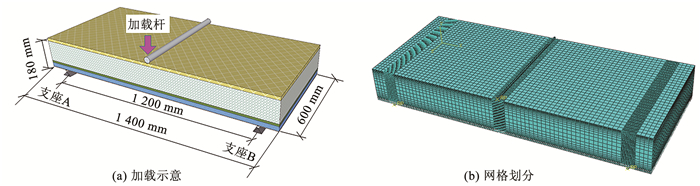
2 RW-CIEF承载力有限元分析 2.1 RW-CIEF抗弯性能 2.1.1 有限元模型建立根据力学性能试验常用标准模板的推荐尺寸[23],RW-CIEF的长度设置为1 400 mm,宽度为600 mm,总厚度为180 mm,跨度为1 200 mm。加载过程中RW-CIEF的内侧加强层朝上,且两个支座设置为完全约束,加载荷载设置为2 000 N。岩棉保温芯材以及内外加强层等各构造层均采用C3D8八结点线性六面体实体单元,耐碱玻纤网格布采用T3D2单元,加荷杆及支座采用R3D4离散刚体单元。岩棉保温芯材和内外加强层平板部分采用六面体单元划分网格,目的是提高网格质量和计算精度。网格划分采用中轴算法,尺寸为20 mm。RW-CIEF在与加载杆和支座接触处厚度方向均采取网格加密,尺寸为2 mm。开槽处采用扫掠网格划分技术,尺寸为2 mm。图 2为加载图和网格划分结果。
|
图 2 加载示意及网格划分 Fig. 2 Loading scheme and grid division |
采用有限元软件ABAQUS对RW-CIEF的抗弯性能进行分析, 结果见图 3。RW-CIEF的挠度与跨度之间呈二次抛物线,且在跨中处的挠度最大,为2.14 mm。进一步对比发现RW-CIEF的顶部挠度大于其底部,这一现象主要归因于岩棉材料弹性模量较小,在三点弯曲荷载作用下岩棉会有一定的压缩。

|
图 3 RW-CIEF底部和顶部竖向挠度 Fig. 3 Vertical deflection of bottom and top of RW-CIEF |
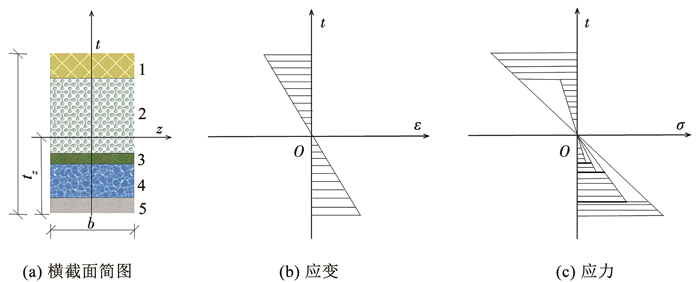
为了验证有限元模型的准确性,建立了RW-CIEF跨中挠度的理论模型,并与有限元分析结果进行比较。图 4为RW-CIEF的横截面计算简图。由谢馨媛[24]的研究可知,当各构造层间紧密黏结时,则在弯曲过程中无相对滑动,此时的叠合梁截面可看作一个整体,因此在小变形情况下满足平截面假定。由平截面假定可知,截面上各点处的纵向线应变沿截面高度的线性变化见图 4(b)。当材料处于线弹性范围内时,各构造层截面上的弯曲正应力与应变符合胡克定律。因此,当材料在线弹性极限之前时,根据胡克定律和静力平衡,可以得到式(8)、(9)。
|
图 4 RW-CIEF的横截面计算简图 Fig. 4 Schematic of cross section calculation of RW-CIEF |
| $ \int_{A_1} E_1 \frac{\left(t_1-t_z\right)}{\rho} \mathrm{d} A_1+\int_{A_2} E_2 \frac{\left(t_2-t_z\right)}{\rho} \mathrm{d} A_2+\int_{A_3} E_3 \frac{\left(t_3-t_z\right)}{\rho} \mathrm{d} A_3+\int_{A_4} E_4 \frac{\left(t_4-t_z\right)}{\rho} \mathrm{d} A_4+\int_{A_5} E_5 \frac{\left(t_5-t_z\right)}{\rho} \mathrm{d} A_5=0 $ | (8) |
| $ \int_{A_1} E_1 \frac{\left(t_1-t_z\right)^2}{\rho} \mathrm{d} A_1+\int_{A_2} E_2 \frac{\left(t_2-t_z\right)^2}{\rho} \mathrm{d} A_2+\int_{A_3} E_3 \frac{\left(t_3-t_z\right)^2}{\rho} \mathrm{d} A_3+\int_{A_4} E_4 \frac{\left(t_4-t_z\right)^2}{\rho} \mathrm{d} A_4+\int_{A_5} E_5 \frac{\left(t_5-t_z\right)^2}{\rho} \mathrm{d} A_5=M $ | (9) |
其中
| $ M=\frac{P l}{4} $ | (10) |
式中:ρ为中性层的曲率半径;A1~A5为各结构层的面积,mm2;t1~t5分别为各结构层形心至外侧加强层外缘的距离,mm;E1~E5为各结构的弹性模量;tz为中性轴至外加强层外缘的距离;M为RW-CIEF横截面上的弯矩;P为荷载;l为跨度。
由式(8)可得出中性轴位置tz=78.92 mm。由式(9)、(10)以及平行移轴公式(11)可求得截面各构造层上的弯曲正应力以及弯曲刚度。在三点弯曲试验中,RW-CIEF的弯曲挠度应为弯矩产生的挠度和剪力产生的挠度之和[24],如式(12)所示。
| $ I_i=\frac{b h_i^3}{12}+t_i^2 A_i $ | (11) |
| $ \varDelta=\frac{P l^3}{48 K_{\mathrm{EI}}}+\frac{2 M(1+v) h^3}{E_2 b h^{\prime 2}} $ | (12) |
式中:P为荷载;l为RW-CIEF的跨度;KEI为总弯曲刚度,通过将各构造层的弯曲刚度相加得到;M为弯矩;E2为岩棉保温芯材料的弹性模量;h2为岩棉保温芯材料的厚度; b为RW-CIEF的宽度; υ为泊松比;h′为岩棉保温芯材上下构造层之间的形心距离,为171.5 mm; Ii为构造层i的惯性矩;hi为构造层i的厚度;ti为构造层i的形心与中性轴之间的距离,mm;Ai为构造层i的面积,mm2。
由式(12)计算得出RW-CIEF的跨中挠度理论值为2.25 mm,与有限元分析结果具有较高的一致性。因此,理论计算结果有效地验证了有限元模型的准确性,有理由通过有限元方法来预测RW-CIEF开槽后的弯曲性能。
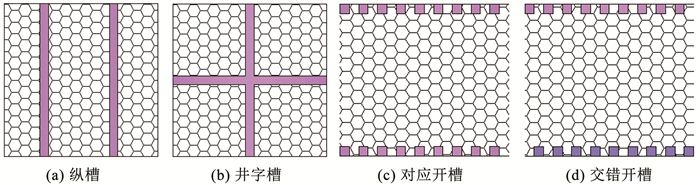
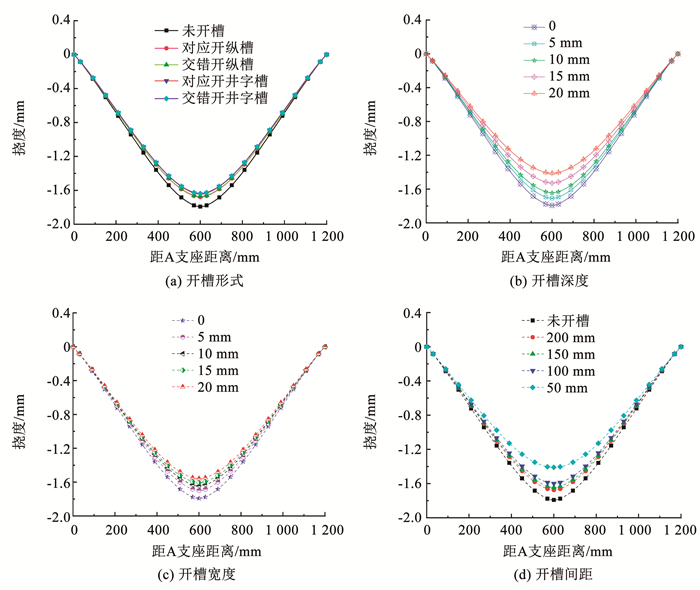
2.1.3 开槽对RW-CIEF抗弯性能影响分析基于ABAQUS有限元软件讨论了开槽形式、开槽宽度、开槽深度和开槽间距对RW-CIEF抗弯性能的影响, 共设置4种开槽形式,分别为对应开纵槽、交错开纵槽、对应开井字槽、交错开井字槽, 图 5为开槽形式分类结果。当研究某一变量时,始终保持开槽形式为对应开井字槽, 开槽深度为10 mm,开槽宽度为10 mm,开槽间距为150 mm。即当研究开槽形式对RW-CIEF抗弯性能的影响时,保持开槽深度为10 mm,开槽宽度为10 mm,开槽间距为150 mm,以此类推。
|
图 5 开槽形式分类结果 Fig. 5 Classification results of groove forms |
开槽对RW-CIEF抗弯性能的影响结果见图 6。从图 6(a)可看出,开槽可以显著提高RW-CIEF的弯曲性能, 其中,交错开井字槽最为明显,跨中竖向挠度减小约8.63%。由图 6(b)、(c)可知,随着开槽深度和宽度的增加,RW-CIEF的跨中挠度持续减小。当开槽深度为20 mm时,跨中挠度减小了21.20%;当开槽宽度为20 mm时,跨中挠度减小了13.11%。由图 6(d)可知,随着开槽间距的减小,RW-CIEF的跨中挠度逐渐减小, 其中,当沟槽间距为50 mm时,RW-CIEF的抗弯性能明显提高,相比未开槽的RW-CIEF,跨中挠度减小了约21.30%。从以上分析可看出,开槽处理有利于提高RW-CIEF的抗弯性能。综合RW-CIEF的热工性能和加工角度,本文建议开槽形式采用对应开井字槽或对应开纵槽,同时建议开槽深度选取10 mm,开槽宽度选取10 mm,开槽间距选取150 mm。
|
图 6 开槽对RW-CIEF抗弯性能的影响 Fig. 6 Effect of grooving on bending properties of RW-CIEF |
建筑模板结构主要由面板、支撑结构和连接件3部分组成。其中,面板(RW-CIEF)是直接接触新浇混凝土的承重板,主要起到约束混凝土成型的作用。而支撑结构是支撑面板、混凝土以及施工荷载的临时结构,支撑结构和面板通过连接件连接成整体。建筑模板结构的传力过程为:RW-CIEF首先将所承受的荷载传递给次楞,次楞依次传递给主楞,最后通过主楞传递给对拉螺栓。因此,建筑模板结构的各部分在使用过程中均需满足抗弯强度要求和抗弯刚度要求[25], 混凝土侧压力根据JGJ 162—2008《建筑施工模板安全技术规范》[23]进行施加。
2.2.1 有限元模型建立利用ABAQUS软件模拟了RW-CIEF在混凝土浇筑过程中的受力情况,通过建立RW-CIEF、主次楞及对拉螺栓的传力体系,分析了RW-CIEF在施工荷载下的应力及变形情况。模型所选墙体尺寸为6 000 mm(宽)×3 000 mm(高),由10块RW-CIEF拼接而成,现浇混凝土墙体厚度为200 mm。木方次楞的截面尺寸为50 mm×80 mm,木方次楞的间距为150 mm,弹性模量和泊松比分别为7.0×103 MPa和0.20。双钢管主楞采用Φ48 mm×3.5 mm的圆钢管,间距为500 mm,弹性模量和泊松比分别为2.1×105 MPa和0.30。采用M14对拉螺栓,相邻对拉螺栓水平间距为300 mm,竖向间距为500 mm,弹性模量和泊松比分别为3.0×108 MPa和0.30。
由于模型涉及多个接触问题,在相互作用设置上,将RW-CIEF各构造层采用tie约束,每块RW-CIEF之间、RW-CIEF与木方次楞之间、木方次楞与双钢管主楞之间均定义接触。对拉螺栓一端设置为固定,另一端与钢管之间采用绑定约束。为了更方便定义钢管与木方次楞以及对拉螺栓之间的接触面,基于截面惯性矩不变原则,将圆形钢管等效为方形钢管。网格划分方面,对拉螺栓网格尺寸采用4 mm,其余部件网格尺寸采用40 mm。整体有限元建模过程中,在RW-CIEF和木方次楞底部采用约束3个方向位移的铰支约束,RW-CIEF两侧竖向采用约束X方向位移的铰支约束。根据JGJ 162—2008 《建筑施工模板安全技术规范》[23],计算变形时底部混凝土侧压力采用43.45 kPa,计算应力时混凝土侧压力采用49.05 kPa。建立的有限元模型见图 7。

|
图 7 有限元模型 Fig. 7 Finite element model |
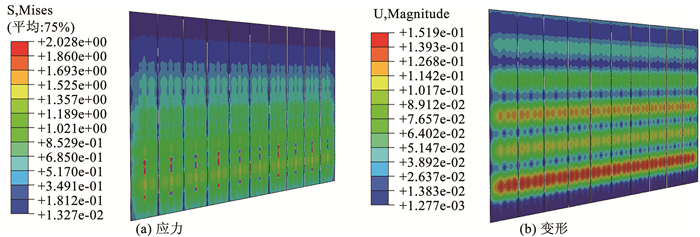
RW-CIEF的外侧加强层受施工侧压力影响较大,因此重点验证了外侧加强层承受施工荷载的能力。现浇混凝土侧压力作用下外侧加强层的应力和变形见图 8。由图 8(a)可知,外侧加强层的最大应力出现在其下部两道钢管之间,最大应力为2.03 MPa。由1.1节所述可知,外侧加强层主要由M15聚合物砂浆和耐碱网格布制成,聚合物砂浆的抗拉强度近似为1.5 MPa。耐碱玻纤网格布可使水泥基板的抗弯承载力提高59%[26],因此外侧加强层的极限承载力可达2.39 MPa。由此可知,荷载作用下的最大应力小于外侧加强层抗拉承载力2.39 MPa。由图 8(b)可知,最大变形同样出现在外侧加强层下部两道钢管之间,变形最大值为0.15 mm,小于规范规定的限值0.375 mm[23]。由此可知,按以上方案设计的RW-CIEF满足施工承载力。
|
图 8 外侧加强层应力及变形 Fig. 8 Stress and deformation of outer reinforcing layer |
考虑到实际工程中的RW-CIEF将长期暴露于环境中,因此一定程度会受到环境影响。其中,复合墙体内外温差是主要影响因素。为此,使用ABAQUS软件进行了有限元分析,并根据理论分析方法验证了有限元结果。复合墙体尺寸为6 000 mm(宽)×3 000 mm(高)。由于所假设的墙体为一整面墙,故有限元分析过程不考虑门窗洞口的影响。另由于钢筋面积占现浇混凝土墙体截面面积极小,对传热过程不会产生较大的影响[27],因此建模过程中暂且不考虑钢筋的影响。
3.1 有限元模型建立复合墙体中的钢筋混凝土墙体四周的4个面固定,由于变形缝的存在,RW-CIEF四周不设置约束,各构造层之间采用tie绑定。每块RW-CIEF之间在法向上建立硬接触,切向摩擦系数设定为0.45。夏季和冬季的室外计算温度分别按最热月和最冷月的极端温度选取。夏季温度约为40 ℃,冬季温度约为-30 ℃,相应的室内计算温度参照黑龙江省地方标准[22]选取,夏季和冬季分别选取26 ℃和18 ℃。根据哈尔滨市冬季和夏季的温度,复合墙体的内表面传热系数均为8.7 W/(m2·K),外表面传热系数分别为23 W/(m2·K)和19 W/(m2·K)。
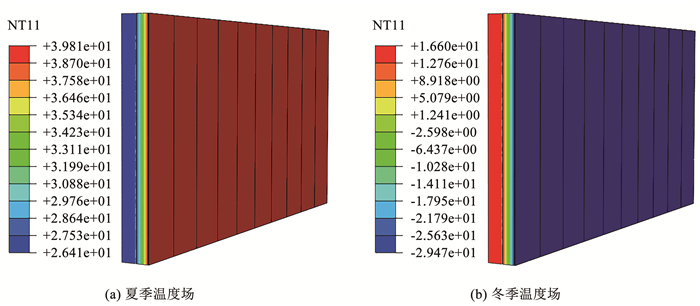
3.2 温度场分析结果温度场有限元分析结果见图 9。在夏季,外侧加强层的温度最高,岩棉保温芯材有效地阻止了热量传递到内部。在冬季,现浇混凝土内墙温度最高,岩棉保温芯材有效防止热量向外散发。此外,根据各构造层由内向外的温度变化趋势可知,夏季和冬季的主要温度变化均发生在岩棉保温芯材。岩棉保温芯材内部靠近墙体的构造层温度变化很小,内侧加强层和现浇混凝土墙的温度几乎没有变化。这一结果反映出RW-CIEF具有良好的保温隔热性能,有利于建筑物的室内热稳定性。
|
图 9 温度场有限元分析结果 Fig. 9 Finite element analysis results of temperature field |
为了验证有限元模型的精确度,基于热工规范公式[15]对各构造层的内表面温度进行计算,见式(13),并与有限元分析结果进行对比。结果显示,复合墙体各构造层的内表面温度理论值与模拟值基本吻合,相对值均低于1%。由此可知,采用有限元模型和热工规范公式均可有效获得RW-CIEF各构造层两侧的温度。但是相比有限元模型,热工规范公式存在一定的局限性,该公式无法获得各构造层内每点的温度,且不适用于开槽、开孔等复杂构造层温度的确定。而有限元模型可以弥补这一缺陷,能实现从外侧到内侧温度的整个线性变化过程及整个温度的传导过程。
| $ \theta_m=t_{\mathrm{i}}-\frac{t_{\mathrm{i}}-t_{\mathrm{e}}}{R_0} \times\left(R_{\mathrm{i}}+\sum\limits_{k=1}^{k=m} R_k\right) $ | (13) |
式中:θm为m结构层内表面温度,m=0为混凝土内表面温度;ti为室内计算温度;te为室外计算温度;R0为复合墙体的总热阻;Ri为内表面传热阻力,Ri=0.11 (m2·K)/W;Rk为k结构层的热阻。
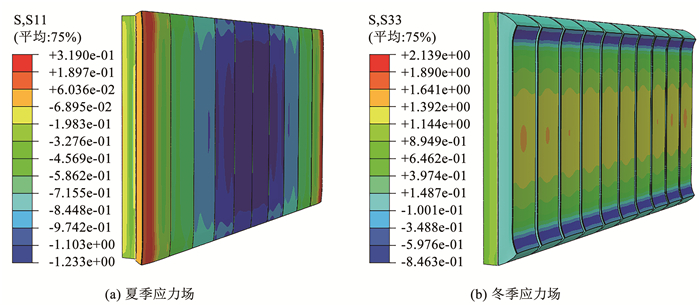
3.3 复合墙体温度应力分析结果夏季和冬季温度效应引起的复合墙体应力见图 10。RW-CIEF在夏季内外温差的影响下出现了膨胀现象。此外,由于中部受到变形限制较大,所以压应力出现在墙体外侧加强层中部,为1.23 MPa。在冬季温度效应下,RW-CIEF出现了收缩现象。最大拉伸应力为2.14 MPa,最大压缩应力为0.85 MPa。在实际情况下,可将最大拉应力和压应力与外侧加强层的承载力进行比较。对比发现,最大拉应力和压应力均未超过外侧加强层的承载力。这一结果表明外侧加强层出现夏季空鼓、冬季开裂的概率极小。
|
图 10 复合墙体整体应力场 Fig. 10 Overall stress field of composite wall |
图 11显示了复合墙体在温度作用下产生的变形云图。由于RW-CIEF各结构层的线膨胀系数不同,导致温差作用下的热胀冷缩程度不同。通过比较,发现最大变形均发生在RW-CIEF四周。夏季最大变形为0.52 mm,冬季最大变形为0.90 mm。此外,由于冬季室内外温差大于夏季,所以复合墙体在冬季的变形大于夏季变形。

|
图 11 复合墙体整体变形 Fig. 11 Overall deformation of composite wall |
设计了一种以岩棉为保温芯材的岩棉复合保温外模板(RW-CIEF)。基于数值研究和理论分析方法,验证了RW-CIEF在实际工程中的可行性。通过分析,得出以下结论:
1) 提出的抗弯性能有限元分析方法具有较高的精度,同理论计算方法相比,该方法可以更简便、高效的计算出开槽后RW-CIEF的抗弯性能。开槽处理对RW-CIEF的抗弯性能是有利的。建议开槽形式采用对应开井字槽或对应开纵槽,开槽深度选取10 mm,开槽宽度选取10 mm,开槽间距选取150 mm。
2) RW-CIEF具有出色的承受施工荷载的能力。混凝土浇筑过程对RW-CIEF外侧加强层产生的最大应力低于RW-CIEF外侧加强层自身的承载力,同时最大变形也小于规范规定的限值0.375 mm。
3) 复合墙体各构造层的内表面温度有限元模拟值与理论值吻合度较高,验证了所建立的有限元模型具有较高的精度。此外,更值得注意的是,所建立的有限元模型不仅可以得到各构造层两侧的温度,还可以确定构造层内每一处的温度,且适用于开槽、开孔等复杂构造层温度的确定, 因此建立的有限元模型可解决热工规范公式存在的局限性问题。
4) 所设计的RW-CIEF具有良好的保温隔热性能,有利于建筑物的室内热稳定性。在温度效应下,RW-CIEF的外侧加强层出现夏季空鼓、冬季开裂的概率极小。
| [1] |
DING Yan, WEI Xiaoting, WANG Qiaochu. Optimization approach of passive cool skin technology application for the building's exterior walls[J]. Journal of Cleaner Production, 2020, 256: 120751. DOI:10.1016/j.jclepro.2020.120751 |
| [2] |
阮方, 钱晓倩, 钱匡亮, 等. 人行为模式对外墙内外保温节能效果的影响[J]. 哈尔滨工业大学学报, 2017, 49(2): 109. RUAN Fang, QIAN Xiaoqian, QIAN Kuangliang, et al. Influence on energy saving effects of internal and external wall insulations for different occupant behaviors[J]. Journal of Harbin Institute of Technology, 2017, 49(2): 109. DOI:10.11918/j.issn.0367-6234.2017.02.018 |
| [3] |
NYERS J, KAJTAR L, TOMIC S, et al. Investment-savings method for energy-economic optimization of external wall thermal insulation thickness[J]. Energy and Buildings, 2015, 86: 268. DOI:10.1016/j.enbuild.2014.10.023 |
| [4] |
FANTUCCI S, GARBAACCIO S, LORENZATI A, et al. Thermo-economic analysis of building energy retrofits using VIP-Vacuum Insulation Panels[J]. Energy and Buildings, 2019, 196: 269. DOI:10.1016/j.enbuild.2019.05.019 |
| [5] |
李姝婷. 西安地区高层住宅外墙外保温材料的选用与优化研究[D]. 西安: 西安建筑科技大学, 2020 LI Shuting. Study on selection and optimization of external wall thermal insulation material for high-rise residential buildings in Xi'an[D]. Xi'an: Xi'an University of Architecture and Technology, 2020 |
| [6] |
JEONG J, JEONG J, LEE J, et al. Learning-driven construction productivity prediction for prefabricated external insulation wall system[J]. Automation in Construction, 2022, 141: 104441. DOI:10.1016/j.autcon.2022.104441 |
| [7] |
王新苗. 寒冷地区模板保温与结构一体化技术优化及应用研究[D]. 西安: 西安建筑科技大学, 2019 WANG Xinmiao. Technical optimization and application of formwork insulation and structure integration in cold area[D]. Xi'an: Xi'an University of Architecture and Technology, 2019 |
| [8] |
YUAN Kelong, XIONG Houren, WEN Minjie, et al. Visualization of localized deformation of external thermal insulation composite systems during aging[J]. Applied Thermal Engineering, 2022, 206: 118108. DOI:10.1016/j.applthermaleng.2022.118108 |
| [9] |
苏冬媛. 免拆保温墙模复合剪力墙体系模板设计及寿命周期成本分析[D]. 太原: 太原理工大学, 2008 SU Dongyuan. Designing and life cycle cost analysis on composite shear wall system with heat preservation formwork[D]. Taiyuan: Taiyuan University of Technology, 2008 |
| [10] |
黄婕. 新型保温免拆模板基本力学性能研究[D]. 长沙: 长沙理工大学, 2017 HUANG Jie. The study on basic mechanical properties of new undismantled insulation-template[D]. Changsha: Changsha University of Science & Technology, 2017 |
| [11] |
潘鸿健. MF保温免拆模板与混凝土墙体连接性能及隔热性能研究[D]. 南京: 东南大学, 2019 PAN Hongjian. Study on connection performance between MF thermal insulation wallboard and concrete wall and thermal insulation performance[D]. Nan jing: Southeast University, 2019 |
| [12] |
万桥. 岩棉复合型保温模板设计及试验研究[D]. 西安: 长安大学, 2017 WAN Qiao. The study and design of the composite rock wool thermal insulation board[D]. Xi'an: Chang'an University, 2017 |
| [13] |
吴警. 外墙免拆保温模板连接件合理参数选择研究[D]. 合肥: 安徽建筑大学, 2022 WU Jing. Study on reasonable parameter selection of non-removable thermal insulation formwork connector of exterior wall[D]. Hefei: Anhui Jianzhu University, 2022 |
| [14] |
段芳敏. 免模保温剪力墙抗震性能及结合界面剪切性能研究[D]. 长沙: 湖南大学, 2017 DUAN Fangmin. The research on seismic performance and adjoining-face shear property of non-template insulation shear wall[D]. Changsha: Hunan Uniiversity, 2017 |
| [15] |
民用建筑热工设计规范: GB 50176—2016[S]. 北京: 中国建筑工业出版社, 2016 Code forthermal design of civil building: GB 50176—2016[S]. Beijing: China Architecture & Building Press, 2016 |
| [16] |
WANG Yijiang, WANG Chaochao, GAO Shang, et al. The impact of thermal insulation on cooling energy consumption and optimal insulation thickness for underground tunnel[J]. Sustainable Energy Technologies and Assessments, 2021, 47: 101495. DOI:10.1016/j.seta.2021.101495 |
| [17] |
ALSAYED M F, TAYEH R A. Life cycle cost analysis for determining optimal insulation thickness in Palestinian building[J]. Journal of Building Engineering, 2019, 22: 101. DOI:10.1016/j.jobe.2018.11.018 |
| [18] |
ZHAO Jianjun, LI Shuang. Life cycle cost assessment and multi-criteria decision analysis of environment-friendly building insulation materials-A review[J]. Energy and Buildings, 2022, 254: 111582. DOI:10.1016/j.enbuild.2021.111582 |
| [19] |
WANG Jie, YU Cong, PAN Wei. Relationship between operational energy and life cycle cost performance of high-rise office buildings[J]. Journal of Cleaner Production, 2020, 262: 121300. DOI:10.1016/j.jclepro.2020.121300 |
| [20] |
GOUNNI A, MABROUK M T, EL WAZNA M, et al. Thermal and economic evaluation of new insulation materials for building envelope based on textile waste[J]. Applied Thermal Engineering, 2019, 149: 475. DOI:10.1016/j.applthermaleng.2018.12.057 |
| [21] |
VINCELAS F F C, GHISLAIN T. The determination of the most economical combination between external wall and the optimum insulation material in Cameroonian's buildings[J]. Journal of Building Engineering, 2017, 9: 155. DOI:10.1016/j.jobe.2016.12.008 |
| [22] |
黑龙江省居住建筑节能设计标准: DB 23/1270—2019[S]. 哈尔滨: 黑龙江省住房和城乡建设厅, 2019 Design standard for energy efficiency of residential buildings in Heilongjiang province: DB 23/1270—2019[S]. Harbin: Department of Housing and Urban-Rural Development of Heilongjiang Province, 2019 |
| [23] |
建筑施工模板安全技术规范: JGJ 162—2008[S]. 北京: 中国建筑工业出版社, 2008 Technical code for safety of forms in construction: JGJ 162—2008[S]. Beijing: China Architecture & Building Press, 2008 |
| [24] |
谢馨媛. 轻木夹层板弯曲性能分析[D]. 南宁: 广西大学, 2013 XIE Xinyuan. Bending properties analysis of sandwich plates with balsa core[D]. Nanning: Guangxi University, 2013 |
| [25] |
LIM H, KIM T, CHO H, et al. Simulation-based planning model for table formwork operation in tall building construction[J]. Journal of Asian Architecture and Building Engineering, 2017, 16(1): 115. DOI:10.3130/jaabe.16.115 |
| [26] |
丁一宁, 丁宁, 李冬. 玄武岩纤维和玻璃纤维的耐碱性及其网格布对混凝土双向板弯曲性能的影响[J]. 复合材料学报, 2020, 37(1): 214. DING Yining, DING Ning, LI Dong. Alkaline resistance of basalt fiber and glass fiber and the effect of fiber mesh on biaxial flexural behavior of concrete slab[J]. Acta Materiae Compositae Sinica, 2020, 37(1): 214. DOI:10.13801/j.cnki.fhclxb.20190429.001 |
| [27] |
常晋. 玻化微珠保温混凝土空心剪力墙热工性能研究[D]. 太原: 太原理工大学, 2016 CHANG Jin. Research on thermal performance of thermal insulation glazed hollow bead concrete hollow shear walls[D]. Taiyuan: Taiyuan University of Technology, 2016 |
 2024, Vol. 56
2024, Vol. 56


