2. 结构工程与抗震教育部重点实验室(西安建筑科技大学),西安 710055
2. Key Lab of Structural Engineering and Earthquake Resistance(Xi'an University of Architecture and Technology), Ministry of Education, Xi'an 710055, China
地震作用下,RC构件的非线性变形主要集中于塑性铰区域,包括弯曲、剪切和滑移变形3部分[1]。研究表明,RC柱端部锚固区黏结滑移效应引起的柱顶部水平位移可达总位移的30%以上[2]。对于遭受氯盐侵蚀后的锈蚀RC构件[3-4],其钢筋肋锈损、疏松的锈蚀产物填充在钢筋与混凝土界面处,保护层锈胀开裂和箍筋锈蚀降低约束作用,这些都将严重劣化钢筋与混凝土间黏结性能,进而影响构件整体变形能力。
锈蚀钢筋混凝土黏结性能试验及本构模型是研究黏结性能退化规律,以及开展考虑滑移变形数值模拟的基础[5]。近年来,国内外进行了大量锈蚀黏结性能试验研究,并建立了锈蚀黏结滑移本构模型。如,袁迎曙等[6]、Feng等[7]、Kivell[8]分别基于试验数据建立了各类分段式黏结滑移模型。Jiang等[9]将锈蚀黏结性能的降低归因为材料特性和约束能力的劣化,通过修正现有模型[10]建立了连续的锈蚀黏结滑移模型。然而,现有考虑箍筋锈蚀对黏结性能影响的研究较少,而实际工程中纵筋与箍筋均发生锈蚀,且上述模型大都是分段式模型,不便进行RC构件数值模拟应用。在考虑黏结滑移变形的数值模拟研究方面,Zhao等[11]兼顾计算效率与精度,提出串联零长度纤维单元与普通纤维单元,并将零长度纤维单元中钢筋应力-应变关系替换为应力-滑移关系的思路,广泛用于RC构件数值模拟。如杨红等[12]和Jeon等[13]均采用上述方法对框架结构进行了建模分析,但其滑移量采用经验回归公式计算,且难以考虑纵筋和箍筋锈蚀对黏结性能的影响。
鉴于目前对考虑纵筋和箍筋共同锈蚀后黏结性能劣化规律、本构模型及数值模拟研究方面的不足,采用电渗—恒电流—干湿循环加速锈蚀方法对25个RC试件进行锈蚀,并对其进行拉拔试验,研究了纵筋锈蚀、箍筋锈蚀、保护层厚度和箍筋间距等参数对黏结性能的影响规律,建立并验证了包含各设计参数、箍筋锈蚀和纵筋锈蚀的修正黏结滑移本构模型,进而结合微元算法推导钢筋应力-滑移关系,通过串联零长度纤维单元与普通纤维单元,模拟了锈蚀RC柱抗震性能,并与锈蚀RC柱拟静力试验数据对比验证了模型的可靠性。
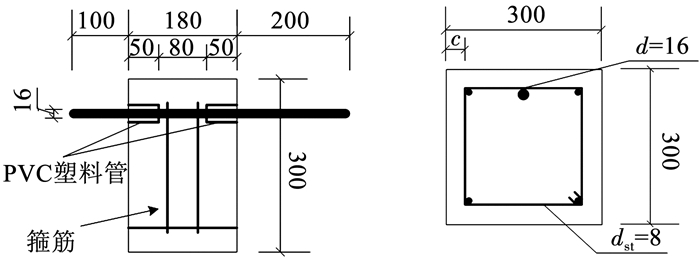
1 试验概况 1.1 试件设计试验以保护层厚度、箍筋间距、锈蚀程度为主要变化参数,共设计制作了25个RC拉拔试件。为使箍筋可以提供有效约束,将试件设置为偏心试件。试件长度为180 mm,截面尺寸为300 mm×300 mm,纵筋和箍筋直径分别为16、8 mm,通过配置不同根数箍筋变化配箍率。为保证黏结力沿锚固长度均匀分布的假定合理,将试件有效黏结长度均设置为5d(d为纵筋直径)。此外,为防止试件端部发生锥形破坏和确保有效黏结长度,在试件两端配置PVC管。试件具体尺寸及配筋见图 1,具体编号见表 1。
|
图 1 试件具体尺寸及配筋(mm) Fig. 1 Specific size and reinforcement of specimen(mm) |
| 表 1 试件参数 Tab. 1 Specimen parameters |
试件采用强度等级为C40的混凝土浇筑,在恒温养护28 d后测得混凝土轴心抗压强度为49.3 MPa,弹性模量为34 500 MPa。试件纵筋采用HRB400钢筋,箍筋采用HPB300钢筋,钢筋力学性能参数见表 2。
| 表 2 钢筋材料的力学性能参数 Tab. 2 Mechanical property parameters of steel bar materials MPa |
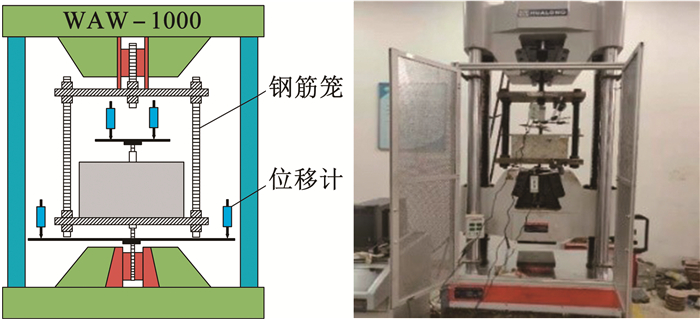
参考文献[14],采用电渗—恒电流—干湿循环的加速锈蚀方法锈蚀钢筋,以获取与自然环境锈蚀形态相似的锈蚀试件。具体锈蚀流程及参数设定方法如下:1)在待锈蚀RC试件两端依次包裹浸润5%氯化钠溶液的吸水海绵,不锈钢网和保水塑料布,将电源负极与靠近纵筋一侧不锈钢网连接,将电源正极与远离纵筋一侧不锈钢网连接,进行电渗试验,参考文献[15],将锈蚀电流密度设置为0.3 mA/cm2,并根据文献[14]确定电渗时长; 2)达到电渗时长后,将电源正极与纵筋连接,作为阳极,电源负极与靠近纵筋一侧不锈钢网连接,作为阴极,进行加速锈蚀; 3)试件恒通电流加速锈蚀4 d后,切断电流,移除试件表面外附吸水海绵,并将试件移至通风处自然干燥3 d,并以此作为一个周期,进行干湿循环。在此锈蚀过程中纵筋和箍筋未隔离将被共同锈蚀。锈蚀完成后,采用WAW-1000电液伺服万能试验机对各试件进行单调拉伸试验,见图 2。采用等速位移控制加载方式对各试件施加单调荷载,加载速率恒为0.4 mm/min,当钢筋被拔出或试件黏结力完全丧失时停止试验。
|
图 2 加载装置 Fig. 2 Loading device |
拉拔试验完成后,将混凝土敲碎,取出锚固段锈蚀钢筋,使用除锈剂对钢筋进行除锈,并量测锈蚀钢筋质量。为反映钢筋实际锈蚀情况,锈蚀钢筋质量损失率计算公式为
| $ \eta=\frac{m_0-m}{m_0} \times 100 \% $ | (1) |
式中m0是钢筋试样锈蚀前质量,m是钢筋试样清除锈蚀产物后的质量。
假定黏结力沿锚固长度均匀分布,各试件平均黏结强度τ及相对黏结强度Rτ分别为:
| $ \bar{\tau}=\frac{P}{\pi d l} $ | (2) |
| $ R_\tau=\frac{\tau_{\mathrm{u}}(\eta)}{\tau_{\mathrm{u}}(0)} $ | (3) |
式中:P为拉拔力,d为钢筋直径,l为锚固长度,τu(0)和τu(η)分别为未锈蚀和锈蚀率为η的构件黏结强度。
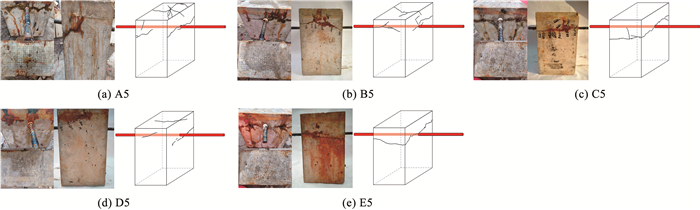
2 试验结果及分析纵筋和箍筋锈蚀都将引起混凝土保护层开裂。纵筋裂缝沿全长发展,箍筋裂缝沿钢筋方向产生放射形微裂纹,未锈蚀箍筋对纵筋裂缝的发展有一定约束作用,但纵筋与箍筋共同锈蚀下裂缝开展模式将更为复杂。图 3展示了严重锈蚀试件的锈胀裂缝扩展图。可以看出,随着箍筋间距减小,锈胀裂缝数量增多,开裂模式更为复杂,这是由于箍筋锈蚀会引起混凝土保护层复杂开裂,并降低对纵筋裂缝的约束,而密排的箍筋和纵筋的锈蚀将直接导致混凝土保护层剥落。随着混凝土保护层厚度的减小,锈胀裂缝数量增多,这是由于混凝土保护层厚度与钢筋直径比值小的试件,锈胀裂缝出现更早,宽度更宽。
|
图 3 试件裂缝扩展 Fig. 3 Crack propagation of specimen |
除锈后的钢筋见图 4。从图 4(a)可以看出,随着目标锈蚀率的增加,钢筋的截面损失程度和坑蚀现象逐渐加重,这是由于钢筋表面存在化学和物理的不均匀性,使得钢筋表面腐蚀性阴离子浓度不同,引起钢筋表面不同位置锈蚀速率不同,进而导致钢筋表面形成宏观蚀坑。此外,从图 4(b)可以看出,钢筋表现出明显的不均匀锈蚀。纵筋靠近混凝土保护层一侧比远离混凝土保护层一侧锈蚀的更严重,箍筋角部锈蚀比较严重,与文献[5, 14, 16]中钢筋锈蚀形态一致。这说明,干湿循环的锈蚀方法可导致钢筋两侧形成氯离子浓度差,造成不均匀锈蚀现象,这与自然环境中钢筋锈蚀是一致的[14]。

|
图 4 除锈后钢筋形态 Fig. 4 Rebar form after rust removal |
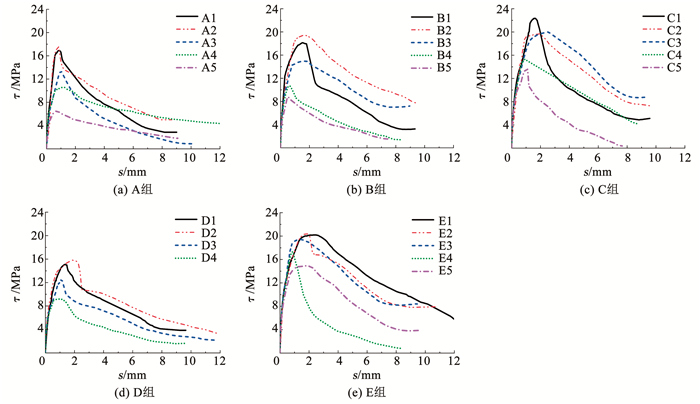
以自由端滑移为横坐标,平均黏结强度为纵坐标,将各试件平均黏结应力-滑移曲线(τ-s)绘制于图 5。由表 3可知,部分试件实际锈蚀率与目标锈蚀率差距较大,且纵筋锈蚀率大于箍筋锈蚀率,可能是由于箍筋的存在使得电化学锈蚀变得更加复杂,导致实际锈蚀结果离散性较大。基于表 3和图 5分析可知,各组试件的黏结强度及相对黏结强度大体上随锈蚀率的增大呈先上升后下降的趋势,这与文献[5, 17-19]研究结果一致,由此可见,锈蚀率较小时,锈蚀会增强钢筋与混凝土间黏结性能,其原因为混凝土发生胀裂破坏前,锈蚀产物会增强外围混凝土对钢筋的握裹作用,进而增加钢筋与混凝土间的摩擦力。但随着锈蚀率增大,锈蚀产物增多,混凝土裂缝逐渐变宽,对钢筋的握裹作用减弱,钢筋截面肋高度和宽度均减小,降低钢筋与混凝土间机械咬合作用,导致试件黏结强度降低。
|
图 5 黏结-滑移曲线 Fig. 5 Bond-slip curves |
| 表 3 拉拔试验结果 Tab. 3 Pull-out test results |
对比A、B、E组试件可知,试件的黏结强度随着保护层厚度的增加逐渐增大,B1试件的黏结强度较A1增加了7.34%,E1试件较B1增加了11.09%。对比B、C、D组试件可知,箍筋间距对黏结强度的影响较大,箍筋间距为40 mm的C1较箍筋间距为60 mm的B1试件黏结强度增加了23.33%,B1较箍筋间距为80 mm的D1试件黏结强度增加了20.31%,由此可知,与保护层厚度相比,箍筋间距对黏结强度的影响更加明显。同时发现在纵筋和箍筋锈蚀率都较低时,箍筋配置较多的C2试件相比于箍筋配置较少的B2、D2试件黏结强度退化速率更快,表明在配箍较高时箍筋锈蚀会对混凝土产生更大的损伤。
3 本构模型建立 3.1 未锈蚀黏结滑移本构模型Wu等[10]提出了统一连续的黏结-滑移模型,简称为Wu模型。该模型考虑了混凝土强度、c/d、箍筋约束等影响因素,可模拟各种钢筋与混凝土界面黏结滑移行为及破坏模式,因此本文基于Wu模型研究锈蚀钢筋混凝土黏结-滑移本构。Wu模型为
| $ \tau=\frac{\tau_{\max }}{\left[\mathrm{e}^{-B \text{In} (B / D) /(B-D)}-\mathrm{e}^{-D \text{In}(B / D) /(B-D)}\right]}\left(\mathrm{e}^{B s}-\mathrm{e}^{D s}\right) $ | (4) |
其模型计算参数为:
| $ \tau_{\max }=\frac{2.5}{1+3.1 \mathrm{e}^{-0.47 K} }\sqrt{f_\mathrm{c}} $ | (5a) |
| $ K=K_{\mathrm{co}}+33 K_{\mathrm{st}} $ | (5b) |
| $ K_{\mathrm{co}}=c / d $ | (5c) |
| $ K_{\mathrm{st}}=A_{\mathrm{st}} /\left(n S_{\mathrm{st}} d\right) $ | (5d) |
| $ B=\frac{0.025\;4+K_{\mathrm{st}}}{-0.023\;2-8.34 K_{\mathrm{st}}} $ | (5e) |
| $ D=3 \text{ln} \left(\frac{0.371\;5+K}{5.176+0.333\;3 K}-0.13\right)-3.375 $ | (5f) |
式中:fc为混凝土强度,Kco和Kst分别为混凝土保护层约束效应和箍筋约束效应,K为混凝土保护层和箍筋约束组合效应,c为保护层厚度,d为纵筋直径,Ast为箍筋肢数总面积,n为受拉纵筋数量,Sst为箍筋间距,s为纵筋滑移,τ为混凝土未锈蚀前的黏结应力。
3.2 锈蚀黏结滑移本构模型钢筋与混凝土接触面间黏结力包括摩擦阻力、化学黏着力和机械咬合力3部分。锈蚀产物导致钢筋与混凝土接触界面软化,从而降低摩擦系数,破坏化学黏着力。纵筋与箍筋锈蚀产物增加,导致钢筋与混凝土间产生较大压力,引起周围混凝土逐渐开裂形成微裂缝,进而降低该区域混凝土强度,劣化机械咬合力。锈蚀过程中,少量锈蚀产物有填充间隙的作用,故轻微锈蚀可在一定程度上增大约束效应,从而增大黏结力。因此,考虑钢筋锈蚀对材料特性和约束效应的影响[9],基于Wu模型[10]建立锈蚀钢筋黏结滑移模型。
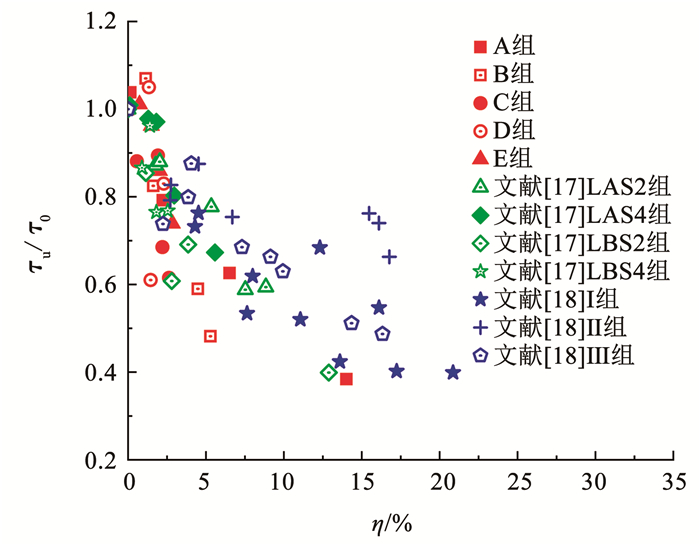
由于试验数据有限,故基于以下原则收集现有研究中钢筋混凝土黏结性能试验数据:1)包含箍筋的拉拔试验,同时保证有效保护层厚度和箍筋提供有效约束; 2)纵筋或箍筋至少有1种被锈蚀。文献[17-18]中箍筋约束试件的相对黏结强度随纵筋锈蚀率的变化见图 6。图 6中每组试件设计参数除锈蚀程度不同外均相同。由图 6可知,不同组试件的相对黏结强度随锈蚀率的退化趋势是不同的,表明锈蚀程度和设计参数对黏结强度影响存在耦合作用。因此,本节基于试验数据,通过多参数非线性拟合方式同时考虑纵筋锈蚀程度、箍筋锈蚀程度和设计参数的耦合作用,建立锈蚀黏结滑移本构模型。
|
图 6 箍筋约束试件黏结强度变化 Fig. 6 Variation of bond strength of stirrup-confined specimens |
纵筋和箍筋锈蚀都将劣化钢筋混凝土材料特性,因此,在Wu模型[10]中引入混凝土强度折减系数F(η, ηstave)来考虑钢筋锈蚀对材料特性的影响,表达式为
| $ \left(\sqrt{f_{\mathrm{c}}}\right)_{\left(\eta, \eta_{\text {stave }}\right)}=\sqrt{f_{\mathrm{c}}} F\left(\eta, \eta_{\text {stave }}\right) $ | (6) |
式中
1) 当纵筋与箍筋未锈蚀时,不影响黏结强度,即F(η=0, ηstave=0)=1;
2) 当纵筋与箍筋完全锈蚀时,黏结强度为0,即F(η=1, ηstave=1)=0;
3) 当纵筋完全锈蚀时,F(η, ηstave)恒等于0;
4) 随着η与ηstave的增加,F(η, ηstave)单调减小。
基于上述条件和试验数据分析,F(η, ηstave)表达式为
| $ \begin{aligned} F\left(\eta, \eta_{\text {stave }}\right)= & \cos \left(\frac{\pi}{2} \eta^{k_1}\right) \times \\ & \left(0.5+0.5 \cos \left(\frac{\pi}{2}\left(\eta^{k_1}+\eta_{\text {stave }}^{k_2}\right)\right)\right) \end{aligned} $ | (7) |
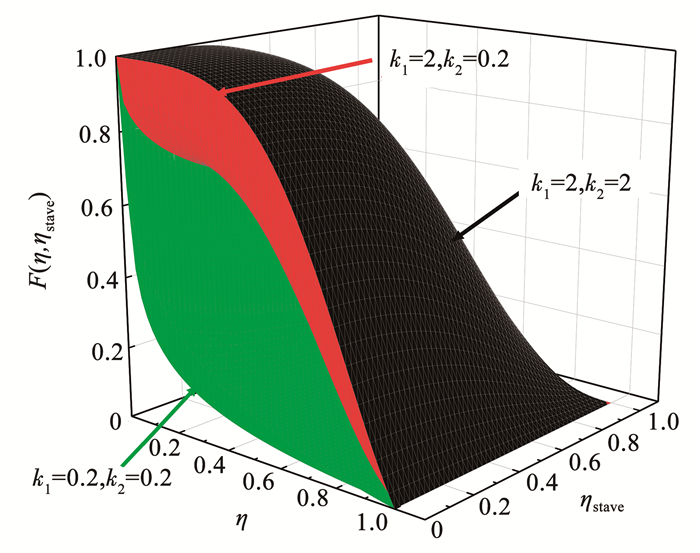
式中k1、k2是待定系数,分别控制F(η, ηstave)随η、ηstave的下降速率,见图 7。通过组合k1、k2的取值,可提供多种类型的等效混凝土强度退化趋势。
|
图 7 F(η, ηstave)随k1 和k2变化趋势 Fig. 7 Change trend of F(η, ηstave) with k1 and k2 |
Wu模型[10]中对约束的考虑包括保护层对纵筋约束效应Kco和箍筋约束效应Kst两方面。因此,可考虑纵筋锈蚀对Kco的影响,以及箍筋锈蚀对Kst的影响,在Wu模型引入保护层约束折减系数G(η)和箍筋约束折减系数H(ηstave),表达式为:
| $ \left(K_{\mathrm{co}}\right)_{(\eta)}=G(\eta) K_{\mathrm{co}} $ | (8) |
| $ \left(K_{\mathrm{st}}\right)_{\left(\eta_{\mathrm{stave}}\right)}=H\left(\eta_{\text {stave }}\right) K_{\mathrm{st}} $ | (9) |
式中:(Kco)(η)和(Kst)(ηstave)(Kco和Kst)分别为锈蚀(未锈蚀)钢筋的保护层约束效应和箍筋约束效应,G(η)和H(ηstave)为修正系数。
根据前述钢筋锈蚀对黏结力影响的分析,以及文献[5, 17-19]可知,当纵筋和箍筋轻微锈蚀时,可在一定程度上增大约束效应,因此,G(η)和H(ηstave)应满足以下条件:
1) 当纵筋未锈蚀(或者,箍筋未锈蚀)时,约束效应不受影响,即G(η=0)=1(或者,H(ηstave=0)=1);
2) 当纵筋完全锈蚀(或者,箍筋完全锈蚀)时,保护层对纵筋约束效应(箍筋约束效应)消失变为0,即G(η=1)=0(或者,H(ηstave=1)=0);
3) 随着η(ηstave)增大,G(η)(H(ηstave))先增大后减小。
基于上述分析和试验数据的变化规律,G(η)和H(ηstave)表达式为:
| $ G(\eta)=\frac{1-\eta}{\left(k_3 \eta^2+k_4 \eta+1\right)} $ | (10) |
| $ H\left(\eta_{\text {stave }}\right)=\frac{1-\eta_{\text {stave }}}{k_5 \eta_{\text {stave }}^2+k_6 \eta_{\text {stave }}+1} $ | (11) |
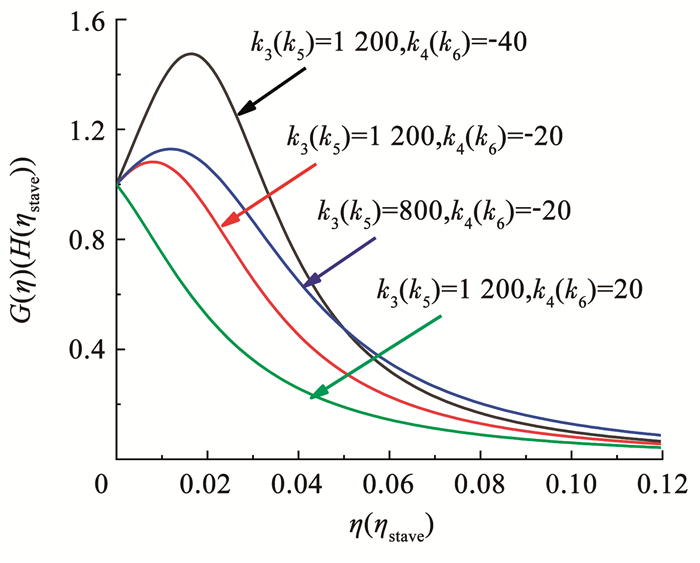
式中k3、k4、k5、k6为待定系数。可通过改变k3、k4、k5、k6的取值获得各种曲线趋势,见图 8。
|
图 8 G(η)(H(ηstave))随不同系数变化趋势 Fig. 8 Change trend of G(η)(H(ηstave)) with different coefficients |
考虑纵筋和箍筋锈蚀影响的(τmax)(η, ηstave)计算公式为
| $ \left(\tau_{\text {max }}\right)_{\left(\eta, \eta_{\text {stave }}\right)}=\frac{2.5\left(\sqrt{f_{\mathrm{c}}}\right)_{\left(\eta, \eta_{\text {stave }}\right)}}{1+3 \cdot 1 \mathrm{e}^{-0.47\left(\left(K_{\text {co }}\right)_{(\eta)}+33\left(K_{\mathrm{st}}\right)_{\eta_{\text {stave }}}\right)}} $ | (12) |
将式(12)和式(7)代入式(3)中,相对黏结强度
| $ R_\tau\left(\eta, \eta_{\text {stave }}\right)=\frac{F\left(\eta, \eta_{\text {stave }}\right)\left[1+3.1 \mathrm{e}^{-0.47\left(K_{\mathrm{co}}+33 K_{\mathrm{st}}\right)}\right]}{1+3.1 \text {e}^{-0.47\left(\frac{1-\eta}{1+k_3 \eta+k_4 \eta^2} K_{\text {co }}+33 \frac{1-\eta_{\text {stave }}}{1+k_5 \eta_{\text {stave }}+k_6 \eta_{\text {stave }}^2} K_{\text {st }}\right)}} $ | (13) |
基于公式(13)与表 3及文献[17-18]试验数据(η、ηstave、Kco、Kst和Rτ),通过非线性拟合分析求取各个待定系数如下:k1=0.346、k2=0.727、k3=-20.100、k4=3.247、k5=0.911、k6=-2.266。
综上所述,所提出锈蚀钢筋黏结-滑移本构模型为
| $ \tau_{\left(\eta, \eta_{\text {stave }}\right)}=\frac{\left(\tau_{\text {max }}\right)_{\left(\eta, \eta_{\text {stave }}\right)}}{\left[\mathrm{e}^{-B \text{In}(B / D) /(B-D)}-\mathrm{e}^{-D \text{In} (B / D) /(B-D)}\right]}\left(\mathrm{e}^{B s}-\mathrm{e}^{D s}\right) $ | (14) |
其模型计算参数为:
| $ \left(\tau_{\max }\right)_{\left(\eta, \eta_{\text {stave }}\right)}=\frac{2.5\left(\sqrt{f_{\mathrm{c}}}\right)_{\left(\eta, \eta_{\mathrm{stave}}\right)}}{1+3.1 \mathrm{e}^{-0.47\left(\left(K_{\mathrm{co}}\right)_{(\eta)}+33\left(K_{\mathrm{st}}\right) \eta_{\text {stave }}\right)}} $ | (15a) |
| $ \begin{aligned} \left(\sqrt{f_{\mathrm{c}}}\right)_{\left(\eta, \eta_{\mathrm{stave}}\right)}= & \sqrt{f_{\mathrm{c}}} \cos \left(\frac{\pi}{2} \eta^{0.346}\right) \times \\ & \left(0.5+0.5 \cos \left(\frac{\pi}{2}\left(\eta^{0.346}+\eta_{\mathrm{stave}}^{0.727}\right)\right)\right) \end{aligned} $ | (15b) |
| $ (K)_{\left(\eta, \eta_{\text {stave }}\right)}=\left(K_{\mathrm{co}}\right)_{(\eta)}+33\left(K_{\mathrm{st}}\right)_{\eta_{\text {stave }}} $ | (15c) |
| $ \left(K_{\mathrm{co}}\right)_{(\eta)}=\frac{c}{d} \frac{1-\eta}{-20.100 \eta^2+3.247 \eta+1} $ | (15d) |
| $ \left(K_{\mathrm{st}}\right)_{\left(\eta_{\mathrm{stave}}\right)}=\frac{A_{\mathrm{st}}}{\left(n S_{\mathrm{st}} d\right)} \frac{1-\eta_{\mathrm{stave}}}{0.911 \eta_{\mathrm{stave}}^2-2.266 \eta_{\mathrm{stave}}+1} $ | (15e) |
| $ B=\frac{0.025\;4+\left(K_{\mathrm{st}}\right)_{\eta_{\mathrm{stave}}}}{-0.023\;2-8.34\left(K_{\mathrm{st}}\right)_{\eta_{\text {stave }}}} $ | (15f) |
| $ D=3 \text{ln} \left(\frac{0.731\;5+K_{\left(\eta, \eta_{\text {stave }}\right)}}{5.176+0.333\;3 K_{\left(\eta, \eta_{\text {stave }}\right)}}-0.13\right)-3.375 $ | (15g) |
式中:τ(η, ηstave)表示滑移量为s时锈蚀钢筋与混凝土界面黏结应力,K(η, ηstave)为考虑纵筋和箍筋锈蚀影响的混凝土保护层和箍筋组合约束效应, 式中其他参数含义见前文所述。
3.3 模型验证文献[17]建立了同时考虑箍筋和纵筋锈蚀的黏结强度计算公式:
| $ \tau_{\mathrm{u}}\left(\eta, \eta_{\text {stave }}\right)=\tau_{\mathrm{u}}(0) R_{\mathrm{st}} R_{\mathrm{m}} $ | (16a) |
| $ \begin{array}{l} \tau_{\mathrm{u}}(0)=13.5\left(\frac{f_{\mathrm{cm}}}{25}\right)^{0.25}\left(\frac{d}{l}\right)^{0.45}\left(\frac{25}{d}\right)^{0.2} \times \\ \;\;\;\;\;\;\;\;\;\;\;{\left[\left(\frac{c_{\text {min }}}{d}\right)^{0.25}\left(\frac{c_{\text {max }}}{c_{\text {min }}}\right)^{0.1}+k_{\mathrm{m}} K_{\mathrm{tr}}\right]} \end{array} $ | (16b) |
| $ R_{\mathrm{m}}=\left\{\begin{array}{cc} 1, & \eta \leqslant 1.5 \% \\ \mathrm{e}^{-\delta(\eta-1.5 \%)}, & \eta>1.5 \% \end{array}\right. $ | (16c) |
| $ R_{\mathrm{st}}=1-0.68 \eta_{\text {stave }} $ | (16d) |
式中:τu(0)为未锈蚀黏结强度,Rst和Rm分别为考虑箍筋锈蚀和纵筋锈蚀的黏结强度修正系数,其他参数含义见文献[17]。
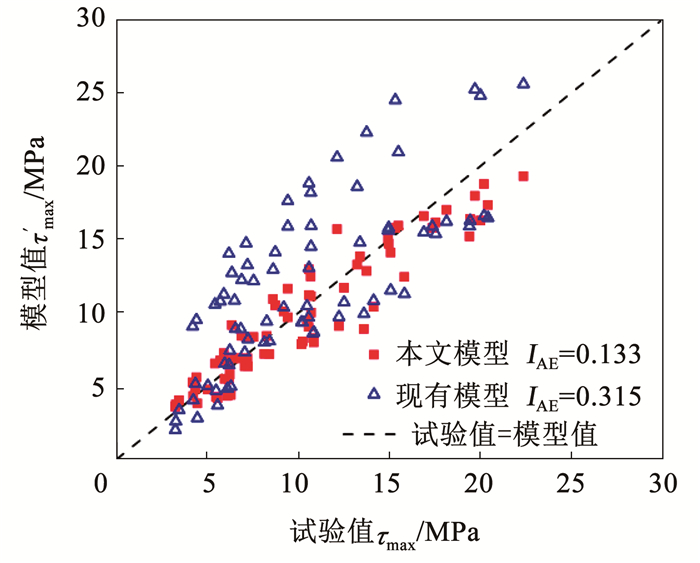
采用现有模型(式(16))和本文模型(式(15))分别计算各试件的黏结强度,并与试验值进行对比,见图 9。采用整体误差指数IAE[9]说明试验数据与模型预测结果的吻合程度,采用计算误差Ef说明计算试验曲线与模型曲线的误差,并将曲线对比图绘制于图 10。IAE和Ef计算公式分别为:
| $ I_{\mathrm{AE}}=\sum \frac{\left|V_{\mathrm{t}}-V_{\mathrm{m}}\right|}{\sum\left|V_{\mathrm{t}}\right|} $ | (17) |
| $ E_{\mathrm{f}}=\frac{1}{\max \left(\left|\tau_i\right|\right)} \sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\tau_i-\tau_i^{\prime}\right)^2} $ | (18) |
|
图 9 模型与试验黏结强度对比 Fig. 9 Comparison of bond strength between model and test |
|
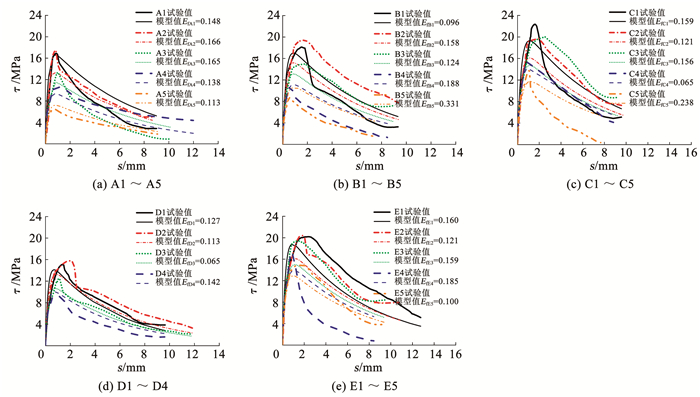
图 10 所建模型与试验黏结-滑移曲线对比 Fig. 10 Comparison of bond-slip curves between model and test |
式中:Vt和Vm分别为试验和理论结果,IAE越小表明模型结果与理论结果吻合程度越好,i代表第i个数据点,n为数据点总数,τi、τi′分别为第i个数据点黏结应力的试验值与计算值。
从图 9可以看出,本文模型预测结果的离散程度显著小于现有模型,且其与试验结果吻合程度远大于现有模型,表明本文模型具有更高的预测精度。随着试件锈蚀程度的增加,现有模型中不同设计参数下试件的黏结强度退化规律相同,而本文模型可以考虑不同设计参数下锈蚀黏结强度退化规律的差异性,这与试验结果一致。由图 10可以看出,所建模型黏结滑移曲线与拉拔试验黏结滑移曲线形状吻合程度较好,大部分试件的Ef小于0.2。综上,所建模型在计算锈蚀钢筋混凝土黏结强度上具有较好精度和适用性。
4 考虑黏结滑移的锈蚀RC构件数值模拟参考文献[11],本节基于OpenSees平台,将现有的锈蚀材料本构模型应用于上部纤维单元,以模拟构件弯曲变形,并结合微元算法[20]及3.2节所提模型,推导出修正的纵筋应力-滑移本构模型,用于底部零长度截面单元,以模拟构件黏结滑移变形,建立了考虑黏结滑移的锈蚀RC构件纤维模型。
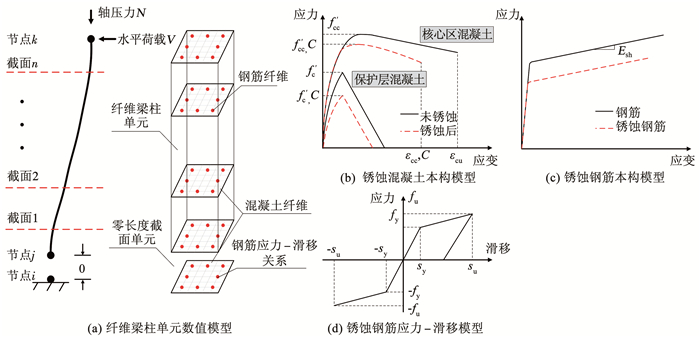
4.1 数值建模方法基于OpenSees平台,采用纤维梁柱单元模拟RC构件弯曲变形,并将钢筋滑移纳入纤维分析,采用零长度纤维截面单元模拟滑移变形[11],建立了可考虑黏结滑移行为的锈蚀RC构件数值模型,见图 11。其中,节点i和j之间为零长度截面单元。
|
图 11 锈蚀RC构件数值模型 Fig. 11 Numerical model of corroded RC components |
约束混凝土应力-应变曲线采用Mander模型[21]计算,保护层混凝土应力-应变曲线采用Kent-Scott-Park模型[22]计算。钢筋锈蚀会引起混凝土保护层开裂,强度退化,箍筋对核心区混凝土约束能力降低,因此,参考文献[23-24]分别对保护层混凝土和核心区混凝土单轴材料特性进行修正。纤维梁柱单元截面中的钢筋本构采用Steel02本构模型,参考文献[25]对锈蚀钢筋屈服强度和极限强度进行修正。数值模型中各类锈蚀材料特征点参数计算如上述所示,滞回规则参数定义与未锈蚀材料相同。
零长度截面中钢筋的本构由纵筋应力-滑移模型代替。基于OpenSees中Hysteretic材料建立钢筋应力-滑移关系,该关系中骨架曲线控制参数包括钢筋达到屈服应力和极限应力时的滑移值,根据4.2节推导过程确定。滞回规则控制参数取值如下:参考文献[11],变形捏缩控制参数取值为0,力捏缩控制参数取值为0.02,由于不考虑基于延性和基于能量的损伤退化,损伤参数均取值为0。此外,为保证上部纤维单元与零长度截面单元变形协调[1, 26],不改变混凝土应力,修正零长度截面单元中混凝土应变为
| $ \varepsilon_{\mathrm{cs}}=\frac{\varepsilon_{\mathrm{c}} s_{\mathrm{y}}}{\varepsilon_{\mathrm{y}}} $ | (19) |
式中:εcs为修正混凝土应变,εc为混凝土峰值应变,sy为钢筋屈服时滑移值,εy为钢筋屈服应变。
4.2 纵筋应力-滑移模型基于上述所建黏结-滑移本构关系,结合微元算法[20](见图 12),可推导出构件端部纵筋达到屈服应力和极限应力时的滑移值。由图 12可知,在微段内纵筋同时满足平衡方程与相容方程:
| $ A_{\mathrm{s}} \times \mathrm{d} f_{\mathrm{s}}=\tau \times C \mathrm{d} x $ | (20) |
| $ \mathrm{d} s=\varepsilon_{\mathrm{s}} \times \mathrm{d} x $ | (21) |

|
图 12 微元算法过程 Fig. 12 Infinitesimal algorithm process |
式中:As为纵筋截面积,dfs为微段内纵筋应力增量,τ为黏结力,C为纵筋截面周长,dx为所取微段。ds为微段的滑移,εs为纵筋应变。
假设微段dx内黏结应力均匀分布,基于平衡方程和相容方程,在一定容许误差范围内,考虑钢筋应力传递结束点的边界条件(τ=0,fs=0,s=0,εs=0),通过微元算法可迭代求解构件端部纵筋达到屈服应力和极限应力时的滑移值。
具体过程如下:
1) 将钢筋加载端处滑移s(1)赋值为较小值δ。为寻找滑移值s(1)=δ时的纵筋应力fs(1),同时将初始值fs0(1)赋值给钢筋加载端处应力。
2) 假定各微段黏结力均匀分布,根据锈蚀黏结-滑移本构模型(式(14)、(15))计算黏结应力τ(1)。
3) 由平衡方程(式(20))计算第二段l2开始处纵筋应力fs(2)=fs0(1)-(τ(1)Cdx)/As,随后根据相容方程(式(21))计算相应的纵筋滑移s(2)=s(1)-εs(1)dx。
4) 根据平衡方程和相容方程逐步计算后续微段的纵筋应力和滑移,并不断修改初始值fs0(1)的值,直至满足钢筋应力传递结束点(该点定为m)的边界条件(fs(m)=0,s(m)=0),此时修改后的fs(1)就是相应s(1)的解。
5) 叠加步骤1)中较小值δ(δ=δ+Δδ),并重复步骤3)~步骤5),即可得到构件端部纵筋达到屈服应力和极限应力时的滑移值。
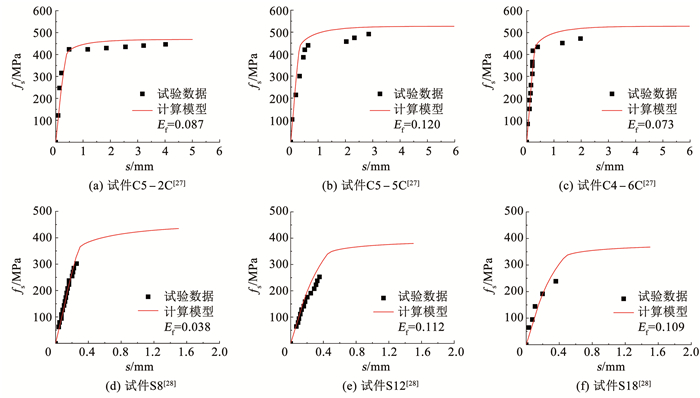
为验证本文提出的纵筋应力-滑移计算模型的准确性,所选取的钢筋锚固长度需足够充分,且保证拉拔试验过程中试件自由端未产生滑移,因此搜集文献[27-28]的拉拔试验结果进行验证。其中,试验数据选取加载端处钢筋应力滑移值。绘制试验结果与模型计算的钢筋应力-滑移曲线对比图,见图 13。采用式(18)计算试验应力数据与模型钢筋应力值的误差Ef,可以看出,所有试件的Ef均小于0.15,所建应力-滑移模型与试验数据吻合程度较好,且可以反映钢筋屈服后的硬化现象。综上可知,所提出的钢筋应力-滑移本构模型具有良好的精度,可综合反映钢筋弹塑性变形下的滑移情况,为RC结构数值模拟提供理论支撑。
|
图 13 试验数据与所建纵筋应力-滑移模型对比 Fig. 13 Comparison between test data and established longitudinal reinforcement stress-slip model |
选取文献[29]中的弯曲破坏锈蚀RC柱作为模拟对象。所选RC柱均进行了加速腐蚀试验和拟静力试验,试验变量为锈蚀程度和轴压比,设计参数和数值模拟中使用的材料特性参数见表 4,试件的具体截面尺寸和配筋细节见文献[29]。
| 表 4 RC试验柱参数及数值模拟计算参数 Tab. 4 RC test column parameters and numerical simulation calculation parameters |
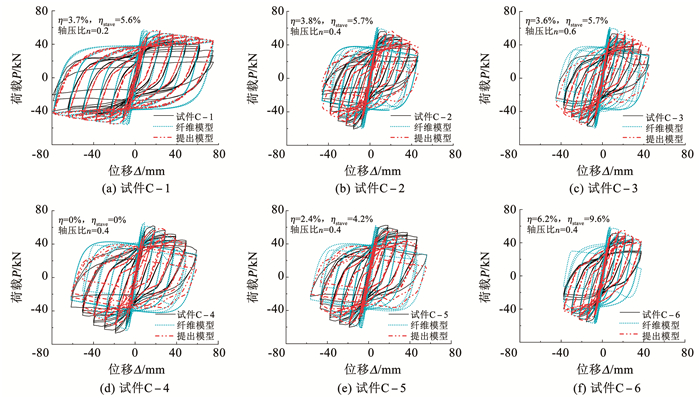
分别采用考虑材料特性退化的纤维模型和考虑黏结效应的数值模型(见图 11,以下称为提出模型)对锈蚀RC柱的拟静力试验结果进行数值模拟,模拟结果见图 14。试验曲线与两种模型模拟曲线的承载力误差Eforce、耗能误差Eenergy[30]和极限位移误差Edisp计算公式为:
| $ E_{\text {force }}=\sqrt{\frac{\sum\limits_{i=1}^n\left(F_{\mathrm{c}}^i-F_{\mathrm{t}}^i\right)^2}{n\left(\max \left(F_{\mathrm{t}}\right)\right)^2}} $ | (22) |
| $ E_{\text {energy }}=\left|\frac{\varOmega_{\mathrm{c}}-\varOmega_{\mathrm{t}}}{\varOmega_{\mathrm{t}}}\right| $ | (23) |
| $ E_{\text {disp }}=\left|\frac{\mathit{\Delta}_{\mathrm{c}}-\mathit{\Delta}_{\mathrm{t}}}{\mathit{\Delta}_{\mathrm{t}}}\right| $ | (24) |
|
图 14 滞回曲线对比 Fig. 14 Hysteretic curves comparison |
式中:Eforce为承载力误差,Eenergy为累积耗能误差,Edisp为极限位移误差,计算结果见表 5,Fci和Fti分别为滞回曲线第i圈滞回环峰值荷载模拟值与试验值,n为滞回环数量,max(Ft)为所有滞回环的最大峰值荷载试验值,Ωc和Ωt分别为滞回曲线累积耗能模拟值与试验值,Δc和Δt分别为极限位移模拟值与试验值。
| 表 5 模拟与试验误差对比 Tab. 5 Comparison of simulation and test errors |
由图 14可知,相对未考虑黏结滑移效应的纤维模型,提出模型的计算滞回曲线与试验数据更为接近。不同锈蚀程度和轴压比下,提出模型计算结果与试验承载能力和滞回环形状均吻合较好,可反映出锈蚀程度增加引发滑移量增大及捏缩程度加剧现象。由表 5可知,提出模型的承载力、累计耗能和极限位移误差均值分别为7.8%、14.5%和10.2%,比纤维模型分别降低12.8%、23.5%和14.2%,计算精度明显提高。上述验证分析表明: 黏结滑移变形是影响锈蚀RC柱整体响应的重要因素,需被包括在构件响应分析中;采用3.2节所建立的锈蚀黏结滑移本构关系以及基于纤维模型的数值建模方法,可准确预测锈蚀RC柱的整体响应并合理计算钢筋滑移的贡献。
5 结论基于25组短锚固锈蚀拉拔试验数据,建立并验证了包含保护层厚度、箍筋间距、箍筋锈蚀率和纵筋锈蚀率等参数的锈蚀钢筋混凝土黏结滑移本构模型,随后结合微元算法、纤维梁柱单元和零长度截面单元,将锈蚀钢筋混凝土黏结滑移模型应用到锈蚀RC柱数值模型中, 主要结论如下:
1) 纵筋和箍筋轻微锈蚀对黏结力有一定增强作用,但随着锈蚀率增大,黏结强度不断降低。增加保护层厚度可略微增加黏结强度,而加密箍筋对黏结强度提升明显。
2) 将锈蚀对黏结性能的影响归因于材料性能和约束能力劣化,在Wu模型中引入混凝土强度折减系数、保护层约束折减系数和箍筋约束折减系数,建立了锈蚀钢筋混凝土黏结滑移模型,且与锈蚀拉拔试验结果吻合较好。
3) 基于微元算法、纤维梁柱单元和零长度截面单元,将锈蚀钢筋混凝土黏结滑移模型应用到锈蚀RC柱数值模型中,为锈蚀RC构件抗震性能模拟提供理论参考。
| [1] |
张艺欣, 郑山锁, 荣先亮, 等. 考虑粘结滑移的冻融损伤纤维梁柱模型研究[J]. 工程力学, 2020, 37(9): 208. ZHANG Yixin, ZHENG Shansuo, RONG Xianliang, et al. Research on freeze-thaw damage model of fiber beam-column considering reinforcement slip effect[J]. Engineering Mechanics, 2020, 37(9): 208. DOI:10.6052/j.issn.1000-4750.2019.11.0657 |
| [2] |
SAATCIOGLU M, ALSIWAT J M, OZCEBE G. Hysteretic behavior of anchorage slip in R/C members[J]. Journal of Structural Engineering, 1992, 118(9): 2439. DOI:10.1061/(ASCE)0733-9445(1992)118:9(2439) |
| [3] |
张白, 陈俊, 杨鸥, 等. 试件尺寸对锈蚀钢筋与混凝土间黏结性能的影响[J]. 哈尔滨工业大学学报, 2018, 50(12): 89. ZHANG Bai, CHEN Jun, YANG Ou, et al. Influence of specimen size on bond performance between corroded reinforcing steel bars and concrete[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 89. DOI:10.11918/j.issn.0367-6234.201803017 |
| [4] |
王朝阳, 杨鸥, 霍静思. 锈蚀钢筋与混凝土间黏结性能试验[J]. 哈尔滨工业大学学报, 2018, 50(8): 150. WANG Chaoyang, YANG Ou, HUO Jingsi, et al. Experimental study on bond performance between corroded bar and concrete[J]. Journal of Harbin Institute of Technology, 2018, 50(8): 150. DOI:10.11918/j.issn.0367-6234.201707144 |
| [5] |
林红威. 单调及重复荷载作用下锈蚀钢筋混凝土粘结性能试验研究[D]. 杭州: 浙江大学, 2017
|
| [6] |
袁迎曙, 余索, 贾福萍. 锈蚀钢筋混凝土的粘结性能退化的试验研究[J]. 工业建筑, 1999, 29(11): 47. YUAN Yingshu, YU Suo, JIA Fuping. Deterioration of bond behavior of corroded reinforced concrete[J]. Industrial Construction, 1999, 29(11): 47. DOI:10.3321/j.issn:1000-8993.1999.11.011 |
| [7] |
FENG Qian, VISINTIN P, OEHLERS D J. Deterioration of bond-slip due to corrosion of steel reinforcement in reinforced concrete[J]. Magazine of Concrete Research, 2016, 68(15): 768. DOI:10.1680/jmacr.15.00217 |
| [8] |
KIVELL A. Effects of bond deterioration due to corrosion on seismic performance of reinforced concrete structures[D]. Christchurch: University of Canterbury, 2012
|
| [9] |
JIANG Cheng, WU Yufei, DAI Mingjiang. Degradation of steel-to-concrete bond due to corrosion[J]. Construction and Building Materials, 2018, 158: 1073. DOI:10.1016/j.conbuildmat.2017.09.142 |
| [10] |
WU Yufei, ZHAO Xuemei. Unified bond stress-slip model for reinforced concrete[J]. Journal of Structural Engineering, 2013, 139(11): 1951. DOI:10.1061/(ASCE)ST.1943-541X.0000747 |
| [11] |
ZHAO J, SRITHARAN S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI Structural Journal, 2007, 104(2): 133. |
| [12] |
杨红, 徐海英, 王志军. 考虑柱底纵筋滑移的纤维模型及框架地震反应分析[J]. 建筑结构学报, 2009, 30(4): 130. YANG Hong, XU Haiying, WANG Zhijun. Seismic responses analysis of RC frame based on fiber model considering bar slippage at column bottom section[J]. Journal of Building Structures, 2009, 30(4): 130. DOI:10.3321/j.issn:1000-6869.2009.04.016 |
| [13] |
JEON J S, LOWES L N, DESROCHES R, et al. Fragility curves for non-ductile reinforced concrete frames that exhibit different component response mechanisms[J]. Engineering Structures, 2015, 85: 127. DOI:10.1016/j.engstruct.2014.12.009 |
| [14] |
金伟良, 夏晋, 王海龙. 内置电极模拟混凝土中钢筋非均匀锈蚀的加速试验方法: CN101762453B[P]. 2010-06-30
|
| [15] |
LIN Hongwei, ZHAO Yuxi, OŽBOLT J, et al. Bond strength evaluation of corroded steel bars via the surface crack width induced by reinforcement corrosion[J]. Engineering Structures, 2017, 152: 506. DOI:10.1016/j.engstruct.2017.08.051 |
| [16] |
金南国, 何家豪, 付传清, 等. 钢筋加速非均匀锈蚀试验方法和锈蚀形态研究[J]. 浙江大学学报(工学版), 2020, 54(3): 483. JIN Nanguo, HE Jiahao, FU Chuanqing, et al. Study on experimental method and morphology of accelerated non-uniform corrosion of steel bars[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(3): 483. DOI:10.3785/j.issn.1008-973X.2020.03.008 |
| [17] |
LIN Hongwei, ZHAO Yuxi, YANG Jiaqi, et al. Effects of the corrosion of main bar and stirrups on the bond behavior of reinforcing steel bar[J]. Construction and Building Materials, 2019, 225: 13. DOI:10.1016/j.conbuildmat.2019.07.156 |
| [18] |
LIN Hongwei, ZHAO Yuxi. Effects of confinements on the bond strength between concrete and corroded steel bars[J]. Construction and Building Materials, 2016, 118: 127. DOI:10.1016/j.conbuildmat.2016.05.040 |
| [19] |
ZHOU Haijun, LU Jinlong, XV Xi, et al. Effects of stirrup corrosion on bond-slip performance of reinforcing steel in concrete: an experimental study[J]. Construction and Building Materials, 2015, 93: 257. DOI:10.1016/j.conbuildmat.2015.05.122 |
| [20] |
HASKETT M, OEHLERS D J, MOHAMED ALI M S. Local and global bond characteristics of steel reinforcing bars[J]. Engineering Structures, 2008, 30(2): 376. DOI:10.1016/j.engstruct.2007.04.007 |
| [21] |
MANDER J, PRIESTLEY M. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [22] |
SCOTT B D, PARK R, PRIESTLEY M. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal, 1982, 79(1): 13. |
| [23] |
CORONELLI D, GAMBAROVA P. Structural assessment of corroded reinforced concrete beams: modeling guidelines[J]. Journal of Structural Engineering, 2004, 130(8): 1214. DOI:10.1061/(ASCE)0733-9445(2004)130:8(1214) |
| [24] |
VU N S, YU Bo, LI Bing. Stress-strain model for confined concrete with corroded transverse reinforcement[J]. Engineering Structures, 2017, 151: 472. DOI:10.1016/j.engstruct.2017.08.049 |
| [25] |
IMPERATORE S, RINALDI Z, DRAGO C. Degradation relationships for the mechanical properties of corroded steel rebars[J]. Construction and Building Materials, 2017, 148: 219. DOI:10.1016/j.conbuildmat.2017.04.209 |
| [26] |
ZHANG Yixin, BICICI E, SEZEN H, et al. Reinforcement slip model considering corrosion effects[J]. Construction and Building Materials, 2020, 235: 117348. DOI:10.1016/j.conbuildmat.2019.117348 |
| [27] |
AMLEH L, MIRZA M S, AHWAZI B B N, et al. Bond deterioration of reinforcing steel in concrete due to corrosion[C]//Challenges of Concrete Construction: Volume 3, Repair, Rejuvenation and Enhancement of Concrete: Proceedings of the International Seminar held at the University of Dundee. Scotland: Thomas Telford, 2002. DOI: 10.1680/RRAEOC.31753.0026
|
| [28] |
郑晓燕. 锈蚀钢筋与混凝土动态粘结性能研究[D]. 南京: 河海大学, 2004
|
| [29] |
郑山锁, 董立国, 左河山, 等. 人工气候环境下锈蚀RC框架柱抗震性能试验研究[J]. 建筑结构学报, 2018, 39(4): 28. ZHENG Shansuo, DONG Liguo, ZUO Heshan, et al. Experimental investigation on seismic behaviors of corroded RC frame columns in artificial climate[J]. Journal of Building Structure, 2018, 39(4): 28. DOI:10.14006/j.jzjgxb.2018.04.004 |
| [30] |
LI Lei, LUO Guangxi, WANG Zhuohan, et al. Prediction of residual behavior for post-earthquake damaged reinforced concrete column based on damage distribution model[J]. Engineering Structures, 2021, 234: 111927. DOI:10.1016/j.engstruct.2021.111927 |
 2024, Vol. 56
2024, Vol. 56



 16
16