2. 中铁十六局集团路桥工程有限公司,北京 101500
2. China Railway 16th Bureau Group Road & Bridge Engineering Co., Ltd., Beijing 101500, China
煤矸石是煤炭在开采、加工时产生最多的矿业固体废弃物,利用率低,占用土地资源。煤矸石自燃、堆放和崩塌还带来了严重的环境污染,造成财产损失、资源浪费等[1-2],如何合理利用煤矸石是当下研究的热点。
煤矸石可通过煅烧提高其活度,配制的煤矸石混凝土具有较高的抗压强度和劈裂强度,可以满足混凝土的工程要求[3-4]。Yz等[5]研究煤矸石取代率和粒径分布对混凝土力学性能的影响,发现当取代率为100%时,抗压强度、抗拉强度和弹性模量分别下降19.4%、36.1%和32.2%,而煤矸石粒径分布对混凝土力学性能的影响不显著。Zhang等[6]采用正交试验设计方法,研究煤矸石的取代率对混凝土抗压强度、导热系数、施工性能和干密度的影响,结果表明,煤矸石取代率为30%时,混凝土的综合强度最佳。Zhou等[7]采用自燃煤矸石取代天然碎石制备混凝土,进行力学试验与微观结构特征表征,结果表明,随取代率的提升,破坏形式由剪切破坏变为纵向劈裂破坏,峰值应力减小,但峰值应变增加。Long等[8]研究了废弃煤矸石骨料加固新型水泥土的力学性能和耐久性,发现煤矸石的掺入显著提高了水泥土的抗腐蚀能力,并减少酸溶液的渗透。由现有研究可知,煤矸石在建筑行业的资源化利用是疏导煤矸石堆放的正确途径,解决骨料短缺问题的同时减少了碳排放。但由于煤矸石属于碳质页岩或灰岩,强度远低于传统骨料的火成岩(花岗岩、玄武岩),煤矸石骨料的掺入不仅降低混凝土的强度和弹模,而且导致应力-应变曲线峰后脆性特征更明显。如何更好地发挥煤矸石混凝土的力学性能是亟待解决的问题。
钢管混凝土是将混凝土填充于钢管内的组合结构[9]。钢管混凝土充分利用两种材料的优势,钢管对混凝土提供横向约束,使混凝土处于三轴受压状态,从而提高混凝土强度,避免发生脆性破坏。同时,混凝土的填充避免或延缓了钢管的局部屈曲。多年来,针对钢管煤矸石混凝土柱,研究人员开展了相关工作。Zhang等[10]开展玻璃纤维增强聚合物-煤矸石混凝土-钢管柱轴压试验,结果表明,粗骨料被煤矸石取代后,虽然承载力有所降低,但试件的延性得到显著提升。Li等[11]采用试验研究与理论分析相结合的方法,分析核心混凝土强度对钢管煤矸石混凝土极限承载力的影响,提出了核心混凝土极限抗压强度计算公式。李帼昌等[12-13]研究了含钢率对钢管煤矸石混凝土受弯力学性能的影响,提出了钢管煤矸石混凝土受弯承载力计算公式。方晨[14]利用有限元软件对钢管煤矸石混凝土柱-煤矸石柱连接节点的力学特性进行了模拟分析,与试验结果的对比表明,钢管内的煤矸石混凝土强度对节点性能的影响可以忽略。Gao等[15]将煤矸石混凝土作为钢管混凝土短柱的核心混凝土,分析煤矸石取代率对钢管煤矸石混凝土短柱轴压强度的影响,验证了煤矸石应用于钢管混凝土的可行性。Zhang等[16-17]开展了钢管混凝土和钢管煤矸石混凝土短柱轴压试验,结果表明,煤矸石混凝土较普通混凝土具有更好的横向约束作用。为解决软岩巷道中的大变形问题,并且吸收围岩所带来的变形能量,需要钢管混凝土有一定可压缩性。在深地软岩巷道支护中,常采用煤矸石取代部分粗骨料,制作钢管煤矸石混凝土墩柱,通过在混凝土端部加设垫块使仅混凝土受压,钢管主要起约束作用,受力方式、特点有别于传统钢管混凝土结构[18]。综上,钢管煤矸石混凝土的试验研究已经取得成功,加载方式主要集中于钢-混凝土同时受压的状态,尚缺乏不同加载方式对钢管煤矸石混凝土承载能力影响及破坏机制的报道。
本文以圆钢管煤矸石混凝土为对象开展轴心受压试验,探究加载方式、钢管径厚比和煤矸石取代率对承载力的影响规律,分析各因素对承载力影响的显著程度。为钢管煤矸石混凝土在实际工程中,特别是矿山建设领域的应用提供参考。
1 试验 1.1 试件设计试验共有9组18个钢管煤矸石混凝土试件,具体参数见表 1,其中,CFST代表钢管混凝土。钢管试验尺寸参数: 外径D为127、140、158 mm,壁厚为4 mm,试件长度L为381、420、474 mm,长径比L/D为3,径厚比D/t为31.75、35、39.5。采用C40混凝土,其中,煤矸石取代粗骨料的取代率r为0、50%、100%。煤矸石骨料购自灵寿县沃阳矿产品加工厂,天然放射性核素镭-226、钍-232、钾-40的放射性比活度同时满足内照射指数IRa>2.0和外照射指数Iγ>2.0,可按正常生产工艺要求自由掺配。
| 表 1 试件参数 Tab. 1 Parameters of specimens |
试验用的钢管为直缝焊接钢管,直缝焊接钢管是钢板经过卷曲成型后采用埋弧焊工艺制作而成。拉伸试件取自卷管前的同批次钢板,按GB/T 228.1 —2010《金属材料拉伸试验》[19],设计并制作钢板拉伸试件。钢管试件厚度均为4 mm,故进行3个钢材标准拉伸试件的拉伸试验。拉伸试件尺寸如图 1,试验结果见表 2。

|
图 1 试样尺寸 Fig. 1 Specimen size |
| 表 2 钢管力学性能指标 Tab. 2 Mechanical properties index of steel tube |
按照JGJ 55—2011《普通混凝土配合比设计规程》[20]进行配合比设计,以煤矸石取代率为主要变化参数,目标设计强度等级为C40,采用单位重量法计算各类材料的用量。采用煤矸石作为粗骨料,按照取代率0、50%、100%取代石子。3种取代率煤矸石混凝土各预留制作3块标准立方体试块。采用万能试验机测定抗压强度。煤矸石混凝土配合比及试验结果见表 3。可以看出,煤矸石取代率由0提升至50%,fcu下降8.5 MPa,下降幅度为16%;取代率提升至100%,fcu下降20.3 MPa,下降幅度为38%。煤矸石混凝土立方体抗压强度随煤矸石取代率的增加而减小。
| 表 3 煤矸石混凝土配合比及试验结果 Tab. 3 Coal gangue concrete mix proportion and test results |
本试验采用200 t压力试验机,在钢管两侧布置2个位移传感器,用于测定试件的轴向变形量。在试件中部每隔45°布置8组横、纵向应变片,测定加载过程中钢管的应变变化,布置形式见图 2(a)。竖向荷载有两种加载方式:加载方式A,轴向荷载施加在钢管和混凝土横截面上;加载方式B,轴向荷载仅作用于混凝土。在加载方式B中,因试件对称性,沿上半部纵向均匀布置4组应变片,布置形式见图 2(b)。为使荷载仅作用于混凝土,混凝土上下两端各布置一个圆形钢垫块。在试件上端加入球铰进行自动找平,减小在加工、浇筑过程中试件加载端接触面不平整造成的误差。

|
图 2 应变片、位移计测点布置 Fig. 2 Layout of measuring points for strain gauges and displacement meters |
正式试验前,首先对试件几何对中,进行3次预加载,检查位移计和应变片的工作状况是否正常。加载方案采用位移控制,开始速率为0.1 mm/min,当荷载达到极限荷载之后,缓慢增加加载速率至1~3 mm/min。为保证试验现象显著的同时兼顾安全性,钢管轴向压缩量达极限荷载对应位移的5倍时停止加载。
2 试验结果与分析 2.1 试验现象与破坏形态图 3为试件的最终破坏形态。钢管煤矸石混凝土受加载方式的影响显著,加载方式A为剪切型破坏,加载方式B为腰鼓型破坏。钢管径厚比和煤矸石取代率在本文范围内变化时,并没有影响试件的最终破坏形态。

|
图 3 试件破坏形态 Fig. 3 Failure mode of specimens |
选取CFST-A1为加载方式A的典型试件,破坏形式见图 3(a)~(c)。加载前期处于弹性阶段,钢管与混凝土共同承担竖向荷载,由于混凝土弹性阶段泊松比小于钢材,横向变形小于钢管,二者相互作用较弱,试件外观无明显变化。竖向荷载超过极限荷载70%后,混凝土内部裂缝进入快速发育阶段,泊松比变大,混凝土横向变形大于钢管,二者相互作用显著增强,持续加载,剪切滑移线开始在钢管端部产生,
并逐渐向试件中部延伸。超过极限荷载后,钢管滑移线两端鼓起明显,试件变形速度加快,内部混凝土沿剪切滑移线形成剪切面,最终呈现出剪切型破坏。选取CFST-B1为加载方式B的典型试件,破坏形式见图 3(d)~(f)。仅混凝土受压时,破坏形态为腰鼓型破坏,变形沿试件中部向外鼓起。弹性阶段,仅混凝土承受纵向荷载,试件外观无明显变化。弹塑性阶段至最终破坏,核心混凝土内部开始出现微裂缝而向外膨胀挤压钢管,钢管开始约束混凝土,二者相互约束,钢管中部逐渐鼓曲直至破坏。加载方式B的破坏形式与加载方式A不同,因为前者钢管不承受纵向荷载,主要承受混凝土环向膨胀引起的环向拉力,提供于核心混凝土的约束更大,钢管屈服的主要原因是环向应力,因此, 变形会更为均匀。在轴压试验之后,切割并移除钢管,研究内部核心混凝土的破坏形式。由图 3可以观察到,试件中混凝土的破坏形式与试件整体破坏形式对应一致,许多裂缝的连接形成了核心混凝土的压碎区域。由于钢管的约束作用,混凝土内部的孔隙变得致密,微裂缝闭合,改善了混凝土的力学性能。因此,无论是否加入煤矸石作为粗骨料,试件都表现出相似的破坏形式。
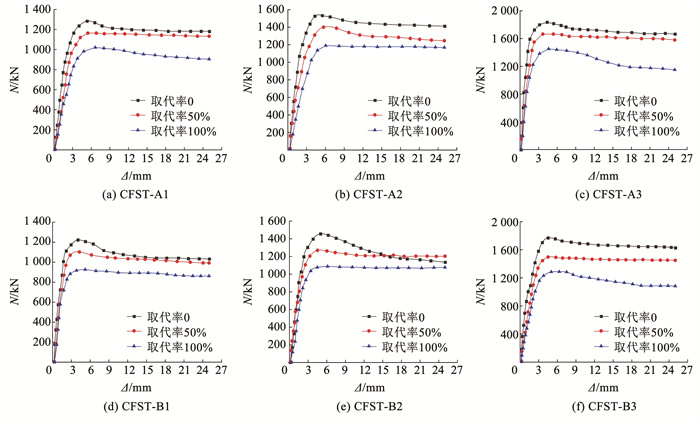
2.2 试件荷载-位移曲线钢管煤矸石混凝土轴压试验极限承载力Nu见表 4。试验竖向荷载-位移曲线如图 4所示。可以看出,弹性阶段各试件的刚度基本一致,近似呈线性关系,上升趋势相同。继续施加荷载,试件进入屈服状态并产生塑性变形,混凝土所产生的裂缝受到钢管的约束抑制,从而提升了试件塑性变形能力,因此,在弹塑性阶段,试件承受的荷载仍会缓慢升高。荷载达到极限荷载时钢管鼓起,煤矸石混凝土内部裂缝开始扩展,最终形成贯通裂缝,核心混凝土压碎,试件破坏,荷载-位移曲线出现下降段。由于钢管的约束效应,荷载-位移曲线在峰值后的下降并不明显,直到加载结束仍具有一定的残余强度,钢管混凝土峰后延性得到显著提升。由于煤矸石粗骨料强度比传统石子低,煤矸石混凝土强度低于普通混凝土,钢管煤矸石混凝土的极限承载力随煤矸石取代率的提升而降低。
| 表 4 试件极限承载力 Tab. 4 Ultimate bearing capacity of specimens |
|
图 4 竖向荷载-位移曲线 Fig. 4 Load - displacement curve |
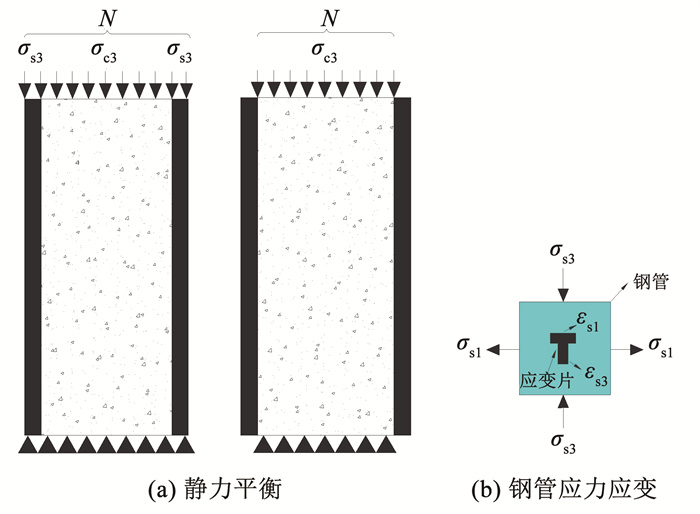
图 5为两种加载方式作用下试件的受力状态。加载过程中钢管混凝土在轴向受压时满足静力平衡条件。
|
图 5 受力状态 Fig. 5 Stress state |
加载方式A:
| $ N=N_{\mathrm{c}}+N_{\mathrm{s}}=A_{\mathrm{c}} \sigma_{\mathrm{c} 3}+A_{\mathrm{s}} \sigma_{\mathrm{s} 3} $ | (1) |
式中:Nc和Ns分别为混凝土和钢管所承担荷载,σc3、σs3分别为混凝土和钢管的纵向应力,Ac和As分别为混凝土和钢管横截面积。
加载方式B:
| $ N=N_\mathrm{c}=A_\mathrm{c} \sigma_{\mathrm{c} 3} $ | (2) |
根据文献[21]钢管应力-应变关系分为3个阶段,见图 5(b)。
1) 弹性工作阶段。根据广义虎克定律得
| $ \left\{\begin{array}{l} \varepsilon_{\mathrm{s} 1}=\frac{1}{E_{\mathrm{s}}}\left(\sigma_1-\mu_{\mathrm{s}} \sigma_{\mathrm{s} 3}\right) \\ \varepsilon_{\mathrm{s} 3}=\frac{1}{E_{\mathrm{s}}}\left(\sigma_{\mathrm{s} 3}-\mu_{\mathrm{s}} \sigma_{\mathrm{s} 1}\right) \end{array}\right. $ | (3) |
式中:εs1和εs3分别为钢管的环向应变和纵向应变,σs1、σs3分别为钢管环向拉应力和纵向压应力。
由式(3)联立推导得
| $ \left\{\begin{array}{l} \sigma_{\mathrm{s} 1}=\left(\frac{E_{\mathrm{s}}}{1-\mu_{\mathrm{s}}^2}\right) \varepsilon_{\mathrm{s} 1}+\left(\frac{E \mu_{\mathrm{s}}}{1-\mu_{\mathrm{s}}^2}\right) \varepsilon_{\mathrm{s} 3} \\ \sigma_{\mathrm{s} 3}=\left(\frac{E_{\mathrm{s}}}{1-\mu_{\mathrm{s}}^2}\right) \varepsilon_{\mathrm{s} 3}+\left(\frac{E \mu_{\mathrm{s}}}{1-\mu_{\mathrm{s}}^2}\right) \varepsilon_{\mathrm{s} 1} \end{array}\right. $ | (4) |
应力强度:
| $ \sigma_{\mathrm{s} 1}^2+\sigma_{\mathrm{s} 3}^2-\sigma_{\mathrm{s} 1} \sigma_{\mathrm{s} 3}=\sigma_i^2 $ | (5) |
σi=fp为弹性阶段和弹塑性阶段的分界点,fp为比例极限。
2) 弹塑性工作阶段。在广义虎克定律的基础上,利用弹性增量理论得
| $ \mathrm{d} \sigma_{\mathrm{s} 1}=\left[\frac{E_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2}\right] \mathrm{d} \varepsilon_{\mathrm{s} 1}+\left[\frac{E_{\mathrm{s}}^{\mathrm{t}} \mu_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2}\right] \mathrm{d} \varepsilon_{\mathrm{s} 3} $ | (6) |
| $ \mathrm{d} \sigma_{\mathrm{s} 3}=\left[\frac{E_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2}\right] \mathrm{d} \varepsilon_{\mathrm{s} 3}+\left[\frac{E_{\mathrm{s}}^{\mathrm{t}} \mu_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2}\right] \mathrm{d} \varepsilon_{\mathrm{s} 1} $ | (7) |
式中:Est为切线模量,μst为弹塑性阶段的泊松比。
Est、μst由下式确定:
| $ E_{\mathrm{s}}^{\mathrm{t}}=\frac{\left(f_{\mathrm{y}}-\sigma_{\mathrm{i}}\right) \sigma_{\mathrm{i}}}{\left(f_{\mathrm{y}}-f_{\mathrm{p}}\right) f_{\mathrm{p}}} E_{\mathrm{s}} $ | (8) |
| $ \mu_{\mathrm{s}}^{\mathrm{t}}=0.217 \frac{\sigma_{\mathrm{i}}-f_{\mathrm{p}}}{f_{\mathrm{y}}-f_{\mathrm{p}}}+0.283 $ | (9) |
叠加式(6)与(7)得
| $ \begin{gathered} \sigma_{\mathrm{s} 1}=\sigma_{\mathrm{s} 1 \mathrm{p}} \sum\limits_{i=k+l}^l\left[\frac{E_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2} \mathrm{~d}\left(\varepsilon_{\mathrm{s} 1(i+1)}-\varepsilon_{\mathrm{s} 1 i}\right)+\right. \\ \left.\frac{E_{\mathrm{s}}^{\mathrm{t}} \mu_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2} \mathrm{~d}\left(\varepsilon_{\mathrm{s} 3(i+1)}-\varepsilon_{\mathrm{s} 3 i}\right)\right] \end{gathered} $ | (10) |
| $ \begin{gathered} \sigma_{\mathrm{s} 3}=\sigma_{\mathrm{s} 3 \mathrm{p}} \sum\limits_{i=k+l}^l\left[\frac{E_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2} \mathrm{~d}\left(\varepsilon_{\mathrm{s} 3(i+1)}-\varepsilon_{\mathrm{s} 3 i}\right)+\right. \\ \left.\frac{E_{\mathrm{s}}^{\mathrm{t}} \mu_{\mathrm{s}}^{\mathrm{t}}}{1-\left(\mu_{\mathrm{s}}^{\mathrm{t}}\right)^2} \mathrm{~d}\left(\varepsilon_{\mathrm{s} 1(i+1)}-\varepsilon_{\mathrm{s} 1 i}\right)\right] \end{gathered} $ | (11) |
σi=fy是弹塑性阶段和塑性阶段得分界点,fy为屈服极限。
3) 塑性工作阶段。根据伊留辛全量理论方程,得出应力和应变关系:
| $ \sigma_{\mathrm{s} 1}=\frac{2 f_y}{3 \varepsilon_{\mathrm{i}}}\left(\varepsilon_{\mathrm{s} 1}-\varepsilon_{\mathrm{s} 2}\right) $ | (12) |
| $ \sigma_{\mathrm{s} 3}=\frac{2 f_y}{3 \varepsilon_{\mathrm{i}}}\left(\varepsilon_{\mathrm{s} 3}-\varepsilon_{\mathrm{s} 2}\right) $ | (13) |
| $ \varepsilon_{\mathrm{i}}=\frac{\sqrt{2}}{3}\left[\left(\varepsilon_{\mathrm{s} 3}-\varepsilon_{\mathrm{s} 1}\right)^2+\left(\varepsilon_{\mathrm{s} 1}-\varepsilon_{\mathrm{s} 2}\right)^2+\left(\varepsilon_{\mathrm{s} 2}-\varepsilon_{\mathrm{s} 3}\right)^2\right]^{1 / 2} $ | (14) |
式中:εi为应变强度,εs2为钢管径向应变。
加载方式A,通过实测应变值,根据式(3)~(14)求出钢管在加载过程中纵向应力,从而求出整个加载过程中钢管所承担的荷载。根据式(1)静力平衡条件,将实测承载力减去钢管所承担的承载力,得到核心煤矸石混凝土承担的承载力。加载方式B,由于钢管不直接承受纵向荷载,实测承载力即为核心混凝土承载力。因此,加载方式A核心混凝土承载力相对变化为(N-Ns)/Acfcu,加载方式B核心混凝土承载力相对变化为N/Acfcu。
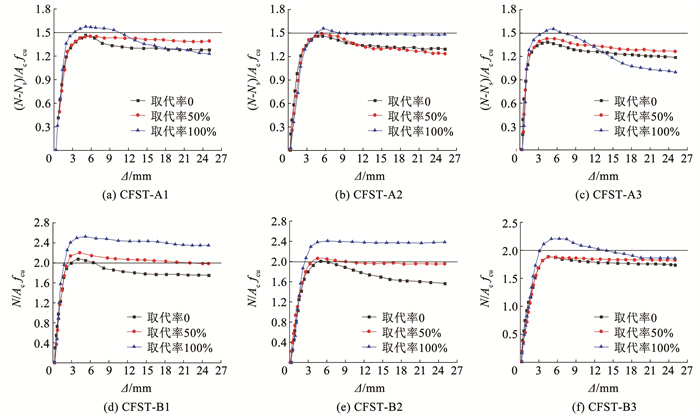
为进一步反映钢管煤矸石混凝土中核心混凝土承载力的相对变化,研究核心煤矸石混凝土的强度提升程度,绘制相应曲线。由图 6(a)~(c)可以看出,在加载方式A中,不同取代率试件在弹性阶段,核心混凝土承载力相对变化基本一致,这是由于钢管与混凝土还未产生显著约束效应。进入弹塑性阶段之后,明显可看出核心混凝土承载力的提升幅度随取代率的增大而增大,表明相对普通混凝土,钢管约束作用对煤矸石混凝土强度提升幅度更大。在不同取代率下,3种径厚比的承载力相对比在1.38~1.57。
|
图 6 核心煤矸石混凝土承载力相对变化 Fig. 6 Relative change of bearing capacity of core coal gangue concrete |
由图 6(d)~(f)可以看出,在加载方式B中,不同取代率试件在整个加载阶段与加载方式A的提升趋势基本一致。不同的是,加载方式B钢管不直接承受纵向荷载,主要对混凝土起到约束作用,约束作用明显高于加载方式A,产生更大的围压。加载方式B中核心混凝土承载力相对比在1.88~2.52,高于加载方式A,表明核心混凝土抗压强度提升更为显著。但随着径厚比的提升,比值呈现降低趋势,钢管对核心煤矸石混凝土的约束作用下降。
两种加载方式作用下,煤矸石混凝土提升幅度均大于普通混凝土,表明钢管煤矸石混凝土更能充分发挥煤矸石混凝土的轴心受压性能。
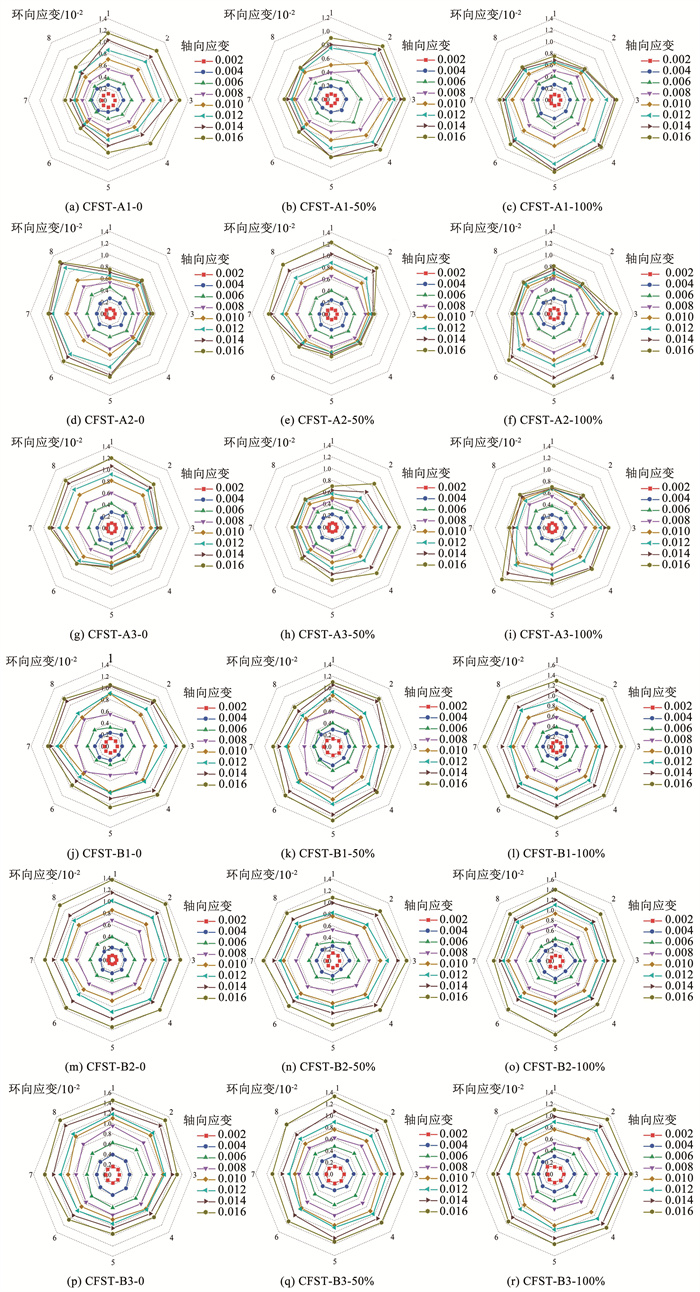
2.4 钢管环向应变分布由钢管环向应变片测得的环向应变绘制试件的钢管环向应变分布,见图 7。图中每一圈由内至外,对应轴向应变0.002~0.016下测点实测的环向应变,1~8表示测点1~8。
|
图 7 钢管应变分布 Fig. 7 Strain distribution of steel tubes |
由图 7(a)~(i)可以看出,加载方式A中弹性阶段各测点环向应变均匀递增,且分布均匀。弹性阶段之后,不同测点对应的环向应变差距逐渐增大。进入塑性阶段后试件产生剪切滑移线,逐渐发生剪切破坏,破坏面测点的环向应变会迅速增大直至破坏,环向应变分布与试件破坏形态高度吻合。在剪切面上发生剪切破坏后,钢管鼓起并产生滑移线,环向应力增大的同时横向变形增大,所对应的环向应变会有突增现象且分布不均匀。另外可看出,煤矸石取代率增加对环向应变分布规律的影响不明显。
由图 7(j)~(r)可以看出,在弹性阶段加载方式B与加载方式A一致,环向应变在各个方向上均匀增加。区别在于弹性阶段之后,发生腰鼓变形,在各个方向上破坏形式较为均匀,环向应变分布均匀。加载方式B中,随着取代率的增加,受煤矸石混凝土强度降低的影响,钢管提供更强的环向约束,环向应变分布更均匀。由于煤矸石混凝土的弹性模量低于普通混凝土,而泊松比高于普通混凝土,与普通混凝土相比,煤矸石混凝土在受压过程中产生的变形更大,核心煤矸石混凝土横向变形发展迅速,钢管对煤矸石混凝土约束效应将更早出现。因此,相对普通混凝土,钢管对煤矸石混凝土可提供更好的横向约束。
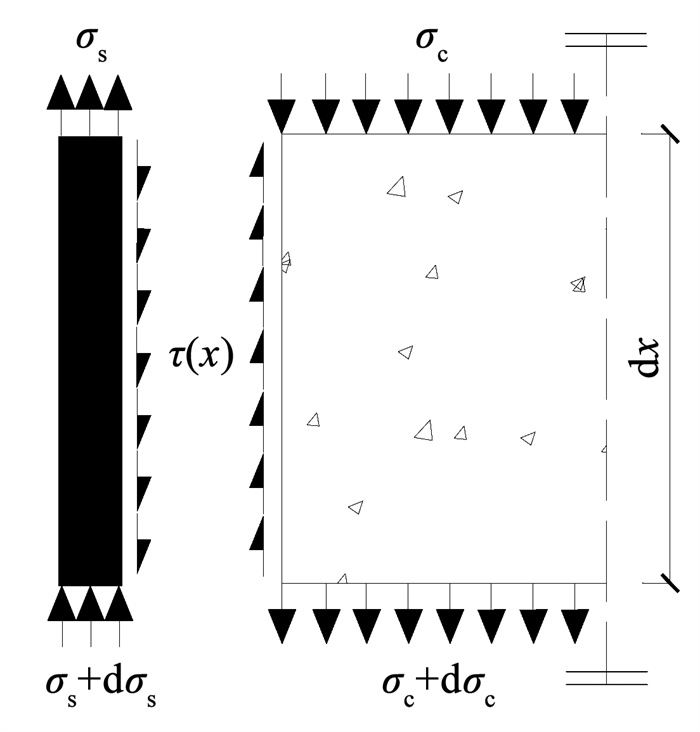
2.5 钢管煤矸石混凝土黏结应力加载方式B作用下仅混凝土受压,图 8为黏结应力平衡关系。根据钢管纵向应变片的变化率与黏结应力的关系可求出黏结应力[22]:
| $ \tau(x) \pi(D-2 t) \mathrm{d} x-A_{\mathrm{s}} E_{\mathrm{s}} \mathrm{~d} \varepsilon_{\mathrm{L}}(x)=0 $ | (15) |
| $ \begin{aligned} \tau(x)= & \frac{A_{\mathrm{s}} E_{\mathrm{s}}}{\pi(D-2 t)} \frac{\mathrm{d} \varepsilon_{\mathrm{L}}(x)}{\mathrm{d} x} \approx \\ & \frac{A_{\mathrm{s}} E_{\mathrm{s}}}{\pi(D-2 t)} \frac{\Delta \varepsilon_{\mathrm{L}}(x)}{\Delta x} \end{aligned} $ | (16) |
|
图 8 黏结应力平衡关系 Fig. 8 Bond stress equilibrium relationship |
式中:As为钢管横截面积,Es为钢管的弹性模量,τ为黏结应力,εL为钢管纵向应变。
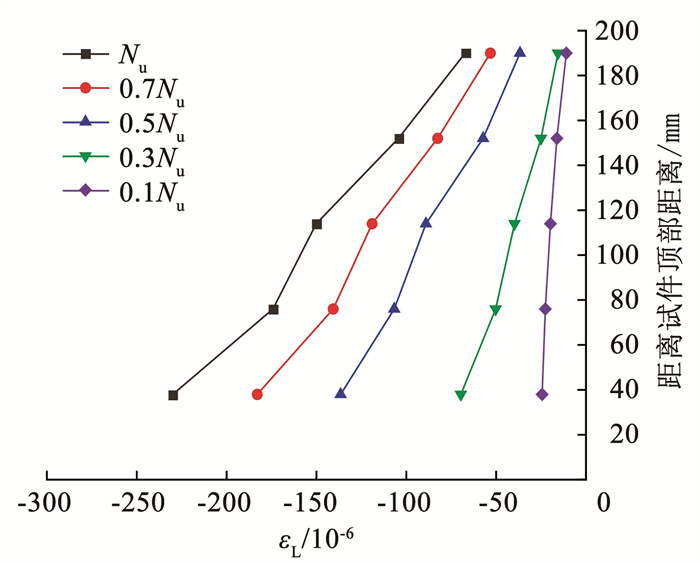
将纵向上半部5组应变片实测值代入式(16),可得试件的黏结应力。分析发现,随荷载增大黏结应力有增大趋势,并且黏结应力越靠近中部越低。图 9为试件CFST-B1-50%在0.1Nu、0.3Nu、0.5Nu、0.7Nu和Nu时钢管纵向应变分布曲线。混凝土轴向受压后会横向膨胀,为钢管壁提供了较大的法向压力,从而使得截面摩擦力逐渐增大。同时,由于试件的对称性,中部无位移,试件变形向中部集中,但应变差逐渐变小,因而黏结应力更低。
|
图 9 钢管应变分布曲线 Fig. 9 Strain distribution curve of steel tube |
利用试验应变求得峰值荷载下各试件极限黏结应力,结果见表 5,可以看出,黏结应力仅为1 MPa左右,表明加载方式B作用下钢管对竖向承载力的贡献可忽略。随着径厚比的提升,试件的黏结应力呈下降趋势。相同径厚比时,随着取代率的提升煤矸石混凝土强度虽然下降,但黏结应力有所提升。因此,在相同取代率下,钢管煤矸石混凝土可通过适当降低径厚比来提升钢管与煤矸石混凝土之间的极限黏结应力。
| 表 5 极限黏结应力计算值 Tab. 5 Calculation of ultimate bond strength |
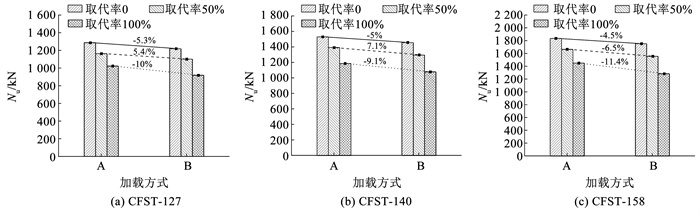
图 10为加载方式对极限承载力的影响。其他参数相同时,加载方式B的极限承载力低于加载方式A。将3种径厚比在不同加载方式的极限承载力降低幅度取平均值。取代率为0~50%时,极限承载力平均下降幅度由4.9%增至6.3%,下降幅度基本一致;取代率为50%~100%时,极限承载力平均下降幅度由6.3%增至10.2%,下降幅度增长1.6倍。破坏形态由剪切破坏变为腰鼓破坏,表明加载方式B中钢管提供约束能力更强,核心煤矸石混凝土强度提升程度更高,但由于失去钢管的竖向抗力,混凝土强度的提升并不能完全弥补钢管缺失导致的承载力降低,因此,加载方式B的极限承载力低于加载方式A。
|
图 10 加载方式对试件极限承载力的影响 Fig. 10 Effect of loading methods on ultimate bearing capacity of specimens |
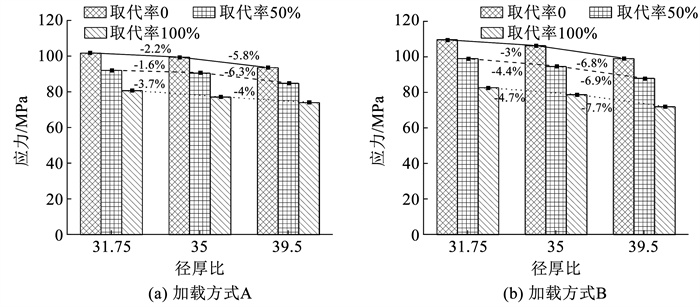
图 11为在两种加载方式下,径厚比对试件极限承载力的影响。由于本文构件为3种尺寸,试件在轴心受压时,为反映径厚比对试件承载能力的影响,采用极限应力强度,即极限承载力与截面面积的比。可以看出,随着径厚比的增加,不同取代率试件极限应力减少。
|
图 11 径厚比对试件极限承载力的影响 Fig. 11 Effect of diameter to thickness ratio on ultimate bearing capacity of specimens |
加载方式A,径厚比由31.75提升至35,3种取代率钢管煤矸石混凝土承载应力降低幅度分别为2.2%、1.6%、3.7%;径厚比由35提升至39.5,3种取代率钢管煤矸石混凝土承载应力降低幅度分别为5.8%、6.3%、4%。可见煤矸石取代率等比例增大时,相同径厚比试件的承载应力均降低,但是降低幅度出现一定的波动。加载方式A作用下,钢混凝土试件的破坏形式为剪切破坏,混凝土材料剪切面传力机制复杂,时变会造成一定的数据离散。加载方式B作用下,径厚比由31.75提升至35,3种取代率钢管煤矸石混凝土承载应力降低幅度分别为3%、4.4%、4.7%;径厚比由35提升至39.5,3种取代率钢管煤矸石混凝土承载应力降低幅度分别为6.8%、6.9%、7.7%。可见,加载方式B下不同径厚比的承载应力降低幅度相比加载方式A略有提升。
因此,两种加载方式中径厚比对不同取代率的钢管煤矸石混凝土的极限承载力影响基本一致。可适当降低径厚比,增加钢管对核心混凝土的约束作用,从而提升核心混凝土强度,充分发挥钢管与煤矸石混凝土的性能,提升试件承载力。
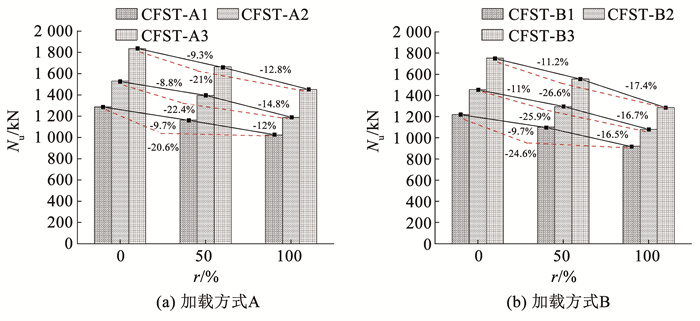
3.3 取代率的影响图 12为煤矸石取代率对试件极限承载力的影响,加载方式A作用下,试件极限承载力随煤矸石取代率的增大而减小,取代率0~50%与50%~100%相比,试件极限承载力下降幅度基本一致,整体降低幅度在11%左右。取代率由0提升至50%,3种径厚比的极限承载力平均降低幅度为9.26%,最大降低程度为9.7%;取代率由50%提升至100%,3种径厚比的极限承载力平均降低幅度为13.2%,最大降低程度为14.8%;取代率由0提升至100%,3种径厚比的极限承载力平均降低幅度为21.1%,最大降低程度为22.4%。
|
图 12 取代率对试件极限承载力的影响 Fig. 12 Effect of replacement rate on ultimate bearing capacity of specimens |
图 12(b)表明,加载方式B作用下试件极限承载力呈降低趋势,与加载方式A相似。取代率0~50%与50%~100%相比,加载方式B下极限承载力平均降低幅度由10.6%增至16.8%。取代率由0提升至100%,极限承载力平均降低幅度为25.7%,试件极限承载力最大降低程度为26.6%。
取代率0~50%,两种加载方式极限承载力下降幅度基本一致;但取代率50%~100%与取代率0~100%,加载方式B极限承载力降低幅度明显高于加载方式A。因此,就取代率而言,加载方式A更适用于钢管煤矸石混凝土,钢管承受纵向荷载可更好地弥补煤矸石混凝土强度的降低。
两种加载方式下钢管煤矸石混凝土承载力平均下降幅度为23.4%,而立方体抗压强度降低幅度为38%,降幅为前者的1.62倍。由于混凝土受压过程中的泊松比效应,对钢管横向挤压,钢管起到约束混凝土膨胀的作用,其实质就是钢管与核心煤矸石混凝土从单向受压转变为三向受压,充分发挥出钢管与煤矸石混凝土力学性能方面的优势,从而在一定程度弥补了核心混凝土因煤矸石取代率提升导致的钢管煤矸石混凝土极限承载力降低的幅度。
4 结论1) 煤矸石混凝土中煤矸石取代率为50%、100%与取代率0相比,fcu分别下降8.5、20.3 MPa,降低幅度为16%和38%。煤矸石混凝土立方体抗压强度随煤矸石取代率的增加而减小。
2) 加载方式A作用下呈现剪切型破坏,环向应变在剪切面有突增现象,分布不均匀,极限承载力高;在加载方式B作用下呈现腰鼓型破坏,环向应变分布较为均匀,但极限承载力低于加载方式A。两种加载方式各有优势,均可在实际工程中应用。
3) 加载方式B作用下,钢管和混凝土间有滑移,黏结应力随竖向荷载的增大而增大,且沿试件高度方向越靠近中部越低。极限黏结应力仅为1 MPa左右,表明加载方式B作用下钢管对竖向承载力的贡献较小,主要提供横向约束作用。
4) 煤矸石取代率是3种变化参数中极限承载力的最显著影响因素,极限承载力随取代率的增大而降低。取代率由0增大至100%,钢管煤矸石混凝土极限承载力降幅平均值为煤矸石混凝土立方体抗压强度降幅的1/1.62,表明钢管煤矸石混凝土可很好地弥补煤矸石混凝土自身强度低的特点。
| [1] |
王晨. 《工业固体废物资源综合利用评价管理暂行办法》和《国家工业固体废物资源综合利用产品目录》发布[J]. 精细与专用化学品, 2018, 26(6): 1. WANG Chen. "Interim measures for the evaluation and management of comprehensive utilization of industrial solid waste resources" and "National industrial solid waste resources comprehensive utilization product catalog" released[J]. Fine and Specialty Chemicals, 2018, 26(6): 1. |
| [2] |
钱鸣高. 煤炭产能扩张引发中西部环境隐忧[J]. 资源环境与发展, 2011(4): 5. QIAN Minggao. Coal production capacity expansion caused environmental concerns in the central and western regions[J]. Resources, Environment and Development, 2011(4): 5. |
| [3] |
LI D, SONG X, GONG C, et al. Research oncementitious behavior and mechanism of pozzolanic cement with coal gangue[J]. Cement & Concrete Research, 2006, 36(9): 1752. DOI:10.1016/j.cemconres.2004.11.004 |
| [4] |
LIU Changjiang, DENG Xiaowei, LIU Jian, et al. Mechanical properties and microstructures of hypergolic and calcined coal gangue based geopolymer recycled concrete[J]. Construction and Building Materials, 2019, 221: 691. DOI:10.1016/j.conbuildmat.2019.06.048 |
| [5] |
YZ A, QWA B, MEI Z C, et al. Mechanical properties of concrete with coarse spontaneous combustion gangue aggregate (SCGA): experimental investigation and prediction methodology[J]. Construction and Building Materials, 2020, 255: 119337. DOI:10.1016/j.conbuildmat.2020.119337 |
| [6] |
ZHANG Y, MA G, LIU Y, et al. Mix design for thermal insulation concrete using waste coal gangue as aggregate[J]. Materials Research Innovations, 2016, 19(Sup.5): S5-878-S5-884. DOI:10.1179/1432891714Z.0000000001212 |
| [7] |
ZHOU Mei, DOU Yanwei, ZHANG Yuzhuo, et al. Effects of the variety and content of coal gangue coarse aggregate on the mechanical properties of concrete[J]. Construction and Building Materials, 2019, 220: 386. DOI:10.1016/j.conbuildmat.2019.05.176 |
| [8] |
LONG Guangcheng, LI Linhao, LI Wengui, et al. Enhanced mechanical properties and durability of coal gangue reinforced cement-soil mixture for foundation treatments[J]. Journal of Cleaner Production, 2019, 231: 468. DOI:10.1016/j.jclepro.2019.05.210 |
| [9] |
蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2003. CAI Shaohuai. Modern steel tube confined concrete structures[M]. Beijing: China Communication Press, 2003. |
| [10] |
ZHANG Ni, ZHAO Zhongwei, ZHENG Chenyang. Compression behavior of GFRP-coal gangue concrete-steel tubular columns[J]. International Journal of Pressure Vessels and Piping, 2022, 197: 104650. DOI:10.1016/j.ijpvp.2022.104650 |
| [11] |
LI Guochang, ZHONG Shaotong. Strength and lateral deformation coefficient of gangue concrete restrained by steel tube[J]. Journal of Harbin University of Civil Engineering and Architecture, 2002, 35(3): 20. DOI:10.1007/s11769-002-0073-1 |
| [12] |
李帼昌, 钟善桐. 钢管约束下煤矸石混凝土的强度及横向变形系数[J]. 哈尔滨建筑大学学报, 2002, 35(3): 4. LI Guochang, ZHONG Shantong. Strength and lateral deformation coefficient of gangue concrete restrain by steel tube[J]. Journal of Harbin University of Civil Engineering & Architecture, 2002, 35(3): 4. |
| [13] |
李帼昌. 钢管煤矸石混凝土受弯构件的承载力分析[J]. 沈阳建筑大学学报(自然科学版), 2005(6): 654. LI Guochang. Bearing capacity of gangue concrete filled steel tubular member under moment[J]. Journal of Shenyang Jianzhu University (Natural Science), 2005(6): 654. DOI:10.3321/j.issn:1671-2021.2005.06.012 |
| [14] |
方晨. 钢管煤矸石砼柱—煤矸石砼梁连接节点的力学性能分析[D]. 沈阳: 沈阳建筑大学, 2013 FANG Chen. Analysis on mechanical property of joint between gangue concrete filled steel tubular column and gangue concrete beam[D]. Shenyang: Shenyang Jianzhu University, 2013 |
| [15] |
GAO S, GUO L. Utilization of coal gangue as coarse aggregates in structural concrete[J]. Construction and Building Materials, 2021, 268: 121212. DOI:10.1016/j.conbuildmat.2020.121212 |
| [16] |
ZHANG Y, XU Q, WANG Q, et al. Axial compressive behavior of circular concrete-filled steel tube stub columns prepared with spontaneous-combustion coal gangue aggregate[J]. Journal of Building Engineering, 2022, 48: 103987. DOI:10.1016/j.jobe.2021.103987 |
| [17] |
XU Q, ZHANG Y, LIU H, et al. Effect of spontaneous-combustion coal gangue aggregate on axial performance of square concrete-filled steel tube stub columns[J]. Structures, 2022, 44: 216. |
| [18] |
黄万朋. 钢管混凝土墩柱沿留空巷技术研究与应用[M]. 北京: 应急管理出版社, 2020. HUANG Wanpeng. Research and application of concrete filled steel tube pier column along gob-side entry technology[M]. Beijing: Emergency Management Press, 2020. |
| [19] |
钢铁研究院. 金属材料拉伸试验第1部分: 室温试验方法GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010 Iron & Steel Research Institute. Metallic materials-tensile testing-Part 1: method of test at room temperature: GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2010 |
| [20] |
中华人民共和国住房和城乡建设部. 普通混凝土配合比设计规程: JGJ 55—2011[S]. 北京: 中国建筑工业出版社, 2011 Ministry of Housing and Urban Rural Development of the People's Republic of China. Design specification for ordinary concrete mix proportion: JGJ 55—2011[S]. Beijing: China Construction Industry Press, 2011 |
| [21] |
钟善桐. 钢管混凝土结构[M]. 北京: 清华大学出版社, 2003. ZHONG Shantong. The concrete-filled steel tubular structures[M]. Beijing: Tsinghua University Press, 2003. |
| [22] |
赵卫平, 王振兴, 陈佳麟, 等. 考虑几何缺陷的钢管混凝土黏结滑移数值模拟[J]. 哈尔滨工业大学学报, 2021, 53(10): 52. ZHAO Weiping, WANG Zhenxing, CHEN Jialin, et al. Numerical simulation of bond-slip of concrete filled steel tube considering geometric defects[J]. Journal of Harbin Institute of Technology, 2021, 53(10): 52. DOI:10.11918/202011001 |
 2024, Vol. 56
2024, Vol. 56


