冷弯型钢(简称CFS)结构低层住宅体系具有低碳、低能耗、轻质高强、环保经济、工期短等优点[2-3],符合中国加强推进住宅构件工厂化、产业化发展方向。但是,由于CFS较薄,截面宽厚比相对较大,易发生屈曲破坏,严重影响了建筑结构的安全性和舒适性。因此,一种新型轻钢轻混凝土结构体系在工业上普遍应用。其在保留了CFS结构住宅体系工业化程度高、建造快等优点的基础上,克服了CFS结构整体安全性、舒适性等方面的不足。
地聚物主要是以粉煤灰、矿渣、尾矿等固体废物为主要原料,经过适当的工艺流程,在碱性环境下发生化学反应生成的无机胶凝材料,是一种新型绿色建材[4]。将其浇筑进CFS柱中可消除现有轻钢结构体系中存在的空鼓声,在废物利用、节能环保、抗侧刚度和抗震性能上都有良好表现。相比早期的钢筋混凝土柱、钢管混凝土柱,冷弯型钢-类地聚物泡沫混凝土柱(简称CFS-GFC柱)的高延性及吸能性使其具有更好的抗震性能,与传统施工方法相比更经济,减少劳动力需求,允许快速施工[5-7],不仅符合中国建筑产业化的发展方向,也顺应了建筑业节能减排的发展趋势。
朴泓任[8]对钢管发泡混凝土柱展开数值模拟研究,分析了混凝土强度、摩擦因数、钢材强度等参数对构件受力性能的影响,结果表明,构件摩擦力越大,则极限承载力越大,内部填充泡沫混凝土可以有效提高构件承载力。李振远[9]采用试验和有限元模拟对比的方法,研究了泡沫混凝土填充拼合C型钢柱的轴压承载力。首先通过空心CFS柱和CFS-泡沫混凝土柱进行轴心受压试验,分析了破坏现象及其变化过程,研究了泡沫混高凝土干密度、截面高宽比和长细比等因素对CFS-泡沫混凝土组合柱峰值承载力、刚度和延性的影响,提出了CFS-泡沫混凝土立柱的正截面轴压承载力计算公式。Thumrongvut等[10]对内部填充泡沫混凝土的矩形钢管柱进行了轴压试验,并与纯泡沫混凝土柱的轴向承载力进行了对比,然后,将试验结果与美国规范(ACI)[11]中设计方程得到的计算荷载进行比较,结果表明,泡沫混凝土矩形钢管柱在达到其最大荷载的80%~90%之前荷载-应变关系呈线性变化,其轴向荷载的大小由管壁的局部屈曲性能控制,ACI设计方程可以很好地预测泡沫混凝土矩形钢管柱的轴压承载力。Salgar等[12]对内部填充轻质混凝土的方形钢管、矩形钢管和圆形钢管进行了轴压试验,结果表明,相比普通混凝土柱,轻质混凝土柱自重降低了25.3%,长细比一定时,构件的承载力随着深度与厚度之比(D/t)的减小而增加。侯亚杰[13]对冷弯薄壁C型钢柱和CFS-轻混凝土组合柱轴压性能进行对比分析,发现填充轻混凝土不仅可以有效提升构件承载力,也限制了构件的畸变屈曲变形。利用ABAQUS进行建模,分析了构件在不同尺寸,加劲方式、边界条件和混凝土强度等参数对构件受力性能的影响,建议采用日本AIJ规范预测CFS-轻混凝土柱承载力。
CFS-泡沫混凝土柱是轻钢轻混凝土结构体系中重要的部分,适合于多层别墅住宅等其他低层民用房屋。为加大该类型构件在社会层面的推广使用,很多学者对其开展了相关研究,但是对于内部填充地聚物泡沫混凝土的CFS组合柱研究并不多,对于填充地聚物泡沫混凝土对CFS管屈曲承载力及屈曲模式的影响并没有详细的讨论,对于填充的地聚物泡沫混凝土的密度对CFS管的屈曲承载力及屈曲模式的影响也没有明确的结论。更重要的是,并没有一本现行的规范针对性地提出CFS-GFC柱的承载力计算方法。因此,有必要对CFS-GFC柱在轴压作用下的受力特点及破坏模式进行分析,讨论二者在轴压荷载下的工作性能及相互约束关系,从而探索CFS-GFC柱的计算公式。
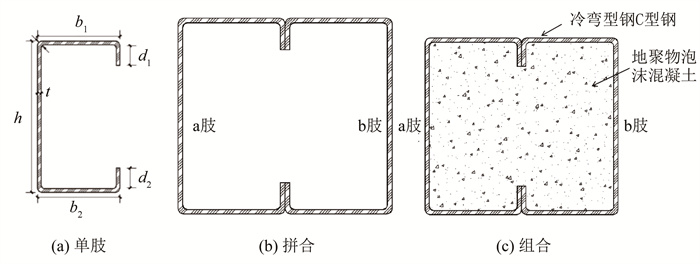
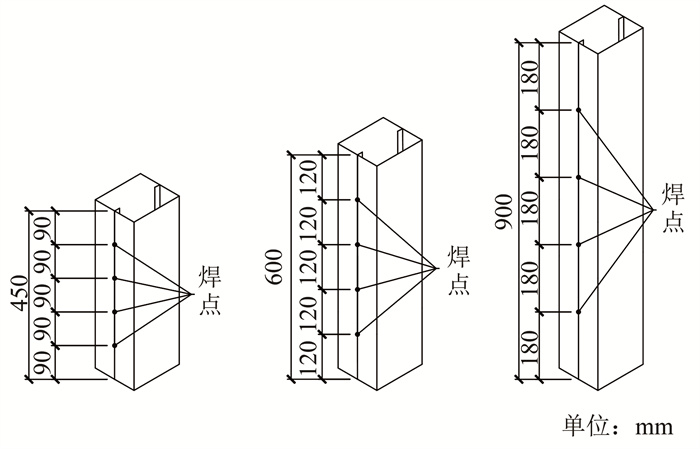
1 试验 1.1 试件设计与制作本试验共设计CFS单肢柱、CFS拼合柱、CFS-GFC组合柱3种截面类型,如图 1所示。单肢柱腹板高为140 mm,翼缘宽为50 mm,卷边长度为15 mm,每种截面形式的构件都分别选取了450、600、900 mm 3种长度。试件两端通过焊接各连接一块200 mm×240 mm的钢板。此外,每种构件设置了3个平行构件,以保证试验数据的准确性。试验试件的实际测量尺寸见表 1。CFS拼合柱由单肢C型柱通过点焊方式卷边对卷边焊接制成,根据《冷弯薄壁型钢结构技术规范》[14]要求,每种长度类型的构件均设置4处焊点。在CFS拼合柱空腔内浇灌注入类地聚物泡沫混凝土浆体并进行养护得到CFS-GFC组合柱。焊点位置及试件如图 2所示。
|
图 1 构件件截面详图 Fig. 1 Member section details |
| 表 1 构件信息汇总 Tab. 1 Summary of specimen information |
|
图 2 拼合构件焊点位置简图 Fig. 2 Schematic diagram of welding point location of assembled components |
本试验类地聚物泡沫混凝土以矿渣和粉煤灰为原材料。将固体NaOH和水玻璃按照一定比例溶于水中搅拌至NaOH完全溶解,冷却至室温作为碱激发剂,选用植物型发泡剂制备泡沫,如图 3所示。类地聚物泡沫混凝土材料配合比见表 2。

|
图 3 植物型发泡剂 Fig. 3 Plant foaming agent |
| 表 2 类地聚物泡沫混凝土材料配合比 Tab. 2 Mix proportion of geopolymer foam concrete |
构件材料为Q235钢材,板件厚度为1.8 mm,材性试验试样分别取自立柱的腹板与翼缘板(沿立柱长度方向截取)。本次材性试验共截取6个标准构件,其中,两个由腹板截取,两个由左翼缘板截取,两个由右翼缘板截取。采用100 kN微机控制电子万能试验机拉伸构件,试验方法及过程、标准试样尺寸及加工要求均按照GB/T 228.1—2021《金属材料拉伸试验第一部分:室温试验方法》[15]中的规定进行。构件实测力学性能指标见表 3。
| 表 3 材性试验结果 Tab. 3 Material performance test results |
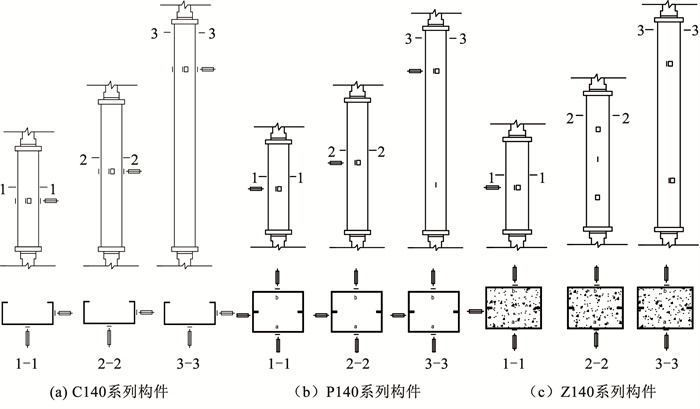
对于长度为450、600 mm的构件,由于其长度较短,构件的屈曲位置多为跨中截面处,因此,对于冷弯薄壁C型钢单肢柱,分别在其腹板及左右翼缘板的中间位置粘贴应变片,位移计则布置在腹板及单侧翼缘板的中间位置。对于CFS拼合和CFS组合柱,分别在其a肢柱及b肢柱腹板的中间位置粘贴应变片,位移计则布置在a肢柱及b肢柱腹板的中间位置和单侧翼缘和卷边交线的位置。对于长度为900 mm的构件,考虑其出现屈曲破坏的位置在构件长度1/3及2/3位置,对于冷弯薄壁C型钢单肢柱,在沿构件长度1/3及2/3位置的腹板上粘贴应变片,位移计布置在腹板及一侧翼缘的1/3位置。对于CFS拼合柱和CFS组合柱,分别在其a肢柱及b肢柱腹板长度1/3及2/3位置粘贴应变片,位移计则布置在a肢柱翼缘与卷边交线的1/3位置及b肢柱腹板的1/3位置。具体测点布置如图 4所示。
|
图 4 应变片及位移计布置 Fig. 4 Layout of strain gauge and displacement meter |
采用WA-1000CI型电液伺服万能试验机加载系统,试验装置如图 5所示,构件两端固定约束。在加载前将构件进行几何对中,试验前对焊接在试件两端的端板标注试件的形心,加载时将试件的形心与加载装置的中心对中,以确保为轴心受压。加载过程分为两个阶段,首先为施加预压力阶段,调整下横梁使构件固定,并施加1 kN的初始荷载,观察应变片与位移计是否可以正常使用,同时消除构件与加载装置之间的空隙。然后进行位移加载,加载速率为0.2 mm/min,在启动加载装置施加荷载的同时,开始采集应变片及位移计的数据,以保证数据准确。当构件发生破坏后,荷载降至极限荷载的70%时停止加载,保存数据,结束试验。

|
图 5 构件加载装置与构件安装 Fig. 5 Specimen loading device and specimen installation |
由于篇幅限制,仅介绍CFS单肢C140-600试件。C140-600构件在加载初期并无异常状态,在加载过程中端部发生局部压屈现象,此后翼缘与卷边交线不再保持直线,构件发生畸变屈曲破坏,破坏特征如图 6所示。对比3根平行构件可以看出,构件在距离端部1/2位置发生翼缘-卷边棱线内收的畸变屈曲,但是由于初始缺陷的影响,变形最大的位置略有不同。

|
图 6 C140-600构件破坏形式 Fig. 6 C140-600 members failure mode |
在加载过程中,P140-600构件端部出现轻微鼓起,构件长度1/2位置出现屈曲波纹。随着荷载持续增大,变形逐渐明显,达到峰值荷载后,构件1/2长度板件向内凹陷,发生局部屈曲。构件破坏特征如图 7所示,可以看出,P140-600构件破坏形式为腹板的局部屈曲破坏,P140-600-1与P140-600-3构件破坏位置在构件中部,P140-600-2破坏位置在中部偏上,焊点并未拉断。

|
图 7 P140-600构件破坏形式 Fig. 7 P140-600 members failure mode |
加载初期,Z140-600构件处于弹性阶段,此时构件并无异常。随着荷载持续增加,构件端部出现向外鼓曲的局部屈曲现象。当荷载增加至屈服荷载时,构件中部腹板出现轻微鼓曲现象,其间,内部混凝土发出破坏爆裂声响。达到峰值荷载后,构件变形明显,主要变形方式为a肢柱下端部鼓曲,中间位置轻微鼓曲,b肢柱下端部鼓曲,上端部轻微鼓曲。构件破坏特征如图 8所示,型钢与混凝土黏结较好。

|
图 8 Z140-600构件破坏形式 Fig. 8 Z140-600 members failure mode |
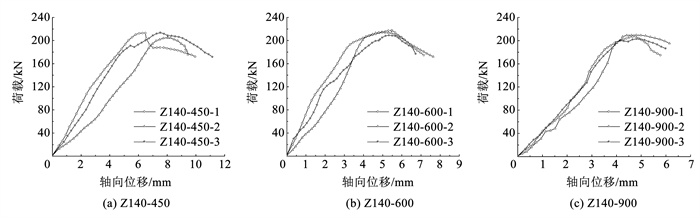
27个短柱试件轴压试验结果见表 4。限于篇幅,图 9仅展示了CFS-GFC组合柱的轴向荷载-位移关系曲线。可以看出,在受荷前期曲线近似为直线,混凝土与钢管共同受力良好,内部填充的泡沫混凝土限制了外钢管板件的屈曲,从而提高了构件的极限荷载。在构件达到极限荷载后,由于内部泡沫混凝土发生破坏,无法继续约束,荷载快速下降。
| 表 4 承载力试验结果 Tab. 4 Test results of bearing capacity |
|
图 9 荷载-轴向位移曲线 Fig. 9 Load-displacement curve |
不同高度各截面形式构件的极限承载力及破坏模式见表 4,内部填充类地聚物泡沫混凝土组合构件的极限承载力相比空心拼合构件最高提升1.4倍,同时,拼合构件及组合构件的屈曲破坏模式相比单肢构件的畸变屈曲变成了局部屈曲破坏,组合构件的破坏模式为板件的轻微鼓曲变形及内填类地聚物泡沫混凝土的压碎。
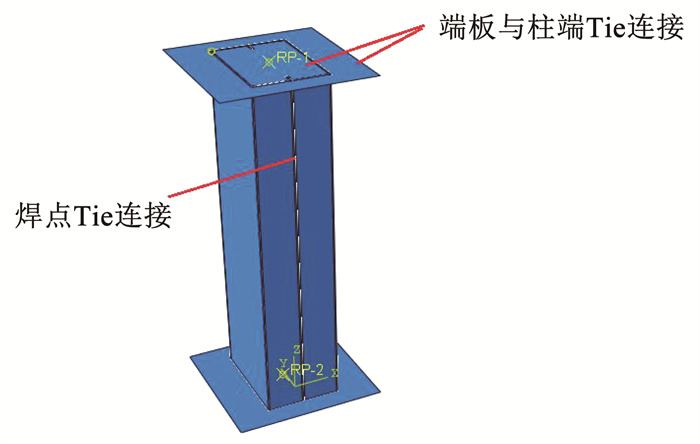
3 有限元分析 3.1 有限元模型的建立 3.1.1 单元类型选择及材料本构采用ABAQUS软件建立如图 10所示有限元模型,构件的上、下端板均采用刚性单元R3D4模拟,CFS部分采用4节点缩减积分S4R壳体单元,类地聚物泡沫混凝土部分采用8节点缩减积分C3D8R实体单元。根据试验分析确定焊点连接处并未破坏,采用绑定方式模拟焊点。钢材本构根据材性试验结果,屈服强度为267.5 MPa,弹性模量为174 GPa,泊松比为0.3。地聚物泡沫混凝土采用的本构关系是李肖等[16]提出的,该本构关系以韩林海[17]提出的钢管混凝土本构模型关系为基础,同时考虑了钢管管壁设置加劲肋对混凝土约束效应的有利影响,引入加劲肋约束效应系数(见式(1)),采用ABAQUS自带的CDP(混凝土塑性损伤)模型。
| $ y=\left\{\begin{array}{l} 2 x-x^2, x \leqslant 1 \\ \frac{x}{\beta_0(x-1)^n+x}, x>1 \end{array}\right. $ | (1) |
|
图 10 有限元模型建立 Fig. 10 Establishment of finite element model |
式中:
有限元建模均采用构件实际尺寸,构件的钢垫板与冷弯薄壁C型钢和混凝土的两端采用绑定(Tie)连接;CFS与类地聚物泡沫混凝土之间采用面面接触,切线方向为“罚”接触,其摩擦因数为0.25,法线方向为“硬”接触;两组冷弯薄壁C型钢采用绑定(Tie)连接方式模拟焊点。为便于轴向荷载的施加,分别在上、下端板中心位置建立参考点RP-1和RP-2,并与端板设置耦合约束。RP-2点约束所有自由度,RP-1点仅释放轴向平动自由度并施加轴向荷载。在不同网格划分情况下多次进行有限元分析,有限元模型的各部件网格尺寸设置为5 mm×5 mm。
3.2 有限元模型的验证图 11和表 4分别给出CFS-GFC组合柱的试验与有限元破坏模式和极限荷载对比。由图 11可以看出,有限元模型Z140-450、Z140-600和Z140-900试件的破坏特征是板件局部鼓曲,腹板上出现凸凹波,其破坏特征和破坏位置与试验现象吻合较好。由表 4可以看出,有限元极限荷载与试验结果比值的平均值为1.03,标准差为0.03,且二者极限荷载非常接近。综上,说明本文建立的有限元模型可以比较精确地模拟CFS-GFC短柱的轴压受力过程,且能准确得到构件的轴压刚度和轴压承载力。

|
图 11 试验与有限元破坏模式对比 Fig. 11 Comparison of experimental and FEA failure modes for a part of specimens |
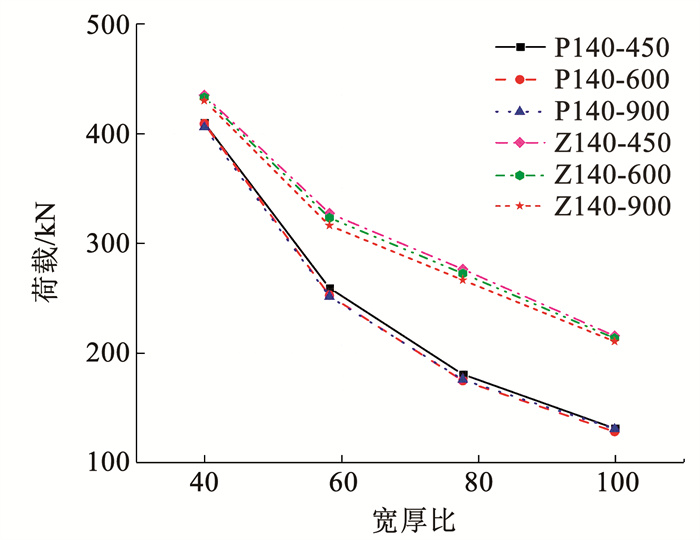
为拓展试验参数范围,全面分析CFS拼合柱和CFS-GSC组合结构的轴压性能,选取腹板截面宽厚比分别为40、58、78、100,对应的厚度分别为3.5、2.4、1.8、1.4 mm,共计24个构件。参数分析结果如图 12所示。随截面宽厚比增加,构件极限荷载降幅逐渐减小,截面宽厚比为40~60时,曲线下降段更陡,截面宽厚比为60~100时,曲线下降段相对平缓,说明截面宽厚比为40~60时对极限荷载的影响更为显著。此外,截面宽厚比为40时,CFS拼合柱与CFS组合柱的极限荷载较为接近,但随着宽厚比逐渐增大,组合柱的极限荷载开始明显大于拼合柱,此现象在宽厚比大于60后尤其明显。说明随宽厚比的增大,构件的厚度逐渐减小,板件易发生局部屈曲,而内部填充的类地聚物泡沫混凝土对厚度较小板件的限制作用明显,此时可以发挥内部填充物的作用,达到增大钢柱极限荷载的目的。而随着截面宽厚比的减小,构件厚度变大,内部填充物利用率较低。
|
图 12 不同构件荷载-宽厚比关系曲线 Fig. 12 Load-width-thickness ratio curve |
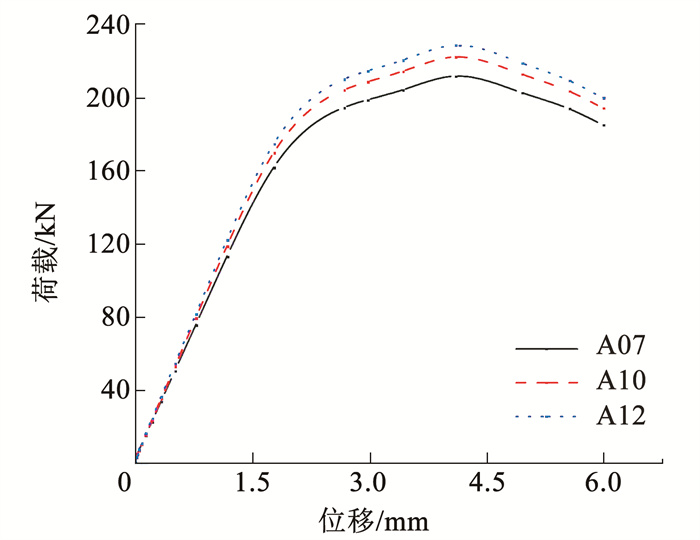
图 13为不同泡沫混凝土密度等级时CFS-GFC组合柱的荷载-轴向位移曲线。可以看出,随着泡沫混凝土密度的增大,组合柱的极限荷载也随之增加。在弹性阶段,泡沫混凝土的弹性模量随其密度的增加而增大,导致CFS-GFC组合柱的刚度也变大。泡沫混凝土密度每提高一个等级,CFS-GFC组合柱的极限荷载约增加1.5%。因此,提高泡沫混凝土的密度等级可以增加组合柱的刚度同时提高组合柱的轴向承载能力。
|
图 13 不同密度等级下的荷载-轴向位移曲线 Fig. 13 Load axial displacement curves |
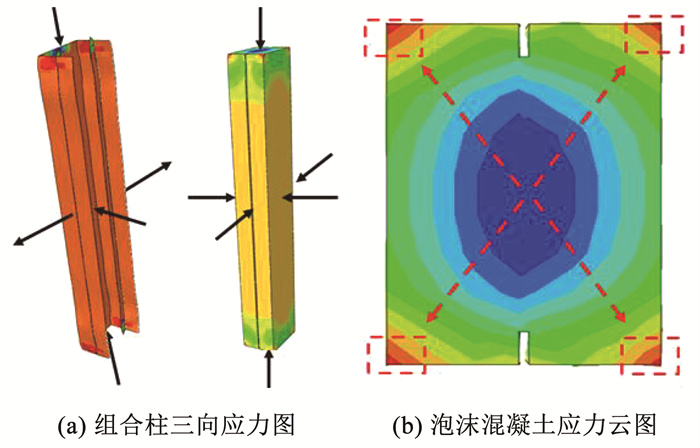
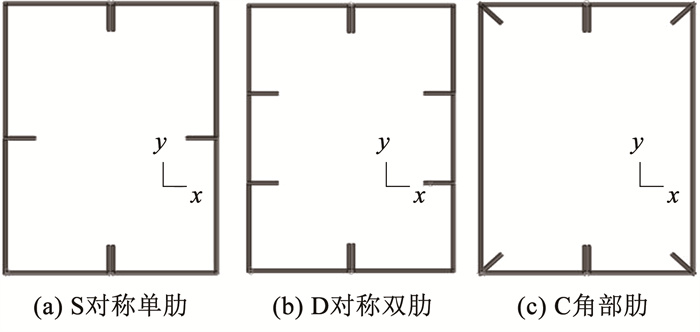
由于CFS内壁较为光滑,CFS与填充混凝土的协同作用效果并不理想,图 14为内部混凝土的应力云图,可以看出,越靠近中心混凝土的应力越小,越靠近边缘混凝土应力越大,同时,在混凝土的角部应力达到最大,说明CFS对角部混凝土的约束效果明显,而边缘处约束效果较弱。为探究腹板加劲对CFS-GFC组合柱构件极限荷载的提升效果以及对混凝土的约束效应,考虑对CFS内壁附加加劲肋,有限元模型截面如图 15所示。其中,S截面为在CFS腹板设置一道对称的加劲肋,D截面为在CFS腹板设置两道对称的加劲肋,C截面为在CFS的角部设置加劲肋,加劲肋的板宽均为15 mm。加劲肋与CFS通过Tie连接。对比表 5可以看出,带肋截面极限荷载的提高系数为1.12~1.22,说明加劲肋可以明显提高CFS-GFC组合柱的极限荷载,其中,C截面的提高系数最大, 为1.223,D截面提高系数略小于C截面的提高系数,为1.217。比较提高系数1与提高系数2可以看出,S截面构件承载力提高系数大于D截面与C截面的构件,从材料用钢量的角度考虑,设置对称单肋可以以较少的材料用量获取更好的极限荷载提高效果。
|
图 14 CFS-GFC组合柱应力图 Fig. 14 Stress diagram of cold-formed thin-walled steel composite column |
|
图 15 CFS加劲肋形式 Fig. 15 Stiffening rib form of CFS |
| 表 5 不同加劲形式构件极限荷载对比 Tab. 5 Comparison of ultimate load of specimens with different stiffeners |
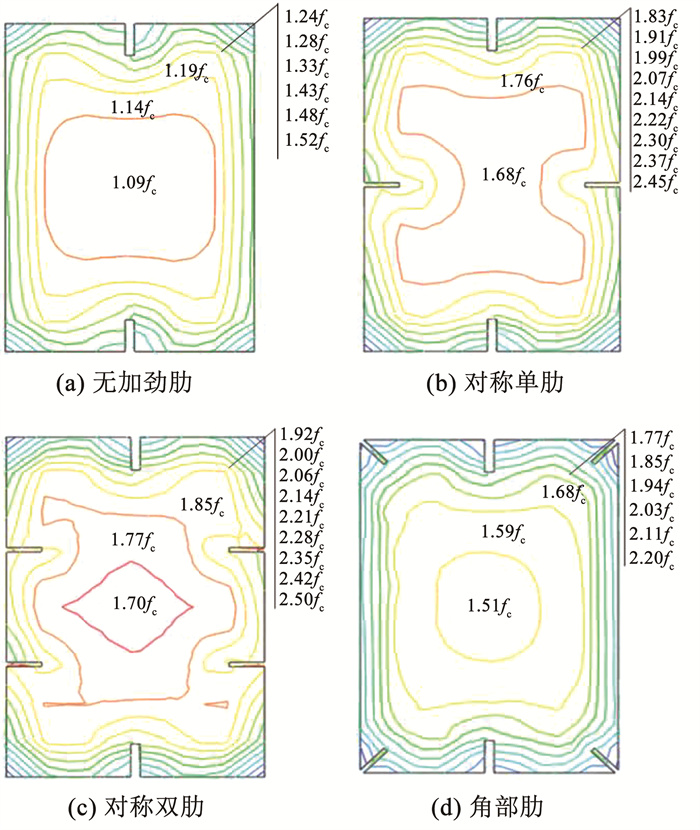
图 16为各类截面构件中部截面混凝土纵向应力分布图,图中曲线代表类地聚物泡沫混凝土轴向应力等值曲线,fc为试验测得的混凝土抗压强度。由图 16可以看出,所有构件在达到极限承载力时,类地聚物泡沫混凝土的最大应力均出现在角部,且应力随与角部距离的增大而减小。无肋、单肋、双肋、角肋构件角部混凝土最大应力分别为1.52fc、2.45fc、2.5fc、2.2fc,表明设置加劲肋提高了类地聚物泡沫混凝土的应力,且随着加劲肋个数的增多,应力也随之提高。对称单肋、双肋及角部肋构件在边缘位置的混凝土纵向应力分别达到了1.91fc、2.0fc和2.03fc,与无肋构件边部混凝土应力1.28fc相比分别提高了49.2%、56.2%和58.6%,表明加劲肋的设置提高了类地聚物泡沫混凝土的轴向应力,从而增大了CFS-GFC组合柱的极限荷载。
|
图 16 泡沫混凝土纵向应力图 Fig. 16 Longitudinal stress diagram of foam concrete |
基于本文两端固结组合柱试验和有限元研究结果,对JGJ 138—2016《组合结构技术规范》[1]中的承载力计算公式(见式(2))进行如下修正:
1) 外钢管的约束效应提高了内部混凝土的轴心受压强度,因此考虑引入泡沫混凝土轴心受压强度增强系数ωc。
2) 外钢管的拼合导致其与普通矩形钢管具有不同的截面形式,从设置加劲肋的角度看,加劲肋位置及个数的不同影响了组合柱的整体承载力,因此考虑引入组合柱截面形状影响系数γ。
| $ N \leqslant 0.9 \psi \gamma\left(\alpha_1 \omega_{\mathrm{c}} f_{\mathrm{c}} b_{\mathrm{c}} h_{\mathrm{c}}+2 f_{\mathrm{a}} b t+2 f_{\mathrm{a}} h_{\mathrm{c}} t\right) $ | (2) |
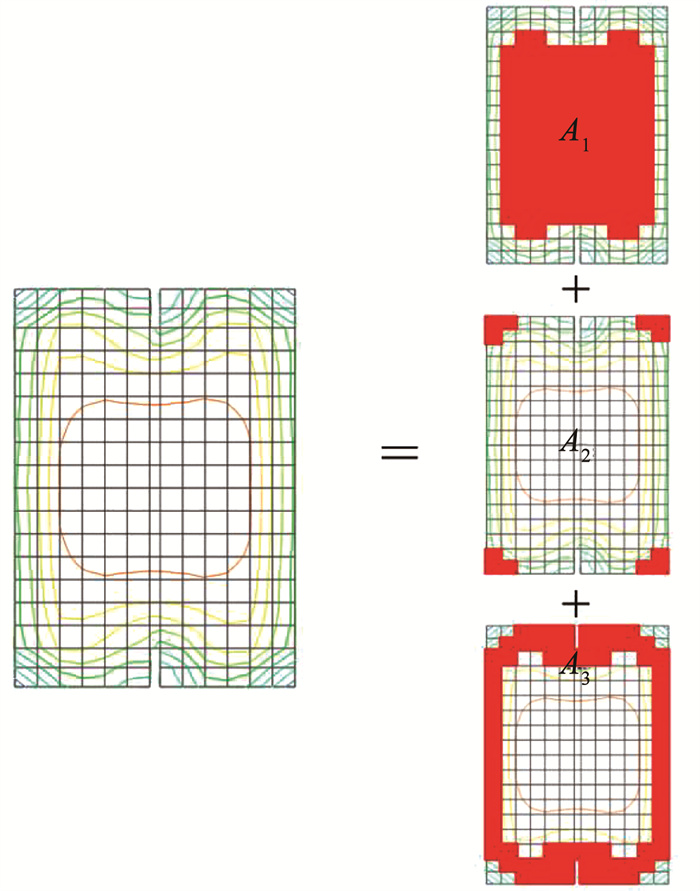
研究发现,CFS-GFC柱内部核心混凝土的强度被加强。在靠近中心位置,泡沫混凝土的应力较小,靠近边缘的泡沫混凝土应力较大,同时,在混凝土的角部应力达到最大,其应力分布及不同应力区域面积划分如图 17所示。根据泡沫混凝土的应力分布图,将不同的应力区域面积进行划分,分为中部泡沫混凝土应力加强区面积A1、角部泡沫混凝土应力加强区面积A2、边缘泡沫混凝土应力加强区面积A3。图 17中每个小正方形的面积为58.6 mm2,每个小长方形的面积为28.29 mm2,总面积Ac为13 053.92 mm2。由此可以推算得出:中部泡沫混凝土应力加强区面积A1=7 840.28 mm2,角部泡沫混凝土应力加强区面积A2=703.2 mm2,边缘泡沫混凝土应力加强区面积A3=4 510.18 mm2。则各部分面积与总面积(Ac)关系为A1=0.6Ac,A2=0.05Ac,A3=0.35Ac。
|
图 17 类地聚物泡沫混凝土应力区域划分 Fig. 17 Stress zone division of geopolymer foam concrete |
由图 17可知,中部泡沫混凝土应力分布(由内到外)值分别为1.09fc、1.14fc、1.19fc,平均值为1.14fc;角部泡沫混凝土应力分布(由内到外)值为1.38fc、1.43fc、1.48fc、1.52fc,平均值为1.45fc;边缘泡沫混凝土应力分布(由内到外)值为1.24fc、1.28fc、1.33fc,平均值为1.28fc。由此可得
| $ \omega_{\mathrm{c}} f_{\mathrm{c}} A_{\mathrm{c}}=1.14 f_{\mathrm{c}} A_1+1.45 f_{\mathrm{c}} A_2+1.28 f_{\mathrm{c}} A_3 $ | (3) |
将换算面积代入可得
| $ \omega_{\mathrm{a}} f_{\mathrm{c}} A_{\mathrm{c}}=1.2045 f_{\mathrm{c}} A_{\mathrm{c}} $ | (4) |
即本文中泡沫混凝土轴心受压强度增强系数ωc=1.204 5。
4.2 截面形状影响系数JGJ 138—2016《组合结构设计规范》[1]给出的承载力计算仅针对矩形截面构件,本文构件截面类型类似于矩形截面并加对称单肋形式,根据有限元分析结果可知,加劲肋数量与位置的不同对构件的极限承载力有显著影响,因此,考虑引入截面形状影响系数,进而使公式的计算结果满足本文构件模型。
有限元分析结果表明:构件设置对称单肋时,其承载力相比不加肋时的提高系数为1.124;构件设置对称双肋时,其承载力相比设置对称单肋时的提高系数为1.083;构件设置角部肋时,其承载力相比设置对称单肋时的提高系数为1.088,因此,截面形状影响系数γ=(1.124+1.083+1.088)/3=1.098 33。
综上,基于拟混凝土理论设计的JGJ 138—2016《组合结构技术规范》[1]中钢管混凝土柱的轴心受压承载力计算公式预测本文构件的承载力较为合理,但是由于其理论值与试验值误差较大,考虑在该公式基础上对其泡沫混凝土轴心受压强度增强系数和截面形状影响系数进行修正,提出适用于本文CFS-GFC组合柱的承载力计算公式,具体如下:
| $ N \leqslant 0.9 \times 1.098 \varphi\left(1.204\;5 \alpha_1 f_{\mathrm{c}} b_{\mathrm{c}} h_{\mathrm{c}}+2 f_{\mathrm{a}} b t+2 f_{\mathrm{a}} h_{\mathrm{c}} t\right) $ | (5) |
式中:N为矩形钢管柱轴压承载力设计值,φ为轴心受压柱稳定系数,fc为内填混凝土抗压强度设计值,fa为矩形钢管抗压和抗拉强度设计值,bc为矩形钢管内填混凝土的截面宽度,hc为矩形钢管内填混凝土的截面高度,b为矩形钢管截面宽度,t为矩形钢管的管壁厚度。
表 6给出了现有承载力计算公式与试验结果的对比,日本AIJ规范[18]和美国LRFD规范[19]计算的CFS-GFC组合柱承载力偏大,且与试验测得的组合柱承载力比Nu, A/Pt、Nu,L/Pt的平均值为1.26、1.21,说明依据日本AIJ规范[18]和美国LRFD规范[19]计算本文构件承载力偏不安全,因此,两种材料承载力相互叠加的理论和拟钢理论给出的计算公式并不适用于本文构件。其可能的原因之一是在实际受力过程中钢材的强度并未充分利用,而强度公式中均未对钢材强度进行相应的折减,使得计算得到的理论结果较试验值偏大。JGJ 138—2016《组合结构设计规范》[1]计算得出的组合柱承载力小于试验值,Nu, J/Pt平均值为0.87,说明由《组合结构设计规范》计算得出的理论值较保守,因此,本文冷弯薄壁型钢组合柱承载力计算公式可根据拟混凝土理论进行设计。但是由于试验构件均为短柱,该规范对于长细比小于28(即本文构件长度l<1 616.72 mm) 时的稳定系均为1,因此,在柱长小于1 616.72 mm时构件发生的均为强度破坏。CECS 28:2012《钢管混凝土结构技术规程》[20]计算得出的组合柱承载力略高于试验值,其与试验结果的比Nu, G/Pt平均值为1.12,说明基于统一理论给出的组合柱承载力计算公式可以作为预测本文构件轴心受压承载力的公式,但偏于不安全。
| 表 6 规范公式计算值与试验值比较 Tab. 6 Comparison between calculated value of standard formula and test value |
将该公式计算值与试验及有限元结果进行对比分析,以验证本文提出公式计算CFS-GFC组合短柱的适用性,结果如图 18所示。可以看出,理论计算值与试验及有限元值整体吻合较好,平均值为0.95,标准差为0.07,且理论计算值与试验及有限元值误差集中在5%左右,说明本文提出的CFS-GFC柱轴心受压承载力计算公式具有准确性。

|
图 18 理论计算值与试验及有限元值误差 Fig. 18 Discrepancy between theoretical calculations and test and finite element values |
1) 内部填充类地聚物泡沫混凝土的组合构件极限承载力相比空心拼合构件提高了1.4倍,单肢构件发生畸变屈曲破坏,拼合构件发生局部屈曲破坏,而组合构件的破坏模式为板件沿高度变化出现多处的轻微鼓曲变形,及内填类地聚物泡沫混凝土的压碎;组合柱的承载力受长细比的影响较大,且内部填充的类地聚物泡沫混凝土对构件极限荷载的影响随长细比的增大而减小。
2) CFS拼合柱与CFS-GFC组合柱的极限荷载随着宽厚比的增大而减小,板件宽厚比为60~100时,类地聚物泡沫混凝土利用率较高;内部填充的类地聚物泡沫混凝土延缓了CFS板件局部屈曲的发生,且宽厚比越大时效果越明显。
3) 提高泡沫混凝土的密度等级可以增加组合柱的刚度,同时提高组合柱的轴向承载能力,泡沫混凝土密度每提高一级,CFS组合柱的极限荷载约增加1.5%。设置加劲肋可以提高组合柱极限荷载,但提高幅值逐渐减小,加劲肋的设置提高了类地聚物泡沫混凝土的轴向应力,从而增大了CFS-类地聚物泡沫混凝土组合柱的极限荷载。
4) JGJ 138—2016《组合结构技术规范》[1]中的计算公式符合本文CFS-GFC柱承载力计算预期结果,但其理论值相比试验值误差超过10%,因此,建议对泡沫混凝土轴心受压强度增强系数和截面形状影响系数进行修正,以充分发挥CFS-GFC组合柱材料性能优势。
| [1] |
中国建筑科学研究院. 组合结构设计规范: JGJ 138—2016[S]. 北京: 中国建筑工业出版社, 2016 China Academy of Building Research. Code for design of composite structures: JGJ 138—2016[S]. Beijing: China Building Industry Press, 2016 |
| [2] |
YU W W, LABOUBE R A. Cold-formed steel design[J]. Wiley&Sons, 2010, 38(3): 217. DOI:10.1002/9780470949825 |
| [3] |
刘洋, 谢伟平, 蔡玉春. 冷弯型钢发展与应用综述[J]. 钢结构, 2004(6): 36. LIU Yang, XIE Weiping, CAI Yuchun. Summary of development and application of cold-formed steel[J]. Steel Construction, 2004(6): 36. DOI:10.3969/j.issn.1007-9963.2004.06.013 |
| [4] |
MEYER C. The greening of the concrete industry[J]. Cement & Concrete Composites, 2009, 31(8): 601. DOI:10.1016/j.cemconcomp.2008.12.010 |
| [5] |
GAJALAKSHMI P, HELENA H J. Behaviour of concrete-filled steel columns subjected to lateral cyclic loading[J]. Journal of Constructional Steel Research, 2012(75): 55. DOI:10.1016/j.jcsr.2012.03.006 |
| [6] |
JI Xiaodong, KANG Hongzhen, CHEN Xingchen, et al. Seismic behavior and strength capacity of steel tube-reinforced concrete composite columns[J]. Earthquake Engineering & Structural Dynamics, 2014, 43(4): 487. DOI:10.1002/ege.2354 |
| [7] |
PATELV I, LIANG Qingquan, HADI M N S. Numerical analysis of high-strength concrete-filled steel tubular slender beam-columns under cyclic loading[J]. Journal of Constructional Steel Research, 2014, 92(1): 183. DOI:10.1016/j.jcsr.2013.09.008 |
| [8] |
朴泓任. 钢管发泡混凝土轴心受压构件受力性能研究[D]. 长春: 长春工程学院, 2018 PIAO Hongren. Study on the mechanical properties of steel tube foamed concrete axial compression members[J]. Changchun: Changchun Institute of Engineering, 2018 |
| [9] |
李振远. 冷弯薄壁型钢-泡沫混凝土柱轴压性能研究[D]. 青岛: 山东科技大学, 2020 LI Zhenyuan. Study on axial compression performance of cold-formed thin-walled steel-foam concrete columns[J]. Qingdao: Shandong University of Science and Technology, 2020. DOI: 10.27275/d.cnki.gsdku.2020.000508 |
| [10] |
THUMRONGVUT J, TIWJANTUK P. Strength and axial behavior of cellular lightweight concrete-filled steel rectangular tube columns under axial compression[J]. Materials Science Forum, 2018, 2417. DOI:10.4028/www.scientific.net/MSF.941.2417 |
| [11] |
COMMITTEE ACI, WIGHT J K, BARTH F G, et al. Buckling code requirements for structural concrete and commentary (ACI 318M-05)[M]. Michigan: American Concrete Institute, 2005.
|
| [12] |
SALGAR P B, PATIL P S. Experimental investigation on behavior of high-strength light weight concrete-filled steel tube strut under axial compression[J]. Transactions of the Indian National Academy of Engineering, 2019, 4: 207. DOI:10.1007/s41403-019-00077-7 |
| [13] |
侯亚杰. 冷弯薄壁型钢-轻混凝土柱畸变屈曲轴压性能研究[D]. 郑州: 华北水利水电大学, 2022 HOU Yajie. Study on distortional buckling axial compression performance of cold-formed thin-walled steel-lightweight concrete columns[D]. Zhengzhou: North China University of Water Resources and Hydropower, 2022. DOI: 10.27144/d.cnki.ghbsc.2022.000687 |
| [14] |
中南建筑设计院. 冷弯薄壁型钢结构技术规范: GB 50018—2002[S]. 北京: 中国计划出版社, 2002 Central-South Architectural Design Institute. Technical code for cold-formed thin-walled steel structures: GB 50018—2002[S]. Beijing: China Plan Publishing House, 2002 |
| [15] |
钢铁研究总院. 金属材料拉伸试验第一部分: 室温试验方法GBT 228.1—2010[S]. 北京: 中国标准出版社, 2011 Central Iron & Steel Research Institute. Tensile test of metal materials Part I: room temperature test method: GBT 228.1—2010[S]. Beijing: China Standard Press, 2011 |
| [16] |
李肖, 张元植. 设平板加劲肋矩形钢管混凝土柱静载下ABAQUS本构模型的研究[J]. 建筑钢结构进展, 2021, 23(8): 84. LI Xiao, ZHANG Yuanzhi. Study on ABAQUS constitutive model of concrete-filled rectangular steel tubular columns with flat stiffeners under static load[J]. Development of Building Steel Structure, 2021, 23(8): 84. DOI:10.13969/j.cnki.cn31-1893.2021.08.010 |
| [17] |
韩林海. 钢管混凝土结构: 理论与实践[M]. 3版. 北京: 科学出版社, 2007. HAN Linhai. Concrete filled steel tubular structures: theory and practice[M]. 3rd ed.. Beijing: Science Press, 2007. |
| [18] |
AIJ. Recommendations for design and construction of concrete filled steel tubular structures[S]. Tokyo: Architectural Institute of Japan(AIJ), 1997
|
| [19] |
Load and resistance factor design specification for structural steel buildings[S]. Chicago: American Institute of Steel Construction(AISC-LRFD), 1999
|
| [20] |
哈尔滨工业大学. 钢管混凝土结构技术规程: CECS 28: 2012[S]. 北京: 中国计划出版社, 2012 Harbin Institute of Technology. Technical specification for concrete filled steel tubular structures: CECS 28: 2012[S]. Beijing: China Plan Press, 2012 |
 2024, Vol. 56
2024, Vol. 56


