2. 岩土力学与工程国家重点实验室(中国科学院武汉岩土力学研究所),武汉 430071
2. State Key Laboratory of Geomechanics and Geotechnical Engineering (Institute of Rock and Soil Mechanics, Chinese Academy of Sciences), Wuhan 430071, China
由GB 50157—2013《地铁设计规范》[1]可知,地铁车站主体结构设计使用年限不应低于100 a,在漫长的服役期间,地铁车站结构的老化锈蚀问题也逐渐引起关注。众所周知,相对地上结构,地铁车站主体结构埋置于水土气三相环境中[2-4],面临着极其复杂的内外环境,杂散电流、混凝土的碳化和氯离子侵入是造成地铁车站结构钢筋锈蚀的主要原因。中国大部分地铁线路集中在经济发达的近海城市,近海环境的海水、海风、海雾以及地下水均含有大量的氯盐[5],氯离子渗透到地铁车站结构中,钢筋表面钝化膜逐渐被破坏,引起钢筋锈蚀,钢筋锈蚀生成的膨胀产物会造成混凝土开裂破坏。地铁主体结构设计使用年限长达100 a,在此服役期间,氯离子对地铁车站结构的破坏是导致结构锈蚀的主因[6]。由中国耐久性区划图[7]及第五代地震动参数区划图[8]可知,大部分含轨道交通网的城市同时位于地震高烈度区及耐久性环境恶劣区。因此,如何评估地铁车站结构在钢筋锈蚀和地震威胁双重作用下的抗震性能意义重大。
自20世纪90年代Okada等[9]开展锈蚀钢筋混凝土梁的低周反复荷载试验以来,众多学者对锈蚀钢筋混凝土结构的抗震性能进行了大量的研究。代旷宇等[10]对框架结构进行建模分析,结果显示,钢筋锈蚀会引起结构的自振周期延长、地震需求变化及抗震能力衰减;Celarec[11]、Berto[12]和Inci等[13]采用塑性铰模型进行锈蚀框架结构模拟,结果表明,钢筋锈蚀对结构受弯承载力影响较小,而对受剪承载力影响较大;Biondini等[14]通过研究结构柱横截面的弯矩-曲率关系变化探究锈蚀结构的时变性能;Simon等[15]分别采用静力Pushover分析和动力时程分析研究锈蚀桥梁在地震作用下的反应,并进行地震损伤评估。近年来,有学者也开始对锈蚀地下结构的抗震性能进行了研究。Song等[16]基于蒙特卡罗算法预测了100 a使用年限中隧道钢筋被腐蚀的概率;Yang等[17]提出一个时间相关的可靠度方法评估隧道的失效概率,利用该方法可以对劣化隧道结构的剩余使用寿命进行预测;Argyroudis等[18]考虑了氯离子侵蚀对浅埋圆形隧道结构横断面损伤的影响,提出基于IDA方法的时变地震易损性分析框架。迄今为止,与锈蚀钢筋混凝土框架结构或锈蚀桥梁结构相比,锈蚀地下结构抗震性能研究仍相当有限,并且地下结构受各层土体特性及约束作用的影响,土层沿深度方向和水平方向振动随埋深存在差异,锈蚀地下结构响应规律必然会与锈蚀地上结构存在很大差异。
为此,对氯离子侵蚀作用下的近海两层3跨地铁车站结构进行抗震性能研究,利用OpenSees有限元软件分别建立锈蚀和未锈蚀土-地铁车站结构相互作用的有限元模型,并依赖现有锈蚀钢筋混凝土柱拟静力试验,验证建模方法的可靠性。分析土-结构整体模型在两种不同频率成分的地震动作用下的结构响应。重点关注地铁车站的中柱损伤,并解释锈蚀地下结构地震响应规律。
1 氯离子侵蚀引起的材料退化模型 1.1 钢筋材性退化模型针对近海地区氯离子侵蚀环境下的地铁车站结构,采用Lee等[19]对氯盐环境锈蚀钢筋材料退化模型的相关研究成果考虑锈蚀对钢筋屈服强度和弹性模量的影响,能够较好地模拟氯蚀钢筋点蚀现象造成的钢筋强度退化。式(1)、(2)为锈蚀后钢筋屈服强度和弹性模量计算公式:
| $ f_{\mathrm{yc}}=\left[1-1.98\left(\mathit{\Delta }_{\mathrm{w}} / 100\right)\right] f_{\mathrm{y} 0} $ | (1) |
| $ E_{\mathrm{sc}}=\left[1-1.15\left(\mathit{\Delta }_{\mathrm{w}} / 100\right)\right] E_{\mathrm{s}} $ | (2) |
式中:fyc和fy0分别为完好及锈蚀钢筋的屈服强度,Esc和Es分别为完好及锈蚀钢筋的弹性模量,Δw为钢筋质量锈蚀率。
1.2 保护层混凝土材性退化模型钢筋锈蚀后体积增大,保护层混凝土受到锈胀力,在锈胀力的影响下保护层混凝土将产生微裂缝,进而导致钢筋混凝土构件承载能力降低。因此,采用Coronelli等[20]提出的Coronelli-Gambarova模型考虑锈蚀引起的外包混凝土强度退化。退化后混凝土强度fc可以用式(3)来计算:
| $ f_{\mathrm{c}}^*=\frac{f_{\mathrm{c}}}{1+K \varepsilon_1 / \varepsilon_{\mathrm{co}}} $ | (3) |
式中:K为与钢筋粗糙度和直径有关的系数(对于中等直径带肋钢筋取0.1),εco为峰值压应力fc对应的应变,ε1为锈蚀试件锈胀破裂后混凝土的平均横向应变。篇幅所限,式中参数取值及计算方法见文献[20]。
1.3 约束混凝土材性退化模型箍筋的混凝土保护层厚度通常小于纵向钢筋的混凝土保护层厚度,较低的混凝土保护层厚度使箍筋更容易接触侵蚀性氯离子。而锈后箍筋能够给核心混凝土提供的约束降低,进而核心混凝土强度的退化不可避免,选择一个合适的箍筋锈后核心混凝土本构模型尤为重要。因此,采用Zhang等[21]提出的锈蚀箍筋约束混凝土抗压强度计算公式,该公式是通过一系列氯离子加速腐蚀下锈蚀箍筋约束混凝土柱抗压试验,并在Mander等[22]提出的约束混凝土本构模型基础上提出的:
| $ f_{\mathrm{c}0}^{\mathrm{c}}=f_{\mathrm{c}0}\left(-1.254+2.254 \sqrt{1+7.94 \alpha_{\mathrm{s}} \frac{f_{\mathrm{lc}}}{f_{\mathrm{c} 0}}}-2 \alpha_{\mathrm{s}} \frac{f_{\mathrm{lc}}}{f_{\mathrm{c}0}}\right) $ | (4) |
式中:fc0c为箍筋锈蚀后约束混凝土的强度,fc0为箍筋锈蚀前约束混凝土的强度,f1c为锈蚀箍筋的有效水平压力,αs为正常强度混凝土的系数。篇幅所限,公式中各参数的取值及计算方法见文献[21-22]。
1.4 黏结强度退化模型采用潘志宏等[23]提出的锈蚀后钢筋混凝土间屈服滑移量计算公式(5)。OpenSees中提供了Bond-SP01材料来考虑节点钢筋黏结滑移的恢复力关系,因此,本文选择的修正模型可以方便地用于OpenSees平台当中。
| $ s_{\mathrm{y}}^*=\left[\frac{d f_{\mathrm{y}}^2\left(1-7.365 \eta_{\mathrm{s}}\right)^{0.4}}{10 E_{\mathrm{s}} \mathit{\Phi}_{\mathrm{u}} \sqrt{f_{\mathrm{c}}}}\right]^{0.714} $ | (5) |
式中:sy*为锈蚀后钢筋混凝土间屈服滑移量,d为钢筋直径,fy为钢筋屈服强度,ηs为钢筋质量锈蚀率,Es为钢筋弹性模量,Φu为受锈蚀率影响的折减系数,fc为混凝土抗压强度。篇幅所限,公式中各参数的取值及计算方法见文献[23]。
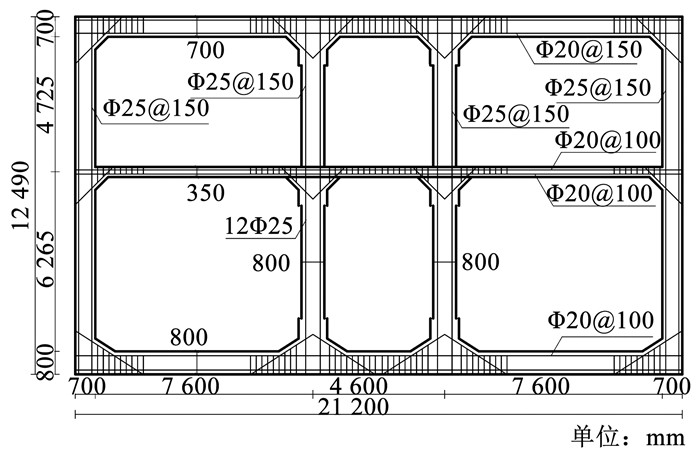
2 氯蚀地铁车站建模与模型验证 2.1 土-结构有限元模型建立 2.1.1 土-结构模型及参数以典型两层3跨地铁车站结构为对象,研究锈蚀前后大型地铁车站结构的非线性地震响应规律。车站结构顶板位置埋深为10 m,场地模型厚度为6 m,场地土层参数如表 1所示,按照GB 50909—2014[24]结构所处场地为Ⅱ类场地,结构的横断面尺寸如图 1所示。混凝土采用C40,钢筋采用HRB400。结构顶板底板配筋率为1.1%,中层隔板的配筋率为1.7%,中柱为1.0%,侧墙为0.65%。
| 表 1 Ⅱ类场地土层参数 Tab. 1 Physical parameters of Ⅱ site soil layers |
|
图 1 地铁车站结构横断面示意 Fig. 1 Schematic of cross-section of subway station structure |
根据土体自振周期[25]计算公式即可求得所采用工程场地自振周期约为0.95 s。
| $ T=\sum\limits_{i=1}^n \frac{4 H_i}{V_{\mathrm{s} i}} $ | (6) |
式中:T为工程场地自振周期,Hi为场地第i土层厚度,Vsi为场地第i土层剪切波速。
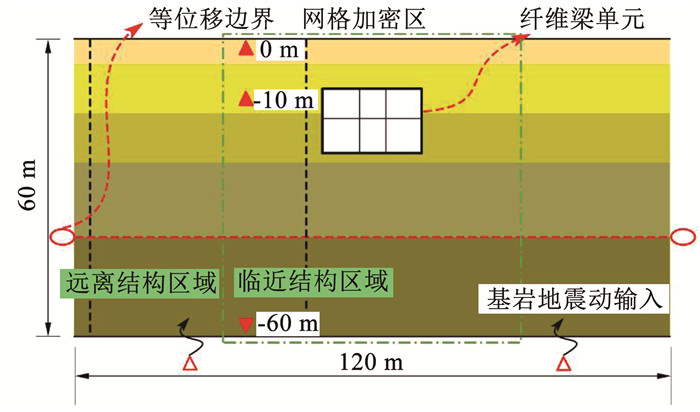
2.1.2 有限元模型建立利用OpenSees有限元软件建立了如图 2所示二维土-结构相互作用分析模型。
|
图 2 地铁车站二维整体有限元模型示意 Fig. 2 2D integrated finite element model of soil-structure interaction system |
土体宽度为120 m,为结构宽度的5倍以上,尽可能消除边界效应对地下结构地震反应的影响[24];计算高度取至距地表 60 m的工程基岩面。模型底部采用固定边界,顶部自由,水平地震动采用基底一致激励进行输入;侧边设置等位移边界,强制相同埋深两侧边界上土节点的水平向位移相同;土体和结构接触采用绑定接触,不考虑结构与土体的接触滑移。在划分网格时,结构单元网格尺寸为1.0 m,并将结构周围的土体网格进行了加密,该划分方式既保证了结构计算结果的准确性,也提高了计算效率。
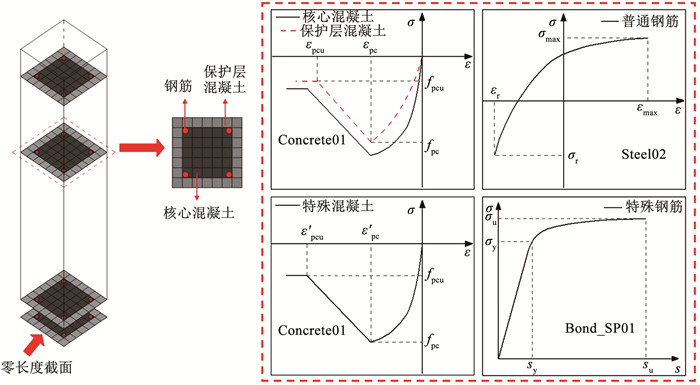
在建立车站结构模型时,钢筋混凝土梁和柱均采用基于位移的非线性梁柱单元(disp beam column)进行模拟,采用纤维截面模拟钢筋混凝土截面,截面划分为核心混凝土、保护层混凝土和钢筋。钢筋选用Steel02本构[26]进行模拟,该材料采用Giuffre-Menegotto-Pinto双线性本构模型,能较好地模拟反复加载下的包辛格效应和等向应变强化效应;混凝土选用Concrete01本构进行模拟;核心混凝土则采用Mander本构模型[22]考虑箍筋对混凝土的约束效应。为了考虑钢筋混凝土的黏结滑移,在梁柱端部增加一个零长度截面,该截面仍为纤维截面,与普通纤维截面不同的是,该截面采用Bond_SP01定义钢筋的本构关系,对于混凝土[27]则将零长度截面单元处全截面均考虑为受约束混凝土,零长度截面单元处的混凝土极限应变应放大100倍,零长度截面单元处的混凝土峰值应变应乘以渗透影响的某一个长度。图 3总结了上述地铁车站结构的非线性有限元建模方法。
|
图 3 锈蚀和未锈蚀钢筋混凝土框架结构的有限元建模示意 Fig. 3 Finite element modeling of corroded and uncorroded reinforced concrete frame structure |
需要注意的是中柱在车站纵向并不连续,而是以9.12 m为柱距均匀分布的,因此,Huo等[28]提出在保证中柱质量不变前提下,通过折减钢筋混凝土的材料参数使其具有与原中柱相同的截面抗弯刚度,等效为适合平面应变问题的连续墙体。
针对氯离子侵蚀下地铁车站结构,建模过程中采用第2节中提到的退化模型对材料力学性能进行修正,以考虑氯离子侵蚀引起的钢筋强度降低、外包混凝土开裂、约束混凝土强度降低和钢筋混凝土黏结能力的退化,同时假设结构产生均匀锈蚀。
基于文献[29]已验证的土体建模分析方法,采用四节点平面应变单元模拟土体在动力荷载下的力学行为。砂土采用对孔隙水压变化较为敏感的多屈服面弹塑性材料(pressure depend multi yield material, PDMY),其属于一种多屈服面弹塑性本构模型,可以模拟对压力敏感的材料,如砂土在动力荷载下的力学行为,屈服面采用Drucker-Prager模型(如图 4(a)所示)。对于黏土,采用对孔隙水压力变化不敏感的多屈服面弹塑性材料(pressure independ multi yield material),其可以模拟对固结状态变化敏感的材料,如黏土在动力荷载下的力学行为,PIMY材料的塑性是基于多屈服面的概念实现的,屈服面为Von Mises类型(如图 4(b)所示)。采用的土体本构模型中关键材料参数取值如表 2和3所示。

|
图 4 PDMY和PIMY本构屈服面 Fig. 4 PDMY and PIMY constitutive yield surface |
| 表 2 黏土材料参数取值 Tab. 2 Values of clay material parameters |
| 表 3 中砂材料参数取值 Tab. 3 Values of medium sand material parameters |
基于Fick第二定律的Life-365[30]软件可计算求得地铁车站起锈时间为20.6 a;基于Vu等[31]提出的钢筋时变腐蚀电流密度表达式,在时域内积分可获得钢筋腐蚀深度随时间变化公式:
| $ \begin{aligned} x_{\text {corr }}\left(t_i\right)= & \int_0^t 0.0116 i_{\text {corr }}(t) \mathrm{d} t= \\ & 0.525 \frac{(1-w / c)^{-1.64}}{d_{\mathrm{c}}} t_i^{0.7} \end{aligned} $ | (7) |
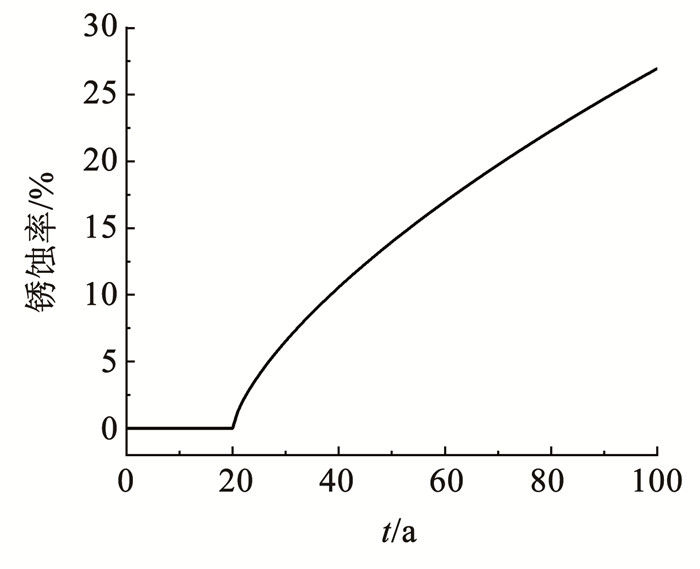
根据式(7)即可求得如图 5所示氯离子侵蚀下结构服役期内锈蚀率逐年变化。由图 5可知,结构在建成后40 a左右钢筋锈蚀率已达到10%,在建成后70 a左右钢筋锈蚀率已达到20%,这将对结构性能造成很大的影响。为此,以这两种锈蚀率作为极限情况,不考虑结构非均匀锈蚀,建立相应有限元模型,研究钢筋锈蚀对结构响应规律的影响。
|
图 5 氯离子侵蚀下钢筋锈蚀率逐年变化 Fig. 5 Change of corrosion rate of steel bar subjected to chloride-induced corrosion |
为了验证本文采用的有限元建模方法的准确性和合理性,对文献[32]中开展的编号为RCC-i(i为锈蚀率,i=5,10,15,20)的4个不同锈蚀率的钢筋混凝土柱的拟静力试验结果进行验证。篇幅所限,上述试验的设计参数和试验结果见文献[32]。
图 6为有限元模拟结果与文献[32]试验结果对比,可以看出,本文采用的锈蚀钢筋混凝土柱有限元建模方法能够较好地模拟不同锈蚀程度下钢筋混凝土柱的滞回性能,试验结果与模拟结果具有较好的一致性。

|
图 6 有限元模拟结果与试验结果对比 Fig. 6 Comparison of finite element simulation results with experimental results |
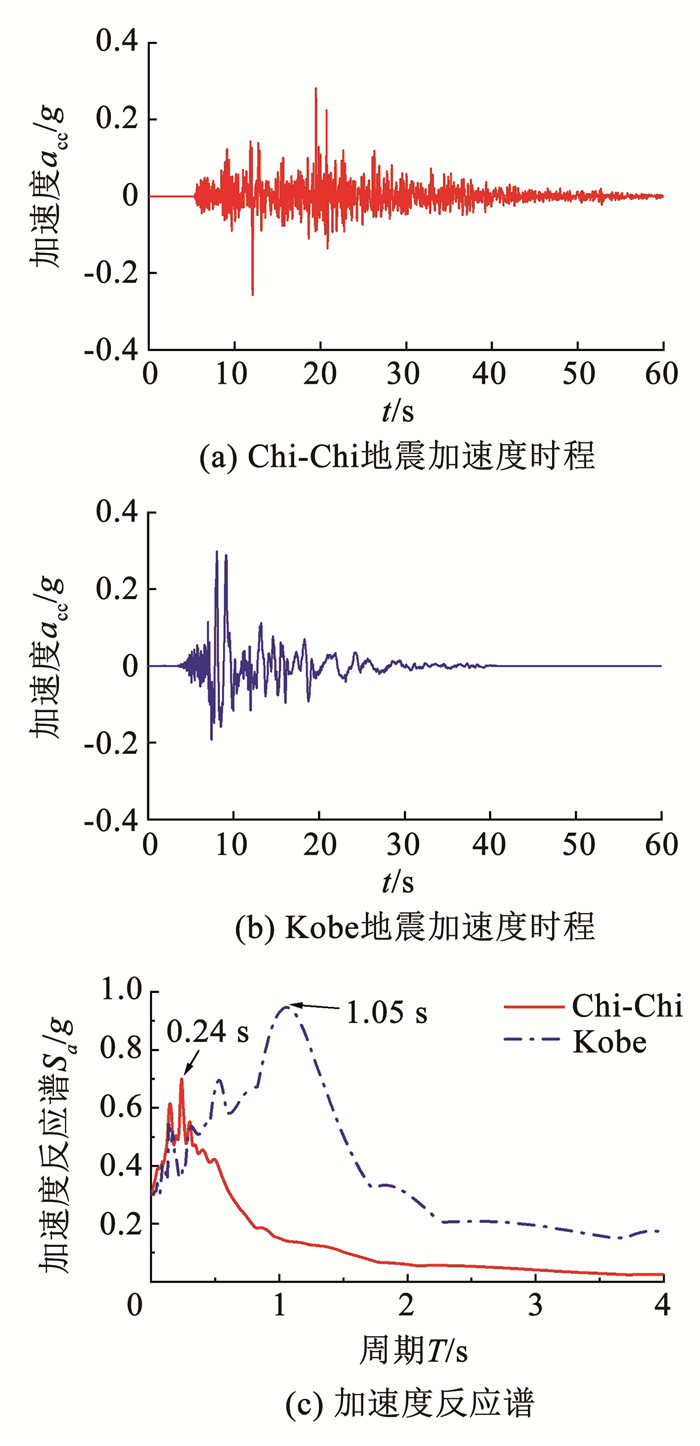
选取由日本Port Island台站记录的Kobe地震和中国台湾WNT台站记录的Chi-Chi地震,探究不同频率成分地震动对锈蚀地铁车站结构地震响应的影响,两条地震动信息如表 4所示。这两条地震动被人工调幅至0.3g后作为地震作用输入到有限元模型中进行计算,图 7(a)、(b)为调幅后地震动加速度时程曲线, 图 7(c)为调幅后地震动加速度时程对比。从图 7可以看出,两次地震记录在频率含量上有显著差异,Kobe地震以低频长周期成分为主,Chi-Chi地震以高频短周期成分为主。
| 表 4 地震动信息 Tab. 4 Ground motion information |
|
图 7 输入地震动 Fig. 7 Input ground motion |
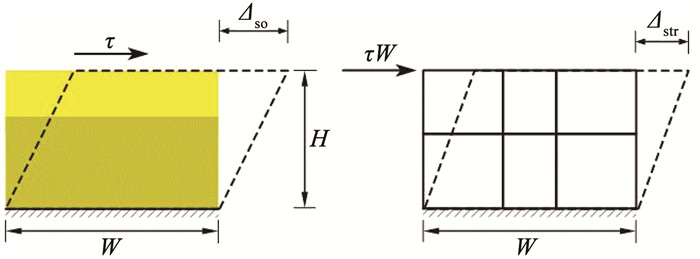
在地下结构施工过程中,需要挖除与结构位置同体积的土体。以氯离子侵蚀前后地下结构和等代土单元为对象,采用数值计算方法分别计算其在水平荷载下的变形比,即土-结构柔度比,计算简图如图 8所示。
|
图 8 柔度计算方法示意 Fig. 8 Flexibility calculation diagram |
针对所建两层3跨地铁车站的计算模型及场地参数,可获得未锈蚀、10%锈蚀率及20%锈蚀率下土-结构柔度比,分别为0.088、0.083和0.072,即相对完好状态,10%与20%锈蚀率下土-结构柔度比分别下降了6%和18%。由此可知,本文典型地铁车站结构抗侧刚度要远小于同体积的土体刚度,且随着锈蚀率的增加结构刚度在不断下降。
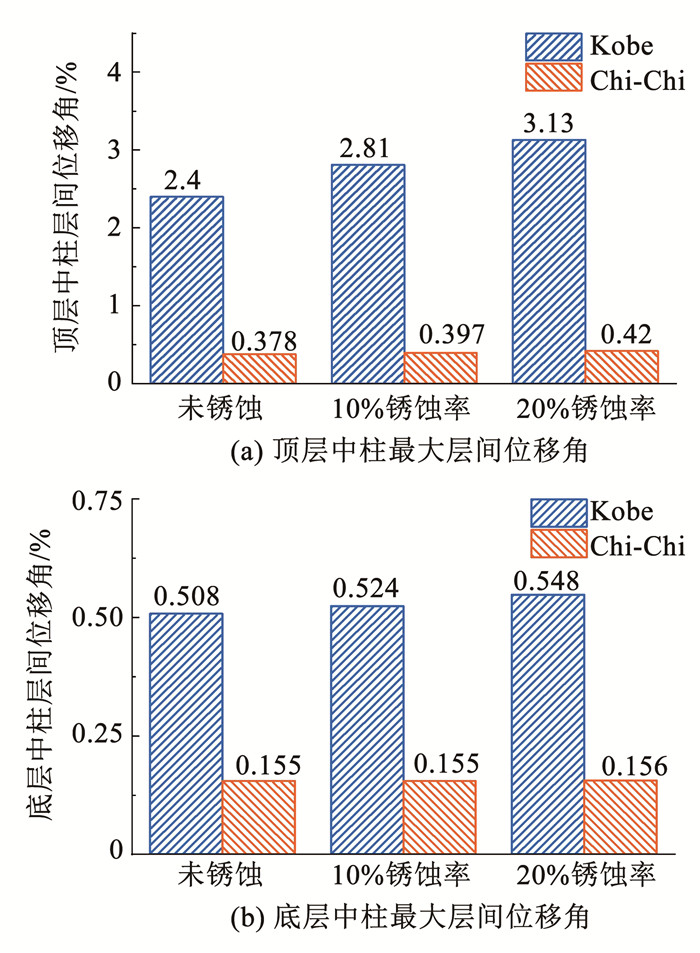
3.2.1 地铁车站中柱层间位移角响应分析从图 9(a)可以看出,在两条地震动作用下,锈蚀地铁车站顶层中柱最大层间位移角有不同程度的增加,而在Kobe地震下增加幅度更为显著,10%锈蚀率和20%锈蚀率的地铁车站顶层中柱最大层间位移角相比完好结构分别增加了17%和30%左右,而在Chi-Chi地震下增幅分别仅有5%和11%。
|
图 9 地铁车站中柱最大层间位移角响应分析 Fig. 9 Response analysis of maximum inter-story drift ratio of central column in subway station |
从图 9(b)可以看出,在Chi-Chi地震下,锈蚀地铁车站底层中柱最大层间位移角没有任何变化,而在Kobe地震下有一定程度的增加,10%锈蚀率和20%锈蚀率的地铁车站底层中柱最大层间位移角相比完好结构分别增加了3%和8%左右。
由于结构抗震薄弱环节底层中柱的层间位移角随锈蚀率的增加变化并不明显,不能直观反映结构安全性的变化。为研究锈蚀对地下结构安全性的影响,定义地下结构安全系数
| $ \kappa=\frac{\theta_{\text {Push }}}{\theta_{\mathrm{Dyn}}} $ | (8) |
式中:θPush为Pushover曲线中极限荷载点所对应的层间位移角,θDyn为动力时程分析后所得最大层间位移角。
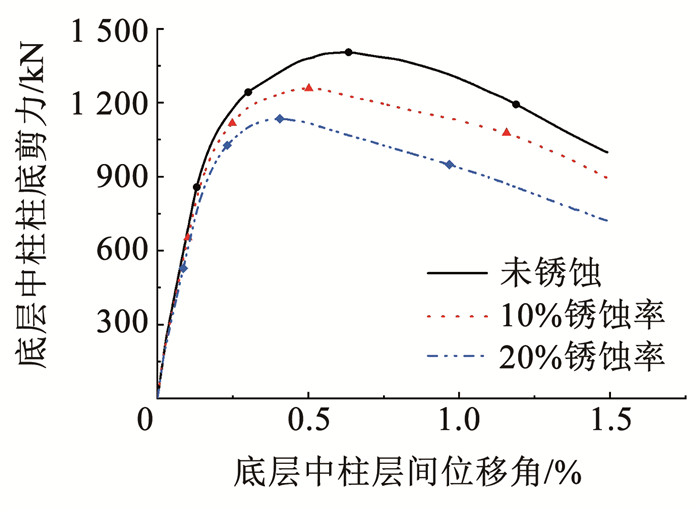
图 10为地铁车站结构底层中柱在不同锈蚀状态下的Pushover曲线,未锈蚀、10%锈蚀率及20%锈蚀率下曲线极限荷载点对应的层间位移角分别为1.18%、1.10%和0.96%。由此计算可得,Chi-Chi地震下未锈蚀、10%锈蚀率及20%锈蚀率下结构安全系数k分别为7.61、7.09和6.19,Kobe地震下分别为2.32、2.09和1.75,即结构安全性随锈蚀率的增加不断降低,且相同幅值地震动下,场地自振周期与地震动卓越周期越接近,结构越不安全。
|
图 10 地铁车站结构在不同锈蚀状态下Pushover曲线 Fig. 10 Pushover curves of a subway station under different level corrosion damage |
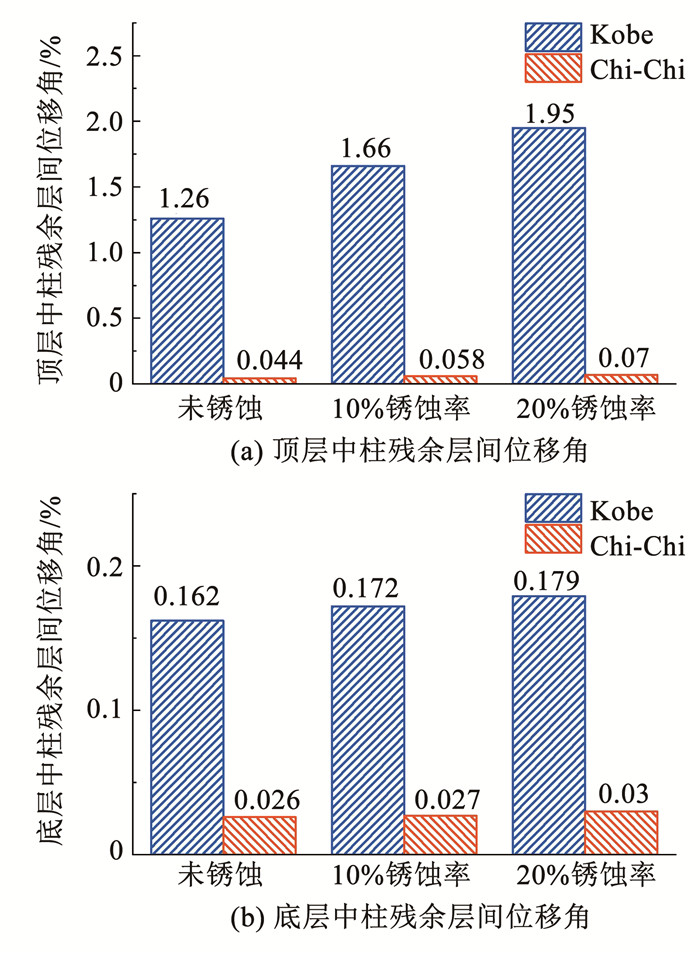
地震过程中土体的强非线性、滞回变形积累,导致周围土体发生不可逆的残余体积变形,结构也随之产生残余变形。由图 11可知,地铁车站中柱残余层间位移角响应规律与最大层间位移角的响应规律类似,即随着锈蚀率的增加,底层中柱残余层间位移角变化幅度不大,当锈蚀率为10%和20%时,顶层中柱残余层间位移角相比完好状态分别增加了5%和10%左右;而顶层中柱残余层间位移角变化幅度明显,增幅分别为32%和55%左右。由于Kobe地震强震持时显著小于Chi-Chi地震,Kobe地震下的中柱残余变形明显大于Chi-Chi地震下中柱残余变形。
|
图 11 地铁车站中柱残余层间位移角响应 Fig. 11 Residual inter-story drift ratios of central column in subway station |
提取两条地震动下不同锈蚀状态的车站结构侧墙与中柱内力,以式(9)定义的冗余度R为分析指标,研究钢筋锈蚀程度对地铁车站构件承载力的影响:
| $ R=\left(1-F_{\mathrm{c} i}^{\prime} / F_{\mathrm{c} i}\right) \times 100 $ | (9) |
式中:F′ci为在地震动作用下不同锈蚀状态的地铁车站结构侧墙或中柱最大底部内力,Fci为不同锈蚀状态下侧墙或中柱极限承载力。
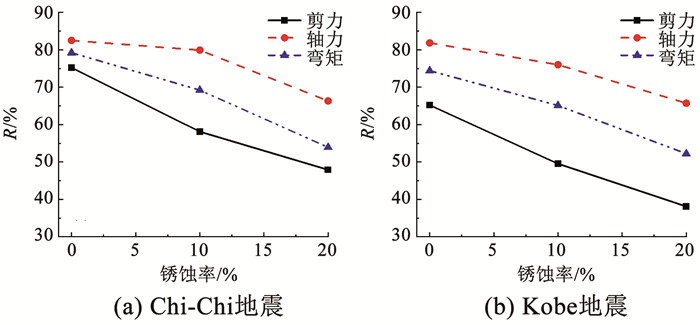
从图 12和13可以看出,随着锈蚀率的增加,结构中柱和侧墙的轴力以及底部剪力弯矩冗余度均有不同程度的下降,即构件由于钢筋锈蚀变得不安全。相比弯矩和剪力,锈蚀引起的构件轴力冗余度变化幅度较小,这是因为锈蚀引起的构件最大轴力增幅不明显,仅构件的极限抗压承载力在下降。相比结构中柱,侧墙的最大内力冗余度大于中柱,且随锈蚀率的增加变化不太明显,可以认为地铁车站结构锈蚀后,中柱仍为整个结构中的抗力最薄弱环节。相比Chi-Chi地震,在Kobe地震作用下构件冗余度小10%左右,即当场地自振周期与地震动卓越周期越接近,构件越不安全。
|
图 12 锈蚀与初始工况中柱柱底内力之比 Fig. 12 Ratio between the internal forces at the base of the column under corroded and non-corroded conditions |

|
图 13 锈蚀与初始工况侧墙墙底内力之比 Fig. 13 Ratio between the internal forces at the base of the sidewall under corroded and non-corroded conditions |
提取两条地震动下不同锈蚀状态的车站结构顶底层中柱纤维截面最大剪力,计算求得纤维截面中钢筋与混凝土各自的剪力占比。从图 14可知,对于未锈蚀结构,在Chi-Chi地震下,无论是底层中柱还是顶层中柱,纤维截面中混凝土都承担了超过80%的剪力,钢筋仅仅承担了15%左右的剪力;而在Kobe地震下,纤维截面中钢筋剪力占比要大于Chi-Chi地震下钢筋剪力占比,且底层与顶层剪力分配有明显的差异,顶层中柱钢筋剪力占比要大于底层中柱剪力占比近一倍。而随着锈蚀率的增加,钢筋强度降低结构自身性能下降,其所能承担的剪力占比不断下降。

|
图 14 地铁车站中柱纤维截面剪力分布 Fig. 14 Shear force distribution of column fiber section in subway station |
为进一步解释锈蚀前后地铁车站中柱响应规律,重点分析结构高度范围内临近结构区域土体响应,提取距离地铁车站结构右侧墙1.2 m的结构上下两层层高范围土体内剪切变形(该层上下两点土体位移差除以层高)。
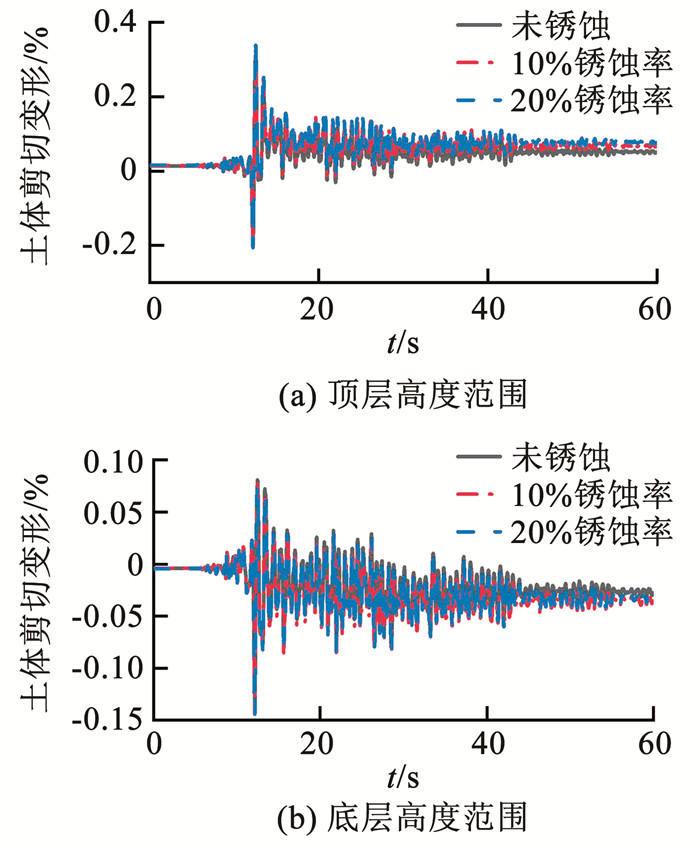
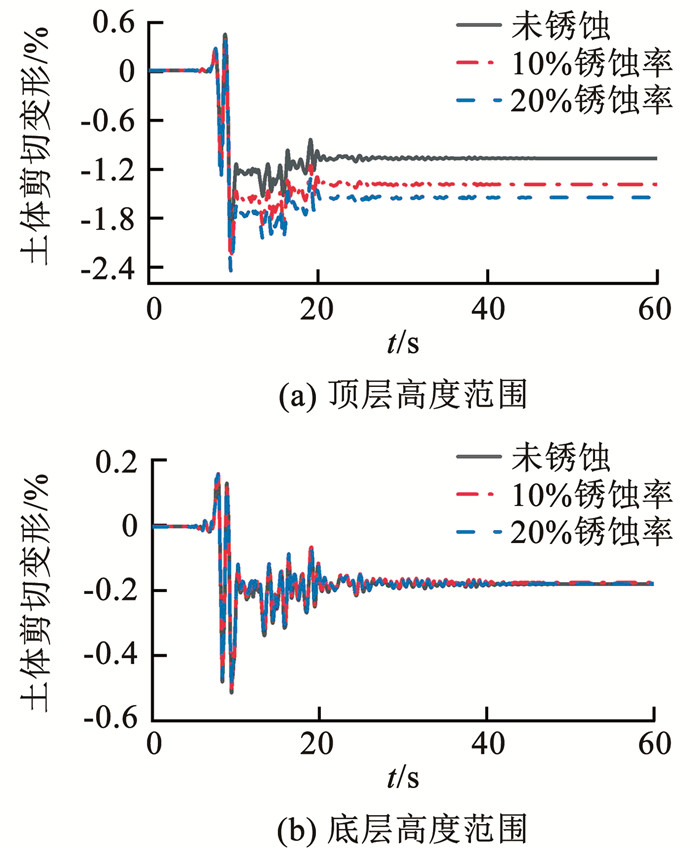
如图 15和16所示,并结合图 14分析可知,在Chi-Chi地震作用下,结构顶底层高度范围内土体剪切变形均相对较小,土体仍能对结构起到一种约束保护作用,使得中柱纤维截面中混凝土承担了绝大部分剪力,因此,钢筋锈蚀对于层间位移角并未有太大影响;而在Kobe地震作用下,结构顶底层高度范围内土体剪切变形变大,且顶层高度范围内的土体剪切变形要明显大于底层高度范围内的土体剪切变形,土体推动结构产生破坏,钢筋承担的剪力百分比变大,此时,钢筋的锈蚀会造成自身性能下降,进而对层间位移角响应产生了影响。
|
图 15 Chi-Chi地震下结构高度范围内临近结构区域土体剪切变形 Fig. 15 Shear deformation of soil in the area adjacent to the structure within the height range of the structure under Chi-Chi earthquake |
|
图 16 Kobe地震下结构高度范围内临近结构区域土体剪切变形 Fig. 16 Shear deformation of soil in the area adjacent to the structure within the height range of the structure under Kobe earthquake |
在Chi-Chi和Kobe地震作用下底层高度范围内临近结构区域土体的剪切变形并不会随结构的锈蚀有很明显的变化。观察Kobe地震作用下顶层高度范围内临近结构区域土体剪切变形可知,结构顶层高度范围内临近结构区域土体剪切变形随锈蚀率的增加而增加,当结构锈蚀率为10%和20%时,相比完好结构,土体最大剪切变形分别增加了16%和24%。由此可看出,当结构因为锈蚀造成变形的大幅增加时,反过来也会引起临近结构区域土体响应变化。
4 结论1) 在10%和20%钢筋锈蚀率下的结构相对完好结构,虽然地铁车站结构抗侧刚度下降,土-结构柔度比下降幅度分别为6%和19%,但由于地下结构周围受土体约束,在相同地震作用下其底层中柱最大层间位移角没有明显变化。
2) 底层中柱作为抗震薄弱环节,随着钢筋锈蚀率的增加,中柱的变形能力和承载能力不断劣化,导致地铁车站结构整体抗震能力和安全系数降低,下降幅度为10%和20%左右。
3) 锈蚀后结构中柱最大层间位移角增幅与场地响应有关,低频成分丰富的地震作用下土体产生大变形,使得顶底层中柱纤维截面中钢筋剪力占比约为40%和20%,此时,钢筋锈蚀将对其地震响应产生较大影响。而高频成分地震作用下土体变形较小,钢筋仅承担了15%左右的剪力,此时钢筋锈蚀产生的影响可忽略不计。
| [1] |
北京市规划委员会. 地铁设计规范: GB 50157—2013[S]. 北京: 中国建筑工业出版社, 2013 Beijing Municipal Commission of Planning. Code for subway design: GB 50157—2013[S]. Beijing: China Architecture & Building Press, 2013 |
| [2] |
张广超. 地下结构中钢筋锈胀对钢筋混凝土整体结构影响问题的研究[D]. 成都: 西南交通大学, 2013 ZHANG Guangchao. Research on the effect of the corroded expansive force of rebar on reinforced concrete structure in underground structures[D]. Chengdu: Southwest Jiaotong University, 2013 |
| [3] |
王海军. 地铁车站主体结构服役期可靠度及检测维修成本优化研究[D]. 北京: 北京交通大学, 2018 WANG Haijun. Research on the reliability and optimization of inspection and maintenance cost during the service life of subway station main structure[D]. Beijing: Beijing Jiaotong University, 2018 |
| [4] |
张立伟. 碳化与锈蚀对地下结构服役性能的研究[D]. 上海: 同济大学, 2008 ZHANG Liwei. Study on service capability of carbonization and corrosion to underground stuctures[D]. Shanghai: Tongji University, 2008 |
| [5] |
BANERJE E, SWAGAT A, PRASAD G, et al. Seismic risk assessment of reinforced concrete bridges in flood-prone regions[J]. Structure & Infrastructure Engineering: Maintenance, Management, Life-Cycle, 2013(9): 12. DOI:10.1080/15732479.2011.649292 |
| [6] |
赵筠. 钢筋混凝土结构的工作寿命设计-针对氯盐污染环境[J]. 混凝土, 2004(1): 3. ZHAO Yun. Service life design of reinforced concrete structures exposed to chloride environment[J]. Concrete, 2004(1): 3. |
| [7] |
吕清芳. 混凝土结构耐久性环境区划标准的基础研究[D]. 杭州: 浙江大学, 2007 LV Qingfang. Fundamental research on durability environmental zonation standard(DEZS) of concrete structures[D]. Hangzhou: Zhejiang University, 2007 |
| [8] |
中国地震局地球物理研究所. 中国地震动参数区划图: GB 18306—2015[S]. 北京: 中国标准出版社, 2015 Institute of Geophysics, China Earthquake Administration. Seismic ground motion parameters zonation map of China: GB 18306—2015[S]. Beijing: Standards Press of China, 2015 |
| [9] |
OKADA K, KOBAYASHI K, MIYAGAWA T. Influence of longitudinal cracking due to reinforcement corrosion on characteristics of reinforced concrete members[J]. コンクリート工学年次講演会論文集, 1988, 85(2): 134. |
| [10] |
代旷宇, 于晓辉, 李雨适, 等. 锈蚀钢筋混凝土结构地震易损性分析[J]. 建筑结构学报, 2022, 43(8): 20. DAI Kuangyu, YU Xiaohui, LI Yushi, et al. Seismic fragility analysis of reinforced concrete structures considering reinforcement corrosion[J]. Journal of Building Structures, 2022, 43(8): 20. |
| [11] |
CELAREC D, VAMVATSIKOS D, DOLEK M. Simplified estimation of seismic risk for reinforced concrete buildings with consideration of corrosion over time[J]. Bulletin of Earthquake Engineering, 2011, 9(4): 1137. DOI:10.1007/s10518-010-9241-3 |
| [12] |
BERTO L, VITALIANI R, SAETTA A, et al. Seismic assessment of existing RC structures affected by degradation phenomena[J]. Structural Safety, 2009, 31(4): 284. DOI:10.1016/j.strusafe.2008.09.006 |
| [13] |
INCI P, GOKSU C, ILKI A, et al. Effects of reinforcement corrosion on the performance of RC frame buildings subjected to seismic actions[J]. Journal of Performance of Constructed Facilities, 2013, 27(6): 683. DOI:10.1061/(ASCE)CF.1943-5509.0000378 |
| [14] |
BIONDINI F, CAMNASIO E, TITI A. Seismic resilience of concrete structures under corrosion[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(14): 2445. DOI:10.1002/eqe.2591 |
| [15] |
SIMON J, BRACCI J M, GARDONI P. Seismic response and fragility of deteriorated reinforced concrete bridges[J]. Journal of Structural Engineering, 2010, 136(10): 1273. DOI:10.1061/(ASCE)ST.1943-541X.0000220 |
| [16] |
SONG H W, PACK S W, ANN K Y. Probabilistic assessment to predict the time to corrosion of steel in reinforced concrete tunnel box exposed to sea water[J]. Construction & Building Materials, 2009, 23(10): 3270. DOI:10.1016/j.conbuildmat.2009.05.007 |
| [17] |
YANG Wei, BAJI H, LI C Q. Time-dependent reliability method for service life prediction of reinforced concrete shield metro tunnels[J]. Structure and Infrastructure Engineering, 2018, 14(8): 1095. DOI:10.1080/15732479.2017.1401094 |
| [18] |
ARGYROUDIS S, TSINIDIS G, GATTI F, et al. Effects of SSI and lining corrosion on the seismic vulnerability of shallow circular tunnels[J]. Soil Dynamics and Earthquake Engineering, 2017, 98: 244. DOI:10.1016/j.soildyn.2017.04.016 |
| [19] |
LEE H S, CHO Y S. Evaluation of the mechanical properties of steel reinforcement embedded in concrete specimen as a function of the degree of reinforcement corrosion[J]. International Journal of Fracture, 2009, 157(1): 81. DOI:10.1007/s10704-009-9334-7 |
| [20] |
CORONELLI D, GAMBAROVA P G. Structural assessment of corroded reinforced concrete beams: modeling guidelines[J]. Journal of Structural Engineering, 2004, 130: 1214. DOI:10.1061/(ASCE)0733-9445(2004)130:8(1214) |
| [21] |
ZHANG Guanghui, CAO Xinhu, FU Qiuni. Experimental study on residual strength of concrete confined with corroded stirrups[J]. Canadian Journal of Civil Engineering, 2016, 43(6): 583. DOI:10.1139/cjce-2016-0138 |
| [22] |
MANDER J, PRIESTLEY M. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [23] |
潘志宏, 李爱群, 孙义刚. 反复荷载下锈蚀黏结退化的RC结构数值模拟[J]. 中国矿业大学学报, 2010, 39(3): 362. PAN Zhihong, LI Aiqun, SUN Yigang. Numerical simulation of reinforced concrete structures under cyclic loads: the effects of bond deterioration due to reinforcement corrosion[J]. Journal of China University of Mining and Technology, 2010, 39(3): 362. |
| [24] |
中华人民共和国住房和城乡建设部. 城市轨道交通结构抗震设计规范: GB 50909—2014[S]. 北京: 中国计划出版社, 2014 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of urban rail transit structure: GB 50909—2014[S]. Beijing: China Plans Publishing House, 2014 |
| [25] |
高广运, 吴世明, 周健, 等. 场地卓越周期的讨论与测定[J]. 工程勘察, 2000(5): 29. GAO Guangyun, WU Shiming, ZHOU Jian, et al. Discussion and determination of site-specific design spectral acceleration[J]. Engineering Investigation and Surveying, 2000(5): 29. |
| [26] |
FILIPPOU F C, POPOV E P, BERTERO V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints[R]. Berkeley: Earthquake Engineering Research Center, University of California, 1983
|
| [27] |
高王鑫. 钢筋与套管约束CFRP纵筋混合配筋混凝土柱抗震性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 GAO Wangxin. Study on seismic performance of concrete columns reinforced by hybrid steel and duct-confined CFRP bars[D]. Harbin: Harbin Institute of Technology, 2017 |
| [28] |
HUO H, BOBET A, FERNANDEZ G, et al. Load transfer mechanisms between underground structure and surrounding ground: evaluation of the failure of the Daikai Station[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(12): 1522. DOI:10.1061/(ASCE)1090-0241(2005)131:12(1522) |
| [29] |
钟紫蓝, 甄立斌, 申轶尧, 等. 基于耐震时程分析法的地下结构抗震性能评价[J]. 岩土工程学报, 2020, 42(8): 1482. ZHONG Zilan, ZHEN Libin, SHEN Yiyao, et al. Seismic performance evaluation of underground structures using endurance time a analysis[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1482. |
| [30] |
Life-365 Consortium Ⅱ. Life-365 Service Life Prediction Model and computer program for predicting the service life and life-cycle cost of reinforced concrete exposed to chlorides[M]. Washington DC: SFA, 2012.
|
| [31] |
VU K A T, STEWART M G. Structural reliability of concrete bridges including improved chloride-induced corrosion models[J]. Building Technique Development, 2007, 22(4): 313. DOI:10.1016/S0167-4730(00)00018-7 |
| [32] |
杨淑雁. 锈蚀钢筋混凝土柱在地震作用下的滞回行为研究[D]. 上海: 上海交通大学, 2014 YANG Shuyan. Research on hysteretic behavior of corroded reinforced concrete column under seismic load[D]. Shanghai: Shanghai Jiao Tong University, 2014 |
 2024, Vol. 56
2024, Vol. 56


