2. 地震灾害防治应急管理部重点实验室,哈尔滨 150080
2. Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin 150080, China
烈度是衡量一次地震对建筑物破坏程度的重要指标。震后快速生成烈度场对精准应急救援有着至关重要的作用[1],也是地震烈度速报中的一项关键技术[2]。由于宏观调查烈度需要花费大量的时间而难以满足地震应急救援的需求,采用强震动观测记录换算成仪器地震烈度,进而通过插值技术生成烈度等震线图是目前常用的一种手段[3-4]。
受震源、传播路径及局部场地的控制,烈度场的空间分布满足特定的衰减规律;而受局部场地及地形的影响,烈度场也存在一定的空间相关性[5]。Schenkova等[6]将克里金插值应用到烈度等值线图的绘制中,通过半变异函数实现对空间相关性的考虑;陈鲲等[7]和邵国良等[8]利用地质统计学中的半变异函数方法对地震动峰值加速度(PGA)、地震动峰值速度(PGV)及加速度反应谱(Sa)的空间相关性进行了研究;Schiappapietra等[9]总结了PGA、PGV、Sa、阿里亚斯烈度(Ia)和累计绝对速度(CAV)等参数的空间相关性分析模型。地震动的空间分布满足一定的衰减规律,尤其大震的近源效应对地震动的空间分布有重要影响,利用地震动衰减规律进行空间地震动场分布估计也是常用的一种手段。
然而,克里金插值法是一种无源插值方法,在进行烈度等值线图的绘制时,不能考虑震源与观测点及待插值点之间的关系。利用克里金插值方法仅仅能够考虑地震动场的空间相关性或局部特征,难以考虑地震动的震源效应。因此,克里金插值法用于仪器烈度的空间插值时,往往存在烈度等值线图形状不规则的问题,与实际调查产生的烈度等值线图存在较大的偏差[10]。中国考虑空间相关性的地震动场估计方法研究还处于探索阶段,无法满足实际应用的需求。本文在克里金插值方法的基础上提出了一种既能考虑震源的信息,又能考虑地震动空间相关性的插值方法,并利用实际地震观测数据验证了方法的合理性,可以为国家地震烈度速报与预警工程提供技术支持。
1 方法克里金插值法又称空间自协方差最佳插值法,是以法国人Krige的名字命名的一种最优内插法[11]。克里金插值方法的原理是根据各已知点获得的观测值进行空间的结构分析,并拟合出合适的理论半变异函数模型,对待插值点的值进行预测[12]。
1.1 融合克里金插值方法假设空间内存在一个待插值点x0,将待插值点x0周围已知点的观测值进行线性组合,可以获得待插值点x0的估计值[13]。在进行空间插值的过程中,克里金插值仅考虑点与点之间的空间相关性,即各点之间相关的程度。为了在插值过程中既能考虑空间相关性,又能考虑震源效应,本文采取了融合插值,如式(1)所示:
| $ z^*=q_1 z_1^*+q_2 z_2^*=q_1 \sum\limits_{i=1}^n \lambda_i z_i+q_2 \sum\limits_{i=1}^n \varphi_i z_i $ | (1) |
式中:z*为融合克里金插值方法中待插值点x0的估计值;z1*为考虑空间相关性的待插值点x0的估计值;z2*为考虑震源效应的待插值点x0的估计值;λi和φi为克里金插值中观测点i相对于待插值点x0的权重系数;zi为待插值点周围观测点i的观测值;n为待插值点周围观测点的数量;q1和q2分别为克里金插值和考虑震源效应的克里金插值的比例系数,满足条件q1+q2=1。
融合克里金插值中的权重系数λi和φi的求法如下,为了使待插值点x0的估计值具有无偏估计性,需保证
| $ z_{\mathrm{var}}=\operatorname{var}\left[z_1^*-z_0\right]=2 \sum\limits_{i=1}^n \lambda_i \gamma_{i 0}-\sum\limits_{i=1}^n \sum\limits_{j=1}^n \lambda_i \lambda_j \gamma_{i j} $ | (2) |
式中:z0为待插值点的真实值;γi0为观测点i与待插值点x0之间的半变异函数值,通过拟合的理论半变异函数模型求解;γij为观测点i与观测点j之间的半变异函数值,其公式为
为了使得估计值与真实值相等,估计方差必须最小,即满足
| $ \left[\begin{array}{ccccc} \gamma_{11} & \gamma_{12} & \cdots & \gamma_{1 n} & 1 \\ \gamma_{21} & \gamma_{22} & \cdots & \gamma_{2 n} & 1 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ \gamma_{n 1} & \gamma_{n 2} & \cdots & \gamma_{n n} & 1 \\ 1 & 1 & \cdots & 1 & 0 \end{array}\right] \times\left[\begin{array}{c} \lambda_1 \\ \lambda_2 \\ \vdots \\ \lambda_n \\ \mu \end{array}\right]=\left[\begin{array}{c} \gamma_{10} \\ \gamma_{20} \\ \vdots \\ \gamma_{n 0} \\ 1 \end{array}\right] $ | (3) |
使用拟合出的理论半变异函数模型解出式(3),即可得到已知点在待插值点处的权重系数λi和拉格朗日乘数μ,代入估计值误差的方差表达式(2)可求得估计方差zvar。考虑震源效应的克里金插值的权重系数φi计算方式与λi相同,不同之处在于半变异函数中距离项的定义不同。
克里金插值方法的核心是半变异函数,既能描述区域化变量的空间结构性变化,又能描述其随机性变化。在插值过程中选用的半变异函数模型及其相关参数会直接影响克里金插值的精度及效果[15]。当改变半变异函数的自变量时,就能获得一个不同的理论半变异函数模型。在权重系数λi的求解过程中,距离h的定义采用两点之间的距离,即
| $ h_{i j}=\sqrt{\left(x_i-x_j\right)^2+\left(y_i-y_j\right)^2} $ | (4) |
式中(xi, yi)和(xj, yj)分别为第i和j个观测点的位置坐标。
为研究震源对仪器烈度影响场的影响,在φi的求解过程中引入了一个新的距离自变量h*,其含义为两点到震源的距离之差,即
| $ h_{i j}^*=\left|R_{j \mathrm{~b}}^i-R_{j \mathrm{~b}}^j\right| $ | (5) |
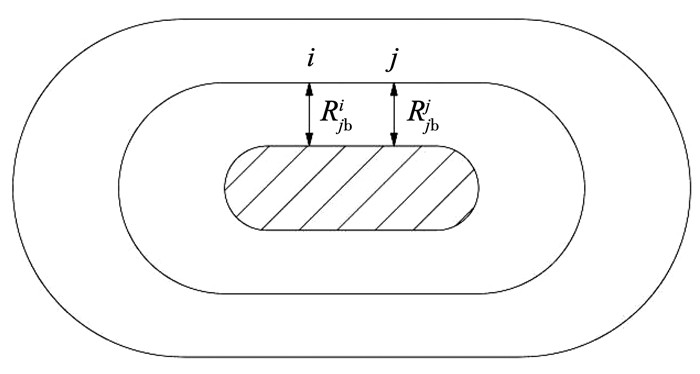
式中:Rjbi和Rjbj分别为观测点i和j到震源的断层投影距离(km);hij*为观测点i和j到震源的断层投影距离差(如图 1所示)。
|
图 1 断层投影距 Fig. 1 Fault projection distance |
图 1中阴影部分是震源的断层在地面上的投影,Rjbi为观测点i到断层面在地面投影的最短距离,Rjbj为观测点j到断层面在地面投影的最短距离[16]。“跑道”为断层投影距相等的点连成的线,根据地震动衰减规律,当两点到震源的距离相等时,两点的地震动也相等。因此,当Rjbi=Rjbj时,i和j两点的烈度值在理论上一致,这就是基于震源距的地震动衰减模型。本文通过点到震源之间的距离差实现了对地震动震源效应的考虑,使用这种新的距离自变量拟合出考虑震源效应的理论半变异函数模型,进而可以获得考虑震源效应的克里金插值结果。
1.2 理论半变异函数的拟合地质统计学领域中,对区域化变量进行结构分析是一项关键的工作。其中,最主要的内容是计算数据的实验半变异函数,然后用实验半变异函数拟合理论半变异函数模型[17]。目前,拟合理论半变异函数模型还没有一个理想的方法。以往许多学者使用的方法是人工拟合,但这种方法具有较强的主观性,缺乏客观的统一标准,阻碍了计算过程的自动化[18]。为了快速高效地确定理论半变异函数模型的相关参数C0, C, a,使用了粒子群优化算法。粒子群优化算法是一种进化计算方法,是模拟鸟群捕食行为而提出的[19]。粒子群优化算法收敛速度快,能快速高效地对理论半变异函数模型进行拟合。
粒子群优化算法先设置若干数量的随机粒子,作为拟合模型的随机解。每一个粒子具有一个初始位置和初始速度,第i个粒子的初始位置和初始速度可以设为Si=(si1, si2, …, siD)T和Vi=(vi1, vi2, …, viD)T,其中,D为粒子的维数,即需要求解的参数的个数;Si作为拟合模型的一个可能解,可以计算出拟合模型的值,进而获得该粒子对拟合模型的适应度,根据适应度可以判断粒子的优劣;Vi作为粒子的当前速度,是粒子向最优解靠近的快慢程度。粒子们不断向解空间的最优粒子靠近,以迭代的方式寻找最优解。每个粒子在迭代的过程中追踪两个当前的最优粒子,一个是个体历史最优位置Pi=(pi1, pi2, …, piD)T,另一个是全局历史最优位置Pg=(pg1, pg2, …, pgD)T,每个粒子根据两个最优粒子的位置更新当前位置和当前速度[18]。
第i个粒子更新自己的第d维参数时公式如下:
| $ s_{i d}^{k+1}=s_{i d}^k+v_{i d}^{k+1} $ | (6) |
| $ v_{i d}^{k+1}=w v_{i d}^k+c_1 r_1\left(p_{\mathrm{i} d}^k-x_{\mathrm{i} d}^k\right)+c_2 r_2\left(p_{\mathrm{g} d}^k-x_{\mathrm{g} d}^k\right) $ | (7) |
式中:k为当前进化代数;c1、c2为学习因子;r1、r2为均匀分布于(0, 1)区间的随机数;w为惯性权重,是调整算法全局搜索能力和局部搜索能力的平衡因子,较大的w有利于跳出局部极小点,较小的w有利于算法收敛[20]。
设置随着迭代的进行,w由最大的wmax线性减小到wmin,即
| $ w=w_{\max }-\left(w_{\max }-w_{\min }\right) u / u_{\max } $ | (8) |
式中:u为当前迭代次数,umax为总迭代次数。
采用待插值点实验半变异函数与理论半变异函数模型在各种距离条件下的差值的平方和作为目标函数,即粒子群优化算法中的适应度函数[21]
| $ f=\sum\limits_{i=1}^m\left[\gamma^*(h)-\gamma(h)\right]^2 $ | (9) |
式中:γ*(h)代表实验半变异函数,γ(h)代表理论半变异函数,m表示插值点的个数。
2 算例分析为了验证方法的合理性,选取强震动记录丰富的日本地区4次实际震例进行分析。为便于实际观测结果对比,震例中的仪器烈度采用该地区使用的JMA尺度[22-23],JMA仪器地震烈度是根据在大约0.5 Hz下进行带通滤波的三分量加速度计算得出的。
JMA仪器地震烈度的原始计算算法对于实时计算来说是不稳定的,因为该算法使用快速傅里叶变换(FFT)来滤波波形,需要较高的计算成本。为了实时计算观测到的地震烈度,采用了Kunugi等[24]提出的技术,使用递归滤波器代替FFT,并以较低的计算成本实时提供高精度的JMA仪器地震烈度近似[25]。
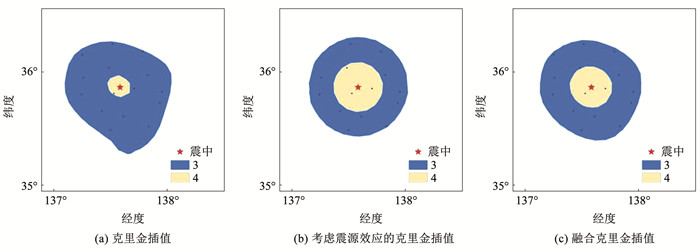
2.1 日本地震插值仪器烈度图 2.1.1 点源模型的中小地震日本长野县地震发生于2017年6月25日,此次地震震中(35.867°N,137.585°E)位于日本长野县南部,震级为5.6级,震源深度约为7 km。对此次地震进行插值,获得仪器烈度如图 2所示。
|
图 2 日本长野县地震仪器烈度 Fig. 2 Instrument intensity of Nagano earthquake in Japan |
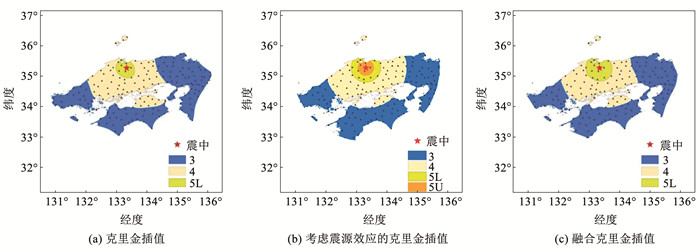
1) 日本鸟取7.3级地震。日本鸟取地震是2000年10月6日发生于日本鸟取县的一场地震,此次地震造成2人死亡,106人受伤。地震震中(35.278°N,133.345°E)位于鸟取县西部,震级为7.3级,震源深度约为11 km。对此次地震进行插值,获得的仪器烈度如图 3所示,其中,5 L和5 U是JMA的烈度尺度,分别对应5度弱和5度强。
|
图 3 日本鸟取地震仪器烈度 Fig. 3 Instrument intensity of Tottori earthquake in Japan |
克里金插值获得的烈度图在烈度3区存在不规则现象,高烈度区形状较规则。考虑震源效应的克里金插值在震中附近出现了5U烈度区,这种插值考虑了震源的影响,以震中为圆心,烈度值逐级递减,震中附近存在少数高烈度值点,会形成小范围的高烈度区。而克里金插值中少数的高烈度值点在进行空间分析时,会受周围低烈度值点影响,所以,少数的高烈度值点无法形成区域。
2) 日本岩手7.2级地震。日本岩手地震发生于东京时间2008年6月14日,震中(39.028°N,140.880°E)位于日本岩手县内陆南部,岩手县东南100 km,东京以北375 km。此次地震震级为7.2,震源深度约为8 km,插值时使用的震源模型是2011年Asano等[26]提出的,根据此次地震的震源反演结果,计算了断层面在地表的投影面(如图 4(b)中的黑色矩形区域)。对此次地震进行插值,获得的仪器烈度如图 4所示。

|
图 4 日本岩手地震仪器烈度 Fig. 4 Instrument intensity of Iwate earthquake in Japan |
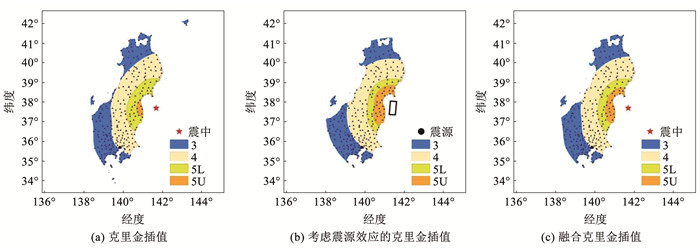
日本本州东部地震发生于当地时间2022年3月16日,截至当地时间2022年3月19日,该地震已造成3人死亡,205人受伤。此次地震震级为7.4,震源深度约为60 km,震中位于日本本州东部(37.7°N,141.7°E),采用USGS对此次地震的震源反演结果,计算了断层面在地表的投影面(如图 5(b)中的黑色矩形区域)。此次地震为海域地震,台站全部位于震源的同一侧,对此次地震进行插值,获得的仪器烈度如图 5所示。
|
图 5 日本本州东部地震仪器烈度 Fig. 5 Instrument intensity of eastern Honshu earthquake in Japan |
通过4次日本地震的仪器烈度图可以看出,克里金插值在对仪器烈度进行插值时,会使低烈度区出现形状不规则现象,高烈度区的烈度值较真实情况偏低,且容易不以震中为中心分布;考虑震源效应的克里金插值以震源为中心向外均匀扩散,在形状上满足震源模型的烈度衰减关系;融合克里金插值考虑了震源效应,使低烈度区的形状变得规则,将高烈度区的范围修正,使仪器烈度图整体更符合地震动衰减规律。
为了验证克里金插值及融合克里金插值获得的仪器烈度图和台站记录的仪器烈度值的相符程度,计算了观测仪器烈度值与插值仪器烈度图相符的比率。为了使数据更具有参考价值,计算时只取JMA烈度3以上的台站,并允许插值获得的仪器烈度图有±0.5度的烈度偏差,震例的4次地震相符率如表 1所示。可以看出,不论是克里金插值还是融合克里金插值,都具有较高的相符率,且融合克里金插值的仪器烈度图准确率基本不低于克里金插值,在考虑了震源效应的基础上保证了仪器烈度图具有较高的准确性。
| 表 1 仪器烈度相符率 Tab. 1 Consistency rate of instrument intensity |
为了验证融合克里金插值方法的合理性,使用粒子群优化算法将以上4次日本地震200 km[27]以内的台站记录数据和融合克里金插值结果分别拟合烈度衰减关系,并进行对比分析,本文使用的烈度衰减关系公式参考了汪素云等[28]提出的公式,形式如下
| $ I=b_1+b_2 M-b_3 R-b_4 \lg (R+10) $ | (10) |
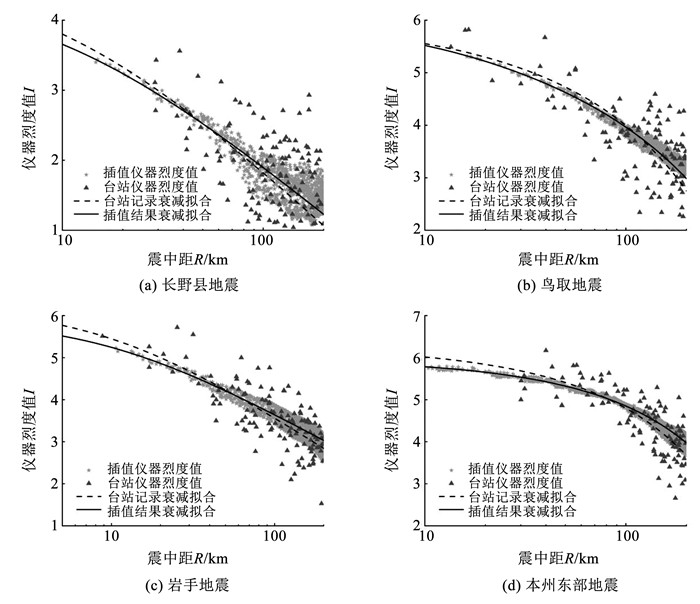
烈度衰减关系的拟合参数如表 2所示,各次地震拟合的烈度衰减关系如图 6所示。
| 表 2 烈度衰减关系参数拟合结果 Tab. 2 Fitting results of intensity attenuation relationship parameters |
|
图 6 融合克里金插值及台站记录的烈度衰减拟合 Fig. 6 Intensity attenuation fitting based on station records and fusion Kriging interpolation |
通过4次地震烈度衰减拟合的共同趋势可以看出,由于场地效应的影响,震源各方向的仪器烈度值在震中距相同时差异较大,且随着震中距增大,各方向台站相距更远,场地条件差异增大,仪器烈度值的差值也随之增大;与台站记录相比,融合克里金插值存在震中距100 km以内小幅度烈度低估,震中距100 km以外小幅度烈度高估现象;融合克里金插值的衰减拟合与台站记录的衰减拟合十分接近,在衰减速度上基本吻合,且离散性较小,可以反映出一次地震随震中距的烈度衰减趋势,同时证明了本文融合克里金插值方法的合理性。
3 讨论 3.1 理论半变异函数模型的选择在地质统计学和地震学中克里金插值常用的两种理论半变异函数模型是球状模型和指数模型,两种半变异函数的计算公式如下。
球状模型:
| $ \gamma(h)=\left\{\begin{array}{l} 0, h=0 \\ C_0+C\left(\frac{3}{2} \frac{h}{a}-\frac{1}{2} \frac{h^3}{a^3}\right), 0 <h \leqslant a \\ C_0+C, h>a \end{array}\right. $ | (11) |
指数模型:
| $ \gamma(h)=\left\{\begin{array}{l} 0, h=0 \\ C_0+C\left(1-\mathrm{e}^{-\frac{3 h}{a}}\right), h>0 \end{array}\right. $ | (12) |
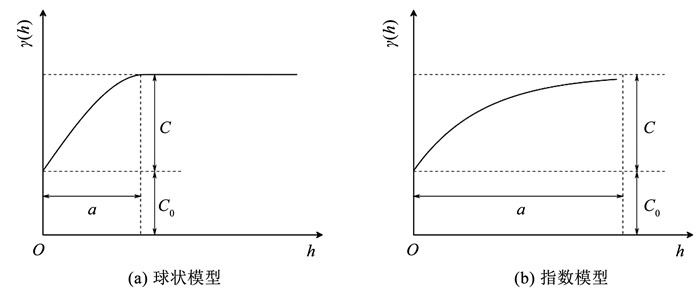
式中:h为半变异函数的自变量,通常为两点之间的距离;C0为块金值,表示当观测点和待插值点距离很小时,两点之间值的差异;a为变程,表示半变异函数模型达到水平状态时的距离,当h>a时,通常认为两点之间不相关;C为偏基台值,表示半变异函数模型在变程处所获得的基台值与块金值的差。
两种理论半变异函数模型如图 7所示。
|
图 7 理论半变异函数模型 Fig. 7 Theoretical semivariogram model |
为了验证两种模型对地震台站记录数据的适应度,选取日本熊本地震进行比较分析。日本熊本地震是当地时间2016年4月16日在日本九州岛熊本县(32.753°N,130.762°E)发生的7.3级地震,震源深度约为12 km。
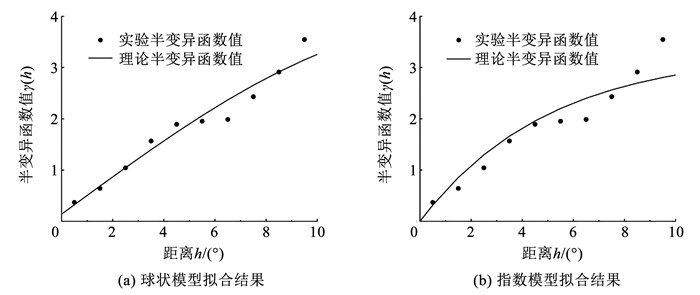
使用粒子群优化算法,将日本熊本地震的台站记录数据拟合到两种理论半变异函数模型,拟合结果如图 8所示。其中,球状模型的适应度为0.422 0,指数模型的适应度为0.971 6,球状模型比指数模型具有更优的适应度,因此,选择球状模型作为克里金插值的理论半变异函数模型。
|
图 8 两种理论半变异函数模型拟合结果 Fig. 8 Fitting results of two theoretical semivariogram models |
在第2节的算例分析中,对于克里金插值和考虑震源效应的克里金插值的融合比例系数,选取了q1=q2=0.5。为了分析不同比例系数对融合插值方法的影响,选取了日本熊本7.3级地震进行验证。
将两种插值以不同的比例进行融合,对获得的融合克里金插值仪器烈度图进行分析并确认最佳比例,使用的比例系数如表 3所示。
| 表 3 插值融合比例 Tab. 3 Fusion ratio of interpolation |
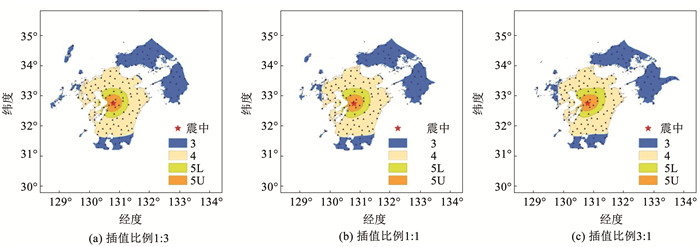
以表 3中的比例将此次地震的插值结果融合,融合克里金插值仪器烈度如图 9所示。
|
图 9 不同比例的融合克里金插值 Fig. 9 Fusion Kriging interpolation with different proportions |
以烈度区的形状作为参考,由图 9可以看出,增大克里金插值所占的比例,会使融合克里金插值更多地考虑插值的空间相关性,减少对震源效应的体现,从而使烈度图更不规则。而增大考虑震源效应的克里金插值的比例,则会使融合克里金插值更满足地震动衰减规律,不能很好地体现插值的空间相关性,使烈度图趋近于烈度衰减关系的同心圆模型。因此,为了对空间相关性和震源效应进行兼顾考虑,最终选用了1∶ 1的融合比例。
3.3 插值对比为了比较融合克里金插值与其他插值结果的差异,选取了2010年金星等[29]使用的基于烈度衰减关系及反距离权重法的插值方法(以下称为金星衰减插值)进行对比分析。
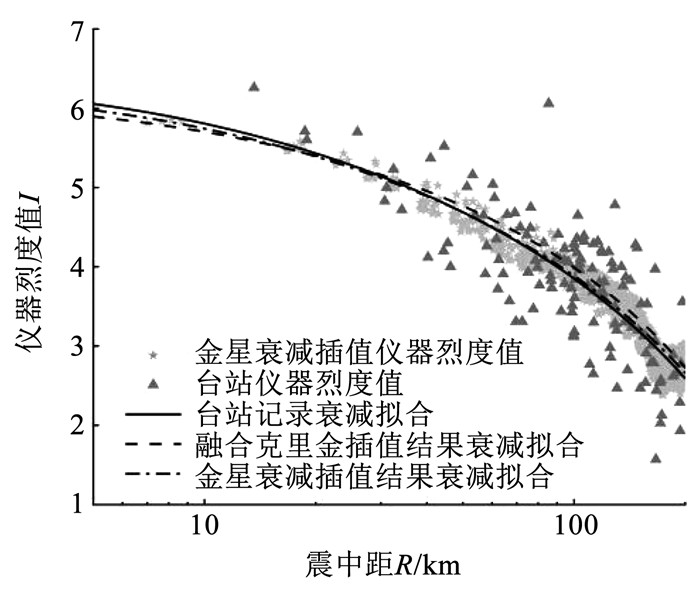
选取2016年日本熊本7.3级地震作为震例,由于金星衰减插值的实现需要烈度衰减关系,将此次地震台站记录拟合的烈度衰减关系I=0.572+1.027M-0.007 88R-1.681lg(R+10)作为金星衰减插值的烈度衰减关系。使用粒子群优化算法,将台站记录、融合克里金插值结果和金星衰减插值结果进行烈度衰减拟合,结果如图 10所示。可以看出,两种插值结果的衰减拟合均与台站记录的衰减拟合十分接近,说明两种方法均能很好地展现出一次地震的烈度衰减情况。
|
图 10 熊本地震烈度衰减拟合 Fig. 10 Intensity attenuation fitting of Kumamoto earthquake |
为了更直观地看出两种插值结果的差异,将两种插值的仪器烈度进行对比,如图 11所示。
|
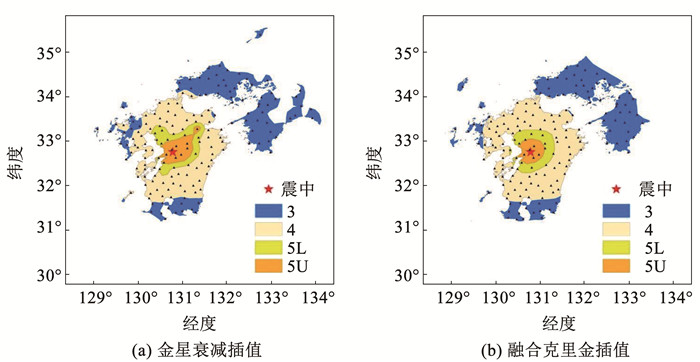
图 11 熊本地震插值仪器烈度图对比 Fig. 11 Comparison of interpolation instrument intensity maps of Kumamoto earthquake |
金星衰减插值和融合克里金插值获得的烈度图在烈度区范围和烈度分布总体趋势一致,金星衰减插值在高烈度区和低烈度区均存在形状不规则现象,融合克里金插值获得的烈度图整体形状较规则,这是因为反距离权重法只考虑已知观测点和待插值点的距离远近,克里金插值法还通过半变异函数和结构分析,考虑了已知观测点的空间分布及与待插值点的空间方位关系,能较好地反映客观地质规律[30-31]。
另外,在插值的过程中,融合克里金插值需要的数据是震中位置及各台站的记录数据,所需参数较少,易于实现;金星衰减插值除了需要上述数据外,还需要地震发生区域的烈度衰减关系,此烈度衰减关系会直接影响插值的结果。在应用范围上,金星衰减插值适用于点源模型的中小地震[29],融合克里金插值可以应用于点源、线源和面源模型,应用范围较广。
3.4 台站分布不均匀情况下的插值效果日本的地震台站分布密集且均匀,使用日本的地震数据进行插值时,克里金插值获得的仪器烈度图并没有大范围的不规则现象,因此,使用融合克里金插值时,对克里金插值进行的修正有限。为了验证当地震台站分布稀疏且不均匀时融合克里金插值的效果,对一次中国地震进行了插值。
中国芦山地震是北京时间2013年4月20日发生于四川省雅安市芦山县(30.299°N,103.000°E)的7.0级地震,震源深度约为13 km。据中国地震局网站消息,截至24日14时30分,地震共造成196人死亡,失踪21人,11 470人受伤。
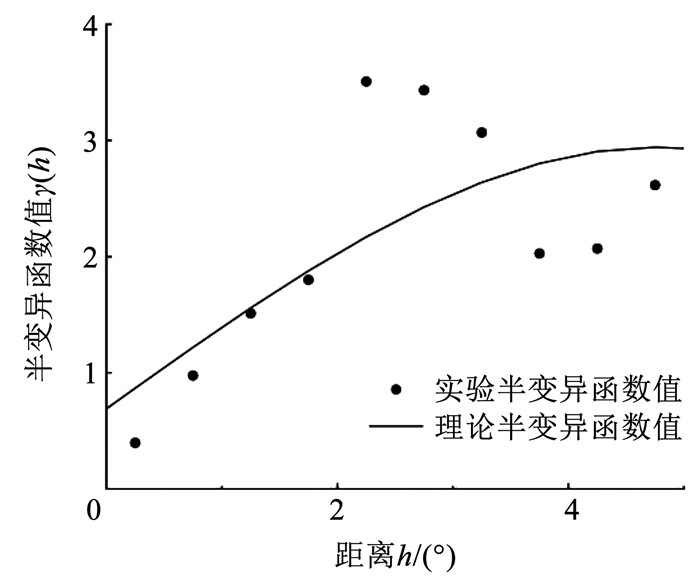
对此次地震进行半变异函数拟合,结果如图 12所示。
|
图 12 芦山地震理论半变异函数模型 Fig. 12 Theoretical semivariogram model of Lushan earthquake |
由于台站分布稀疏且不均匀,芦山地震的半变异函数出现了部分异常值,将此次地震的理论半变异函数模型和日本熊本地震对比,拟合参数如表 4所示。相比熊本地震,芦山地震的半变异函数块金值较大,表示芦山地震的数据在两点相近时差异性较大;芦山地震变程值较小,说明台站分布稀疏导致数据在空间上的相关性减弱,只在较小范围内存在相关性。
| 表 4 芦山地震和熊本地震理论半变异函数模型对比 Tab. 4 Comparison of theoretical semivariogram models for Lushan earthquake and Kumamoto earthquake |
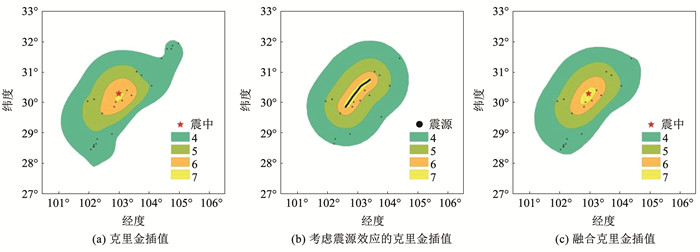
对芦山地震进行融合克里金插值,插值时使用的震源模型是2013年王卫民等[32]提出的,根据此次地震的震源反演结果,计算了断层面在地表的投影面[33](如图 13(b)中的黑色线形区域)。获得的仪器烈度如图 13所示,本次地震使用的仪器烈度是中国烈度标准[34]。
|
图 13 中国芦山地震仪器烈度 Fig. 13 Instrument intensity of Lushan earthquake in China |
由图 13可以看出,克里金插值获得的仪器烈度图在低烈度区形状不规则,烈度7区范围与震中产生了偏差,并不以震中为中心。本次地震触发的台站数为75,烈度值4以上的台站数为23,台站分布稀疏且不均匀。其中,烈度值达到7的台站仅有4个,且均位于震源的同一侧,这直接导致了烈度7区插值的不规则现象。考虑震源效应的克里金插值以线源为中心,满足烈度衰减关系的跑道模型,将两种插值融合后获得的仪器烈度图高烈度区的范围以震中为中心向外均匀扩散,低烈度区的形状规则,仪器烈度图总体符合烈度衰减关系,证明融合克里金插值对稀疏台站有较好的适应性。
4 结论1) 提出一种考虑地震动空间相关性及大震震源效应的融合克里金插值方法。考虑地震动空间相关性及震源效应的融合克里金插值比单独采用两点之间距离的克里金插值获得的仪器烈度图有更规则的形状,符合烈度衰减特征。
2) 对融合克里金插值和台站记录进行烈度衰减关系拟合,发现融合克里金插值在震中距100 km以内有小幅度烈度低估,在震中距100 km以外有小幅度烈度高估,但两者在衰减速度上基本吻合,且融合克里金插值离散性较小,可以反映一次地震的烈度衰减趋势。
3) 计算了4次地震台站的仪器烈度值与插值获得的仪器烈度图的相符率,克里金插值和融合克里金插值均有较高的相符率,表明融合克里金插值获得的仪器烈度图基本不损失仪器烈度的准确性。
4) 将融合克里金插值和金星衰减插值进行对比分析,发现融合克里金插值在仪器烈度图绘制上形状更规则,且在插值方法实现难易程度及应用范围上要优于金星衰减插值。最后以2013年中国芦山地震进行算例分析,验证了融合克里金插值方法在台站稀疏情况下的可行性。
5) 本文使用的震源模型包括点源、线源和面源模型,在对一次地震进行烈度速报时,由于地震刚发生不久,震源的模型和破裂机制往往还未获得。FinDer方法[35-36]是一种用于地震预警的实时震源参数估计方法,可以快速获取断层面在地面的投影,在实际应用中建议采用该方法获取震源参数。
| [1] |
OTAKE R, KURIMA J, GOTOH, et al. Deep learning model for spatial interpolation of realtime seismic intensity[J]. Seismological Research Letters, 2020, 91(6): 1. DOI:10.1785/0220200006 |
| [2] |
李山有, 金星, 陈先, 等. 地震动强度与地震烈度速报研究[J]. 地震工程与工程振动, 2002, 22(6): 1. LI Shanyou, JIN Xing, CHEN Xian, et al. Rapid reporting of peak strong motion and seismic intensity[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(6): 1. DOI:10.13197/j.eeev.2002.06.001 |
| [3] |
郝敏, 谢礼立. 921台湾集集地震的烈度等震线[J]. 哈尔滨工业大学学报, 2007, 39(2): 169. HAO Min, XIE Lili. The isoseismal of seismic intensity for the 9.21 Taiwan Chi-Chi earthquake of 1999[J]. Journal of Harbin Institute of Technology, 2007, 39(2): 169. DOI:10.3321/j.issn:0367-6234.2007.02.001 |
| [4] |
SPAGNUOLO E, FAENZA L, CULTRERA G, et al. Accounting for source effects in the ShakeMap procedure: the 2000 Tottori and the 2008 Miyagi earthquakes[J]. Geophysical Journal International, 2013, 194(3): 1836. DOI:10.1093/gji/ggt195 |
| [5] |
BOORE D M, GIBBS J F, JOYNER W B, et al. Estimated ground motion from the 1994 Northridge, California, earthquake at the site of the interstate 10 and La Cienega Boulevard Bridge collapse, west Los Angeles, California[J]. Bulletin of the Seismological Society of America, 2003, 93(6): 2737. DOI:10.1785/0120020197 |
| [6] |
SCHENKOVA Z, SCHENK V, KALOGERAS I, et al. Isoseismal maps drawing by the Kriging method[J]. Journal of Seismology, 2007, 11(3): 345. DOI:10.1007/s10950-007-9056-0 |
| [7] |
陈鲲, 俞言祥, 高孟潭, 等. 地震动的空间相关性——以纳帕地震为例[J]. 地震地质, 2020, 42(5): 1218. CHEN Kun, YU Yanxiang, GAO Mengtan, et al. Study on spatial correlation of ground-motion: a case study of Napa earthquake[J]. Seismology and Geology, 2020, 42(5): 1218. DOI:10.3969/j.issn.0253-4967.2020.05.012 |
| [8] |
邵国良, 冀昆, 温瑞智, 等. 基于密集观测数据的强震动参数空间相关性分析[J]. 地震工程与工程振动, 2022, 42(6): 114. SHAO Guoliang, JI Kun, WEN Ruizhi, et al. Spatial correlation analysis of strong motion parameters based on high-density observation recordings[J]. Earthquake Engineering and Engineering Dynamics, 2022, 42(6): 114. DOI:10.13197/j.eeed.2022.0612 |
| [9] |
SCHIAPPAPIETRA E, DOUGLAS J. Modelling the spatial correlation of earthquake ground motion: insights from the literature, data from the 2016-2017 Central Italy earthquake sequence and ground-motion simulations[J]. Earth-Science Reviews, 2020, 203. DOI:10.1016/j.earscirev.2020.103139 |
| [10] |
LI Wei, LI Shanyou. Generation methodology of isolines of earthquake ground motion[J]. Earthquake Engineering and Engineering Vibration, 2010, 9(4): 473. DOI:10.1007/s11803-010-0029-x |
| [11] |
CRESSIE N. The origins of Kriging[J]. Mathematical Geology, 1990, 22(3): 239. DOI:10.1007/BF00889887 |
| [12] |
李俊晓, 李朝奎, 殷智慧. 基于ArcGIS的克里金插值方法及其应用[J]. 测绘通报, 2013(9): 87. LI Junxiao, LI Chaokui, YIN Zhihui. ArcGIS based Kriging interpolation method and its application[J]. Bulletin of Surveying and Mapping, 2013(9): 87. DOI:10.1007/s12204-013-1367-4 |
| [13] |
OLIVER M A, WEBSTER R. A tutorial guide togeostatistics: computing and modelling variograms and Kriging[J]. Catena, 2014, 113: 56. DOI:10.1016/j.catena.2013.09.006 |
| [14] |
王秋实, 丁文其, 赵志坚, 等. 基于克里金插值与朴素贝叶斯的盾构开挖面上软下硬分类及风险评估[J]. 土木工程学报, 2022, 55(增刊2): 66. WANG Qiushi, DING Wenqi, ZHAO Zhijian, et al. Classification of upper-soft lower-hard shield tunnel face and risk evaluation based on Kriging method and Naive Bayes[J]. China Civil Engineering Journal, 2022, 55(Sup.2): 66. DOI:10.15951/j.tmgcxb.2022.s2.04 |
| [15] |
CRESSIE N. Kriging nonstationary data[J]. Journal of the American Statistical Association, 2012, 81(395): 625. DOI:10.1080/01621459.1986.10478315 |
| [16] |
JOYNER W B, BOORE D M. Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 imperial valley, California, earthquake[J]. Bulletin of the Seismological Society of America, 1981, 71(6): 2011. DOI:10.1785/BSSA0710062011 |
| [17] |
魏达, 孙章庆. 利用地质统计学反演预测砂岩型铀矿体的变差函数求取方法[J]. 石油地球物理勘探, 2021, 56(6): 1381. WEI Da, SUN Zhangqing. Calculation method of variation function for predicting sand-stone-type uranium ore bady by geostatistical inversion[J]. Oil Geophysical Prospecting, 2021, 56(6): 1381. DOI:10.13810/j.cnki.issn.1000-7210.2021.06.020 |
| [18] |
陈学工, 陈婷, 肖晓芳. 混沌粒子群算法自动拟合理论变差函数[J]. 计算机工程与应用, 2012, 48(4): 37. CHEN Xuegong, CHEN Ting, XIAO Xiaofang. Chaos Particle Swarm Optimization algorithm to match theoretical variogram automatically[J]. Computer Engineering and Applications, 2012, 48(4): 37. DOI:10.3778/j.issn.1002-8331.2012.04.010 |
| [19] |
谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2): 129. XIE Xiaofeng, ZHANG Wenjun, YANG Zhilian. Overview of Particle Swarm Optimization[J]. Control and Decision, 2003, 18(2): 129. DOI:10.3321/j.issn:1001-0920.2003.02.001 |
| [20] |
梁昔明, 肖晓芳. 基于PSO算法的变差函数球状模型参数拟合[J]. 计算机工程, 2011, 37(14): 155. LIANG Ximing, XIAO Xiaofang. Parameter fitting of variogram spherical model based on Particle Swarm Optimization algorithm[J]. Computer Engineering, 2011, 37(14): 155. DOI:10.3969/j.issn.1000-3428.2011.14.051 |
| [21] |
张琦, 马艳宁, 王肖骏, 等. 基于优化克里金插值方法的隧道主结构面建模[J]. 土木工程学报, 2022, 55(增刊2): 74. ZHANG Qi, MA Yanning, WANG Xiaojun, et al. Modeling of main structural plane of tunnel based on optimized Kriging interpolation method[J]. China Civil Engineering Journal, 2022, 55(Sup.2): 74. DOI:10.15951/j.tmgcxb.2022.s2.07 |
| [22] |
Japan Meteorological Agency(JMA). Seismic intensity[M]. Tokyo: [s.n.], 1996: 238.
|
| [23] |
HOSHIBA M, OHTAKE K, IWAKIRI K, et al. How precisely can we anticipate seismic intensities? A study of uncertainty of anticipated seismic intensities for the Earthquake Early Warning method in Japan[J]. Earth, Planets and Space: EPS, 2010, 62(8): 611. DOI:10.5047/eps.2010.07.013 |
| [24] |
KUNUGI T, AOI S, NAKAMURA H, et al. An improved approximating filter for real-time calculation of seismic intensity[J]. Zisin(Journal of the Seismological Society of Japan 2nd ser), 2013, 65(3): 223. DOI:10.4294/zisin.65.223 |
| [25] |
KODERA Y, YAMADA Y, HIRANO K, et al. The Propagation of Local Undamped Motion (PLUM) method: a simple and robust seismic wavefield estimation approach for Earthquake Early Warning[J]. Bulletin of the Seismological Society of America, 2018, 108(2): 983. DOI:10.1785/0120170085 |
| [26] |
ASANO K, IWATA T. Characterization of stress drops on asperities estimated from the heterogeneous kinematic slip model for strong motion prediction for inland crustal earthquakes in Japan[J]. Pure and Applied Geophysics, 2011, 168(1/2): 105. DOI:10.1007/s00024-010-0116-y |
| [27] |
李伟, 俞言祥, 肖亮. 阿里亚斯强度衰减关系分析[J]. 地震学报, 2017, 39(6): 921. LI Wei, YU Yanxiang, XIAO Liang. Attenuation relationship of Arisa intensity[J]. Acta Seismologica Sinica, 2017, 39(6): 921. DOI:10.11939/jass.2017.06.010 |
| [28] |
汪素云, 俞言祥, 高阿甲, 等. 中国分区地震动衰减关系的确定[J]. 中国地震, 2000, 16(2): 5. WANG Suyun, YU Yanxiang, GAO Ajia, et al. Development of attenuation relations for ground motion in China[J]. Earthquake Research in China, 2000, 16(2): 5. DOI:10.3969/j.issn.1001-4683.2000.02.001 |
| [29] |
金星, 张红才, 韦永祥, 等. 基于地震监测台网资料近实时插值计算震动图的初步研究[J]. 防灾减灾学报, 2010, 26(1): 1. JIN Xing, ZHANG Hongcai, WEI Yongxiang, et al. Preliminary study of real-time interpolation calculation of shakemap based on seismic monitoring network's information[J]. Journal of Disaster Prevention and Reduction, 2010, 26(1): 1. DOI:10.13693/j.cnki.cn21-1573.2010.01.010 |
| [30] |
于江, 和仕芳, 卢永坤, 等. 基于空间插值方法的2021年云南漾濞Ms6.4地震仪器地震烈度影响场分析[J]. 地震研究, 2021, 44(3): 414. YU Jiang, HE Shifang, LU Yongkun, et al. Analysis of the influence field of the instrumental seismic intensity of the 2021 Yangbi, Yunnan Ms6.4 earthquake based on spatial interpolation method[J]. Journal of Seismological Research, 2021, 44(3): 414. DOI:10.3969/j.issn.1000-0666.2021.03.013 |
| [31] |
靳国栋, 刘衍聪, 牛文杰. 距离加权反比插值法和克里金插值法的比较[J]. 长春工业大学学报(自然科学版), 2003, 24(3): 53. JIN Guodong, LIU Yancong, NIU Wenjie. Comparison between Inverse Distance Weighting method and Kriging[J]. Journal of Changchun University of Technology, 2003, 24(3): 53. |
| [32] |
王卫民, 郝金来, 姚振兴. 2013年4月20日四川芦山地震震源破裂过程反演初步结果[J]. 地球物理学报, 2013, 56(4): 1412. WANG Weimin, HAO Jinlai, YAO Zhenxing. Preliminary result for rupture process of Apr. 20, 2013, Lushan Earthquake, Sichuan, China[J]. Chinese Journal of Geophysics, 2013, 56(4): 1412. DOI:10.6038/cjg20130436 |
| [33] |
谢俊举, 李小军, 温增平, 等. 芦山7.0级地震近断层地震动的方向性[J]. 地球物理学报, 2018, 61(4): 1266. XIE Junju, LI Xiaojun, WEN Zengping, et al. Variations of near-fault strong ground motion with directions during the 2013 Lushan Ms7.0 earthquake[J]. Chinese Journal of Geophysics, 2018, 61(4): 1266. DOI:10.6038/cjg2018K0686 |
| [34] |
中国地震局工程力学研究所. 中国地震烈度表: GB/T 17742—2020[S]. 北京: 地震出版社, 2021
|
| [35] |
BOSE M, HEATON T H, HAUKSSON E. Real-time finite fault rupture detector (FinDer) for large earthquakes[J]. Geophysical Journal International, 2012, 191(2): 803. DOI:10.1111/j.1365-246X.2012.05657.x |
| [36] |
卢建旗, 李山有. 地震预警断层参数实时识别方法(FinDer)详解及其性能初步评价[J]. 世界地震工程, 2021, 37(1): 152. LU Jianqi, LI Shanyou. Detailed analysis and preliminary performance evaluation of the FinDer: a real-time finite fault rupture detector for earthquake early warning[J]. World Earthquake Engineering, 2021, 37(1): 152. |
 2024, Vol. 56
2024, Vol. 56


