2. 山西建筑工程集团有限公司,太原 030006;
3. 山西二建集团有限公司,太原 030013
2. Shanxi Construction Engineering Group Co., Ltd., Taiyuan 030006, China;
3. Shanxi Erjian Group Co., Ltd., Taiyuan 030013, China
实际工程应用中,竖向预制构件的钢筋节点连接主要为套筒灌浆对接连接,但该连接现场施工时存在施工困难、浇筑质量差、造价高等缺陷。基于现有套筒灌浆对接接头存在的问题,2015年,余琼[1]提出一种新型套筒灌浆搭接接头,简称APC(all vertical members precasted in concrete structures)接头,分为Ⅰ型和Ⅱ型APC接头,见图 1。APC接头具有内径大、工艺简单、方便施工、灌浆密实、成本低等优点。2017年,余琼等[2]以搭接长度为变量,研究了Ⅰ型APC接头单向拉伸时的静力性能;2018年,余琼等[3]以钢筋直径和套筒尺寸为变量进行了Ⅰ型APC接头中心拉拔试验,分析了接头的受力机制;2018年,许坤[4]以搭接长度和套筒截面尺寸为变量,研究了Ⅰ型APC接头单拉时的静力性能;2019年,匡轩[5]以搭接长度和钢筋直径为变量,利用ABAQUS对Ⅰ型APC接头建立数值模型,研究其单向拉伸性能;2022年,Yu等[6]以搭接长度为变量,分析了Ⅰ型APC接头单拉时的力学机制;2022年,余琼等[7]以钢筋直径和后插入钢筋位置为变量,通过试验和数值模拟,研究了Ⅰ型APC接头单拉时的黏结强度和极限承载能力。可见,当前对Ⅰ型APC接头的破坏机制、延性、承载能力和黏结强度等研究较为充分,但Ⅱ型APC接头单拉力学性能尚不明确,有必要展开系统研究。
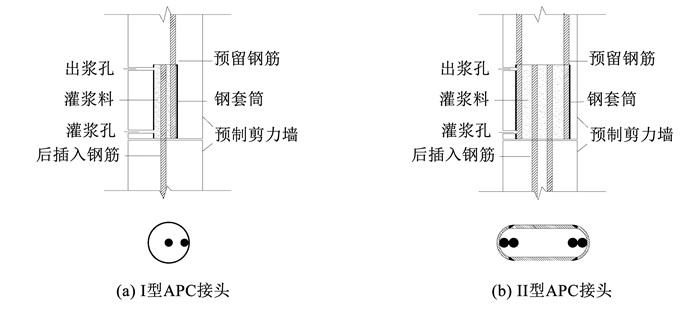
|
图 1 APC接头示意 Fig. 1 Schematic of APC connector |
本文进行了36个Ⅱ型APC接头的单拉试验,研究防偏转措施、钢筋直径和后插入钢筋位置等对Ⅱ型APC接头受力性能的影响。并利用ABAQUS建立了16个该接头的精细化模型进行数值模拟,以后插入钢筋位置为变量,设计与4种试验后插入钢筋位置不同的4种后插入钢筋位置套筒模型,补充研究后插入钢筋位置对接头力学性能的影响。
1 试验 1.1 材料性能灌浆料采用H40型灌浆料。测得40 mm×40 mm×160 mm试件的抗折、抗压强度分别为12.1、65.3 MPa[8],150 mm×150 mm×150 mm试件劈裂抗拉强度为3.4 MPa,150 mm×150 mm×300 mm试件的轴心抗压强度为75.5 MPa。
套筒采用Q235B无缝钢管(壁厚4 mm)与钢板(厚6 mm)焊接而成,测得其平均屈服强度分别为372.2、322.7 MPa,平均极限强度分别为489.4、462.5 MPa[9]。试验采用HRB400级钢筋,材料性能见表 1。
| 表 1 钢筋材料性能 Tab. 1 Material properties of rebar |
为模拟实际工程中接头的施工方法,上、下两根预留钢筋点焊在套筒上、下内壁(固定钢筋位置)。本试验设计了3种钢筋直径(14、16、18 mm)和4种潜在的不同后插入钢筋位置(位置一、位置二、位置三和位置四),共12组36个试件,不同后插入钢筋位置试件示意见图 2。

|
图 2 后插入钢筋位置示意 Fig. 2 Schematic of positions of post-installed rebar |
位置一和位置四试件钢筋沿长轴对称布置,区别在于钢筋间距不同,位置二、位置三试件钢筋紧贴套筒偏心布置,但钢筋间距不同。实际工程中,套筒被混凝土包裹,基本不发生偏转,为模拟实际工况,避免因钢筋非对称布置而产生偏转,试验中位置二、三的2、3号试件采取防偏转措施。
根据前期试验[10],为保证大多数试件发生钢筋拔出破坏,搭接长度(套筒长度)均取为8d(d为钢筋直径)。此时改变后插入钢筋位置和钢筋直径,研究其对极限承载力和黏结强度的影响更有代表性。套筒尺寸见图 3。
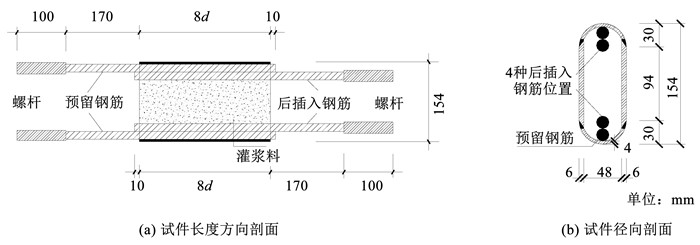
|
图 3 套筒尺寸示意 Fig. 3 Schematic diagram of sleeve size |
不同后插入钢筋位置及套筒应变测点位置见图 4。在套筒中部沿套筒纵向贴放4个应变片Z1~Z4,沿套筒环向贴放4个应变片H1~H4,编号为H和Z的应变片分别测量套筒中部环向应变和纵向应变。
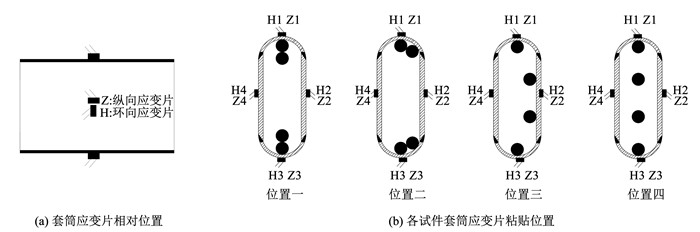
|
图 4 不同后插入钢筋位置试件套筒应变片粘贴位置 Fig. 4 Locations of strain gauges on specimens with different positions of post-installed rebar |
加载采用200 t电液伺服作动器,试验装置见图 5。试验开始以2 kN/s的加载速率匀速加载至接近钢筋屈服,屈服后以5~10 mm/min的速率进行位移控制,直至试件发生破坏[7, 11]。
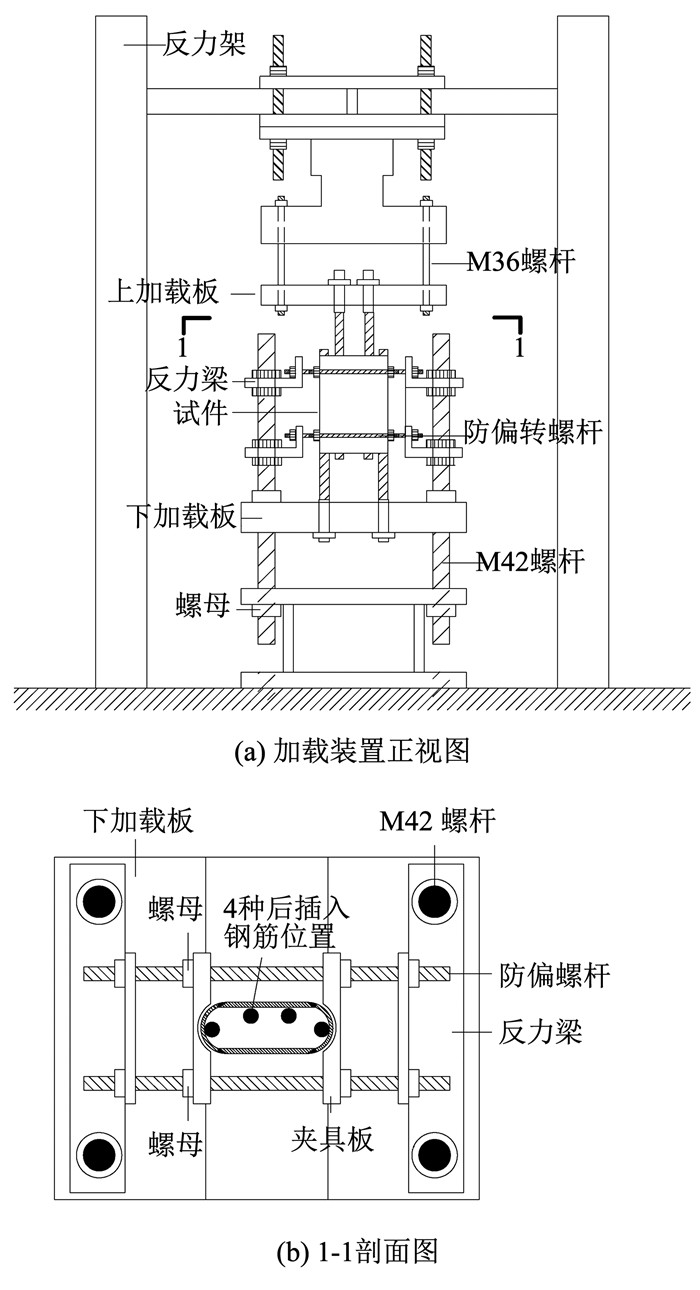
|
图 5 试验装置示意 Fig. 5 Setup of the test |
各试件的屈服强度fy、极限强度fu、屈服荷载位移δy、极限荷载位移δu、极限平均黏结应力τu和破坏形态见表 2。试件有两种破坏形式,即钢筋拉断破坏和钢筋拔出破坏,前者分为一根钢筋拉断和两根钢筋拉断,钢筋均拉断于母材处。试件破坏情况见图 6。
| 表 2 试验结果统计 Tab. 2 Statistics of test results |

|
图 6 试件破坏情况 Fig. 6 Failure modes of specimens |
钢筋直径为14 mm时,位置一试件均发生钢筋拉断破坏,其余后插入钢筋位置试件发生钢筋拔出破坏。这是由于位置一试件钢筋沿长边对称紧贴布置,接头几乎不发生偏转,接头承载力高。位置四试件钢筋虽对称布置,但后插入钢筋未紧贴布置,而是靠近套筒中部布置,套筒长边约束比短边弱,故接头承载力低于位置一试件,发生拔出破坏。位置二、三试件钢筋偏心布置,加载时易引起钢筋弯曲变形[7],灌浆料破损严重;且钢筋紧贴套筒布置,易形成灌浆缺陷,故接头承载力偏低。发生拔出破坏试件,固定端出现沿长边方向裂缝,加载端灌浆料随钢筋一起拔出。试件端部破坏情况见图 7。

|
图 7 试件端部破坏情况 Fig. 7 Failure modes at the end of specimens |
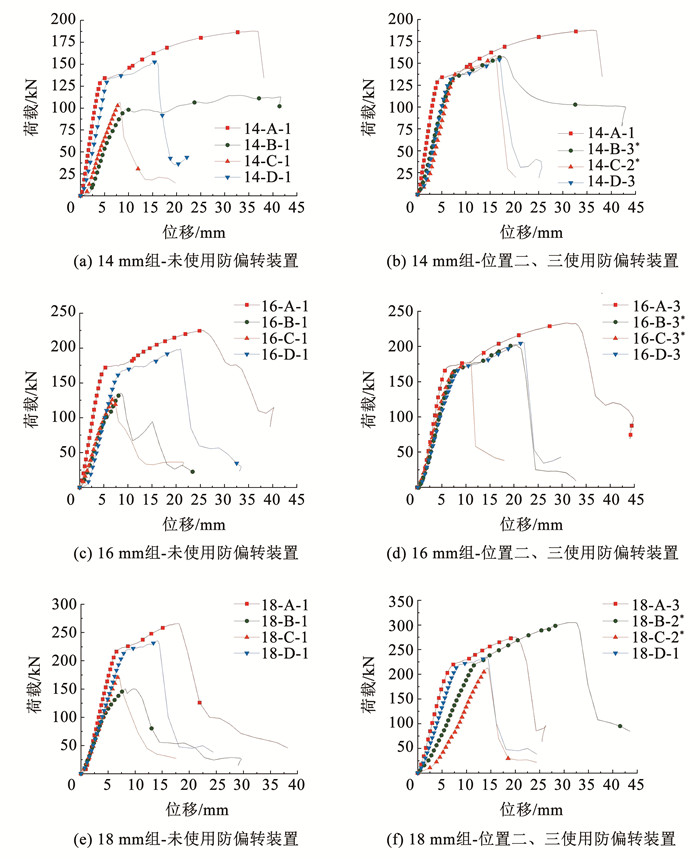
图 8为试件典型荷载-位移曲线。其中,图 8(a)、(c)、(e)中位置二、三试件均未采取防偏转措施,对于未设防偏转措施的试件,试件的极限承载能力按后插入钢筋位置一、四、二、三次序逐渐减小,位置二、三试件的极限承载力接近;在曲线上升的弹性段,荷载相同时,位置二、三试件对应的位移大于位置四试件、位置一试件,说明位置二、三试件的初始刚度小于位置四、位置一试件。这是由于位置二、三试件内部钢筋非对称布置,加载时产生偏转,降低了试件的初始刚度。
|
图 8 试件典型荷载-位移曲线 Fig. 8 Typical load-displacement curves of specimens |
位置一、四试件曲线有明显的强化段,而位置二、三组试件无明显强化段,即钢筋未屈服就已拔出。位置一、四试件曲线在加荷初期,处于弹性上升段;加荷到屈服荷载时,随灌浆料裂缝发展,试件刚度下降,进入强化段;加荷到极限荷载时,灌浆料破碎,随钢筋拔出,曲线进入突降段。位置二、三试件曲线在加荷初期,处于弹性上升段;随荷载增加,还未进入强化段,灌浆料就因试件偏转被压碎,随钢筋拔出,达到极限荷载,曲线快速下降。
图 8(b)、(d)、(f)中位置二、三试件均使用防偏转装置进行辅助加载,可见位置二、三试件极限承载力与初始刚度有所提高。由于防偏转装置为位置二、三试件提供侧向约束,减轻试件的偏转程度,延缓内部灌浆料的破坏,其极限承载力与初始刚度提高。18 mm组位置二、三试件初始刚度提高不明显,这是由于试件极限承载力随钢筋直径增加而增大,但防偏转装置刚度有限,试件刚度提升不明显。
2.2 接头延性分析接头位移延性系数Rd应满足Rd≥4[12-13]。Rd=δu/δy,δy为试件屈服荷载对应的位移,δu为极限荷载对应的位移。位置二、三试件不防偏转时,荷载-位移曲线未出现明显屈服平台,故未统计其位移延性系数。试件位移延性系数见表 2。除14-A组试件发生钢筋拉断破坏,其余试件均发生钢筋拔出破坏,故位移延性系数较小。
2.2.1 后插入钢筋位置对延性的影响由表 2可知,试件的延性系数按后插入钢筋位置一、二、四、三次序逐渐减小。位置一试件钢筋对称紧贴布置于套筒中心线上,钢筋紧贴几乎不偏心,其延性系数最大;位置二试件钢筋紧贴但两根钢筋均与套筒接触,灌浆存在缺陷,延性系数次之;位置四试件钢筋布置于套筒中心线上,但后插入钢筋位于套筒中部,套筒长边对其约束较弱,延性系数偏小;位置三试件后插入钢筋位于套筒中部,且偏心程度最大,故接头延性系数最小。
接头延性主要受3种因素影响,即钢筋间距、后插入钢筋偏心程度与后插入钢筋是否紧贴套筒布置。后插入钢筋布置于套筒中部,钢筋间距大,套筒长边约束弱,接头延性降低;后插入钢筋偏心布置,易产生弯曲变形,接头延性降低;后插入钢筋紧贴套筒布置易产生灌浆缺陷,接头延性降低。
2.2.2 钢筋直径对延性的影响钢筋直径由14 mm增加到18 mm,试件延性系数逐渐降低。这主要是由于更大直径的钢筋对试件锚固长度的要求更高,虽然试件相对搭接长度(均为8d) 相同,但较大直径钢筋延性发挥程度相对更低。
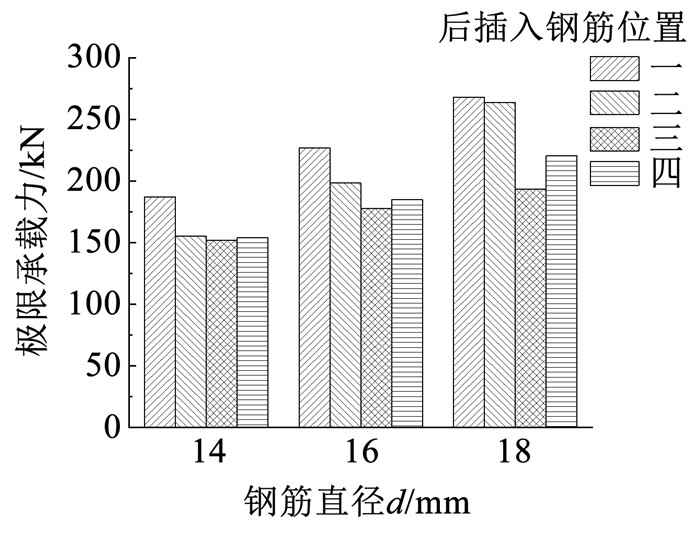
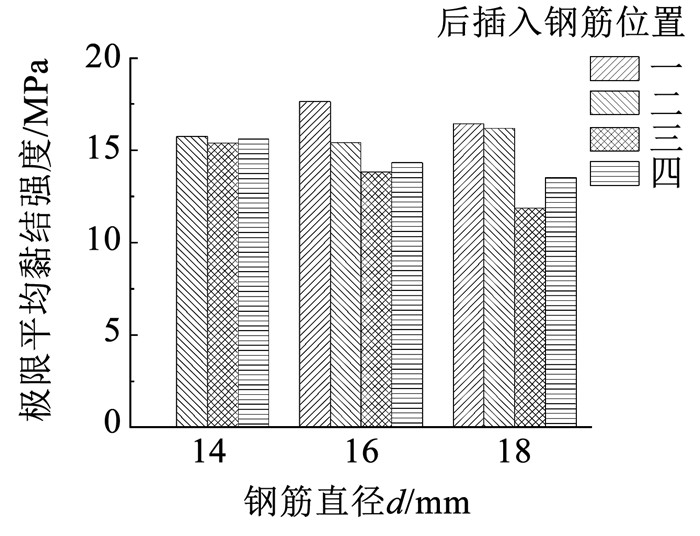
2.3 接头极限承载力及黏结强度分析 2.3.1 后插入钢筋位置对极限承载力及黏结强度影响图 9、10为后插入钢筋位置对极限承载力及黏结强度的影响(均为防偏转试件)。由于位置一钢筋直径14 mm试件发生拉断破坏,图 10中未统计其黏结强度。可以看出,钢筋直径相同时,后插入钢筋对称紧贴布置于长轴时(位置一),极限承载力和黏结强度最高;后插入钢筋偏心且紧贴套筒短边布置时(位置二),极限承载力和黏结强度次之;后插入钢筋平均对称布置在套筒中心线时(位置四),极限承载力和黏结强度有所下降;后插入钢筋偏心且紧贴套筒长边布置时(位置三),极限承载力和黏结强度最低。
|
图 9 后插入钢筋位置对各试件极限承载力的影响 Fig. 9 Impact of the position of post-installed rebar on the ultimate bearing capacity of each specimen |
|
图 10 后插入钢筋位置对平均黏结强度的影响 Fig. 10 Impact of position of post-installed rebar on average bond strength |
位置一试件,后插入钢筋紧贴预留钢筋沿长边对称布置在套筒中心线上,套筒短边约束强,且后插入钢筋未偏心,未紧贴套筒布置,故极限承载力和黏结强度最高。位置二试件,后插入钢筋虽靠近但紧贴套筒布置,易产生灌浆缺陷,故位置二试件极限承载力和黏结强度有所下降。
位置四试件,后插入钢筋对称布置在套筒中心线,但位于套筒中部,套筒长边对其约束弱,故位置四试件极限承载力和黏结强度较小。
位置三试件,后插入钢筋偏心且紧贴套筒长边布置,由于钢筋与套筒内壁间空隙狭小,易形成灌浆料缺陷,灌浆料与钢筋无法充分接触,且后插入钢筋偏心布置易引起钢筋弯曲变形[7],从而使试件极限承载力和黏结强度最低。
接头极限承载力和黏结强度也主要受3种因素影响,即钢筋间距、后插入钢筋是否偏心布置与后插入钢筋是否紧贴套筒布置。后插入钢筋远离预留钢筋,靠近套筒中部布置,套筒长边对其约束弱,接头极限承载力及黏结强度降低;后插入钢筋偏心布置,预留钢筋与后插入钢筋易产生弯曲变形,接头极限承载力及黏结强度降低;后插入钢筋紧贴套筒布置易产生灌浆缺陷,接头极限承载力及黏结强度降低。
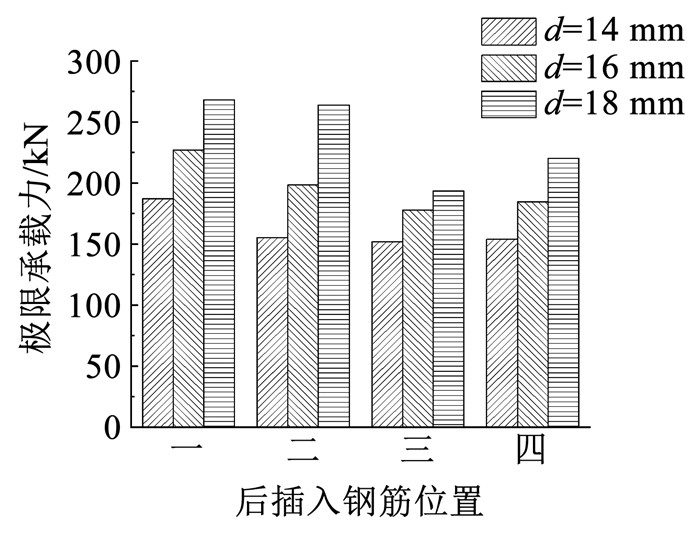
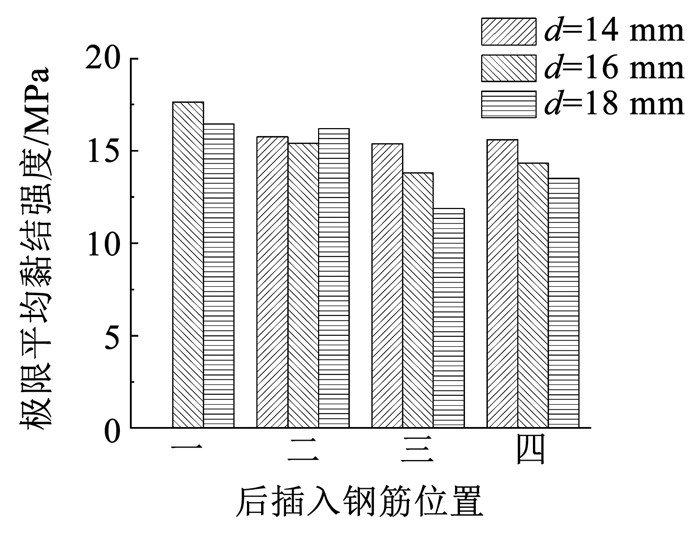
2.3.2 后插入钢筋直径对极限承载力及黏结强度的影响图 11、12为后插入钢筋直径对极限承载力及黏结强度的影响(均为防偏转试件)。由于位置一钢筋直径14 mm试件发生拉断破坏,图 12中未统计其黏结强度。可以看出,后插入钢筋位置和相对搭接长度相同时,随钢筋直径增加,试件极限承载力逐渐增大,但黏结强度逐渐降低。
|
图 11 钢筋直径对极限承载力的影响 Fig. 11 Impact of rebar diameter on ultimate bearing capacity |
|
图 12 钢筋直径对平均黏结强度的影响 Fig. 12 Impact of rebar diameter on average bond strength |
相对搭接长度相同时,随钢筋直径增大,钢筋-灌浆料相互作用长度增大,更多的钢筋横肋与灌浆料相互作用,从而提高了试件的极限承载力;随钢筋直径增加,钢筋表面积增大,故试件黏结强度逐渐降低。
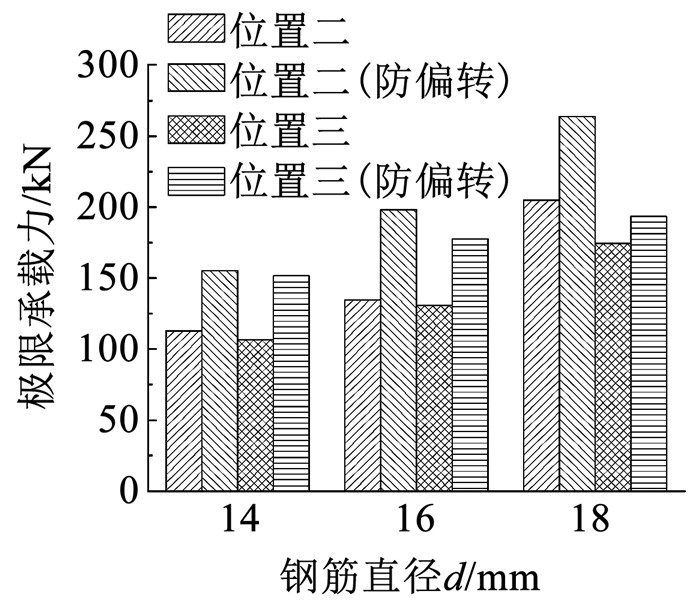
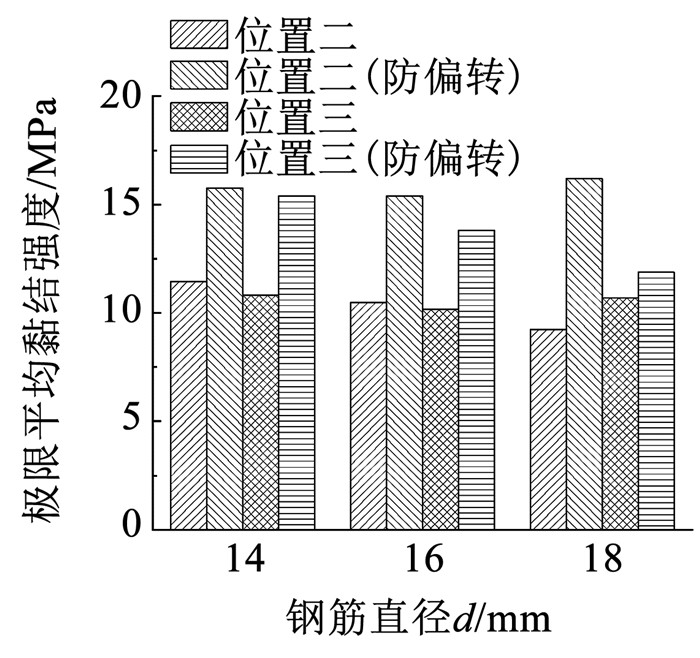
2.3.3 防偏转装置对极限承载力及黏结强度的影响图 13、14为防偏转装置对极限承载力及黏结强度的影响。可以看出,位置二、三试件使用防偏转装置可以有效约束试件的偏转,提高试件的极限承载力和黏结强度。
|
图 13 防偏转装置对极限承载力的影响 Fig. 13 Impact of anti-deflection device on ultimate bearing capacity |
|
图 14 防偏转装置对平均黏结强度的影响 Fig. 14 Impact of anti-deflection device on average bond strength |
不使用防偏转装置时,套筒端部灌浆料因试件偏转被压碎,试件锚固长度减小,故试件极限承载力降低,而防偏转装置可以提供环向约束,有效限制试件偏转,防止灌浆料因偏转提前压碎;加载时内部灌浆料会膨胀变形,防偏转装置约束套筒,抑制裂缝产生与发展,进而提高试件的极限承载力和黏结强度。
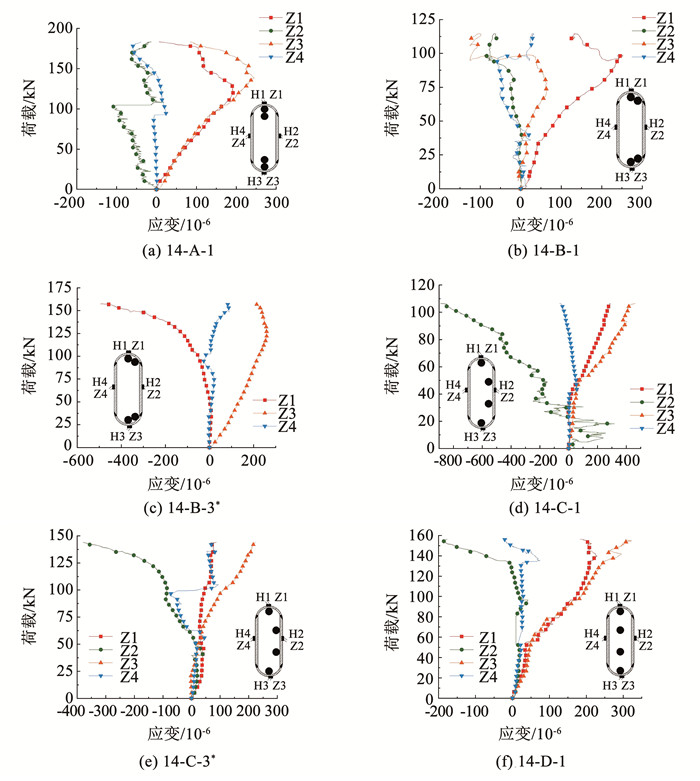
2.4 套筒1/2截面荷载-纵向应变曲线图 15为套筒1/2截面典型荷载-纵向应变曲线(压应变为负)。最大压应变为890×10-6,最大拉应变为462×10-6,均小于2 000×10-6,说明在整个加载过程中套筒1/2截面处在弹性阶段。
|
图 15 套筒中部截面典型荷载-纵向应变曲线 Fig. 15 Typical load-longitudinal strain curves of middle section of sleeve |
由图 15可知,各试件套筒短边侧纵向应变Z1、Z3在加载初期存在受拉趋势,随荷载增加,套筒应变出现受压趋势,加载过程中套筒应变表现为拉应变。原因为加载初期随着荷载的增加,钢筋-灌浆料黏结力逐渐增加,沿套筒纵向的应力分量也增大,灌浆料存在随钢筋一起纵向拔出的趋势,而套筒阻止灌浆料和钢筋的纵向拔出,导致套筒纵向受拉;加载后期,根据钢筋互锁机制[14],套筒纵向受拉程度随外荷载增加先增大后减小,随后逐渐呈受压趋势,但仍为拉应变。
各试件套筒长边侧纵向应变Z2、Z4在加载初期很小,随荷载增加套筒应变逐渐变大,且为压应变。这是由于钢筋黏结力产生的剪应力会使套筒受轴向力,随着荷载增大,套筒由纵向受拉转变为受压[14];同时,灌浆料膨胀使套筒纵向受压,两者叠加套筒压应变逐渐变大。
2.5 套筒1/2截面荷载-环向应变曲线图 16为套筒1/2截面典型荷载-环向应变曲线。可以看出,套筒1/2截面环向应变以拉应变为主,最大拉应变为1 331×10-6,小于2 000×10-6,说明在整个加载过程中套筒1/2截面处在弹性阶段。
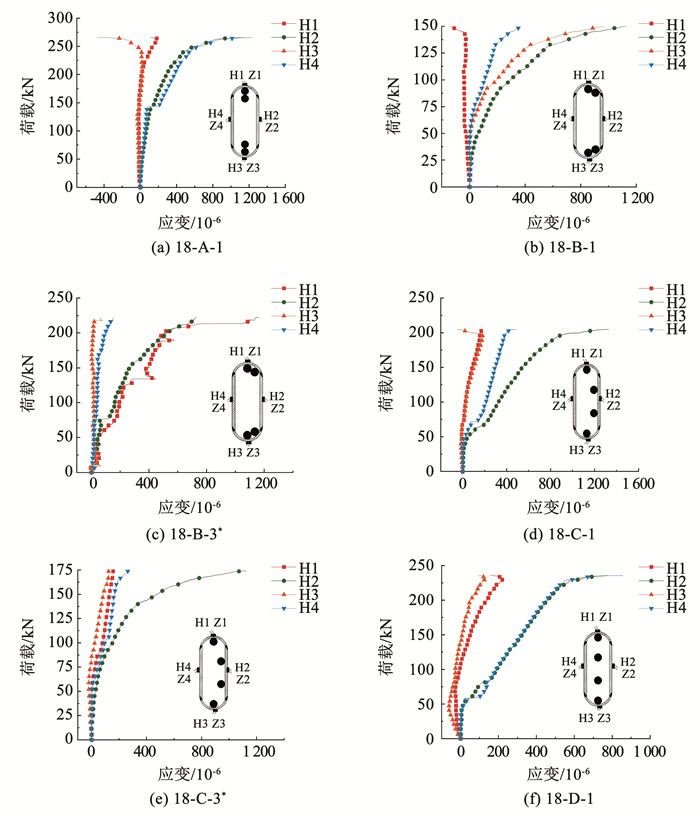
|
图 16 套筒中部截面典型荷载-环向应变曲线 Fig. 16 Typical load-circumferential strain curves of middle section of sleeve |
在加载初期,由于灌浆料与钢筋间黏结力使套筒纵向受拉,此时拉应力较小,因泊松效应套筒环向存在受压趋势;荷载增加,灌浆料随之膨胀变形,套筒环向受拉;加载后期,灌浆料与钢筋间黏结力使套筒环向受拉[14],与灌浆料膨胀引起的套筒环向受拉叠加,受拉趋势更明显。
短边侧套筒环向应变(H1、H3)较小,长边侧套筒环向应变(H2、H4)较大,这是由于灌浆料膨胀变形引起的套筒环向应变较大,为套筒环向受拉的主要因素。抵抗灌浆料膨胀时,套筒长边侧比短边侧薄弱,长边侧类似薄板受弯,其面外刚度较小,抗弯能力差;短边类似于拱,抗弯能力强,故长边变形更大。
未防偏转约束试件(图 16(b)、(d))H2处环向拉应变较大,由于偏转产生的钢筋弯曲变形会使套筒纵向受压,套筒环向拉应变更大。
3 有限元模拟与参数分析 3.1 材料本构关系 3.1.1 灌浆料本构灌浆料模拟采用混凝土塑性损伤模型。并依据试验数据,参考文献[15-16]得到灌浆料应力-应变本构。
3.1.2 钢筋本构在实际加载过程中,采用名义应力和名义应变误差较大,不能准确反映材料的实际应力-应变情况,无法满足计算要求。因此,输入材料参数时要转化为符合实际的真实应力-真实应变。根据文献[17]计算得到套筒和钢筋的真实应力-真实应变关系。直径为16 mm的钢筋应力-应变关系见图 17(a)。
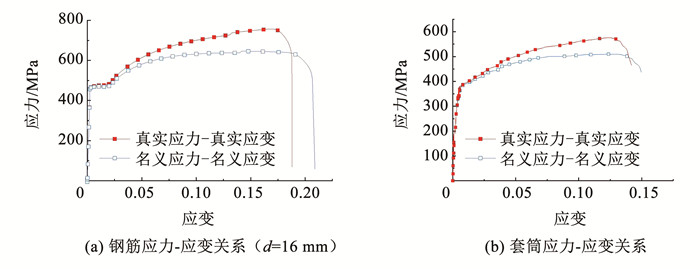
|
图 17 本构关系 Fig. 17 Constitutive relation |
本模型钢材的塑性硬化类型为各向同性。参考材性结果,取其杨氏模量为206 GPa,屈服强度为362.2 MPa,屈服应变为0.005 5,极限强度为509.5 MPa,极限应变为0.127 8。套筒应力-应变关系见图 17(b)。
3.2 有限元模型建立以钢筋直径和后插入钢筋位置为变量,建立12个精细化模型,将模拟结果与试验结果进行对比。同时,为考虑施工误差导致的不同后插入钢筋位置对接头力学性能的影响,设计与4种试验后插入钢筋位置不同的4种后插入钢筋位置接头模型,其位置示意见图 18。接头整体模型及网格划分见图 19。
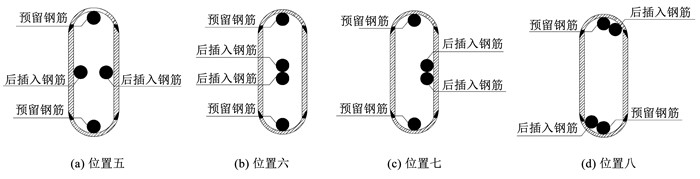
|
图 18 后插入钢筋位置示意 Fig. 18 Schematic of positions of post-installed rebar |
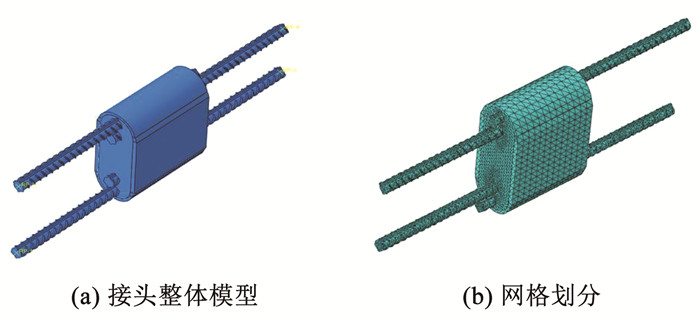
|
图 19 接头整体模型及网格划分 Fig. 19 Overall model of the connector and mesh division |
各部件中存在较多不规则的部件模型,而四面体实体单元对大变形和接触问题的模拟有足够高的精度,因此,本文模拟采用四面体实体单元C3D10M。
分析步类型为“动力,显式”,以保证模型能够在合理增量步内顺利运行。由于收敛速度高且预期法向应力低,为更好模拟黏结滑移,采用硬接触设定法向行为和“罚函数法”,摩擦因数设为0.5。
为模拟套筒单向拉伸作用下的约束,采用以下边界条件:1)套筒偏转模型, 预留钢筋端为固定端(U1、U2、U3、UR1、UR2、UR3均设置为0),后插入钢筋端Z方向(U3)根据试验实际情况设置位移,其他位移约束(U1、U2、UR1、UR2、UR3)设置为0;2)套筒防偏转模型, 在套筒偏转模型边界条件的基础上,在套筒短边X、Y方向(U2、U1)设置位移约束,Z方向(U3)的位移不设置约束。
3.3 模拟结果与试验结果对比模拟结果见表 3。试件典型破坏形式见图 20。试件的典型破坏形式主要有两种:一是固定端两根预留钢筋同时拉断破坏;二是加载端两根后插入钢筋同时拔出破坏。由表 3可知,各试件模拟破坏形式与试验结果基本相同,极限荷载试验值和模拟值相对误差未超过10%,表明参数设置合理,模拟方法可行。
| 表 3 模拟结果统计 Tab. 3 Statistics of simulation results |

|
图 20 试验和模拟典型破坏形式对比 Fig. 20 Comparison of typical failure modes between experiments and simulations |
部分模拟试件与试验试件的荷载-位移曲线对比见图 21。其中,图 21(a)、(b)中模拟试件与试验试件均未采取防偏转措施,模拟曲线与试验曲线趋势基本相同,模拟曲线弹性段和强化段与试验曲线较吻合,而下降段模拟曲线与试验曲线有所偏差。弹性阶段模拟曲线刚度大于试验曲线,这是因为试验中灌浆料存在一定缺陷。曲线下降段有所偏差,模拟曲线较早出现下降段是因为在模拟中灌浆料因变形过大被删除,不再约束钢筋拔出;而试验中发生破坏的灌浆料仍在套筒中,对钢筋有约束作用。
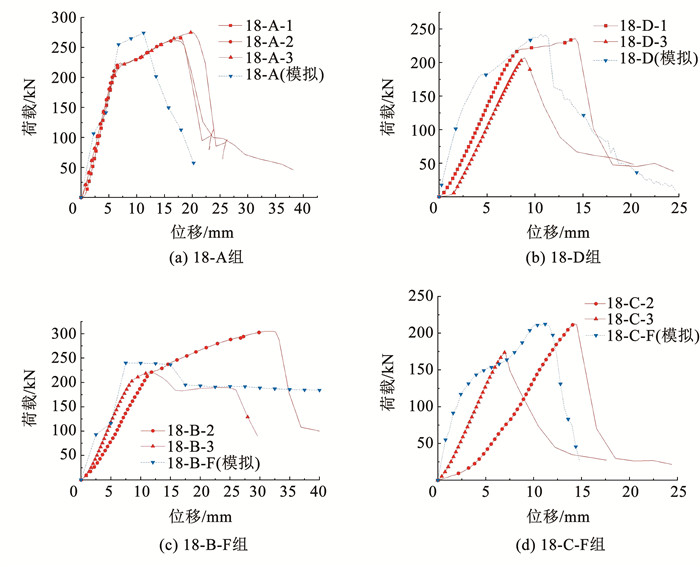
|
图 21 试件荷载-位移曲线 Fig. 21 Load-displacement curves of deflectable specimen |
图 21(c)、(d)中模拟试件与试验试件均采取防偏转措施,防偏转试件模拟结果在上升段拟合良好,模拟曲线的刚度略大于试验曲线,具体原因同上文。可见,各试件模拟曲线与试验曲线整体吻合良好,模拟方法可行。
4 后插入钢筋位置对接头承载力的影响后插入钢筋位置为位置二、三、七时设置防偏转约束条件,其余位置不出现偏转,故8种后插入钢筋位置试件均在防偏转约束条件下进行模拟分析。不同后插入钢筋位置模拟试件的极限荷载见图 22。钢筋直径均为16 mm,搭接长度均为8d,试件均发生钢筋拔出破坏。
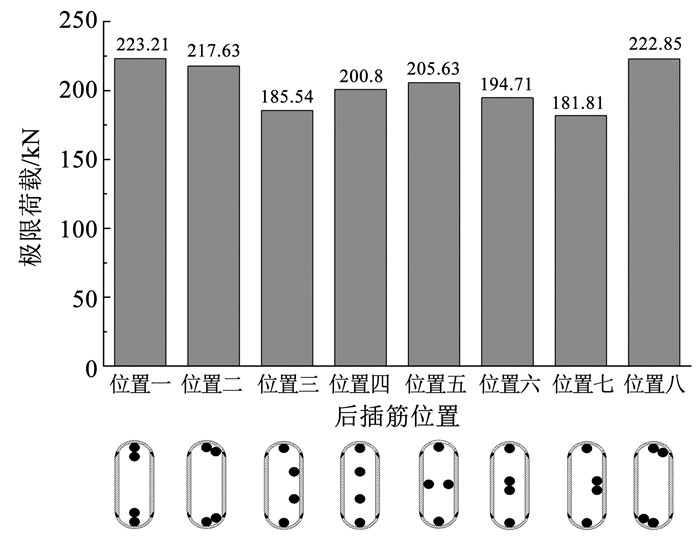
|
图 22 试件破坏时极限荷载 Fig. 22 Ultimate load during specimen failure |
由图 22可知,后插入钢筋对称紧贴布置于长轴时(位置一)试件极限荷载最大,后插入钢筋偏心紧贴布置时(位置二、八)试件极限荷载其次,位置三、四、五、六试件极限荷载有所下降,后插入钢筋紧贴套筒长边中部布置时(位置七)试件极限荷载最小。
位置一试件的后插入钢筋紧贴预留钢筋沿长边对称布置在套筒中心线上,钢筋几乎不偏心且套筒短边对其约束较强;位置二、八试件的后插入钢筋,虽紧贴预留钢筋布置,但与套筒内壁接触,形成的空隙易引起灌浆缺陷,故极限荷载小于位置一试件。
后插入钢筋为位置一、二、八的试件,预留钢筋紧贴套筒内壁,后插入钢筋紧贴预留钢筋,套筒短边约束能力强;其余位置试件,后插入钢筋距预留钢筋远,布置于套筒长边中部,套筒长边约束能力弱,故试件极限荷载小。
与位置四试件相比,位置三试件后插入钢筋虽均匀布置在套筒长边侧,但紧贴套筒内壁布置,易产生灌浆缺陷,且后插入钢筋偏心布置易引起钢筋弯曲变形,极限荷载小于位置四试件。与位置六试件相比,位置七试件后插入钢筋虽紧贴布置在套筒长边中部,但与套筒内壁接触,易产生灌浆缺陷,且后插入钢筋偏心布置易引起钢筋弯曲变形,极限荷载小于位置六试件。
模拟结果进一步证明接头极限荷载主要受3种因素影响,即钢筋间距、后插入钢筋是否偏心布置与后插入钢筋是否紧贴套筒布置。与前文2.3.1中试验结果一致。
位置一试件极限荷载最大;位置七试件极限荷载最小,且为位置一试件的0.81倍。为试验方便,后续接头试验一般采用位置一试件,承载力公式中引入折减系数ω(ω取0.8)考虑不同后插入位置影响。
5 结论1) 防偏转装置可明显限制试件的偏转现象,提高试件的极限承载力和初始刚度。
2) 接头极限荷载和延性主要受3种因素影响,即钢筋间距、后插入钢筋是否偏心布置及是否紧贴套筒布置。后插入钢筋布置于套筒中部,钢筋间距大,套筒长边约束弱,接头极限荷载和延性降低;后插入钢筋偏心布置,易产生弯曲变形,接头极限荷载和延性降低;后插入钢筋紧贴套筒布置易产生灌浆缺陷,接头极限荷载和延性降低。
3) 两钢筋紧贴对称布置于长轴时,弧形短边对其约束程度强且钢筋偏心程度小,试件极限承载力、黏结强度和延性最大。随后插入钢筋偏离长轴中心线程度的增加,加载时试件偏转程度增大,试件极限承载力、黏结强度和延性有所降低。
4) 后插入钢筋位置和相对搭接长度相同时,随钢筋直径增加,试件极限承载力逐渐增大,试件黏结强度逐渐降低。
5) 极限荷载时,套筒短边侧纵向应变为拉应变,但存在受压趋势,套筒长边侧纵向应变为压应变;套筒短边侧环向应变较小,套筒长边侧环向应变较大,套筒长边约束灌浆料膨胀变形的能力比套筒短边约束能力差。
6) 模拟试件的端部破坏情况、荷载-位移曲线、极限承载力等与试验结果基本吻合,验证了模拟方法的可行性。模拟分析进一步表明,后插入钢筋布置越靠近套筒中部、偏离接头长轴中心线程度越大、与套筒紧贴试件极限承载力越低;钢筋位置不同时,极限荷载最小值约为最大值的80%;建议接头承载力公式中引入折减系数ω(ω取0.8)考虑不同后插入位置影响。
| [1] |
余琼. 一种新型的约束搭接套筒: ZL 201420656653.0[P]. 2015-04-01 YU Qiong. A new confined lapping sleeve: ZL 201420656653.0[P]. 2015-04-01 |
| [2] |
余琼, 许雪静, 袁炜航, 等. 不同搭接长度下套筒约束浆锚搭接接头力学试验研究[J]. 湖南大学学报, 2017, 44(9): 82. YU Qiong, XU Xuejing, YUAN Weihang, et al. Mechanical experimental study on sleeve binding slurry anchor lap joints with different lap lengths[J]. Journal of Hunan University, 2017, 44(9): 82. DOI:10.16339/j.cnki.hdxbzkb.2017.09.010 |
| [3] |
余琼, 孙佳秋, 袁炜航. 带肋钢筋与套筒约束灌浆料黏结性能试验[J]. 哈尔滨工业大学学报, 2018, 50(12): 98. YU Qiong, SUN Jiaqiu, YUAN Weihang. Experimental study on bond behavior between ribbed steel bars and sleeve constrained grouting material[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 98. DOI:10.11918/j.issn.0367-6234.201701088 |
| [4] |
余琼, 刘言, 唐子鸣, 等. 套筒截面尺寸对套筒灌浆搭接接头拉伸性能影响试验[J]. 湖南大学学报, 2023, 50(1): 22. YU Qiong, LIU Yan, TANG Ziming, et al. Experimental study on influence of sleeve section size on tensile performance of grouted sleeve lapping connectors[J]. Journal of Hunan University, 2023, 50(1): 22. DOI:10.16339/j.cnki.hdxbzkb.2023003 |
| [5] |
匡轩. 钢筋套筒灌浆搭接连接有限元模拟[D]. 上海: 同济大学, 2019 KUANG Xuan. Finite element simulation of reinforcement sleeve grouting lap connection[D]. Shanghai: Tongji University, 2019 |
| [6] |
YU Qiong, ZHANG Liang, TANG Peiyan, et al. Experimental study and in-depth tensile mechanism analysis of grouted sleeve lapping connectors[J]. Latin American Journal of Solids and Structures, 2022, 19(2): e428. DOI:10.1590/1679-78256935 |
| [7] |
余琼, 唐子鸣, 张星魁, 等. 后插钢筋位置等对APC接头拉伸性能的影响[J]. 哈尔滨工业大学学报, 2022, 54(10): 84. YU Qiong, TANG Ziming, ZHANG Xingkui, et al. Influence of position of post-installed rebar and other factors on tensile performance of APC connector[J]. Journal of Harbin Institute of Technology, 2022, 54(10): 84. DOI:10.11918/202112130 |
| [8] |
中国建筑科学研究院. 普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2003 China Academy of Building Research. Standard for test method for mechanical properties on ordinary concrete: GB/T 50081—2002[S]. Beijing: China Architecture and Building Press, 2003 |
| [9] |
钢铁研究总院. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010 tIron and Steel Research Institute. Metallic materials: tensile testing. Part 1: method of test at room temperature: GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2010 |
| [10] |
余琼, 魏晋文, 魏雨桐, 等. 套筒约束两根钢筋浆锚搭接拉伸试验研究[J]. 湖南大学学报, 2019, 46(11): 20. YU Qiong, WEI Jinwen, WEI Yutong, et al. Experimental study of grouted sleeve lapping connectors of two bars under tensile load[J]. Journal of Hunan University, 2019, 46(11): 20. DOI:10.16339/j.cnki.hdxbzkb.2019.11.003 |
| [11] |
中国建筑科学研究院. 钢筋套筒灌浆连接应用技术规程: JGJ 355—2015[S]. 北京: 中国建筑工业出版社, 2015 China Academy of Building Research. Technical specification for grout sleeve splicing of rebars: JGJ 355—2015[S]. Beijing: China Construction Industry Press, 2015 |
| [12] |
ACI Committee 318. Building code requirements for structural concrete: ACI 318-14[S]. Michigan: American Concrete Institute, 2014
|
| [13] |
Technical Committee B/525. Structural use of concrete. Part 1: code of practice for design and construction: BS 8110-1[S]. London: British Standards Institution, 1997
|
| [14] |
余琼, 王子沁, 白少华, 等. 套筒灌浆搭接接头拉伸试验及受力机理分析[J]. 哈尔滨工业大学学报, 2021, 53(4): 96. YU Qiong, WANG Ziqin, BAI Shaohua, et al. Tensile test and stress mechanism analysis of grouted sleeve lapping connectors for rebars[J]. Journal of Harbin Institute of Technology, 2021, 53(4): 96. DOI:10.11918/202006123 |
| [15] |
LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892. DOI:10.1061/(ASCE)0733-9399(1998)124:8(892) |
| [16] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015 Ministry of Housing and Urban Rural Development of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Construction Industry Press, 2015 |
| [17] |
刘希月, 王元清, 石永久. 基于微观机制的高强度钢材及其焊缝断裂预测模型研究[J]. 建筑结构学报, 2016, 37(6): 231. LIU Xiyue, WANG Yuanqing, SHI Yongjiu. Micromechanical fracture prediction model of high strength steel and its weld[J]. Journal of Building Structures, 2016, 37(6): 231. DOI:10.14006/j.jzjgxb.2016.06.028 |
 2024, Vol. 56
2024, Vol. 56


