2. 长安大学 建筑工程学院,西安 710061
2. School of Civil Engineering, Chang′an University, Xi′an 710061, China
当前,3D打印技术[1-4]与纤维增强树脂基复合材料(fiber reinforced polymer, FRP)[5-8]在桥梁等土木工程领域的应用备受关注,3D打印FRP技术将上述两项技术的优势相结合,工程应用前景广阔,例如锚具及结构复杂构件的制作等用途。然而,由于其制备工艺的特殊性以及材料自身的结构性,导致3D打印FRP材料易发生分层损伤失效,使得该种材料所制作构件在受载后容易发生沿材料层间的破坏,严重制约了该项技术的推广[9]。因此,针对3D打印FRP材料的层间力学性能,国内外学者展开了相关研究。
文献[10-11]利用纤维施胶及微螺杆原位挤出工艺提高了材料的层间强度, 展开了相关研究; 文献[12-13]利用调节基体黏度、预浸渍以及等离子体-激光协同辅助等方式显著提高了打印材料的层间强度;文献[14]设计了一种气体辅助喷头,提高了打印件的层间强度;文献[15-16]选取不同打印参数为研究变量,对试件层间性能进行了试验研究;文献[17]将退火与否作为研究变量进行了研究。上述研究仅从3D打印的工艺及设备入手进行研究,缺乏细观角度分析。文献[18-19]研究了低压退火参数对于试件层间性能和细观组织的影响;文献[20]通过合成增塑剂提高了试件层间黏结性能,并从细观角度进行分析;文献[21]通过对短碳纤维进行表面改性,研究了对试件层间黏结强度的影响,并分析其细观原因。上述在研究打印工艺影响的基础上增加了细观机理探索,但缺乏参数化细致分析。文献[22]对碳纤维/尼龙打印层压板的层内与层间性能进行研究,并分析了最终成型材料的缺陷对试件横向及层间力学性能的影响;文献[23]通过力学试验,分析层厚对试件Ⅰ型层间断裂韧性的影响通过研究打印温度的影响,提出了最佳打印温度及温度补偿本构模型;文献[24]通过研究打印温度的影响,提出了最佳打印温度及温度补偿本构模型。上述研究虽均进行了3D打印FRP层间力学性能的分析,但仍存在两点限制:1)缺少科学合理的层间预制裂纹试件制备方法;2)尚未对材料层间力学性能的影响因素展开系统的理论分析。本文提出了一种全新的3D打印FRP材料层间预制裂纹试件制备方法-断层替换法,基于该方法较为系统的量化研究了两类打印参数对Ⅰ型层间断裂韧性的影响趋势; 同时,基于内聚区理论及surface-based cohesive关系构建了双悬臂梁(double cantilever beam, DCB)试验的仿真模型,通过试验与仿真相互佐证的方式验证了断层替换法的合理性及稳定性。
1 试验 1.1 打印原材料本文将研究对象聚焦为3D打印碳纤维增强树脂基复合材料(carbon fiber reinforced polymer, CFRP),该材料由增强相短切碳纤维(carbon fiber, CF)及基体相聚酰胺(polyamide 6-PA6)组成。具体型号为polymidePA6-CF印材,横截面直径为1.75 mm,玻璃态转变温度为220 ℃,该原材料碳纤维表面经过化学处理后层间强度明显提高,其中碳纤维含量为25%(质量分数)。
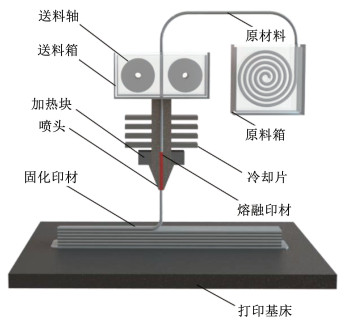
1.2 成型材料细观结构熔丝制造3D打印技术的成型原理为将印材送入加热端加热至熔融态并挤出,挤出的印材在层积过程中冷却固化,随着喷头移动与基床下降逐层打印试件,打印技术原理如图 1所示。打印过程中,印材底部因接触到已固化材料时发生塑性流动而变得扁平,而上部在固化过程中仍然保持圆形轮廓。因此,印材间形成贯通倒三角形空隙,削弱了材料的层间力学性能,试件沿打印方向的断裂面细观结构如图 2所示,该细观结构通过扫描电子显微镜(scanning electron microscope, SEM)获得,图 2坐标中,1方向为印材打印方向,2方向为层内垂直于印材的方向,3方向为试件厚度方向。
|
图 1 熔丝制造3D打印技术原理 Fig. 1 Principles of fused filament fabrication 3D printing technology |

|
图 2 3D打印碳纤维增强树脂基复合材料的细观结构 Fig. 2 Meso-structures of 3D printing carbon fiber reinforced polymer(CFRP) |
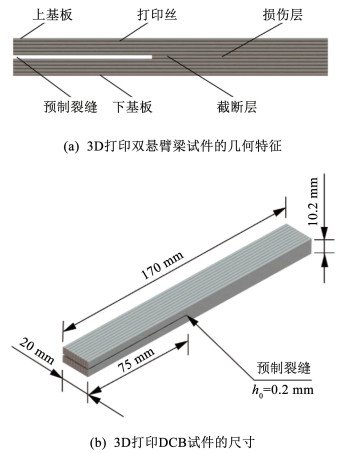
本文参考ASTM D5528-13[25]完成Ⅰ型层间断裂韧性试验试件的设计及制备,具体试验方法为双悬臂梁(double cantilever beam,DCB)试验。如图 3所示,3D打印DCB试件分为上基板、损伤层与下基板三部分,其中损伤层包括预制裂纹及截断层。为适应打印技术的特征,试件尺寸在规范给定的基础上进行了微调,具体为170 mm×20 mm×10.2 mm,预制裂纹长度为75 mm,上、下基板厚度设计为5 mm,损伤层厚度为0.2 mm。
|
图 3 3D打印DCB试件 Fig. 3 3D printing DCB specimens |
根据前期预研资料,打印温度及速度对印材层间力学性能影响较为明显,因此将上述两类参数作为敏感参数进行系统性分析。考虑印材的热力学特征,打印温度的分别选取为245、255、265、275 ℃及285 ℃。当打印速度过大时,印材被喷头拖拉而产生脱层现象[26],削弱层间力学性能;当打印速度过小时,已成型印材热量散失过快,影响层间黏结特性,故打印速度的分别选取为20、30、40、50 mm/s及60 mm/s。此外,当研究打印温度的影响时,打印速度固定为40 mm/s;当研究打印速度的影响时,打印温度固定为275 ℃。试件共有9组不同的参数设置,各组试件的打印温度和速度见表 1。试件其他打印参数:填充率为99%,喷头直径为0.6 mm,机床温度为90 ℃,打印层厚为0.2 mm。
| 表 1 试件打印参数 Tab. 1 Printing parameters of specimens |
考虑熔丝制造3D打印技术的工艺特点,本文提出断层替换法完成预制裂纹试件的制备,打印过程如图 4所示,具体流程如下:1)上传模型文件,打印喷头及基床预热,在基床打印位置处涂胶,保证打印过程印材与基床保持黏结状态;2)采用熔丝制造3D打印工艺对试件底板、下基板与损伤层进行打印,损伤层打印完成后打印机自动暂停;3)利用无黏结非光滑纸代替试件的预制裂纹,为防止上基板变形,与下基板黏结削弱,纸张应放置平整且迅速,纸张放置时间应控制在10 s左右,借助磁铁块放置纸张。由于打印机基床温度设为90 ℃,并在打印过程中恒定,延缓了印材在放置纸张过程中冷却速度,防止印材在纸张放置后固化。纸张宽度控制为73.5 mm,保证试件前端1.5 mm内上、下基板黏结,防止上基板翘曲, 该操作及纸张的性质使得试件上、下基板分离的同时防止试件变形,使得预制裂缝尖端的力学性能不受影响; 4)纸张放置完成后,重启打印机,继续打印完成试件剩余部分,试件打印完成后,从基床上移除试件,去除试件底板及纸张多余部分。

|
图 4 预制裂纹试件打印方法 Fig. 4 Printing method of pre-crack specimens |
根据ASTM D5528-13[25],本文采用铰链传递拉伸荷载使试件发生Ⅰ型分层,进而完成DCB试验。其中,铰链由贴片、辊轴与夹片构成,辊轴使得夹片在加载过程中可绕贴片转动,保证上、下基板自由弯曲,铰链的具体构造如图 5所示。

|
图 5 铰链详细构造 Fig. 5 Details of hinge structure |
试件打印完后,去除多余纸张,在试件端部粘贴铰链。从预制裂纹末端开始涂白,并对涂白部位标注刻度线,共标注20 mm,前5 mm及后5 mm分度为1 mm,其余分度为5 mm,具体如图 6所示。

|
图 6 Ⅰ型层间断裂韧性测试试件准备 Fig. 6 Preparation for specimens of mode Ⅰ fracture toughness |
本文采用万能试验机与电子显微镜完成相关试验,试验具体分两步:1)预拉伸;2)正式拉伸。首先是预拉伸阶段,利用试验机夹头固定试件,采用较快加载速度进行预拉(5~10 mm/s),撕开试件前端黏结部分后立即停止加载。其次为正式加载阶段,开启电子显微镜并将镜头对准裂纹尖端,以1~2 mm/s的速度进行位移加载(准静载)。加载过程中牵引力-位移曲线由试验机系统记录,裂纹扩展长度借助电子显微镜观察,并根据万能试验机记录不同裂纹长度相应牵引力值,直至裂纹扩展完整个标注范围。试验设备及测试过程如图 7所示,试件裂纹扩展过程如图 8所示。为避免试验数据的偶然性,每种工况设置3组平行试验进行数据采集,并将3组平行试验的数据进行平均,作为与仿真分析对比的依据。

|
图 7 试验设备及测试过程 Fig. 7 Experimental equipment and testing process |

|
图 8 试件裂纹扩展过程 Fig. 8 Crack propagation process of specimens |
采用柔度校准法完成Ⅰ型层间断裂韧性的计算,原理根据ASTM D5528-13[25]规定,DCB试件断裂过程中层间断裂韧性可按式(1)计算:
| $ G_{\mathrm{IC}}=-\frac{1}{b} \cdot \frac{\mathrm{~d} U}{\mathrm{~d} a} $ | (1) |
式中:U为试件总应变能,
DCB试样的柔度C采用式(2)计算:
| $ C=\frac{\delta}{P} $ | (2) |
根据Berry[26]提出的柔度C与裂纹长度a成比例假设,柔度的表达式为
| $ C=Z a^n $ | (3) |
式中Z、n为回归参数。
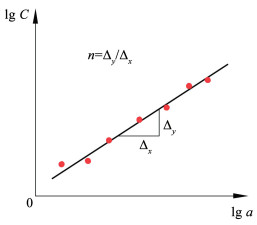
上述回归参数Z、n可对式(3)取对数后,对lg C与lg a的试验数据进行最小二乘拟合得到,如图 9所示。将式(1)、(2)、(3)联列,得到柔度校准法Ⅰ型断裂韧性值计算式:
| $ G_{\text {IC }}=\frac{n P \delta}{2 b a} $ | (4) |
式中P、δ及a均取裂纹开始扩展时的值进行计算。
2 仿真分析 2.1 计算理论 2.1.1 内聚区模型采用内聚区模型模拟打印材料层间力学行为,如图 10所示,该理论认为复合材料在发生分层过程中,裂纹分为彻底分离自由面与存在内聚力的裂纹尖端两部分。内聚力在裂纹尖端范围内呈非线性分布,其内聚力发展情况在分层损伤过程中,受牵引-分离定律控制。

|
图 10 内聚区裂纹扩展 Fig. 10 Crack propagation of cohesive zone |
随着牵引点相对位移增大,裂纹尖端界面发生相对位移,界面间内聚力随之增大;当牵引点相对位移达到临界值δm0,材料开始出现不可逆损伤,内聚力σ随牵引点相对位移增大开始减小。当裂纹尖端能量释放率达到材料的层间断裂韧性GΙC之后,裂纹尖端完全张开,内聚力减小为0,内聚区黏结失效,新的裂纹形成并向前扩展,断裂韧性值GΙC可由σ-δ曲线所围面积求出,计算式为
| $ G_{\mathrm{IC}}=\int \sigma \mathrm{d} \delta=\int f(\delta) \mathrm{d} \delta $ | (5) |
在ABAQUS模型中,内聚力本构模型计算分为未损伤阶段、损伤起始及损伤演化阶段,各个阶段的本构关系不同。未损伤阶段采用如式(6)所示本构关系:
| $ \begin{aligned} & \boldsymbol{\sigma}=\left[\begin{array}{l} \sigma_{\mathrm{n}} \\ \sigma_{\mathrm{s}} \\ \sigma_{\mathrm{t}} \end{array}\right]=\left[\begin{array}{lll} E_{\mathrm{nn}} & E_{\mathrm{ns}} & E_{\mathrm{nt}} \\ E_{\mathrm{sn}} & E_{\mathrm{ss}} & E_{\mathrm{st}} \\ E_{\mathrm{tn}} & E_{\mathrm{ts}} & E_{\mathrm{tt}} \end{array}\right]\left[\begin{array}{l} \varepsilon_{\mathrm{n}} \\ \varepsilon_{\mathrm{s}} \\ \varepsilon_{\mathrm{t}} \end{array}\right]= \\ & \boldsymbol{E} \cdot \boldsymbol{\varepsilon}=\left[\begin{array}{lll} K_{\mathrm{nn}} & K_{\mathrm{ns}} & K_{\mathrm{nt}} \\ K_{\mathrm{sn}} & K_{\mathrm{ss}} & K_{\mathrm{st}} \\ K_{\mathrm{tn}} & K_{\mathrm{ts}} & K_{\mathrm{tt}} \end{array}\right]\left[\begin{array}{l} \delta_{\mathrm{n}} \\ \delta_{\mathrm{s}} \\ \delta_{\mathrm{t}} \end{array}\right]=\boldsymbol{K} \cdot \boldsymbol{\delta} \end{aligned} $ | (6) |
| $ K_{\mathrm{nn}}=\frac{E_{\mathrm{nn}}}{T_0} $ | (7) |
| $ K_{\mathrm{ss}}=\frac{E_{\mathrm{ss}}}{T_0} $ | (8) |
| $ K_{\mathrm{tt}}=\frac{E_{\mathrm{t}}}{T_0} $ | (9) |
式中:σ为内聚力单元牵引应力矢量,ε为内聚力应变矢量,E为内聚力单元弹性矩阵,K为与黏结性能相关的内聚力单元界面初始刚度矩阵。
损伤起始按照最大名义应力准则来判断损伤是否发生,判据如式(10)及式(11)所示:
| $ \max \left(\frac{\left\langle\sigma_{\mathrm{n}}\right\rangle}{\sigma_{\mathrm{n}}^{\max }}, \frac{\sigma_{\mathrm{s}}}{\sigma_{\mathrm{s}}^{\max }}, \frac{\sigma_{\mathrm{t}}}{\sigma_{\mathrm{t}}^{\max }}\right)=1 $ | (10) |
| $ \left\langle\sigma_{\mathrm{n}}\right\rangle=\left\{\begin{array}{l} \sigma_{\mathrm{n}}, \sigma_{\mathrm{n}} \geqslant 0 \\ 0, \sigma_{\mathrm{n}}<0 \end{array}\right. $ | (11) |
损伤演化阶段采用如式(14)所示的本构关系:
| $ \sigma_{\mathrm{n}}=\left\{\begin{array}{l} (1-D) \bar{\sigma}_{\mathrm{n}}, \bar{\sigma}_{\mathrm{n}} \geqslant 0 \\ \bar{\sigma}_{\mathrm{n}}, \bar{\sigma}_{\mathrm{n}}<0 \end{array}\right. $ | (12) |
式中:D与式(13)意义相同,按照式(16)计算,σn为材料未发生损伤时相应位移所对应的应力,下标n代表Ⅰ型层间断裂工况,为方便表示后文下标用Ⅰ来代替。
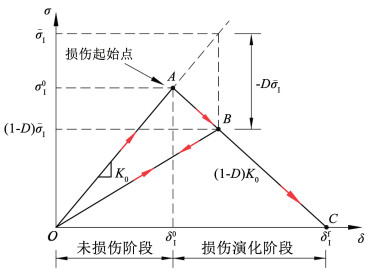
整个加载过程采用双线性内聚区本构关系模拟,牵引内聚力σ与张开位移δ的关系如图 11所示,未损伤阶段对应图 11中的OA段,损伤起始点对应图 11中的A点,损伤演化阶段对应图 11中的AC段,双线性本构模型中内聚力与张开位移的本构关系见式(13)及式(14):
| $ \sigma_{\mathrm{I}}=\left\{\begin{array}{l} K_0 \delta_{\mathrm{I}}, \delta_{\mathrm{I}} \leqslant \delta_{\mathrm{I}}^0 \\ (1-D) K \delta_{\mathrm{I}}, \delta_{\mathrm{I}}^0 <\delta_{\mathrm{I}}<\delta_{\mathrm{I}}^{\mathrm{I}} \\ 0, \delta_{\mathrm{I}} \geqslant \delta_{\mathrm{I}}^{\mathrm{I}} \end{array}\right. $ | (13) |
| $ D=\frac{\delta_{\mathrm{I}}^{\mathrm{f}}\left(\delta_{\mathrm{I}}^{\max }-\delta_{\mathrm{I}}^0\right)}{\delta_{\mathrm{I}}^{\max }\left(\delta_{\mathrm{I}}^{\mathrm{f}}-\delta_{\mathrm{I}}^0\right)} $ | (14) |
|
图 11 内聚区双线性本构模型 Fig. 11 Bilinear constitutive model of cohesive zone |
式中:σΙ为Ⅰ型断裂模式下界面内聚牵引力;K0为初始界面刚度;δΙ为界面分离位移;D为损伤变量,D=0时材料未损伤,D=1时材料完全损伤;δΙ0为损伤起始点的裂纹张开位移;δfΙ为临界裂纹张开位移;δΙmax为加载过程等效位移最大值;GΙC为内聚力单元Ⅰ型断裂下模式下断裂韧性。
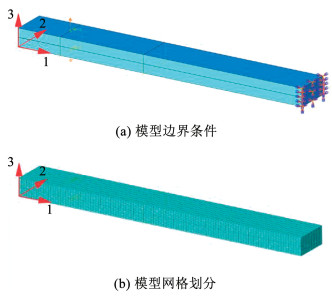
2.2 仿真模型 2.2.1 模型概况本文仿真基于ABAQUS/Explicit开展,模型由上、下基板构成,基板尺寸为170 mm×20 mm×5 mm,单元类型为C3D8R。模型采用surface-based cohesive实现上、下基板黏结,并考虑损伤层厚度的影响。模型在裂纹侧距离试件端部20 mm处,即试件铰链辊轴位置处建立分割面,并在该面上、下边中点处建立基准点作为加载点,将基准点与分割面设置为耦合关系,对所建立基准点进行位移加载。模型裂纹端不进行约束,另一端将模型侧面完全固结,试件的仿真模型建立如图 12所示。
|
图 12 DCB试件仿真模型 Fig. 12 Simulation model of DCB specimens |
本文仿真中,参考相关研究成果[28-31]获得试件初始界面刚度K0及初始界面强度σ0的取值范围。同时,结合预实验研究及仿真分析,最终确定打印速度为40 mm/s及打印温度为275 ℃时各工况下K0及σ0的值并在表 2与表 3中给出。
| 表 2 打印速度为40 mm/s下的不同打印温度的初始界面刚度K0及初始界面强度σ0 Tab. 2 Initial interface stiffness K0 and initial interface strength σ0 with printing temperature at 40 mm/s |
| 表 3 打印温度为275 ℃下的不同打印速度的初始界面刚度K0及初始界面强度σ0 Tab. 3 Initial interface stiffness K0 and initial interface strength σ0 with printing speed at 275 ℃ |
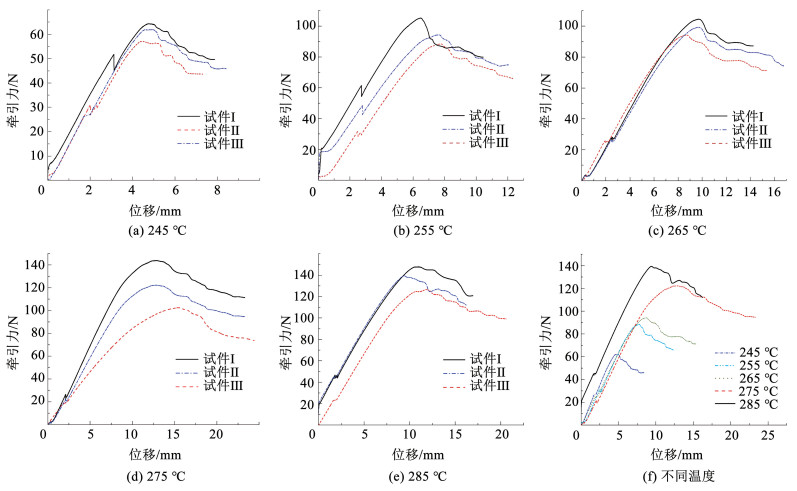
不同打印温度下DCB试件的牵引力-位移曲线在图 13(a)~13(e)中给出,同时将同一打印温度下不同试件的测试数据进行平均,实现不同打印温度下试验测试数据的对比分析,结果如图 13(f)所示。由图 14(f)可知,不同打印温度下牵引力-位移曲线上升段的斜率近似相同,牵引力峰值随着打印温度的增加而增加,表明随打印温度的提高,试件的层间界面强度也会明显提高;且牵引力峰值对应位移,也随温度增加而增加(除285 ℃外)。基于牵引力-位移试验数据,分别计算得到不同打印温度下材料的Ⅰ型层间断裂韧性值,在表 4中给出。此外,牵引力峰值在表 5中给出。
|
图 13 不同打印温度下的牵引力-位移试验曲线 Fig. 13 Experimental traction-separation curves with different printing temperatures |
|
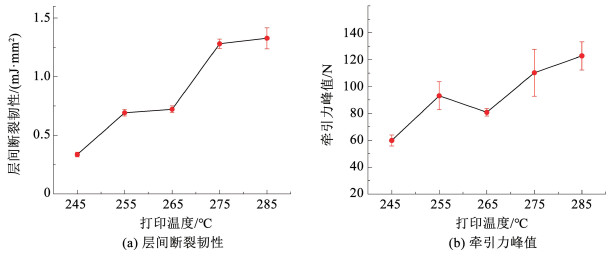
图 14 不同打印温度试件的层间断裂韧性与牵引力峰值 Fig. 14 Inter-layer fracture toughness and traction peak of specimens with different printing temperatures |
| 表 4 不同打印温度下试件的Ⅰ型层间断裂韧性值 Tab. 4 ModeⅠ inter-layer fracture toughness of specimens with different printing temperatures |
| 表 5 不同打印温度下试件的牵引力峰值 Tab. 5 Traction peak of specimens with different printing temperatures |
Ⅰ型层间断裂韧性及牵引力峰值随打印温度的变化曲线如图 14所示,由图 14(a)可知,Ⅰ型层间断裂韧性随打印温度的升高而增大,当温度由245 ℃升至255 ℃时,断裂韧性增加105.95%,由265 ℃升至275 ℃时,增加77.39%,此区间内增加速度较快;其余温度区间则增加速度较小,由255 ℃升至265 ℃时,增加2.89%,由275 ℃升至285 ℃时,增加3.67%。由图 14(b)可知,牵引力峰值的变化规律总体与层间断裂韧性相同,但在265 ℃为例外情况,该温度下的牵引力峰值较255 ℃下降了13.24%。
本文通过SEM观察不同打印温度下试件细观结构的差异,从细观尺度解释打印温度对层间力学性能的影响机理,不同打印温度下试件横断面细观结构如图 15所示,图中仅标注较大空隙。图中可见,随着打印温度提高,试件内的空隙面积变小,原因为当打印温度升高时,熔融印材温度更高,使得印材固化时间更长,固化前会充分发生塑性流动,减小了层内及层间空隙;此外,已固化印材的温度也更高,后挤出印材可与其更好黏结。同时,由图 14(a)可知,当打印温度较高时,再增加温度,试件断裂韧性不再显著增加,对于所研究温度范围,275 ℃为较合理的打印温度,285 ℃时,断裂韧性仅提高3.67%。其原因为此时试件质量已处于较好状态,其力学性能趋于传统压塑工艺,层间断裂韧性不再显著变化。

|
图 15 不同打印温度下试件的细观结构 Fig. 15 Meso-structures of specimens with different printing temperatures |
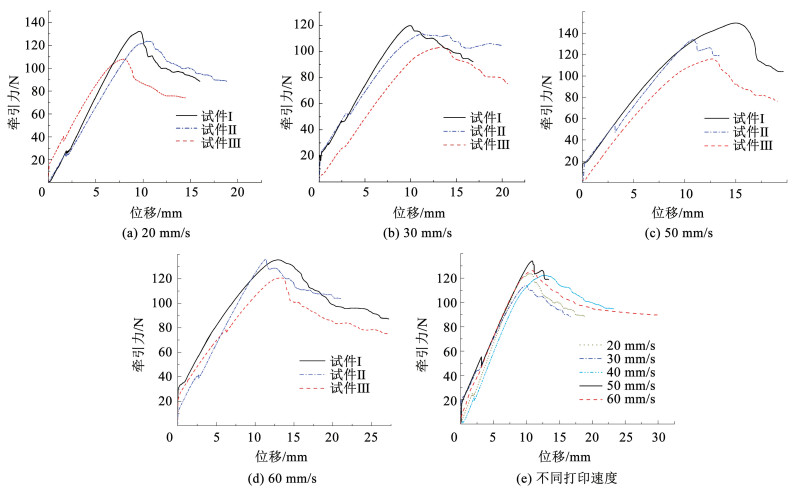
将不同打印速度工况试件测得牵引力- 位移曲线绘制如图 16(a)~16(d)所示,打印速度40 mm/s时的试验曲线与图 13(d)曲线相同,故不再重复。并对各组试件的牵引力-位移曲线进行平均作为该打印速度下结果,如图 16(e)所示。
|
图 16 不同打印速度下的牵引力-位移试验曲线 Fig. 16 Experimental traction-separation curves with different printing speeds |
由图 16(e)可知,改变打印速度时,牵引力-位移曲线上升段的斜率也近似相同。各工况下牵引力峰值随打印速度增加而增加(除60 mm/s、20 mm/s),说明提高打印速度时试件层间界面强度也会提高。基于试验数据,分别计算各组试件的层间断裂韧性在表 6中给出,牵引力峰值在表 7中给出。
| 表 6 不同打印速度下试件的Ⅰ型层间断裂韧性值 Tab. 6 ModeⅠ inter-layer fracture toughness of specimens with different printing speeds |
| 表 7 不同打印速度下试件的牵引力峰值 Tab. 7 Traction peak of specimens with different printing speeds |
Ⅰ型层间断裂韧性及牵引力峰值随打印速度变化曲线如图 17所示,由图 17(a)可知,Ⅰ型层间断裂韧性随速度升高而增大,但增加缓慢,打印速度达到30 mm/s时仅增加3.16%;达到40 mm/s时增加18.64%;达到50 mm/s时,断裂韧性几乎不变,达到60 mm/s时增加4.06%。由图 17(b)可知,当打印速度改变时,试件的牵引力峰值的变化不明显,只有速度为30 mm/s时降低了12.76%,其余工况下牵引力峰值几乎相等。

|
图 17 不同打印速度试件的层间断裂韧性与牵引力峰值 Fig. 17 Inter-layer fracture toughness and traction peak of specimens with different printing speeds |
本文通过SEM观察不同打印速度下试件细观结构的差异,从细观尺度解释打印速度对层间力学性能的影响机理,不同打印速度下试件横断面细观结构如图 18所示,打印速度为40 mm/s时的结果与图 15(d)相同,故不再重复。图 18中仅标注出较大空隙。由图 18可见,随着打印速度提高,试件内的空隙面积变小,原因为当打印速度加快时,印材沉积过程中散失的热量更少,已沉积印材与新挤出印材在固化前能发生充分的塑性流动。但由图 17可知,打印速度较高时,层间Ⅰ型层间断裂韧性改善不显著。其原因为虽然此时印材散失的热量减少且黏结较好,但由于打印速度过快印材发生脱层或不完全沉积的概率增大,两种效应对断裂韧性的影响趋势是负相关的。在所研究打印速度范围内,40 mm/s为推荐打印速度,60 mm/s的速度下层间断裂韧性仅提高4.22%。

|
图 18 不同打印速度下试件的细观结构 Fig. 18 Meso-structures of specimens with different printing speeds |
网格尺寸是影响计算时间及精度的重要因素,应选取适当的网格尺寸进行仿真分析。在分析网格尺寸对收敛性的影响时,选取打印温度为275 ℃、打印速度为40 mm/s的基准工况进行。将网格尺寸选取为2.5、2、1.5、1 mm和0.75 mm 5种,分别计算5种网格尺寸下基准工况的牵引力-位移曲线,网格尺寸为2.5 mm至0.75 mm范围时,牵引力峰值从120.21 N变化为134.42 N,相应计算结果如图 19所示。

|
图 19 不同网格尺寸下牵引力-位移曲线 Fig. 19 Traction-displacement curves with different mesh sizes |
由图 19可知,随着网格的不断加密,仿真模型的解逐渐趋于收敛,但网格过密会明显降低计算效率。研究表明,采用自定义模式进行网格划分及计算,计算时间可被缩短,且计算结果精度高。因此,本文采取自定义网格的方式来对模型进行网格划分,模型厚度方向上网格尺寸定为0.625 mm,宽度方向上定为2.5 mm,长度方向上定为1.5 mm,牵引力峰值为134.48 N。
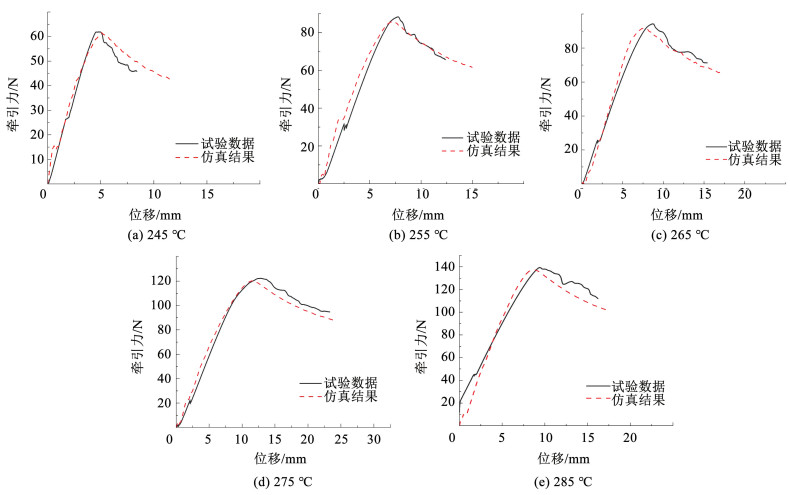
3.2.2 变打印温度工况图 20中给出了不同打印温度下,牵引力-位移曲线仿真计算结果与试验测试数据的对比分析。在曲线的峰值附近,材料不再处于线弹性阶段,此时试件力学性能不稳定,仅需关注牵引力峰值及峰值对应位移,保证仿真计算结果与试验测试数据间的相对误差在15%之内即可。对曲线牵引力峰值及峰值对应位移的相对误差进行计算,计算结果在表 8中给出。
|
图 20 不同打印温度下仿真计算结果与实验测试数据对比 Fig. 20 Comparison between simulation results and experimental data with different printing temperatures |
| 表 8 不同打印温度下仿真计算结果与试验测试数据间的相对误差 Tab. 8 Relative error between simulation results and experimental data with different printing temperatures |
由表 8可知,牵引力峰值的相对误差较小,而峰值对应位移的相对误差较大。其原因:1)试验过程中,牵引力的持续增加引起夹头与铰链之间相对滑移,导致所测量位移值整体偏大;2)在加载初期铰链容易突然小范围打滑,造成骤然卸载,进一步导致试验所测峰值力对应位移偏大。但仿真计算结果与试验测试数据间的相对误差均保持在15%内,表明仿真计算结果与试验测量数据之间可以相互佐证。
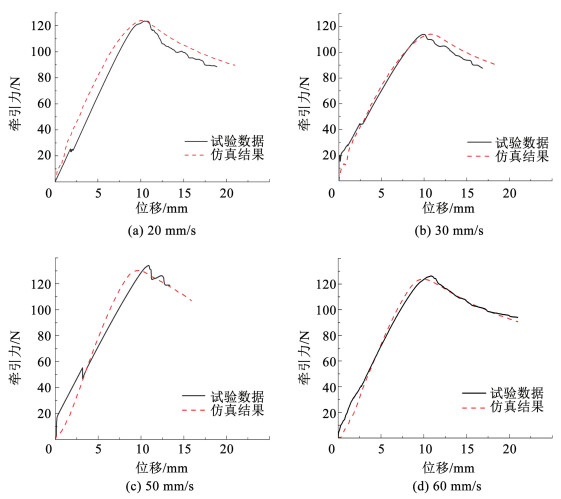
3.2.3 变打印速度工况图 21给出了不同打印速度下仿真计算结果与试验测试数据的对比分析,打印速度为40 mm/s时的计算曲线与图 20(d)相同,对牵引力峰值及峰值对应位移的相对误差进行计算,计算结果在表 9中给出。由表 9可知,变打印速度工况下仿真计算结果及试验测试数据之间的相对误差规律与变打印温度工况一致,牵引力峰值的相对误差较小,而峰值对应位移的误差较大,其原因与变打印温度工况下相同,为试验机夹头与铰链相对滑移以及加载初期铰链滑脱等。
|
图 21 不同打印速度下仿真计算结果与实验测试数据对比 Fig. 21 Comparison between simulation results and experimental data with different printing speeds |
| 表 9 不同打印速度下仿真计算结果与试验测试数据间的相对误差 Tab. 9 Relative error between simulation results and experimental data with different printing speeds |
本文对3D打印CFRP Ⅰ型层间断裂性能进行了系统性研究,设计了新型预制裂纹试件制备方法,将试验测试及仿真分析两种方法相结合,分析了Ⅰ型层间断裂韧性对打印温度及打印速度的敏感性,得到如下结论:
1) 提出的断层替换法可用于层积成型3D打印复合材料的层间力学性能分析,该方法具有效率高、操作简单等优势,同时获取的试验数据稳定可靠,采用surface-based cohesive关系可以正确描述材料的Ⅰ型层间失效现象。
2) 打印材料的Ⅰ型层间断裂韧性随打印温度及速度的提高而增大,但存在上界,打印温度超过275 ℃或者打印速度超过40 mm/s后,其变化幅度很小,分别为3.67%及4.22%。此外,峰值牵引力对打印速度不敏感。
3) 材料细观研究表明,随着打印温度及速度的提高,印材在固化前能发生更充分的塑性流动,使得印材间空隙更小,层间力学性能更好,从细观层次对材料的层间力学性能变化机理作了合理解释。
由于篇幅限制,本文仅对Ⅰ型层间断裂韧性进行分析,后期可对Ⅱ型层间断裂韧性进行相应研究。
| [1] |
GENG Songyuan, LUO Qiling, LIU Kun, et al. Research status and prospect of machine learning in construction 3D printing[J]. Case Studies in Construction Materials, 2023, 18: e01952. DOI:10.1016/j.cscm.2023.e01952 |
| [2] |
冯鹏, 张汉青, 孟鑫淼, 等. 3D打印技术在工程建设中的应用及前景[J]. 工业建筑, 2019, 49(12): 154. FENG Peng, ZHANG Hanqing, MENG Xinmiao, et al. The prospects and applications of printing for construction[J]. Industrial Construction, 2019, 49(12): 154. DOI:10.13204/j.gyjz201912027 |
| [3] |
李施展. 3D打印技术在香溪长江大桥施工测量中的应用[J]. 测绘通报, 2021(增刊2): 121. LI Shizhan. Application of 3D printing technology in construction survey of Xiangxi Yangtze River bridge[J]. Bulletin of Surveying and Mapping, 2021(Sup.2): 121. DOI:10.13474/j.cnki.11-2246.2021.0601 |
| [4] |
朱彬荣, 潘金龙, 周震鑫, 等. 3D打印技术应用于大尺度建筑的研究进展[J]. 材料导报, 2018, 32(23): 4150. ZHU Binrong, PAN Jinlong, ZHOU Zhenxin, et al. Advances in large-scale three-dimensional printing technology applied in construction industry[J]. Materials Reports, 2018, 32(23): 4150. DOI:10.11896/j.issn.1005-023X.2018.23.017 |
| [5] |
刘志明, 陈静芬, 毛欢, 等. 纤维增强复合材料混合模式分层破坏数值模拟研究[J]. 应用力学学报, 2023, 40(3): 545. LIU Zhiming, CHEN Jingfen, MAO Huan, et al. Numerical simulations of mixed-mode delamination in fiber-reinforced composite materials[J]. Chinese Journal of Applied Mechanics, 2023, 40(3): 545. DOI:10.11776/j.issn.1000-4939.2023.03.006 |
| [6] |
娄逸群, 彭晖, 兰川云, 等. 端部嵌贴CFRP板加固RC结构的斜嵌段黏结性能试验[J]. 复合材料学报, 2024, 41(2): 871. LOU Yiqun, PENG Hui, LAN Chuanyun, et al. Experiment of bonding performance of inclined embedded section of RC structure reinforced with near-end enhanced embedded CFRP strip[J]. Acta Materiae Compositae Sinica, 2024, 41(2): 871. DOI:10.13801/j.cnki.fhclxb.20230530.001 |
| [7] |
白玉磊, 张玉峰, 梅世杰, 等. 大应变FRP加固连续梁桥地震易损性分析[J]. 哈尔滨工业大学学报, 2023, 55(9): 84. BAI Yulei, ZHANG Yufeng, MEI Shijie, et al. Seismic fragility of continuous grider bridge reinforced with large rupture strain FRP[J]. Journal of Harbin Institute of Technology, 2023, 55(9): 84. DOI:10.11918/202111054 |
| [8] |
刘昌永, 孙士鹏, 胡清, 等. FRP-钢夹层复合管混凝土桥墩轴压承载力试验[J]. 哈尔滨工业大学学报, 2018, 50(12): 31. LIU Changyong, SUN Shipeng, HU Qing, et al. FRP-interlayer-steel tube concrete column piers under axial compression[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 31. DOI:10.11918/j.issn.0367-6234.201801162 |
| [9] |
赵丽滨, 龚愉, 张建宇. 纤维增强复合材料层合板分层扩展行为研究进展[J]. 航空学报, 2019, 40(1): 171. ZHAO Libin, GONG Yu, ZHANG Jianyu. A survey on delamination growth behavior in fiber reinforced composite laminates[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 171. DOI:10.7527/S1000-6893.2018.22509 |
| [10] |
LIU Tengfei, TIAN Xiaoyong, ZHANG Manyu, et al. Interfacial performance and fracture patterns of 3D printed continuous carbon fiber with sizing reinforced PA6 composites[J]. Composites Part A: Applied Science and Manufacturing, 2018, 114: 368. DOI:10.1016/j.compositesa.2018.09.001 |
| [11] |
LIU Tengfei, TIAN Xiaoyong, ZHANG Yayuan, et al. High-pressure interfacial impregnation by micro-screw in-situ extrusion for 3D printed continuous carbon fiber reinforced nylon composites[J]. Composites Part A: Applied Science and Manufacturing, 2020, 130: 105770. DOI:10.1016/j.compositesa.2020.105770 |
| [12] |
LUO Meng, TIAN Xiaoyong, SHANG Junfan, et al. Impregnation and interlayer bonding behaviours of 3D-printed continuous carbon-fiber-reinforced poly-ether-ether-ketone composites[J]. Composites Part A: Applied Science and Manufacturing, 2019, 121: 130. DOI:10.1016/j.compositesa.2019.03.020 |
| [13] |
LUO Meng, TIAN Xiaoyong, SHANG Junfang, et al. Bi-scale interfacial bond behaviors of CCF/PEEK composites by plasma-laser cooperatively assisted 3D printing process[J]. Composites Part A: Applied Science and Manufacturing, 2020, 131: 105812. DOI:10.1016/j.compositesa.2020.105812 |
| [14] |
肖建华, 许煌翔, 刘晓波. 一种FDM成形中气体辅助喷头的设计及其对打印件力学性能的影响[J]. 塑性工程学报, 2023, 30(1): 208. XIAO Jianhua, XU Huangxiang, LIU Xiaobo. Design of a gas-assisted nozzle in FDM molding and its influence on mechanical properties of printing parts[J]. Journal of Plasticity Engineering, 2023, 30(1): 208. DOI:10.3969/j.issn.1007-2012.2023.01.027 |
| [15] |
王琛, 任思雨, 张晨赟. 成型参数对3D打印柔性聚氨酯制件层间黏结性能的影响[J]. 塑料工业, 2023, 51(5): 181. WANG Chen, REN Siyu, ZHANG Chenyun. Effect of molding parameters on interlaminar bonding properties of 3D printed flexible polyurethane parts[J]. China Plastics Industry, 2023, 51(5): 181. DOI:10.3969/j.issn.1005-5770.2023.05.027 |
| [16] |
徐奔, 张守玉, 水锋, 等. 连续碳纤维增强聚苯硫醚复合材料的3D打印及力学性能优化[J]. 高分子材料科学与工程, 2022, 38(7): 84. XU Ben, ZHANG Shouyu, SHUI Feng, et al. 3D printing and mechanical properties optimization of continuous carbon fiber reinforced polyphenylene sulfide composites[J]. Polymer Materials Science & Engineering, 2022, 38(7): 84. DOI:10.16865/j.cnki.1000-7555.2022.0148 |
| [17] |
喻红, 杨孟茹, 吴悠, 等. 3D打印参数对制品层间黏结性能的影响[J]. 中国塑料, 2018, 32(6): 92. YU Hong, YANG Mengru, WU You, et al. Effect of 3D printing parameters on interlayer adhesive properties of printed parts[J]. China Plastics, 2018, 32(6): 92. DOI:10.19491/j.issn.1001-9278.2018.06.014 |
| [18] |
YU Xiao, SONG Wenzhe, ZHENG Jinghua, et al. Effects of low-pressure annealing on the performance of 3D printed CF/PEEK composites[J]. Chinese Journal of Mechanical Engineering: Additive Manufacturing Frontiers, 2023, 2(2): 100076. DOI:10.1016/j.cjmeam.2023.100076 |
| [19] |
YILMAZ M, YILMAZ N F, KALLAN M F. Rheology, crystallinity, and mechanical investigation of interlayer adhesion strength by thermal annealing of polyetherimide (PEI/ULTEM 1010) parts produced by 3D printing[J]. Journal of Materials Engineering and Performance, 2022, 31(12): 9900. DOI:10.1007/S11665-022-07049-Z |
| [20] |
LYU Yang, CHEN Yanlu, LIN L, et al. Architecture of covalent bonds between filament layers to enhance performance of 3D printing biodegradable polymer blends[J]. Polymer Testing, 2022, 106: 107456. DOI:10.1016/j.polymertesting.2021.107456 |
| [21] |
ZHANG Zimeng, LIU Ruochen, LI Wei, et al. Frontal polymerization-assisted 3D printing of short carbon fibers/dicyclopentadiene composites[J]. Journal of Manufacturing Processes, 2021, 71: 753. DOI:10.1016/j.jmapro.2021.10.014 |
| [22] |
IRAGI M, PASCUAL-GONZALEZ C, ESNAOLA A, et al. Ply and interlaminar behaviours of 3D printed continuous carbon fibre-reinforced thermoplastic laminates; effects of processing conditions and microstructure[J]. Additive Manufacturing, 2019, 30: 100884. DOI:10.1016/j.addma.2019.100884 |
| [23] |
SOMIREDDY M, SINGH C V, CZEKANSKI A. Mechanical behaviour of 3D printed composite parts with short carbon fiber reinforcements[J]. Engineering Failure Analysis, 2020, 107: 104232. DOI:10.1016/j.engfailanal.2019.104232 |
| [24] |
ZHU Kaiyang, DENG Zichen, DAI Shi, et al. Temperature-compensated constitutive model of fused filament fabrication 3D printed PLA materials with full extrusion temperatures[J]. Rapid Prototyping Journal, 2021, 28(1): 41. DOI:10.1108/RPJ-04-2021-0101 |
| [25] |
ASTM International. Standard test method for mode Ⅰ interlaminar fracturetoughness of unidirectional fiber reinforced polymer matrix composites: ASTM D5528-13[S]. West Conshohocken, PA, USA: ASTM International, 2013
|
| [26] |
BERRY J. Determination of fracture surface energies by the cleavage technique[J]. Journal of Applied Physics, 1963, 34(1): 62. DOI:10.1063/1.1729091 |
| [27] |
贾艳波. 增材制造碳纤维复合材料层间损伤失效试验研究与数值分析[D]. 西安: 长安大学, 2020 JIA Yanbo. Experimental study and numerical analysis of interlaminar damage failure of additively manufactured carbon fiber reinforced composites[D]. Xi'an: Chang'an University, 2020 |
| [28] |
BORG R, NILSSON L, SIMONSSON K. Modeling of delamination using a discretized cohesive zone and damage formulation[J]. Composites Science and Technology, 2002, 62(10): 1299. DOI:10.1016/S0266-3538(2)00070-2 |
| [29] |
WISNOM M, CHANG F. Modelling of splitting and delamination in notched cross-ply laminates[J]. Composites Science and Technology, 2000, 60(15): 2849. DOI:10.1016/S0266-3538(00)00170-6 |
| [30] |
HARPER P W, SUN L, HALLETT S R. A study on the influence of cohesive zone interface element strength parameters on mixed mode behavior[J]. Composites Part A: Applied Science and Manufacturing, 2012, 43(4): 722. DOI:10.1016/j.compositesa.2011.12.016 |
| [31] |
尹世豪, 张建宇, 龚愉, 等. 新型三线性本构内聚力模型的界面参数研究[J]. 重庆大学学报, 2020, 43(2): 91. YIN Shihao, ZHANG Jianyu, GONG Yu, et al. Studies on the critical interfacial parameters in a novel three-linear cohesive zone model[J]. Journal of Chongqing University, 2020, 43(2): 91. DOI:10.11835/j.issn.1000-582X.2019.253 |
 2024, Vol. 56
2024, Vol. 56