直升机因其独特的悬停能力,在抢险救灾、海上救援、森林防火等任务中能起到不可替代的作用。直升机执行此类任务时,常常需要驾驶员快速操纵,规避地面障碍,保证飞行安全。随着直升机设计与制造技术的不断进步,人们对直升机机动飞行提出了更高的要求。为更精确地模拟直升机机动飞行过程,需要放弃旋翼转速恒定的假设,分析旋翼转速的动态变化对直升机机动飞行的影响[1-2]。为此需要建立能够考虑发动机动态特性影响的直升机飞行动力学模型。
在直升机飞行动力学研究早期,由于发动机本身的复杂性与特殊性,加之研究人员对发动机的特性了解有限,在建模与分析中通常忽略发动机或使用简化的发动机模型。而发动机建模与控制设计中,也会对直升机模块进行简化[3-6]。随着直升机技术的进步和飞行要求的提高,继续使用孤立模型,忽略直升机与发动机之间耦合特性的建模方法已经不能满足人们的需要。为此,人们开始建立直升机/发动机耦合模型。Mihaloew等[7]为研究直升机与发动机之间的共振问题与动稳定性问题,建立了直升机/发动机耦合模型。Liu等[8]将旋翼模型与发动机模型高度简化,同时忽略旋翼与机身之间的耦合关系,使用该简化模型研究旋翼与发动机之间的耦合关系对发动机输出转速的影响。Misté等[9-10]使用GENHEL模型研究发动机动力涡轮转速变化对旋翼性能的影响。国内的相关研究起步稍晚一些,曾庆福等[11]研究旋翼状态变化对发动机燃油流量的影响,并对旋翼/发动机耦合模型动态响应结果进行计算。姚文荣等[12]构建了包含直升机功率计算模块的发动机模型,对发动机控制系统进行优化设计,张海波等[13]在此基础上使用旋翼转速变化率对发动机燃油流量进行优化控制,降低了发动机输出滞后引起的旋翼转速波动。严旭飞等[14]分析了变转速直升机单发失效下的飞行性能。韩东等[15-16]对变转速旋翼与变体旋翼进行研究,给出以最小油量消耗为目标的旋翼转速变化曲线。汪勇等[17-18]通过建立直升机/发动机耦合模型,在优化转速过程中考虑了发动机特性的影响。杨庶[19]使用直升机/发动机耦合模型设计控制律,实现直升机的高度,姿态控制与动力涡轮转速边界保护功能。上述研究针对各自研究情景下的直升机与发动机之间的耦合关系,使用一定程度的简化模型,达到了比较好的计算效果。但这些研究都没有考虑机动飞行过程中发动机动态特性对旋翼转速与偏航方向扭矩的影响,不能直接用于分析直升机机动飞行响应结果。
基于上述研究结果,为研究机动飞行过程中旋翼/发动机耦合特性的影响,建立了一种直升机/发动机耦合模型。首先,建立旋翼飞行动力学模型和发动机部件级气动热力学模型。在此基础上,依照功率匹配关系,建立直升机/发动机综合分析模型。根据UH-60A直升机飞行试验数据,验证直升机模型的配平和动态响应计算结果。最后,对直升机垂直隐蔽(bob up and remask)机动飞行进行仿真计算。研究结果表明,有助于加深对现有直升机与发动机耦合关系的认识,对直升机/发动机综合控制系统的设计具有指导意义。
1 直升机飞行动力学模型的建立 1.1 旋翼分段法模型的建立旋翼是直升机上最重要的部件,同时起到升力面、操纵面和推进器的作用,旋翼内部存在复杂的耦合关系[5]。为研究直升机机动飞行,首先需要建立准确的旋翼模型。使用功率计算模型等简化旋翼模型不能准确描述转速变化后的旋翼动态响应,因为旋翼转速变化后,桨叶微段的气动力,惯性力均会随之改变,引起桨叶运动与诱导速度变化, 因此采用叶素理论建立旋翼模型,诱导速度使用Pitt-Peters动态入流模型计算。采用刚性桨叶假设,桨叶弹性变形根据经验公式计算得到[20]:
| $ \theta_{\mathrm{D}}=\theta_{\mathrm{DYN}}\left\{0.28+0.72 \sin \left[90\left(y_2+\xi\right)\right]\right\} $ | (1) |
式中:θDYN为弹性扭转系数,y2为量纲一的桨叶微段位置,ξ为量纲一的挥舞铰位置。
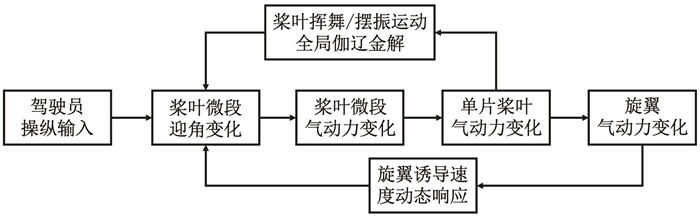
旋翼非定常气动力计算流程见图 1。首先根据操纵输入与初值输入计算桨叶微段气动力,求和得到桨叶气动力,计算旋翼挥舞,摆振运动[21]。然后求解旋翼气动力,根据动态入流公式求解桨盘平面诱导速度分布。旋翼气动力计算中存在桨叶运动与诱导速度两个迭代计算过程。当两个迭代过程结束,旋翼达到稳定状态后,得到旋翼非定常气动力。
|
图 1 旋翼非定常气动力计算流程 Fig. 1 Flow chart of rotor unsteady aerodynamic force |
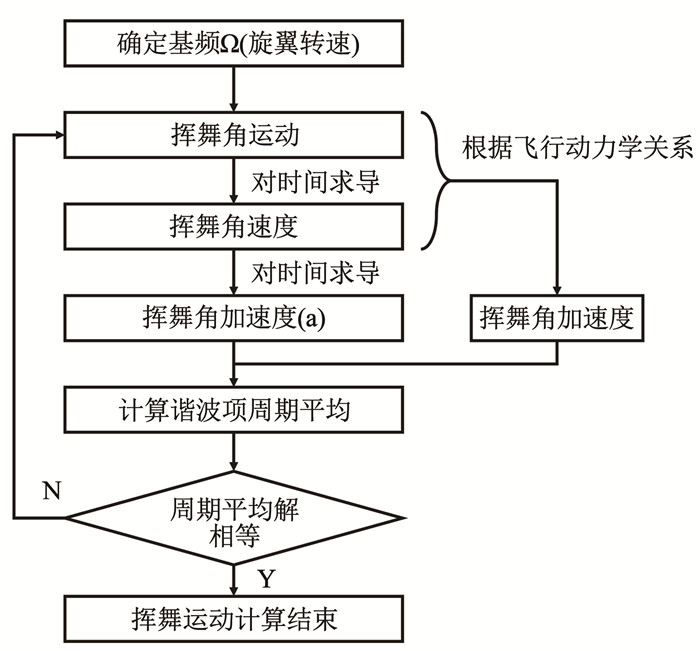
桨叶的挥舞,摆振运动使用全局伽辽金法求解[21]。全局伽辽金法即谐波平衡法(Harmonic-Balance method, HB),假定外激励频率是基频的整数倍,将运动项与激励项展开成傅里叶级数,求解对应的系数方程。挥舞运动的全局伽辽金法求解过程见图 2。
|
图 2 全局伽辽金法计算流程 Fig. 2 Flow chart of global Galerkin method |
以挥舞运动计算过程为例说明全局伽辽金法计算流程。首先以旋翼转速作为基频,将挥舞运动进行傅里叶展开,得到各片桨叶的挥舞角随方位角变化的公式。将方位角对时间求导得到桨叶挥舞角速度与挥舞角加速度。同时,将计算得到的挥舞角度与挥舞角速度代入旋翼模型,根据飞行动力学关系计算挥舞角加速度。全局伽辽金法假设,两种方法计算得到的挥舞加速度对整个桨盘积分结果相等时,旋翼挥舞运动达到稳定状态。旋翼挥舞运动的全局伽辽金法计算公式如下:
| $ \left\{\begin{array}{l} \int\left(\ddot{\beta}-\ddot{\beta}_a\right) \mathrm{d} \psi=0 \\ \int\left(\ddot{\beta}-\ddot{\beta}_a\right) \cos k \psi \mathrm{~d} \psi=0 \\ \int\left(\ddot{\beta}-\ddot{\beta}_a\right) \sin k \psi \mathrm{~d} \psi=0 \end{array}\right. $ | (2) |
与桨叶任意运动法相比,全局伽辽金法消除桨叶初始方位角的影响,易于编程计算。全局伽辽金法计算挥舞运动时,常系数与一阶谐波系数恰好等于桨盘平面假设中使用的挥舞锥度角、后倒角、侧倒角。但是挥舞运动的高阶项和摆振运动的系数没有具体物理意义。摆振计算方法与挥舞运动类似,此处不再赘述。
使用全局伽辽金法计算桨叶运动时,假设外激励为傅里叶级数将会引入截断误差。该误差对配平计算影响不大,但会影响动态响应计算结果,因此需要使用直接打靶法[21]计算旋翼模型桨叶运动的精确解。
直接打靶法计算结果用两点非线性边界值确定:状态量xrotor(0)=xrotor(2nπ),其中n为转动圈数。xrotor=[β1, β2, β3, β4, ζ1, ζ2, ζ3, ζ4, vi0, vis, vic]分别为各片桨叶的挥舞角、摆振角与旋翼动态入流的3个分量。使用直接打靶法消除了全局伽辽金法引入的截断误差,计算结果可以直接作为动态响应计算的初值。
1.2 发动机部件级气动热力学模型的建立过去直升机建模中,往往使用简化模型代替涡轴发动机。因为在稳定工作状态下,涡轴发动机动力涡轮输出转速恒定,发动机与直升机可以视为是解耦的。然而在机动飞行过程中,直升机飞行状态快速改变引起发动机负载快速变化,导致旋翼转速波动。使用简化发动机模型无法准确描述发动机输出变化的动态过程,因此,需要建立能反映负载与燃油流量快速变化影响的发动机动态模型。
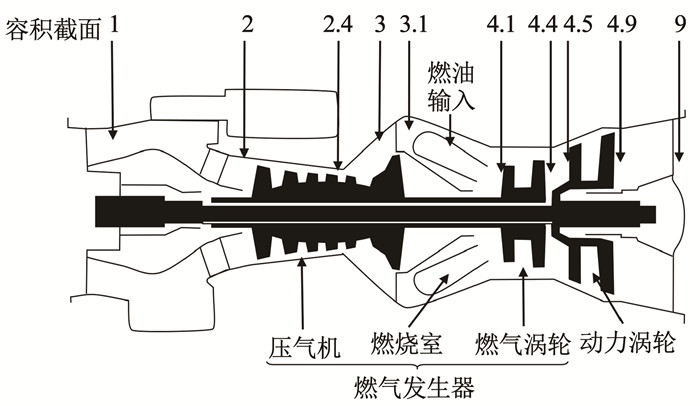
根据容积动力学、传热动力学与转子动力学关系,建立涡轴发动机部件级气动热力学模型[22]。发动机建模中假设气流一维流动,燃烧室是绝热的,忽略部件热惯性,雷诺数和大气湿度的影响。本文使用的样例发动机,GE-T700型涡轴发动机见图 3。图 3中数字编号表示涡轴发动机内部容积截面(其中:1为进气道,2为压气机,2.4为压气机冷却放气,3为压气机出口,3.1为燃烧室入口。4.1为燃气涡轮入口,4.4为燃气涡轮出口,4.5为动力涡轮入口,4.9为动力涡轮出口,9为排气管出口)。在两级涡轴发动机中,提供高温,高压气体的压气机,燃烧室与燃气涡轮的组合被称为燃气发生器。
|
图 3 GE-T700型涡轴发动机示意 Fig. 3 Schematic of GE-T700 turboshaft engine |
根据发动机内部部件与工作截面的气动热力学关系与转子动力学关系,得到涡轴发动机共同工作方程:
| $ \left\{\begin{array}{l} p_3=K_{\mathrm{V} 3} \int T_3\left(W_{\mathrm{A} 3}-W_{\mathrm{A} 3 \mathrm{~bl} }-W_{\mathrm{A} 31}\right) \mathrm{d} t \\ p_{41}=K_{\mathrm{V} 41} \int T_{41}\left(W_{\mathrm{A} 31}-W_{\mathrm{f}}-W_{41}\right) \mathrm{d} t \\ p_{45}=K_{\mathrm{V} 45} \int T_{45}\left(W_{41}-W_{45}+B_3 K_{\mathrm{bl} } W_{\mathrm{A} 2}\right) \mathrm{d} t \\ N_{\mathrm{G}}=\frac{60}{2 {\rm{ \mathsf{ π} }}} \int \frac{Q_{\mathrm{GT}}-Q_{\mathrm{C}}}{J_{\mathrm{GT}}} \mathrm{~d} t \\ N_{\mathrm{P}}=\frac{60}{2 {\rm{ \mathsf{ π} }}} \int \frac{Q_{\mathrm{PT}}-Q_{\mathrm{req}}}{J} \mathrm{~d} t \end{array}\right. $ | (3) |
式中:p为压强,T为温度,W为燃气流量,WA为空气流量,Wf为燃油流量,KV为容积系数,Kbl为放气系数,N为转速(其中:下标G为燃气发生器,燃气发生器包括发动机高速轴上的部件:压气机,燃气涡轮与两者之间的燃烧室;下标P为动力涡轮)。Q为扭矩(其中:下标C、GT、PT、req分别为压气机需用扭矩、燃气涡轮输出扭矩、动力涡轮输出扭矩与直升机需用扭矩),J为转动惯量。发动机模型主要参数见表 1[22]。
| 表 1 发动机参数 Tab. 1 Engine parameters |
为研究直升机/发动机耦合引起的转速变化动态过程,需建立发动机燃油调节系统。发动机燃油流量控制系统使用比例-积分-微分(proportional integral derivative,PID)控制器与总距信号输入共同组成。发动机燃油流量控制系统计算公式如下:
| $ W_{\mathrm{f}}=K_\theta \theta_{\mathrm{c}}+K_{\mathrm{P}} \Delta N_{\mathrm{P}}+K_{\mathrm{I}} \int \Delta N_{\mathrm{P}}+K_{\mathrm{D}} \Delta \dot{N}_{\mathrm{P}} $ | (4) |
式中: Kθ为旋翼总距前馈系数,KP为控制器比例系数,KI为积分系数,KD为微分系数, ΔNP为发动机动力涡轮实际转速与目标转速之间的误差,Wf为燃油流量。
为研究直升机与发动机之间的耦合关系,首先根据发动机动力涡轮输出轴上的扭矩平衡关系,建立旋翼/发动机耦合模型,分析旋翼转速动态变化过程。使用定传动比减速器,根据设计传动比计算旋翼和尾桨的转速,具体计算过程如下:
| $ \left\{\begin{aligned} Q_{\mathrm{PT}}= & 778.12 \cdot \frac{60}{2 {\rm{ \mathsf{ π} }}} \cdot \frac{1}{N_{\mathrm{G}}} W_{45} \Delta H_{\mathrm{PT}}- \\ & K_{\text {damp }} \cdot \frac{2 {\rm{ \mathsf{ π} }}}{60} \cdot\left(N_{\mathrm{P}}-N_{\mathrm{Pdes}}\right) \\ N_{\mathrm{P}}= & \frac{60}{2 {\rm{ \mathsf{ π} }}} \int \frac{Q_{\mathrm{PT}}-Q_{\mathrm{req}}}{J} \mathrm{~d} t \end{aligned}\right. $ | (5) |
式中:ΔHPT为动力涡轮焓变化量,Kdamp为动力涡轮转速阻尼系数,NPdes为动力涡轮设计转速,动力涡轮轴上的转动惯量J由3部分组成:动力涡轮转动惯量、传动系统转动惯量以及旋翼和尾桨的等效转动惯量。
1.3 直升机飞行动力学模型的建立为分析直升机机动飞行动态过程,需要建立准确的直升机模型。使用UH-60A直升机作为样例直升机,以现有的GENHEL模型[20]为基础建立直升机飞行力学模型。其中,直升机尾桨使用桨盘积分法建模,代替GENHEL中使用的Bailey简化模型,使用均匀入流模型计算尾桨诱导速度。机身、垂尾和平尾的气动力(矩)使用风洞试验数据插值计算得到。根据前飞速度确定平尾安装角。使用单向耦合方法计算直升机部件间的气动干扰,仅考虑旋翼对其他部件的气动干扰。
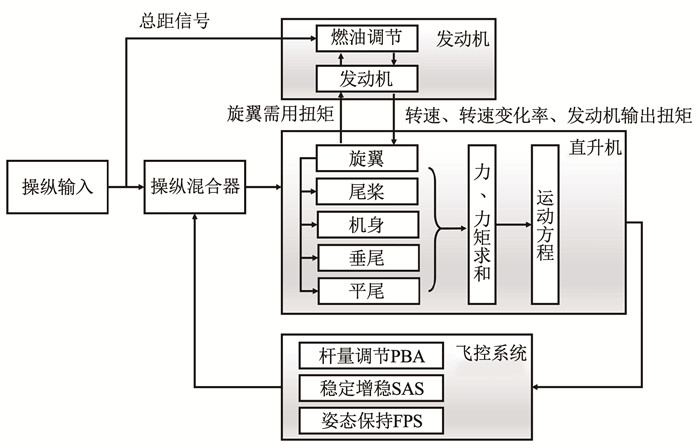
旋翼/发动机之间存在复杂的双向耦合关系,这表现在直升机需用功率改变后,发动机动态特性决定旋翼转速的动态变化,旋翼转速改变会引起旋翼拉力与反扭矩的变化,又会改变旋翼的需用功率。同时,旋翼与直升机其他部件之间也存在复杂的耦合关系。本文建立的直升机模型见图 4。
|
图 4 直升机飞行动力学模型示意 Fig. 4 Schematic of helicopter aerodynamic model |
直升机飞行动力学模型是一种强耦合的非线性动力系统。将旋翼挥舞、摆振方程与诱导速度方程与直升机自身状态变量共同求解,得到直升机飞行动力学方程组。该方程组可以写成一阶微分方程组的形式:
| $ \dot{\boldsymbol{x}}=f(\boldsymbol{x}, \boldsymbol{u}, t) $ | (6) |
式中:x=[xrotor, xheli, xeng]为状态量(其中:xrotor为旋翼状态量,xheli=[u, v, w, p, q, r, φ, θ, ψ]为直升机状态量(其中:u, v, w为直升机线速度,p, q, r为直升机角速度,φ, θ, ψ为直升机欧拉角), xeng=[Ng, P3, P41, P45]为发动机状态量),u=[δ0, δ1c, δ1s, δt, NPset]为控制量(其中:δ0为驾驶员总距杆量,δ1c为横向周期变距,δ1s为纵向周期变距,δt为脚蹬操纵量,NPset为动力涡轮目标转速),t为时间。
直升机/发动机耦合模型配平与动态响应计算流程见图 5。由于发动机内部热力学过程与直升机飞行动力学相比,可以认为是瞬时发生的,因此,在直升机/发动机耦合模型配平计算时,可以假设旋翼转速恒定,对直升机与发动机模块分别进行配平。使用c++编写计算程序,实现直升机/发动机耦合模型配平计算。根据直升机配平结果得到的需用扭矩和发动机输出转速,然后计算发动机的状态量。使用c++程序编译的matlab可执行文件(mex文件),通过S-function模块在matlab/simulink环境下构建直升机/发动机耦合模型与飞行控制系统。使用配平值作为响应计算初值输入,计算直升机/发动机耦合模型的动态响应。

|
图 5 直升机/发动机耦合模型计算流程 Fig. 5 Flow chart of helicopter/engine coupling model calculation |
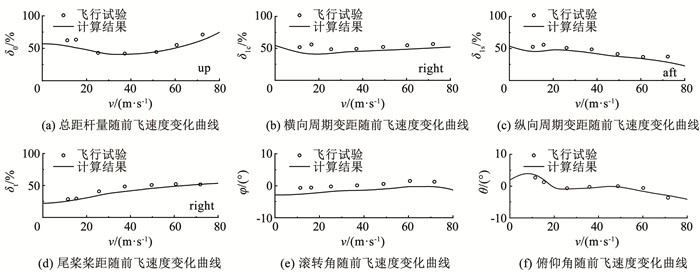
使用UH-60直升机作为样例直升机,直升机质量7 257.0 kg,密度高度1 600.0 m,重心位置坐标(8.92, 0, 5.88) m,旋翼转速27 rad/s。直升机模型配平计算结果与AEFA(USA army aviation engineering flight activity)飞行试验结果[22]的对比见图 6。模型计算结果与飞行试验结果之间的误差均在13%以内,最大误差出现在15 m/s前飞状态,这表明本文建立的直升机模型是准确的。
|
图 6 直升机配平计算结果 Fig. 6 Helicopter trim result |
根据涡轴发动机台架试验结果对发动机模型计算结果进行验证。发动机需用扭矩输入分别为122.2,201.1,280.0 N·m。模型共同工作方程组计算结果与试验结果[23]对比如图 7所示,计算结果与试验结果误差在13%以内,表明本文建立的发动机模型是准确的。

|
图 7 发动机模型稳态共同工作方程计算结果 Fig. 7 Engine's steady-state common working equation result |
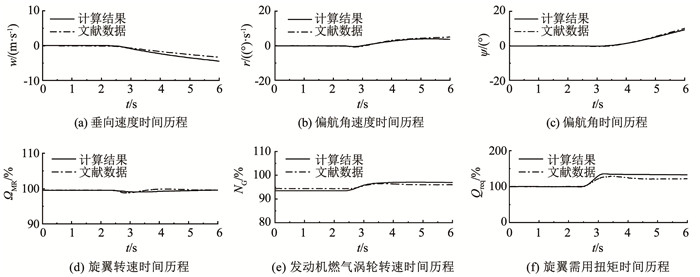
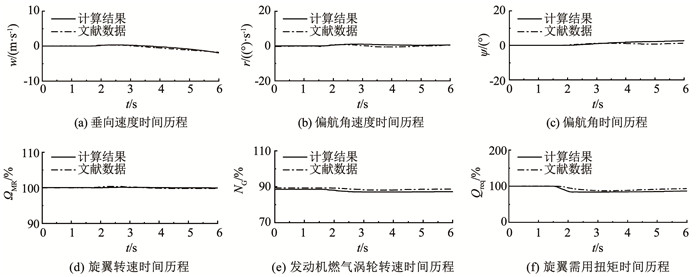
本文选取UH-60A直升机作为样例直升机。计算样例直升机悬停和前飞状态给定操纵下的直升机与发动机的耦合模型动态响应计算结果,并与AEFA飞行试验结果[22]进行比较。悬停总距阶跃操纵输入下的动态响应计算结果见图 8。此时直升机质量为7 271.21 kg,重心位置(9.13, 0, 5.91) m,飞行密度高度为1 649.27 m,旋翼额定转速26.87 rad/s,总距杆向上升2.54 cm。60节(30.87 m/s)前飞总距阶跃操纵输入下的动态响应计算结果见图 9。此时直升机质量为7 130.59 kg,重心位置(8.93, 0, 5.89) m,密度高度1 680.97 m,旋翼额定转速26.90 rad/s,总距杆向下降1.27 cm。
|
图 8 悬停状态下直升机发动机耦合模型动态响应 Fig. 8 Dynamic response of helicopter-engine coupling model in hovering state |
|
图 9 前飞状态下直升机发动机耦合模型动态响应 Fig. 9 Dynamic response of helicopter-engine coupling model in forward flight state |
根据图 8、9中的悬停,30.87 m/s前飞的直升机发动机耦合模型动态响应计算结果与飞行试验结果对比可知,本文建立的直升机发动机耦合模型的直升机线速度,角速度与姿态角的动态响应计算结果与飞行试验结果吻合较好,发动机内部燃气涡轮转速与动力涡轮转速变化趋势与实际飞行一致,旋翼需用扭矩计算存在误差,误差小于10%。综上所述,可以认为本文建立的直升机发动机耦合模型是准确的,能够用于直升机机动飞行特性与动态响应的分析。
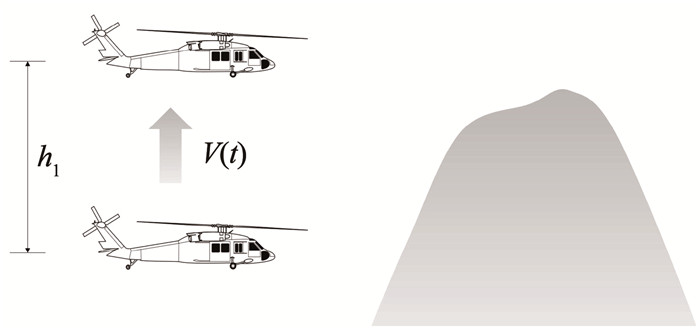
3 直升机机动飞行直升机因其独特的悬停和低速飞行特性,常常需要执行贴地飞行(nap of the earth, NOE)任务。在众多NOE机动中,悬停状态下的垂直跃升(bob-up)机动飞行任务(图 10)最能体现直升机与发动机之间耦合特性的影响。当直升机执行垂直跃升机动飞行任务时,驾驶员需要快速拉动总距杆。此时直升机旋翼扭矩变化非常剧烈,发动机输出滞后会造成旋翼转速明显变化,对直升机机动飞行造成不利影响。
|
图 10 直升机垂直跃升机动飞行任务示意 Fig. 10 Schematic of helicopter bob-up maneuver flight |
悬停状态下,驾驶员快速操纵总距杆,引起旋翼拉力快速变化,改变直升机垂向位置,完成垂直跃升机动飞行。样例直升机质量7 546.87 kg,重心位置坐标为(9.13, 0, 5.91) m,飞行密度高度为0 m,旋翼额定转速27.00 rad/s。直升机/发动机耦合模型垂直隐蔽科目计算结果与AACT(U.S Army air-to-air combat test)飞行试验结果[24]对比结果见图 11。

|
图 11 直升机垂直跃升动态响应计算结果 Fig. 11 Results of helicopter bob-up maneuver dynamic response |
垂直跃升开始阶段,驾驶员增加总距杆量,旋翼需用功率迅速增加,发动机输出滞后引起旋翼转速降低。同时,作用在旋翼轴的扭矩与尾桨反扭矩相比也存在滞后,引起直升机偏航方向的运动,造成总距-偏航不良耦合。随着驾驶员降低总距杆量,旋翼需用功率降低,发动机输出功率大于旋翼需用功率,引起旋翼转速增加。随着仿真时间的增加,直升机模型计算结果与飞行试验结果间的误差逐渐增加,图 11(d)中,偏航角响应结果在7 s后误差逐渐增大,在12 s时误差达到最大值3.37 °。模型误差主要来自以下几个方面:一是发动机建模假设引起的误差,二是仿真过程中的数值积分引起的数值误差。
从图 11(d)旋翼转速的动态响应结果可以发现,在对称的总距操纵输入下,直升机旋翼转速的变化趋势并不对称,这是由于发动机在加速与减速的动态过程特性不同所引起的。使用简化发动机模型不能反映发动机动态特性的变化,因此无法对垂直跃升任务进行准确模拟。在飞行过程中,发动机输出滞后会引起旋翼转速快速变化,改变旋翼拉力,同时引起偏航方向耦合运动,对直升机执行垂直隐蔽飞行任务造成不利影响。
4 结论本文建立一种耦合了发动机气动热力学特性的直升机飞行动力学模型,并使用飞行试验结果验证了耦合模型的准确性。在此基础上,对垂直隐蔽机动科目进行仿真计算。结果表明:
1) 使用全局伽辽金法与直接打靶法结合的方法计算桨叶运动,消除了全局伽辽金法配平计算引入的截断误差,旋翼配平计算结果可以直接用于响应计算。
2) 总距操纵信号快速变化时,发动机输出滞后引起旋翼转速改变,对直升机机动飞行过程造成不利影响。同时,发动机动态特性会引起直升机偏航轴方向不利的耦合运动,影响直升机机动科目的执行。
3) 总距信号增加与减小时,旋翼转速的变化过程是不对称的,因此,在对直升机机动飞行,尤其是以总距杆量快速变化的机动动作进行仿真计算时,不能忽略发动机动态特性的影响。直升机/发动机耦合模型将发动机动态特性纳入直升机飞行动力学模型中,考虑发动机输出引起的旋翼转速与偏航扭矩变化,对以垂直跃升机动为代表的机动飞行过程进行较为准确的仿真计算。
| [1] |
CHEN Renliang, YUAN Ye, THOMSON D. A review of mathematical modelling techniques for advanced rotorcraft configurations[J]. Progress in Aerospace Sciences, 2021, 120: 100681. DOI:10.1016/j.paerosci.2020.100681 |
| [2] |
陈仁良, 李攀, 吴伟, 等. 直升机飞行动力学数学建模问题[J]. 航空学报, 2017, 38(7): 520915. CHEN Renliang, LI Pan, WU Wei, et al. A review of mathematical modeling of helicopter flight dynamics[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 520915. DOI:10.7527/S1000-6893.2017.520915 |
| [3] |
HOUCK J A, MOORE F L, HOWLETT J J, et al. Rotor systems research aircraft simulation mathematical model: NASA-TM-78629 [R]. Hampton: NASA, 1977
|
| [4] |
陆陶冶, 陈仁良, 吉洪蕾, 等. 共轴双旋翼悬停地面效应分析[J]. 哈尔滨工业大学学报, 2017, 49(10): 45. LU Taoye, CHEN Renliang, JI Honglei, et al. Performance analysis of coaxial-rotorfor hovering in ground effect[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 45. DOI:10.11918/j.issn.0367-6234.201607105 |
| [5] |
王军杰, 陈仁良, 王志瑾, 等. 倾转旋翼机涡环状态数值模拟及数学建模[J]. 哈尔滨工业大学学报, 2023, 55(4): 35. WANG Junjie, CHEN Renliang, WANG Zhijin, et al. Numerical simulation and mathematical modeling of vortex ring state of Tiltrotor aircraft[J]. Journal of Harbin Institute of Technology, 2023, 55(4): 35. DOI:10.11918/202203036 |
| [6] |
严旭飞, 陈仁良. 倾转旋翼机短距起飞单发失效着陆的轨迹优化[J]. 哈尔滨工业大学学报, 2017, 49(10): 38. YAN Xufei, CHEN Renliang. Trajectory optimization of tilt-rotor aircraft landing in short takeoff after one engine failure[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 38. DOI:10.11918/j.issn.0367-6234.201604113 |
| [7] |
MIHALOEW J R, BALLIN M G, RUTTLEDGE D C G. Rotorcraft flight-propulsion control integration: an eclectic design concept: NASA-TP-2815[R]. Hampton: NASA, 1988
|
| [8] |
LIU Ketao, MITTAL M, PRASAD J V R, et al. A study of coupled engine/rotor dynamic behavior[C]//51st Annual of the American Helicopter Society. Fort Worth, Texas: American Helicopter Society, Inc., 1995, 51: 1335
|
| [9] |
MISTÉ G A, BENINI E. Performance of a turboshaft engine for helicopter applications operating at variable shaft speed[C]//ASME 2012 Gas Turbine India Conference. Mumbai: ASME, 2013: 701. DOI: 10.1115/GTINDIA2012-9505
|
| [10] |
MISTÉ G A, BENINI E, GARAVELLO A, et al. A methodology for determining the optimal rotational speed of a variable RPM main rotor/turboshaft engine system[J]. Journal of the American Helicopter Society, 2015, 60(3): 1. DOI:10.4050/jahs.60.032009 |
| [11] |
曾庆福, 谢光华, 李挺. 直升机旋翼/发动机一体化仿真模型[J]. 航空学报, 1997, 18(5): 563. ZENG Qingfu, XIE Guanghua, LI Ting. Integrated simulation model of a helicopter rotor/engine system[J]. Acta Aeronautica et Astronautica Sinica, 1997, 18(5): 563. |
| [12] |
姚文荣, 孙健国. 基于变旋翼转速的涡轴发动机优化控制[J]. 航空动力学报, 2007, 22(9): 1573. YAO Wenrong, SUN Jianguo. Optimizing control of turboshaft engines based on variable rotor speed[J]. Journal of Aerospace Power, 2007, 22(9): 1573. DOI:10.3969/j.issn.1000-8055.2007.09.030 |
| [13] |
张海波, 孙立国, 孙健国. 直升机/涡轴发动机综合系统鲁棒抗扰控制设计[J]. 航空学报, 2010, 31(5): 883. ZHANG Haibo, SUN Liguo, SUN Jianguo. Robust disturbance rejection control design for integrated helicopter system/turbo-shaft engine[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 883. |
| [14] |
严旭飞, 池骋, 陈仁良, 等. 变转速旋翼直升机单发失效低速回避区分析[J]. 航空学报, 2018, 39(10): 84. YAN Xufei, CHI Cheng, CHEN Renliang. Analysis of low speed height velocity diagram of variable speed rotor helicopter in one engine inoperative situation[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(10): 84. DOI:10.7527/S10006893.2018.22107 |
| [15] |
韩东. 变转速旋翼直升机性能及配平研究[J]. 航空学报, 2013, 34(6): 1241. HAN Dong. Study on the performance and trim of helicopters with variable speed rotors[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1241. DOI:10.7527/S1000-6893.2013.0228 |
| [16] |
韩东, 林长亮, 李建波. 旋翼变体技术对直升机性能的提升[J]. 航空动力学报, 2014, 29(9): 2017. HAN Dong, LIN Changliang, LI Jianbo. Helicopter performance improvement by rotor morphing technologies[J]. Journal of Aerospace Power, 2014, 29(9): 2017. DOI:10.13224/j.cnki.jasp.2014.09.001 |
| [17] |
汪勇, 刘明磊, 宋劼, 等. 一种直升机/发动机系统最经济旋翼转速综合优化方法[J]. 推进技术, 2022, 43(1): 64. WANG Yong, LIU Minglei, SONG Jie, et al. Integrated optimization method of the most economical rotor speed for helicopter/engine system[J]. Journal of Propulsion Technology, 2022, 43(1): 64. DOI:10.13675/j.cnki.tjjs.200451 |
| [18] |
WANG Yong, SONG Jie, ZHONG Wencheng, et al. Rotational speed optimization of coaxial compound helicopter and turboshaft engine system[J]. Journal of Aerospace Engineering, 2023, 36(5): 4023042. DOI:10.1061/jaeeez.aseng-4546 |
| [19] |
杨庶. 具有边界保护性能的直升机飞-发一体化控制律[J]. 航空学报, 2023, 44(增刊1): 77. YANG Shu. Helicopter integrated flight-engine control with envelope protections[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(Sup.1): 77. DOI:10.7527/S1000-6893.2022.27560 |
| [20] |
HOWLETT J J. UH-60A black hawk engineering simulation program volume. Ⅰ: mathematical model: NASA-CR-166309[R]. Hampton: NASA, 1981
|
| [21] |
KIM F D, CELI R, TISCHLER M B. Forward flight trim and frequency response validation of a helicopter simulation model[J]. Journal of Aircraft, 1993, 30(6): 854. DOI:10.2514/3.46427 |
| [22] |
BALLIN M G. Validation of a real-time engineering simulation of the UH-60A helicopter: NASA-TM-88360, [R]. Hampton: NASA, 1987
|
| [23] |
BALLIN M G. A high fidelity real-time simulation of a small turboshaft engine: NASA-TM-100991[R]. Hampton: NASA, 1988
|
| [24] |
RUTTLEDGE D G C. A rotorcraft flight/propulsion control integration study: NASA-CR-179574[R]. Hampton: NASA, 1986
|
 2024, Vol. 56
2024, Vol. 56


