2. 新疆大学 智能科学与技术学院(未来技术学院),乌鲁木齐 830017
2. School of Intelligence Science and Technology (School of Future Technology), Xinjiang University, Urumqi 830017, China
随着风电场群规模和装机容量不断扩大,风力发电对电网的安全运行越来越重要[1]。风速具有间歇性、波动性和随机性的特点[2],大规模的风电集成到电网中,对电网的安全稳定运行是极大的挑战[3],高效准确的风速预测可以为电网的运行和调度提供可靠的依据和保障[4]。常用的风速预测方法主要分为统计法、物理法和人工智能法,随着历史采样数据的积累和深度学习的发展,典型的深度学习网络框架也广泛地应用在风速预测领域。毕贵红等[5]采用双通道卷积神经网络(convolutional neural network, CNN)对风速特征进行提取。王岩等[6]通过结合互信息理论和循环神经网络(recurrent neural network,RNN)对短期风速进行预测。何锦华等[7]提出根据台风的Holland气压场模型和Batts梯度风模型,构建融合物理信息的神经网络,然后使用含时序模式注意力机制的长短期记忆神经网络(long short-term memory,LSTM)模型对风速进行训练和预测。随着Vaswani等[8]模型的提出,模型所具有的自注意力机制在风速数据特征提取方面取得了广泛的应用[9-10],学者针对Transformer预测提出了多种变体,例如卷积自注意力[11]、生成式解码器[12]、基于注意力的深度神经网络架构[13]、季节趋势分解架构[14]以及频率增强机制[15]、Non-stationary Transformer[16]等。
上述方法主要依赖于单一风电场的历史数据,没有考虑到风电场集群存在的空间相关性。针对风电场集群相关性问题多是从地理位置来分类,孙亦皓等[17]提出通过图卷积神经网络提取风速空间特征,并构造了一种从强度、时滞两个维度分别表征相关关系的复数邻接矩阵,充分挖掘相邻多风场之间的空间相关性。Yang等[18]提出分析风电场集群内每个风电场风速与参考风电场之间的灰度相关性划分为不同子集群,利用分形变换理论建立子集群的局部输出与风电场集群总体输出的放射关系,通过对相关度的最高子集群的预测来实现对风电场集群的风功率预测。潘超等[19]通过风电场的地理位置分布,构建了风速空间信息特征集,通过卷积神经网络模型进行空间特征提取,对整场风速进行预测。
上述方法多是对风电场群从地理角度进行分类,忽略其整体相关性。Friedman等[20]提出投影寻踪算法,由于投影寻踪算法可以满足高维非正态数据分析的需要,可以有效地找到样本数据间的内在联系,在工业[21]、农业[22]、经济[23]等多个领域得到了广泛的应用。投影寻踪算法可以有效地对高维数据进行分类,因此,针对高维风电场群风速数据,可以引入投影寻踪算法对其进行分类,有望实现更好的风速预测结果。
根据上述分析,现有文献对风电场的整体空间相关性的分析研究较少,同时由于风速数据波动特性复杂,会对风速预测的准确性造成影响。因此,本文引入投影寻踪算法实现风电场群风速的聚类,并提出NS-L-Transformer模型实现对风速的预测。
综上所述,本文首先对风速数据进行了预处理,通过信号分解和小波变换降低采集过程中噪声对数据的干扰;在此基础上,首次引入了粒子群- 投影寻踪聚类算法,通过分析风电场风速的波动特性对风电场群风速的相关性进行准确划分,并根据类内相关性,将相关风电场的风速作为目标风电场风机风速的特征量,构造了新的数据集;最后,针对新构造的风速数据集存在的短期局部波动特性,使用长短时记忆网络替换Non-stationary Transformer模型的编码器位置,构造了NS-L-Transformer模型,进一步加强了风速数据局部信息的提取能力,一定程度上提高了模型的预测精度。
1 数据预处理由于风速信号具有非平稳、波动性强等特点,对风速的评估工作的准确性有很大的影响,在预测前对数据进行预处理可以很大程度的提高预测的精度。
变分模态分解[24](variational mode decomposition, VMD)要求各模态的估计带宽之和最小,约束条件设定为所有模态之和与原始信号相等。在实际对信号进行分解时,由于样本采样不足及样条插值均会产生过分解现象。这些多余的分量称为伪分量,会使风速数据分析变得复杂,进而影响风速预测结果, 因此,本文提出对伪分量进行识别并剔除,提高VMD的信号降噪效果。通过计算各IMF(intrinsic mode function)分量与原始信号的相关系数来判别该IMF分量是否为伪分量,即
| $ Q=\frac{\sum\limits_{t=0}^n y(t) I_{\mathrm{MF}, i}(t)}{\sqrt{\sum\limits_{t=0}^n y^2(t) \sum\limits_{t=0}^n I_{\mathrm{MF}, i}^2(t)}} $ | (1) |
式中:y(t)为原始风速信号,IMF,i(t)为y(t)经过分解后得到的各IMF分量。
对分解得到的各分量进行去除伪处理,具体判断方法为:首先计算各IMF分量与原始信号的相关系数,本文选取最大相关系数的1/10作为判定阈值;然后,比较各IMF分量与原始信号的相关系数与阈值的大小,如果相关系数小于阈值,则认为该相关系数对应的IMF分量为伪分量。
由于外部环境和信号采集传输的影响,实际采集到的风速信号往往存在不同程度的噪声干扰,如何有效滤除噪声是风速预测中十分重要的环节。二十世纪八十年代,小波变换凭借其良好的时域局部化特性,完美解决了时序信号中局部有效信息与滤除噪声之间的矛盾,在信号降噪领域得到了广泛的应用。其中,Donoho等[25]提出的小波阈值法计算量较小且实现过程简单,是目前小波去噪领域最常使用的方法。具体实现步骤为:
Step1 选取合适的基小波以及分解层数,对风速信号f(n)进行多尺度小波分解,得到不同尺度下的小波分解系数。
Step2 确定一个合适的阈值,对各尺度下的小波分解系数进行阈值处理,得到阈值处理后的估计小波分解系数。
Step3 利用小波逆变换将估计小波系数进行信号重构,得到去噪后的风速信号。
小波降噪的阈值对去噪有着非常重要的影响,目前,常用的阈值确定规则有如下几种[26]:
1) VisuShrink阈值。VisuShrink阈值是一种固定阈值,可定义为
| $ \lambda_1=\sigma_n \sqrt{2 \ln N} $ | (2) |
式中:σn为标准噪声差,N为风速信号长度。
2) Rigrsure阈值。Rigrsure阈值是一种基于史坦无偏似然估计的自适应阈值,可定义为
| $ \lambda_2=\sigma_n \sqrt{\rho_\alpha} $ | (3) |
式中:σn为标准噪声差,pα为风险值。
3) HeurSure阈值。HeurSure阈值是一种启发式阈值,综合前两种阈值来确定最优变量阈值。设n个小波系数的平方和为e,η=(e-n)/n,
| $ \lambda_3= \begin{cases}\lambda_1, & \eta<\mu \\ \min \left(\lambda_1, \lambda_2\right), & \eta \geqslant \mu\end{cases} $ | (4) |
在实际计算中,多采用启发式阈值来进行小波变换。
在小波降噪中,常见的阈值函数有软阈值函数和硬阈值函数两种,本文通过软阈值函数对分解后的风速信号进行处理,软阈值函数表达式如下:
| $ \hat{z}= \begin{cases}\operatorname{sgn}(z)(|z|-\lambda), & |z| \geqslant \lambda \\ 0, & |z|<\lambda\end{cases} $ | (5) |
式中:
投影寻踪(projection pursuit, PP)算法于1974年首次由美国Stanford大学的Friedman和Tukey提出并命名为Projection Pursuit,用来分析和处理高维观测数据,通过将高维数据投影到低维子空间上,达到对原始高维数据分析和评价的目的。
设xij(i=1, 2, …, n; j=1, 2, …, m)为第i个风电场风速的第j个指标,n为风电场个数,m为风速指标个数。随机抽取若干初始投影方向a(a1, a2, …, am),投影寻踪就是将投影于 a得到其投影值z(i),即
| $ z_i=\sum\limits_{j=1}^m \boldsymbol{a}(j) x(i, j) $ | (6) |
按照局部集中、整体散开的原则,构造投影指标函数Q(a)为
| $ Q(a)=s(a) d(a) $ | (7) |
式中:s(a)为类间距离,d(a)为类内密度。
根据定义,投影指标函数Q(a)越大越好,本文通过粒子群算法[27-28](particle swarm optimization, PSO)对投影方向进行优化。利用种群规模为n粒子群在D维空间进行寻优,基于个体和种群历史的最优位置点进行迭代变化,原则如下:
| $ \begin{aligned} v_i(k+1)= & \omega \cdot v_i(k)+c_1 \cdot r \cdot\left(p_i-x_i(k)\right)+ \\ & c_2 \cdot r \cdot\left(p_g-x_i(k)\right) \end{aligned} $ | (8) |
| $ x_i(k+1)=x_i(k)+v_i(k) $ | (9) |
式中: pi为粒子的历史最优位置,pg为全局最优位置,c1、c2为学习因子,影响算法的收敛速度;r为随机数,在0~1之间。
本文通过PSO-PPC算法,对风电场群在空间所具有的相关性进行聚类划分,具体流程见图 1。

|
图 1 PSO-PPC算法流程 Fig. 1 Flowchart of PSO-PPC algorithm |
Non-stationary Transformer模型是针对非平稳时序问题的一个网络模型。
通过在Transformer模型结构上添加了包含序列平稳化模块和去平稳化注意力模块(见图 2)。通过序列平稳化模块,增强输入数据的平稳性,从而解决实际应用中风速信号过平稳的问题。
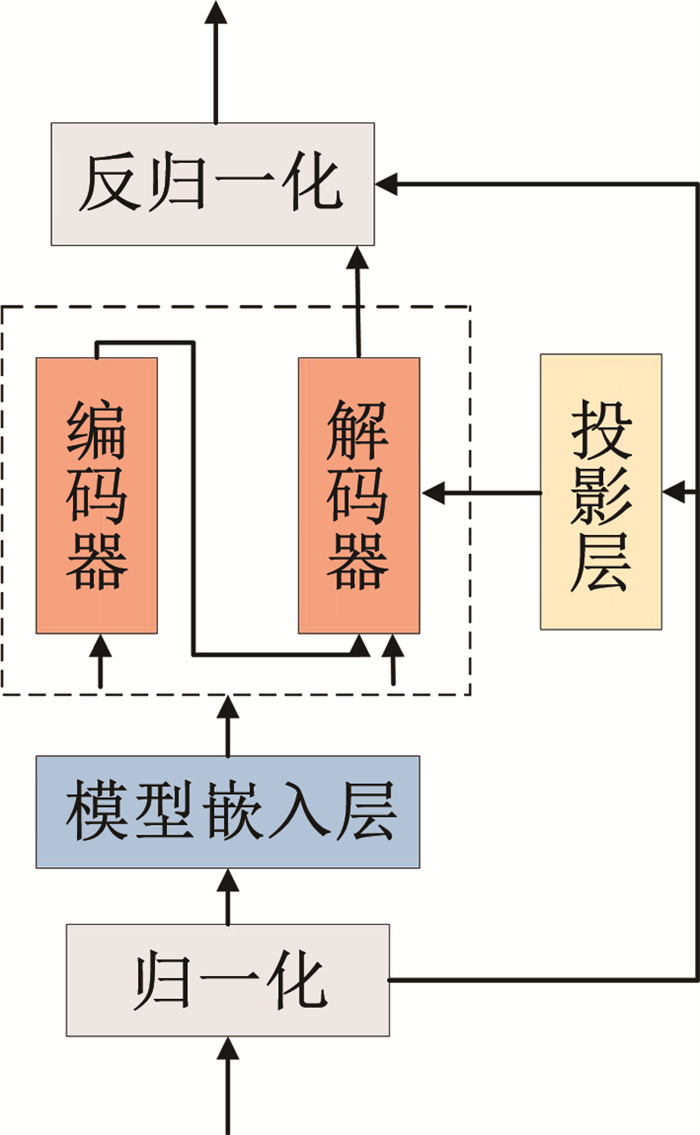
|
图 2 序列平稳框架 Fig. 2 Stationary sequence framework |
模型的平稳化包括窗口归一化和反归一化两个阶段,如式(10)、(11)所示,归一化作为一种平稳化技术,增强了数据的可预测性的同时对原本数据的分布造成了不可逆的退化,因此需要用归一化之前存储的各个窗口内序列原本的均值和方差重新对模型的输出进行反向尺度变换,恢复其归一化是丢失的分布信息。
| $ \mu_x=\frac{1}{S} \sum\limits_{i=1}^S x_i $ | (10) |
| $ \begin{aligned} \sigma_x^2 & =\frac{1}{S} \sum\limits_{i=1}^S\left(x_i-\mu_x\right)^2 \\ x_i^{\prime} & =\frac{1}{\sigma_x} \odot\left(x_i-\mu_x\right) \end{aligned} $ | (11) |
| $ \begin{aligned} & y^{\prime}=\boldsymbol{H}\left(x^{\prime}\right) \\ & \hat{y}_i=\sigma_x \odot\left(y_i^{\prime}+\mu_x\right) \end{aligned} $ | (12) |
式中:⊙为Hadamard乘积,μx为原始输入均值,
Transformer模型的自注意力机制和前馈网络层,可提高模型的计算训练,Non-stationary Transformer模型在Transformer模型的基础上添加了序列平稳化模块,可以提高非平稳时间序列的可预测性。但针对所构造的多维风速预测数据集,目标风电场的风速与类内风电场的风速存在着一定的类内相关性,LSTM模型可以更好地捕捉多维时序特征,因此,在基于传统Transformer的编码器-解码器结构中,本文提出使用LSTM编码器来替代Non-stationary Transformer的编码器位置。通过LSTM模块对经过平稳化处理后的多维风速序列进行编码,提取多维风速时间序列特征,使用Non-stationary Transformer的解码器生成输出序列,更好地提高模型提取数据局部位置信息的能力,模型结构见图 3。
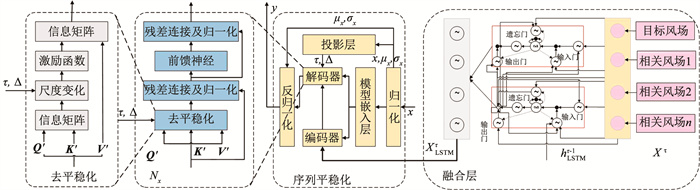
|
图 3 NS-L-Transformer模型结构框架 Fig. 3 Structurel framework of NS-L-Transformer model |
模型的去平稳化注意力模块主要是在模型内部,使用过归一化后的输入和归一化时存储的均值方差等量,根据Transformer的注意力机制,以及进行序列平稳化时,模型输入在时间维进行的尺度变换,基于模型嵌入层和前向传播层在时间维度的线性关系,导出注意力层的输入 Q, K,通过简化,可得到目标注意力,具体计算如下:
| $ \left\{\begin{array}{l} \operatorname{Attn}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Soft} \max \left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_{\boldsymbol{k}}}}\right) \boldsymbol{V} \\ \boldsymbol{Q}^{\prime}=\frac{\left(\boldsymbol{Q}^{-1} \mu_{\boldsymbol{Q}}^{\mathrm{T}}\right)}{\sigma_x} \\ \boldsymbol{K}^{\prime}=\frac{\left(\boldsymbol{K}^{-1} \mu_{\boldsymbol{K}}^{\mathrm{T}}\right)}{\sigma_x} \\ \operatorname{Soft} \max \left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_{\boldsymbol{k}}}}\right)=\operatorname{Soft} \max \left(\frac{\sigma_x^2 \boldsymbol{Q}^{\prime} \boldsymbol{K}^{\prime \mathrm{T}}+1\left(\mu_{\boldsymbol{Q}}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}}\right)}{\sqrt{d_{\boldsymbol{k}}}}\right) \end{array}\right. $ | (13) |
式中:Attn为原Transformer的注意力计算公式,Q、K、V分别为查询矩阵、索引矩阵和内容矩阵,Q′、K ′、V′分别为平稳化后的 Q、K、V,dk为基于K矩阵的维度。
Xτ表示经过分解降噪重构处理后的同一个分类里面各个风电场的风速,多特征数据首先经过LSTM层,通过LSTM模型的遗忘门和记忆单元机制,更好地捕捉发风速序列的时序特征。通过LSTM模型的门控单元,在多维数据中提取相关时序特征作为隐藏状态,用于存储和处理序列中的时序信息。
由于Transformer模型具有的自注意力机制,更关注当前预测量的关键特征通过学习目标风电场历史数据,结合同一分类风电场风速值来预测目标风速。
通过多头注意力并行操作,可以关注到序列中的不同位置,增加模型的捕捉不同范围依赖性的能力。LSTM编码器处理完输入序列后的输出。首先对数列进行归一化处理,通过LSTM编码器处理完输入序列后,接着通过两个卷积层和Dropout层后,送入解码器。通过Non-stationary Transformer的解码器部分的多头注意力并行操作,可以关注到序列中的不同位置,增加模型的捕捉不同范围依赖性的能力,从而实现较为准确的风速预测。
4 风电场群风速预测模型 4.1 预测流程基于以上所述原理,针对风电场群风速预测,本文提出一种基于PSO-PPC和NS-L-Transformer模型的预测路线,具体流程如下(见图 4)。
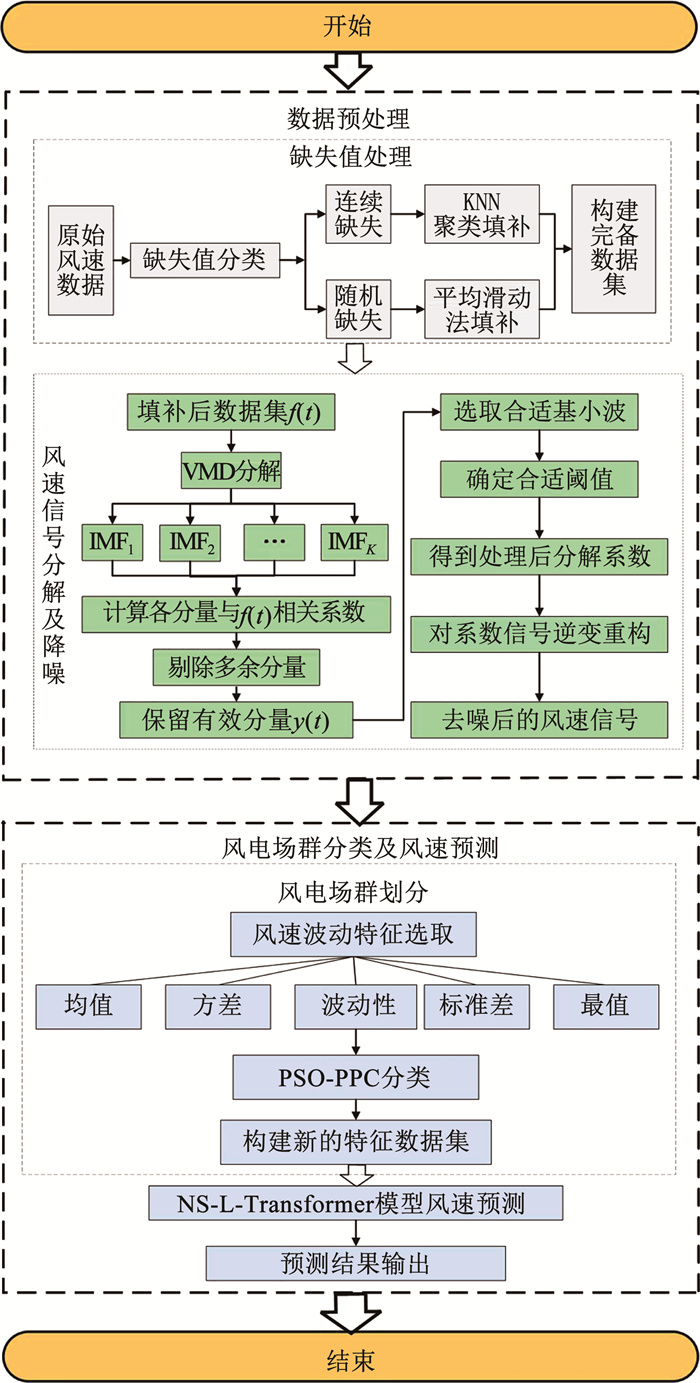
|
图 4 风电场群风速预测流程 Fig. 4 Flow chart for predicting wind speed in wind farm clusters |
Step1(缺失值处理) 对于所采集的数据集中,存在的数据缺失问题,设定固定阈值10,判断连续缺失值的多少,若连续缺失值小于阈值,则采用均值插补法对缺失值进行填充,若连续缺失值大于阈值,平均滑动法对缺失值进行填补。
Step2(数据分解与去伪) 使用VMD将填补处理后的风速数据分解,设置K=7,通过分解得到7个分量。利用式(1)计算各分量与原始风速信号的相关系数,设定小于最大系数1/10的分量为伪分量,去除伪分量。
Step3(数据去噪及重构) 保留其余分量后得到若干个有效分量。通过小波变换对有效分量进行去噪,对去噪之后的信号进行重构。
Step4(风电场聚类) 从风速的均值、最大最小值、方差、标准差、波动性来构造评价指标,使用PSO-PPC算法对20个风场的风速进行分类。通过计算分类后风电场的相关系数对分类的准确性进行评估。
Step5(数据集构建) 根据分类,在每一个分类中,选定一个风电场风速作为目标风电场风速,以类内相关风电场的风速作为目标风电场风速的特征值,构造新的数据集。
Step6(预测数据集) 通过所提的NS-L- Transformer模型对构造的数据集进行风速预测。
4.2 评价指标本文选用皮尔逊相关系数ρ对风电场群的聚类进行评价分析,选取均方根误差εRMSE、平均绝对误差εMAE和拟合优度R2对风速多步预测构架评价指标,分别如下:
| $ \rho=\frac{\sum\limits_{i=1}^n\left(x_i-x_{\mathrm{avg}}\right) \sum\limits_{i=1}^n\left(y_i-y_{\mathrm{avg}}\right)}{\sqrt{\sum\limits_{i=1}^n\left(x_i-x_{\mathrm{avg}}\right)^2 \sum\limits_{i=1}^n\left(y_i-y_{\mathrm{avg}}\right)^2}} $ | (14) |
| $ \varepsilon_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{x}_i-x_i\right)^2} $ | (15) |
| $ \varepsilon_{\mathrm{MAE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|x_i-\hat{x}_i\right| $ | (16) |
| $ R^2=\left(1-\frac{\sum\limits_{i=1}^n\left(x_i-\hat{x}_i\right)^2}{\sum\limits_{i=1}^n\left(\hat{x}_i-x_{\mathrm{avg}}\right)^2}\right) $ | (17) |
式中:xi为目标风电场实际风速值,xavg为目标风电场平均风速值,yi为相关风电场的实际风速值,yavg为相关风电场的平均风速值,
使用中国东南地区某区域2023年3月1日—2023年5月30日的数据来验证所用模型的可行性,总共有20个风电场,风电场群的分布见图 5。采样间隔时间为15 min,总样本数为8 640×20(4×24×90)。

|
图 5 风电场群分布 Fig. 5 Distribution of wind farm clusters |
为消除噪声对风速产生的误差,并提取风速关键特征,本文使用VMD分解方法对原始风速信号进行分解,设置模态个数K为7,得到分量IMF1~IMF7。
以1号风电场为例,风速原始数据集共8 640个采样点,将1号风场的风速输入VMD分解模型,得到分解结果见图 6。从图 6中可知,VMD将风速按照频率分解总共得到7条IMF序列,各个序列按照高频到低频的方式排列。
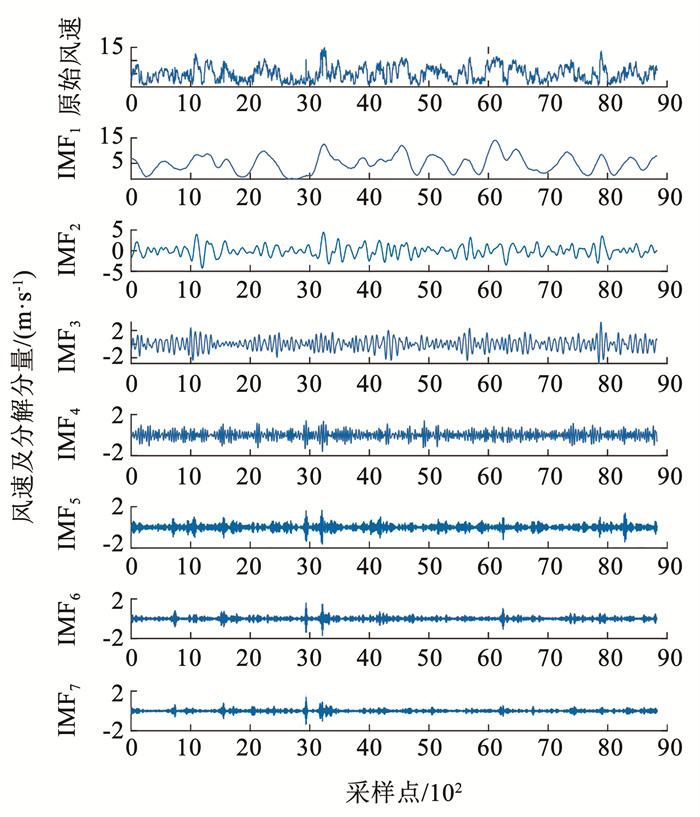
|
图 6 风速信号分解后的各分量 Fig. 6 IMFs after decomposing wind speed sequences |
使用式(1)分析分解后的各分量与原始分量的相关系数,具体数值见表 1。保留大于最大系数1/10的分量,在1号风电场中保留相关系数大于0.094 81的所有分量,即1号风电场中所保留的有效分量为IMF1~IMF4。
| 表 1 各分量与原始风速相关系数 Tab. 1 Correlation coefficient between IMFs and original wind speed |
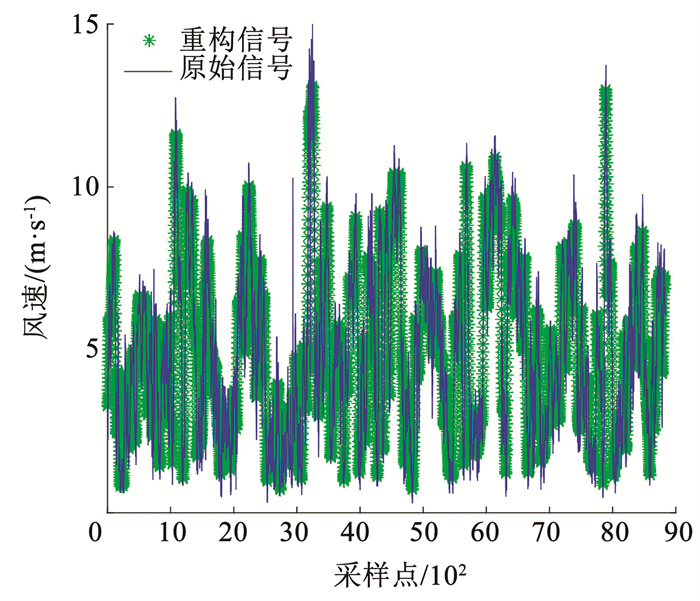
将保留的有效分量通过小波变换进行去噪,小波基函数为Db5、分解层数为3。对去噪后的信号通过相加进行重构,重构后的信号与原始信号对比见图 7。由图 7分析可知,降噪后的风速波动较原始信号更平稳,便于预测模型对风速特征进行捕捉。
|
图 7 降噪后信号重构 Fig. 7 Signal reconstruction after noise reduction |
选用春季(3月1日-5月30日)的数据对集群进行分类,选择风速的平均值、方差、标准差和风速的波动性作为评价指标,通过PSO寻优算法确定投影寻踪的最佳方向,PSO的初始值设定为粒子数目200,学习因子1和学习因子2分别为0.5和2.0,惯性权重为0.7,迭代次数为200,问题维数为6。
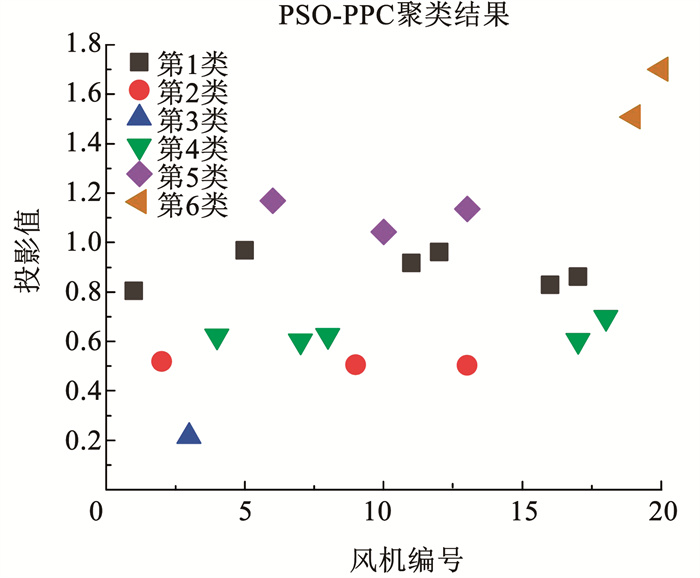
分别采用传统的投影寻踪算法与PSO-PPC算法对机群的进行评估,评估结果相近的风机风速划分为一类,机群聚类的结果见表 2和图 8。
| 表 2 风电场风速聚类结果 Tab. 2 Results of wind farm wind speed clustering |
|
图 8 风电场风速聚类结果 Fig. 8 Results of wind farm wind speed clustering |
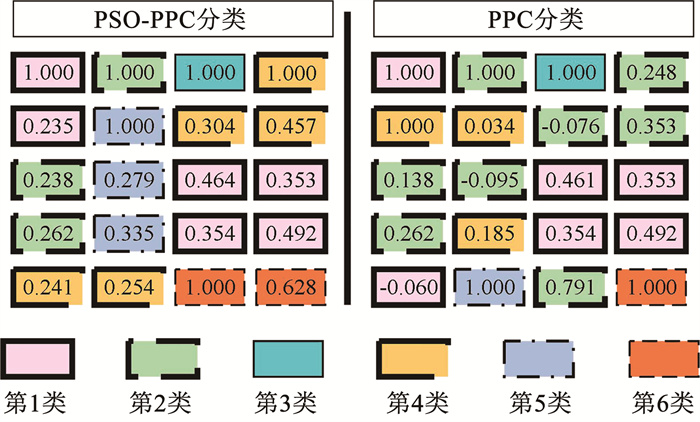
在图 8中,将颜色形状相同的点划分为同一类,可以明显看出,同一个分类的点的投影值较为接近。投影寻踪算法可以很好地解决样本数据的高维度问题分类。不难看出,由于存在风机能量转化过程中的损耗和尾流效应的影响,聚类结果受空间的分布影响相对较小,并未按照风机的地理分布呈现出片区式划分。通过皮尔逊分析对划分的样本类进行验证,分别对PPC和PSO-PPC的风机聚类结果进行评估,总共20个风场,使用4×5单元格按照从左至右、从上至下的顺序排列。两种聚类都将20个风机分为6类,相同颜色表示同一类风电场,目标风电场与自身的皮尔逊相关系数为1,具体相关性见图 9。
|
图 9 皮尔逊评价分类 Fig. 9 Pearson evaluation classification |
通过皮尔逊系数分析可以明显看出,因为PSO-PPC算法较传统的投影寻踪算法可以更准确找到最大的投影方向,因此通过PSO-PPC算法分类所得到的每一类机群较投影寻踪算法分类所得到的机群分类,类内的风机数量较为平均,且通过PSO-PPC算法分类后的类内机群的风速与该类中目标风机的风速的相关系数均为正相关,而传统的投影寻踪算法类内机群的风速与目标风电场的风速会存在负相关系数,会影响后续目标风电场风速的预测精度。
5.4 数据集构建及风速预测以PSO-PPC算法划分后的第1类和第4类数据集为例,由上述分析可得,第1类和第4类同一个分类内风机的风速在3月1日— 5月30日的存在相关性。以同时间段存在相关性的风机风速作为目标风机风速的特征量,重新构建预测数据集,风速数据以3∶ 1∶ 1的比例来划分训练集、验证集和测试集。
本文将所提方法通过消融实验,分别与Transformer、Non-stationary Transformer预测模型进行对比,深度学习模型框架需要选择合适的参数来获得满意的预测结果,通过多次对比试验,选择不同参数,相关参数见表 3。
| 表 3 3种模型主要参数设置 Tab. 3 Main parameters settings of the three models |
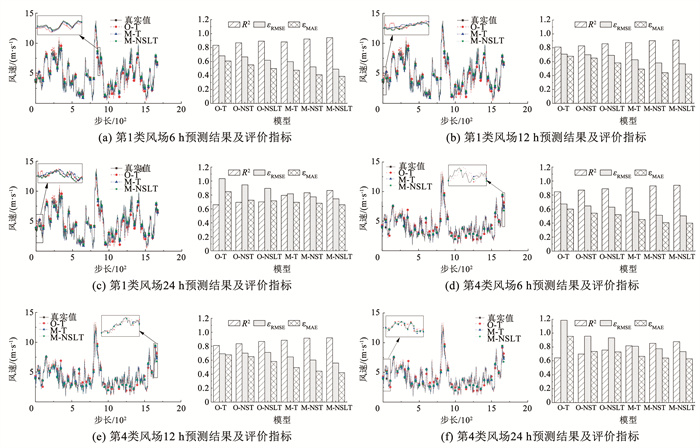
分别采用Transformer、Non-stationary Transformer和NS-L-Transformer对第1类和第4类数据集风电场风速进行预测,并对原有的风机风速数据和构建后的风电场风速数据未来6、12、24 h预测进行仿真,结果见图 10。
|
图 10 不同模型风速预测情况 Fig. 10 Different models in wind speed prediction |
图 10分别展示了第1类和第4类风电场对6、12、24 h的风速序列进行预测的结果,在两类风电场的预测图中均可以看出,使用单一风电场数据集进行风速预测的拟合结果较使用多维数据预测的拟合结果要差一些;在多维数据集中,本文所提的模型较Transformer模型的预测结果能够更好的拟合风电场的真实数据。
为进一步分析预测的结果,使用式(14)~(17)计算不同预测时长和不同模型下的风速预测的误差,以对预测结果进一步分析,误差指标见表 4。表 4中,O-T、O-NST、O-NSLT、M-T、M-NST、M-NSLT分别为单一风电场目标风机风速Transformer预测、单一风电场目标风机风速Non-stationanry Transformer预测、单一风电场目标风机风速NS-L-Transformer预测、类内风电场目标风机风速Transformer预测、类内风电场目标风机风速Non-stationanry Transformer预测、类内风电场目标风机风速NS-L-Transformer预测。
| 表 4 不同预测模型误差指标 Tab. 4 Error index in different prediction models |
对比发现,由于风速的波动性和非平稳性,在两个分类的风电场中,每一种预测模型,24 h的风速预测误差值大于12 h风速预测的误差值,12 h的风速预测误差值大于6 h风速预测的误差值,可以明显看出,预测误差会随着预测步长增加而增大。但是,在不同时刻的预测中,NS-L-Transformer模型的误差仍低于其他模型。
通过对第1类和第4类风电场在不同模型下的对比,可以明显的看出单一风电场的误差预测精度低于所构建的多维数据集的风速预测精度。在本文所提出的NS-L-Transformer模型下,根据均方根误差分析可得第1类场群的24 h预测误差,多维预测较单一预测精度提高了38.63 %,在第4类场群中提高了27.62 %。证明在模型中考虑到风电场风机的空间相关性对风速预测的精度会有提升。
对重新构建后的风电场群风速预测,分析第1类和第4类的风速预测。分别观察单一风电场和重新构建的多维风电场的预测误差,可以看出,使用NS-L-Transformer模型对风速数据进行预测得到的预测精度优于其他模型。根据均方根误差对第1类场群的24 h预测误差进行分析,本文所提出的模型较Transformer模型和Non-stationary Transformer模型在单一风电场中,分别提高了13.8 %和5.8 %;在多维数据中,分别提高了9.58 %和3.75 %。即通过LSTM模型加强对模型提取局部数据信息对预测结果有所提升。
6 结论1) 对原始风速信号通过VMD分解、剔除噪声后,重构所得的信号较原始风速信号更为平缓。
2) 对比改进前、后的PPC算法的分类结果的相关性,经过PSO算法改进的投影寻踪算法可以找到最佳投影方向,利用皮尔逊相关系数对划分的集群进行验证,同一个分类内的风机风速均为正相关性。
3) 根据PSO-PPC算法确定分类风电场群分类,构建新的高维风速数据集。对不同的预测模型中单一风电场风速数据和高维风速数据集仿真分析,结果表明使用多个正相关输入量去预测目标风电场的风速,较使用单一风电场风速预测的精度有所提升,验证了集群分类和高位数据集建立的有效性。
4) 利用Non-stationary Transformer模型中的平稳序列模块,通过Transformer模型的注意力机制来捕捉数据的全局依赖关系,结合LSTM层来加强模型提取数据局部位置信息的能力。对不同的数据集和预测时长的仿真分析,结果均表明所提出的模型的预测精度均有提升,从而验证了所提模型的有效性。
| [1] |
HUANG Chaoming, KUO C J, HUANG Y C. Short-term wind power forecasting and uncertainty analysis using a hybrid intelligent method[J]. IET Renewable Power Generation, 2017, 11(5): 678. DOI:10.1049/iet-rpg.2016.0672 |
| [2] |
PUTZ D, GUMHALTER M, AUER H. A novel approach to multi-horizon wind power forecasting based on deep neural architecture[J]. Renewable Energy, 2021, 178: 494. DOI:10.1016/j.renene.2021.06.099 |
| [3] |
YANG Mao, ZHANG Luobin, CUI Yang, et al. Investigating the wind power smoothing effect using set pair analysis[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1161. DOI:10.1109/TSTE.2019.2920255 |
| [4] |
YANG Mao, SHI Chaoyu, LIU Huiyu. Day-ahead wind power forecasting based on the clustering of equivalent power curves[J]. Energy, 2021, 218: 119515. DOI:10.1016/j.energy.2020.119515 |
| [5] |
毕贵红, 赵鑫, 李璐, 等. 双模式分解CNN-LSTM集成的短期风速预测模型[J]. 太阳能学报, 2023, 44(3): 191. BI Guihong, ZHAO Xin, LI Lu, et al. Dual-mode decomposition CNN-LSTM integrated short-term wind speed forecasting model[J]. Acta Energiae Solaris Sinica, 2023, 44(3): 191. DOI:10.19912/j.0254-0096.tynxb.2021-1307 |
| [6] |
王岩, 陈耀然, 韩兆龙, 等. 基于互信息理论与递归神经网络的短期风速预测模型[J]. 上海交通大学学报, 2021, 55(9): 1080. WANG Yan, CHEN Yaoran, HAN Zhaolong, et al. Short-term wind speed forecasting model based on mutual information and recursive neural network[J]. Journal of Shanghai Jiao Tong University, 2021, 55(9): 1080. DOI:10.16183/j.cnki.jsjtu.2020.433 |
| [7] |
何锦华, 刘洋, 朱誉, 等. 融合物理信息的TPA-LSTM网络应用于台风条件下海上风电场风速多步预测[J]. 电网技术, 2023, 47(10): 4152. HE Jinhua, LIU Yang, ZHU Yu, et al. Physics-informed TPA-LSTM network applied to multi-step wind speed prediction of offshore wind farms under typhoon conditions[J]. Power System Technology, 2023, 47(10): 4152. DOI:10.13335/j.1000-3673.pst.2023.1024 |
| [8] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017: 6000. DOI: 10.48550/arXiv.1706.03762
|
| [9] |
HUANG Siteng, WANG Donglin, WU Xuehan, et al. DSANet: dual self-attention network for multivariate time series forecasting[C]//Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing: ACM, 2019: 2129. DOI: 10.1145/3357384.3358132
|
| [10] |
MAMMADI FARSANI R, PAZOUKI E. A transformer self-attention model for time series forecasting[J]. Journal of Electrical and Computer Engineering Innovations (JECEI), 2021, 9(1): 1. DOI:10.22061/jecei.2020.7426.391 |
| [11] |
LI Shiyang, JIN Xiaoyong, XUAN Yao, et al. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting[EB/OL]. 2019: 1907.00235. https://arxiv.org/abs/1907.00235v3
|
| [12] |
ZHOU Haoyi, ZHANG Shanghang, PENG Jieqi, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(12): 11106. DOI:10.1609/aaai.v35i12.17325 |
| [13] |
LIM B, ARIK S Ö, LOEFF N, et al. Temporal fusion transformers for interpretable multi-horizon time series forecasting[J]. International Journal of Forecasting, 2021, 37(4): 1748. DOI:10.1016/j.ijforecast.2021.03.012 |
| [14] |
WU Haixu, XU Jiehui, WANG Jianmin, et al. Autoformer: decomposition transformers with auto-correlation for long-term series forecasting[EB/OL]. 2021: 2106.13008. https://arxiv.org/abs/2106.13008v5
|
| [15] |
ZHOU Tian, MA Ziqing, WEN Qingsong, et al. FEDformer: frequency enhanced decomposed transformer for long-term series forecasting[EB/OL]. 2022: 2201.12740. https://arxiv.org/abs/2201.12740v3
|
| [16] |
LIU Yong, WU Haixu, WANG Jianmin, et al. Non-stationary transformers: exploring the stationarity in time series forecasting[J]. Advances in Neural Information Processing Systems, 2022, 35: 9881. DOI:10.48550/arXiv.2205.14415 |
| [17] |
孙亦皓, 刘浩, 胡天宇, 等. 基于时空关联特征与GCN-FEDformer的风速短期预测方法[J]. 中国电机工程学报, 2024, 44(21): 8496. SUN Yihao, LIU Hao, HU Tianyu, et al. Short-term wind speed forecasting based on GCN and FEDformer[J]. Proceedings of the CSEE, 2024, 44(21): 8496. DOI:10.13334/j.0258-8013.pcsee.231140 |
| [18] |
YANG Mao, YAN Qi, DAI Bozhi, et al. An improved spatial upscaling method for producing day-ahead power forecasts for wind farm clusters[J]. IET Generation, Transmission & Distribution, 2022, 16(19): 3860. DOI:10.1049/gtd2.12569 |
| [19] |
潘超, 李润宇, 王典, 等. 基于风速时空关联的多步预测方法[J]. 太阳能学报, 2022, 43(2): 458. PAN Chao, LI Runyu, WANG Dian, et al. Multi-step wind speed prediction method based on wind speed spatial-time correlation[J]. Acta Energiae Solaris Sinica, 2022, 43(2): 458. DOI:10.19912/j.0254-0096.tynxb.2020-0410 |
| [20] |
FRIEDMAN J H, TUKEY J W. A projection pursuit algorithm for exploratory data analysis[J]. IEEE Transactions on Computers, 1974, C -23(9): 881. DOI:10.1109/T-C.1974.224051 |
| [21] |
赵静远, 熊智新, 梁龙, 等. 投影寻踪分类模型在常见造纸纤维原料综合评价中的应用[J]. 中国造纸学报, 2020, 35(3): 53. ZHAO Jingyuan, XIONG Zhixin, LIANG Long, et al. Application of projection pursuit classification model in comprehensive evaluation of common papermaking materials[J]. Transactions of China Pulp and Paper, 2020, 35(3): 53. DOI:10.11981/j.issn.1000-6842.2020.03.53 |
| [22] |
李芳. 中国式现代化背景下数字农业发展水平测度与空间区位分布[J]. 饲料研究, 2023, 46(19): 186. LI Fang. Measurement of digital agriculture level and spatial location distribution in the context of Chinese-stylemodernization[J]. Feed Research, 2023, 46(19): 186. DOI:10.13557/j.cnki.issn.1002-2813.2023.19.037 |
| [23] |
方必和, 程志宏, 刘慧萍. 投影寻踪模型在国民经济综合评价中的应用[J]. 运筹与管理, 2005, 14(5): 85. FANG Bihe, CHENG Zhihong, LIU Huiping, et al. Application of projection pursuit model in integrated evaluation of national economy[J]. Operations Research and Management Science, 2005, 14(5): 85. |
| [24] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531. DOI:10.1109/TSP.2013.2288675 |
| [25] |
DONOHO D L, JOHNSTONE I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200. DOI:10.1080/01621459.1995.10476626 |
| [26] |
邵忍平, 曹精明, 李永龙. 基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J]. 振动与冲击, 2012, 31(8): 96. SHAO Renping, CAO Jingming, LI Yonglong. Gear fault pattern identification and diagnosis using Time-Frequency Analysis and wavelet threshold de-noising based on EMD[J]. Journal of Vibration and Shock, 2012, 31(8): 96. DOI:10.13465/j.cnki.jvs.2012.08.014 |
| [27] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth: IEEE, 1995: 1942. DOI: 10.1109/ICNN.1995.488968
|
| [28] |
张利彪, 周春光, 马铭, 等. 基于粒子群算法求解多目标优化问题[J]. 计算机研究与发展, 2004, 41(7): 1286. ZHANG Libiao, ZHOU Chunguang, MA Ming, et al. Solutions of multi-objective optimization problems based on particle swarm optimization[J]. Journal of Computer Research and Development, 2004, 41(7): 1286. |
 2024, Vol. 56
2024, Vol. 56


