2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 哈尔滨工业大学 土木工程学院, 哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
防屈曲支撑因良好的延性和耗能能力在抗震钢结构中广泛应用[1],但支撑大幅屈服后残余变形较大,将影响震后结构的使用功能[2-3]。为控制支撑的残余变形,有学者采用形状记忆合金[4]、复合纤维筋[5]和高强钢绞线[6]等构建复位系统,并和防屈曲支撑并联组成自复位防屈曲支撑。与常用中心支撑的布置原则相同,自复位支撑在结构平面上应满足基本对称布置等要求,且在结构高度方向应满足连续布置等要求。因结构层间剪切变形可更好地发挥支撑轴向变形能力[7],自复位支撑适用于层间侧移中剪切变形起主导作用的抗震结构。
然而,形状记忆合金昂贵且大侧移下自复位支撑的残余变形仍较大[4]。复合纤维筋锚固困难,纤维筋在锚固区的断裂会劣化支撑的延性[5]。高强钢绞线较经济,但施加预拉力后可用的弹性变形能力有限,需串联多重组件来增大复位系统的弹性变形能力[6],这导致传力路径增大且对组件加工和装配精度要求提高等不足。
组合碟簧轴向承载和变形能力较好,已用于构建自复位防屈曲支撑[8-11]。然而,当并联两串预压组合碟簧提供复位力时[8, 10],存在两串碟簧轴向受力难以一致进而对复位系统制作和安装精度有较高要求等问题。防屈曲支撑的内置钢板支撑多采用变截面的方式[8-11],而试验表明,变截面方式使制作中内置支撑屈服段在靠近弹性过渡段处易出现局部截面削弱而引发较早低周疲劳断裂[8-9]。内置钢板支撑两端采用较长的连接段,大幅降低了屈服段的长度[8, 10-11],使相同楼层侧移下屈服段塑性变形能力需求增大,易导致钢板支撑较早低周疲劳断裂[8]。这些均表明有必要进一步探索合理的构造。
上述自复位防屈曲支撑[4-6, 8-11]在构造上均采用两端刚接,将导致支撑大侧移后端部承受较大的弯矩。这使支撑实际受力与目前结构设计和分析中普遍采用支撑端部铰接按轴心受力构件进行设计的力学模型不符,且额外受弯使自复位支撑受力性能复杂化,将劣化支撑的延性。试验表明,端部刚接支撑大侧移后,复位系统部件受力复杂且因受弯较大甚至产生屈服[9],有悖于复位系统处于弹性的能力设计原则。此外,常定义组合碟簧初始复位力与防屈曲支撑屈服后, 某侧移角下的承载力之比为复位比率[8-11],目前主要研究该比率变化对支撑残余变形的影响,关于碟簧的组合方式和相应的组合碟簧刚度变化对自复位支撑受力性能影响的探索较少。
针对以上问题,本文内置支撑采用等宽度的钢板制作,构建了端部铰接和刚接的自复位防屈曲支撑(SBRB)。对3个纯自复位支撑(DS)和3个组合碟簧自复位防屈曲支撑(SBRB)进行了拟静力试验,重点考察了组合碟簧刚度、端部连接形式、复位比率等关键参数对SBRB滞回性能的影响。
1 试件准备 1.1 自复位系统的组成和工作原理单片碟簧的尺寸见图 1。依据试验设计,选取A系列的碟簧,不同组合碟簧的轴向力-变形关系接近线性。采用两种规格的碟簧和组合碟簧,见表 1。
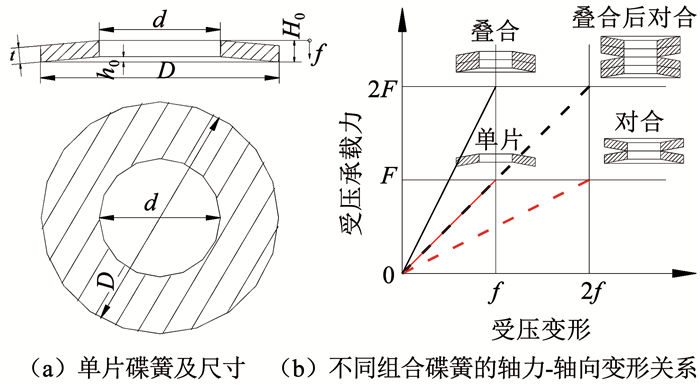
|
图 1 碟簧的尺寸和组合 Fig. 1 Dimension and combination of disc springs |
| 表 1 碟簧尺寸和组合方式 Tab. 1 Dimension and combination of disc springs |
自复位系统由上下部推拉块、上下部预压块、螺杆组合、组合碟簧组成,见图 2。各部件由螺杆组合连成整体,每根螺杆上布置3处螺母,分别位于上下部预压块端板和推拉块内端板处。螺杆受拉分两阶段,第一阶段为组合碟簧施加预压力, 第二阶段为支撑受拉时传递拉力。第一阶段中12根螺杆通过Ⅱ、Ⅲ类螺母之间螺杆与组合碟簧形成自平衡体系,此时Ⅰ、Ⅱ类螺母之间螺杆不受力。当支撑受压变形2δ时,下部推拉块推动下部预压块,上部推拉块推动上部预压块,二者相向运动2δ,使组合碟簧产生2δ的压缩量;当支撑受拉变形2δ时,下部推拉块通过Ⅰ、Ⅲ类螺母拉动上部预压块,上部推拉块通过Ⅰ、Ⅲ类螺母拉动下部预压块,使上、下部预压块仍相向运动2δ,组合碟簧仍然产生2δ的压缩量。从而实现支撑无论受压还是受拉,组合碟簧均进一步受压,可为支撑提供复位力。
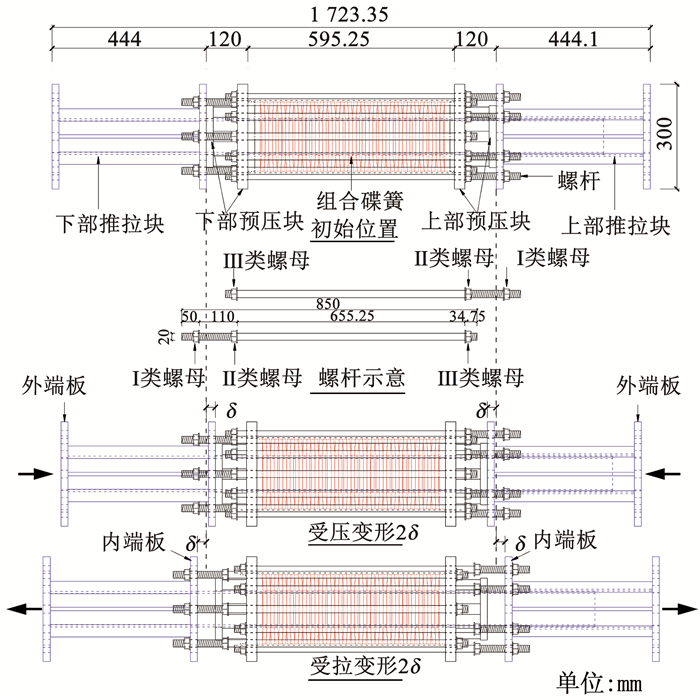
|
图 2 复位系统的工作机制 Fig. 2 Working mechanism of self-centering system |
碟簧施加预压力前,先将各部件按图 2严格就位在一起,螺杆均松动。再将下部推拉块底部固定,对上部推拉块顶施加轴压力,适时量测组合碟簧的轴向压缩变形和轴压力。当压力达到预定的启动力值时,持荷等待并将12根螺杆的Ⅱ、Ⅲ类螺母处通过双螺母均匀拧紧初步固定。然后卸载并重新加载至组合碟簧启动(即螺杆均再次松动,对应的轴压力为启动力),记录组合碟簧的受压荷载-位移曲线,并查验启动力值。若发现启动力偏高或偏低,则压缩碟簧来松动Ⅱ、Ⅲ类螺母以调整启动力值并重新初步固定和查验启动力值。初步固定后,重复至少加、卸载3次,若所得加、卸载下的荷载-位移曲线均重合且启动力值满足要求,则通过进一步紧固双螺母的外侧螺母来最终固定Ⅱ、Ⅲ类螺母。这样,两预压块、12根螺杆和组合碟簧形成自平衡体系(12根螺杆均受拉)。之后,再将每端6根螺杆通过Ⅰ类双螺母与推拉块的内端板连接,Ⅰ类螺母仅作就位固定,确保6根螺杆区段基本不受预拉力。
1.2 防屈曲支撑组成防屈曲支撑由内部钢板支撑和由高强螺栓连接的开孔钢板、开孔填板、开孔薄铁皮等外部约束构件组成,钢管与开孔钢板采用角焊缝连接,见图 3。
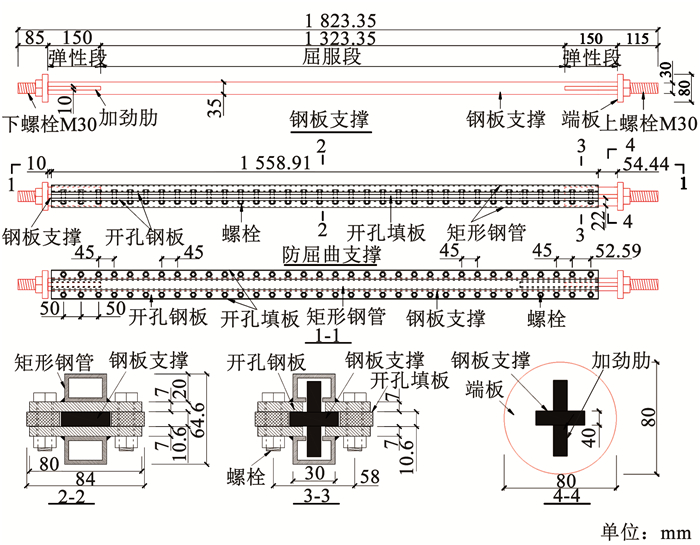
|
图 3 防屈曲支撑(BRB)的构造 Fig. 3 Constructional details of BRB |
钢板支撑作为耗能构件分为弹性段和屈服段,弹性段两端设置带螺杆的圆形端板,用于与连接端部进行连接,支撑屈服段截面为35 mm×10 mm。矩形钢管、开孔钢板为钢板支撑提供厚度方向的约束;开孔填板为钢板支撑提供宽度方向的约束,并留置沿宽度方向上的间隙;开孔薄铁皮为钢板支撑留置沿厚度方向上的间隙。沿钢板支撑厚度和宽度方向每侧分别留置0.15、1 mm的空隙。与文献[9]的构造不同,不设置钢板支撑截面变化的过渡段,整块钢板支撑截面等宽,可避免加工制作中支撑屈服段端部因刀具切削转换导致的截面局部削弱。
1.3 自复位防屈曲支撑组成整个自复位支撑由复位系统、防屈曲支撑、连接端部组成,有端部铰接和刚接两种形式,见图 4。连接端部中的上、下并联板使复位系统和防屈曲支撑并联受力,见图 4(a)。
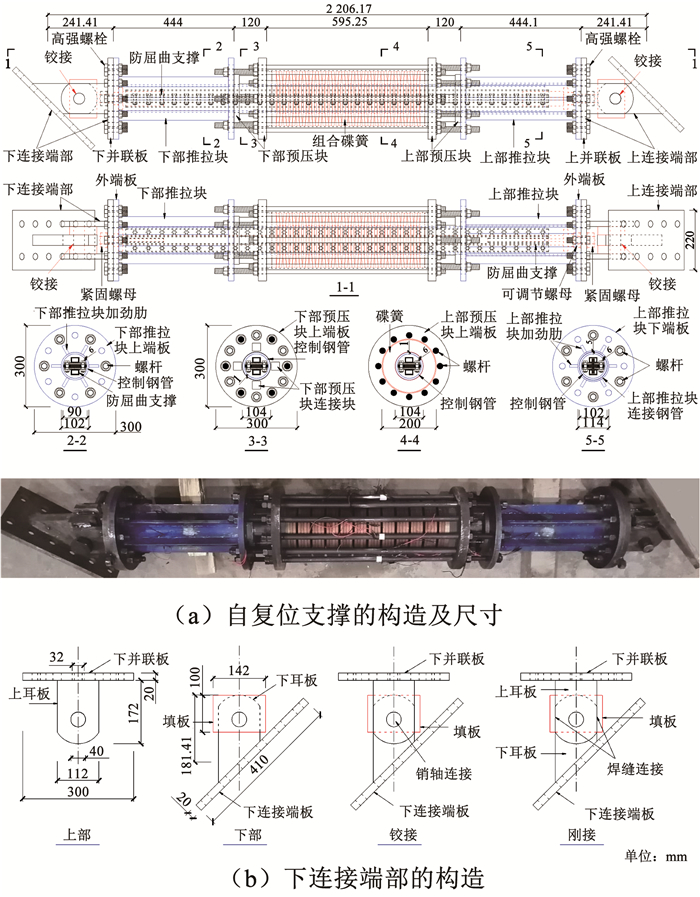
|
图 4 自复位防屈曲支撑(SBRB)的构造 Fig. 4 Constructional details of SBRB |
以下连接端部为例,其上部由两块上耳板与下并联板焊接而成,下部由填板、下耳板、下连接端板焊接而成,铰接连接时将上下两部分用销轴连接,刚接连接时采用角焊缝连接,见图 4(b)。上、下并联板与上、下部推拉块外端板各用12个M20高强螺栓相连;并联板采用高强螺母与防屈曲支撑端板预先焊接的M30高强螺栓相连。上端M30螺杆较长且上并联板内外各采用一个高强螺母,以实现防屈曲支撑轴向安装长度可调节,避免因各部件制作和装配误差使防屈曲支撑承受初始轴向力。
上、下连接端部以及复位系统和防屈曲支撑各自制作和组装完成后,先将防屈曲支撑沿轴向穿过控制钢管就位,并将防屈曲支撑与复位系统的下部与下并联板精确就位。之后,通过12个高强螺栓将复位系统下推拉块端板与下并联板连接固定,通过下并联板外一个紧固螺母(图 4(a))将防屈曲支撑的下螺栓(图 3)与下并联板也连接固定。然后,调节防屈曲支撑上螺栓上的用于上并联板内部一侧的可调节螺母(图 4(a))的位置,使该螺母外边缘与上部推拉块端板外边缘在一个平面内。进而,将上连接端部精确就位,并通过12个高强螺栓将复位系统上推拉块端板与上并联板连接固定,上并联板外侧的一个紧固螺母将防屈曲支撑的上螺栓与上并联板也连接固定。这样就完成了整个支撑的组装。
此外,由图 4(a)、图 2和图 5可知,当支撑上、下端相对水平侧移后,支撑端部铰接时,下部推拉块的控制钢管和上部推拉块的连接钢管间可沿轴向自由相对错动而基本无其他相互作用;而支撑端部刚接时,二者除了轴向相对错动还会在垂直轴向有相互接触作用,使控制钢管通过抗剪和轴向摩擦作用来为整个支撑提供额外的抗侧力作用。
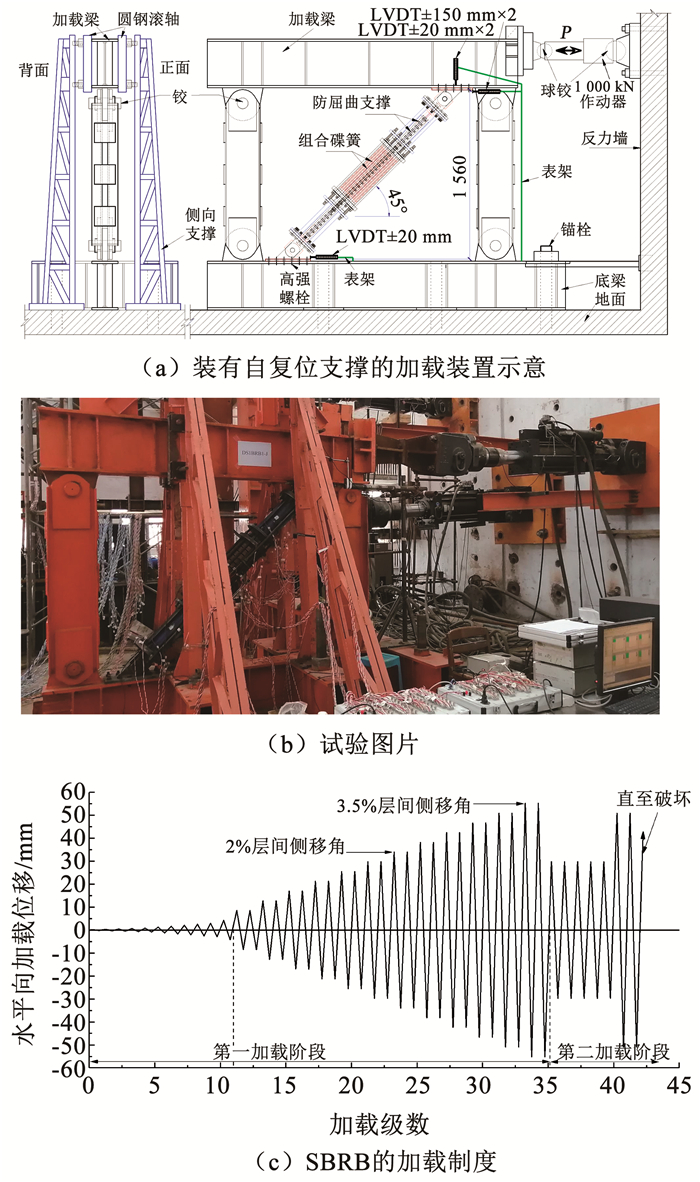
|
图 5 装有自复位支撑(SBRB)的加载装置和加载制度 Fig. 5 Test rig with a SBRB and loading rule |
试验的6个试件组成见表 2。根据图 4所示构造,当复位系统和防屈曲支撑均设置时,根据连接端部和组合碟簧的不同,包括3个自复位支撑。如果去除防屈曲支撑部分,仅有复位系统时,根据连接端部和组合碟簧的不同,包括3个纯自复位支撑。
| 表 2 试件的组成 Tab. 2 Formation of specimens |
钢板支撑采用Q235B钢,通过标准材性试件的单调拉伸试验获得的实测屈服强度和抗拉强度分别为314.12、455.64 MPa,弹性模量和泊松比分别为192 GPa和0.28,伸长率为26.8%。碟形弹簧采用60Si2MnA钢,厂家提供的屈服应力和极限应力分别为1 477、1 647 MPa。
1.4 试验加载和量测方案加载装置由铰接框架、侧撑和作动器组成,见图 5(a)和(b)。安装时,将支撑试件上、下连接端部与框架的加载梁和底梁用M20高强螺栓连接。
试验采用两阶段加载。依据文献[1]和[12],试验第一加载阶段采用位移幅值渐增的加载制度。为进一步考察自复位支撑构件的最终破坏模式和极限累积非弹性变形性能等,通过第二加载阶段附加了两个恒定位移幅值下的额外加载。文献[13]表明,自复位支撑钢框架结构可能经历比防屈曲支撑钢框架结构更大的层间变形,建议两种结构位移幅值渐增的加载阶段中最大层间侧移角需分别达到0.04和0.035(最大位移幅值下加载一圈)。考虑第一阶段位移幅值基本呈线性增长,且最大位移幅值下加载两圈,对SBRB试件取最大加载侧移角约为0.035(因支撑高1 560 mm(图 5(a)),对应水平加载位移约±55.15 mm,见图 5(c))。
以支撑上、下端相对水平位移作为控制位移进行加载。对于SBRB试件,依据钢板支撑材性实测值和支撑几何尺寸,水平向加载制度中近似取屈服位移Δy=4.24 m。第一阶段,在位移±Δy之前,每级加载一圈。之后,因防屈曲支撑明显屈服,每级位移增量为Δy,每级加载两圈,直至约±55.15 mm(±13Δy)。若防屈曲支撑未破坏,进入第二加载阶段,先进行±29.70 mm(±7Δy)下循环5圈,若还未破坏,再进行±50.91 mm(±12Δy)下若干圈循环加载直至钢板支撑受拉断裂,加载制度详见图 5(c)。对于DS试件,因基本处于弹性,每级加载仅循环一圈,起初采用小的位移增量,从±4.24 mm起,每级位移增量约为2Δy,直至±63.64 mm(±15Δy,对应加载侧移角约为0.041)。加载位移负值和正值分别表示推出和拉回作动器,即支撑分别受压和受拉。
2 试验结果 2.1 试件的破坏模式3个DS试件无破坏。3个SBRB试件在第二加载阶段的±12Δy循环中均发生了钢板支撑屈服段低周疲劳受拉断裂破坏,SBRBJ1、SBRBJ2和SBRBG分别在第7圈、第21圈和第4圈中受拉断裂。其他部件均保持完好。复位系统的部件基本处于弹性,实现了重复利用。刚接试件断裂出现在屈服段端部,其余铰接试件均出现在屈服段中部,表明端部刚接情况下屈服段塑性变形更易集中于端部。同时,文献[8-9]提及钢板支撑设置过渡段时,制作中过渡段与屈服段的交界处易出现屈服段局部截面削弱,加之端部刚接,局部截面削弱更易导致较早断裂。可见不设置过渡段的等宽钢板支撑构造有利于避免制作缺陷。因钢板支撑与约束构件间设置间隙,支撑发生了多波弯曲变形(图 6),又因沿钢板宽度方向间隙较大,变形也较明显。可见,本文采用螺栓组装支撑,当用于支撑钢框架结构中时,震后仅需检修或更换钢板支撑,其余部件均有望重复利用。
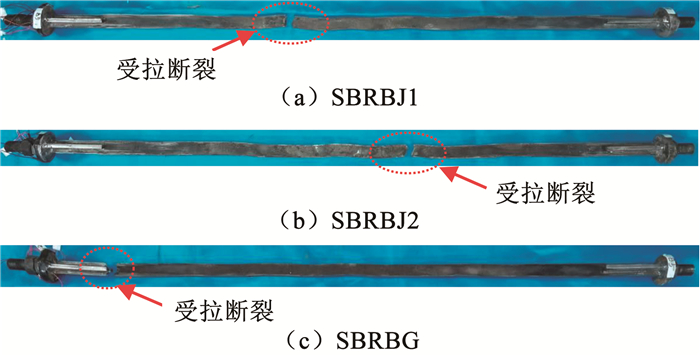
|
图 6 内置钢板支撑的断裂 Fig. 6 Fracture of inner plate braces |
试件的水平力-位移滞回曲线见图 7。因实际加载控制有误差,第一加载阶段最大加载侧移角范围为0.033~0.041。可见DS和SBRB试件都呈稳定的旗帜型滞回曲线,相对于每级加载最大位移,卸载到零荷载SBRB的残余变形得到大幅削减,表明设置复位系统有效控制了防屈曲支撑的残余变形。由图 7可知,SBRB试件直至钢板支撑断裂前滞回曲线较稳定。支撑断裂后,因为复位系统的存在以及多波弯曲变形的内置钢支撑与约束构件间存在摩擦力,循环加载中仍表现出一定的耗能能力。特别是,与SBRBG相比,SBRBJ1和SBRBJ2支撑在出现断裂的那圈加载中受拉断裂较早(图 7(f)、(i)),很可能导致多波弯曲变形没有被很好地拉直(图 6),支撑与约束构件间的摩擦作用较强,曲线加、卸载所包围的面积较大。还需说明的是,因加载中受端部销轴间隙和滑移影响,适时调整了SBRBJ2水平控制位移,使正、负向位移出现较多差异(图 7(g)~(i))。
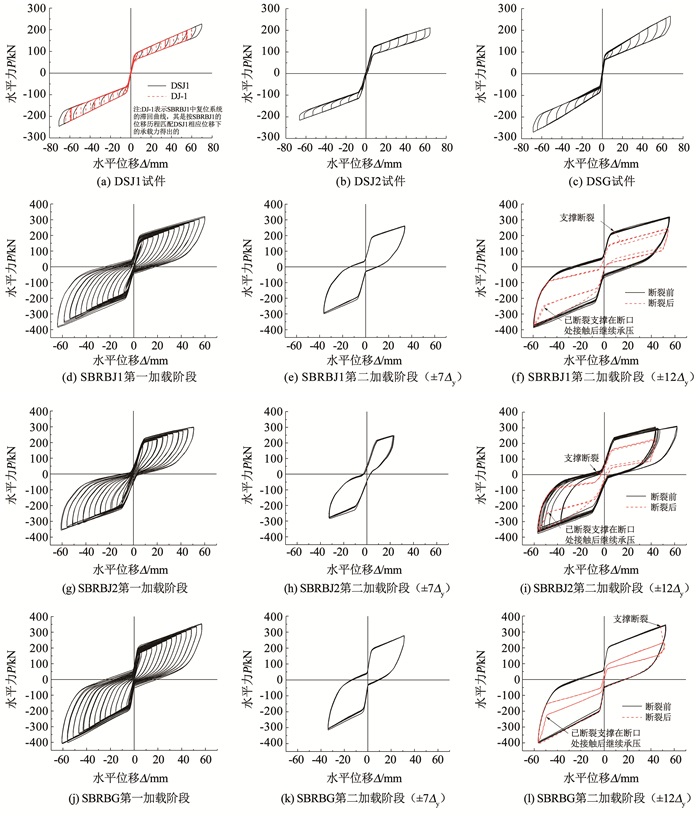
|
图 7 试件的滞回曲线 Fig. 7 Hysteretic curves of specimens |
因3个DS试件工作稳定,为了考察每个SBRB中复位系统和防屈曲支撑部分各自的承载力和耗能等情况,假定复位系统在SBRB试件中仍表现出类似图 7(a)~(c)中的曲线。对于复位系统和端部连接相同的两试件DS和SBRB,可根据SBRB的位移加载历程来匹配出相应位移下DS的承载力,进而获得这个SBRB中复位系统的滞回曲线。然后,将相同位移下SBRB的承载力和配出的复位系统(DS)部分的承载力作差,便可得到这个SBRB中防屈曲支撑(BRB)部分的滞回曲线。SBRBJ1、SBRBJ2和SBRBG中匹配出的DS部分分别记为DJ-1、DJ-2和DG;作差获得的BRB部分分别记为BJ-1、BJ-2和BG,BRB部分的承载力记为PBRB。以SBRBJ1为例,匹配出其内部复位系统DJ-1的滞回曲线见图 7(a),BJ-1的滞回曲线见图 8(a)。每个SBRB试件及其内部的DS部分和BRB部分的骨架曲线分析表明,DS部分和BRB部分的骨架曲线均呈双折线,拐点处的位移分别对应启动位移Δs和屈服位移Δy,又因二者差别不大,总体上SBRB的骨架曲线也呈双折线。以SBRBJ1为例,骨架曲线见图 8(b)。
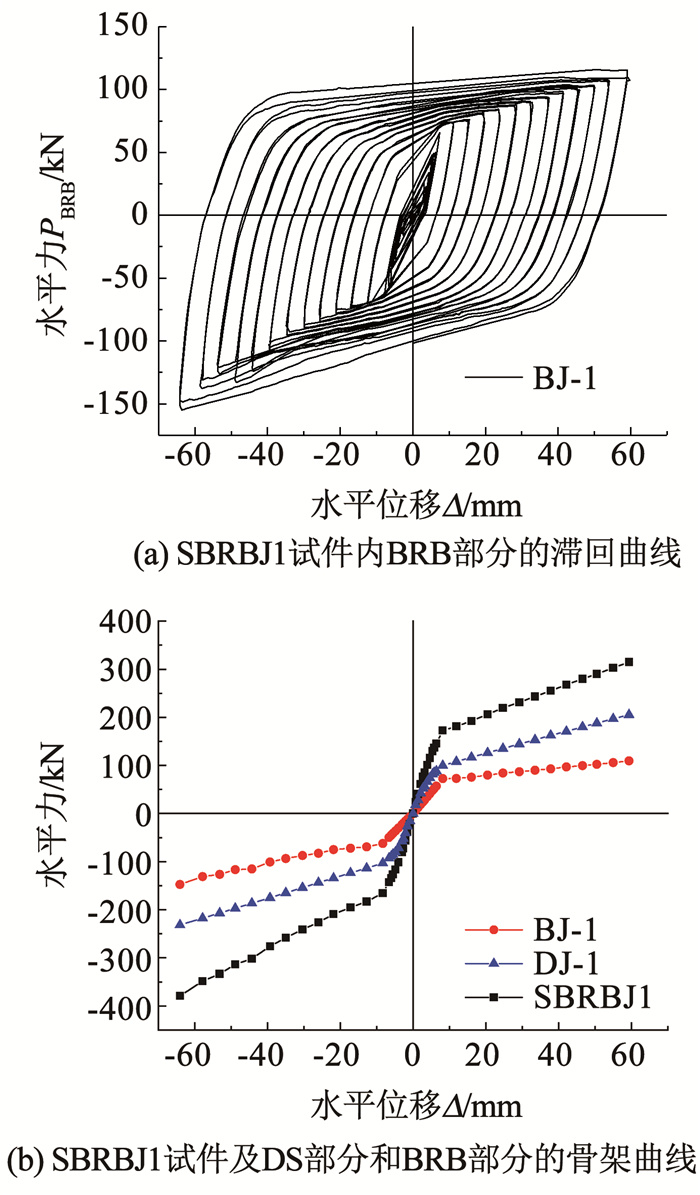
|
图 8 SBRBJ1的曲线 Fig. 8 Curves for the SBRBJ1 |
由图 9(a)可知,因每个DS试件启动前、后的荷载-位移关系基本呈线性,为了确定其启动力和启动位移,可对其拉压两侧启动前、后的骨架曲线进行线性拟合,得到两条直线l1(l3)和l2(l4),见图 9(b),两条直线交点对应的位移即为启动位移Δs,在骨架曲线上此位移对应的荷载即为启动力P0。
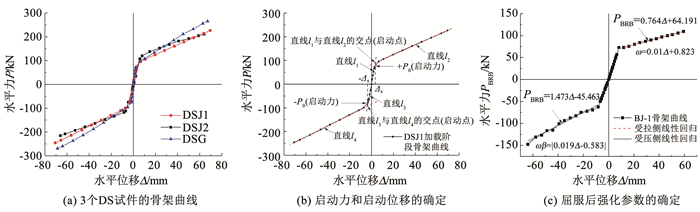
|
图 9 骨架曲线和参数的确定 Fig. 9 Backbone curves and determination of parameters |
由图 7(a)~(c)可知,因组合碟簧内以及控制钢管和连接钢管等复位系统内的部件间存在摩擦效应,且加、卸载阶段摩擦力方向相反,其加载阶段和卸载阶段的荷载-位移曲线不重合,即DS试件加载和卸载时的启动力不同。据此,可以按类似图 9(b)的做法分别获得加、卸载阶段的-P0和+P0,而加、卸载阶段的启动位移Δs几乎相同(见表 3)。表 3给出了各DS试件的启动位移Δs和启动力P0,可以看出,与DSJ1相比,DSJ2启动前刚度较低,但其启动力较大,导致实测启动位移较大(图 9(a))。
| 表 3 启动位移和启动力 Tab. 3 Start displacements and forces |
需说明的是,按理想状态,启动前,组合碟簧与12根螺杆并联,螺杆轴向刚度远大于组合碟簧。因此,理论上DSJ1和DSJ2启动前刚度基本相同。但由于试验中支撑端部销轴间隙和滑移的影响且其影响对各试件可能不同,虽然在水平力P接近0 kN时间隙导致的明显滑移已从滞回曲线上消去,但因部分间隙的影响随受力变化而夹杂在滞回曲线中,难于完全从滞回曲线上消除其影响,导致实测的DSJ2启动前刚度稍低。又因DSJ2启动力大,启动位移也较大。而刚接时,因上部推拉块连接钢管和下部推拉块的控制钢管间额外的相互作用参与抗侧力,DSG的刚度略大于DSJ1,启动位移较小。
各试件的BRB部分在屈服后因钢材应变硬化和受压时钢板支撑与约束构件间的摩擦效应导致其承载力PBRB进一步增大,文献[1]通过定义受拉承载力调整系数ω=+Pu/Pyc和受压承载力调整系数β=|-Pu/+Pu|来分别考虑受拉和受压承载力的提高。其中,+Pu和-Pu分别为试验实测水平方向受拉、受压峰值荷载,Pyc为钢板支撑由实测的屈服应力和截面尺寸计算所得的水平向屈服承载力。考虑BRB的骨架曲线基本呈双折线,为了应用方便,对BRB屈服后骨架曲线进行线性回归(图 9(c)),便可计算出ω和β随加载位移变化的表达式,见表 4。各BRB部分在1/50侧移角时受压承载力调整系数β1/50均小于1.5,满足设计条文[1]的要求。
| 表 4 BRB部分的强化参数 Tab. 4 Hardening parameters for BRB parts |
比较图 7和图 8(a)可知,与BRB部分相比,复位系统并入后形成SBRB试件可有效地降低相同加载位移幅值卸载后支撑的残余变形。BRB部分屈服后,提取3个SBRB试件及其BRB部分在每级第一圈加载位移幅值下对应的残余位移,见图 10(a)。随加载位移增大,BJ-1、BJ-2和BG的残余位移基本呈线性增大,相同加载侧移下,三者的残余位移较接近,BG的稍大。在加载1/50侧移角(对应Δ=31.2 mm)下,BG在拉、压两侧的残余侧移角分别约为+1.69%和-1.70%;而SBRBJ1、SBRBJ2和SBRBG受拉(压)侧的残余侧移角分别为+0.4%(-0.43%)、+0.1%(-0.16%)和+0.37%(-0.49%),均小于文献[2]中0.5%的限值,表明复位效果良好。其中,SBRBJ2的残余变形Δr为+1.56 mm(-2.50 mm),均小于对应DSJ2试件的启动位移(表 3),几乎完全消除了残余变形。
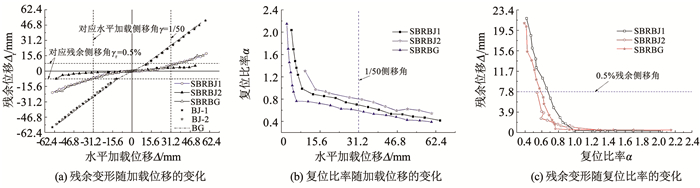
|
图 10 残余变形和复位比率 Fig. 10 Residual deformation and self-centering ratios |
因相同位移幅值下受压侧残余变形较大,按受压侧的DS部分启动力和BRB部分的屈服后承载力计算整个自复位支撑复位比率α=|-P0/(ωβPyc)|。再考虑拉、压作用下均是DS部分卸载阶段的力来控制BRB部分的残余变形,因此,复位比率计算中统一采用表 3受压卸载阶段的启动力。
由图 10(b)可知,因防屈曲支撑屈服后承载力随加载位移增大而增加,3个SBRB试件复位比率α均随加载位移幅值的增大而减小。1/50侧移角下,SBRBJ1、SBRBJ2和SBRBG的复位比率分别约为0.7、0.8和0.6。各试件残余位移随复位比率的变化见图 10(c)。可以看出,随α增加,Δr减小,α<0.9时,随α增加Δr减幅明显;当α>0.9时,Δr减幅趋缓;当α>1.2后,随α的增加Δr减幅甚微。以0.5%作为残余变形角的限值,当α>0.7时可满足要求,而当α>0.9时Δr已经极小(残余变形角小于0.1%)。考虑复位比率过大不会再明显减小残余变形,还将提高对DS部分的设计要求,故建议加载1/50侧移角下的复位比率取0.7~0.9。实际设计中,在获得整根支撑总设计轴力后,因复位系统和防屈曲支撑并联受力和分配总轴力,在预估了防屈曲支撑拟采用的屈服轴力以及相应的调整系数ω和β后,组合碟簧的预压力可根据复位比率在上述合理范围内取值的原则确定,进而确定碟簧的组合方式、防屈曲支撑的截面组成等。
由图 10(a)可知,其他构造基本相同时,SBRBJ1和SBRBG对比表明,相同受压加载位移下,刚接试件残余变形稍大,但总体上,端部连接形式对残余变形影响不大。SBRBJ1和SBRBJ2相比,前者组合碟簧的刚度更大,导致DS部分启动后承载力增幅较多(图 9(a)),而SBRBJ2的启动力更大(表 3),进而相同位移下复位比率更大(图 10(b)),使大的加载侧移下支撑残余位移更小(图 10(a)和(c))。
3.2 承载力、延性和耗能相同加载位移下,每个SBRB试件中DS部分和BRB部分的承载力和整个支撑承载力的比值见图 11(a)。可以看出,DS部分承载力占比高于BRB部分,是SBRB试件承载力的主要来源。在大位移幅值下,各部分承载力占比趋于稳定,DS部分和BRB部分占比分别为57%~69%和31%~43%。
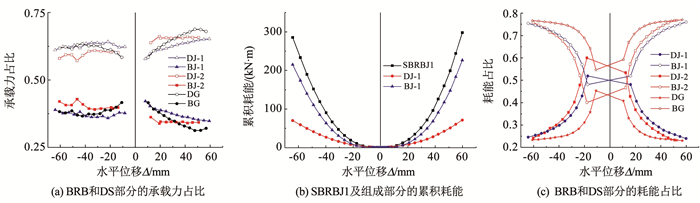
|
图 11 第一加载阶段的承载力和累积耗能 Fig. 11 Bearing capacity and cumulative energy dissipation in the first loading stage |
以SBRBJ1为例,第一加载阶段的累积耗能见图 11(b)。可以看出,耗能主要源自BRB部分,因两推拉块钢管间的相互作用、组合碟簧内部以及其他部件之间的摩擦作用,DS部分也有一定的耗能能力。由图 11(c)可知,加载位移31.2 mm(对应1/50侧移角)后,BRB部分和DS部分耗能占比分别为64%~77%和23%~36%。各SBRB在支撑受拉断裂导致承载力下降前的总累积耗能Ep见表 5,可见其他构造相同时,因端部铰接更有利于支撑轴心受力,与SBRBG相比,铰接的SBRBJ1耗能能力更大,而端部刚接会在钢板支撑中产生附加弯矩,易使钢板支撑较早断裂。
| 表 5 试验的承载力、变形和耗能结果 Tab. 5 Test results of bearing capacity, deformation and energy dissipation |
表 5的水平力和位移中正、负号分别表示受拉和受压。Δy和Py为BRB部分屈服时对应SBRB试件的屈服位移和屈服承载力,Δy取BRB部分骨架曲线拐点处对应的位移。Δu和Pu分别为最大加载位移和最大承载力,P1/50为1/50侧移角下的承载力。BRB部分的累积非弹性变形系数η按文献[14]计算,见表 5,且η值远大于文献[1]BRB的η至少为200的要求,表明支撑延性较好。
4 结论1) SBRB中钢板支撑断裂位置不总出现在屈服段端部,表明不设置过渡段的等宽钢板支撑更有利于避免制作中屈服段局部截面削弱。与端部刚接时钢板支撑更早断裂相比,端部铰接更有利于实现支撑轴心受力,支撑的累积耗能能力更好。
2) SBRB的主要承载和耗能能力分别来自DS和BRB部分,在侧移角接近1/50及更大时,占比分别为57%~69%和64%~77%。因组合碟簧间的摩擦作用等因素,DS部分也具有一定的耗能能力。
3) 加载侧移角1/50下,SBRBJ1、SBRBJ2和SBRBG的最大残余侧移角约为0.49%;而对应防屈曲支撑部分BJ-1、BJ-2和BG的约为1.70%。总体上,SBRB残余变形Δr随复位比率α的增加而逐渐减小。若以0.5%作为残余变形角限值,建议加载1/50侧移角下的复位比率取0.7~0.9。总体上,端部连接形式对残余变形影响不大。
| [1] |
American Institute of Steel Construction. Seismic provisions for structural steel buildings: ANSI/AISC 341-16[S]. Chicago: AISC, 2016
|
| [2] |
中华人民共和国住房和城乡建设部. 建筑抗震韧性评价标准: GB/T 38591—2020[S]. 北京: 中国标准出版社, 2020 Ministry of Housing and Urban Rural Development of the People's Republic of China. Standard for seismic resilience assessment of buildings: GB/T 38591—2020[S]. Beijing: Standards Press of China, 2020 |
| [3] |
DING Yukun, ZHENG Rui, ZHANG Wenyuan. Tests of chevron panel buckling-restrained braced steel frames[J]. Journal of Constructional Steel Research, 2018, 143: 233. DOI:10.1016/j.jcsr.2017.12.024 |
| [4] |
MILLER D J, FAHNESTOCK L A, EATHERTON M R. Development and experimental validation of a nickel-titanium shape memory alloy self-centering buckling-restrained brace[J]. Engineering Structures, 2012, 40: 288. DOI:10.1016/j.engstruct.2012.02.037 |
| [5] |
ZHOU Z, XIE Q, LEI X C, et al. Experimental investigation of the hysteretic performance of dual-tube self-centering buckling-restrained braces with composite tendons[J]. Journal of Composites for Construction, 2015, 19(6): 04015011. DOI:10.1061/(ASCE)CC.1943-5614.0000565 |
| [6] |
CHOU C C, TSAI W J, CHUNG P T. Development and validation tests of a dual-core self-centering sandwiched buckling-restrained brace (SC-SBRB) for seismic resistance[J]. Engineering Structures, 2016, 121: 30. DOI:10.1016/j.engstruct.2016.04.015 |
| [7] |
MOUSAVI S A, ZAHRAI S M, PASAND A A. Drift-based seismic design procedure for buckling restrained braced frames[J]. Structures, 2021, 30: 62. DOI:10.1016/j.istruc.2020.12.077 |
| [8] |
DING Yukun, LIU Yangtao. Cyclic tests of assembled self-centering buckling-restrained braces with pre-compressed disc springs[J]. Journal of Constructional Steel Research, 2020, 172: 106229. DOI:10.1016/j.jcsr.2020.106229 |
| [9] |
汤孟轲. 同轴组装自复位碟簧内置防屈曲支撑滞回性能与设计方法[D]. 哈尔滨: 哈尔滨工业大学, 2019 TANG Mengke. Hysteretic behavior and design methods for self-centering buckling-restrained brace coaxially assembled in disc springs[D]. Harbin: Harbin Institute of Technology, 2019 |
| [10] |
XU Longhe, CHEN Peng, LI Zhongxian. Development and validation of a versatile hysteretic model for pre-compressed self-centering buckling-restrained brace[J]. Journal of Constructional Steel Research, 2021, 177: 106473. DOI:10.1016/j.jcsr.2020.106473 |
| [11] |
JIN S S, AI P P, ZHOU J T, et al. Seismic performance of an assembled self-centering buckling-restrained brace and its application in arch bridge structures[J]. Journal of Constructional Steel Research, 2022, 199: 107600. DOI:10.1016/j.jcsr.2022.107600 |
| [12] |
中国建筑科学研究院. 建筑抗震试验规程: JGJ/T 101—2015[S]. 北京: 中国建筑工业出版社, 2015 China Academy of Building Sciences. Specification for seismic test of buildings: JGJ/T 101—2015[S]. Beijing: China Architecture and Building Press, 2015 |
| [13] |
FANG C, PING Y, CHEN Y. Loading protocols for experimental seismic qualification of members in conventional and emerging steel frames[J]. Earthquake Engineering & Structural Dynamics, 2020, 49: 155. DOI:10.1002/eqe.3231 |
| [14] |
NEWELL J, UANG C M, BENZONI G. Subassemblage testing of corebrace bucking-restrained braces (G series): TR-2006/01[R]. San Diego: University of California, 2006
|
 2024, Vol. 56
2024, Vol. 56


