为淘汰电力行业的落后产能,国家须关闭污染物排放量大、煤电转换率低的小型火电机组[1]。冷却塔是火电机组的必要配套设施,其拆除是一项危险且复杂的工作。因此,冷却塔的拆除常采用爆破设计简单、倒塌方向易控制的定向拆除。目前,关于冷却塔定向拆除的研究主要集中在国内,国外在这方面的研究较少。主要采用有限元研究各种爆破参数对倒塌形态的影响[2-4],而对冷却塔定向拆除的力学机制研究较少。在研究冷却塔定向拆除的力学机制时,一般将爆破后的冷却塔简化成图 1所示。对于保留筒壁的验算,上官子昌等[5]和汪高龙等[6]基于保留筒壁的抗弯承载力给出了冷却塔的倾倒验算公式,戴俊[7]基于筒壁的材料强度给出了冷却塔的倾倒验算公式。对于保留柱的验算,顾祥林等[8]基于保留柱的抗弯承载力给出了冷却塔的倾倒验算公式。
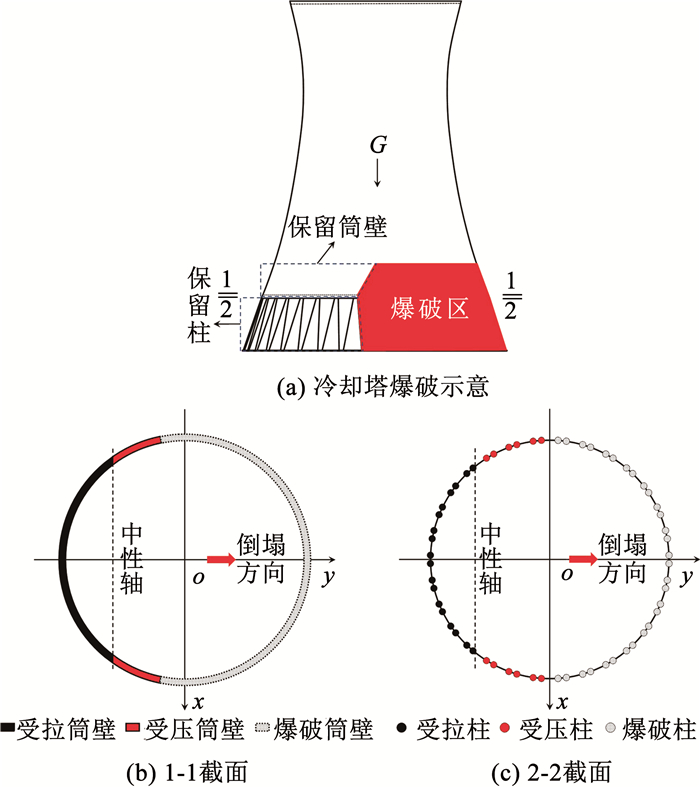
|
图 1 冷却塔爆破后计算简图 Fig. 1 Calculation diagram of cooling tower after blasting |
然而在实际工程中,冷却塔的拆除设计仍然依靠爆破工程师的工程经验,其主要原因是现有的理论是基于整个截面上的平截面假定推导而来,而实际上爆破后的冷却塔在整个截面上并不满足平截面假定。此外,大多数现有的理论只适用于保留筒壁,适用于保留柱的理论较少,而在工程案例中很多冷却塔的倒塌是由保留柱的失效所引起[9-11]。
从力学角度出发,针对保留柱提出一种可指导冷却塔定向拆除的理论公式。首先根据力的相似关系给出支柱Z向力与其轴向力的换算关系,然后基于所有保留柱上的平截面假定推导了保留柱Z向力的计算公式,随后根据模拟结果假设爆破后的冷却塔仅在部分保留柱上满足平截面假定对公式进行修正,并使用不同冷却塔检验了修正后公式的适用性。研究结果可从力学角度为冷却塔的定向拆除提供理论支撑,使冷却塔的拆除设计更加科学合理,拆除工作更加安全可控。
1 理论推导爆破后冷却塔的计算简图如图 2(a)所示,选取支柱柱顶所在的截面作为验算截面,验算截面上各保留柱的编号如图 2(b)所示。
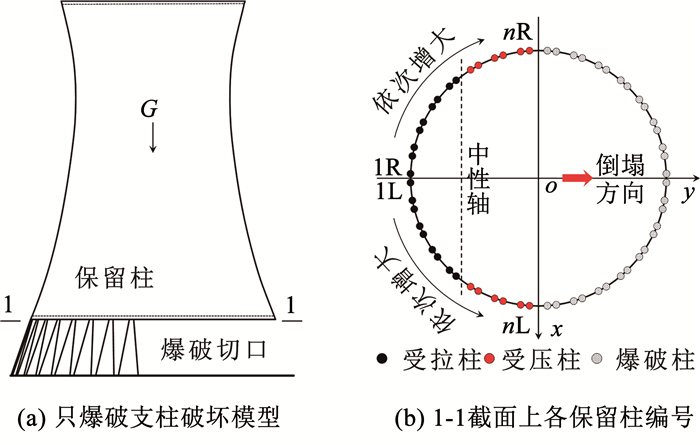
|
图 2 计算模型及保留柱编号 Fig. 2 Calculation model and retained columns number |
基于支柱材料的抗压强度提出只爆破支柱破坏模型的倾倒验算准则,即当第n排保留柱的压应力达到支柱材料的抗压强度时,爆破后的冷却塔即可沿着预定的方向发生倒塌,倾倒验算公式为
| $ \sigma_n \geqslant k \sigma_{\mathrm{c}}^{\mathrm{z}} $ | (1) |
式中:σn为第n排保留柱(nR和nL)所受的压应力值,σn=FNn/A。其中,FNn为第n排保留柱的轴向压力,A为支柱横截面面积。σcz为支柱材料的静态抗压强度,k为动态荷载作用下建筑材料强度的放大系数。
1.2 保留柱轴向力计算公式根据有限元结果,在计算时可将第n排保留柱简化为一个两端铰支且作用有弯矩和轴力大小相等、方向相反的压弯构件。在该简化计算模型中,由于保留柱的轴力大小不受端部弯矩的影响,在求解保留柱Z向力和轴向力的换算关系式时,可将第n排保留柱视为两端铰接的二力杆。
由于保留柱Z向力和轴向力之间的关系与支柱的位置和朝向无关,以图 3所示的支柱为例,给出保留柱Z向力与其轴向力之间的换算关系式。
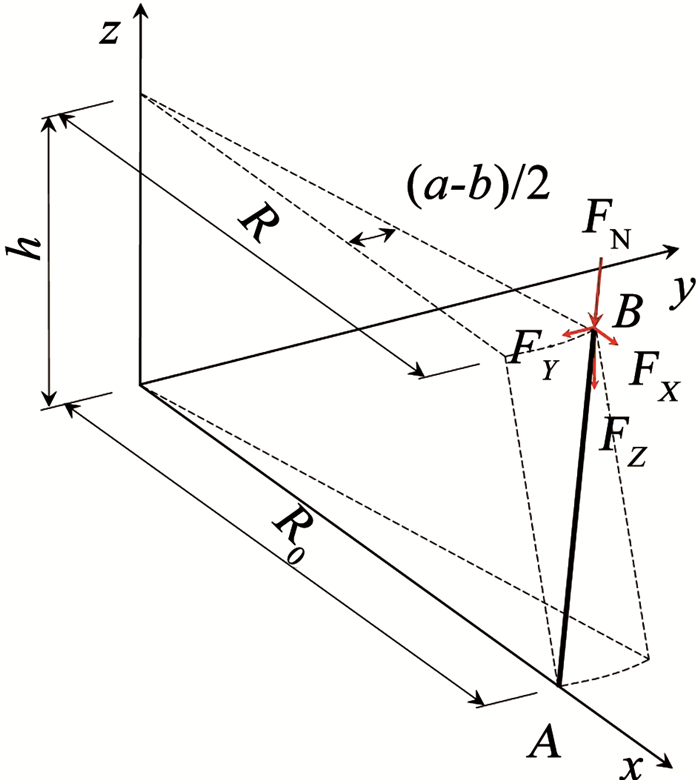
|
图 3 单根支柱几何关系示意 Fig. 3 Geometric relationship diagram of single column |
根据空间几何关系可得支柱AB的空间向量
| $ \boldsymbol{A B}=\left(R \cos \frac{a-b}{2}-R_0, R \sin \frac{a-b}{2}, h\right) $ |
式中:R0和R分别为支柱柱底和柱顶处的半径;h为支柱的高度;a、b分别为相邻柱柱顶所对应的圆心角(如图 4所示),且a>b。
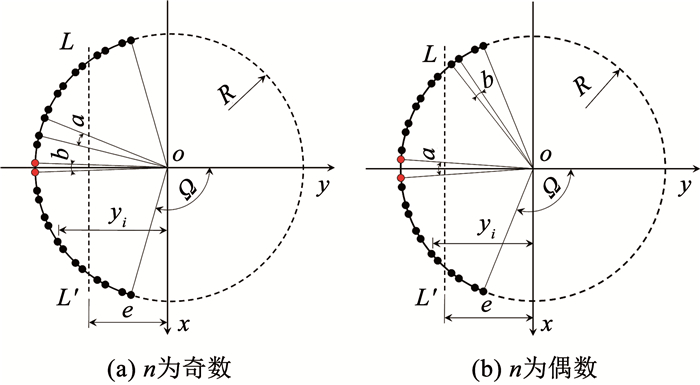
|
R为柱顶处冷却塔的半径,a、b分别为两种相邻柱柱顶所对应的圆心角(a>b),yi为第i排保留柱到x轴的距离,e为保留柱中性轴LL′到x轴的距离,Ω为爆破圆心角的1/2。 图 4 验算截面示意 Fig. 4 Diagram of calculation section |
由力的相似关系可得第n排保留柱轴向力
| $ F_{\mathrm{N} n}=\frac{\sqrt{\left(R \cos \frac{a-b}{2}-R_0\right)^2+\left(R \sin \frac{a-b}{2}\right)^2+h^2}}{h} \cdot F_{Z n} $ | (2) |
式中FZn为第n排保留柱Z向力。
1.3 保留柱Z向力计算公式假设只爆破支柱破坏模型满足以下假定:1)爆破后y轴两侧保留柱的受力及变形完全对称;2)各保留柱在Z方向上的变形与其y轴坐标之间满足线性关系,即爆破后的冷却塔在所有保留柱上满足平截面假定;3)保留柱上部结构的重心通过环梁的圆心;4)支柱为均质线弹性材料。
为计算不同n值下FZn的大小,按照n值的奇偶性,分别推导了n为奇数时和n为偶数时FZn的计算公式。
1.3.1 n为奇数当n为奇数时,验算截面上各保留柱的分布如图 4(a)所示。由几何关系可得,第i排保留柱到x轴的距离yi如式(3)所示,其中i=1,2,3,…,n。
| $ y_i=\left\{\begin{array}{l} R \cos \left[\frac{i-1}{2}(a+b)+\frac{b}{2}\right], i \text { 为奇数 } \\ R \cos \left[\frac{i}{2}(a+b)-\frac{b}{2}\right], i \text { 为偶数 } \end{array}\right. $ | (3) |
第i排保留柱到中性轴LL′的距离di为
| $ d_i=y_i-e $ | (4) |
由各保留柱Z向力的分布满足平截面假定可得各保留柱Z向力与其Z向位移的关系为
| $ \frac{F_{Z 1}}{d_1}=\frac{F_{Z 2}}{d_2}=\cdots=\frac{F_{Z n}}{d_n} $ | (5) |
根据验算截面在LL′上的力矩平衡和验算截面在Z方向上力的平衡可得
| $ \begin{gathered} \sum M_{L L^{\prime}}=2\left(F_{Z 1} d_1+F_{Z 2} d_2+\cdots+F_{Z n} d_n\right)=G e \\ 2 \sum F_{Z i}=-G \end{gathered} $ | (6) |
将式(4)和(5)代入式(6)可得保留柱中性轴LL′到x轴距离e的计算公式,如式(7)所示,各保留柱Z向力FZi的计算公式如式(8)所示。
| $ e=\frac{\sum\limits_{i=1}^n y_i^2}{\sum\limits_{i=1}^n y_i} $ | (7) |
| $ F_{Z i}=G e \frac{d_i}{2 \sum\limits_{i=1}^n d_i^2} $ | (8) |
当n为偶数时,各保留柱Z向力计算公式的推导方法与n为奇数时完全相同,且保留柱中性轴LL′到x轴的距离e仍按式(7)计算,各保留柱Z向力FZi仍按式(8)计算。不同之处在于:第i排保留柱到x轴距离的计算公式发生改变,当n为偶数时验算截面上各保留柱的分布如图 4(b)所示。
由几何关系可得,当n为偶数时,第i排保留柱到x轴的距离yi为
| $ y_i=\left\{\begin{array}{l} R \cos \left[\frac{i-1}{2}(a+b)+\frac{a}{2}\right], i \text { 为奇数 } \\ R \cos \left[\frac{i}{2}(a+b)-\frac{a}{2}\right], i \text { 为偶数 } \end{array}\right. $ | (9) |
为探究环梁和支柱的弹性模量、支柱高度、保留柱数量以及相邻柱柱顶所对应的圆心角等参数对保留柱Z向力的影响,根据文献[12-13]建立一座64.5 m高的钢筋混凝土冷却塔模型,采用ANSYS Workbench中的Static模块对冷却塔进行分析。
该冷却塔由人字柱、环梁以及筒壁共同组成,其中筒壁与环梁由36对人字柱支撑,人字柱的截面为内径0.4 m的正八边形,环梁高1.9 m,冷却塔的具体尺寸如表 1所示。
| 表 1 64.5 m高冷却塔尺寸参数 Tab. 1 Size parameters of 64.5 m cooling tower |
重点关注冷却塔支柱的受力情况,在建立有限元模型时,将钢筋混凝土等效为一种均质线弹性材料。等效后钢筋混凝土的密度根据钢筋与混凝土的质量等效确定,其弹性模量根据刚度等效确定(以受压为主的构件可根据抗压刚度等效确定,以受弯为主的构件可根据抗弯刚度等效确定)。等效后的钢筋混凝土采用SOLID186单元,冷却塔各部位材料信息如表 2所示。
冷却塔模型仅考虑重力作用,支柱-环梁以及环梁-筒壁之间采用Bonded接触进行连接,各层筒壁之间采用共节点进行连接,支柱底部采用固定约束。
2.2 有效性验证建立一座60.0 m高钢筋混凝土冷却塔的有限元模型,通过对比其前四阶频率的模拟值与实测值来验证建模方法的有效性。该冷却塔的几何信息和材料信息详见文献[14],有限元分析时取该钢筋混凝土冷却塔的弹性模量为25.6 GPa,密度为2 500 kg/m3,泊松比为0.2。由表 3可知,冷却塔前四阶频率的模拟值与实测值的相对误差均在5%以内,由此可证明建模方法的有效性。
| 表 3 60.0 m高冷却塔前四阶频率 Tab. 3 First four-order frequency of 60.0 m cooling tower |
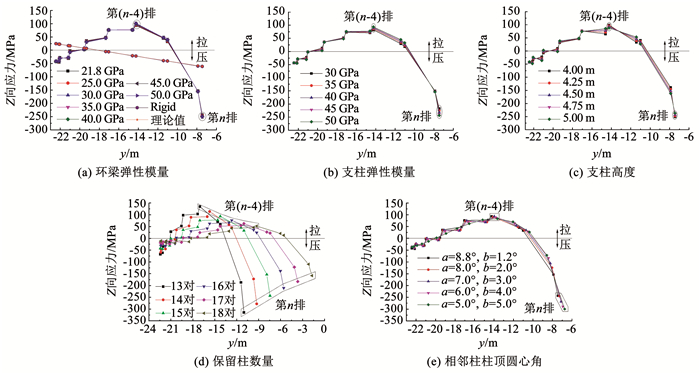
参数分析时维持其他参数不变,仅改变单个参数的取值。根据规范[15-16]对环梁和支柱配筋率及混凝土强度的要求,分别取环梁的弹性模量为21.8~50.0 GPa、支柱的弹性模量为30~50 GPa进行参数分析。根据规范[15]对冷却塔进风口面积与支柱柱顶处冷却塔的面积之比的要求,取支柱的高度为4.0~5.0 m进行参数分析。根据工程常用爆破圆心角的取值(190°~240°),取保留柱的数量为13~18对进行参数分析。根据64.5 m高冷却塔的几何特征,取相邻柱柱顶圆心角b为1.2°~5.0°进行参数分析。5种参数的分析结果如图 5所示。
|
图 5 各参数对保留柱Z向应力的影响 Fig. 5 Effects of various parameters on Z-direction stress of retained columns |
由图 5(a)可知,当环梁的弹性模量无穷大时,各保留柱的Z向应力值与理论计算值基本相同,而弹性模量为21.8~50.0 GPa时,理论计算值与模拟值存在较大差异,但不同环梁弹性模量下各保留柱Z向应力的分布曲线基本重合;由图 5(b)和(c)可知,不同支柱弹性模量下和不同支柱高度下,各保留柱Z向应力的大小及分布总体上相差不大,仅在个别保留柱上存在差异。其中,随着支柱弹性模量的增加和支柱高度的减小,第15排保留柱的Z向应力值呈小幅度递增,但支柱弹性模量从30 GPa增到50 GPa,第15排保留柱Z向应力的增幅不超过12%,支柱高度从5.00 m减小到4.00 m,第15排保留柱Z向应力的增幅不超过6%;由图 5(d)和(e)可知,保留柱数量和相邻柱柱顶圆心角对各保留柱Z向应力值的影响较大,且随着保留柱数量的减小和柱顶圆心角a的减小,第15排保留柱的Z向应力值呈递增趋势,但保留柱数量和相邻柱柱顶圆心角并不影响各保留柱Z向应力的分布规律。
通过分析可知,基于平截面假定得到的理论计算值与实际值存在较大偏差,其主要原因为爆破后的冷却塔在所有保留柱上并不满足平截面假定;在实际工程范围内,环梁和支柱的弹性模量以及支柱高度对各保留柱Z向应力值的影响较小,保留柱数量与相邻柱柱顶圆心角对保留柱Z向应力值的影响较大;在实际工程范围内,各保留柱的Z向力沿着y轴方向上的分布呈现“两端受压,中间受拉”的分布形态,且各保留柱Z向力的分布始终呈现以下规律:保留柱中的最大压力始终出现在第n排保留柱上,最大拉力始终出现在第(n-4)排保留柱上。
3 理论修正及其计算精度由于爆破后的冷却塔在所有保留柱上不满足平截面假定,且冷却塔的支柱是一个空间三维构件,保留柱Z向力的大小除了与柱顶Z向位移有关外,还与其X和Y方向上的位移有关。因此,要想准确计算出保留柱Z向力的大小需知道柱顶在X、Y、Z 3个方向上的位移,而这是一个复杂且困难的过程。为了给出一个计算过程便捷的第n排保留柱轴向力的计算公式,根据参数分析的结果对1.3节公式进行了修正。
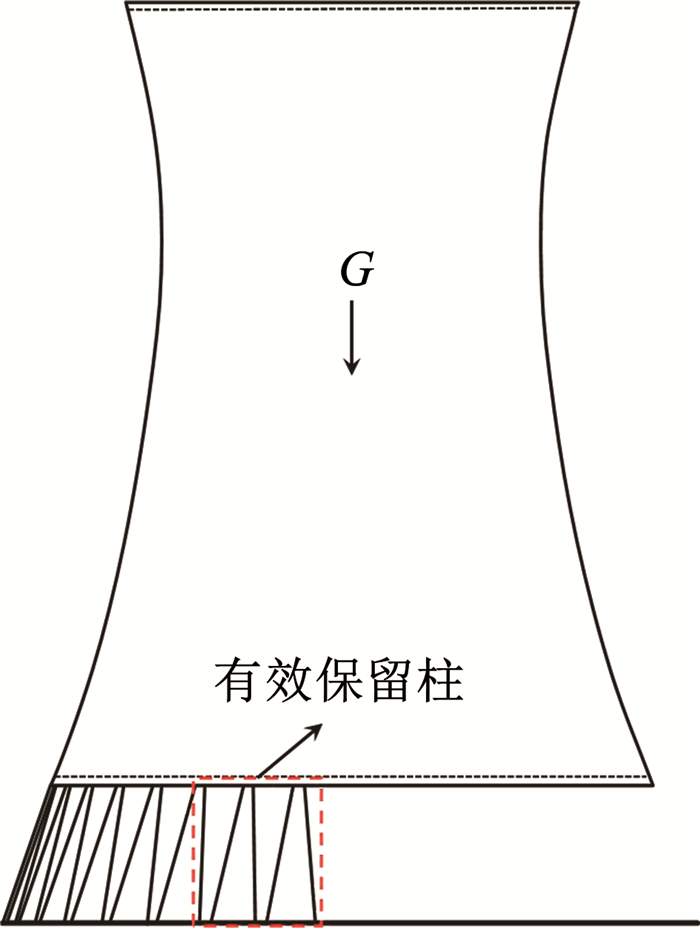
3.1 计算公式的修正根据“保留柱中的最大压力始终出现在第n排保留柱上,最大拉力始终出现在第(n-4)排保留柱上”这一特征,提出一种“有效保留柱修正法”,即无论保留柱数量为多少,均取靠近爆破切口的前5排柱作为有效保留柱(如图 6所示)。
|
图 6 有效保留柱示意 Fig. 6 Diagram of effective retained column |
在有效保留柱修正法中,假定爆破后的倾倒力矩全部由有效保留柱承担,且爆破后的冷却塔在有效保留柱范围内满足平截面假定。
假设在倾倒力矩的作用下,有效保留柱的中心轴到x轴的距离为e′,则各有效保留柱柱顶到中性轴的距离d′i为
| $ d_i^{\prime}=y_i-e^{\prime} $ | (10) |
由Z向力的分布满足平截面假定可得
| $ \frac{F_{Z n}^{\prime}}{d_n^{\prime}}=\frac{F_{Z(n-1)}^{\prime}}{d_{n-1}^{\prime}}=\frac{F_{Z(n-2)}^{\prime}}{d_{n-2}^{\prime}}=\frac{F_{Z(n-3)}^{\prime}}{d_{n-3}^{\prime}}=\frac{F_{Z(n-4)}^{\prime}}{d_{n-4}^{\prime}} $ | (11) |
由验算截面上力的平衡关系可得
| $ \begin{gathered} \sum M=2 \sum\limits_{i=n-4}^n F^{\prime}{ }_{Z i} d^{\prime}{ }_i=G e \\ \sum F=2 \sum\limits_{i=n-4}^n F^{\prime}{ }_{Z i}=-G \end{gathered} $ | (12) |
将式(10)和(11)代入式(12)可得,有效保留柱的中心轴到x轴的距离e′为
| $ \begin{aligned} e_{1, 2}^{\prime}&=\frac{\left(5 e+2 \sum\limits_{i=n-4}^n y_i\right)}{10} \pm \\ &\frac{\sqrt{\left(5 e+2 \sum\limits_{i=n-4}^n y_i\right)^2-20\left(e \sum\limits_{i=n-4}^n y_i+\sum\limits_{i=n-4}^n y_i^2\right)}}{10} \end{aligned} $ | (13) |
修正后各有效保留柱Z向力F′Zi为
| $ F_{Z i}^{\prime}=G e \frac{d_i^{\prime}}{2 \sum\limits_{i=n-4}^n d_i^{\prime 2}} $ | (14) |
则修正后第n排保留柱轴向力F′Nn为
| $ F_{\mathrm{N} n}^{\prime}=\frac{\sqrt{\left(R \cos \frac{a-b}{2}-R_0\right)^2+\left(R \sin \frac{a-b}{2}\right)^2+h^2}}{h} \cdot F_{Z n}^{\prime} $ | (15) |
为了检验修正后公式的计算精度,分别将不同保留柱数量和不同相邻柱柱顶圆心角下第n排保留柱轴向应力的计算值与有限元模拟值进行对比。
3.2.1 计算过程以13对保留柱为例,给出第n排保留柱轴向应力的计算过程。已知保留柱上部冷却塔自重(G)为29 376 kN,冷却塔在柱底和柱顶处半径(R0和R)分别为24.0、22.441 m,支柱高度(h)和横截面面积(A)分别为4.5 m和0.113 137 m2,两种相邻柱柱顶所对应的圆心角(a和b)分别为8.8°和1.2°。
由式(3)得各保留柱柱顶y轴的坐标,由此可得
| $ \begin{aligned} & \sum\limits_{i=1}^{13} y_i=233.345 \mathrm{~m}, \sum\limits_{i=1}^{13} y_i^2=4383.955 \mathrm{~m}^2 \\ & \sum\limits_{i=9}^{13} y_i=68.327 \mathrm{~m}, \sum\limits_{i=9}^{13} y_i^2=958.346 \mathrm{~m}^2 \end{aligned} $ |
由式(7)可得修正前中性轴到x轴的距离
| $ e=4383.955 \div 233.345=18.787 \mathrm{~m} $ |
由式(8)可得修正前第13排保留柱Z向力
| $ F_{\mathrm{Z} 13}=\frac{29376651 \times 18.787 \times(-7.771)}{2 \times 204.632}=-10479320 \mathrm{~N} $ |
由式(1)和(2)可得修正前第13排保留柱轴向应力
| $ \begin{aligned} \sigma_{13}= & \frac{\sqrt{\left(22.441 \cos 3.8^{\circ}-24\right)^2+\left(22.441 \sin 3.8^{\circ}\right)^2+4.5^2}}{4.5 \times 0.113137} \times \\ & (-10479320)=-103.014 \mathrm{MPa} \end{aligned} $ |
由式(13)可得修正后中心轴到x轴的距离
| $ e^{\prime}=\frac{230.591-\sqrt{230.591^2-20 \times 2242.03}}{10}=13.931 \mathrm{~m} $ |
由式(10)可得各有效保留柱到修正后中性轴的距离,再由式(14)可得修正后第13排保留柱Z向力
| $ \begin{aligned} F_{Z 13}^{\prime}= & \frac{29376651 \times 18.787 \times(-2.915)}{2 \times 24.993}= \\ & -32184732 \mathrm{~N} \end{aligned} $ |
由式(1)和(15)可得修正后第13排保留柱轴向应力
| $ \sigma_{13}^{\prime}=-103.014 \times 32185 \div 10479=-316.391 \mathrm{MPa} $ |
不同保留柱数量与不同相邻柱柱顶圆心角下,修正前后第n排保留柱轴向应力的计算值和有限元模拟值如表 4和5所示。可以看出,无论是不同保留柱数量下,还是不同相邻柱柱顶圆心角下,修正后的计算精度相比修正前均得到有效提升,且修正后的计算值与模拟值的相对误差较小;当爆破圆心角为190°~240°时,修正后第n排保留柱轴向应力计算值的相对误差在23%以内;不同相邻柱柱顶圆心角下,修正后第n排保留柱轴向应力计算值的相对误差在10%以内。
| 表 4 不同保留柱数量下第n排保留柱的轴向应力 Tab. 4 The axial stress of the nth retained column under different number retained columns |
| 表 5 不同相邻柱柱顶圆心角下第n排保留柱的轴向应力 Tab. 5 The axial stress of the nth retained column under different central angles of the top of adjacent column |
为了检验修正后计算公式在不同冷却塔中的适用性,分别建立一座177 m高和一座191 m高的钢筋混凝土冷却塔模型,对比不同保留柱数量下第n排保留柱轴向应力的计算值和模拟值。
两座钢筋混凝土冷却塔的筒壁均由48对人字柱支撑,且人字柱截面均为直径1.3 m的圆。其中,177 m高冷却塔相邻柱柱顶所对应的圆心角a、b分别为6.3°、1.2°,筒身重力为455 535 kN。191 m高冷却塔相邻柱柱顶所对应的圆心角a、b分别为6.1°、1.4°,筒身重力为452 002 kN。两座冷却塔的尺寸与材料信息详见文献[17-18],材料参数如表 6所示。
| 表 6 177、191 m高冷却塔各部分材料参数 Tab. 6 Material parameters of 177 and 191 m cooling tower |
经计算与模拟可得,不同保留柱数量下177、191 m高钢筋混凝土冷却塔的第n排保留柱的轴向应力分别如表 7和8所示。可以看出,当爆破圆心角为190°~240°时,177 m高冷却塔修正后的理论计算值和有限元模拟值的相对误差在23%以内,191 m高冷却塔修正后的理论计算值和有限元模拟值的相对误差在33%以内。
| 表 7 177 m高冷却塔第n排保留柱轴向应力 Tab. 7 The axial stress of the nth retained column of 177 m cooling tower |
| 表 8 191 m高冷却塔第n排保留柱轴向应力 Tab. 8 The axial stress of the nth retained column of 191 m cooling tower |
由表 4、5、7、8可以看出,无论是64.5 m高的冷却塔还是177、191 m高的冷却塔,修正后第n排保留柱轴向力的计算精度均得到大幅提升,且当爆破圆心角为200°~240°时,修正后的计算值和有限元模拟值的相对误差均在21%以内;当爆破圆心角为210°~220°时,修正后的计算公式在3座冷却塔中均取得良好的计算精度,其相对误差均在12%以内。由此可以说明修正后的计算公式具有较好的适用性。
5 结论1) 基于所有保留柱上平截面假定得到的各保留柱Z向力的计算值与其实际值相差较大,其主要原因为爆破后的冷却塔在所有保留柱上并不满足平截面假定。
2) 在实际工程范围内,环梁弹性模量、支柱弹性模量、支柱高度、保留柱数量以及相邻柱柱顶所对应的圆心角5种参数并不影响保留柱Z向应力的分布特征,各保留柱Z向力沿y轴方向的分布呈现“两端受压,中间受拉”的形态,且保留柱中的最大压力始终出现在第n排保留柱上,最大拉力始终出现在第(n-4)排保留柱上。
3) 在实际工程范围内,修正后的第n排保留柱轴向力的计算公式具有较好的计算精度,且该公式可适用于不同高度的冷却塔,具有良好的适用性。修正后的计算公式与基于支柱材料强度的倾倒验算公式从力学角度为冷却塔的定向拆除提供了理论支撑,可增加冷却塔拆除工作的安全性。
| [1] |
佚名. 上大压小节能减排[J]. 上海企业, 2007(4): 5. |
| [2] |
付天杰, 赵超群, 梁儒, 等. 竖向切缝在高大冷却塔拆除爆破中的作用[J]. 工程爆破, 2011, 17(4): 58. FU Tianjie, ZHAO Chaoqun, LIANG Ru, et al. Application of vertical cut in demolition blasting of tall cooling tower[J]. Engineering Blasting, 2011, 17(4): 58. |
| [3] |
张建华, 谌彪, 黄刚, 等. 卸荷槽对冷却塔拆除爆破的数值模拟研究[J]. 爆破, 2020, 37(3): 122. ZHANG Jianhua, CHEN Biao, HUANG Gang, et al. Numerical simulation study on the influence of unloading tank for cooling tower blasting demolition[J]. Blasting, 2020, 37(3): 122. DOI:10.3963/j.issn.1001-487X.2020.03.021 |
| [4] |
张宝岗, 赵明生, 余红兵, 等. 切口角度对冷却塔爆破拆除影响研究[J]. 爆破, 2018, 35(1): 109. ZHANG Baogang, ZHAO Mingsheng, YU Hongbing, et al. Study on influence of cut angle on explosive demolition of cooling tower[J]. Blasting, 2018, 35(1): 109. DOI:10.3963/j.issn.1001-487X.2018.01.018 |
| [5] |
上官子昌, 李守巨, 刘书贤, 等. 定向爆破拆除冷却塔倾倒条件的研究[C]//第四届全国岩石动力学学术会议. 武汉: 湖北科学技术出版社, 1994: 120
|
| [6] |
汪高龙, 王潇, 李跟, 等. 复杂环境90 m高双曲线冷却塔拆除爆破[J]. 工程爆破, 2021, 27(1): 62. WANG Gaolong, WANG Xiao, LI Gen, et al. Demolition blasting of 90 m high hyperbola cooling tower in complicated environment[J]. Engineering Blasting, 2021, 27(1): 62. DOI:10.19931/j.EB.20200204 |
| [7] |
戴俊. 筒形建筑物爆破拆除缺口参数的力学分析[J]. 爆破器材, 1995, 24(5): 16. DAI Jun. Mechanical analyses on cutting-section parameters for demolishing a tube-shaped construction by blasting[J]. Explosive Materials, 1995, 24(5): 16. |
| [8] |
GU Xianglin, YU Qianqian, LI Yi, et al. Collapse process analysis of reinforced concrete super-large cooling towers induced by failure of columns[J]. Journal of Performance of Constructed Facilities, 2017, 31(5): 04017037. DOI:10.1061/(ASCE)CF.1943-5509.0001023 |
| [9] |
李洪伟, 颜事龙, 郭进, 等. 爆破拆除切口形状对冷却塔爆破效果影响及数值模拟[J]. 爆破, 2013, 30(4): 92. LI Hongwei, YAN Shilong, GUO Jin, et al. Numerical simulation of effect of cut parameters on explosive demolition of cooling towers[J]. Blasting, 2013, 30(4): 92. DOI:10.3963/j.issn.1001-487X.2013.04.020 |
| [10] |
谢先启, 姚颖康, 贾永胜, 等. 冷却塔爆破拆除失稳机制与变形破坏特征研究[J]. 爆破, 2017, 34(2): 40. XIE Xianqi, YAO Yingkang, JIA Yongsheng, et al. Study on instability mechanism and deformation characteristics of hyperbolic cooling tower explosive demolition[J]. Blasting, 2017, 34(2): 40. DOI:10.3963/j.issn.1001-487X.2017.02.007 |
| [11] |
张继春, 曾庆福, 严军, 等. 成都华能电厂106.6 m钢筋砼冷却塔控制爆破拆除[J]. 爆破, 2010, 27(1): 58. ZHANG Jichun, ZENG Qingfu, YAN Jun, et al. Controlled explosive demolition of 106.6 m reinforced concrete cooling tower in Chengdu Huaneng plant[J]. Blasting, 2010, 27(1): 58. DOI:10.3963/j.issn.1001-487X.2010.01.015 |
| [12] |
卢子冬, 张世平, 张昌锁. 永济市热电厂三座特殊结构冷却塔爆破拆除[J]. 爆破, 2014, 31(3): 114. LU Zidong, ZHANG Shiping, ZHANG Changsuo. Explosive demolition of three cooling towers with special construction in Yongji[J]. Blasting, 2014, 31(3): 114. DOI:10.3963/j.issn.1001-487X.2014.03.022 |
| [13] |
卢子冬. 烟囱、冷却塔、框架结构楼房爆破拆除数值模拟研究[D]. 太原: 太原理工大学, 2015 LU Zidong. Numerical simulation study of chimney, cooling tower and frame structure's demolition blasting[D]. Taiyuan: Taiyuan University of Technology, 2015 |
| [14] |
王朋国. 钢筋混凝土双曲冷却塔结构抗震性能分析及加固方法研究[D]. 北京: 北京交通大学, 2017 WANG Pengguo. Seismic performance and strengthening method of reinforced concrete hyperbolic cooling tower[D]. Beijing: Beijing Jiaotong University, 2017 |
| [15] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 工业循环水冷却设计规范: GB/T 50102—2014[S]. 北京: 中国计划出版社, 2014
|
| [16] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 混凝土结构设计规范: GB 50010—2014[S]. 北京: 中国建筑工业出版社, 2010
|
| [17] |
张宗方. 大型自然通风冷却塔失效分析与优化设计[D]. 大连: 大连理工大学, 2011 ZHANG Zongfang. Failure analysis and optimization design of large-scale natural draft cooling tower[D]. Dalian: Dalian University of Technology, 2011 |
| [18] |
杨亚. 大型冷却塔结构不同建模方式对比研究[D]. 重庆: 重庆交通大学, 2017 YANG Ya. Comparative study on different modeling methods of large cooling tower[D]. Chongqing: Chongqing Jiaotong University, 2017 |
 2024, Vol. 56
2024, Vol. 56


