2. 同济大学 土木工程学院, 上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
作为上部结构与基础连接的关键部位,柱脚将底层柱的轴力、剪力和弯矩传递至基础,是保证结构承载力和刚度的关键。1995年阪神淡路大地震中,24.5%的钢结构破坏均因柱脚受损造成[1]。典型的钢结构柱脚包括外露式、外包式及埋入式3类。其中,埋入式柱脚将钢柱伸入基础,由基础钢筋混凝土提供竖向及侧向支撑,其受弯承载力和刚度均较大,耗能性能好,在多高层及超高层结构中应用广泛。埋入式柱脚在结构计算中通常视为理想刚接,但有学者[3]指出这种假设可能过高地估计了柱脚节点的刚度。相应地,柱脚实际存在的柔性会降低第一层柱反弯点的位置,增加柱顶的抗弯需求,导致实际层间位移大于按理想刚接假定计算得到的层间位移。因此,埋入式柱脚的理想刚接假定可能会导致偏于不安全的结构设计。特别是,地铁上盖结构柱脚及大型复杂工程中的巨型柱脚往往无法达到规范规定的埋深。此类浅埋柱脚受埋入深度影响,其刚度可明显低于深埋柱脚,故整体结构设计时,若仍假定为理想刚接将导致严重的整体结构不安全。鉴于此,近年来,越来越多学者开始关注埋入式钢柱脚刚度的计算方法。
Morino等[4]仅考虑在混凝土承压应力反向点以上埋入柱段与混凝土的变形,且假定该柱段下端(即混凝土承压应力反向点处)的边界条件为固接,从而计算埋入式柱脚刚度。Cui[5]考虑3个组件对埋入式柱脚刚度的贡献,即锚栓、承压侧混凝土和翘起侧混凝土。Richards等[6]考虑了浅埋柱脚中的钢柱底板,使用转动弹簧代表底板的转动约束,基于Hetenyi [7]推导的弹性地基梁理论求解埋入式柱脚刚度,该刚度模型经文献[8]的试验结果验证。Rodas等[9]沿用文献[10]强度模型中对弯矩分配和应力分布的假定,对埋入柱段受力进行简化,进而基于Timoshenko梁理论[11]计算埋入式柱脚刚度,并通过文献[12]的试验结果进行了验证。
但上述刚度模型均存在一定不足。Morino等[4]对于埋入柱段在混凝土承压应力反向点处为固接的假定无可靠依据;Cui[5]对于混凝土承压应力分布形式的假定过于简化,且未考虑埋入柱段的剪切变形及底板的转动约束;Richards等[6]忽略了埋入柱段自身的剪切变形;Rodas等[9]未考虑钢柱底板对转动刚度的贡献。另外,柱脚的转动刚度与承载力均受钢柱内轴力的影响[2],但该影响未被已有模型考虑。鉴于已有模型的不足,本文建立了可综合考虑轴力影响与底板转动约束作用的埋入式柱脚节点的简化地基梁模型。在此基础上,推导了Winkler地基上考虑轴力影响的Timoshenko梁的解析解,提出了底板转动约束的计算方法,并最终给出埋入式柱脚转动刚度模型。使用文献[13]中的试验结果和经校验的有限元模型参数分析结果,验证了本文提出的理论模型的准确性,并与已有文献中最新的刚度模型[6, 9]进行比对。
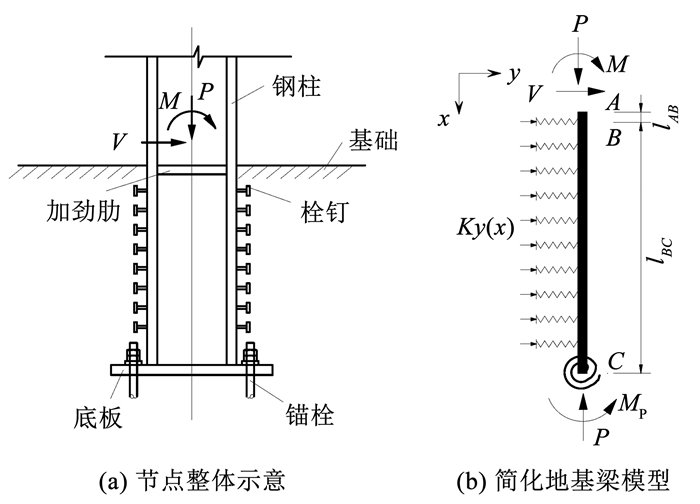
1 埋入式柱脚简化地基梁模型图 1(a)展示了埋入式柱脚节点的基本构造,主要包括钢柱埋入段、混凝土基础、柱底板、加劲肋、栓钉和锚栓。假定埋入柱段在弹性阶段的行为可以用地基梁模型描述,如图 1(b)所示。AB段代表水平加劲肋,AB段长度lAB等于加劲肋厚度;BC段代表在水平加劲肋下方和底板上方b×h矩形截面范围内的钢柱与混凝土(可视作由钢柱与翼缘间外包混凝土组成的组合钢柱),其中b和h分别为H型钢柱的宽与高,BC段长度lBC为该组合钢柱的高度。
|
图 1 柱脚节点示意 Fig. 1 Schematic diagram of column base |
忽略钢柱与混凝土界面间有限的抗拉黏结强度,仅考虑埋入柱段翼缘外侧混凝土因承受来自柱翼缘的局部承压作用而产生的刚度贡献。同时考虑底板的抗弯作用,用转动弹簧代表底板的转动约束。将埋入柱段视作地基上的梁,翼缘外受压混凝土视作地基,等效为受压弹簧,假定钢柱与受压混凝土间的受力与变形关系满足Winkler地基假设;若将弹簧置于钢柱一侧,则分布于两侧翼缘外的受压混凝土可同时由单侧的拉压弹簧表示,如图 1(b)所示。V和M分别为钢柱传递至柱脚顶面的剪力和弯矩,P为柱脚受到的轴力,MP为锚栓和周围混凝土对底板的约束弯矩,K为单位长度上柱侧等效弹簧的刚度,y(x)为埋入柱段在距基础表面x处的挠度,则Ky(x)为翼缘在单位长度上对混凝土的承压力。忽略栓钉挤压传力的影响,假定K在深度方向上为常数;柱侧上方混凝土靠近基础表面,没有或仅受到个别栓钉的挤压力,柱侧下方混凝土由于应力的扩散作用受到栓钉的挤压力也有限,而柱侧上下方混凝土恰是承受翼缘承压作用的主要区域。因此,忽略了栓钉的挤压传力,避免变化的K值带来的模型求解困难。
埋入式柱脚的变形主要由3部分组成,即钢柱自身的弯曲和剪切变形、埋入柱段两侧混凝土的承压变形以及底板上下方混凝土的承压变形。该简化地基梁模型可体现各部分对刚度的贡献:钢柱与两侧混凝土的变形即地基梁和弹簧的变形,底板上下混凝土的变形即弹簧的转动。
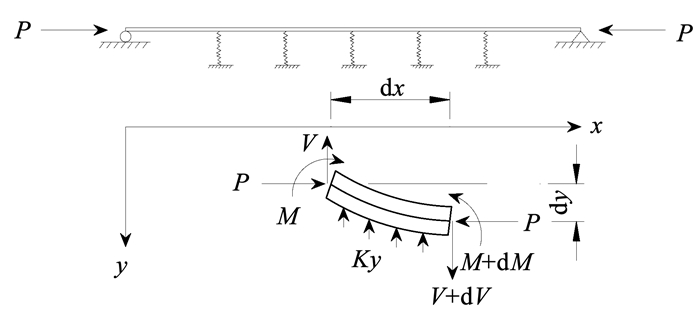
2 Winkler地基上考虑轴力的Timoshenko梁解析解文献[14]推导了Winkler地基上无轴力作用的Timoshenko梁的解析解,此节研究的有轴力的情况是对前述研究的拓展。对于Winkler地基上的Timoshenko梁,当存在轴力P时,微段隔离体的受力如图 2所示,建立竖向力和弯矩的平衡微分方程为
| $ \left\{\begin{array}{l} -\frac{\mathrm{d}}{\mathrm{d} x}\left[C\left(\frac{\mathrm{d} y}{\mathrm{~d} x}-\varphi\right)\right]+K y=0 \\ -\frac{\mathrm{d}}{\mathrm{d} x}\left(D \frac{\mathrm{d} \varphi}{\mathrm{d} x}\right)-C\left(\frac{\mathrm{d} y}{\mathrm{~d} x}-\varphi\right)-P \frac{\mathrm{d} y}{\mathrm{~d} x}=0 \end{array}\right. $ | (1) |
|
图 2 考虑轴力的Winkler地基上Timoshenko梁及受力微元体 Fig. 2 Timoshenko beam subject to axial force on the Winkler foundation and free body |
式中:y为梁中性轴的挠度,φ为由弯曲变形引起的截面转角,dy/dx-φ为截面剪切角或平均剪应变;K=k0b,k0为地基的基床系数,b为梁宽;D=EI为基础梁截面抗弯刚度,E为弹性模量,I为截面惯性矩;C=μGA为基础梁截面抗剪刚度,μ为剪切修正系数,G为抗剪模量,A为截面面积。
采用龙驭球提出的初参数法[15]对式(1)进行求解。初参数法的基本思路是:用梁初始截面的4个参数(称为初参数),即挠度y0、转角φ0、剪力V0和弯矩M0作为积分常数,使积分常数具有明确的物理意义,从而简化计算。采用初参数表示的基本解如下
| $ \left\{\begin{array}{l} y(x)=a_1(x) y_0+b_1(x) \varphi_0+c_1(x) V_0+d_1(x) M_0 \\ \varphi(x)=a_2(x) y_0+b_2(x) \varphi_0+c_2(x) V_0+d_2(x) M_0 \\ V(x)=a_3(x) y_0+b_3(x) \varphi_0+c_3(x) V_0+d_3(x) M_0 \\ M(x)=a_4(x) y_0+b_4(x) \varphi_0+c_4(x) V_0+d_4(x) M_0 \end{array}\right. $ | (2) |
式中a1(x)~a4(x),b1(x)~b4(x),c1(x)~c4(x),d1(x)~d4(x)的具体表达式详见附录A。
3 埋入式柱脚转动刚度模型 3.1 简化地基梁模型求解埋入式柱脚转动刚度为钢柱在基础顶面(A点)处的弯矩与转角之比。地基梁模型的始端(A点)和终端(C点)共有8个边界条件,分别为A、C两点处的挠度、转角、剪力和弯矩。假定柱脚受到的外荷载(即A点处的剪力V和弯矩M)已知,同时,因柱脚剪力在埋入段完全传递,底板处(C点)剪力为0,8个边界条件中仍有5个未知量。式(2)仅提供了4个方程,故需建立一补充方程方可求解全部未知量。以底板处的弯矩-转角关系作为补充条件。
对于地基梁AB段,由式(2)可求解B点的挠度yB、转角φB、剪力VB和弯矩MB:
| $ \left\{\begin{array}{l} y_B=a_1 y_A+b_1 \varphi_A+c_1 V+d_1 M \\ \varphi_B=a_2 y_A+b_2 \varphi_A+c_2 V+d_2 M \\ V_B=a_3 y_A+b_3 \varphi_A+c_3 V+d_3 M \\ M_B=a_4 y_A+b_4 \varphi_A+c_4 V+d_4 M \end{array}\right. $ | (3) |
式中:yA、φA、V和M分别为A点的挠度、转角、剪力和弯矩;ai=ai(x=lAB),bi=bi(x=lAB),ci=ci(x=lAB),di=di(x=lAB), 其中, i=1, 2, 3, 4。
对于地基梁BC段,底板受锚栓和周围混凝土约束而产生抵抗转动的弯矩,有MC=MP。由式(2)有
| $ \left\{\begin{array}{l} y_C=a_1^{\prime} y_B+b_1^{\prime} \varphi_B+c_1^{\prime} V_B+d_1^{\prime} M_B \\ \varphi_C=a_2^{\prime} y_B+b_2^{\prime} \varphi_B+c_2^{\prime} V_B+d_2^{\prime} M_B \\ 0=a_3^{\prime} y_B+b_3^{\prime} \varphi_B+c_3^{\prime} V_B+d_3^{\prime} M_B \\ M_{\mathrm{P}}=a_4^{\prime} y_B+b_4^{\prime} \varphi_B+c_4^{\prime} V_B+d_4^{\prime} M_B \end{array}\right. $ | (4) |
式中:yC、φC分别为C点的位移和转角;ai=ai(x=lBC),bi=bi(x=lBC),ci=ci(x=lBC),di=di(x=lBC),其中,i=1, 2, 3, 4。由AB段与BC段在B点的变形连续条件,将式(3)代入式(4),可得
| $ \left\{\begin{array}{l} y_C=e_1 y_A+f_1 \varphi_A+g_1 V+h_1 M \\ \varphi_C=e_2 y_A+f_2 \varphi_A+g_2 V+h_2 M \\ 0=e_3 y_A+f_3 \varphi_A+g_3 V+h_3 M \\ M_{\mathrm{P}}=e_4 y_A+f_4 \varphi_A+g_4 V+h_4 M \end{array}\right. $ | (5) |
式中
| $ \left(\begin{array}{llll} e_1 & f_1 & g_1 & h_1 \\ e_2 & f_2 & g_2 & h_2 \\ e_3 & f_3 & g_3 & h_3 \\ e_4 & f_4 & g_4 & h_4 \end{array}\right)=\left(\begin{array}{cccc} a_1^{\prime} & b_1^{\prime} & c_1^{\prime} & d_1^{\prime} \\ a_2^{\prime} & b_2^{\prime} & c_2^{\prime} & d_2^{\prime} \\ a_3^{\prime} & b_3^{\prime} & c_3^{\prime} & d_3^{\prime} \\ a_4^{\prime} & b_4^{\prime} & c_4^{\prime} & d_4^{\prime} \end{array}\right)\left(\begin{array}{llll} a_1 & b_1 & c_1 & d_1 \\ a_2 & b_2 & c_2 & d_2 \\ a_3 & b_3 & c_3 & d_3 \\ a_4 & b_4 & c_4 & d_4 \end{array}\right) $ |
由式(5)后两式可得由MP表示的yA和φA:
| $ \left(\begin{array}{l} y_A \\ \varphi_A \end{array}\right)=\left(\begin{array}{ll} e_3 & f_3 \\ e_4 & f_4 \end{array}\right)^{-1}\left[\left(\begin{array}{c} 0 \\ M_{\mathrm{P}} \end{array}\right)-\left(\begin{array}{ll} g_3 & h_3 \\ g_4 & h_4 \end{array}\right)\left(\begin{array}{l} V \\ M \end{array}\right)\right] $ | (6) |
将式(6)代入式(5)前两式,可得C点的挠度与转角:
| $ \begin{aligned} \left(\begin{array}{l} y_C \\ \varphi_C \end{array}\right)= & \left(\begin{array}{ll} e_1 & f_1 \\ e_2 & f_2 \end{array}\right)\left(\begin{array}{ll} e_3 & f_3 \\ e_4 & f_4 \end{array}\right)^{-1}\left(\begin{array}{l} 0 \\ M_{\mathrm{P}} \end{array}\right)- \\ & \left(\begin{array}{ll} e_1 & f_1 \\ e_2 & f_2 \end{array}\right)\left(\begin{array}{ll} e_3 & f_3 \\ e_4 & f_4 \end{array}\right)^{-1}\left(\begin{array}{ll} g_3 & h_3 \\ g_4 & h_4 \end{array}\right)\left(\begin{array}{l} V \\ M \end{array}\right)+ \\ & \left(\begin{array}{ll} g_1 & h_1 \\ g_2 & h_2 \end{array}\right)\left(\begin{array}{l} V \\ M \end{array}\right) \end{aligned} $ | (7) |
若底板转动刚度kp已知(3.3节介绍计算方法),则φC与MP之间有关系:
| $ \varphi_C=\frac{M_{\mathrm{P}}}{k_{\mathrm{p}}} $ | (8) |
联立式(7)和(8)可得
| $ \begin{aligned} M_{\mathrm{P}}= & \frac{k_{\mathrm{p}}\left[\left(e_4 f_2-e_2 f_4\right)\left(V g_3+M h_3\right)-\left(V g_4+M h_4\right)\right]}{e_3 f_4-e_4 f_3+\left(e_2 f_3-e_3 f_2\right) k_{\mathrm{p}}}+ \\ & \frac{k_{\mathrm{p}}\left(e_3 f_4-e_4 f_3\right)\left(V g_2+M h_2\right)}{e_3 f_4-e_4 f_3+\left(e_2 f_3-e_3 f_2\right) k_{\mathrm{p}}} \end{aligned} $ | (9) |
将MP代入式(6)即可求解φA,进而得到柱脚转动刚度KCB为
| $ K_{C B}=\frac{M}{\varphi_A} $ | (10) |
在求解过程中,BC段截面的抗弯刚度为EI=EsIs+EcIc,抗剪刚度为GA=ksABGsAs+ksBCGcAc。其中,Es和Ec分别为钢材和混凝土的弹性模量,Is和Ic分别为BC段截面中钢柱和混凝土的截面惯性矩,Gs和Gc分别为钢材和混凝土的剪切模量,As和Ac分别为BC段截面中钢柱和混凝土的截面面积,ksAB和ksBC分别为截面中钢柱和混凝土的剪切修正系数,ksAB=2/3[14],ksBC=Asw/As,Asw为钢柱腹板的面积。
地基系数k0是求解过程中涉及的另一重要参数。关于其取值,目前有荷载试验法、查表法以及经验公式法等。荷载试验法较精确,但试验费用高;查表法受经验因素影响较大。经验公式法综合考虑了土层性质的差异、荷载大小和基础底面积的影响,故应用较广。不同的经验公式有着相似的表达式[16]:
| $ k_0=a \frac{E_{\mathrm{a}}}{1-\nu^2}\left(\frac{E_{\mathrm{a}} B^4}{E I}\right)^\gamma $ | (11) |
式中:Ea为地基的变形模量;E为基础材料的弹性模量;ν为地基土的泊松比;B为基础宽度;I为基础截面惯性矩;a和γ为公式常数,不同学者取值不同,见表 1。
| 表 1 式(11)的a、γ取值 Tab. 1 Values of a and γ in Eq.(11) |
式(11)及表 1中所示的a和γ均为针对土质地基的研究所得。Richards等[6]基于试验结果指出,将式(11)与表 1常数用于计算埋入式柱脚混凝土地基系数时,结果偏大;应用表 1常数得到的计算结果的平均值与实测值之比为1.75。纠其原因,一方面,如前已述,是因为该式及公式常数均针对土质地基;另一方面,公式假定基床材料保持线弹性,而由于混凝土材料自身的非线性,柱脚节点在受力初始便已表现出非线性行为。因此,在应用时,基于文献[6]的结论,k0取值是将表 1常数用于式(11)得到的计算结果平均值的57%(即1/1.75)。
3.2 底板约束刚度 3.2.1 简化受力模型Richards等[6]在确定底板刚度时,将底板假定为埋置于弹性材料(混凝土)内的仅受弯矩作用的无限刚性板,且刚性板上部混凝土与下部混凝土刚度相等。但实际上,两者承载机制不同造成刚度有差异。
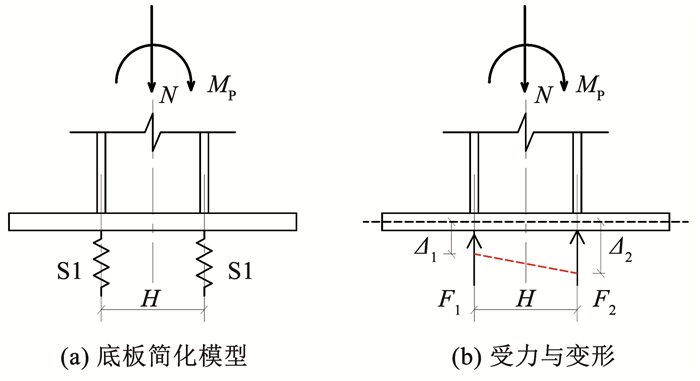
底板与混凝土间的应力分布较为复杂,将其简化为如图 3所示的受力模型。由于截面弯矩主要由两侧翼缘内的拉压内力形成的力偶承担,且翼缘对底板具有显著的加劲作用,底板受到周围混凝土的约束作用主要通过两侧翼缘传递,将该约束等效为位于柱翼缘下方的两线性弹簧S1与S2,弹簧力形成的力偶即作用于底板的约束弯矩。
|
图 3 底板简化模型与受力简图 Fig. 3 Simplified model and force diagram of base plate |
假定底板处钢柱截面轴力N和弯矩MP完全通过两侧翼缘传递,即忽略腹板的承压贡献,可计算两侧翼缘分别传递的内力为
| $ F_1=\frac{N}{2}-\frac{M_{\mathrm{P}}}{H} $ | (12) |
| $ F_2=\frac{N}{2}+\frac{M_{\mathrm{P}}}{H} $ | (13) |
式中:F1与F2即为传递至弹簧S1和S2的内力,H为翼缘中心的距离。
由胡克定律,有
| $ \Delta_1=\frac{F_1}{k_{\mathrm{S} 1}}=\frac{\frac{N}{2}-\frac{M_{\mathrm{P}}}{H}}{k_{\mathrm{S} 1}} $ | (14) |
| $ \Delta_2=\frac{F_2}{k_{\mathrm{S} 2}}=\frac{\frac{N}{2}+\frac{M_{\mathrm{P}}}{H}}{k_{\mathrm{S} 2}} $ | (15) |
式中:Δ1和Δ2分别为弹簧S1和S2的变形,kS1和kS2分别为弹簧S1和S2的刚度。
由几何关系,可得底板的转角为
| $ \theta_{\mathrm{P}}=\frac{\Delta_2-\Delta_1}{H}=\frac{1}{2 H^2}\left(\frac{N H+2 M_{\mathrm{P}}}{k_{\mathrm{S} 2}}-\frac{N H-2 M_{\mathrm{P}}}{k_{\mathrm{S} 1}}\right) $ | (16) |
则底板的约束刚度kp为
| $ k_{\mathrm{p}}=\frac{M_{\mathrm{P}}}{\theta_{\mathrm{P}}}=\frac{2 H^2 M_{\mathrm{P}}}{\frac{N H+2 M_{\mathrm{P}}}{k_{\mathrm{S} 2}}-\frac{N H-2 M_{\mathrm{P}}}{k_{\mathrm{S} 1}}} $ | (17) |
当F1<0,即MP>NH/2时,弹簧S1受拉,弹簧S2受压。此时,kS1=kt,kS2=kb。其中,kt与kb分别为在钢柱受拉翼缘侧底板上部混凝土的刚度与在钢柱受压翼缘侧底板下部混凝土的刚度。将kt与kb(通过3.2.3节中的方法计算)代入式(17)即可计算得到kp。
当F1≥0,即MP≤NH/2时,弹簧S1和S2均受压。此时,kS1=kS2=kb,则式(17)可简化为
| $ k_{\mathrm{p}}=\frac{M_{\mathrm{P}}}{\theta_{\mathrm{P}}}=\frac{k_{\mathrm{b}} H^2}{2} $ | (18) |
受压翼缘侧底板下部混凝土刚度kb的计算可参考文献[25]中基于组件法计算外露式柱脚刚度时对受压混凝土组件的刚度计算方法,表达式为
| $ k_{\mathrm{b}}=\frac{E_{\mathrm{c}} \sqrt{b_{\text {eff }} l_{\text {eff }}}}{1.275} \cong \frac{E_{\mathrm{c}} \sqrt{t_{\mathrm{w}} l_{\text {eff }}}}{0.72} $ | (19) |
式中:beff和leff分别为等效T型件的宽和长,tw为等效T型件的腹板厚度。式(19)中第1个等式为欧洲钢结构设计规范Eurocode 3 Part 1-8[26]中外露式柱脚受压混凝土组件的刚度计算公式,第2个等式为文献[25]基于实际底板等效T型件典型尺寸,令beff=3.125 tw,作出便于实际应用的简化。
在计算kt时,需要考虑受拉翼缘侧底板上部混凝土和锚栓对刚度的共同贡献。
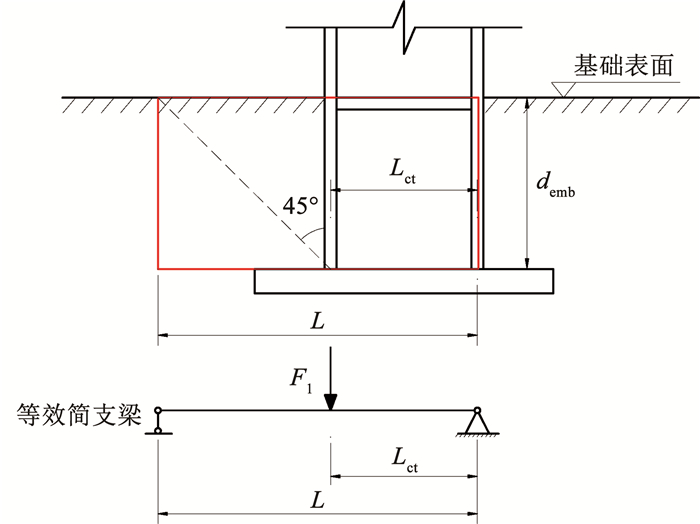
将受拉翼缘侧受到底板翘起作用的混凝土块简化为等效简支梁,如图 4所示。其中,L为等效梁长,Lct为钢柱两侧翼缘中面间距(即两弹簧间距),demb为埋深。等效简支梁右端支座位于底板的转动中心,为简化计算,近似取为受压翼缘中面处。假定翘起作用在混凝土内的应力扩散角为45°[25],左端支座距受拉翼缘的距离为demb。因此,等效简支梁长L=Lct+demb。柱宽度以外的底板由于没有翼缘的加劲作用而具有较小的弯曲刚度,底板对混凝土的作用力主要集中在柱宽范围内,简支梁截面宽度取为柱翼缘宽度。
|
图 4 受拉翼缘侧底板上部混凝土等效简支梁 Fig. 4 Equivalent simply supported beam modeling the concrete on top of base plate |
简支梁在荷载F1的作用下,荷载处的位移Δ1由梁的弯曲变形Δ1M和剪切变形Δ1V构成。令α=Lct/L,有
| $ \Delta_{1 \mathrm{M}}=\frac{F_1 L^3}{3 E I} \alpha^2(1-\alpha)^2 $ | (20) |
| $ \Delta_{1 \mathrm{~V}}=\frac{F_1 L}{G A} \alpha(1-\alpha) $ | (21) |
则等效简支梁的刚度kbeam为
| $ \begin{aligned} k_{\text {beam }}= & \frac{F_1}{\Delta_1}=\frac{F_1}{\Delta_{1 \mathrm{M}}+\Delta_{1 \mathrm{~V}}}= \\ & \frac{1}{\frac{L^3}{3 E I} \alpha^2(1-\alpha)^2+\frac{L}{G A} \alpha(1-\alpha)} \end{aligned} $ | (22) |
上述计算过程没有考虑周边配筋对刚度的贡献。基础梁的箍筋和钢柱周边的补强垂直纵向主筋和箍筋,垂直于等效简支梁的受力方向,对简支梁刚度的贡献可以忽略。而基础梁的纵向主筋常在柱身附近弯折后从两侧绕过钢柱,同时,底板对混凝土的作用力主要集中在柱宽范围内且靠近受拉翼缘,因此,也忽略了基础梁纵筋对刚度的贡献。
受拉锚栓组件的刚度kab参照Eurocode 3 Part 1-8[26]中外露柱脚底板受弯和锚栓受拉的刚度得
| $ k_{\mathrm{ab}}=\frac{1}{\frac{1}{\frac{0.425 l_{\mathrm{eff}} t_{\mathrm{p}}^3}{m^3}}+\frac{1}{\frac{2 A_{\mathrm{s}}}{L_{\mathrm{b}}}}} $ | (23) |
式中:leff为等效T型件的长;tp为底板厚度;m为一规定几何尺寸,取值见Eurocode 3 Part 1-8[26];As为受拉锚栓面积;Lb为锚栓拉伸长度。
根据受拉翼缘侧底板上部混凝土和锚栓两者的并联机制,kt可取为
| $ k_{\mathrm{t}}=k_{\text {beam }}+k_{\text {ab }} $ | (24) |
除混凝土和锚栓对底板的约束外,栓钉的挤压传力也会提供一定的转动约束。受压翼缘内力除传至底板下方混凝土外,还通过栓钉传递至侧面混凝土,在模型中可表现为kb的增大;受拉翼缘内力除通过底板传递至其上方混凝土外,还通过栓钉传递至侧面混凝土,两种传力机制作用于同一混凝土区,若考虑栓钉的贡献,则该侧混凝土对底板的约束也将同时减小,因此,在kt计算中实际上隐含了混凝土对栓钉和底板的共同约束。由于混凝土承压刚度明显大于翘起刚度,一般而言,kb显著大于kt,使得底板转动中心靠近受压翼缘,kb的变化对底板转动中心的位置和转动刚度kp的影响很小。对于埋深有限的浅埋柱脚,栓钉的数量也十分有限,大部分翼缘内力将由底板传递至混凝土。因此,为简化模型,在计算中忽略了栓钉的影响。
3.3 埋入式柱脚转动刚度综上,计算柱脚转动刚度KCB的流程可总结为:1)柱脚弯矩M与轴力N已知,由式(12)和(13)计算F1与F2;2)由式(19)和(24)计算kb和kt;3)联立式(9)和(17)求解kp和MP;4)由式(6)计算φA;5)由式(10)计算KCB。
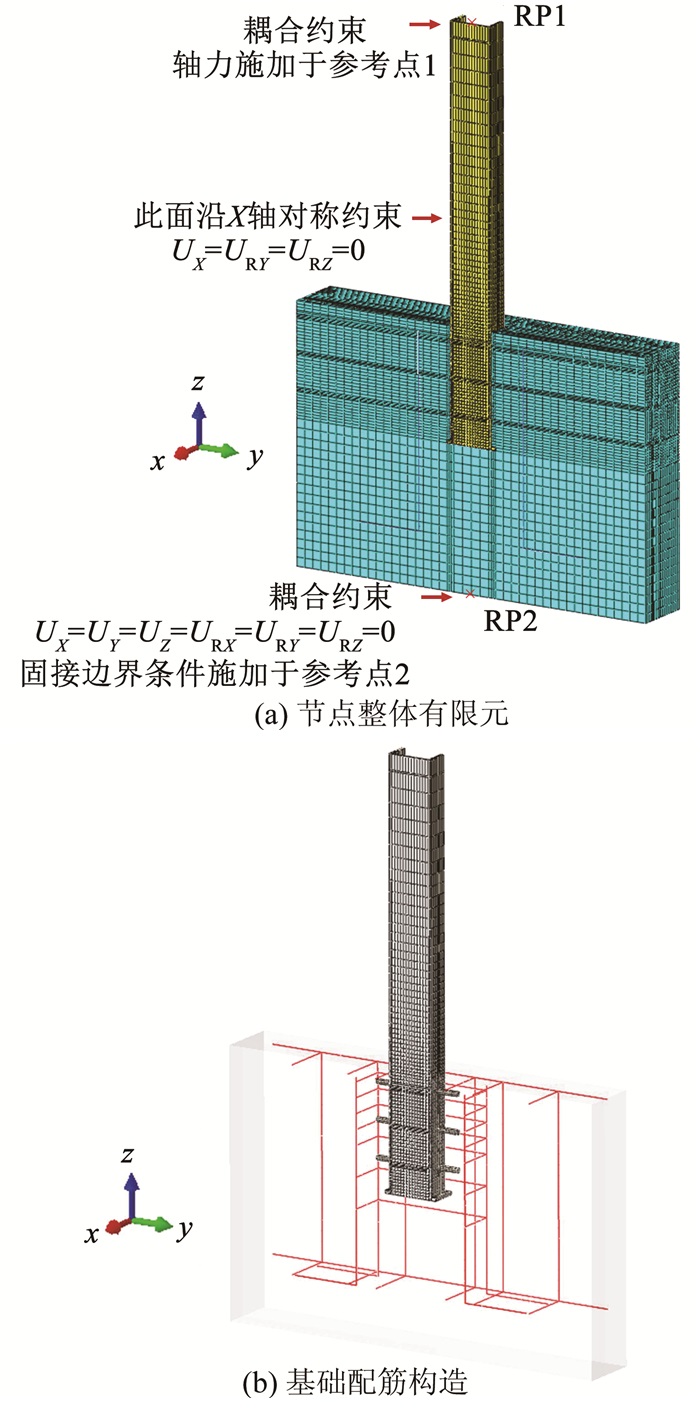
4 埋入式柱脚转动刚度模型验证本节将对上一节提出的埋入式柱脚节点转动刚度的理论模型进行验证。过往埋入式柱脚试验数据较少,特别是已有试验的研究参数无法体现出埋深与轴力对柱脚刚度的影响。因此,首先基于ABAQUS有限元软件对文献[13]中的埋入式柱脚试验进行模拟,验证有限元模型精度,而后基于已验证的有限元模型进行参数分析,研究埋深、轴力以及底板约束对柱脚刚度的影响,验证理论模型的准确性。
4.1 有限元模型与验证文献[13]中的埋入式柱脚试件,钢柱为Q235B牌号截面规格为150 mm×150 mm×7 mm×10 mm的H型钢,钢柱外露高度1 000 mm;钢柱在埋入段上端向下30 mm处设有厚度为5 mm的加劲肋;底板平面尺寸为180 mm×180 mm,厚度为10 mm。基础混凝土强度等级为C40,尺寸为400 mm×870 mm×1 300 mm。钢筋等级为HRB335,如图 5(b)所示,在埋入柱段翼缘外侧各配置3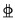
图 5以EBC3-2为例展示了在ABAQUS中基于对称性建立的原试件1/2有限元模型。钢柱与混凝土均采用C3D8R实体单元模拟;钢筋采用T3D2桁架单元模拟,并采用“embedded”约束嵌入至混凝土单元。为准确模拟节点的受力性态,钢柱板件厚度方向均划分4层网格,同时细化节点局部区域的网格尺寸。钢柱翼缘、下底板及水平加劲肋与基础混凝土在变形过程中会发生接触。接触面法向方向设置“硬接触”,切向方向采用库伦摩擦模型,摩擦因数为0.3。有限元模型采用与试验一致的边界条件,同时考虑1/2模型的对称性,在对称面上施加相应的位移约束。钢材和钢筋本构选用双线性模型,钢材弹性模量Es=206 GPa,屈服强度fy=290 MPa,屈服后模量E′=0.01Es,泊松比为0.3;钢筋弹性模量Es=200 GPa,屈服强度fy=405 MPa,屈服后模量E′=0.01Es,泊松比为0.3。混凝土选用塑性损伤模型,单轴受压应力-应变关系取自GB 50010—2010《混凝土结构设计规范》[27],弹性模量Ec=34.6 GPa,立方体抗压强度标准值fcu, k=50.27 MPa。泊松比为0.2。
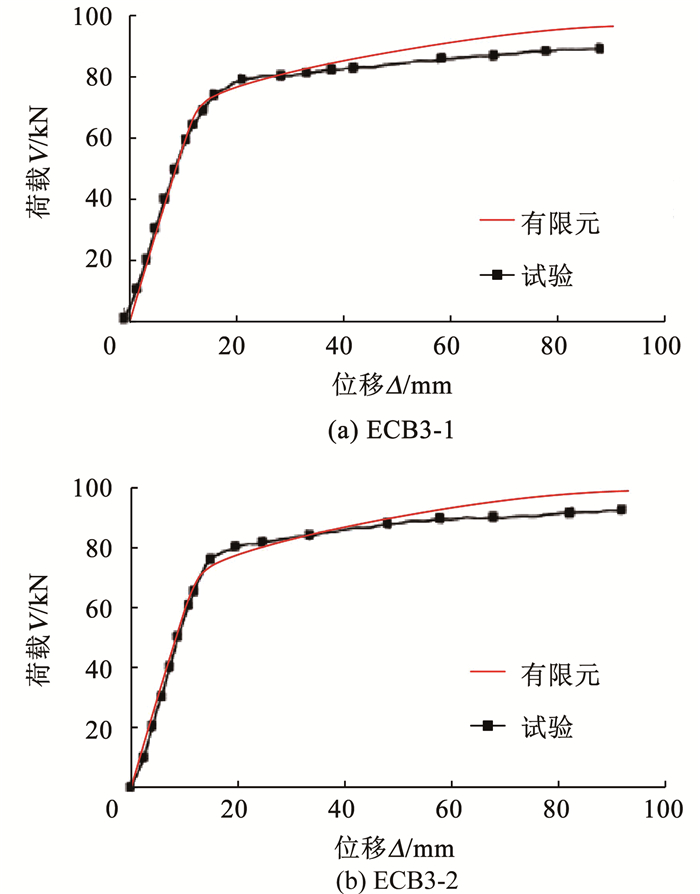
图 6展示了有限元结果与试验结果的对比,横纵坐标分别为柱顶加载点(即图 5(a)中的参考点RP1)处的水平位移和施加的荷载大小。有限元模型较好地重现了试件的全过程性态,包括试件的初始刚度、承载力和强化段。试验中,试件ECB3-1和ECB3-2柱顶分别加载至15、17 mm时,荷载-位移曲线的斜率逐步减小,基础表面垂直于钢柱翼缘宽度方向的裂缝逐渐开展,当位移为25、30 mm时,钢柱外露段底部屈服,最终当位移达到90 mm时,钢柱外露段受压侧翼缘出现明显屈曲,此时在基础表面出现典型的呈发散状的冲切裂缝。有限元结果显示,最终柱脚因钢柱外伸段弯曲屈服和随后的塑性屈曲而破坏,与试验结果一致。在受压翼缘外,混凝土因局部承压出现明显的受压损伤区域,而在受拉翼缘侧,混凝土出现受拉损伤,基础表面贯通的损伤区域垂直于翼缘,与试验结果吻合。另外,有限元结果提取了埋入柱段翼缘在深度方向上的纵向应变:在加载初期,纵向应变沿深度方向基本呈线性变化;随荷载增加,埋入段翼缘上部进入屈服,而下部应变仍较小。上述结果验证了有限元模型的可靠性。
|
图 6 荷载位移曲线的有限元与试验结果对比 Fig. 6 Comparison between FE and test results of load displacement curves |
基于经校验的有限元模型,探究钢柱埋深比、轴压力和底板约束作用对柱脚转动刚度的影响,进而验证理论模型的准确性。试件加劲肋布设于基础表面以下30 mm处,有限元分析表明,在此范围内布设的加劲肋,其位置对柱脚转动刚度影响甚微。因此,参数分析时将加劲肋布设于基础表面处,以与理论模型相应。由于钢柱脚弯矩-转角曲线在加载初期就表现出一定的非线性行为,随着荷载继续增加,柱侧混凝土进入明显的非线性阶段,割线刚度也逐渐降低。通常取弯矩-转角曲线在柱顶位移与柱高之比达到弹性层间位移角限值1/250时的割线刚度作为钢柱脚转动刚度[5-6]。理论模型涉及的所有几何与材料参数均取试验实测值。对于地基系数k0,将混凝土弹性模量代入式(11),并采用表 1中的公式常数进行计算,所得k0的平均值为221 N/mm3;因此,理论模型中,k0=221/1.75=125 N/mm3。
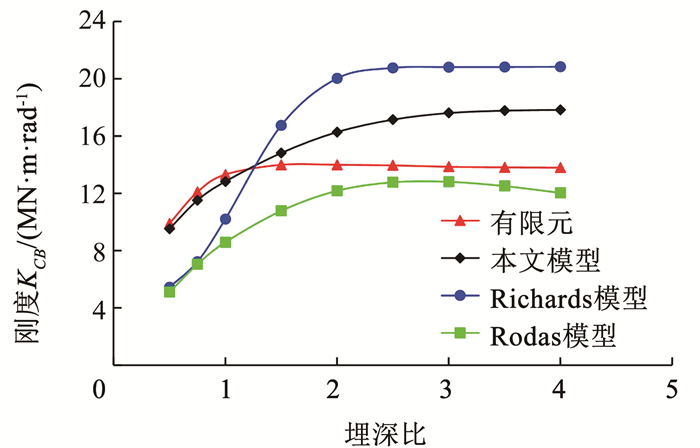
由图 7可知,对于文献[13]中的试件,当埋深比由0.5增大到1.5时,柱脚转动刚度增大了41.4%,此后趋于不变。本文模型能够很好地反映埋深比对于柱脚刚度的影响:在埋深比较小时,柱脚刚度随埋深比的增加快速增大;埋深比增加到一定程度后,其对柱脚刚度几乎无影响。由于埋深比较大时可以将柱脚近似为固接,对于柱脚刚度计算的关键在于浅埋柱脚。对于浅埋柱脚,本文理论模型与有限元结果具有非常高的吻合度。在埋深比为0.5~1.5时,理论模型与有限元结果的平均比值为0.98。埋深较大时,理论模型的精度略有降低。在埋深比为3.0时,理论模型与有限元结果的比值为1.27。Richards模型[6]和Rodas模型[9]也可体现出埋深比对于柱脚转动刚度的影响,但其对于刚度的计算精度与本文模型具有明显的差距,特别是对于埋深比小于1.5的浅埋柱脚。
|
图 7 柱脚转动刚度受埋深比的影响 Fig. 7 Dependence of rotational stiffness on embedded depth ratio |
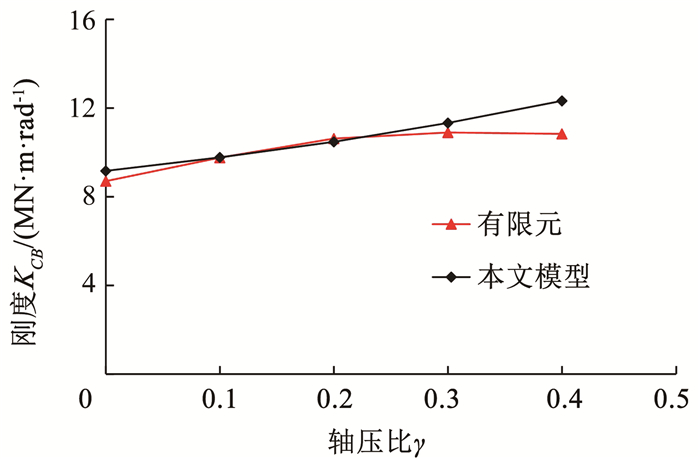
定义用于衡量轴压力大小的无量纲参数γ=N/(Afy)(类似于混凝土柱的轴压比)。图 8给出了埋深比为0.5的柱脚的转动刚度在工程常用γ范围内的变化。当柱脚在无轴力工况下增加到轴压比为0.4时,其刚度增大了24.6%。本文理论模型不仅可以较准确地预测柱脚转动刚度的具体数值,也能较好地反应柱脚转动刚度随钢柱轴力增加而增大的趋势。Richards模型[6]与Rodas模型[9]均无法考虑轴力对于柱脚刚度的影响。
|
图 8 柱脚转动刚度受轴压比的影响 Fig. 8 Dependence of rotational stiffness on axial force ratio |
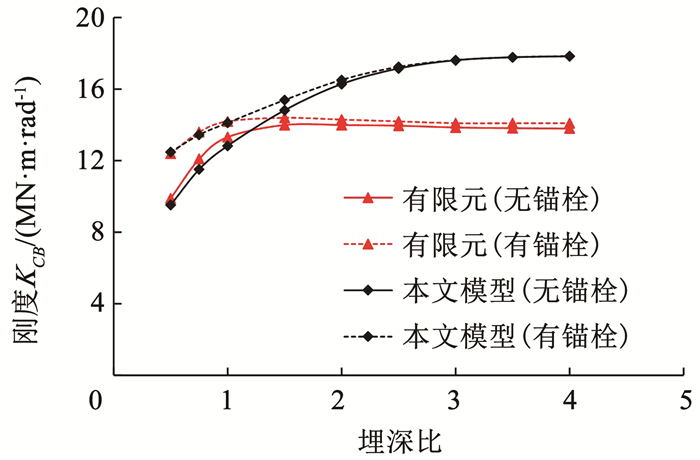
实际工程中,锚栓通常仅起安装固定作用,但若锚栓布置于柱翼缘以外,同样对柱脚刚度有一定提升。图 9展示了锚栓布置与否对于柱脚刚度的影响。算例中,布置锚栓的柱脚节点,在两侧柱翼缘外各设置两根锚栓。对于浅埋柱脚节点,锚栓对其刚度的影响较大,不能忽略。当埋深比为0.5时,单侧布置两根锚栓可使柱脚刚度增大25.3%。随着埋深的增大,锚栓的影响逐渐减小。
|
图 9 柱脚转动刚度受锚栓布置的影响 Fig. 9 Dependence of rotation stiffness on the presence of anchor bolts |
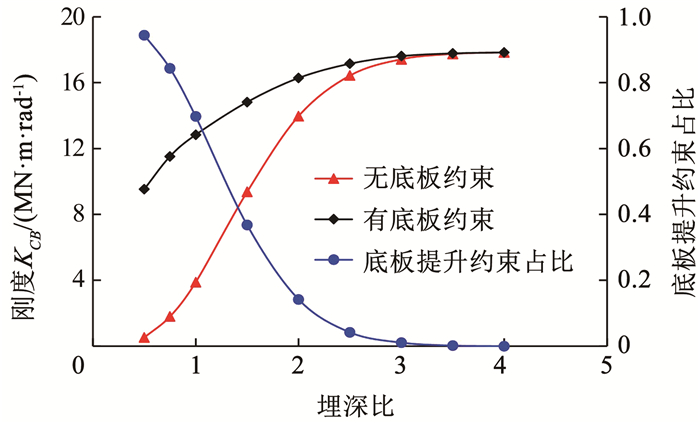
为进一步体现底板约束的有利作用,图 10给出了无锚栓情况下考虑和不考虑底板约束时柱脚转动刚度随埋深变化的理论解,以及底板约束带来的刚度提升占柱脚总转动刚度的比值。当埋深比小于2.5时,底板约束的影响变得突出;当埋深比继续减小至1.5以下时,底板约束提供的转动刚度将超过总刚度的1/2,节点的行为向外露式柱脚靠近。根据柱脚刚度随埋深的变化以及底板约束对刚度的贡献,将埋深比小于1.5和大于2.5的柱脚节点定义为浅埋和深埋柱脚,其间为中等埋深柱脚。对于浅埋柱脚节点,底板对柱脚刚度的贡献十分重要,若忽略将造成对节点刚度的严重低估,且刚度随埋深增加快速增长,对于深埋柱脚,底板的约束可以忽略,且柱脚刚度随埋深的增加基本不再变化。
|
图 10 柱脚刚度受底板约束的影响 Fig. 10 Dependence of rotational stiffness on the restraint of base plate |
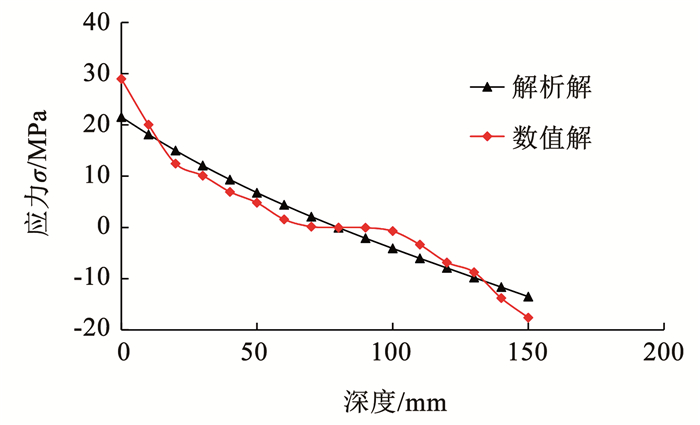
钢柱脚埋入段的弹性行为可用Winkler地基上的深梁描述是本文提出的刚度模型的重要假设和前提,该模型准确预测了埋深比不超过1.5的柱脚的初始转动刚度。为进一步验证该假设的合理性,在有限元中提取了钢柱翼缘对混凝土在不同高度上的承压应力,并与理论预测值(由地基系数k0乘以挠度y(x)得到)进行了对比。图 11以埋深比为1、无锚栓有底板、不考虑轴力的柱脚样本为例,给出了在弹性阶段35 kN水平荷载作用下承压应力的有限元和理论结果。横坐标为与基础表面的距离,应力的正负号指承压应力分布在不同翼缘侧。
|
图 11 承压应力的理论与有限元结果的对比 Fig. 11 Comparisons between analytical and FE results of the bearing stresses |
从图 11可以看出,理论模型得到的应力分布与有限元结果比较吻合。承压应力反向点(即应力为0的位置)均位于90 mm处。尽管有限元结果存在一定的零应力区,两侧的变化趋势和幅值基本相当。可见,采用Winkler地基上的Timoshenko梁理论描述埋入式柱脚的行为是合理的。
5 结论1) 将埋入式柱脚节点的埋入段视作轴力作用下的Timoshenko梁,采用Winkler地基模型描述柱侧混凝土的侧向约束,通过梁端转动弹簧表征混凝土和锚栓对底板的转动约束,从而建立起了能够综合反映柱脚埋深、埋入段剪切变形、轴力和底板约束影响的埋入式钢柱脚转动刚度模型。
2) 采用初参数法对考虑轴力影响的Winkler地基上的Timoshenko梁模型进行求解;通过将底板周围混凝土和锚栓的作用等效为底板上的两线性弹簧,结合合理假定,计算表征不同约束机制的等效弹簧刚度,进而得到了底板的转动约束刚度。
3) 本文提出的埋入式柱脚节点转动刚度理论模型可以较好地预测试验与精细建模有限元分析的结果,尤其是对于埋深比为0.5~1.5的浅埋柱脚节点,并可很好地反映埋深比和轴力对转动刚度的影响:在埋深比较小时,柱脚刚度随埋深比的增加快速增大,埋深比增加到一定程度后,其对柱脚刚度几无影响;柱脚转动刚度随钢柱轴压力增加而增大;底板转动约束对埋深比小于1.5的节点刚度具有显著影响,当埋深比增大至2.5,其影响可以忽略。
附录A| $ \begin{gathered} a_1(x)=\operatorname{ch}(\alpha x) \cos (\beta x)+\frac{\alpha^2-\beta^2+P / D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \\ b_1(x)=\frac{\operatorname{ch}(\alpha x) \sin (\beta x)}{2 \beta}+\frac{\operatorname{sh}(\alpha x) \cos (\beta x)}{2 \alpha} \\ c_1(x)=\frac{\left(\alpha^2-3 \beta^2+P / D\right) \operatorname{ch}(\alpha x) \sin (\beta x)}{2 \beta K}+ \\ \frac{\left(3 \alpha^2-\beta^2+P / D\right) \operatorname{sh}(\alpha x) \cos (\beta x)}{2 \alpha K} \\ d_1(x)=-\frac{\operatorname{sh}(\alpha x) \sin (\beta x)}{2 \alpha \beta D} \end{gathered} $ |
| $ \begin{gathered} a_2(x)=\frac{\left(\alpha^2+\beta^2\right)(1+P / C)}{2 \alpha} \operatorname{sh}(\alpha x) \cos (\beta x)- \\ \frac{\left(\alpha^2+\beta^2\right)(1+P / C)}{2 \beta} \operatorname{ch}(\alpha x) \sin (\beta x) \\ b_2(x)=\operatorname{ch}(\alpha x) \cos (\beta x)- \\ \frac{\alpha^2-\beta^2+P / D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \\ c_2(x)=-\frac{(1+P / C)}{2 \alpha \beta D} \operatorname{sh}(\alpha x) \sin (\beta x) \\ d_2(x)=\frac{\left(\alpha^2-3 \beta^2+P / D\right) \operatorname{ch}(\alpha x) \sin (\beta x)}{2 \beta\left(\alpha^2+\beta^2\right) D}-\\ \frac{\left(3 \alpha^2-\beta^2+P / D\right) \operatorname{sh}(\alpha x) \cos (\beta x)}{2 \alpha\left(\alpha^2+\beta^2\right) D} \end{gathered} $ |
| $ \begin{gathered} a_3(x)=\frac{K+\left(\alpha^2+\beta^2\right) P}{2 \beta} \operatorname{ch}(\alpha x) \sin (\beta x)+ \\ \frac{K-\left(\alpha^2+\beta^2\right) P}{2 \alpha} \operatorname{sh}(\alpha x) \cos (\beta x) \\ b_3(x)=\frac{\left(\alpha^2+\beta^2\right)^2 D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \\ c_3(x)=\operatorname{ch}(\alpha x) \cos (\beta x)+ \\ \frac{\alpha^2-\beta^2+P / D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \\ d_3(x)=\frac{\alpha^2+\beta^2}{2 \alpha} \operatorname{sh}(\alpha x) \cos (\beta x)- \\ \frac{\alpha^2+\beta^2}{2 \beta} \operatorname{ch}(\alpha x) \sin (\beta x) \end{gathered} $ |
| $ \begin{gathered} a_4(x)=\frac{\left(\alpha^2+\beta^2\right)^2(1+P / C) D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \\ b_4(x)=\frac{\left(\alpha^2+\beta^2+P / D\right) D}{2 \beta} \operatorname{ch}(\alpha x) \sin (\beta x)- \\ \frac{\left(\alpha^2+\beta^2-P / D\right) D}{2 \alpha} \operatorname{sh}(\alpha x) \cos (\beta x) \\ c_4(x)=\frac{1+P / C}{2 \alpha} \operatorname{sh}(\alpha x) \cos (\beta x)+ \\ \frac{1+P / C}{2 \beta} \operatorname{ch}(\alpha x) \sin (\beta x) \\ d_4(x)=\operatorname{ch}(\alpha x) \cos (\beta x)- \\ \frac{\alpha^2-\beta^2+P / D}{2 \alpha \beta} \operatorname{sh}(\alpha x) \sin (\beta x) \end{gathered} $ |
| $ \alpha=\sqrt{\sqrt{\frac{K}{4 D}}+\frac{1}{4}\left(\frac{K}{C}-\frac{P}{D}\right)}, \beta=\sqrt{\sqrt{\frac{K}{4 D}}-\frac{1}{4}\left(\frac{K}{C}-\frac{P}{D}\right)} $ |
| [1] |
TREMBLAY R, FILIATRAULT A, BRUNEAU M, et al. Seismic design of steel buildings: lessons from the 1995 Hyogo-ken Nanbu earthquake[J]. Canadian Journal of Civil Engineering, 1996, 23(3): 727. DOI:10.1139/l96-885 |
| [2] |
XU Wu, HAN Linhai, LI Wei. Seismic performance of concrete-encased column base for hexagonal concrete-filled steel tube: experimental study[J]. Journal of Constructional Steel Research, 2016, 121: 352. DOI:10.1016/j.jcsr.2016.02.003 |
| [3] |
ZAREIAN F, KANVINDE A. Effect of column-base flexibility on the seismic response and safety of steel moment-resisting frames[J]. Earthquake Spectra, 2013, 29(4): 1537. DOI:10.1193/030512EQS062M |
| [4] |
MORINO S, TSUJI A, KADOYA H. Strength and stiffness of CFT semi-embedded type column base[C]//Advances in Structures: Proceedings of the International Conference on Advances in Structures (ASSCCA'03). Sydney, Australia: CRC Press, 2003: 3
|
| [5] |
CUI Yao. Development of joint systems using SFRCC for enhanced seismic performance of steel structures[D]. Kyoto: Kyoto University, 2009
|
| [6] |
RICHARDS P W, BARNWELL N V, TRYON J E, et al. Flexural strength and stiffness of block-out connections for steel columns[J]. Engineering Structures, 2018, 173: 404. DOI:10.1016/j.engstruct.2018.06.055 |
| [7] |
HETÉNYI M. Beams on elastic foundation: theory with applications in the fields of civil and mechanical engineering[M]. Ann Arbor: University of Michigan Press, 1946.
|
| [8] |
BARNWELL N V. Experimental testing of shallow embedded connections between steel columns and concrete footings[D]. Provo: Brigham Young University, 2015
|
| [9] |
RODAS P T, ZAREIAN F, KANVINDE A. Rotational stiffness of deeply embedded column-base connections[J]. Journal of Structural Engineering, 2017, 143(8): 04017064. DOI:10.1061/(asce)st.1943-541X.0001789 |
| [10] |
GRILLI D A, KANVINDE A M. Embedded column base connections subjected to seismic loads: strength model[J]. Journal of Constructional Steel Research, 2017, 129: 240. DOI:10.1016/j.jcsr.2016.11.014 |
| [11] |
TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1921, 41(245): 744. DOI:10.1080/14786442108636264 |
| [12] |
GRILLI D, JONES R, KANVINDE A. Seismic performance of embedded column base connections subjected to axial and lateral loads[J]. Journal of Structural Engineering, 2017, 143(5): 04017010. DOI:10.1061/(asce)st.1943-541x.0001741 |
| [13] |
杨建. 水平荷载下埋入式钢柱脚基础段受力性能研究[D]. 苏州: 苏州科技学院, 2009 YANG Jian. Study on mechanical behavior of embedded steel column base foundation section under horizontal load[D]. Suzhou: Suzhou University of Science and Technology, 2009 |
| [14] |
夏桂云. 考虑剪切变形影响的杆系结构理论与应用[M]. 北京: 人民交通出版社, 2008. XIA Guiyun. Frame structure theory including shear deformation effect and its applications[M]. Beijing: China Communications Press, 2008. |
| [15] |
龙驭球. 弹性地基梁的计算[M]. 北京: 高等教育出版社, 1981. LONG Yuqiu. Calculation method in elastic foundation beam[M]. Beijing: Higher Education Press, 1981. |
| [16] |
SALL O A, FALL M, BERTHAUD Y, et al. Influence of the elastic modulus of the soil and concrete foundation on the displacements of a mat foundationg[J]. Open Journal of Civil Engineering, 2013, 3(4): 228. DOI:10.4236/OJCE.2013.34027 |
| [17] |
BIOT M A. Bending of an infinite beam on an elastic foundation[J]. Journal of Applied Mechanics, 1937, 4(1): 1. |
| [18] |
VESIC A B. Beams on elastic subgrade and the Winkler's hypothesis[C]//Proceedings of 5th International Conference on Soil Mechanics and Foundation Engineering. Paris: [s. n. ], 1961: 845
|
| [19] |
LIU F L. Rectangular thick plates on Winkler foundation: differential quadrature element solution[J]. International Journal of Solids and Structures, 2000, 37(12): 1743. DOI:10.1016/S0020-7683(98)00306-0 |
| [20] |
DALOGLU A T, VALLABHAN C V G. Values of k for slab on Winkler foundation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(5): 463. DOI:10.1061/(ASCE)1090-0241(2000)126:5(463) |
| [21] |
FISCHER F D, GAMSJÄGER E. Beams on foundation, Winkler bedding orhalfspace: a comparison[J]. Technische Mechanik-European Journal of Engineering Mechanics, 2008, 28(2): 152. |
| [22] |
YANG K. Analysis of laterally loaded drilled shafts in rock[D]. Akron: University of Akron, 2006
|
| [23] |
HENRY M T. Train-induced dynamic response of railway track and embankments on soft peaty foundations[D]. Saskatoon: University of Saskatchewan, 2007
|
| [24] |
JAYACHANDRAN S A, SEETHARAMAN S, ABRAHAM S. Simple formulation for the flexure of plates on nonlinear foundation[J]. Journal of Engineering Mechanics, 2008, 134(1): 110. DOI:10.1061/(ASCE)0733-9399(2008)134:1(110) |
| [25] |
IVANYI M. Semi-rigid connections in structural steelwork[M]. New York: America, Springer Wien, 2000.
|
| [26] |
European Committee for Standardization (CEN). Eurocode 3: design of steel structures, Part 1-8: design of joints[S]. Brussels: [s. n.], 2005
|
| [27] |
中国建筑研究院. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010
|
| [28] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2015
|
 2024, Vol. 56
2024, Vol. 56