2. 中铁十六局集团路桥工程有限公司,北京 101500;
3. 北京市政建设集团有限责任公司,北京 100048
2. China Railway 16th Bureau Group Road & Bridge Engineering Co., Ltd., Beijing 101500, China;
3. Beijing Municipal Construction Co., Ltd., Beijing 100048, China
梁柱节点是框架结构的关键部位,承担着分配弯矩、传递剪力和轴力的作用。强震来临时,梁柱节点位置易发生损伤破坏,塑性铰出现在框架柱中甚至可能导致框架结构建筑物倒塌[1-3]。保证节点具有足够的抗震能力是框架结构抗震设计的主要目标之一。
为评估节点的抗震性能,学者们完成了大量的试验。Hakuto等[4]研究了梁纵筋黏结滑移对节点抗弯能力和延性性能的影响,发现黏结性能的损伤退化是梁柱节点力学性能降低的重要原因。吕西林等[5-6]对往复荷载作用下节点核心区的纵筋黏结滑移进行了研究,指出梁纵筋滑移引起的梁外端附加挠度占梁柱组合体外端总挠度的30%以上。Braga等[7]通过试验发现受拉钢筋的黏结滑移会显著降低梁柱节点的刚度、延性和耗能能力。曹子建等[8]对有缺陷装配式梁柱节点的抗震性能进行了试验研究,结果表明,纵筋的黏结滑移降低了节点的抗震性能,加剧了滞回曲线的捏缩效应。建立梁柱节点有限元分析模型时,需要考虑钢筋与混凝土间的黏结退化效应。
考虑黏结滑移作用的精细化有限元模型可弥补宏观试验数据采集的短板,受到越来越多的关注。Elmorsi等[9]基于二维平面单元建立了梁柱节点有限元分析模型,采用黏结滑移单元模拟钢筋与混凝土间的黏结滑移作用,结果表明模拟结果与试验结果较为一致。Lowes等[10-12]开发了节点单元用于模拟节点核心区非弹性变形,利用57个节点试验对节点单元进行标定,由于其较高的计算效率和超短的计算周期,被纳入OpenSees有限元平台。赖少颖[13]为准确模拟梁柱节点的抗震性能,采用ABAQUS用户单元子程序开发了一种四节点平面黏结滑移单元用于模拟钢筋与混凝土的黏结劣化现象。赵雯桐等[14]基于OpenSees提出了修正梁柱节点单元,以边节点试验数据为依据,校核了模型计算的准确性和适用性。
上述梁柱节点有限元分析模型大多基于一维梁单元和二维平面单元建立,主要优势是求解稳定和模型计算周期短,其缺点是无法准确显示结构内部的应力状态和裂缝发展。节点捏缩效应的实现主要通过节点拟静力试验结果反推试算确定,往复荷载作用下的黏结退化机制并未真正体现,实际上已将分析和评价过程结合在一起,对所试算的模型及试验可以做到较高的吻合程度,但方法的通用性和可移植性仍然存疑。本文采用组合弹簧单元实现往复荷载作用下钢筋与混凝土间的黏结退化效应,基于损伤理论提出往复荷载作用下黏结滑移本构预测模型,运用APDL(ANSYS parametric design language)[15]进行简单的二次开发即可将黏结退化本构植入ANSYS环境,模拟得到的滞回曲线、骨架曲线、刚度退化曲线与试验结果的对比验证了有限元模型的适用性和准确性。
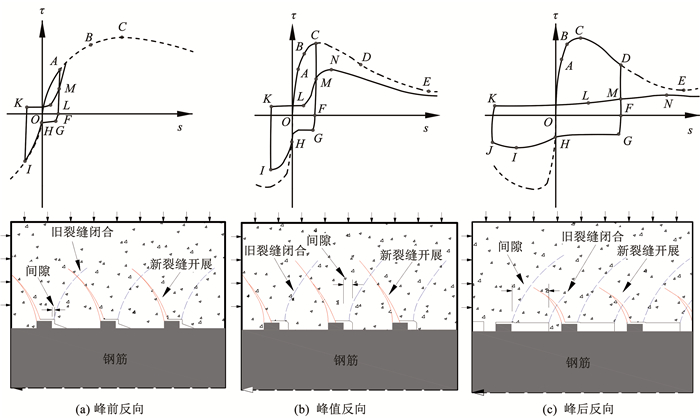
1 组合弹簧单元 1.1 往复荷载作用下钢筋与混凝土的黏结退化机制图 1为往复荷载作用下钢筋与混凝土的黏结退化机制。图中OABCDE为单调黏结滑移曲线,往复荷载作用下的黏结滑移曲线与单调加载差异明显,黏结性能的损伤退化取决于加载历程,随着循环周次及加载位移的逐步增加,钢筋与混凝土间的黏结强度和刚度会出现明显的损伤退化。进行结构抗震分析时,必须考虑钢筋与混凝土间的黏结退化行为。
|
图 1 往复荷载作用下的黏结退化机制 Fig. 1 Bond degradation mechanism under eciprocating loading |
为实现往复荷载作用下黏结性能的损伤退化,基于非线性弹簧单元和间隙弹簧单元建立了组合弹簧单元模型。
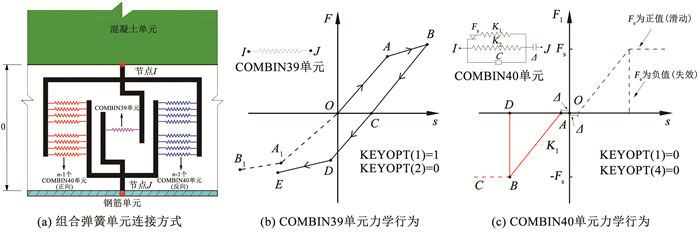
图 2(a)为组合弹簧单元的连接方式,组合弹簧单元由1个COMBIN39单元与n-1对COMBIN40单元并联组成[15],节点I和节点J分别为混凝土单元和钢筋单元的节点,钢筋单元的其他节点均采用相同的方式与混凝土节点相连。
|
图 2 组合弹簧单元连接方式与力学行为 Fig. 2 Connection mode and mechanical behavior of composite spring elements |
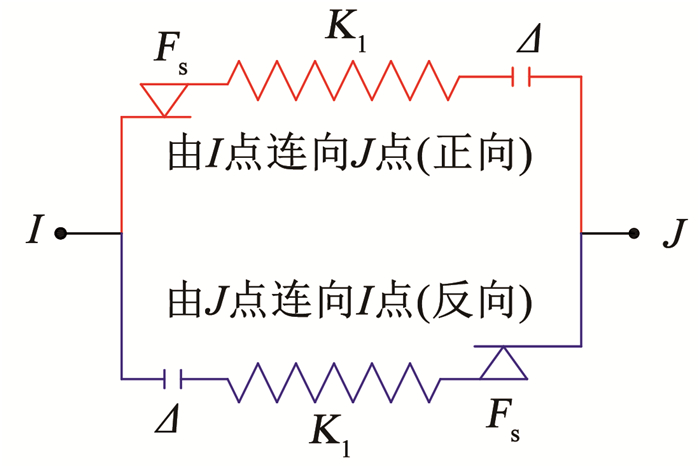
图 2(b)为COMBIN39单元的力学行为,通过设置对应的关键选项(KEYOPT选项)可激活该单元的非保守力行为,进而实现往复加载过程中的能量耗散。图 2(c)为COMBIN40单元的力学行为,输入的参数有弹簧刚度K1、极限滑动力Fs和间隙GAP(Δ),Fs设为负值可激活单元的失效行为,实现往复加载过程中黏结性能的损伤退化。COMBIN40单元是由节点连接顺序决定的单向弹簧(仅受压),为实现弹簧既能抗拉又能抗压的效果,将两个COMBIN40单元反向并联后成对使用,连接方式见图 3。
|
图 3 COMBIN40弹簧对 Fig. 3 COMBIN40 spring pair |
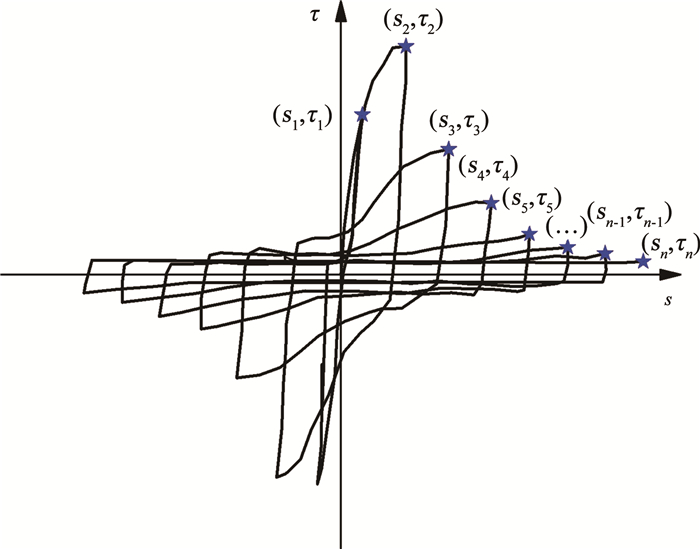
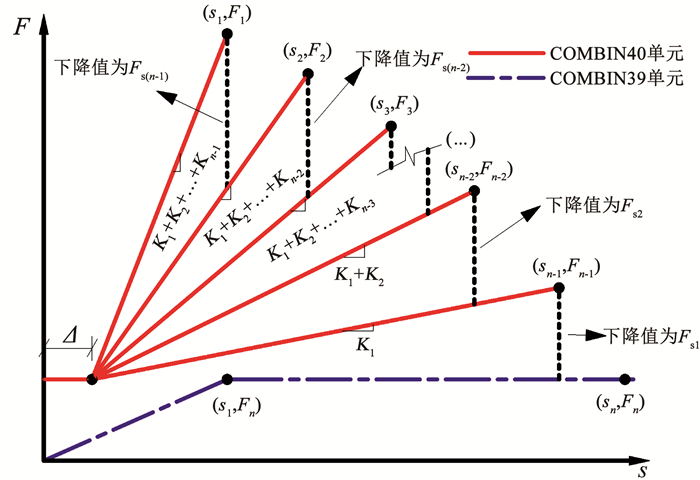
图 4为典型的黏结滑移退化曲线,(si, τi)为各正向加载历程中最大滑移量对应的特征数据点,根据数据点(si, τi)标定组合弹簧单元的参数。标定方式见图 5,首先将数据点(si, τi)采用式(1)转换为(si, Fi)。
| $F_i=\tau_i \pi d l$ | (1) |
|
图 4 往复荷载作用下的黏结滑移曲线 Fig. 4 Bond-slip curve under reciprocating loading |
|
图 5 组合弹簧单元参数标定示意 Fig. 5 Indication ofcalibration of composite spring elements |
式中:τi为黏结应力,d为钢筋的直径,l为钢筋单元的长度。
采用COMBINE39单元模拟残余黏结力,单元的F-s曲线可根据残余黏结力确定,特征数据点为(s1, Fn)和(sn, Fn)。CONBINE40单元用于模拟往复荷载作用下的黏结损伤,特征数据点按下述方法确定。
第1对COMBIN40弹簧的极限滑动力Fs1和刚度K1根据(sn-1, Fn-1)和(sn, Fn)确定:
| $F_{\mathrm{s} 1}=F_{n-1}-F_n$ | (2) |
| $K_1=\frac{F_{\mathrm{s} 1}}{s_{n-1}-\varDelta}$ | (3) |
第2对COMBIN40弹簧的极限滑动力Fs2和刚度K2根据(sn-2, Fn-2)和(sn, Fn)确定:
| $F_{\mathrm{s} 2}=F_{n-2}-F_n-K_1\left(s_{n-2}-\varDelta\right)$ | (4) |
| $K_2=\frac{F_{\mathrm{s} 2}}{s_{n-2}-\varDelta}$ | (5) |
依此类推,可标定各对COMBIN40弹簧的极限滑动力Fsi和刚度Ki,即
| $F_{\mathrm{s} i}=F_{n-i}-F_n-\sum\limits_{j=1}^{i-1} K_j\left(s_{n-i}-\varDelta\right)$ | (6) |
| $K_i=\frac{F_{\mathrm{s} i}}{s_{n-i}-\varDelta}$ | (7) |
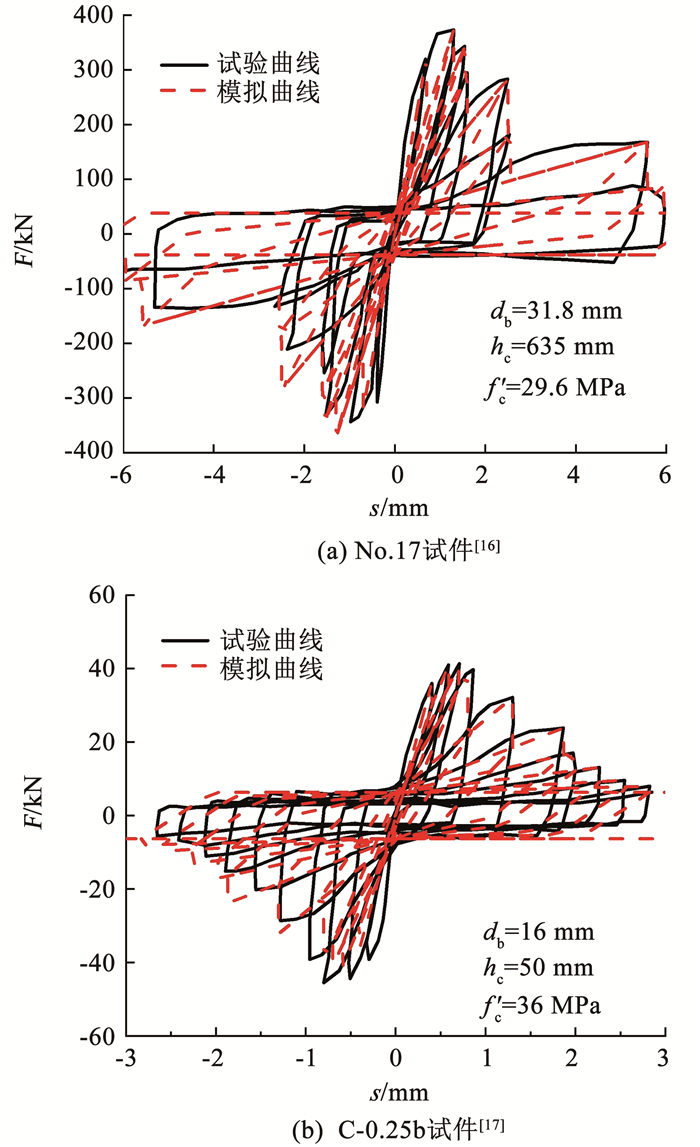
根据以上算法,可利用实测数据对组合弹簧进行标定,根据文献[16-17]的试验数据标定组合弹簧单元参数,标定结果与试验结果的对比见图 6。
|
db为钢筋直径,hc为钢筋埋入长度,f′c为混凝土圆柱体抗压强度 图 6 标定结果与试验结果对比 Fig. 6 Comparison of calibration and experimental results |
结果表明,根据实测数据和式(2)~(7)可完成组合弹簧单元的参数标定,组合弹簧单元成功地反演了往复荷载作用下黏结滑移曲线强度和刚度的退化。
2 往复荷载作用下的黏结滑移本构预测模型 2.1 基于损伤理论的黏结滑移本构预测模型组合弹簧单元的参数标定依赖于实测试验数据,为提高模型的适用性和可移植性,当无实测试验数据时,提出了基于损伤理论的黏结滑移本构预测模型。根据CEB-FIP Model Code 2010[18]确定钢筋与混凝土的单调黏结滑移曲线:
| $\tau=\left\{\begin{array}{l}\tau_{\text {max }}\left(\frac{s}{s_1}\right)^{0.4}, 0 \leqslant s \leqslant s_1 \\ \tau_{\text {max }}, s_1 \leqslant s \leqslant s_2 \\ \tau_{\text {max }}-\frac{\left(\tau_{\text {max }}-\tau_{\mathrm{f}}\right)\left(s-s_2\right)}{s_{\mathrm{R}}-s_2}, s_2 \leqslant s \leqslant s_{\mathrm{R}} \\ \tau_{\mathrm{f}}, s>s_{\mathrm{R}}\end{array}\right.$ | (8) |
式中:
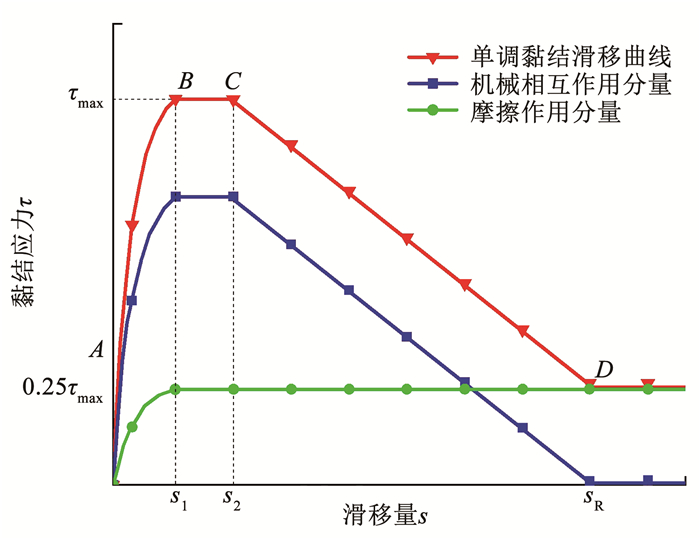
钢筋与混凝土之间的黏结力由化学胶着力、摩擦力和机械咬合力3部分组成[19]。相对滑移发生后,化学胶结力随即丧失,黏结应力可分解为机械作用分量(τb=0.75τmax)和摩擦作用分量(τf=0.25τmax),见图 7。
|
图 7 单调黏结滑移曲线及组成 Fig. 7 Monotonic bond-slip curve and its composition |
损伤参数采用Murcia-Delso损伤模型[20]确定:
| $d_{\mathrm{b}}=1-1.2 \mathrm{e}^{-2.7\left(\frac{\bar{S}_{\max }}{S_{\mathrm{R}}}\right)^{p .8}} \geqslant 0$ | (9) |
| $d_{\mathrm{f}}=\frac{\min \left(s_{\text {max }}^{+}+s_{\text {max }}^{-}, s_{\mathrm{R}}\right)}{s_{\mathrm{R}}}\left[1-\mathrm{e}^{-0.45\left(\frac{s_{\text {acc }}}{s_{\mathrm{R}}}\right)^{0.75}}\right]$ | (10) |
| $\bar{s}_{\max }=0.75 \max \left(s_{\max }^{+}, s_{\max }^{-}\right)+0.25\left(s_{\max }^{+}+s_{\max }^{-}\right)$ | (11) |
式中:db为机械作用损伤参数;df为摩擦作用损伤参数;smax+为正方向上最大滑移量,smax-为负方向上最大滑移量的绝对值;sacc为累计滑移量,为避免大量小周期加载对摩擦作用分量损伤的过高估计,当滑移量小于s1时,sacc取0。
损伤后的黏结应力根据损伤参数确定:
| $\begin{aligned} \tau_{\mathrm{b}, \mathrm{d}} & =\left(1-d_{\mathrm{b}}\right) \tau_{\mathrm{b}} \\ \tau_{\mathrm{f}, \mathrm{d}} & =\left(1-d_{\mathrm{f}}\right) \tau_{\mathrm{f}} \\ \tau_{\mathrm{d}} & =\tau_{\mathrm{b}, \mathrm{d}}+\tau_{\mathrm{f}, \mathrm{d}}\end{aligned}$ | (12) |
式中:τb, d为损伤后的机械作用分量,τf, d为损伤后的摩擦作用分量,τd为损伤后的总黏结应力。
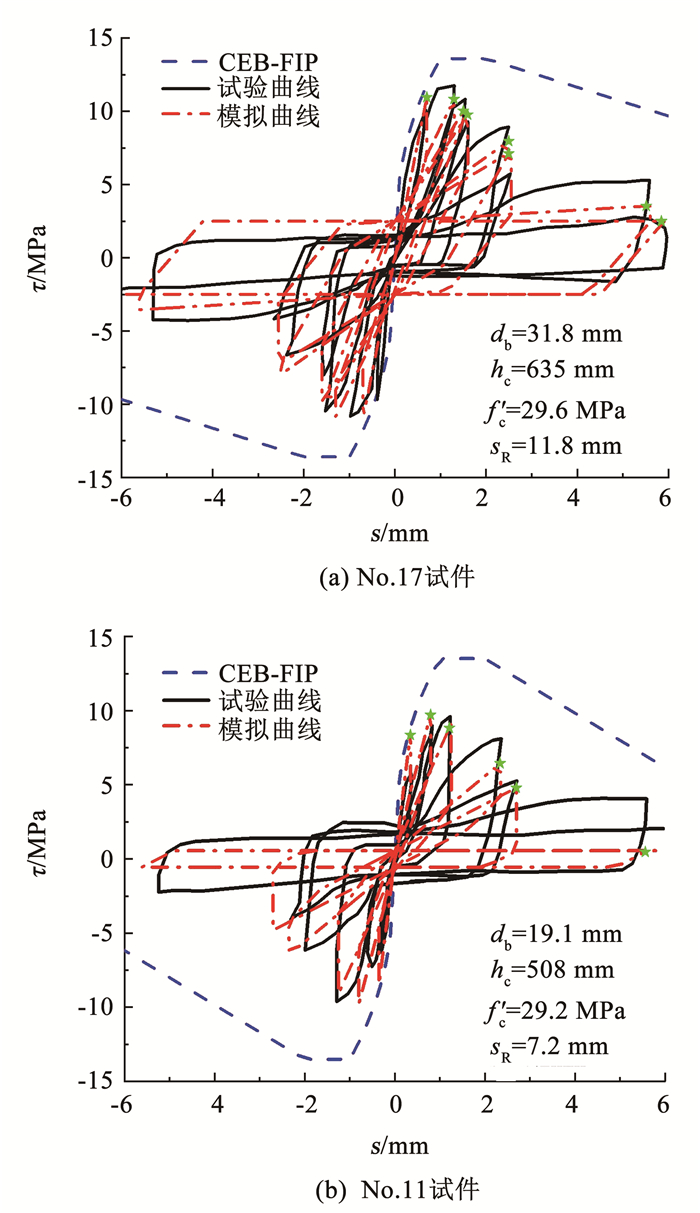
2.2 黏结滑移本构预测模型有效性验证为验证黏结滑移本构预测模型的有效性,使用黏结滑移本构预测模型对文献[16]中的黏结滑移试验曲线进行相应预测,主要变化参数为钢筋直径和黏结长度,将预测结果与试验结果进行对比,结果见图 8。
|
图 8 预测结果与试验结果对比 Fig. 8 Comparison between predicted and experimental results |
图 8中虚线为由CEB-FIP Model Code 2010预测得到的单调黏结滑移曲线,直线为试验黏结滑移曲线,点划线为采用组合弹簧单元模拟得到的黏结滑移曲线,其中星标为用损伤模型预测得到的标定组合弹簧单元参数的特征点。试验与模拟结果对比表明,预测模型可以较好地预测往复荷载作用下钢筋与混凝土的黏结滑移退化趋势。
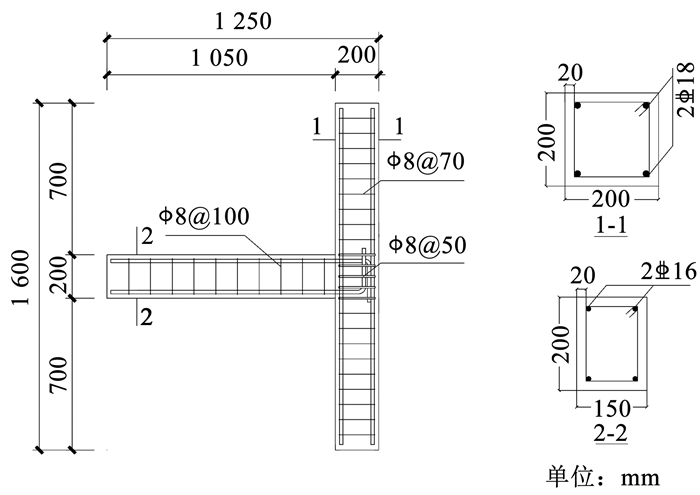
3 边节点有限元模型 3.1 试验概况根据文献[21]的试验设计建立梁柱边节点有限元模型,节点的几何尺寸如图 9所示,柱横截面尺寸为200 mm×200 mm,梁横截面尺寸为150 mm×200 mm。
|
图 9 试件几何尺寸 Fig. 9 Geometric dimension of experimental specimen |
梁柱边节点试件的材料参数见表 1和2,梁柱纵筋为HRB400E钢筋,箍筋为HPB300钢筋,箍筋直径均为8 mm。
| 表 1 梁柱边节点试件的材料参数 Tab. 1 Material parameters of exterior beam-column joint specimens |
| 表 2 钢筋力学性能指标 Tab. 2 Mechanical property index of reinforcement |
混凝土受压应力-应变曲线公式[22]如下:
| $\sigma_{\mathrm{c}}=\left\{\begin{array}{l}f_{\mathrm{ck}}\left[1-\left(1-\varepsilon_{\mathrm{c}} / \varepsilon_{\mathrm{c} 0}\right)^n\right], \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{c} 0} \\ f_{\mathrm{ck}}\left[1-0.15\left(\frac{\varepsilon_{\mathrm{c}}-\varepsilon_{\mathrm{c} 0}}{\varepsilon_{\mathrm{cu}}-\varepsilon_{\mathrm{c} 0}}\right)\right], \varepsilon_{\mathrm{c} 0}<\varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{cu}}\end{array}\right.$ | (13) |
| $n=2-\frac{1}{60}\left(f_{\mathrm{ck}}-50\right)$ | (14) |
| $\varepsilon_0=0.002+0.5\left(f_{\mathrm{ck}}-50\right) \times 10^{-5}$ | (15) |
| $\varepsilon_{\mathrm{cu}}=0.0033-0.5\left(f_{\mathrm{ck}}-50\right) \times 10^{-5}$ | (16) |
式中:εc0为峰值应力对应的压应变,εcu为极限压应变。
混凝土单轴受拉应力-应变曲线公式[22]如下:
| $\sigma_{\mathrm{t}}=\left\{\begin{array}{l}E_0 \varepsilon_{\mathrm{t} 0}, \varepsilon_{\mathrm{t}} \leqslant \varepsilon_{\mathrm{t} 0} \\ 0.6 f_{\mathrm{ct}}\left(1.2-0.2 \frac{\varepsilon_{\mathrm{t}}}{\varepsilon_{\mathrm{t} 0}}\right), \varepsilon_{\mathrm{t} 0}<\varepsilon_{\mathrm{t}} \leqslant \varepsilon_{\mathrm{tu}}\end{array}\right.$ | (17) |
式中:E0为受拉区的初始弹性模量,可根据式(13)的原点切线模量确定;fct=0.19fck0.75,为抗拉强度;εt0为极限拉应力对应的拉应变;εtu=6εt0,为极限拉应变。
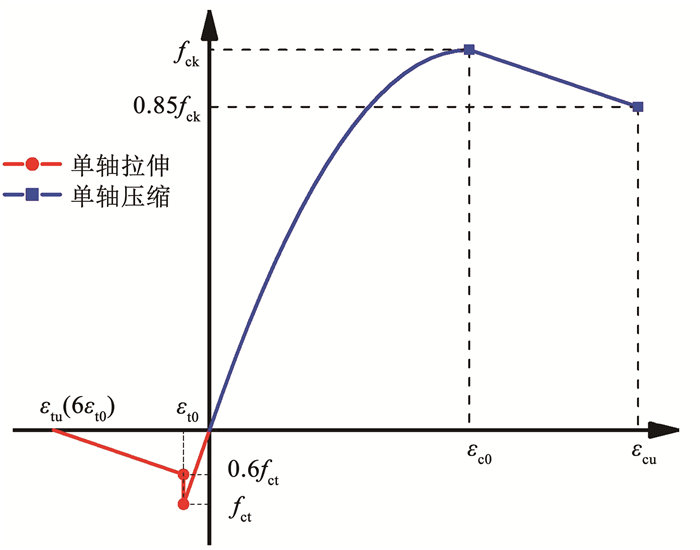
混凝土的应力-应变曲线见图 10。
|
图 10 混凝土应力-应变曲线 Fig. 10 Stress strain curve of concrete |
采用混合强化模型定义HRB400E钢筋的本构关系,混合强化模型由Voce非线性等向强化模型和Chaboche非线性随动强化模型组成[23]。Voce非线性等向强化模型的屈服应力演化可用下式表示:
| $\sigma_{\mathrm{Y}}=\sigma_0+R_0 \hat{\varepsilon}^{\mathrm{pl}}+R_{\infty}\left[1-\exp \left(-b \hat{\varepsilon}^{\mathrm{pl}}\right)\right]$ | (18) |
式中:σY为屈服应力,σ0为初始屈服应力,R0为饱和应力的斜率,R∞为饱和应力与初始屈服应力的差值,
Chaboche非线性随动强化模型的背应力演化可用下式表示:
| $X_k=\frac{C_k}{\gamma_k}\left(1-\mathrm{e}^{-\gamma_k \varepsilon^{\mathrm{pl}}}\right)+X_{k, 1} \mathrm{e}^{-\gamma_k \varepsilon^{\mathrm{pl}}}$ | (19) |
| $X=\sum\limits_{k=1}^n X_k$ | (20) |
式中:Xk为背应力,εpl为塑性应变值,Ck和γk为随动强化参数。
根据文献[24]的实测数据对往复荷载作用下钢筋的本构关系进行标定,等向强化模型材料参数和随动强化模型材料参数分别见表 3和4。
| 表 3 Voce非线性等向强化模型材料参数 Tab. 3 Material parameters of Voce nonlinear isotropic hardening model |
| 表 4 Chaboche非线性随动强化模型材料参数 Tab. 4 Material parameters of Chaboche nonlinear kinematic hardening model |
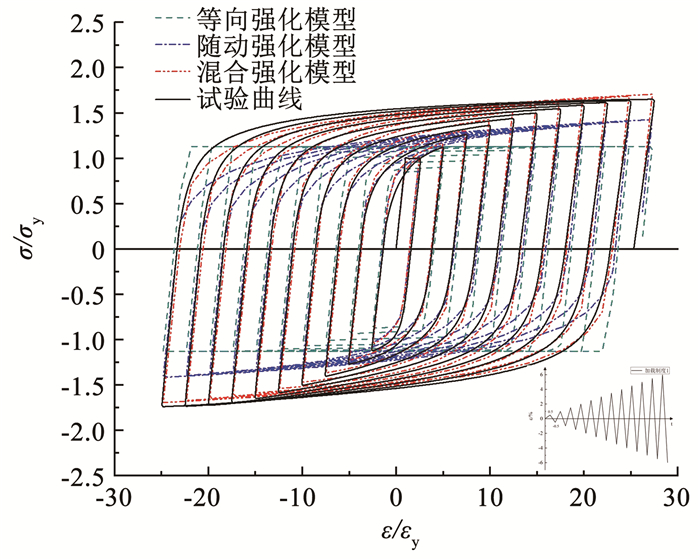
图 11为等向强化模型、随动强化模型和混合强化模型对比。循环荷载作用下,正向应变首次达2%时,3种本构关系的相对误差分别为23.7%、8.4%和4.7%。混合强化模型包含等向强化模型和随动强化模型的特征,能更好地描述钢筋在往复荷载作用下的滞回响应。
|
图 11 正则化钢筋滞回曲线 Fig. 11 Regularized reinforcement hysteretic curves |
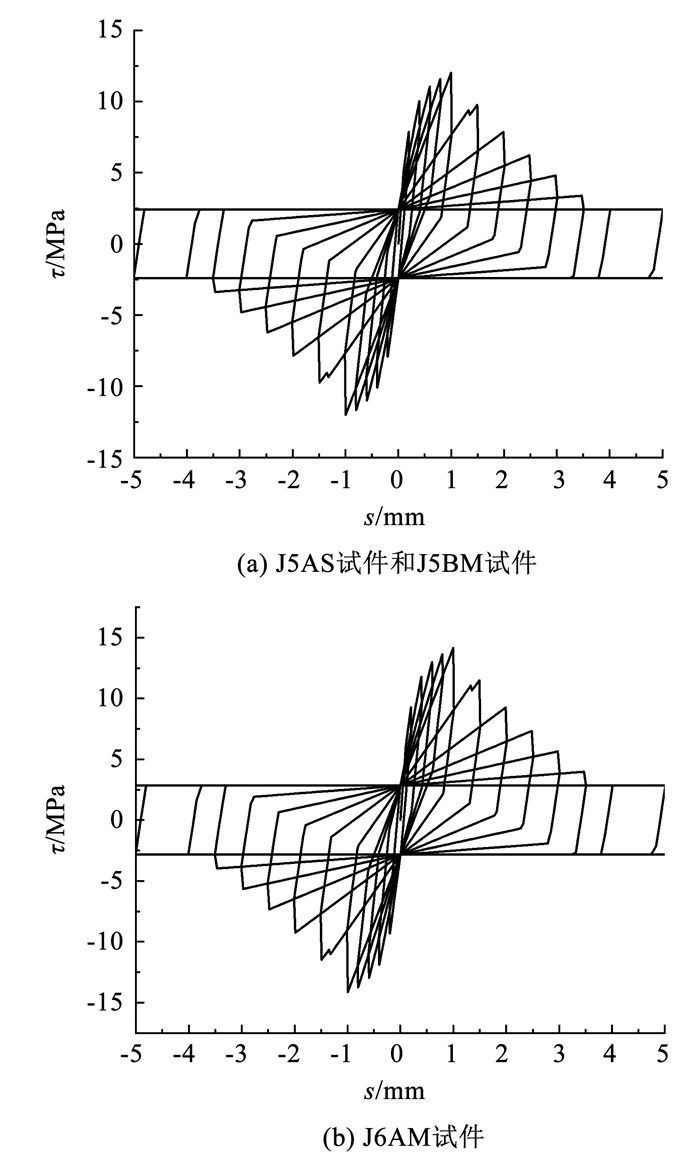
基于表 1和2中试验参数,利用式(8)~(12)即实现对文献[21]中往复荷载作用下黏结滑移本构关系的预测,见图 12。
|
图 12 黏结滑移本构关系 Fig. 12 Bond-slip constitutive relation |
采用ANSYS建立梁柱边节点有限元分析模型,钢筋与混凝土单元不共用节点,在钢-混界面植入开发的组合弹簧单元,模拟加载过程中钢筋与混凝土间黏结性能的退化。
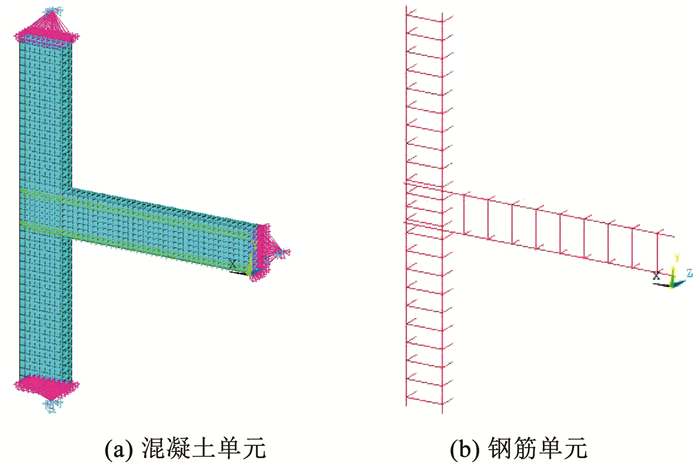
根据对称性,采用SOLID65实体单元建立混凝土1/2模型,如图 13(a)。模型在梁长范围内的单元尺寸为25 mm×25 mm×25 mm,其他区域混凝土单元尺寸为25 mm×25 mm×35 mm。为方便施加荷载和约束,使用MASS21单元作为主节点,梁端及柱端处节点作为从节点,采用约束方程建立耦合关系,在MASS21单元上施加与试验一致的柱顶轴力和梁端往复位移荷载。梁柱边节点模型对称面上约束Z方向平移自由度,柱下方MASS21节点施加X、Y和Z方向的约束,柱体上方MASS21节点施加X、Z方向约束,并施加750 kN的竖向荷载,梁端施加Z方向的约束,在梁端的MASS21节点上施加往复位移荷载。
|
图 13 有限元模型 Fig. 13 Finite element model |
采用LINK180单元建立钢筋1/2模型,如图 13(b)。梁纵筋的单元尺寸为25 mm,与混凝土单元对应,在钢筋单元与混凝土单元之间插入长度为0的组合弹簧单元。
3.4 数值模拟结果分析数值模拟采用与试验相同的加载制度,将模拟结果与试验结果进行对比,进而验证梁柱边节点有限元模型的有效性。
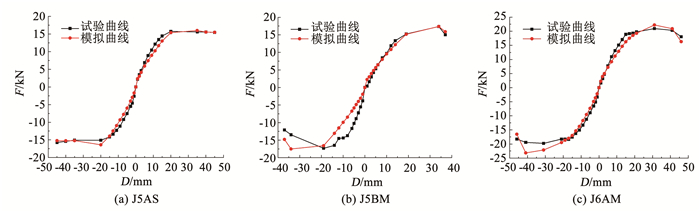
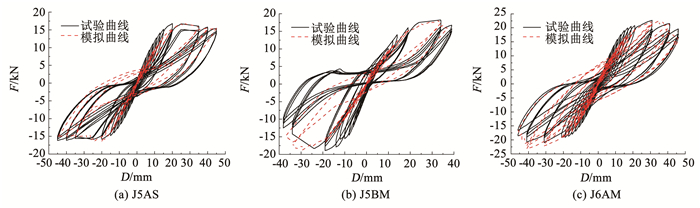
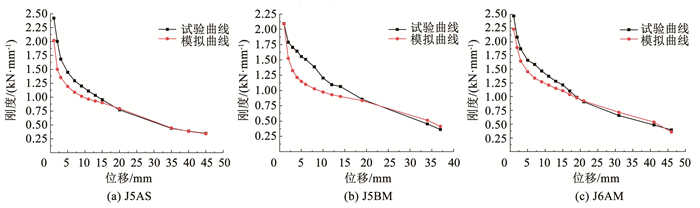
3.4.1 骨架曲线、滞回曲线和刚度退化曲线图 14、15、16分别为骨架曲线、滞回曲线和刚度退化曲线有限元计算结果与试验对比。节点拟静力加载数值模拟结果基本对称,试验曲线后期骨架曲线在1、3象限有些差异,有限元未能考虑这些变化,所以, 图 14(b)、(c)数值模拟与实测结果有一定差异。根据图 10混凝土本构关系,ANSYS中SOLID65混凝土单元开裂时拉应力降为抗拉强度的0.6倍,将过高估计刚度的退化,混凝土充分开裂后又逐渐趋近试验结果,因此,图 16(a)~(c)数值模拟的5 mm左右刚度低于试验结果。模拟得到的骨架曲线、滞回曲线和刚度退化曲线基本反映了拟静力加载试验曲线的特征,模拟得到的滞回曲线展现了明显的捏缩效应,证实了模型的有效性与合理性,表明利用组合弹簧单元结合钢筋的Voce-Chaboche混合强化本构关系可以较好地模拟梁柱边节点在往复荷载作用下的抗震性能。
|
图 14 骨架曲线 Fig. 14 Skeleton curve |
|
图 15 滞回曲线 Fig. 15 Hysteresis curves |
|
图 16 刚度退化曲线 Fig. 16 Stiffness degradation curves |
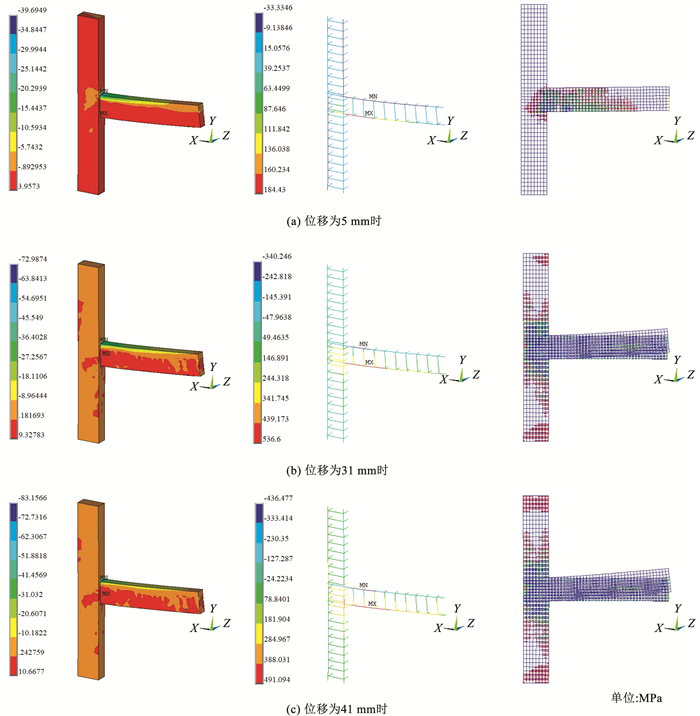
ANSYS中SOLID65单元采用最大拉应力准则作为开裂判据,达到最大拉应力随即出现与拉应力正交的裂缝,后处理选项可以查看指定荷载步下梁柱边节点的应力状态及裂缝发展。图 17为位移分别为5、31、41 mm时节点J6AM的混凝土应力图、钢筋应力图与裂缝。由混凝土应力云图可知,混凝土上的最大拉压应力均出现在梁柱节点核心区,且随着加载位移的增加,混凝土上的应力也逐步增大。由钢筋应力云图可知,加载位移由5 mm增加至31 mm时,钢筋的最大拉应力呈现增长趋势,而当位移由31 mm增加至41 mm时,钢筋的最大拉应力由536.6 MPa减小至491.094 MPa,钢筋与混凝土之间黏结性能的退化是导致钢筋应力在循环加载后期降低的原因。由裂缝发展图可知,随着加载位移的增加,裂缝从梁柱节点核心区逐步向梁端与柱端发展。
|
图 17 应力云图和裂缝发育 Fig. 17 Stress nephogram and crack development |
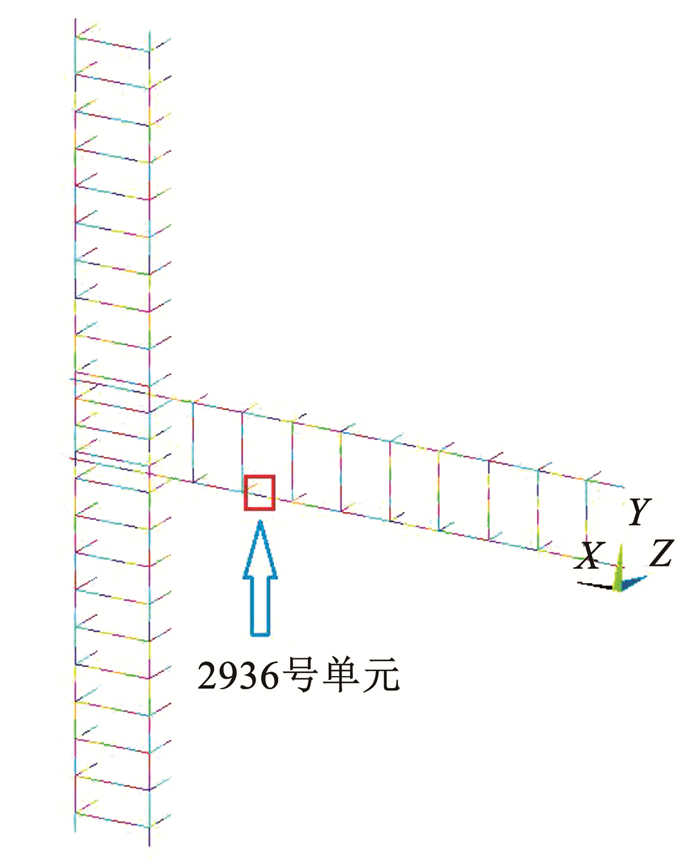
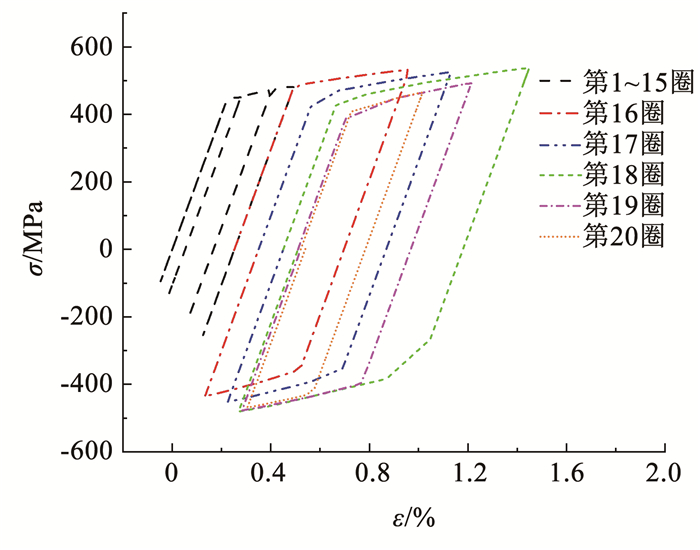
为直观地了解梁柱边节点内部钢筋的滞回响应,提取了J6AM试件2936号钢筋单元(图 18)的应力-应变曲线,见图 19。结果表明,随着梁端对称加载位移的逐步增加,钢筋的塑性伸长致使应变出现漂移,加载后期(第18~20圈)钢筋应力-应变滞回环甚至反方向漂移;组合弹簧单元成功地反演了往复加载过程中黏结性能的退化机制,在钢筋塑性漂移和黏结退化的双重作用下,往复加载后期钢筋的应力反而有所降低,与图 17中的钢筋最大拉应力云图的分析一致。
|
图 18 应变考察单元位置 Fig. 18 Location of strain observation element |
|
图 19 钢筋应力-应变曲线 Fig. 19 Stress-strain curve of reinforcement |
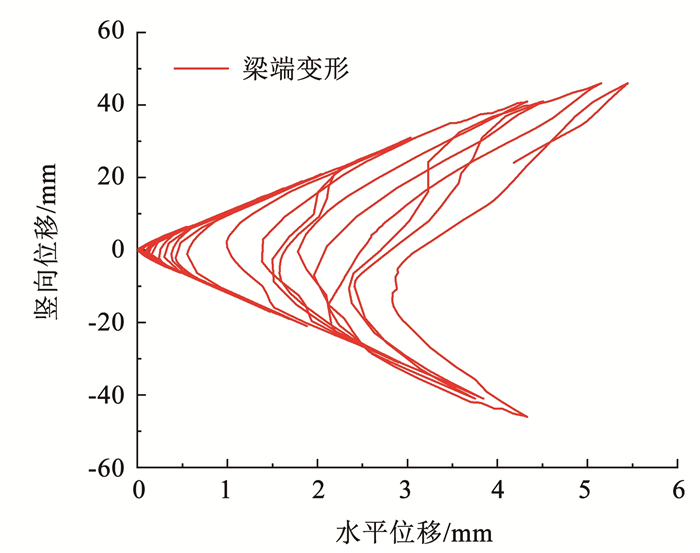
图 20为J6AM节点梁端竖向位移和水平位移的关系。随着梁端竖向往复位移的逐步增加,梁端水平残余变形也逐渐增大,表明往复荷载作用下节点梁中塑性铰的发育会导致梁的伸长。目前,对梁柱节点的研究主要集中于构件层面的抗震性能和抗剪性能,而梁的伸长对边节点的影响并未引起足够的重视。
|
图 20 梁端竖向位移与水平位移的关系 Fig. 20 Relationship between vertical displacement and horizontal displacement of beam end |
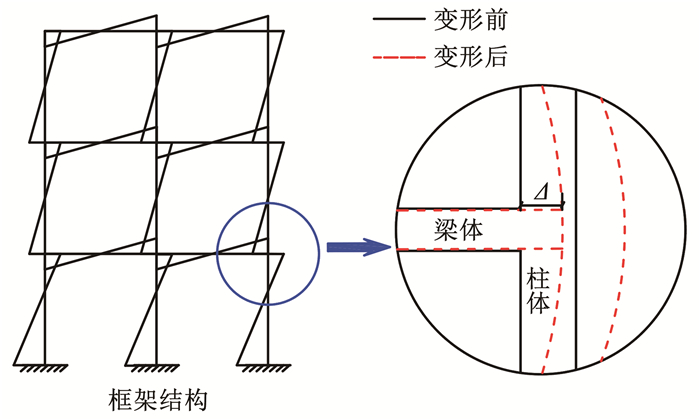
如图 21所示,在水平地震荷载作用下,首层框架结构边柱的反弯点位于1/2柱高以上[25],柱根部弯矩明显大于柱顶。然而,汶川震灾调查结果表明[26],多层混凝土框架结构边柱的主要破坏位置集中于弯矩较小的柱顶(图 22),梁端的塑性伸长迫使边柱发生侧移是导致首层边柱柱顶破坏的主要原因之一。近年来,中国一直致力于推广高品质钢材在建筑行业的应用,从2007年开发的细晶粒钢筋到2018年带“E”牌号的抗震钢筋[27],伸长率和耗能能力均有明显提升,然而无论是结构内力计算还是抗震设计,均未考虑梁塑性伸长对边柱的影响,研究工作亟待开展。
|
图 21 多层框架结构弯矩图与边柱侧移 Fig. 21 Bending moment of multi-story frame structure and exterior column side shift |

|
图 22 首层柱顶节点破坏形式 Fig. 22 Failure mode of column top joint on the first floor |
1) 组合弹簧单元可以有效地模拟往复荷载作用下钢筋与混凝土之间的黏结退化特性,弹簧单元力学参数可根据实测数据或文中预测模型进行标定。
2) 循环荷载作用下,正向应变首次达2%时,等向强化模型、随动强化模型和混合强化3种钢筋本构的相对误差分别为23.7%、8.4%和4.7%,混合强化本构能更好地描述往复荷载作用下的滞回响应。
3) 考虑黏结退化机制的梁柱边节点有限元模型,可以实现往复加载过程中滞回曲线的捏缩效应,与试验结果的对比证明了模型的可靠性和准确性。
4) 往复荷载作用下节点梁中塑性铰的发育导致梁塑性伸长,将对边节点柱造成不利影响。
5) 组合弹簧单元结合精细化有限元建模技术,丰富了节点相关研究的内容也增加了对细节的把控,在一定程度上可弥补宏观试验在测试上的不足。
| [1] |
钱凯, 何畔, 原小兰, 等. 中柱失效下预制装配式框架结构抗连续倒塌性能研究[J]. 建筑结构学报, 2022, 43(7): 131. QIAN Kai, HE Pan, YUAN Xiaolan. Progressive collapse resistance of precast frame structure subjected to loss of a middle column[J]. Journal of Building Structures, 2022, 43(7): 131. DOI:10.14006/j.jzjgxb.2020.0226 |
| [2] |
钱辉, 李宗翱, 裴金召, 等. 自复位超弹性SMA筋梁柱节点数值模拟研究[J]. 工程力学, 2020, 37(11): 135. QIAN Hui, LI Zongao, PEI Jinzhao, et al. Numerical simulation on self-centering beam-column joints reinforced with superelastic SMA bars[J]. Engineering Mechanics, 2020, 37(11): 135. DOI:10.6052/j.issn.1000-4750.2019.12.0791 |
| [3] |
赵卫平, 程倩倩, 李雪菡, 等. HRB400E钢筋混凝土梁柱边节点的抗剪性能[J]. 哈尔滨工业大学学报, 2022, 54(10): 20. ZHAO Weiping, CHENG Qianqian, LI Xuehan, et al. Shearing performance of concrete exterior beam-column joints with HRB400E reinforcement[J]. Journal of Harbin Institute of Technology, 2022, 54(10): 20. DOI:10.11918/202111052 |
| [4] |
HAKUTO S, PARK R, TANAKA H. Effect of deterioration of bond of beam bars passing through interior beam-column joints on flexural strength and ductility[J]. ACI Structural Journal, 1999, 96(5): 858. |
| [5] |
吕西林, 郭子雄, 王亚勇. RC框架梁柱组合件抗震性能试验研究[J]. 建筑结构学报, 2001, 22(1): 2. LYU Xilin, GUO Zixiong, WANG Yayong. Seismic reinforced concrete frame[J]. Journal of Building Structures, 2001, 22(1): 2. |
| [6] |
武秀莹. 配置500级纵筋的框架中间层中节点抗震性能试验及设计方法研究[D]. 重庆: 重庆大学, 2008 WU Xiuying. Experimental and design methodological research for the seismic behavior of interior joint with 500 MPa longitudinal bar[D]. Chongqing: Chongqing University, 2008 |
| [7] |
BRAGA F, GIGLIOTTI R, LATERZA M. R/C existing structures with smooth reinforcing bars: experimental behaviour of beam-column joints subject to cyclic lateral loads[J]. Open Construction & Building Technology Journal, 2009, 3(1): 52. DOI:10.2174/1874836800903010052 |
| [8] |
曹子健, 李全旺. 有缺陷的装配式混凝土梁柱节点抗震性能试验研究[J]. 工程力学, 2021, 38(11): 134. CAO Zijian, LI Quanwang. Experimental study on the seismic behavior of precast concrete beam-column joints with connection defects[J]. Engineering Mechanics, 2021, 38(11): 134. DOI:10.6052/j.issn.1000-4750.2020.11.0788 |
| [9] |
ELMORSI M, KIANOUSH M R, TAO W K. Modeling bond-slip deformations in reinforced concrete beam-column joints[J]. Canadian Journal of Civil Engineering, 2000, 27(3): 490. DOI:10.1139/l99-085 |
| [10] |
LOWES L N, ALTOONTASH A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading[J]. Journal of Structural Engineering, 2003, 12(12): 1686. DOI:10.1061/(ASCE)0733-9445(2003)129:12(1686) |
| [11] |
MITRA N, LOWES L N. Evaluation, calibration, and verification of a reinforced concrete beam-column joint model[J]. Journal of Structural Engineering, 2007, 133(1): 105. DOI:10.1061/(ASCE)0733-9445(2007)133:1(105) |
| [12] |
MITRA N. An analytical study of reinforced concrete beam-column joint behavior under seismic loading[D]. Washington: University of Washington, 2007
|
| [13] |
赖少颖. 考虑黏结滑移作用的钢筋混凝土梁柱节点数值分析[D]. 深圳: 深圳大学, 2013 LAI Shaoying. Numerical analysis of reinforced concrete beam-column joints considering bond slip[D]. Shenzhen: Shenzhen University, 2013 |
| [14] |
赵雯桐, 杨红, 傅剑平, 等. 钢筋混凝土中间层边节点模型化方法研究[J]. 建筑结构学报, 2018, 39(增刊1): 254. ZHAO Wentong, YANG Hong, FU Jianping, et al. Modelling of RC exterior beam-column joint[J]. Journal of Building Structures, 2018, 39(Sup.1): 254. |
| [15] |
ANSYS. ANSYS user's manual for version 17.2[M]. Canonsburg: ANSYS Inc, 2016.
|
| [16] |
LUNDGREN K. Pull-out tests of steel-encased specimens subjected to reversed cyclic loading[J]. Materials & Structures, 2000, 33(231): 450. DOI:10.1007/bf02480665 |
| [17] |
HWANG H J, EOM T S, PARK H G. Bond-slip relationship of beam flexural bars in interior beam-column joints[J]. ACI Structural Journal, 2015, 112(6): 827. DOI:10.14359/51687708 |
| [18] |
CEB-FIP. Model code 2010: final draft[S]. Switzerland: Fédération Internationale Du Béton, 2012
|
| [19] |
赵卫平, 肖建庄. 带肋钢筋与混凝土间黏结滑移本构模型[J]. 工程力学, 2011, 28(4): 164. ZHAO Weiping, XIAO Jianzhuang. On bond-slip constitutive model between ribbed steel bars and concrete[J]. Engineering Mechanics, 2011, 28(4): 164. |
| [20] |
MURCIA-DELSO J, STAVRIDIS A, SHING P B. Bond strength and cyclic bond deterioration of large-diameter bars[J]. ACI Structural Journal, 2013, 110(54): 659. DOI:10.14359/51685751 |
| [21] |
赵卫平, 赵芷迎, 雷永旺, 等. 基于正交试验的框架端节点抗震性能影响因素分析[J]. 振动与冲击, 2021, 40(14): 203. ZHAO Weiping, ZHAO Zhiying, LEI Yongwang, et al. Influencing factor analysis on the seismic behaviors of frame exterior joints based on orthogonal experiments[J]. Journal of Vibration and Shock, 2021, 40(14): 203. DOI:10.13465/j.cnki.jvs.2021.14.027 |
| [22] |
王新敏, 李义强, 许宏伟. ANSYS结构分析单元与应用[M]. 北京: 人民交通出版社, 2011. WANG Xinmin, LI Yiqiang, XU Hongwei. Element and application of ANSYS structure analysis[M]. Beijing: China Communications Press, 2011. |
| [23] |
CHABOCHE J L. Time-independent constitutive theories for cyclic plasticity[J]. International Journal of Plasticity, 1986, 2(2): 149. DOI:10.1016/0749-6419(86)90010-0 |
| [24] |
石永久, 王萌, 王元清. 循环荷载作用下结构钢材本构关系试验研究[J]. 建筑材料学报, 2012, 15(3): 293. SHI Yongjiu, WANG Meng, WANG Yuanqing. Experimental study of structural steel constitutive relationship under cyclic loading[J]. Journal of Building Materials, 2012, 15(3): 293. |
| [25] |
钱稼茹, 赵作周, 纪晓东. 高层建筑结构设计[M]. 3版. 北京: 中国建筑工业出版社, 2018. QIAN Jiaru, ZHAO Zuozhou, JI Xiaodong. Design of tall building structures[M]. 3rd ed.. Beijing: China Architecture & Building Press, 2018. |
| [26] |
田志鹏, 张新培, 赵统. 汶川地震中多层钢筋混凝土框架结构房屋震害分析[J]. 建筑结构, 2009, 39(11): 67. TIAN Zhipeng, ZHANG Xinpei, ZHAO Tong. Seismic damage of multilayer reinforced concrete frame structures in Wenchuan Earthquake[J]. Building Structure, 2009, 39(11): 67. DOI:10.19701/j.jzjg.2009.11.018 |
| [27] |
中冶建筑研究总院有限公司. 钢筋混凝土用钢第2部分热轧带肋钢筋: GB/T 1499.2—2018[S]. 北京: 中国建筑工业出版社, 2018
|
 2024, Vol. 56
2024, Vol. 56


