2. 中南大学 高速铁路建造技术国家工程研究中心,长沙 410075;
3. 中建五局第三建设有限公司,长沙 410004
2. National Engineering Research Center of High-speed Railway Construction Technology, Central South University, Changsha 410075, China;
3. The Third Construction Co., Ltd. of China Construction Fifth Engineering Bureau, Changsha 410004, China
装配式组合梁作为一种新型复合材料结构,因其生产效率高、可持续性能好、低碳环保等特点广泛应用于工业与民用建筑中[1-4]。本课题组首次提出了一种新型装配式双拼槽钢-混凝土组合梁,该组合梁是通过高强螺栓将两个预制楼板背靠背连接起来叠合而成,如图 1所示。与现有的装配式组合梁相比,该组合梁实现了全装配施工,无需额外的现场浇筑和焊接,加快了施工速度;此外,混凝土板位于槽钢翼缘下方,有效降低了梁高,增大了建筑使用空间,具有广泛应用前景和巨大商业价值。钢-混组合梁通常是依靠剪力连接件来传递混凝土与钢梁之间的界面剪力,保证两者协同工作。国内外常用的剪力连接件主要包括栓钉、螺栓剪力连接件等[5-7],但对于新型装配式双拼槽钢-混凝土组合梁,常规的剪力连接件无法满足其构造要求。为保证组合梁中混凝土板与槽钢梁之间的组合作用,增强组合梁的整体工作性能,提出一种适用于该组合梁的新型开孔钢板剪力连接件(PSP剪力连接件)。该剪力连接件是在组合梁的上翼缘和纵向加劲肋之间焊接特定的开孔钢板形成(见图 1(b)),其不仅能够有效防止混凝土板的纵向滑移和横向分离,增强组合梁整体工作性能,还能作为槽钢梁加劲肋,防止腹板和翼缘的屈曲和失稳。

|
图 1 新型预制楼板及双拼槽钢-混凝土组合梁 Fig. 1 New type of prefabricated floor slab and double-channel steel-concrete composite beam |
目前,对各类开孔钢板剪力连接件抗剪性能的研究已较为系统。Oguejiofor等[8]研究了开孔钢板孔洞数量、孔洞间距、混凝土强度以及横向钢筋对受剪承载力的影响,并提出了受剪承载力计算方法。Vianna等[9]开展了16组PBL剪力连接件推出试验,讨论了混凝土板厚度、混凝土强度、穿孔钢筋等参数对PBL剪力连接件受剪承载力和刚度的影响并给出了计算建议。Ahn等[10]通过推出试验发现双排PBL连接件的平均受剪承载力约为单排受剪承载力的80%。Kim等[11]提出了一种新的Y型PBL剪力连接件并对其开展了推出试验。Vianna等[12]对18组T型开孔钢板剪力连接件开展了试验研究,结果表明,T型开孔钢板剪力连接件具有较高的受剪承载力。肖林等[13-15]通过静载试验发现PBL连接件受剪承载力及破坏模式取决于开孔钢板厚度,并给出了考虑钢板厚度等参数的承载力计算公式。胡建华等[16]通过开展推出试验发现PBL连接件具有延性破坏特征。卫星等[17]对PBL剪力连接件疲劳性能开展了系统的试验研究,并给出了采用残余滑移量评估疲劳损伤发展的设计建议。张清华等[18-19]通过试验、数值和理论方法研究了PBL剪力连接件群的传力机制,并提出了荷载-滑移变形协调模型和极限承载力计算方法。汪维安等[20]通过静载试验研究了多排PBL连接件荷载-滑移分布特征,并给出了PBL剪力连接件群承载力计算方法。
综上,虽然对开孔钢板剪力连接件(PBL剪力连接件)已开展了大量研究并取得了丰富的研究成果,但主要都是围绕垂直于穿孔钢筋方向受剪的PBL剪力连接件,对于受剪方向平行于穿孔钢筋的开孔钢板剪力连接件的研究较少。本文提出的PSP剪力连接件属于该类开孔钢板剪力连接件,目前对PSP剪力连接件的研究尚属空白。为此,在新型装配式双拼槽钢-混凝土组合梁基础上,设计了7组试件并开展推出试验,探讨了不同参数PSP剪力连接件的受剪承载力及破坏模式。采用有限元方法开展了参数分析,进一步研究了开孔钢板厚度、开孔直径、混凝土强度、连接件间距和穿孔钢筋对PSP剪力连接件力学性能的影响。根据试验及有限元荷载-滑移曲线提出了装配式双拼槽钢-混凝土组合梁中单个PSP剪力连接件荷载滑移曲线计算公式,为装配式双拼槽钢混组合梁的设计提供参考。
1 试验 1.1 试件设计为研究新型装配式双拼槽钢-混凝土组合梁中PSP剪力连接件的力学性能,在双拼槽钢-混凝土组合梁基础上,根据Eurocode4规范设计了标准推出试件,其详细构造及尺寸如图 2所示。

|
图 2 标准推出试件构造及尺寸 Fig. 2 Structure and size of standard specimens |
推出试件整体尺寸为400 mm×100 mm×400 mm。其中,钢梁由沿腹板切割后的32b热轧槽钢和矩形钢板焊接而成,长度为350 mm,矩形钢板厚度为16 mm。PSP剪力连接件三边焊接于钢梁内部,试件中所有焊接均采用一级全融透焊缝。为避免试件底部混凝土发生局部受压破坏,在底部混凝土中设置了箍筋加密区。此外,混凝土浇筑前在钢梁内侧涂抹了润滑油,以减少钢梁与混凝土之间的界面摩擦。
推出试件主要参数如表 1所示。其中,试件SP2-6-30-C40-150和SP2-4-30-C40-150为间距150 mm双剪力连接件试件,其余试件为单剪力连接件试件。所有试件均采用C40或C50混凝土,经28 d自然养护,两种实测混凝土立方体抗压强度分别为42.5、50.4 MPa。试件中槽钢、矩形钢板及PSP剪力连接件钢材材料均为Q235B。钢筋采用HRB400,纵向钢筋直径为8 mm,箍筋直径为6 mm。钢材材料性能如表 2所示。
| 表 1 试件主要参数 Tab. 1 Main parameters of specimens |
| 表 2 钢材材料特性 Tab. 2 Properties of steel material |
试验采用2 000 kN电伺服液压机进行加载,加载装置如图 3所示。为消除混凝土板与基座之间的缝隙,同时检查各仪器仪表是否正常工作,正式加载前进行了2次预加载,加载值为60 kN。进入正式加载阶段后采用位移控制,加载速率为0.2 mm/min,每级位移增量为0.4 mm,直至试件破坏。为保证试件加载过程中受力均匀,在每个试件顶部安装了水平钢板,底部铺设了少量砂垫层。试件相对滑移通过位移计测量获得,加载值则采用顶部压力传感器配合液压机受力读数获得。

|
图 3 试验加载装置 Fig. 3 Test set up |
7个试件在加载初期并没有发生明显变化。随着加载的进行,钢梁与混凝土之间开始产生明显的滑移,钢混交界面处混凝土部分剥落。随着荷载继续增大,试件底部混凝土首先出现竖向裂纹。继续加载,PSP剪力连接件处混凝土开始出现斜裂缝并逐渐向混凝土底部及侧面延伸, 如图 4所示。随着荷载进一步增大,混凝土板两侧产生横向和竖向裂缝,正面斜裂缝继续发展。最终侧面裂缝和正面斜裂缝贯通,底部混凝土保护层大量剥落,试件展示出混凝土压碎破坏形式。

|
图 4 混凝土裂缝 Fig. 4 Concrete cracks |
7个试件拆除混凝土后的PSP剪力连接件变形情况如图 5所示。可以看出,试件SP1-4-50-C40、SP1-4-30-C50、SP1-4-30-C40、SP2-4-30-C40-150以及SP2-6-30-C40-150的PSP剪力连接件都发生了较为明显的弯曲变形,其中,试件SP1-4-30-C50中还观察到PSP剪力连接件的剪切破坏。而试件SP1-10-30-C40的PSP剪力连接件没有观察到明显变形。对于具有双排PSP剪力连接件的SP2-4-30-C40-150和SP2-6-30-C40-150试件,底部PSP剪力连接件比顶部PSP剪力连接件变形更明显,这是由于PSP剪力连接件间距较小导致上下剪力连接件受力不均匀,底部PSP剪力连接件承担更高的剪力。

|
图 5 拆除混凝土后剪力连接件变形 Fig. 5 Deformation of connectors after removing concrete |
所有试件的荷载-滑移曲线如图 6所示。可以看出,PSP剪力连接件荷载-滑移曲线主要分为弹性阶段、弹塑性阶段、平台阶段、破坏阶段。加载初期,试件处于弹性阶段,此时荷载-滑移曲线呈线性增长,直至A点,此时相对滑移约为0.3 mm,对应荷载约为峰值荷载的40%。随着荷载持续增大,混凝土板表面产生斜裂缝,曲线进入弹塑性阶段,此时曲线呈非线性增长,斜率逐渐减小,直至达到峰值荷载B点。随后,曲线进入平台阶段,在这一阶段,混凝土裂缝继续发展并相互贯通,裂缝宽度增大,部分混凝土逐渐退出工作。该阶段中曲线接近水平发展,荷载保持在峰值荷载的95%以上。最后,曲线进入破坏阶段,并迅速下降。在此期间,大量混凝土分离,混凝土压碎。

|
图 6 荷载-滑移曲线 Fig. 6 Load-slip curve |
所有试件的试验结果如表 3所示。可以看出,试件SP1-10-30-C40受剪承载力较SP1-6-30-C40和SP1-4-30-C40提高了17.2%和32.5%,抗剪刚度提高5.6%和32.6%,由此说明,增大开孔钢板厚度可以提高PSP剪力连接件受剪承载力和抗剪刚度。对比试件SP1-4-30-C50与试件SP1-4-30-C40,前者抗剪刚度较后者提高了9.2%,而受剪承载力差异较小,这可能是由于开孔钢板厚度较小导致PSP剪力连接件受剪承载力主要由开孔钢板控制。对比具有相同参数的双剪力连接件试件与单剪力连接件试件,发现试件SP2-4-30-C40-150的极限承载力较试件SP1-4-30-C40提高了50.2%,试件SP2-6-30-C40-150的极限承载力较试件SP1-6-30-C40提高了49.1%。然而,均没有实现两倍的提高,双剪力连接件试件中单个PSP剪力连接件平均受剪承载力均小于单个PSP剪力连接件的受剪承载力,这是由于较小的间距导致PSP剪力连接件受力不充分,其抗剪能力不能完全发挥。
| 表 3 推出试验结果 Tab. 3 The results of push-out tests |
为进一步分析开孔钢板厚度、开孔直径、混凝土强度、剪力连接件间距对PSP剪力连接件力学性能的影响,利用有限元软件ABAQUS对装配式双拼槽钢组合梁中PSP剪力连接件进行了非线性参数分析。有限元模型由6部分组成,包括混凝土板、钢梁、PSP剪力连接件、加载板、底板和钢筋网,如图 7所示。

|
图 7 有限元模型 Fig. 7 Finite element model |
有限元模型中钢梁、PSP剪力连接件、混凝土板采用三维八节点单元(C3D8R),加载板和底板采用离散刚性单元(R3D4),内部钢筋网采用三维双节点桁架单元(T3D2)。此外,内部钢筋网采用“Embedded Region”嵌入到混凝土中发挥作用。部件之间的接触采用接触单元进行模拟,其中,钢梁与混凝土板、PSP剪力连接件与混凝土板、混凝土板与加载板及底板之间的接触采用硬接触模拟法向接触行为,采用库伦摩擦接触模拟切向接触行为。混凝土板与钢梁和PSP剪力连接件的摩擦因数取0.4。由于底板与混凝土板之间存在砂垫层,底板与混凝土板之间的摩擦因数取0.3。为同时保证计算结果准确可靠,对PSP连接件进行了局部精密网格划分。PSP连接件沿厚度方向采用4~8层单元,局部网格尺寸为5 mm,其余部件采用10 mm的网格尺寸。
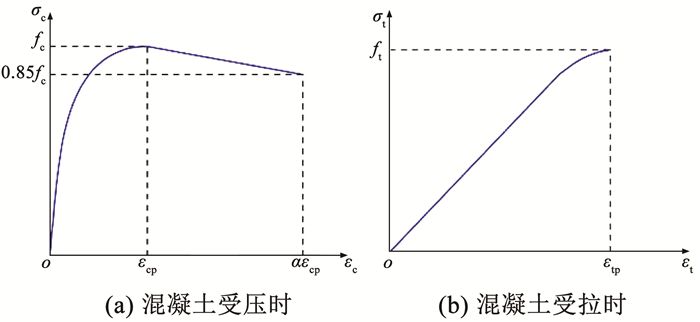
2.3 材料性能 2.3.1 混凝土混凝土拉压本构模型参考文献[21-22],应力-应变曲线如图 8所示。当混凝土受压,应力-应变曲线分为上升和下降段。其中,上升段由式(1)、(2)控制,下降段为一条直线,在达到85%最大抗压强度时终止,此时应变为14εcp。当混凝土受拉,应力-应变曲线由式(3)、(4)控制。
| $\sigma_{\mathrm{c}}=\left[\frac{k \eta-\eta^2}{1+(k-2) \eta}\right] f_{\mathrm{c}}$ | (1) |
| $k=\frac{E_{\mathrm{c}} \varepsilon_{\mathrm{cp}}}{f_{\mathrm{c}}}, \eta=\frac{\varepsilon_{\mathrm{c}}}{\varepsilon_{\mathrm{cp}}}$ | (2) |
| $\sigma_{\mathrm{t}}=\left(1.2 x-0.2 x^6\right) f_{\mathrm{t}}$ | (3) |
| $x=\frac{\varepsilon_{\mathrm{t}}}{\varepsilon_{\mathrm{tp}}}$ | (4) |
|
图 8 混凝土应力-应变曲线 Fig. 8 Stress-strain curves of concrete |
式中:σc和εc分别为曲线上升段的压应力及对应的压应变;fc和εcp分别为最大压应力和最大压应变;Ec为混凝土弹性模量;σt和εt分别为拉应力及对应拉应变;ft和εtp为极限拉应力和极限拉应变。
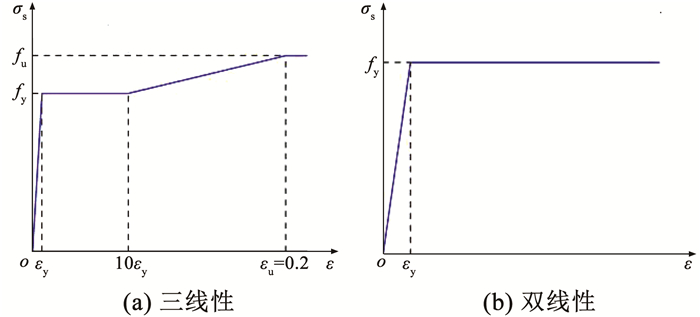
2.3.2 钢材PSP剪力连接件采用三线性等效强化模型进行模拟,其余钢材采用双线性理想模型进行模拟,应力-应变曲线如图 9所示。模型中所有钢材均遵循Mises屈服准则,PSP剪力连接件极限应变取0.2,钢筋泊松比取0.3,其他材料参数见表 2。
|
fy、εy、fu和εu分别为钢材屈服应力、屈服应变、极限应力和极限应变。 图 9 钢材应力-应变曲线 Fig. 9 Stress-strain curves of steel |
图 10以SP1-4-50-C40、SP1-6-30-C40、SP1-10-30-C40为例,给出了推出试验与有限元分析中荷载-滑移曲线对比,可以看出,有限元模拟得到的荷载-滑移曲线与推出试验实测曲线吻合良好。以试件SP1-6-30-C40为例,对比了有限元分析和推出试验中PSP剪力连接件破坏形态,如图 11所示。图 11(a)和(b)为有限元模拟得到的混凝土开裂状态与试验结果对比。图 11(c)为有限元模拟得到的开孔钢板剪力连接件塑性变形与试验结果对比。结果表明,有限元分析得到的破坏模式与实验结果基本一致。因此,本文建立的有限元模型能够较好地反映推出试件中PSP剪力连接件的剪切行为和最终破坏形态。

|
图 10 有限元分析荷载-滑移曲线与试验结果对比 Fig. 10 Comparison of the load-slip curves calculated by the FEM and the test result |

|
图 11 有限元计算结果与试验破坏形态对比 Fig. 11 Comparison of the results calculated by the FEM and the experimental failure modes |
利用验证后的有限元模型,通过改变开孔钢板厚度、开孔直径、混凝土强度、连接件间距、穿孔钢筋,分析PSP剪力连接件不同参数变化对其荷载-滑移曲线及受剪承载力的影响。
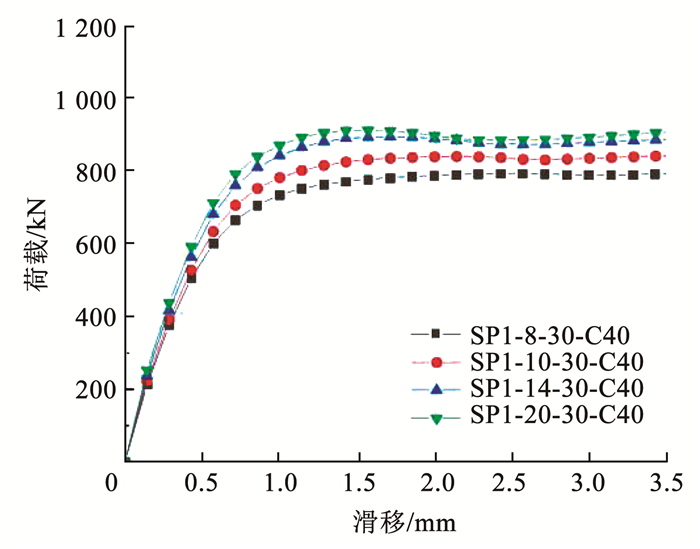
3.1 开孔钢板厚度的影响图 12给出了不同厚度的PSP剪力连接件荷载-滑移曲线。可以看出,随着开孔钢板厚度的增加,PSP剪力连接件抗剪刚度和受剪承载力均得到提高,当开孔钢板厚度从8 mm增加到10、14、20 mm时,PSP剪力连接件受剪承载力分别提高了5.8%、12.6%、14.9%。受剪承载力随开孔钢板厚度呈现非线性增加,随着厚度的增大,受剪承载力增加速度逐渐减小。这是由于开孔钢板厚度的提高使得PSP剪力连接件更不容易产生变形,受剪承载力和抗剪刚度得到提高。然而,当开孔钢板厚度增加到一定程度时,大厚度的开孔钢板使得混凝土提前被压碎,混凝土强度对受剪承载力的影响变得更为敏感,受剪承载力增加速度减小。因此,适当增加开孔钢板厚度可以有效地提高PSP剪力连接件的受剪承载力。
|
图 12 不同开孔钢板厚度的影响 Fig. 12 Effect of different thicknesses of perforated steel plate |
图 13给出了钢板厚度为10 mm时不同开孔直径的PSP剪力连接件荷载-滑移曲线。可以看出,随着开孔直径的增大,荷载-滑移曲线变化不明显,当开孔直径从10 mm增加到50 mm时,开孔钢板受剪承载力仅减小了4.0%,而抗剪刚度没有明显变化。这可能是由于厚度较大的PSP剪力连接件的受剪承载力主要由焊缝周围混凝土提供。在整个加载过程中,钢板未发生明显弯曲或剪切变形,而底部混凝土被压溃。因此,对于大厚度PSP剪力连接件,开孔直径对受剪承载力和抗剪刚度的影响较小。

|
图 13 不同开孔直径的影响 Fig. 13 Effect of different opening diameters |
图 14给出了不同混凝土强度下PSP剪力连接件的荷载-滑移曲线。可以看出,随着混凝土强度的提高,PSP剪力连接件的受剪承载力和抗剪刚度都得到了提高。当混凝土强度从50 MPa增加到60、70、80 MPa时,PSP剪力连接件的受剪承载力分别提高了9%、18%、28%。受剪承载力随混凝土强度的提高近似呈线性增长,提高混凝土强度能有效增大PSP剪力连接件受剪承载力。因此,混凝土强度对PSP剪力连接件的力学性能有显著影响。

|
图 14 不同混凝土强度的影响 Fig. 14 Effect of different strength of concrete |
图 15给出了不同连接件间距下PSP剪力连接件的荷载-滑移曲线。可以看出,连接件间距对PSP剪力连接件的受剪承载力有显著影响。当连接件间距较小时,由于相邻剪力连接件间混凝土应力重叠,顶部与底部PSP剪力连接件受力并不均匀,底部剪力连接件会比顶部连接件分担到更高的剪力,随着连接件间距的增大,应力重叠减小,相邻两个PSP剪力连接件分担的剪力趋于相等。间距为100、150、200、250 mm的单排平均承载力分别达到了单个PSP剪力连接件的66.2%、75.6%、87.7%、91.2%,均小于单个PSP剪力连接件受剪承载力。因此,在实际工程中PSP剪力连接件的间距取值建议大于250 mm。

|
图 15 不同连接件间距的影响 Fig. 15 Effect of different connector spacing |
穿孔钢筋是各种形式开孔钢板连接件中至关重要的研究参数,以试件SP2-6-30-C40-O(无穿孔钢筋)和试件SP2-6-30-C40-I(含直径为16 mm的穿孔钢筋)研究穿孔钢筋对PSP剪力连接件抗剪能力的影响。从图 16可以看出,穿孔钢筋对PSP剪力连接件的受剪承载力和抗剪刚度影响较小。相比试件SP2-6-30-C40-O,试件SP2-6-30-C40-I的受剪承载力仅提高了2.2%。此外,在开孔钢板中设置穿孔钢筋可以在很大程度上提高PSP剪力连接件的面外抗剪能力和抗拉能力。因此,有必要在PSP剪力连接件孔中设置穿孔钢筋,以保证装配式双拼槽钢-混凝土组合梁中混凝土板和钢梁之间的共同工作性能。

|
图 16 穿孔钢筋的影响 Fig. 16 Effect of perforated reinforcement |
剪力连接件的荷载-滑移行为是评价钢-混凝土组合梁界面特性的重要指标。对于大多数钢-混凝土组合梁,在弹性阶段,剪力连接件对组合梁力学性能的影响不显著。而在塑性阶段,组合梁内部剪力连接件、混凝土和钢梁三者之间应力开始重新分布,需要通过荷载-滑移关系考虑剪力连接件变形和钢-混凝土相互作用。而目前对PSP剪力连接件荷载-滑移关系的研究基本属于空白。常见的荷载-滑移曲线公式主要是针对栓钉和螺栓等剪力连接件,表 4总结了不同学者提出的荷载-滑移曲线经验公式。
| 表 4 荷载-滑移曲线经验公式 Tab. 4 Practical formulas of load-slip curve |
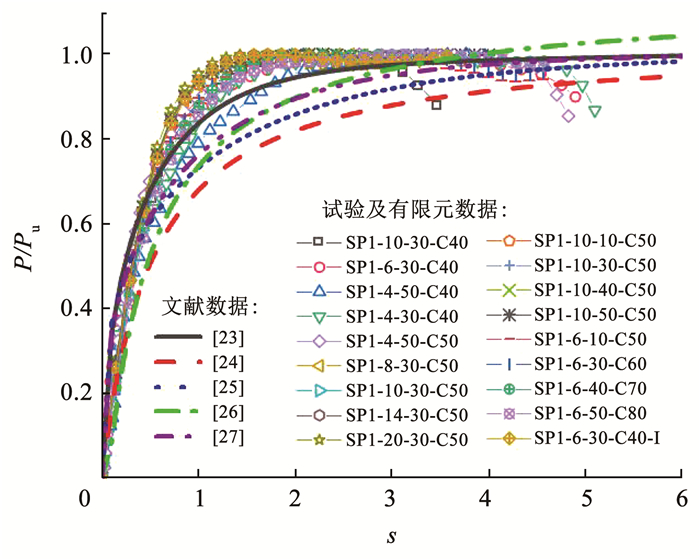
将试验及有限元荷载-滑移曲线与表 4所建议公式进行对比,结果如图 17所示。可以看出,公式与试验及有限元结果拟合精度较差,现存经验公式不适用本文提出的PSP剪力连接件。因此,有必要研究和建立PSP剪力连接件的荷载-滑移曲线关系式。
|
图 17 试验及有限元结果与荷载-滑移预测公式对比 Fig. 17 Comparison between the experimental and finite element results and the prediction equations of load-slip curve |
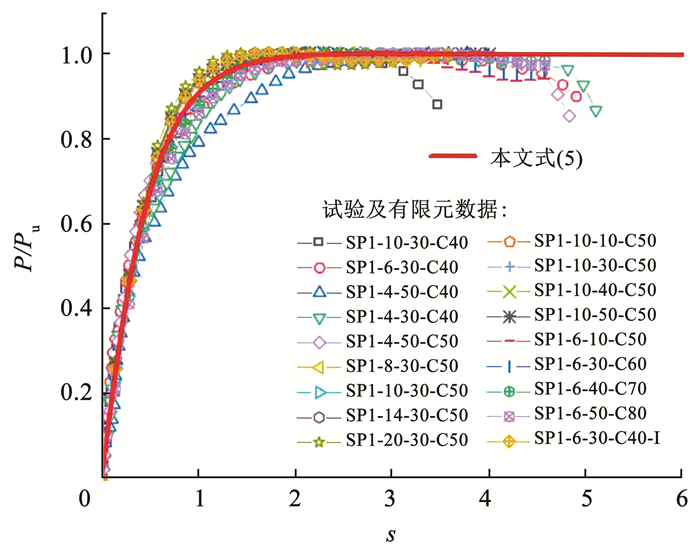
根据试验数据和有限元计算结果,参考文献[25, 27]中的荷载-滑移关系公式形式,拟合得到PSP连接件荷载-滑移关系计算公式(5)。试验数据和有限元计算结果与本文提出公式的对比如图 18所示,该公式适用于不考虑群连接件效应的单个PSP剪力连接件。可以看出,公式预测结果与试验及有限元获得的荷载-滑移曲线吻合良好。
| $\frac{P}{P_{\mathrm{u}}}=\left(1-\mathrm{e}^{-2.49 s}\right)^{1.13}$ | (5) |
|
图 18 试验及有限元结果与本文公式对比 Fig. 18 Comparison between the experimental and finite element results and the proposed equation |
1) 试验结果表明,除10 mm厚度PSP剪力连接件外,所有4 mm与6 mm厚度的PSP剪力连接件均发生了明显弯曲变形,其中,试件SP1-4-30-C50中PSP剪力连接件还观察到了剪切破坏。对于双排连接件试件,底部PSP剪力连接件变形比顶部连接件更明显。所有试件破坏时剪力连接件周围混凝土均出现了斜向裂缝。
2) 增加开孔钢板厚度可以提高PSP剪力连接件受剪承载力。但随着厚度的增大,受剪承载力增加速度逐渐减小。
3) 提高混凝土强度可以显著提高PSP剪力连接件受剪承载力和抗剪刚度,而开孔直径和穿孔钢筋对受剪承载力和抗剪刚度影响较小。
4) 增大连接件间距能够显著提高单排PSP剪力连接件平均受剪承载力,当间距为100、150、200、250 mm时,单排平均承载力分别达到单个PSP剪力连接件的66.2%、75.6%、87.7%、91.2%。因此,实际工程中PSP剪力连接件的间距取值建议大于250 mm。
5) 提出了装配式双拼槽钢-混凝土组合梁中单个PSP剪力连接件荷载-滑移曲线计算公式,为装配式双拼槽钢混组合梁的设计提供参考。
| [1] |
SUWAED A S H, KARAVASILIS T L. Demountable steel-concrete composite beam with full-interaction and low degree of shear connection[J]. Journal of Constructional Steel Research, 2020, 171: 106. DOI:10.1016/j.jcsr.2020.106152 |
| [2] |
刘界鹏, 周保旭, 余洁, 等. 装配整体式钢-混凝土组合梁栓钉抗剪连接件受力性能试验研究[J]. 建筑结构学报, 2017, 38(增刊1): 337. LIU Jiepeng, ZHOU Baoxu, YU Jie, et al. Experimental study on mechanical behavior of shear studs in assembled monolithic steel-concrete composite beam[J]. Journal of Building Structures, 2017, 38(Sup.1): 337. DOI:10.14006/j.jzjgxb.2017.S1.047 |
| [3] |
古金本, 王俊颜, 陆伟. 新型可拆卸式钢-UHPC组合板的抗弯性能[J]. 哈尔滨工业大学学报, 2024, 56(1): 84. GU Jinben, WANG Junyan, LU Wei. Flexural behavior of a novel demountable steel-UHPC composite slab[J]. Journal of Harbin Institute of Technology, 2024, 56(1): 84. DOI:10.11918/202208008 |
| [4] |
赵鹤, 王皓, 支旭东, 等. 装配式板柱钢结构体系建筑产业化技术与示范[J]. 建筑钢结构进展, 2021, 23(10): 32. ZHAO He, WANG Hao, ZHI Xudong, et al. Architectural industrialization technology and demonstration of prefabricated slab-column steel structural systems[J]. Progress in Steel Building Structures, 2021, 23(10): 32. DOI:10.13969/j.cnki.cn31-1893.2021.010.004 |
| [5] |
汪炳, 黄侨, 刘小玲. 疲劳荷载作用下栓钉连接件的抗剪承载力退化规律[J]. 哈尔滨工业大学学报, 2016, 48(9): 76. WANG Bing, HUANG Qiao, LIU Xiaoling. Shear capacity degradation law of stud connectors under fatigue loading[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 76. DOI:10.11918/j.issn.0367-623 |
| [6] |
MOLKENS T, DOBRIC ' J, ROSSI B. Shear resistance of headed shear studs welded on welded plates in composite floors[J]. Engineering Structures, 2019, 197: 109. DOI:10.1016/j.engstruct.2019.109412 |
| [7] |
ATAEI A, ZEYNALIAN M. A study on structural performance of deconstructable bolted shear connectors in composite beams[J]. Structures, 2021, 29: 519. DOI:10.1016/j.istruc.2020.11.065 |
| [8] |
OGUEJIOFOR E C, HOSAIN M U. A parametric study of perfobond rib shear connectors[J]. Canadian Journal of Civil Engineering, 1994, 21(4): 614. DOI:10.1139/l94-063 |
| [9] |
VIANNA J D C, ANDRADE S A L D, VELLASCO P C G D S, et al. Experimental study of perfobond shear connectors in composite construction[J]. Journal of Constructional Steel Research, 2013, 81(81): 62. DOI:10.1016/j.jcsr.2012.11.002 |
| [10] |
AHN J H, LEE C G, WON J H, et al. Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement[J]. Journal of Constructional Steel Research, 2010, 66(10): 1295. DOI:10.1016/j.jcsr.2010.04.008 |
| [11] |
KIM S, PARK S, HEO W, et al. Shear resistance characteristic and ductility of Y-type perfobond rib shear connector[J]. Steel and Composite Structures, 2015, 18(2): 497. DOI:10.12989/scs.2015.18.2.497 |
| [12] |
VIANNA J D C, COSTA-NEVES L F, VELLASCO P C G D, et al. Structural behaviour of T-perfobond shear connectors in composite girders: an experimental approach[J]. Engineering Structures, 2008, 30(9): 2381. DOI:10.1016/j.engstruct.2008.01.015 |
| [13] |
肖林, 强士中, 李小珍, 等. 考虑开孔钢板厚度的PBL剪力键力学性能研究[J]. 工程力学, 2012, 29(8): 282. XIAO Lin, QIANG Shizhong, LI Xiaozhen, et al. Research on mechanical performance of PBL shear connectors considering the perforated plate's thick[J]. Engineering Mechanics, 2012, 29(8): 282. DOI:10.6052/j.issn.1000-4750.2011.06.0343 |
| [14] |
肖林, 卫星, 强士中. 两类PBL剪力键推出试验的对比研究[J]. 土木工程学报, 2013, 46(11): 70. XIAO Lin, WEI Xing, QIANG Shizhong. Comparative study on two kinds of push-out tests of PBL shear connectors[J]. China Civil Engineering Journal, 2013, 46(11): 70. DOI:10.15951/j.tmgcxb.2013.11.025 |
| [15] |
肖林, 叶华文, 卫星, 等. 斜拉桥桥塔钢-混结合段的力学行为和传力机制研究[J]. 土木工程学报, 2014, 47(3): 88. XIAO Lin, YE Huawen, WEI Xing, et al. Study on mechanical behavior and load transfer mechanism of steel-concrete composite joint of cable-stayed bridge pylon[J]. China Civil Engineering Journal, 2014, 47(3): 88. DOI:10.15951/j.tmgcxb.2014.03.003 |
| [16] |
胡建华, 叶梅新, 黄琼. PBL剪力连接件承载力试验[J]. 中国公路学报, 2006, 19(6): 65. HU Jianhua, YE Meixin, HUANG Qiong. Experiment on bearing capacity of PBL shear connectors[J]. China Journal of Highway and Transport, 2006, 19(6): 65. DOI:10.19721/j.cnki.1001-7372.2006.06.013 |
| [17] |
卫星, 肖林, 邵柯夫, 等. 钢-混组合结构PBL剪力键疲劳寿命试验[J]. 中国公路学报, 2013, 26(6): 96. WEI Xing, XIAO Lin, SHAO Kefu, et al. Fatigue performance of perfobond shear connectors in steel-concrete composite structure[J]. China Journal of Highway and Transport, 2013, 26(6): 96. DOI:10.19721/j.cnki.1001-7372.2013.06.014 |
| [18] |
张清华, 李乔, 卜一之. PBL剪力连接件群传力机制研究(Ⅰ): 理论模型[J]. 土木工程学报, 2011, 44(4): 71. ZHANG Qinghua, LI Qiao, BU Yizhi. Load transmission mechanism of PBL shear connector group(Ⅰ): theoretical model[J]. China Civil Engineering Journal, 2011, 44(4): 71. DOI:10.15951/j.tmgcxb.2011.04.006 |
| [19] |
张清华, 李乔, 卜一之. PBL剪力连接件群传力机制研究Ⅱ: 极限承载力[J]. 土木工程学报, 2011, 44(5): 101. ZHANG Qinghua, LI Qiao, BU Yizhi. Load transmission mechanism of PBL shear connector groups Ⅱ: load capacity[J]. China Civil Engineering Journal, 2011, 44(5): 101. DOI:10.15951/j.tmgcxb.2011.05.019 |
| [20] |
汪维安, 李乔, 赵灿晖, 等. 混合结构PBL剪力键群承载力试验研究[J]. 土木工程学报, 2014, 47(6): 109. WANG Weian, LI Qiao, ZHAO Canhui, et al. Experimental study on bearing capacity of PBL shear connector group in hybrid structures[J]. China Civil Engineering Journal, 2014, 47(6): 109. DOI:10.15951/j.tmgcxb.2014.06.016 |
| [21] |
CEB-FIP. Model code 2010, international federation for structural concrete[R]. Switzerland: [s. n.], 2010
|
| [22] |
CABP. Code for design of concrete structures: GB 50010—2010[S]. Beijing: Ministry of Housing and Urban and Rural Construction in People's Republic of China, 2015
|
| [23] |
MOLENSTRA N, JOHNSON R P. Partial shear connection in composite beams for buildings[J]. Proceedings of the Institution of Civil Engineers, 1991, 91: 679. DOI:10.1680/iicep.1991.17485 |
| [24] |
XUE W C, DING M, WANG H, et al. Static behavior and theoretical model of stud shear connectors[J]. Journal of Bridge Engineering, 2008, 13(6): 623. DOI:10.1061/(ASCE)1084-0702(2008)13:6(623) |
| [25] |
SU Qingtian, YANG Guotao, BRADFORD M A. Static behaviour of multi-row stud shear connectors in high-strength concrete[J]. Steel and Composite Structures, 2014, 17: 967. |
| [26] |
AN Li, CEDERWALL K. Push-out tests on studs in high strength and normal strength concrete[J]. Journal of Constructional Steel Research, 1996, 36(1): 15. DOI:10.1016/0143-974X(94)00036-H |
| [27] |
OLLGAARD J G, SLUTTER R G, FISHER J W. Shear strength of stud connectors in lightweight and normal weight concrete[J]. AISC Engineering Journal, 1971, 8(2): 55. |
 2024, Vol. 56
2024, Vol. 56


