2. 北京环境特性研究所,北京 100143
2. Beijing Institute of Environmental Characteristics, Beijing 100143, China
高精度海洋场景红外仿真需对光谱辐射信号在复杂海洋环境中的传输过程进行准确解析。就宏观结构而言,海洋环境由大气层、近海面层以及海洋水体层3部分组成。其中,大气层和海洋水体层的几何结构稳定,其辐射传输作用仅由该层介质自身的种类、质量浓度等因素决定;而近海面层处在大气层与海洋水体层之间,一方面,其结构、成分、物性等因素受到上下两层介质的直接影响而剧烈变化,空间结构高度复杂,另一方面,在辐射传输过程中,该层介质又在中间起到“承上启下”作用,对大气辐射及水体的反射辐射信号均有较强的参与作用(包括自身发射、散射、吸收等)。因此,对由大气层及水体层作用下的海面层介质辐射传输过程展开研究,即是对“气-面-体”的耦合辐射作用展开研究,便成为了复杂海洋环境中红外辐射信号传输过程仿真研究的核心环节。
海况等级与近海面层结构复杂程度直接相关。粗糙海面出现于海况小于3级(浪高小于1.25 m)时,其光学特性主要由小尺度海水平面发射、反射、折射作用决定。当海况大于3级(浪高大于1.25 m)时,海浪开始发生破碎并产生白冠。就演化时间而言,海面白冠可以分为A和B两个阶段,A阶段是位于海浪破碎位置的破碎波,由活跃的碎波和被拖拽的空气组合而成,就光学特性研究而言,破碎波光学特性可以看作海上飞沫、海面泡沫、粗糙海面以及含气泡浅层水体组成的多尺度三维结构体的辐射传输问题。B阶段是衰变过程,称为静态泡沫,发生在A阶段之后,存在于除破碎波以外海面任意位置,具有条状结构和指数衰减特征,在光学特性研究中,静态泡沫可以看作直接覆盖于粗糙海面静态泡沫结构。由于特定海域的海面上静态泡沫和破碎波仅出现在满足海浪破碎发生条件的位置,在海面光学特性研究中,除了探究海况等级与粗糙海面对辐射传输信号的折反射作用之间的变化规律,还须理清含破碎波海面多尺度光学特性。
目前,海面层介质辐射传输特性的研究工作大多数还停留在单组分的阶段。粗糙海面的辐射传输特性由海水的散射特性以及海面的镜面反射特性决定,例如,水色遥感应用中,海面的光学特性主要由纯海水以及海水中杂质散射吸收特性决定[1]。早期的白冠光学散射特性都是基于观测数据和简单的线性模型获取,Frouin等[2]通过接收海面白冠不同角度下的散射辐射,计算海面的双向反射分布函数(FBRD, bidirectional reflectance distribution function),利用3种不同方法推导出海面泡沫层的光谱反射率。在模拟方面的研究则将泡沫层等效为覆盖在海面上的一层或多层大小均匀的空心粒子层,进而在泡沫的等效模型上提出一系列发射率和散射特性计算模型。Guo等[3]将泡沫看作是包裹薄海水涂层的高密度黏性气泡,并采用中等尺寸包覆颗粒密集分布的介质模型对泡沫层进行描述,基于电磁散射理论建立电磁散射模型。考虑到独立散射理论对稠密泡沫层不成立,利用稠密介质辐射传输(DMRT)理论和准晶近似(QCA)理论计算了稠密分布的中等尺寸黏性粒子的表面亮度和温度,研究了泡沫覆盖海面对被动微波遥感测量的影响。Camps等[4]利用文献[3]中的近海面几何结构,以测量泡沫发射率作为盐度、泡沫厚度、入射角和极化的函数,通过海面控制实验给出实验结果,并与以实测泡沫参数作为模型输入参数的双层泡沫发射模型进行比较,证明该发射率模型的正确性。马兰新[5]考虑了更精细的泡沫层几何结构,将泡沫层划分为3层,泡沫层空隙率由上到下逐层递减,分析了泡沫层几何参数和风速对覆盖泡沫层的粗糙海面的双向反射分布函数和光谱反射率,但该研究中并未考虑风速对泡沫层厚度和结构的影响。对于水体中气泡,目前也有学者进行了研究。Zhang[6]发现气泡数密度与风速呈幂律关系,且随深度呈指数衰减,并给出了气泡数密度随风速以及深度变化的关系式。Al-Lashi等[7]利用光学成像方式观察水中气泡的变化过程,并利用相关统计方法给出每个时间段气泡群的数密度和空隙率。Ma等[8]采用蒙特卡罗方法研究了上层海洋气泡层的光谱反射率和双向反射率特征,分析了气泡涂层、叶绿素质量浓度(ρChl,chlorophyll concentration)和气泡数密度对气泡层光谱反射率的影响,以及气泡层在正入射和斜入射情况下双向反射率分布函数的变化。发现在高风速条件下,清澈水域的气泡数量显著影响气泡层的反射特性。Yang等[9]使用平均抽样方法将应用于生物光学领域CUDAMCML程序扩展为CUDAMCML-ocean程序,用来仿真含有彩色溶解有机物(CDOM)和气泡等元素的多种颗粒海水中的辐射传输,并计算了不同风速和叶绿素质量浓度下,含气泡群水体的光谱反射率和透射率。Monahan[10]提出以A和B两个阶段来分类白冠的视觉特征,A阶段的特征是海浪在波峰处发生破碎形成白冠,而B阶段的特征是泡沫群稳定持续存在。Reul等[11]为覆盖泡沫的海面开发了一个动力学模型,作为风速的函数,其是一定尺度下泡沫层持续时间和破断前沿总长度分布的综合函数,该模型可以分别计算不同风速条件下静态泡沫和波峰泡沫的厚度以及海面覆盖率。Li等[12]在上述动力学模型的基础上首次对海面覆盖的泡沫进行了区分,并对海面的电磁散射特性进行了计算。结果表明,与包含任意一种泡沫的海面计算结果相比,同时包含两种泡沫的海面电磁散射特性计算结果更接近真实测量结果。
对于多尺度海面结构体的辐射传输建模问题,Chowdhary等[13-14]介绍了4种常用大气-海洋辐射传输模型,主要解决了包含大气、粗糙海面以及含藻类水体的系统辐射传输问题,部分模型也将海面泡沫的影响考虑到辐射传输过程中,但都将泡沫层假设为朗伯体,与泡沫的实际散射特性严重不符。
基于上述问题,不同于三维场景辐射传输与辐射特性一体化建模方法,针对海面泡沫和破碎波样本重复出现的特点,提出了一种“先拆后建”的研究思路(如图 1所示)。首先将含泡沫和破碎波多尺度海面抽象为粗糙海面、海面泡沫、破碎波的组合,进而拆解出“粗糙海面”、“粗糙海面+泡沫”、“含破碎波粗糙海面”3类典型多尺度海面结构体,分别开展多尺度耦合辐射、散射特性建模研究,构建3类多尺度海面结构体辐射散射方向-光谱特性计算模型;在此基础上,对于大范围海面辐射/散射特性问题,通过海面栅格化、海面结构体匹配、方向-光谱特性重构渲染等方法,由3类典型多尺度海面结构体方向-光谱特性组合重构大范围海面辐射散射特性算法,最终构建完成多尺度海面“体-气-面”耦合辐射/散射特性计算方法。

|
图 1 含泡沫与破碎波多尺度海面的“气-面-体”耦合辐射/散射研究思路 Fig. 1 Architecture of "air-surface-body" coupling radiation/scattering research ideas for multi-scale sea surface covered with foam and breaking wave |
在该研究思路中,构建多尺度海面结构体的辐射传输模型,耦合近海面层各组成部分对光谱传输信号的作用,探究典型多尺度海面结构体光谱辐射传输特性与海况因素的关系是一切研究工作的前提。
为了获取准确的海面典型结构体在可见-近红外波段的辐射传输特性,在已有大气-海洋辐射传输模型的基础上增加了海面泡沫层和海水气泡层两个模块。在海洋水体方面,除了考虑水体及杂质的散射特性外,还加入了对气泡散射问题的分析。在海面结构方面,不再将泡沫假设为朗伯体,而是采用泡沫自身的吸收散射特性来参与辐射传输计算。此外, 区分了波峰泡沫和静态泡沫的不同。为了确定典型结构体的影响因素,本次模型中使用光滑平面代替粗糙海面。围绕多尺度海面结构体辐射传输模型开展以下工作:根据风速参数化对应的海面结构体,计算体元中各种组分的光学特性参数,基于蒙特卡洛法对结构体中的辐射传输过程进行仿真模拟,从而量化不同风速对多尺度海面结构体辐射传输的影响。
1 方法与计算 1.1 多尺度海面结构体几何参数化泡沫浮于海面上,由不同厚度水膜包裹的气泡堆积而成。本文讨论的与风速相关的泡沫层几何参数主要包括泡沫层的厚度结构、泡沫层空隙率分布。
Reul结合海面动力学模型及相关实验观测数据,将波峰泡沫和静态泡沫的平均厚度分布表示为[11]
| $ \bar{\delta}_{\rm c}(c)=\frac{0.4 c^2}{2 g} \text { (波峰) } $ | (1) |
| $ \bar{\delta}_{\mathrm{s}}(c)=\frac{0.4 c^2}{10 {\rm{ \mathsf{ π} }}}\left\{\frac{5 c}{2 g}+\tau^{\prime}\left[1-\exp \left(-\frac{c(10 {\rm{ \mathsf{ π} }}-5)}{g \tau^{\prime}}\right)\right]\right\} \text { (静态) } $ | (2) |
式中: τ′=3.8表示一个指数时间常数;
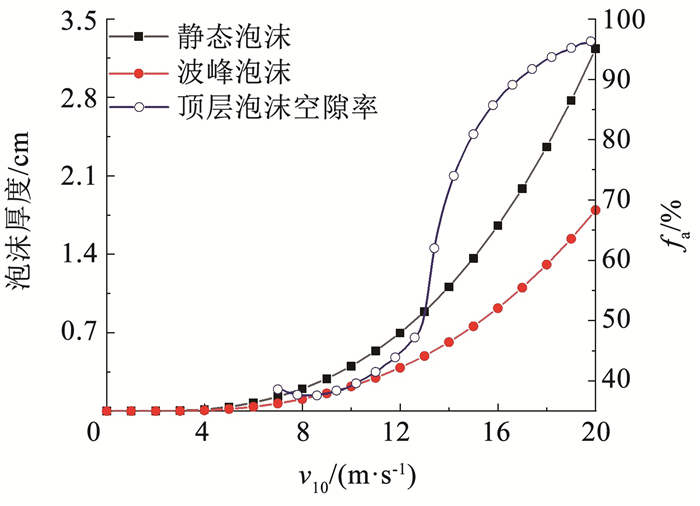
基于实验观察,顶部泡沫层的气泡几乎是空隙率大于90%的干泡。在海洋泡沫底层,气泡层空隙率较低,极限值近似为零。Liu等[15]从Aquarius数据拟合出顶部泡沫层空隙率fa与风速的关系,如图 2所示。其中,泡沫层空隙率fa为表征海面泡沫层结构的一个重要参量,定义如下:
| $ f_{\mathrm{a}} \cong f_{\mathrm{b}}=\frac{1}{N_{\text {total }}} \sum\limits_{N_{\text {total }}} \frac{4 {\rm{ \mathsf{ π} }} r_0^3 / 3}{4 {\rm{ \mathsf{ π} }} r^3 / 3}=\left(\frac{r_0}{r}\right)^3 $ | (3) |
|
图 2 波峰泡沫、静态泡沫厚度以及顶层泡沫空隙率随风速的变化 Fig. 2 Thickness of crest foam, static foam and void fraction of top foam vs wind speed |
式中:r和r0表示双层球气泡的外径和内径,fb为双层球泡沫粒子孔隙率,Ntotal为泡沫数量。
根据上述海面泡沫层结构的描述,将泡沫层简化为厚度分布均匀的3层平行平板结构模型,其剖面结构如图 3所示。双层球形气泡紧密堆积形成单层泡沫,泡沫粒子孔隙率相同,且粒径分布为对数正态分布:
| $ p(r)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} r \ln \sigma_{\mathrm{g}}} \exp \left\{-\frac{1}{2}\left[\frac{\ln (r / \bar{r})}{\ln \sigma_{\mathrm{g}}}\right]\right\} $ | (4) |

|
图 3 海面泡沫层剖面结构示意 Fig. 3 Profile structure of foam layer |
式中:r和σg分别表示气泡平均半径和平均几何偏差,气泡半径取50 μm~10 mm。根据风速分别给出静态泡沫和波峰泡沫厚度以及顶层泡沫的空隙率。为了计算方便,假设每层气泡的平均几何偏差分别为2、1.5、1.2,底层泡沫的空隙率为1%,且3层泡沫的空隙率满足线性的垂向变化。
海浪破碎后会在浅层水体中形成一个水平方向上均匀的气泡层,研究表明,海水中气泡层能够稳定存在的气泡粒径范围为10~150 μm。在气泡层的研究方面,有学者基于观测实验数据提出了Hall-Novarini气泡粒径分布模型[16],并基于该模型推导出了气泡的粒子数密度与风速和深度关系表达式。研究发现气泡数密度N(z)与风速v10符合第四幂律,随深度呈指数衰减:
| $ N(z)=N_0 \exp \left(-z / z_0\right) $ | (5) |
式中: N0=66v104为气泡层上表面气泡数密度,v10为海平面上方10 m处的风速,z0=0.16(v10-2.5)为气泡层下表面深度。
根据Hall-Novarini气泡粒径分布模型和气泡数密度的四次幂律关系式对浅层水体进行几何建模,如图 4所示。在风速一定的情况下,气泡数密度主要与深度有关,因此,对气泡层进行分层处理,在竖直方向上将气泡层划分成若干层,层数取决于初始风速,每一层的气泡数密度遵从第四幂律公式。在水平方向上,使用随机分布模型,给定气泡粒径范围,但不同粒径的气泡位置随机分布在每一层。采用等效介质理论将气泡层简化为球形颗粒随机分布在海水中。

|
图 4 含气泡水体剖面结构示意 Fig. 4 Profile structure of bubble layer |
基于Hall-Novarini气泡粒径分布模型,气泡的粒子数密度分布函数表达式(ρbub, m-3/μm)可以写成:
| $ \rho_{\text {bub }}(r, z)=16000 G(r, z)\left(\frac{v_{10}}{13}\right)^3 \exp \left[-\frac{z}{L\left(v_{10}\right)}\right] $ | (6) |
| $ L\left(v_{10}\right)=\left\{\begin{array}{l} 0.4, v_{10} \leqslant 7.5 \mathrm{~m} / \mathrm{s} \\ 0.4+0.115\left(v_{10}-7.5\right), v_{10}>7.5 \mathrm{~m} / \mathrm{s} \end{array}\right. $ | (7) |
| $ G(r, z)=\left\{\begin{array}{l} {\left[\frac{r_{\text {ref }}(z)}{r}\right]^4, r_{\text {min }}<r \leqslant r_{\text {ref }}(z)} \\ {\left[\frac{r_{\text {ref }}(z)}{r}\right]^{4.37+(z / 2.55)^2}, r_{\text {ref }}(z)<r \leqslant r_{\text {max }}} \end{array}\right. $ | (8) |
式中:z和r分别表示水下深度和气泡半径,单位为m和μm;rmin和rmax分别表示气泡最小和最大半径;rref=54.4+1.984×10-6z,表示随高度变化的参考半径; v10为海拔10 m处的风速,单位为m/s。因此,不同海水深度的气泡数密度Nbub(m-3)可以表示为
| $ \begin{gathered} N_{\text {bub }}(z)=\int_{r_{\text {min }}}^{r_{\text {max }}} \rho_{\text {bub }}(r, z) \mathrm{d} r \approx \\ \left(1.6 \times 10^4\right) \frac{r_{\text {ref }}^4}{r_{\text {min }}}\left(\frac{v_{10}}{13}\right)^3 \exp \left[-\frac{z}{L\left(v_{10}\right)}\right] \end{gathered} $ | (9) |
Hall-Novarini模型中所有气泡半径均大于10 μm,因此,rmin=10 μm。构建的气泡层的深度取决于风速的大小,若每层的厚度设置为1 m,则每层中的平均气泡数密度Nbub可计算为
| $ \bar{N}_{\text {bub }, i}=\int_{z_{1 i}}^{z_{2 i}} N_{\text {bub }}(z) \mathrm{d} z /\left(z_{2 i}-z_{1 i}\right) $ | (10) |
其中,z1i和z2i分别表示第i层的上限和下限。
1.2 多尺度海面结构体组分光学特性计算含破碎波粗糙海面结构体的散射特性由泡沫层、气泡群以及海水的光学特性共同决定,因此,需要分别对上述3种介质的光学特性进行研究。
海面泡沫层是由粒径为50 μm~1 cm的空心球粒子堆积而成,因此,在可见-近红外波段需要采用几何光学的方法求解单个空心球粒子的吸收散射效率因子。对于具有弱吸收性的大尺度粒子,可以忽略粒子之间的相互影响[5],采用独立散射理论,结合2.1给出的泡沫层几何结构参数对泡沫层的吸收散射特性进行计算。
| $ a_{\lambda, \text { foam }}=N_{\text {foam }} \int_{r_{\text {min }}}^{r_{\max }} Q_{\text {abs, foam }}(r, \lambda) {\rm{ \mathsf{ π} }} r^2 p(r) \mathrm{d} r $ | (11) |
| $ \sigma_{\text {s} \lambda, \text { foam }}=N_{\text {foam }} \int_{r_{\text {min }}}^{r_{\text {max }}} Q_{\text {sca, foam }}(r, \lambda) {\rm{ \mathsf{ π} }} r^2 p(r) \mathrm{d} r $ | (12) |
| $ g_{\lambda, \text { foam }}=\frac{1}{\sigma_{\mathrm{s} \lambda}} \int_{r_{\min }}^{r_{\max }} Q_{\text {sca, foam }}(r, \lambda) g_{\mathrm{p}, \text { foam }}(r, \lambda) {\rm{ \mathsf{ π} }} r^2 \mathrm{~d} r $ | (13) |
式中:Nfoam为单位体积内的泡沫总数且
在红外波段,海水具有强吸收性,因此,浅层水体中气泡的辐射特性计算可以利用吸收性介质中的粒子Mie散射理论进行计算。
基于广义Mie散射理论计算了气泡层的散射特性,气泡层的光谱散射系数σsλ, bub(z)和不对称因子gλ, bub可以分别表示为
| $ \sigma_{\mathrm{s} \lambda, \mathrm{bub}}(z)=N_{\mathrm{bub}}(z) \int_{r_{\min }}^{r_{\max }} Q_{\mathrm{sca}, \mathrm{bub}}(r, \lambda) p(r) {\rm{ \mathsf{ π} }} r^2 \mathrm{d} r $ | (14) |
| $ g_{\lambda, \text { bub }}=\frac{1}{\sigma_{\text {s } \lambda, \text { bub }}(z)} \int_{r_{\text {min }}}^{r_{\text {max }}} Q_{\text {sca, bub }}(r, \lambda) g_{\text {p } \lambda, \text { bub }} {\rm{ \mathsf{ π} }} r^2 \mathrm{d} r $ | (15) |
式中:Qsca, bub(r, λ)和gpλ, bub表示单个气泡的散射效率因子和相应的散射相函数。与天然海水相比,气泡(空气)的吸收系数可以忽略不计。
水体固有光学特性(IOP)也影响着浅层海水的辐射特性,包括总光谱吸收系数和总光谱散射系数。叶绿素质量浓度(chlorophyll concentration,ρChl)与有色溶解有机物和浮游生物之间存在相关关系,因此,可用叶绿素质量浓度表征海水的浑浊度。
海水总光谱吸收系数aλ, t可以表征为每种组分吸收系数之和,即
| $ a_{\lambda, \mathrm{t}}=a_{\lambda, \mathrm{w}}+a_{\lambda, \mathrm{ph}}+a_{\lambda, \mathrm{CDOM}} $ | (16) |
其中,采用Krik的实验数据计算纯海水吸收系数aλ, w。浮游植物的吸收系数aλ, ph近似等于叶绿素质量浓度与浮游植物比吸收系数(aph,m2/mg)的乘积。有色溶解有机物的吸收系数aλ, CDOM与波长的关系可以采用如下经验公式描述[17]:
| $ \begin{aligned} a_{\lambda, \mathrm{CDOM}}= & 0.2\left[a_{\lambda, \mathrm{w}}(440)+0.06 \rho_{\mathrm{Chl}}^{0.65}\right] \cdot \\ & \exp [-0.014(\lambda-440)] \end{aligned} $ | (17) |
其中aλ, w(440)为纯水在440 nm处的吸收系数。
由于有色溶解有机物的散射系数很小,海水总光谱散射系数σsλ, t近似等于纯海水散射系数与浮游植物散射系数σsλ, ph之和[18],即
| $ \begin{aligned} \sigma_{\mathrm{s} \lambda, \mathrm{t}}= & \sigma_{\mathrm{s} \lambda, \mathrm{w}}+\sigma_{\mathrm{s} \lambda, \mathrm{ph}}=0.00193\left(\frac{550}{\lambda}\right)^{4.32}+ \\ & 0.3\left(\frac{550}{\lambda}\right) \rho_{\mathrm{Chl}}^{0.62} \end{aligned} $ | (18) |
浮游植物的体散射函数Φph(θ)采用Petzold平均粒子相函数描述。根据Zhang和Hu[19]的研究,纯海水的体散射函数
| $ \widetilde{\Phi}_{\mathrm{w}}(\theta)=\widetilde{\Phi}_{\mathrm{w}}\left(90^{\circ}\right)\left(1+0.925 \cos ^2 \theta\right) $ | (19) |
其中,
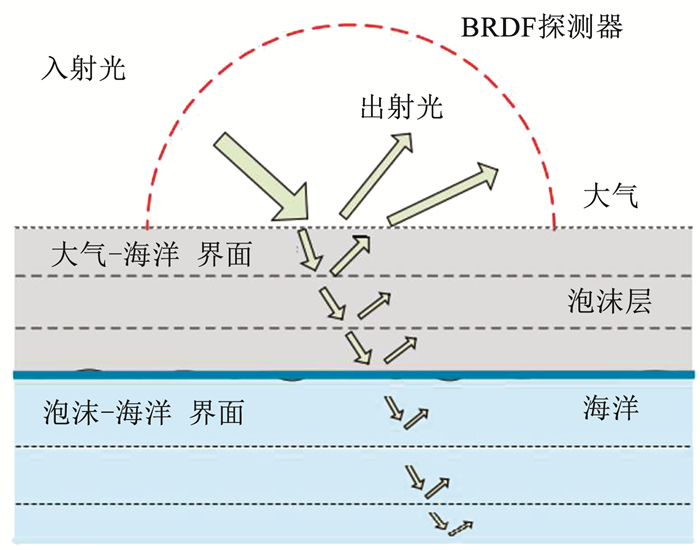
考虑到海面面元的划分尺寸较小,为了更准确地考察风速对破碎浪的影响,本次计算忽略粗糙海面对结构体光谱散射特性的影响,假设结构体是含折反射界面的半无限大多层平行平板介质,如图 5所示。在辐射传输计算中可以根据破碎浪种类,结合1.2节给出的海面各组分的光学特性对平行平板介质各层的光学参数进行设置。
|
图 5 典型结构体中辐射传输过程示意 Fig. 5 Schematic diagram of radiation transfer process for featured multi-scale voxels |
光子按照设定角度(θ, φ=0)入射到结构体上表面的固定位置p0,即为光子的初设位置。被介质散射的光子会按照散射方向行进一段路径长度。路径长度l由0~1的随机数ξ计算得到,即
| $ l=-\ln \xi / \beta_{\lambda, \mathrm{t}} $ | (20) |
其中,βλ, t为每层介质的总衰减系数。由于每层介质的总衰减系数都不同,需通过随机数ξ计算多层介质的光学厚度取值区间再确定光子行进的路径长度l。根据光子散射方向和路径长度,可以确定运动后光子在介质中的位置ptemp。若线段p0ptemp与海面没有交点,ptemp即为光子此次运动的终点p,并根据光子所在介质层确定光子与介质的相互作用。否则,需要先计算线段与海面的交点以及光子与海面相互作用后光子的出射方向,作为该光子的终点p和下一次传输方向。
确定光子所在位置后,光子所在介质的辐射物性也随之确定。此时光子有一定概率被介质散射,该概率由总散射系数和总衰减系数进行计算,即
| $ \omega=\frac{\sigma_{\lambda, \mathrm{t}}}{\beta_{\lambda, \mathrm{t}}} $ | (21) |
式中ω代表光子所在介质层的反照比。给出一个随机数ξω,若ξω>ω,则光子被吸收;反之,光子将发生散射。
对于泡沫层,由于不考虑近海面气溶胶的影响,可认为泡沫层存在于非吸收性介质-空气中,光子被散射后将依据散射相函数gfoam发生散射,散射方向由H-G相函数[20]决定,给出随机数ξfoam1和ξfoam2,则散射天顶角和方位角可由下式计算:
| $ \cos \theta=\left\{\begin{array}{l} \frac{1}{2 g_{\text {foam }}}\left[1+g_{\text {foam }}^2-\left(\frac{1-g_{\text {foam }}^2}{1-g_{\text {foam }}+2 g_{\text {foam }} \xi_{\text {foaml }}}\right)^2\right], g_{\text {foam }} \neq 0 \\ 2 \xi_{\text {foam1 }}-1, g_{\text {foam }}=0 \end{array}\right. $ | (22) |
| $ \varphi=2 {\rm{ \mathsf{ π} }} \xi_{\text {foam2 } } $ | (23) |
定义两个变量η1和η2,对于散射成分较为复杂的浅层水体,根据随机数ξwater与η1和η2的大小关系,确定散射光子的组分(气泡、浮游植物或纯海水)。
| $ \eta_1=\frac{\sigma_{\mathrm{s} \lambda, \mathrm{bub}}}{\sigma_{\mathrm{s} \lambda, \mathrm{bub}}+\sigma_{\mathrm{s} \lambda, \mathrm{ph}}+\sigma_{\mathrm{s} \lambda, \mathrm{w}}} $ | (24) |
| $ \eta_2=\frac{\sigma_{\mathrm{s} \lambda, \mathrm{bub}}+\sigma_{\mathrm{s} \lambda, \mathrm{ph}}}{\sigma_{\mathrm{s} \lambda, \mathrm{bub}}+\sigma_{\mathrm{s} \lambda, \mathrm{ph}}+\sigma_{\mathrm{s} \lambda, \mathrm{w}}} $ | (25) |
当ξwater>η2时,光子被纯海水散射;当ξwater < η1时,光子被气泡散射;否则,光子被浮游植物散射。确定散射主体后,同样依据非对称因子和H-G相函数确定散射天顶角和方位角。
图 6展示了入射光、结构体和探测器的几何位置关系。光子经过结构体各层介质的吸收和散射后,统计从海面出射的光子方位和数量。

|
图 6 典型结构体上表面FBRD探测示意 Fig. 6 Schematic diagram of FBRD detection method for the upper surface of featured multi-scale voxels |
根据统计结果,微元面的双向反射分布函数计算如下:
| $ F_{\text {BRD }}\left(\theta_{\mathrm{i}}, \varphi_{\mathrm{i}}, \theta_{\mathrm{r}}, \varphi_{\mathrm{r}}\right)=\frac{\mathrm{d} I_{\lambda, \mathrm{r}}\left(\theta_{\mathrm{r}}, \varphi_{\mathrm{r}}\right)}{I_{\lambda, \mathrm{i}}\left(\theta_{\mathrm{i}}, \varphi_{\mathrm{i}}\right) \cos \theta_{\mathrm{i}} \mathrm{d} \Omega_{\mathrm{i}}}=\frac{M_{\mathrm{r}}\left(\Omega_{\mathrm{r}}\right)}{M_0 \Omega_{\mathrm{i}} \cos \theta_{\mathrm{i}}} $ | (26) |
式中:θi和φi为投射辐射的天顶角和方位角,θr和φr分别为观测天顶角和方位角,dΩi为入射辐射立体角,Ωr为反射辐射的探测立体角,Iλ, i(θi, φi)和Iλ, r(θr, φr)分别为入射辐射和反射辐射的辐射强度,M0为微元辐射传输仿真过程中入射到海面上的光子总数,Mr(Ωr)为海水表面上半球空间探测器在立体角Ωr内接收到的光子数。
2 典型结构体FBRD计算及分析 2.1 海面泡沫层与气泡层光学特性图 7(a)~(c)给出了0.3~2.0 μm波段内泡沫粒子平均半径r=500 μm和泡沫层空隙率fa=0.5时对应泡沫层的光谱散射系数、吸收系数和不对称因子。与他人研究(0.4~1.7 μm)进行了对比,结果显示本研究使用的计算模型的结果与马兰新的研究结果吻合较好。此外,可以看出,散射系数、吸收系数和不对称因子在可见光波段几乎不变,而在近红外波段有较大变化。在0.3~2.0 μm波段内,散射系数随平均几何偏差的增大而减小。在0.9~2.0 μm波段内,不对称因子则随着平均几何偏差的增大而增大。图 7(d)~(f)展示了0.3~2.0 μm波段内气泡平均半径r=500 μm和平均几何因子σg=1.2时对应泡沫层的光谱散射系数、吸收系数和不对称因子。可以看出,散射系数随泡沫层空隙率的增加而增加,但吸收系数展现出相反的趋势。在0.3~1.9 μm波段内,不对称因子展现出随泡沫层空隙率的增加而增加的趋势。当波长大于1.9 μm时,不对称因子与泡沫层空隙率呈负相关性。

|
图 7 0.3~2.0 μm波段内海面泡沫层的光学特性参数 Fig. 7 Optical properties of foam layer within 0.3-2.0 μm |
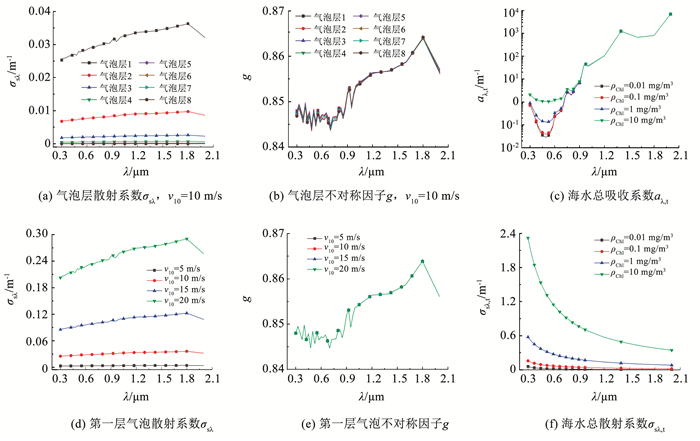
图 8(a)、(b)给出了0.3~2.0 μm波段内风速v10=10 m/s时在深度方向按照1 m间隔划分的每个子气泡层的光谱散射系数和不对称因子。在0.3~2.0 μm波段内,散射系数随着深度的增加而减小,第3层气泡的散射系数基本接近0,而不对称因子基本没有明显变化。在波长λ=1.8 μm时散射和不对称因子会达到最大值。风速对第1层气泡辐射特性的影响如图 8(c)、(d)所示。随着风速的增大,散射系数逐渐增加,而不对称因子不随风速改变。
|
图 8 0.3~2.0 μm波段内气泡层的光学特性参数 Fig. 8 Optical properties of bubble layer and sea water within 0.3-2.0 μm |
图 8(e)、(f)给出了ρChl分别为0.01、0.1、1、10 mg/m3时海水总光谱吸收和散射系数。可以看出,叶绿素是影响海水吸收和散射特性的关键因素。在0.3~2.0 μm波段内,海水总散射系数总体呈现减小趋势。海水总散射系数随叶绿素质量浓度的增加而显著增大,但吸收系数仅在0.35~0.60 μm波段内有明显增加。
2.2 风速和波长对不同结构体FBRD的影响粗糙海面、含泡沫粗糙海面、含破碎波粗糙海面的随风速变化,出射方位角为0°,入射天顶角为60°,波长为0.5、1.2、2 μm。
图 9(a)~(i)分别给出了4种风速(v10=5、10、15、20 m/s)和3种波长(λ=0.5、1.2、2 μm)条件下粗糙海面结构体、含泡沫粗糙海面结构体和含破碎波粗糙海面结构体FBRD(忽略海面镜向分量),其中,入射天顶角θi=60°,入射方位角φi=0°,观测方位角φr=0°。结构体几何结构和光学参数的设置参照1.1和1.2节。从图 9可以看出,不同条件下3种结构体的FBRD之间均存在显著差异,该结果表明,不同几何结构海面的FBRD有显著差异。当风速为5 m/s时,由于气泡和泡沫的散射系数几乎接近于0,可以认为该风速条件下的FBRD为水体结构体的FBRD,且只有当波长为0.5 μm时,粗糙海面结构体的FBRD不为0。对于粗糙海面结构体而言,只有当波长为0.5 μm时,结构体FBRD才存在有效值,且此时结构体FBRD随风速的变化并不明显,4种风速条件下,结构体FBRD的数值均在0.06 sr-1附近震荡,而其他波长下由于水体具有较强的吸收性,粗糙海面结构体的FBRD数值均为0,如图 9(a)~(c)所示。对于含泡沫粗糙海面结构体和含破碎波粗糙海面结构体,结构体的FBRD随出射天顶角的增大逐渐增加。当风速一定时,4种风速对应的FBRD分别随着波长的增大而减小。当波长一定时,两种结构体的FBRD随风速的增大而增大,如图 9(d)~(i)所示。

|
图 9 不同风速及波长条件下典型结构体的FBRD Fig. 9 FBRD of featured multi-scale voxels under different wind speeds and wavelengths |
为探究典型结构体FBRD随入射天顶角和观测方位角的变化规律,计算了风速为20 m/s和3个太阳天顶角(θi=0°、30°、60°)下观测方位角从0°~180°变化的3种典型结构体(粗糙海面结构体、含泡沫粗糙海面结构体以及含破碎波粗糙海面结构体)FBRD分布云图(图 10)。可以看出,太阳斜入射时,FBRD取值在不同观测角度下有较大差异。当入射天顶角θi=0°时,结构体FBRD取值不随方位角变化。而随着入射天顶角增大,FBRD取最大值时对应的方位角逐渐偏转到θr=90°和φr=0°,并且随着观测方位角的增加,同一观测天顶角下的FBRD取值迅速降低至0.05 sr-1以下。

|
图 10 不同入射天顶角条件下典型结构体的FBRD Fig. 10 FBRD of featured multi-scale voxels under different incident zenith angles |
针对高等级海况条件下粗糙海面结构体、含泡沫粗糙海面结构体以及含破碎波粗糙海面结构体3种典型结构体对大气-海洋辐射传输模型进行了补充,通过高等级海况条件下海面的体元几何结构的参数化,使用几何光学、广义MIE散射、独立散射理论以及生物光学模型分别计算了泡沫层、气泡层以及海洋水体的吸收系数、散射系数以及不对称因子3类光学特性。最后计算了不同风速、入射角和波长条件下3种典型结构体的双向反射分布函数。具体结论可归纳如下:
1) 海面结构体的光学特性在可见光波段几乎不变,而在近红外波段有较大变化。散射系数随着泡沫层空隙率的增加而增加,吸收系数随泡沫层空隙率的增加而减小。
2) 随着风速的增大,散射系数逐渐增加,而不对称因子不受风速的影响。
3) 叶绿素是影响海水吸收和散射特性的关键因素。海水总散射系数总体呈现减小趋势。海水总散射系数随叶绿素质量浓度的增加而显著增长,但吸收系数仅在0.35~0.60 μm波段内有明显增加。
4) 对于含泡沫粗糙海面结构体和含破碎波粗糙海面结构体,结构体的FBRD随出射天顶角的增大逐渐增加。当风速一定时,4种风速对应的FBRD分别随波长的增大而减小。当波长一定时,两种结构体的FBRD随风速的增大而增大。
5) 太阳斜入射时,FBRD取值在不同观测角度下有较大差异。当入射天顶角为0°时,结构体FBRD不随方位角变化。而随着入射天顶角增大,FBRD取最大值时对应的方位角逐渐偏转到θr=90°和φr=0°。
利用本研究可以实现不同海况条件下海面辐射特性的快速建模仿真,为大尺度海面辐射特征提取工作提供依据。在今后工作中,将进一步开展不同海况下大尺度海表结构建模、海-气耦合辐射传输计算等工作,实现大尺度海面辐射特征仿真工作。
| [1] |
李敏敏. 我国典型近岸水体悬浮颗粒物后向散射特性研究[D]. 青岛: 国家海洋技术中心, 2013 LI Minmin. Study on the backscattering characteristics of suspended particulate matter in typical nearshore water bodies in China[D]. Qingdao: National Marine Technology Center, 2013 |
| [2] |
FROUIN R, SCHWINDLING M, DESCHAMPS P Y. Spectral reflectance of sea foam in the visible and near-infrared: in situ measurements and remote sensing implications[J]. Journal of Geophysical Research: Oceans, 1996, 101(C6): 14361. DOI:10.1029/96JC00629 |
| [3] |
GUO Jianjun, TSANG L, ASHER W, et al. Applications of dense media radiative transfer theory for passive microwave remote sensing of foam covered ocean[J]. IEEE Trans Geosci Remote Sens, 2001, 39(5): 1019. DOI:10.1109/36.921420 |
| [4] |
CAMPS A, VALL-LLOSSERA M, VILLARINO R, et al. The emissivity of foam-covered water surface at L-band: theoretical modeling and experimental results from the FROG 2003 field experiment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(5): 925. DOI:10.1109/TGRS.2004.839651 |
| [5] |
马兰新. 近海面海浪破碎形成弥散介质辐射传输特性[D]. 哈尔滨: 哈尔滨工业大学, 2017 MA Lanxin. Radiation transfer characteristics of dispersed media formed by breaking waves near the sea surface[D]. Harbin: Harbin Institute of Technology, 2017 |
| [6] |
ZHANG Xiaodong. Influence of bubbles on the water-leaving reflectance[D]. Halifax, Canada: Dalhousie University, 2002
|
| [7] |
AL-LASHI R S, GUNN S R, WEBB E G, et al. A novel high-resolution optical instrument for imaging oceanic bubbles[J]. IEEE Journal of Oceanic Engineering, 2018, 43(1): 1. DOI:10.1109/JOE.2017.2660099 |
| [8] |
MA Lanxin, WANG Fuqiang, WANG Chengan, et al. Monte Carlo simulation of spectral reflectance and BRDF of the bubble layer in the upper ocean[J]. Optics Express, 2015, 23(19): 24274. DOI:10.1364/OE.23.024274 |
| [9] |
YANG Yu, GUO Lixin. Parallel Monte Carlo simulation algorithm for the spectral reflectance and transmittance of the wind-generated bubble layers in the upper ocean using CUDA[J]. Optics Express, 2020, 28(22): 33538. DOI:10.1364/OE.406262 |
| [10] |
MONAHAN E C. Whitecap coverage as a remotely monitorable indication of the rate of bobbie injection into the oceanic mixed layer[C]//Sea Surface Sound. Berlin: Springer Netherlands, 1988. DOI: 10.1007/978-94-009-3017-9_7
|
| [11] |
REUL N. A model of sea-foam thickness distribu-tion for passive microwave remote sensing applica-tions[J]. Journal of Geophysical Research, 2003, 108(C10): 3321. DOI:10.1029/2003JC001887 |
| [12] |
LI Dongfang, ZHAO Zhiqin, ZHAO Yanwen, et al. A modified model for electromagnetic scattering of sea surface covered with crest foam and static foam[J]. Remote Sensing, 2020, 12(5): 788. DOI:10.3390/rs12050788 |
| [13] |
CHOWDHARY J, ZHAI Pengwang, BOSS E, et al. Modeling atmosphere-ocean radiative transfer: a pace mission perspective[J]. Frontiers in Earth Sciences, 2019, 7(100). DOI:10.3389/feart.2019.00100 |
| [14] |
CHOWDHARY J, ZHAI Pengwang, XU Feng, et al. Testbed results for scalar and vector radiative transfer computations of light in atmosphere-ocean systems[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 242. DOI:10.1016/j.jqsrt.2019.106717 |
| [15] |
LIU Shubo, WEI Enbo, LI Yinan, et al. Aquarius semi-theoretical model of sea surface salinity retrieval for foam-covered surface[J]. International Journal of Remote Sensing, 2020, 41(11): 4293. DOI:10.1080/01431161.2020.1714783 |
| [16] |
CZERSKI H, TWARDOWSKI M, ZHANG Xiaodong, et al. Resolving size distributions of bubbles with radii less than 30 μm with optical and acoustical methods[J]. Journal of Geophysical Research Oceans, 2011, 116(C7): 1. DOI:10.1029/2011JC007177 |
| [17] |
MOREL A, GENTILI B. Diffuse reflectance of oceanic waters: its dependence on Sun angle as influenced by the molecular scattering contribution[J]. Appl Opt, 1991, 30(30): 4427. DOI:10.1364/AO.30.004427 |
| [18] |
GORDON H R, MOREL A Y. Remote assessment of ocean color for interpretation of satellite visible imagery: a review[J]. Physics of the Earth & Planetary Interiors, 1983, 37(4): 292. DOI:10.1029/LN004 |
| [19] |
ZHANG Xiaodong, HU Lianbo. Scattering by pure seawater at high salinity[J]. Optics Express, 2009, 17(15): 12685. DOI:10.1364/OE.17.012685 |
| [20] |
谈和平, 夏新林, 刘林华, 等. 红外辐射特性与传输数值计算[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006. TAN Heping, XIA Xinlin, LIU Linhua, et al. Infrared radiation characteristics and numerical calculation of transmission[M]. Harbin: Harbin Institute of Technology Press, 2006. |
 2024, Vol. 56
2024, Vol. 56


