2. 中国科学院大学,北京 100049;
3. 磁共振冻土成冰过程动态分析联合实验室,兰州 730000
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Joint NMR Laboratory for Freeze-Thaw Processes in Soils, Lanzhou 730000, China
土体中吸附水是吸附在土颗粒周围的水分子,且主要存在于小孔隙中[1];而土体中自由水是远离土颗粒表面的水分子,受颗粒表面作用影响较小[2],通常分为重力水和毛细水[3],主要存在于大孔隙中。自由水和吸附水含量影响着土颗粒的物理属性[4-6]。土体冻融过程引起土体中吸附水和自由水重分布,进而导致土体物理性质发生变化。因此,冻融条件下土体中吸附水和自由水的动态变化是评估寒区土体物理特征的关键。
由于土颗粒表面能和毛细作用影响,冻土中始终存在未冻水[7]。针对冻土中未冻水研究,学者提出了许多关于未冻水含量的测量技术及计算方法。例如,量热法[8],时域反射法[9-11],以及计算公式[12-13]。然而,这些方法主要用于测量土体中整体的未冻水含量,无法准确确定冻土中吸附水和自由水含量。20世纪70年代,核磁共振技术被用来测量冻土中未冻水含量[14],之后,有学者基于核磁共振技术测量了土体中吸附水含量,并讨论了土体密度和温度对吸附水含量的影响[15]。近年来,从理论角度分析了土体中吸附水和自由水热力学状态[16-18],然而,土体冻融过程中,孔隙中吸附水和自由水的变化是一个动态过程,但目前对于该动态变化过程的相关研究甚少。
为了研究土体中吸附水和自由水在冻融时的动态变化,本研究采用可分层测量的核磁仪器对含水量(质量分数)分别为21.1%,16.8%和12.0%的粉质黏土进行冻融实验,并对冻融后土样进行SEM扫描。基于实验结果,揭示了粉质黏土在冻融过程中不同冻结深度的吸附水和自由水动态变化的机理,从微观结构角度分析了吸附水和自由水重分布的原因。为探索土体冻融过程中土水之间物理化学过程提供科学参考。
1 材料和方法 1.1 土样的物理性质本研究采用的土壤是青藏高原北麓河地区(92.94°E, 34.83°N)的粉质黏土。采用数显式液塑限测量仪测得土体的液限和塑限分别为22.9%和12.0%。通过Mastersizer 2000测得土颗粒粒径 < 0.005 mm,0.005~0.025 mm, >0.025~0.075 mm和>0.075 mm的占比分别为12%,24%,32%和32%。利用X射线衍射法测得了土体中的主要矿物成分及含量分别是二氧化硅(59.1%)、碳酸钙(14.7%)、钙钠长石(26.2%)。
土壤自然风干、混和、碾碎,过2 mm筛子。利用去离子水与土体充分混合,以达到目标质量含水量21.1%,16.8%和12.0%,其中21.1%土样为近饱和含水量土样。将配置含水量之后的土样静置在塑料密封袋中12 h以上,使得土样水分分布均匀。
1.2 试验设备为了观测冻融过程中土样各层吸附水和自由水动态变化,冻土工程国家重点实验室和苏州纽迈分析仪器科技有限公司联合研制了土体冻融成冰过程动态分析系统(MRI-cryogenic soil-moisture analyzer,MRI-CSMA),图 1(a)是该仪器的结构图。该仪器由温度控制系统、磁体系统、成像系统、控制单元以及温度采集系统构成。温度控制系统由5个冷浴组成,主要用于控制土样的边界温度以及射频线圈和梯度单元的温度。成像系统可以获得土样中液态水的空间分布图。控制单元用于参数设置和数据采集。温度采集系统用于实时监测土样及土样边界温度。磁体系统是仪器的核心部分,由磁体单元、梯度单元、射频线圈及样品容器构成。磁体单元主要是提供发生核磁共振所需的静磁场。梯度单元主要作用是与静磁场形成恒定梯度,将样品从上至下分成均匀的9层(每层11.1 mm),涵盖了土样冻结区及未冻区。射频线圈用于激发静磁场中氢质子。样品仓是射频线圈中央的空腔,用于放置样品容器。样品容器结构如图 1(b)所示。

|
图 1 土体冻融成冰过程动态分析系统 Fig. 1 The MRI-cryogenic soil-moisture analyzer |
在试验进行时将土样置于样品容器中,样品容器可以放置直径90 mm,高100 mm的圆柱型土样进行实验测量。样品容器侧壁内嵌有用于冷冻液循环的环形通道,以控制试样侧面温度。在土样上端和下端分别有内置冷冻液循环腔的上顶板和下底板,主要控制土样上端和下端的温度。在样品管侧面有间距为24 mm的5个圆孔(圆孔直径为2.5 mm) 用于插入温度探头TP1, TP2, TP3, TP4和TP5,基于温度探头实测温度,对应的9个土层的温度通过拟合温度曲线获得。利用MRI-CSMA中的MT-CPMG序列可以获得每一层土样(每层厚11.1 mm)的横向弛豫时间T2分布曲线(即T2分布曲线)。
根据Curie定律,温度对土体中液态水的核磁信号强度有影响,且土体正温时孔隙水的核磁信号与温度成线性关系(顺磁线性回归线)[19-20]。因此,在计算不同温度土样的液态水含量时,将T2分布曲线的面积作为测量信号强度值Sm,根据顺磁线性回归线得到土体中液态水的理论核磁信号值St,故液态水的含量wu可由式(1)计算[21]:
| $ w_{u}=\frac{w_{0} \cdot S_{m}}{S_{t}} $ | (1) |
其中w0为土样正温时液态水含量。
1.3 试验过程将配置好含水量的土样装入样品容器,依次插入侧面的温度探头,连接土样的控温结构。然后开启温度控制系统并设置各个边界温度,待设定的边界温度稳定后设置设备采集参数并接通射频信号传输线开始采集数据。
在土样冻结之前,土样经历5个恒温阶段,此时土样上端,下端以及环境的温度是相同的,5个恒温阶段的设置温度分别是21.5 ℃,16.5 ℃,11.5 ℃,6.5 ℃和1.5 ℃。恒温结束之后进行单向冻结,设置上端温度为-20 ℃(初始含水量为21.1%土样冻结过程,由于仪器故障上端温度为-18 ℃, 这并不影响本研究的核心观点),下端和环境都是1 ℃。在融化阶段,土样上端,下端和环境温度均设为6.5 ℃。其中,初始含水量为21.1%的土样恒温阶段持续的时间约为38 h,冻结阶段持续的时间约为72 h,融化时间为24 h;初始含水量为16.8%的土恒温阶段时间约为59 h,冻结阶段持续时间约为71 h, 融化时间约为28 h;初始含水量为12.0%的土样恒温阶段时间约为59 h,冻结阶段持续时间约为72 h,融化时间约为24 h。
1.4 确定吸附水和自由水吸附水是受土颗粒表面作用影响明显且吸附在土颗粒附近的水,主要存在于小孔隙中,弛豫过程中横向弛豫时间T2较短。相反,自由水主要存在于土体大孔隙中,受到土颗粒的吸附作用较弱,在弛豫时横向弛豫时间较长。根据T2和土体孔隙中水分子的赋存关系,可以选取一个截止值T2c,当T2大于T2c时,T2所表征的是自由水的横向弛豫过程,而小于T2c时,T2所表征的是吸附水的横向弛豫过程[22-23]。采用文献[24]的方法对本试验得到的T2分布曲线分析获得T2c=2.31 ms。因此,本研究中吸附水的横向弛豫时间是0 ms < T2≤2.31 ms,吸附水含量通过T2分布曲线在0 ms < T2≤2.31 ms时的面积计算。自由水的横向弛豫时间是2.31 ms < T2 < 10 000 ms时, 自由水含量通过分布曲线在2.31 ms < T2 < 10 000 ms面积计算。
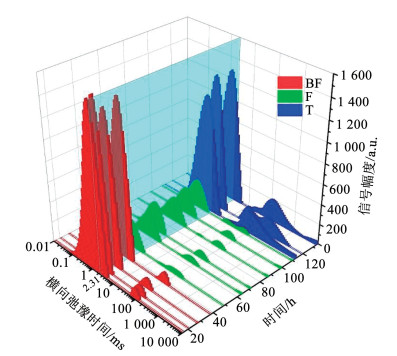
2 试验结果及分析 2.1 T2分布曲线T2分布曲线展示了土体中水分子不同的横向弛豫时间及其强度的分布特征。不同的T2值代表土孔隙中水分子的不同活性状态,而强度表示与T2相对应的水分子的相对含量。图 2展示了含水量为21.1%土样在冻融过程中第2层的T2分布曲线,BF代表冻融前,F代表冻结过程,T代表融化过程。根据1.4节确定的T2c,T2分布曲线分为两部分,T2c左侧的T2分布曲线代表吸附水,T2c的右侧表示自由水。如图 2所示,在冻结过程中,随着温度下降,T2c的左右两侧的核磁信号强度随冻结时间持续而减小。特别地,在冻结初期,T2c右侧的核磁信号强度大幅下降。这表明在冻结过程中,自由水比吸附水更容易发生改变(移动和相变)。在融化过程中,随着温度升高,核磁信号强度增加。融化完成后,T2c右侧的核磁信号强度明显比冻结前高,这表明冻融作用对土样中液体水分子的能量状态及其含量的再分配产生影响。
|
图 2 冻融过程中初始含水量为21.1%土样第2层的T2分布曲线 Fig. 2 The T2 distribution curve of the second layer of soil sample with the initial water content of 21.1% during freezing and thawing |
图 3~5分别展示了含水量为21.1%, 16.8%和12.0%土样冻融过程中各层的吸附水和自由水随温度变化而变化的过程。在冻结阶段,土样各层的吸附水和自由水含量随温度下降而降低,在冻结初期,降低的程度最为明显。图 6展示了初始含量为21.1 %土样在冻结阶段各层的吸附水和自由水变化速率。冻结初期,随着远离土样冷端,吸附水下降速率逐渐减小,第1层下降的速率最大,第9层的下降速率最慢。同样地,自由水的下降速率也呈现相似的规律。这主要是在冻结区,靠近试样冷端,温度越低,相变量越多。在未冻区,越靠近冻结锋面,冷吸力越大,导致水分迁移量越多。另外,冻结区的液态水下降速率整体大于未冻区,这说明冻结区由相变引起的水分减少速率大于在未冻区由水分迁移引起的水分减少速率。

|
图 3 初始含水量为21.1%的土样在冻融过程中吸附水和自由水随温度变化 Fig. 3 The variation of adsorbed water and free water in soil samples with initial moisture content of 21.1% during freezing and thawing processes |
|
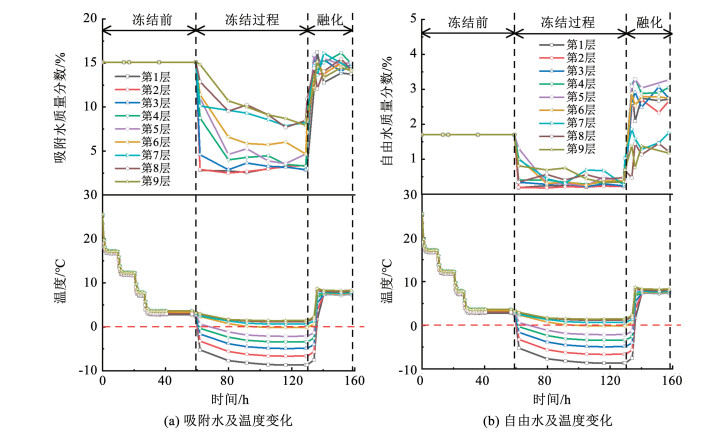
图 4 初始含水量为16.8%的土样在冻融过程中吸附水和自由水随温度变化 Fig. 4 The variation of adsorbed water and free water in soil samples with initial moisture content of 16.8% during freezing and thawing processes |

|
图 5 初始含水量为12.0%的土样在冻融过程中吸附水和自由水随温度变化 Fig. 5 The variation of adsorbed water and free water in soil samples with initial moisture content of 12.0% during freezing and thawing processes |

|
图 6 冻结过程初始含水量为21.1%土样吸附水和自由水的变化速率(R1, R2, R3, …, R8和R9分别是土样的第1层至第9层的变化速率) Fig. 6 The change rate of adsorbed water and free water in the soil sample with initial water content 21.1% under freezing conditions(R1, R2, R3, …, R8, and R9 respect the change rate of adsorbed/free water in the first layer to the ninth layer, respectively) |
在融化阶段,施加正温后,土样各层的吸附水和自由水含量随着温度升高而上升。如图 3所示,初始含水量为21.1%土样在融化2.7 h后,土样第1层到第9层的吸附水相对于施加正温之前分别升高了12.3%,12.0%,11.5%,9.1%,7.4%,4.1%,3.5%,3.8%和3.4%;自由水相对于施加正温之前分别升高了6.1%,6.2%,5.2%,6.2%,5.9%,0.7%,0.7%,0.6%和0.6%。初始含水量为16.8%和12.0%土样在融化过程中,各层的吸附水和自由水均同样出现不同程度的升高。土样冻结区在施加正温后,冰融化成液态水,导致吸附水和自由水含量升高。在未冻区吸附水和自由水含量升高是由于冻结区的冰融化后,部分液态水下渗到未冻区,导致未冻区的吸附水和自由水含量均升高。
2.3 冻结过程中吸附水和自由水相对变化量在初始状态,土样中吸附水含量与自由水含量不相同,例如初始含水量为12.0%的土样,第3层的吸附水和自由水的含量分别是11.0%和1.0%。为了消除初始状态含量差异,本文引入了相对变化量来表征冻结过程中吸附水和自由水的变化程度,其计算如(2)式:
| $ w_{r}=\frac{w_{t}-w_{0}}{w_{0}} \times 100 \% $ | (2) |
其中:wr为相对变化量, wt为冻结时间为t时刻的吸附水/自由水含量, w0为初始正温时吸附水/自由水含量。
图 7为初始含水量为21.1%土样在冻结阶段吸附水和自由水的相对变化量,负号表示吸附水和自由水的含量相对于初始含水量在减小。含水量为16.8%和12.0%土样冻结过程中吸附水和自由水的相对变化量与含水量为21.1%土样的规律相似。后文主要以分析含水量为21.1%土样为主。如图 7所示,冻结时间相同时,土样各层的自由水相对变化量大于吸附水的相对变化量,即在相同的冻结时间内,自由水较吸附水变化更快。例如,初始含水量为21.1%土样在冻结区的第2层冻结10.6 h后,吸附水的相对变化量为77.2%,自由水的相对变化量为83.3%。在未冻结区的第8层冻结10.6 h后,吸附水的相对变化量为12.5%,自由水的相对变化量为30.2%。

|
图 7 冻结阶段初始含水量为21.1%的土样每层吸附水和自由水的相对变化量 Fig. 7 Relative change content of adsorbed/free water in the soil sample with the initial water content of 21.1% at the freezing stage |
冻结过程中,冻结区液态水的变化主要是负温作用下液态水发生相变引起;未冻区液态水在基质吸力作用下向冻结锋面处的迁移引起了未冻区各层土体液态水发生变化。此外,冻结过程中在冻结区和未冻区发生相变和迁移时,自由水的变化要明显快于吸附水,其本质原因是土体吸附水和自由水的热力学状态的差异。
孔隙水压力是表征土体孔隙水热力学状态的关键参数。孔隙水压力的大小很大程度上依赖于水分子距离土颗粒表面的距离。通常孔隙水压力随着距离土体颗粒表面的增加而减小[25-26]。土颗粒表面附近液态水的孔隙水压和冻结温度可以用Clausius-Clapeyron方程描述[17, 27],越靠近土颗粒表面,孔隙水压越大,冻结温度越低,因此,吸附水的冻结温度低于自由水的冻结温度,在孔隙水发生相变时,自由水更容易相变成冰。在微观上,黏度反映了分子运动和相互作用的影响,是液体热力学状态函数,土颗粒附近液态水的孔隙水压力随着距离土颗粒表面的距离减少而增加,土颗粒附近液态水的黏度随着距离土颗粒表面的距离减少而增大,所以,吸附水的黏度大于自由水的黏度,在未冻区,自由水比吸附水更容易迁移。
2.4 冻融前后吸附水和自由水的重分布冻融作用导致土样各层的吸附水和自由水发生重分布,总体上冻结区的吸附水减少,自由水增加;未冻区的吸附水和自由水均减少。图 8是初始含水量为21.1%,16.8%和12.0%土样冻融后各层的吸附水和自由水的变化量。吸附水/自由水的变化量是融化阶段最后时刻的吸附水/自由水含量减去冻结阶段初始时刻的含水量。如图 8所示,初始含水量为21.1%土样在冻融后,第1层到第5层的吸附水含量分别减少1.9%,0.6%,1.7%,2.4%,2.9%;自由水分别增加4.0%,4.0%,3.0%,3.5%,4.0%。在第6层到第9层的吸附水分别减少1.0%,1.0%,1.5%和0.7%;而自由水分别减少1.8%,1.7%,1.8%和1.9%。初始含水量为16.8%土样冻融后吸附水和自由水的分布与初始含水量为21.1%土样具有相似性。初始含水量为12.0%土样的未冻区吸附水和自由水均减少;在冻结区,自由水和吸附水均增加,这与初始含水量为21.1%和16.8%土样在冻结区吸附水的变化规律不同。

|
图 8 冻融前后土体各层中吸附水和自由水含量变化量 Fig. 8 Change content of free and adsorbed water in each layer caused by freezing-thawing action |
吸附水和自由水在土体中的赋存与土体结构相关,冻融作用会改变土体的微观结构。图 9为初始含水量为21.1%土样冻融后的宏观结构及不同位置的SEM图像。如图 9所示,土样在冻融后,宏观上冻结区的孔隙数量比未冻区多,冻结区土体相比未冻区更加松散。这种差异在微观SEM图像上更加明显,冻结区和未冻结区的SEM图像明显不同,相比于未冻区,冻结区的SEM图像中有很多孔隙,而且冻结区的土颗粒团聚现象更加明显。对于未冻区,孔隙数量较少,且土颗粒之间团聚现象并不明显。这些结构的改变是土体冻融的结果,同时结构的改变也影响吸附水和自由水的赋存。在冻结区土颗粒团聚导致土颗粒的比表面积减小,相应地吸附在土颗粒表面的水分子体积减小,引起冻结区吸附水含量减小。在未冻区,土体颗粒排列紧密,孔隙数量较少,这是冻结过程冻结区的法向冻胀应力和自重压密所致,同时使得未冻区的吸附水和自由水在挤压和冻冻结锋面吸力作用下向冻结区移动,使得未冻区的吸附水和自由水均减少,冻结区的自由水含量增加。对于初始含水量为12.0%的土样,在冻结区吸附水含量增加,因为对于低含水量土样而言,初始状态的吸附水含量处于非饱和状态,当土体的水分子迁移至冻结区时,部分水分子受到土颗粒表面的吸附作用形成吸附水,使吸附水含量增加。

|
图 9 初始含水量为21.1%的土样冻融完成后的宏观结构及SEM图像 Fig. 9 Macrostructure and SEM images of soil sample with the initial water content of 21.1% after freezing-thawing |
本研究通过自主研发的新型核磁共振仪分别测量了含水量为21.1%,16.8%和12.0%的粉质黏土。通过该仪器的在线控温和分层扫描,探明土样在冻融过程中不同土层吸附水和自由水的动态变化特征,并采用扫描电镜获得冻融后土样不同位置的微观结构。基于实验结果对土体中吸附水和自由水在冻融过程中的动态变化机理进行分析。主要结论如下:
1) 土样发生冻结时,土样各层中的吸附水和自由水减少。在冻结区主要受相变作用影响,且越靠近土样的冷端相变越剧烈,变化速率越快。在未冻区液态水主要向冻结锋面处迁移,且越靠近冻结锋面,吸力作用越强,迁移量越多。
2) 冻结过程中,冻结区自由水的相变比吸附水更加容易;同样未冻区自由水迁移比吸附水更加容易。吸附水和自由水相变和迁移的差异是土体中自由水和吸附水的热力学状态不同导致。冻结区水分相变时自由水的冻结温度大于吸附水的冻结温度,而未冻区水分迁移时自由水的黏度小于吸附水,其本质是由于土体孔隙中水分子之间的作用势能与距离土颗粒表面的距离相关。
3) 土样冻融导致土体冻结区吸附水减少,自由水增加;未冻区吸附水和自由水均减少,其原因是土体冻融过程中水分迁移和微观结构变化。
4) 在本文中确定吸附水和自由水的方法只是基于实验数据,然而吸附水和自由水在土体中的赋存是一个复杂的物理问题,因此在后续研究中需要从理论和实验数据相结合的方式进一步精确地区分土体中的吸附水和自由水。
| [1] |
TULLER M D, DUDLEY L M. Adsorption and capillary condensation in porous media: liquid retention and interfacial configurations in angular pores[J]. Water Resources Research, 1999, 35(7): 1949. DOI:10.1029/1999WR900098 |
| [2] |
SHANG J Q, LO K Y, QUIGLEY R M. Quantitative-determination of potential distribution in stern-gouy double-layer model[J]. Canadian Geotechnical Journal, 1994, 31(5): 624. DOI:10.1139/t94-075 |
| [3] |
马巍, 王大雁. 冻土力学[M]. 北京: 科学出版社, 2014: 12. MA Wei, WANG Dayan. Frozen soil mechanics[M]. Beijing: Science Press, 2014: 12. |
| [4] |
BAKER R, FRYDMAN S. Unsaturated soil mechanics critical review of physical foundations[J]. Engineering Geology, 2009, 106(1/2): 26. |
| [5] |
KONRAD J M, LEBEAU M. Capillary-based effective stress formulation for predicting shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 2015, 52(12): 2067. DOI:10.1139/cgj-2014-0300 |
| [6] |
ZHOU Annan, HUANG Ruiqiu, SHENG Daichao. Capillary water retention curve and shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 2016, 53(6): 974. DOI:10.1139/cgj-2015-0322 |
| [7] |
徐斅祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2010: 39. XU Xiaozu, WANG Jiacheng, ZHANG Lixin. Physics of frozen soil[M]. Beijing: Science Press, 2010: 39. |
| [8] |
STENBERG L. Determination of unfrozen water content in clay by the calorimeter method[M]. Linköping, Sweden: Swedish National Road and Transport Research Institute, 1975: 232.
|
| [9] |
SEYFRIED M S, MURDOCK M D. Calibration of time domain reflectometry for measurement of liquid water in frozen soils[J]. Soil Science, 1996, 161(2): 87. DOI:10.1097/00010694-199602000-00002 |
| [10] |
SPAANS E J A, BAKER J M. Examining the use of time domain reflectometry for measuring liquid water content in frozen soil[J]. Water Resources Research, 1995, 31(12): 2917. DOI:10.1029/95WR02769 |
| [11] |
STAHLI M, STADLER D. Measurement of water and solute dynamics in freezing soil columns with time domain reflectometry[J]. Journal of Hydrology, 1997, 195(1/2/3/4)): 352. |
| [12] |
ANDERSON D M, TICE A R. Predicting unfrozen water contents in frozen soils from surface area measurements[J]. Highway Research Record, 1972, 393: 12. |
| [13] |
MICHALOWSKI R L. A constitutive model of saturated soils for frost heave simulations[J]. Cold Regions Science and Technology, 1993, 22(1): 47. DOI:10.1016/0165-232X(93)90045-A |
| [14] |
TICE A R, BURROUS C M, ANDERSON D M. Determination of unfrozen water in frozen soil by pulsed nuclear magnetic resonance[C]//Proc 3rd Internat Conf Permafrost. Edmonton: National Research Council Canada, 1978
|
| [15] |
田慧会, 韦昌富. 基于核磁共振技术的土体吸附水含量测试与分析[J]. 中国科学: 技术科学, 2014, 44(3): 295. TIAN Huihui, WEI Changfu. Measurement and analysis of adsorbed water content of soil based on nuclear magnetic resonance technology[J]. Science in China: Science and Technology, 2014, 44(3): 295. |
| [16] |
LU Ning, ZHANG Chao. Soil sorptive potential: concept, theory, and verification[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(4): 13. |
| [17] |
ZHANG Lianhai, ZHUANG Qianlai, WEN Zhi, et al. Spatial state distribution and phase transition of non-uniform water in soils: implications for engineering and environmental sciences[J]. Advances in Colloid and Interface Science, 2021, 294: 12. |
| [18] |
ZHANG Chao, LU Ning. What is the range of soil water density? Critical reviews with a unified model[J]. Reviews of Geophysics, 2018, 56(3): 532. DOI:10.1029/2018RG000597 |
| [19] |
谭龙, 韦昌富, 田慧会, 等. 冻土未冻水含量的低场核磁共振试验研究[J]. 岩土力学, 2015, 36(6): 1566. TAN Long, WEI Changfu, TIAN Huihui, et al. Unfrozen water content in frozen soil by low-field NMR experiments[J]. Rock and Soil Mechanics, 2015, 36(6): 1566. |
| [20] |
泰斯A. R., 奥利丰特J. L., 朱元林, 等. 用脉冲核磁共振法及物理解吸试验测定的冻土中冰和未冻水之间的关系[J]. 冰川冻土, 1983, 5(2): 37. TICE A R, OLIPHANT J L, ZHU Yuanlin, et al. Relationship between the ice and unfrozen water phases in frozen soils as determined by pulsed nuclear magnetic resonance and physical desorption data[J]. Journal of Glaciology and Geocryology, 1983, 5(2): 37. |
| [21] |
SHI Yajun, ZHANG Lianhai, MA Wei, et al. Investigating unfrozen water and its components during freeze-thaw action in loess using a novel NMR technique[J]. European Journal of Soil Science, 2022, 73(4). |
| [22] |
COATES G R, MARSCHALL D, MARDON D, et al. A new characterization of bulk-volume irreducible using magnetic resonance[J]. Log Analyst, 1997, 39(1): 51. |
| [23] |
TIMUR A. Pulsed nuclear magnetic resonance studies of porosity, movable fluid, and permeability of sandstones[J]. Journal of Petroleum Technology, 1969, 21(6): 775. DOI:10.2118/2045-PA |
| [24] |
TIAN Huihui, WEI Changfu. A NMR-based testing and analysis of adsorbed water content[J]. Scientia Sinica Technologica, 2014, 44(3): 295. DOI:10.1360/092013-1133 |
| [25] |
KURTJAK M, URBIC T. Water in the presence of inert Lennard-Jones obstacles[J]. Molecular Physics, 2014, 112(8): 1132. DOI:10.1080/00268976.2013.836608 |
| [26] |
ZHANG Lianhai, YANG Chengsong, WANG Dayan, et al. Freezing point depression of soil water depending on its non-uniform nature in pore water pressure[J]. Geoderma, 2022, 412: 115724. DOI:10.1016/j.geoderma.2022.115724 |
| [27] |
WAGNER W. International equations for the pressure along the melting and along the sublimation curve of ordinary water substance[J]. Journal of Physical and Chemical Reference Data, 1994, 23(3): 515. DOI:10.1063/1.555947 |
 2024, Vol. 56
2024, Vol. 56


