2. 湖南省交通规划勘察设计院有限公司,长沙 410200
2. Hunan Provincial Transportation Planning Survey and Design Institute Co., Ltd., Changsha 410200, China
在城市道路资源有限的情况下,如今城市中路面行驶的大量的小汽车已经造成严重的道路交通拥堵。鼓励居民乘坐公交,可以降低私家车出行,缓解拥堵,降低环境污染。高载客量的公交车已经成为城市公共交通的重要组成部分[1],一些公交优先措施很好地解决了公交车准点率差、通行效率低的问题[2-4]。其中,公交专用道为公交车提供独立路权在拥挤路段效果更好[5-7]。但路网的复杂性、公交车的周期性导致公交专用车道利用率低,而限时共享专用道这种静态共享方案难以适用于多样、复杂的道路网络环境。
目前,主要有间歇性公交车道(intermittent bus lane,IBL)、具有间歇性优先权的公交车道(bus lanes with intermittent priority,BLIP)以及预信号这3种动态共享方案。IBL在公交车接近时为专用道,公交车离开时为普通车道[8-9]。IBL通过信号调整清空专用道内车辆保证公交优先,能够减少车辆的延误[10-13],BLIP则是利用可变信息标志(variable message sign,VMS)提醒车辆离开专用车道[14-15]。而预信号是通过在交叉口上游处设置预信号来控制共享专用道,为交叉口提供额外的车辆通行能力[16-18]。
然而IBL的信号调整会给主干道更多的绿灯时间,在主干道需求低时会增加其他道路的延误;在面对不同路段长度清空专用道内车辆时,BLIP可能会需要大量的信息标志,部署成本较高;预信号增加的额外信号会强制车辆队列末端向后移动。而且这3种策略均无法适应多种路段长度。随着GPS技术的不断发展,在未来环境中GPS可以实现对车辆精确定位。以此为基础,本文提出一种动态公交专用车道共享实时控制方法(以下简称控制方法),建立以减少交叉口车辆总延误为目标的公交专用车道共享控制模型,以实现公交专用车道灵活性、持续性共享。
1 问题描述控制方法是利用GPS定位实时获取交叉口处公交车的位置,并通过交通检测设备获取专用道内小汽车车辆数,结合当前时刻交叉口主信号显示对专用道共享前后交叉口车辆总延误进行比较。比较结果实时反馈给车道信号,当共享公交车道的总延误小于不共享公交车道的总延误时,车道信号显示绿灯,普通车道的车辆可以在到达车道信号之前进入专用道;反之,车道信号显示红灯,普通车道的车辆不允许进入专用道,同时专用道内未到达车道信号的车辆要通过交织区域驶离专用道。其中,交织区域是车道信号与交叉口车道分割实线之间的路段,以保证公交车道内的车辆变换车道时的安全,避免对普通车道的干扰,如图 1所示。

|
图 1 控制原理 Fig. 1 Control principle |
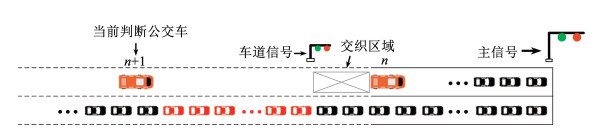
在当前时刻,如果离交叉口最近的第n辆公交车已经到达或者通过车道信号,则此次车道信号的显示情况由相邻的第n+1辆公交车为判断标准,如图 2所示。
|
图 2 公交车的判断标准 Fig. 2 Criteria of selecting buses |
1) 左转公交车流量很少,少量左转公交车可以进入普通左转车道完成左转。
2) 在交叉口路段内公交车以一个平均速度行驶。
3) 考虑到车辆不能及时在主信号显示红灯前刹车,以及车辆一般在显示绿灯时会有起步损失时间,主信号的黄灯时间是绿灯时间的延续,而部分绿灯时间作为红灯时间的延续。
4) 专用道内的车辆都能够顺利通过交织区域进入普通车道,不会对其他车辆造成干扰。
2.2 符号说明参数符号说明见表 1。其中,小汽车和公交车平均司乘系数代表小汽车和公交车每辆车内的平均人数;公交专用车道内i辆车通过交叉口的时间
| $ \left\{\begin{array}{l} l_{r}=r-t, 0 \leqslant t \leqslant r \\ l_{g}=C-t, r<t \leqslant C \end{array}\right. $ | (1) |
| 表 1 参数符号说明 Tab. 1 Parameter symbol description |
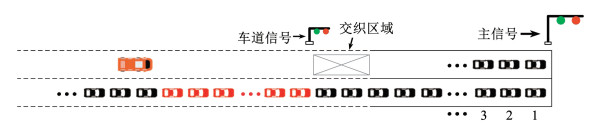
在当前主信号周期内,无法从普通车道通过交叉口的车辆在公交专用车道共享后可以从专用车道通过交叉口,本文将这种车辆定义为受影响车辆(如图 3中的红色车辆)。
|
图 3 受影响车辆 Fig. 3 Affected vehicles |
由于交叉口处的车流密度较大并且车辆运行状态相对均匀,本文认为交叉口处的车辆是均匀排列的。根据当前时刻交叉口车辆的队伍,从交叉口停车线开始对普通车道上的车辆进行编号(停车线后的车辆为第1辆,依次向后编号)。车辆离交叉口的距离和序号满足如下关系:
| $ d_{n}=(n-1)/K $ | (2) |
一个主信号周期绿灯剩余时间内能够通过交叉口的车辆数有限,受影响车辆的序号是位于当前周期能通过交叉口车辆的序号之后,即
| $ n_{\min }=\operatorname{Max}\left(\left[S \cdot l_{g}\right]+1, \left[\left(d_{0}+d_{1}\right) \cdot K\right]+1\right) $ | (3) |
| $ n_{\max }=\operatorname{Min}\left(\left[K \cdot V_{2} \cdot l_{g}\right]+1, \left[\left(d_{B}-e\right) \cdot K\right]+1\right) $ | (4) |
| $ N=n_{\max }-n_{\min }+1 $ | (5) |
| $ N \leqslant\left[S \cdot l_{g}\right]-\bar{N} $ | (6) |
根据实际意义,受影响车辆为正整数。如果专用道内已有车辆数超过绿灯剩余时间所能通过的车辆数,或者编号nmax小于nmin时,则不存在受影响车辆(取N=0),无论是否共享专用车道均不会减少交叉口的总延误。
2.4 控制模型交叉口的总延误包括公交车的延误、受影响车辆的延误以及非受影响车辆的延误,其中非受影响车辆包括在普通车道的车辆以及已在公交专用车道的普通车辆, 即
| $ D=\alpha \cdot D_{N}+\beta \cdot D_{B}+\alpha \cdot D_{M} $ | (7) |
| $ Z=D_{r}-D_{g} $ | (8) |
| $ D_{r}=\alpha \cdot D_{N r}+\beta \cdot D_{B r}+\alpha \cdot D_{M r} $ | (9) |
| $ D_{g}=\alpha \cdot D_{N g}+\beta \cdot D_{B g}+\alpha \cdot D_{M g} $ | (10) |
其中:D为交叉口车辆总延误,DN为受影响车辆延误,DB为离交叉口最近公交车的延误,DM为非受影响车辆延误,Dr为假设车道信号显示红灯时的交叉口总延误,Dg为假设车道信号显示绿灯时的交叉口总延误。
共享公交专用车道不会对非受影响车辆造成干扰,则共享前后非受影响车辆的延误相等。由此可以计算出公交专用车道共享前后交叉口总延误差值:
| $ Z=\alpha \cdot\left(D_{N r}-D_{N g}\right)+\beta \cdot\left(D_{B r}-D_{B g}\right) $ | (11) |
综合上述分析,车道信号显示情况I与当前时刻交叉口共享公交专用车道前后车辆总延误的差值、离交叉口最近的公交车的位置以及受影响车辆有关,由此建立动态公交车道共享实时控制模型(12)。控制方法的流程如图 4所示。
| $ I=\left\{\begin{array}{l} \text { Green, } Z>0 \\ \operatorname{Red}, Z \leqslant 0 \text { 或 } N=0 \end{array}\right. $ | (12) |

|
图 4 整体控制过程 Fig. 4 Overall control process |
在控制模型中最关键的因素就是当前时刻交叉口共享公交专用车道前后的车辆总延误差值,而车辆总延误与当前时刻主信号灯显示情况有着密不可分的关系。当前时刻不同的主信号显示情况以及不同的公交车离交叉口距离都会影响受影响车辆数的大小,对车辆总延误的分析与计算也是不同的。
3.1 当前时刻主信号显示红灯 3.1.1 计算车道信号显示红灯时的延误1) 受影响车辆延误。受影响车辆不仅经历了当前周期的剩余红灯时间,也受到了相邻周期红灯时间的影响,经历额外的延误如图 5所示。而且每辆受影响车辆的延误都与当前周期的红灯剩余时间、车辆从当前位置到达交叉口的行驶时间、前一辆车离开交叉口的时间等因素有关,受影响车辆的总延误是每辆受影响车辆延误的总和, 即
| $ D_{N r}=\sum\nolimits_{i=n_{\text {min }}}^{n_{\text {max }}}\left(r+g+l_{r}+h_{i-n_{\text {min }}}-d_{i}/V_{1}\right) $ | (13) |

|
图 5 在主信号显示红灯情况下车道信号显示红灯时受影响车辆运行状态 Fig. 5 Operating status of affected vehicle when lane signal is red and main signal is red |
2) 公交车延误。离交叉口最近的公交车到达交叉口停车线的行驶时间tB(以下简称公交车行驶时间)会导致主信号显示、专用道内车辆情况的不同,这些因素直接影响公交车的延误。因此,本文针对公交车行驶时间分析如下。
| $ t_{B}=d_{B}/V $ | (14) |
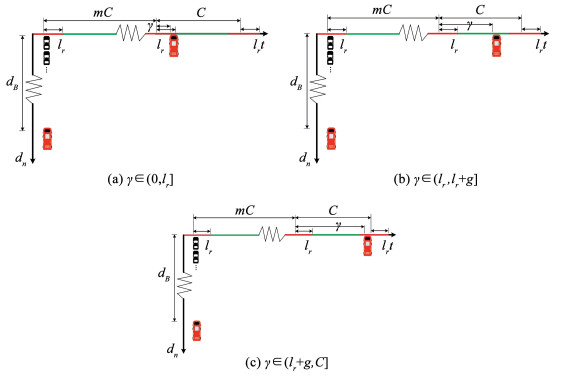
在tB≥C的情况下,当前时刻在专用道内已有车辆在公交车到达交叉口停车线之前已离开交叉口,不会对公交车造成干扰。为了便于情况分析,本文引入m和γ∈(0, C]来描述公交车行驶时间与交叉口主信号周期间的关系。其中,m表示公交车行驶时间与主信号周期的比值, γ则反应了公交车行驶时间与主信号周期比值的余数。m并不会改变公交车到达交叉口停车线时主信号显示情况,而γ的变化会导致公交车到达交叉口停车线时主信号显示情况改变,如图 6所示。
| $ t_{B}=m C+\gamma $ | (15) |
|
图 6 在主信号显示红灯情况下车道信号显示红灯及tB≥C时公交车运行状态 Fig. 6 Operating status of bus when lane signal is red and main signal is red with tB≥C |
当公交车到达交叉口停车线时,主信号可能显示红灯(图 6(a),图 6(c)),主信号也可能显示绿灯(图 6(b))。显然,不同的主信号显示情况会影响公交车的延误,随着γ的变化公交车延误也在变化。
| $ D_{B r}=\left\{\begin{array}{l} l_{r}-\gamma, \gamma \in\left(0, l_{r}\right] \\ 0, \gamma \in\left(l_{r}, l_{r}+g\right] \\ C+l_{r}-\gamma, \gamma \in\left(l_{r}+g, C\right) \end{array}\right. $ | (16) |
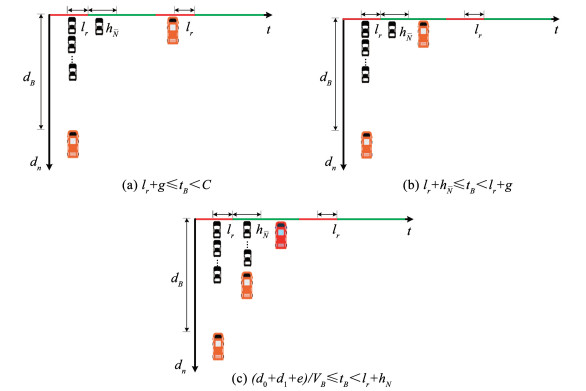
在lr+g≤tB < C的情况下,公交车到达交叉口停车线时主信号显示红灯,专用道内已有车辆全部通过交叉口(如图 7(a)所示)。公交车延误是公交车到达交叉口停车线时下一个主信号周期红灯剩余时间。
| $ D_{B r}=r-\left[t_{B}-\left(l_{r}+g\right)\right] $ | (17) |
|
图 7 在主信号显示红灯情况下车道信号显示红灯时公交车运行状态 Fig. 7 Operating status of bus when lane signal is red and main signal is red |
在
| $ D_{B r}=0 $ | (18) |
在
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B} $ | (19) |
在
当
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B}+\left\{\begin{array}{l} l_{r}-\gamma, \gamma \in\left(0, l_{r}\right] \\ 0, \gamma \in\left(l_{r}, l_{r}+g\right] \\ C+l_{r}-\gamma, \gamma \in\left(l_{r}+g, C\right) \end{array}\right. $ | (20) |
当
| $ \begin{equation*} D_{B r}=l_{r}+h_{\bar{N}}-t_{B}+r-\left[\hat{t}_{B}-\left(l_{r}+g\right)\right] \end{equation*} $ | (21) |

|
图 8 在主信号显示红灯情况下车道信号显示红灯时相邻公交车运行状态 Fig. 8 Operating status of adjacent bus when lane signal is red and main signal is red |
当
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B} $ | (22) |
当
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B}+l_{r}+h_{\bar{N}+1}-\hat{t}_{B} $ | (23) |
如果
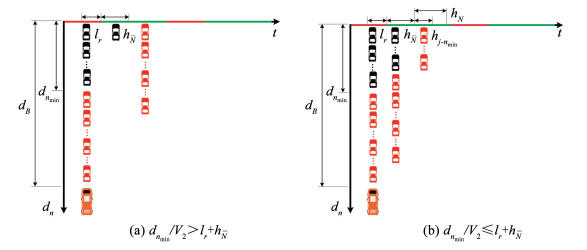
1) 受影响车辆延误。受影响车辆可以进入公交专用车道,但可能会受到专用道内已有车辆的干扰。受影响车辆是从编号nmin开始的车辆队列,如果专用道内车辆在编号nmin的车辆接近时没有全部驶离交叉口,则整个受影响车辆队列均会受到干扰。因此,针对编号nmin的车辆是否被干扰进行分析(如图 9所示)。
|
图 9 在主信号显示红灯情况下车道信号显示绿灯时受影响车辆运行状态 Fig. 9 Operating status of affected vehicle when lane signal is green and main signal is red |
在
| $ D_{N g}=\left\{\begin{array}{l} 0, d_{n_{\min }}/V_{2}>l_{r}+h_{\bar{N}} \\ N \cdot\left(l_{r}+h_{\bar{N}}\right)+\sum\nolimits_{j=n_{\text {min }}}^{n_{\max }}\left(h_{j-n_{\min }}-d_{j}/V_{2}\right), \\ \quad d_{n_{\min }}/V_{2} \leqslant l_{r}+h_{\bar{N}} \end{array}\right. $ | (24) |
2) 公交车延误。同样地,仍然需要对公交车行驶时间进行深入分析。在tB≥C的情况下,公交车的运行状态与主信号显示红灯情况下车道信号显示红灯时一致(如图 6所示),公交车延误与主信号显示红灯情况下车道信号显示红灯时的延误相等(式(16))。
| $ D_{B g}=D_{B r}=\left\{\begin{array}{l} l_{r}-\gamma, \gamma \in\left(0, l_{r}\right] \\ 0, \gamma \in\left(l_{r}, l_{r}+g\right] \\ C+l_{r}-\gamma, \gamma \in\left(l_{r}+g, C\right) \end{array}\right. $ | (25) |
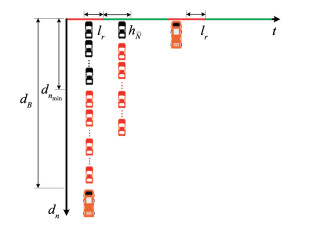
在lr+g≤tB < C的情况下,公交车到达交叉口停车线时主信号显示红灯,专用道内已有车辆全部通过了交叉口(如图 10所示)。公交车延误是公交车到达交叉口停车线时下一个主信号周期红灯剩余时间。
| $ D_{B g}=r-\left[t_{B}-\left(l_{r}+g\right)\right] $ | (26) |
|
图 10
在主信号显示红灯情况下车道信号显示绿灯及 |
在
| $ D_{B g}=\left\{\begin{array}{l} 0, \left(d_{0}+d_{1}+e\right)/V_{B} \leqslant t_{B}\left\langle l_{r}+g, d_{n_{\min }}/V_{2}\right\rangle l_{r}+h_{\bar{N}} \\ 0, l_{r}+h_{\bar{N}}+h_{N} \leqslant t_{B}<l_{r}+g, d_{n_{\min }}/V_{2} \leqslant l_{r}+h_{\bar{N}} \\ l_{r}+h_{\bar{N}}+h_{N}-t_{B}, \left(d_{0}+d_{1}+e\right)/V_{B} \leqslant t_{B}<l_{r}+h_{\bar{N}}+h_{N}, d_{n_{\min }}/V_{2} \leqslant l_{r}+h_{\bar{N}} \end{array}\right. $ | (27) |
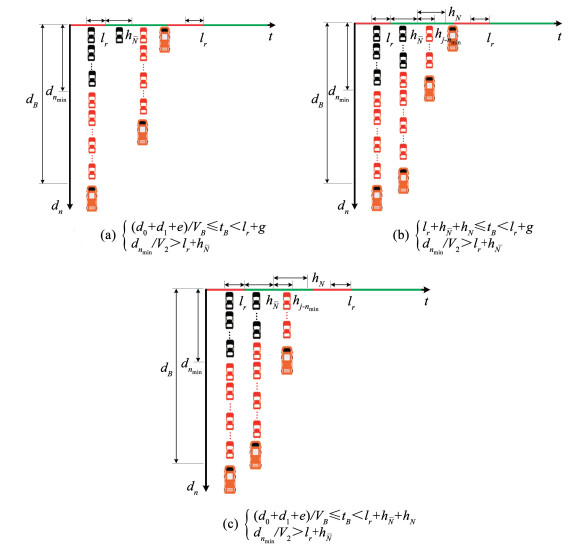
|
图 11
在主信号显示红灯情况下车道信号显示绿灯及 |
在
当
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B}+\left\{\begin{array}{l} l_{r}-\gamma, \gamma \in\left(0, l_{r}\right] \\ 0, \gamma \in\left(l_{r}, l_{r}+g\right] \\ C+l_{r}-\gamma, \gamma \in\left(l_{r}+g, C\right) \end{array}\right. $ | (28) |
当
| $ D_{B r}=l_{r}+h_{\bar{N}}-t_{B}+r-\left[\hat{t}_{B}-\left(l_{r}+g\right)\right] $ | (29) |
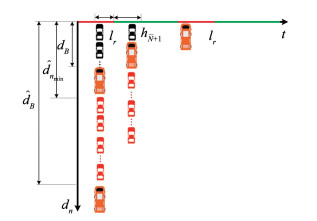
|
图 12
在主信号显示红灯情况下车道信号显示绿灯及 |
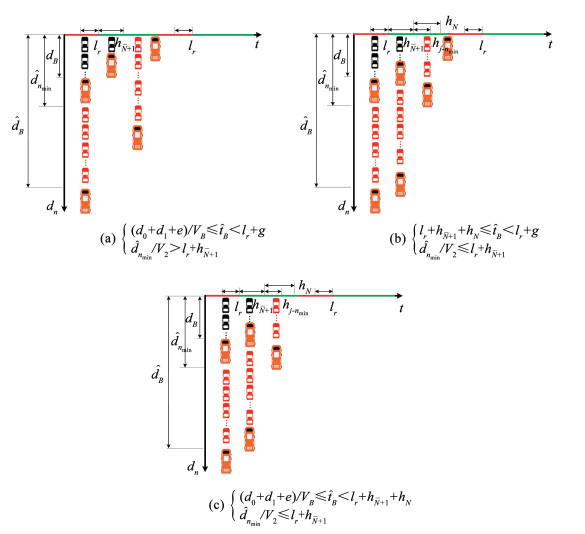
当
| $ D_{B g}=\left\{\begin{array}{l} l_{r}+h_{\bar{N}}-t_{B}, \left(d_{0}+d_{1}+e\right)/V_{B} \leqslant \hat{t}_{B}\left\langle l_{r}+g, \hat{d}_{n_{\min }}/V_{2}\right\rangle l_{r}+h_{\bar{N}+1} \\ l_{r}+h_{\bar{N}}-t_{B}, l_{r}+h_{\bar{N}+1}+h_{N} \leqslant \hat{t}_{B}<l_{r}+g, \hat{d}_{n_{\min }}/V_{2} \leqslant l_{r}+h_{\bar{N}+1} \\ 2 l_{r}+h_{2 \bar{N}+1}+h_{N}-t_{B}-\hat{t}_{B}, \frac{\left(d_{0}+d_{1}+e\right)}{V_{B}} \leqslant \hat{t}_{B}<l_{r}+h_{\bar{N}+1}+h_{N}, \hat{d}_{n_{\min }}/V_{2} \leqslant l_{r}+h_{\bar{N}+1} \end{array}\right. $ | (30) |
|
图 13
在主信号显示红灯情况下车道信号显示绿灯及 |
根据车道信号显示红灯以及绿灯两种情况下求得的受影响车辆延误、公交车延误,可以计算出共享公交专用车道前后交叉口车辆总延误的差值。
离交叉口最近的公交车未驶过车道信号:
1)
| $ Z=\alpha \cdot\left[N \cdot\left(C+l_{r}\right)+\sum\nolimits_{i=n_{\min }}^{n_{\max }}\left(h_{i-n_{\min }}-d_{i}/V_{1}\right)\right] $ | (31) |
2)
| $ Z=\left\{\begin{array}{l} \alpha \cdot p, l_r+h_{\bar{N}}+h_N \leqslant t_B \\ \alpha \cdot p-\beta \cdot\left(l_r+h_{\bar{N}}+h_N-t_B\right), l_r+h_{\bar{N}} \leqslant t_B<l_r+h_{\bar{N}}+h_N \\ \alpha \cdot p-\beta \cdot h_N, \left(d_0+d_1+e\right)/V_B \leqslant t_B<l_r+h_{\bar{N}} \end{array}\right. $ | (32) |
| $ p=N \cdot\left(C-h_{\bar{N}}\right)-\sum\nolimits_{k=n_{\text {min }}}^{n_{\text {max }}}\left(d_{k}/V_{1}-d_{k}/V_{2}\right) $ | (33) |
离交叉口最近的公交车驶过车道信号:
1)
| $ Z=\alpha \cdot\left[N \cdot\left(C+l_{r}\right)+\sum\nolimits_{i=n_{\min }}^{n_{\max }}\left(h_{i-n_{\min }}-\hat{d}_{i}/V_{1}\right)\right] $ | (34) |
2)
| $ Z=\left\{\begin{array}{l} \alpha \cdot \hat{p}, l_r+h_{\bar{N}+1}+h_N \leqslant \hat{t}_B \\ \alpha \cdot \hat{p}-\beta \cdot\left(l_r+h_{\bar{N}+1}+h_N-\hat{t}_B\right), \\ l_r+h_{\bar{N}+1} \leqslant \hat{t}_B<l_r+h_{\bar{N}+1}+h_N \\ \alpha \cdot \hat{p}-\beta \cdot h_N, \left(d_0+d_1+e\right)/V_B \leqslant \hat{t}_B<l_r+h_{\bar{N}+1} \end{array}\right. $ | (35) |
| $ \hat{p}=N \cdot\left(C-h_{\bar{N}+1}\right)-\sum\nolimits_{k=n_{\min }}^{n_{\max }}\left(\hat{d}_k/V_1-\hat{d}_k/V_2\right) $ | (36) |
本部分关于车道信号显示红灯和绿灯两种情况下,受影响车辆延误和公交车延误的分析方法与主信号显示红灯时分析方法一致,共享公交专用车道前后交叉口车辆总延误的差值计算结果如下。
离交叉口最近的公交车未驶过车道信号:
1)
| $ Z=\alpha \cdot\left[N \cdot\left(r+l_{g}\right)+\sum\nolimits_{i=n_{\text {min }}}^{n_{\max }}\left(h_{i-n_{\min }}-d_{i}/V_{1}\right)\right] $ | (37) |
2)
| $ Z=\left\{\begin{array}{l}\alpha \cdot q, h_{\bar{N}}+h_{N} \leqslant t_{B} \\ \alpha \cdot q-\beta \cdot\left(h_{\bar{N}}+h_{N}-t_{B}\right), h_{\bar{N}} \leqslant t_{B}<h_{\bar{N}}+h_{N} \\ \alpha \cdot q-\beta \cdot h_{N}, \left(d_{0}+d_{1}+e\right)/V_{B} \leqslant t_{B}<h_{\bar{N}}\end{array}\right. $ | (38) |
| $ q=N \cdot\left(r+l_{g}-h_{\bar{N}}\right)-\sum\nolimits_{k=n_{\min }}^{n_{\max }}\left(d_{k}/V_{1}-d_{k}/V_{2}\right) $ | (39) |
离交叉口最近的公交车驶过车道信号:
1)
| $ Z=\alpha \cdot\left[N \cdot\left(r+l_{g}\right)+\sum\nolimits_{i=n_{\text {min }}}^{n_{\max }}\left(h_{i-n_{\min }}-\hat{d}_{i}/V_{1}\right)\right] $ | (40) |
2)
| $ Z=\left\{\begin{array}{l}\alpha \cdot \hat{q}, h_{\bar{N}+1}+h_{N} \leqslant \hat{t}_{B} \\ \alpha \cdot \hat{q}-\beta \cdot\left(h_{\bar{N}+1}+h_{N}-\hat{t}_{B}\right), h_{\bar{N}+1} \leqslant \hat{t}_{B}<h_{\bar{N}+1}+h_{N} \\ \alpha \cdot \hat{q}-\beta \cdot h_{N}, \left(d_{0}+d_{1}+e\right)/V_{B} \leqslant \hat{t}_{B}<h_{\bar{N}+1}\end{array}\right. $ | (41) |
| $ \hat{q}=N \cdot\left(r+l_{g}-h_{\bar{N}+1}\right)-\sum\nolimits_{k=n_{\text {min }}}^{n_{\text {max }}}\left(d_{k}/V_{1}-d_{k}/V_{2}\right) $ | (42) |
结合控制模型和交叉口总延误差值表达式可以看出,车道信号显示情况与当前时刻公交车离交叉口的距离、主信号显示情况以及专用道内已有车辆数有关。本文引入示例探究在不同场景下车道信号的显示情况,模型参数设置见表 2。
| 表 2 模型参数设置 Tab. 2 Model instance parameter settings |
本文以主信号周期50 s(绿灯28 s,红灯22 s)为例。图 14展示在公交专用车道内已有车辆数为4辆(图 14(a))、8辆(图 14(b))、12辆(图 14(c))、16辆(图 14(d))的情况下,当前时刻公交车离交叉口不同的距离、交叉口主信号显示情况对车道信号显示的影响。其中,x轴表示交叉口主信号显示时间,用以反映主信号显示情况(0~22 s显示红灯,22~50 s显示绿灯);y轴表示公交车离交叉口的距离。灰色区域表示车道信号显示绿灯的情况,黑色区域表示车道信号显示红灯的情况,区域面积的大小反映了车道信号显示情况的多少。

|
图 14 专用道内车辆数不同的情况下某时刻车道信号的显示情况 Fig. 14 Lane signal display conditions at a certain moment with different number of vehicles in the dedicated lanes |
绿灯剩余时间内能够通过交叉口的车辆数有限,专用道内已有车辆数是影响车道共享的关键因素。如果当前时刻下专用道内车辆数较多,一方面导致受影响车辆数较少,会影响交叉口总体延误;另一方面也增加了公交车接近交叉口时专用道内车辆未能全部驶离交叉口的风险,会干扰公交车正常行驶且增加交叉口延误。整体上,公交专用车道内已有的车辆数越多,黑色区域的面积越大。当专用道内车辆数超过主信号绿灯时间所能允许通过交叉口的车辆数时,车道信号只显示红灯(如图 14(d)所示)。车道信号的控制在有效避免专用道内已有车辆过多的同时,也充分利用专用道减少交叉口总体延误。
公交车离交叉口越远,其到达交叉口的行驶时间越长,共享后车辆有充足的时间驶离交叉口,能够有效减小交叉口车辆延误;在主信号显示红灯的情况下,绿灯剩余时间最大且等于主信号绿灯时间,允许通过交叉口的车辆数也是最大,减少的车辆延误最多。灰色区域主要集中在图像的左上角,符合实际情况。车道信号的控制减少了因公交车距离交叉口较远时专用道的资源浪费,并实现了交叉口当前周期的通过率饱和。
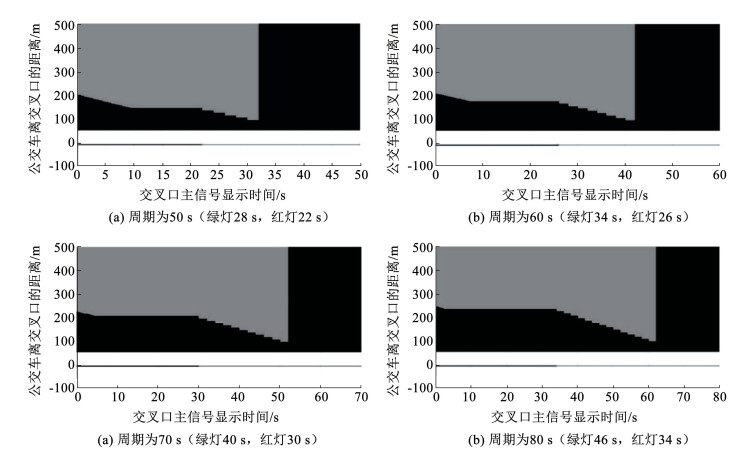
为进一步探究主信号配时对车道信号显示情况的影响,结合前文对主信号周期为50 s(绿灯28 s,红灯22 s)的分析,本部分以公交车道内已有8辆车为例,增加交叉口主信号周期为60 s(绿灯34 s,红灯26 s)、70s(绿灯40 s,红灯30 s)以及80 s(绿灯46 s,红灯34 s)。图 15展示了在不同主信号配时方案下车道信号的显示情况。
|
图 15 不同主信号配时方案情况下的车道信号显示 Fig. 15 Lane signal display conditions under different main signal timing plans |
在不同主信号配时方案下,灰色区域仍然是集中在图像的左上角,这说明车道信号在公交车离交叉口较远、绿灯剩余时间较长时显示绿灯的情况较多,与前文分析结论一致。从整体上看,在主信号显示红灯部分,随着主信号周期的增加,灰色与黑色区域分界线的位置在增加,这也从数据上印证了主信号红灯时间的增加使得在主信号显示红灯部分更难共享专用车道。而在主信号显示绿灯部分,由于公交专用车道内已有车辆数一定,即使主信号配时方案不同,车道信号在绿灯剩余时间小于18 s时也只显示红灯(如图 15所示)。因为此时公交专用车道内已有车辆数已经超过绿灯剩余时间所能通过交叉口的最大车辆数,这从侧面证明了车道信号控制能够充分利用交叉口绿灯时间以减少交叉口延误。
5 结论交叉口拥堵、公交专用车道利用率低是城市交通的重要问题,在考虑未来GPS技术成熟的基础下,本文针对信控交叉口公交专用车道共享问题进行了研究,得出以下结论:
1) 提出一种动态公交专用车道实时共享控制方法。利用GPS定位实时获取交叉口处公交车的位置,并通过交通检测设备获取专用道内小汽车数量,结合主信号显示情况对这些数据进行技术分析,综合判断当前时刻下公交专用道共享前后交叉口整体车辆延误的大小关系,并将判断结果反馈给车道信号。
2) 引入受影响车辆的概念,建立以减少交叉口车辆总延误为目标的车道共享控制模型。针对主信号显示红灯和绿灯两种情况下的交叉口延误进行详细分析,提出一种综合考虑车辆司乘系数、受影响车辆延误、公交车延误以及非受影响车辆延误的交叉口延误计算方法,得出共享公交专用车道前后交叉口车辆总延误差值的表达式。
3) 通过实例数值模拟在不同场景下车道信号的显示情况,可以发现当前时刻下公交专用车道内已有车辆数对专用道共享的影响最大,公交车离交叉口距离以及主信号显示情况对专用道共享的影响相对较小。模拟结果符合客观实际,本文为解决公交专用车道的持续性共享提供了一种新的思路。
为了便于问题分析,本文在示例分析中将交织区域的长度取为一个定值。交织区域是保证车辆变道以及车道共享的关键因素,其长度是需要根据实际情况等综合确定的,这需要今后进一步的研究。
| [1] |
余建平. 论公交专用道系统建设的必要性[J]. 中国公共安全(综合版), 2018(9): 67. YU Jianping. On the necessity of the construction of the bus-only lane system[J]. Chinese Public Security (Comprehensive Edition), 2018(9): 67. |
| [2] |
WU Kan, LU Muyang, GULER S. Modeling and optimizing bus transit priority along an arterial: a moving bottleneck approach[J]. Transportation Research Part C: Emerging Technologies, 2020, 121(5): 102873. |
| [3] |
COLOMBARONI C, FUSCO G, ISAENKO N. A simulation-optimization method for signal synchronization with bus priority and driver speed advisory to connected vehicles[J]. Transportation Research Procedia, 2020, 45: 890. DOI:10.1016/j.trpro.2020.02.079 |
| [4] |
李津, 孙雨彤, 魏小忠, 等. 考虑柔性车道设置的公交优先信号设计[J]. 吉林大学学报(工学版), 2023, 53(2): 448. LI Jin, SUN Yutong, WEI Xiaozhong, et al. Design of bus priority signal considering flexible lane setting[J]. Journal of Jilin University (Engineering Edition), 2023, 53(2): 448. DOI:10.13229/j.cnki.jdxbgxb20210639 |
| [5] |
BEN-DOR G, BEN-ELIA E, BENENSON I. Assessing the impacts of dedicated bus lanes on urban traffic congestion and modal split with an agent-based model[J]. Procedia Computer Science, 2018, 130: 824. DOI:10.1016/j.procs.2018.04.071 |
| [6] |
邵春福, 郭润航, 董春娇, 等. 基于HOV理念的公交专用道交通组织优化[J]. 北京交通大学学报, 2022, 46(1): 61. SHAO Chunfu, GUO Runhang, DONG Chunjiao, et al. Optimization of bus lane traffic organization based on HOV concept[J]. Journal of Beijing Jiaotong University, 2022, 46(1): 61. |
| [7] |
陈伟. 基于车路协同的公交专用道交通管理设施设置[J]. 重庆交通大学学报(社会科学版), 2022, 22(1): 60. CHEN Wei. The setting of traffic management facilities for bus-only lanes based on vehicle-road coordination[J]. Journal of Chongqing Jiaotong University (Social Science Edition), 2022, 22(1): 60. |
| [8] |
VIEGAS J, LU Baichuan. Traffic control system with intermittent bus lanes[J]. IFAC Proceedings Volumes, 1997, 30(8): 865. DOI:10.1016/S1474-6670(17)43930-9 |
| [9] |
VIEGAS J, LU Baichuan. The intermittent bus lane signals setting within an area[J]. Transportation Research Part C: Emerging Technologies, 2004, 12(6): 453. DOI:10.1016/j.trc.2004.07.005 |
| [10] |
ZHU Huibing. Numerical study of urban traffic flow with dedicated bus lane and intermittent bus lane[J]. Physic A: Statistical Mechanics and Its Applications, 2010, 389(16): 3134. DOI:10.1016/j.physa.2010.03.040 |
| [11] |
ZYRYANOV V, MIRONCHUK A. Simulation study of intermittent bus lane and bus signal priority strategy[J]. Procedia Social & Behavioral Sciences, 2012, 48: 1464. |
| [12] |
谢秋峰, 李文权, 贾晓欢, 等. 设置间歇式公交专用进口道的流量条件研究[J]. 交通运输工程与信息学报, 2012, 10(2): 117. XIE Qiufeng, LI Wenquan, JIA Xiaohuan, et al. Research on flow conditions for setting up intermittent bus-only entrances[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 10(2): 117. |
| [13] |
CHIABAUT N, BARCET A. Demonstration and evaluation of an intermittent bus lane strategy[J]. Public Transportation, 2019, 11(3): 443. DOI:10.1007/s12469-019-00210-3 |
| [14] |
EICHLER M, DAGANZO C. Bus lanes with intermittent priority: strategy formulae and an evaluation[J]. Transportation Research Part B: Methodological, 2006, 40(9): 731. DOI:10.1016/j.trb.2005.10.001 |
| [15] |
WU Wei, HEAD L, YAN Sanghuiyu, et al. Development and evaluation of bus lanes with intermittent and dynamic priority in connected vehicle environment[J]. Journal of Intelligent Transportation Systems, 2017, 22(4): 301. |
| [16] |
WU Jianping, HOUNSELL N. Bus priority using pre-signals[J]. Transportation Research Part A: Policy and Practice, 1998, 32(8): 563. DOI:10.1016/S0965-8564(98)00008-1 |
| [17] |
GULER S, MENENDEZ M. Analytical formulation and empirical evaluation of pre-signals for bus priority[J]. Transp Res Part B: Methodol, 2014, 64: 41. DOI:10.1016/j.trb.2014.03.004 |
| [18] |
HE Haitao, GULER S, MENENDEZ M. Adaptive control algorithm to provide bus priority with a pre-signal[J]. Transportation Research Part C: Emerging Technologies, 2016, 64(3): 28. |
 2024, Vol. 56
2024, Vol. 56


