2. 高速铁路建造技术国家工程实验室(中南大学), 长沙 410075
2. National Engineering Laboratory for Construction Technology of High Speed Railway (Central South University), Changsha 410075, China
地下水按含水介质特征分为孔隙水、岩溶水及裂隙水,长期以来学者对前两者进行了广泛的研究,建立的稳定流与非稳定流理论在生产实践中起到了积极的作用。而裂隙水,由于赋存条件及运动的复杂性,在研究方法及水文地质计算方面与工程建设的需求尚存较大距离[1]。
受地质运动的长期作用,岩体内部涌现了大量裂隙[2],控制着岩体力学特性及岩体中流体的渗流,严重影响结构的安全性[3]。光滑裂隙的渗水能力与裂隙宽度的立方成正比[4],而天然裂隙壁面的粗糙程度制约着渗流的非线性特性[5],定量解析和描述裂隙粗糙程度对裂隙渗水特性的影响具有重要意义[6]。文献[6-7]基于单裂隙渗流特性,探讨了裂隙粗糙度及非线性渗流对立方定律的影响机制。文献[9-10]揭示了含组合裂隙时不同流动形态下临界雷诺数、等效水力梯度及非达西参数的演化规律。文献[11]基于围岩孔隙与裂隙结构的二相渗流模型,构建了围岩孔隙及裂隙结构跨尺度的渗流简化计算模型,为孔隙与裂隙结构的耦合计算奠定了理论基础。文献[12]借助三维离散元软件建立了裂隙岩体隧道渗流分析数值模型,揭示了富水裂隙区隧道施工过程中渗流场的演化规律。在隧道涌水灾害处治方面,文献[13-14]基于室内试验分析了浆液流动性的影响因素;文献[15-17]揭示了注浆机理,探讨了动水压力下注浆的可行性及有效性。
针对裂隙控制的隧道涌水问题,学者多借助模型试验及数值模拟手段揭示了单一及组合裂隙下隧道涌水规律及对裂隙涌水灾害的治理进行了分析,而对富水裂隙下涌水预测模型的构建及涌水量计算式的求解鲜有涉及[2]。基于此,视富水裂隙区围岩及注浆区为非均质各向异性介质,初期支护及二次支护结构为均质各向同性结构,构建裂隙围岩下隧道涌水简化计算模型,基于地下水力学理论及流体质量守恒定律推导涌水量计算表达式,通过退化分析及现场试验实测数据检验构建模型的合理性及公式推导的正确性,基于解析解揭示各特征参数对隧道涌水的影响规律,探讨富水裂隙区隧道涌水机制特征。
1 模型建立及基本假定岩体由岩石及结构面组成,岩石的渗透性一般极弱,忽略非裂隙区渗透性,岩体的渗透性仅取决于裂隙的发育程度[18]。考虑实际工况及方便问题解答,深埋富水裂隙区隧道涌水问题作如下假定[19]:1)初期支护及二次支护结构均质且各向同性,围岩与注浆圈非均质且各向异性;2)流体不可压缩;3)隧道为大埋深且渗流处于稳定状态;4)注浆区及支护结构内渗流满足达西定律。
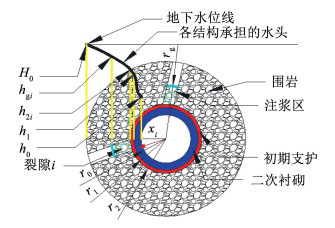
仅考虑围岩内裂隙渗透性时构建富水裂隙围岩下隧道涌水的简化计算模型,如图 1所示。图中二次支护结构内缘、二次支护结构外缘、初期支护外缘及注浆区外缘半径分别为r0、r1、r2及rg,二次支护结构及初期支护渗透系数分别为ke及kc,二次支护结构内缘与外缘承担水头分别为h0及h1,裂隙i内缘及外缘水头分别为h2i及hgi,涌水影响半径处水头为H0。
|
图 1 涌水简化计算模型 Fig. 1 Simplified calculation model of water inflow |
分别计算二次支护结构、初期支护、注浆区及围岩区域渗流场,据流体质量守恒定律,推导渗流稳定时隧道涌水量计算表达式。
2.1 裂隙围岩区假定裂隙围岩及注浆区内渗流为一维流且满足立方定律,计算式[20]为
| $ q_{i}=\frac{\gamma b_{i}^{3}}{12 \mu} \frac{\partial H_{i}}{\partial x_{i}} $ | (1) |
式中:i为裂隙总数为N的裂隙样本中按大小排序为i的序号,qi为裂隙i的单宽流量,γ为流体重度,μ为动力黏滞系数,bi为裂隙i的宽度,Hi为裂隙i内的水头。
对裂隙i有边界条件:
| $ \left\{\begin{array}{l} \left.H_{i}\right|_{x=r_{\mathrm{g}}}=h_{\mathrm{g} i} \\ \left.H_{i}\right|_{x=R}=H_{0} \end{array}\right. $ | (2) |
式中R为渗流影响半径。
联立式(1)、(2),解得裂隙i的流量计算式为
| $ q_{i}=\frac{\gamma b_{i}^{3}}{12 \mu} \frac{H_{0}-h_{\mathrm{g} i}}{R-r_{\mathrm{g}}} $ | (3) |
由式(3)可知
| $ h_{\mathrm{g} i}=H_{0}-12 \mu q_{i} \frac{R-r_{\mathrm{g}}}{\gamma b_{i}^{3}} $ | (4) |
据假定,注浆区水流速度与水力梯度满足达西定律,表达式为
| $ v=k_{\mathrm{g}} J $ | (5) |
式中:v为渗流速度,kg为注浆区渗透系数,J为水力梯度。
注浆区渗流表达式为
| $ q_{i}=A_{i} v_{i}=b_{i} k_{\mathrm{g}} \frac{\partial H_{i}}{\partial x_{i}} $ | (6) |
对注浆区i有边界条件:
| $ \left\{\begin{array}{l} \left.H_{i}\right|_{x=r_{g}}=h_{g i} \\ \left.H_{i}\right|_{x=r_{2}}=h_{2 i} \end{array}\right. $ | (7) |
联立式(6)、(7),解得注浆区i的流量计算公式为
| $ q_{i}=k_{\mathrm{g}} b_{i} \frac{h_{\mathrm{g} i}-h_{2 i}}{r_{\mathrm{g}}-r_{2}} $ | (8) |
由式(8)可得
| $ h_{2 i}=h_{g i}-q_{i} \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}} b_{i}} $ | (9) |
将式(4)代入式(9)可得
| $ h_{2 i}=H_{0}-12 \mu q_{i} \frac{R-r_{\mathrm{g}}}{\gamma b_{i}^{3}}-q_{i} \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}} b_{i}} $ | (10) |
隧道施作支护结构后周边渗水透过围岩、注浆圈及初期支护,经环向排水盲管、纵向排水管及横向排水管流入隧道中心排水沟或侧向排水沟,再依靠纵坡排出隧道。理论分析时常忽略复杂的排水系统,假定等效渗透系数后视支护结构为各向同性均匀介质[21]。据渗流力学原理,无限平面内单孔隧道稳定径向渗流连续性方程的极坐标表达式[22]为
| $ \frac{1}{\rho} \frac{\partial}{\partial \rho}\left(\rho \frac{\partial \psi}{\partial \rho}\right)=0 $ | (11) |
式中:ρ为计算点至隧道中心的距离,ψ为无限平面内计算点的渗流场水头势函数。
渗流稳定时,据地下水力学理论[23]:
| $ h_{R 1}-h_{R 2}=\frac{Q}{2 {\rm{\mathsf{π}}} k} \ln \frac{R_{1}}{R_{2}} $ | (12) |
式中:k为介质渗透系数,R2、R1为距隧道中心的距离,hR2、hR1为计算点位置处的水头高度,Q为渗流稳定时的涌水量。
将式(12)依次应用于二次支护结构及初期支护,可得
| $ h_{1}-h_{0}=\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}} $ | (13) |
| $ h_{2}-h_{1}=\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}} $ | (14) |
联立式(13)、(14),解得
| $ h_{2}=h_{0}+\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}} $ | (15) |
假定围岩裂隙样本数为N,由式(10)计算初期支护外缘水头的平均值为
| $ \begin{gather*} \overline{h_{2}}=\frac{\sum\limits_{i=1}^{N}\left(h_{2 i} b_{i}\right)}{2 {\rm{\mathsf{π}}} r_{2}}= \\ \frac{\sum\limits_{i=1}^{N}\left[\left(H_{0}-12 \mu q_{i} \frac{R-r_{\mathrm{g}}}{\gamma b_{i}^{3}}-q_{i} \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}} b_{i}}\right) b_{i}\right]}{2 {\rm{\mathsf{π}}} r_{2}} \end{gather*} $ | (16) |
联立式(15)、(16),解得
| $ \begin{gather*} h_{0}+\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+\frac{Q}{2 {\rm{\mathsf{π}}} k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}= \\ \frac{\sum\limits_{i=1}^{N}\left[\left(H_{0}-12 \mu q_{i} \frac{R-r_{\mathrm{g}}}{\gamma b_{i}^{3}}-q_{i} \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}} b_{i}}\right) b_{i}\right]}{2 {\rm{\mathsf{π}}} r_{2}} \end{gather*} $ | (17) |
据流体质量守恒定律[24]可知
| $ Q=\sum\limits_{i=1}^{N} q_{i} $ | (18) |
将式(18)代入式(17),并化简得
| $ \begin{gather*} 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+Q \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}}}= \\ H_{0} \sum\limits_{i=1}^{N} b_{i}-12 \mu \frac{R-r_{\mathrm{g}}}{\gamma} \sum\limits_{i=1}^{N}\left(\frac{q_{i}}{b_{i}{ }^{2}}\right) \end{gather*} $ | (19) |
由文献[25]可知地下工程裂隙宽度近似服从帕累托分布,表达式为
| $ b_{i}=\frac{b_{\max }}{i^{\frac{\beta}{3}}} $ | (20) |
式中:bmax为裂隙样本中宽度最大的裂隙宽度,参数β由最小二乘法拟合获取。
由渗流立方定律得
| $ q_{i}=\frac{q_{\max }}{i^{\beta}} $ | (21) |
式中qmax为宽度最大裂隙的涌水量。
将式(20)、(21)代入式(19)并化简得
| $ \begin{align*} & 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+Q \frac{r_{g}-r_{2}}{k_{\mathrm{g}}}= \\ & H_{0} b_{\max } \sum\limits_{i=1}^{N} \frac{1}{i^{\frac{\beta}{3}}}-12 \mu \frac{R-r_{\mathrm{g}}}{\gamma} \frac{q_{\max }}{b_{\text {max }}^{2}} \sum\limits_{i=1}^{N}\left(i^{-\frac{\beta}{3}}\right) \end{align*} $ | (22) |
将式(21)代入式(18),解得
| $ q_{\max }=\frac{Q}{\sum\limits_{i=1}^{N} \frac{1}{i^{\beta}}} $ | (23) |
将式(23)代入式(22),解得涌水量与裂隙分布参数的耦合关系式为
| $ \begin{align*} & 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+Q \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}}}= \\ & H_{0} b_{\max } \sum\limits_{i=1}^{N} \frac{1}{i^{\frac{\beta}{3}}}-12 \mu \frac{R-r_{\mathrm{g}}}{\gamma b_{\text {max }}^{2}} \frac{Q}{\sum\limits_{i=1}^{N} \frac{1}{i^{\beta}}} \sum\limits_{i=1}^{N}\left(i^{-\frac{\beta}{3}}\right) \end{align*} $ | (24) |
考虑到本文主要研究内容为富水裂隙围岩下隧道涌水问题,为验证本文构建的富水裂隙围岩区隧道涌水简化计算模型的合理性及涌水量计算式推导的正确性。假定围岩裂隙无限多且宽度均为b,此时富水裂隙围岩可视为均质围岩,且β=1,N=
| $ \begin{gather*} 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+Q \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}}}= \\ 2 {\rm{\mathsf{π}}} r_{2} H_{0}-12 Q \mu \frac{R-r_{\mathrm{g}}}{\gamma b^{2}} \end{gather*} $ | (25) |
由式(1)可知,富水裂隙围岩区等效渗透系数表达式为
| $ \mu=\frac{\gamma b^{2}}{12 k_{\mathrm{r}}} $ | (26) |
式中kr为富水裂隙围岩区等效渗透系数。
将式(26)代入式(25),并化简得
| $ \begin{gather*} 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+Q \frac{r_{\mathrm{g}}-r_{2}}{k_{\mathrm{g}}}= \\ 2 {\rm{\mathsf{π}}} r_{2} H_{0}-Q \frac{R-r_{\mathrm{g}}}{k_{r}} \end{gather*} $ | (27) |
利用泰勒公式,并忽略高阶无穷小
| $ \ln (x+1) \approx x $ | (28) |
将式(28)代入式(27),解得
| $ \begin{gather*} 2 {\rm{\mathsf{π}}} r_{2} h_{0}+r_{2} \frac{Q}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+r_{2} \frac{Q}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+r_{2} \frac{Q}{k_{\mathrm{g}}} \ln \frac{r_{\mathrm{g}}}{r_{2}}= \\ 2 {\rm{\mathsf{π}}} r_{2} H_{0}-r_{2} \frac{Q}{k_{r}} \ln \frac{R-r_{\mathrm{g}}+r_{2}}{r_{2}} \end{gather*} $ | (29) |
式(29)化简后可得
| $ Q=\frac{2 {\rm{\mathsf{π}}}\left(H_{0}-h_{0}\right) k_{r}}{\frac{k_{r}}{k_{\mathrm{e}}} \ln \frac{r_{1}}{r_{0}}+\frac{k_{r}}{k_{\mathrm{c}}} \ln \frac{r_{2}}{r_{1}}+\frac{k_{r}}{k_{\mathrm{g}}} \ln \frac{r_{\mathrm{g}}}{r_{2}}+\ln \frac{R-r_{\mathrm{g}}+r_{2}}{r_{2}}} $ | (30) |
深埋隧道中,式(30)为均质围岩下隧道运营期涌水量计算式[26]。忽略注浆区,且不考虑支护作用,有
| $ Q=\frac{2 {\rm{\mathsf{π}}} H_{0} k_{r}}{\ln \frac{R}{r_{2}}} $ | (31) |
式(31)为古德曼方程计算裸洞涌水量的解析公式[27]。忽略裂隙围岩的非均质性,本文的计算式可退化到均质围岩下隧道涌水量计算式;不考虑注浆区及支护结构,本文所推导的富水裂隙区隧道涌水量解析式可退化到视围岩为均质且各向同性的半无限平面内隧道开挖后的最大涌水量计算表达式,初步验证了本文视富水裂隙围岩为非均质且各向异性时构建的隧道涌水简化计算模型的合理性及隧道涌水量计算式求解的正确性。
3.2 工程算例依托鸿图隧道在建工程进行现场试验,实时监测涌水量以进一步验证本文构建的富水裂隙区隧道涌水简化计算模型的合理性及公式推导的正确性。
3.2.1 工程简介鸿图隧道位于广东省,长6 336 m,地面标高345~1 060 m,隧道底部设计标高239~344 m,最大埋深约739 m,为深埋特长山岭隧道。隧址区有多条断层及裂隙存在,同时隧道紧邻飞泉电站、飞泉水库、三渡水库及下穿黄棉湖水库,部分断层与大型水体相连,施工期突涌水风险极高。
选取施工期掌子面开挖揭示的裂隙发育段,在相应里程桩号支护结构内埋设智能弦式数码渗压计,保护后由二次支护结构引出。渗压计量程为1.0 MPa,灵敏度为0.001 MPa,现场埋设与测量如图 2所示。

|
图 2 传感器埋设与测量 Fig. 2 Sensor embedding and measurement |
注浆区渗透系数为3.5×10-5 m/s,与初期支护及二次支护结构渗透系数比值分别为15及20,其中二次支护结构渗透系数综合考虑了环向与纵向排水管作用[28],其余所需数据见表 1。
| 表 1 实验数据 Tab. 1 Experimental data |
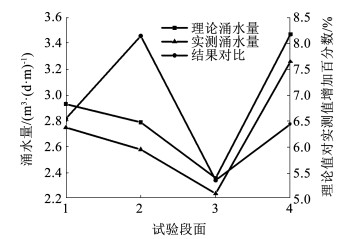
由式(24)计算理论涌水量,并与现场实测值进行对比,绘制曲线如图 3所示。
|
图 3 结果对比 Fig. 3 Results comparison |
4个测试断面中,涌水量理论值与实测值分别相差6.5%、8.1%、5.4%及6.4%,差异较小,在可接受范围内,验证了本文构建的富水裂隙区隧道涌水简化计算模型的合理性及公式推导的正确性,预测误差主要有裂隙分布的复杂性及渗透系数的离散性。
4 特征参数敏感性分析鉴于所推导的隧道涌水量计算表达式(24)影响参数众多,直接分析较为复杂。现基于解析解揭示各特征参数对隧道涌水的影响规律,探讨富水裂隙区隧道涌水机制特征。
假定r0、r1、r2分别为6、6.5、6.8 m;地下水水位线距隧道中心距离为200 m;二次支护结构内缘水头为0 m;流体动力黏滞系数及重度分别为1.01×10-3 Pa · s及9.8×103 N · m-3;影响半径取地下水位高度的2倍。
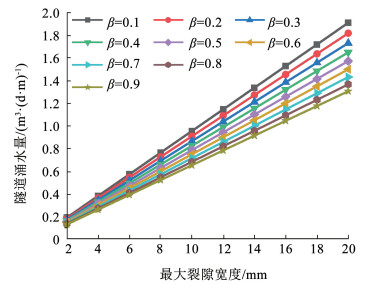
4.1 裂隙分布参数β分析据现场多个断层区实测值及经验假定注浆区渗透系数为1.25×10-5 m/s;注浆区与初期支护结构及二次支护结构渗透系数比值为15与20;注浆区厚度为6 m; 裂隙数目N取10。由式(24)计算涌水量与裂隙的关系,绘制曲线如图 4所示。
|
图 4 隧道涌水量与裂隙的关系 Fig. 4 Relationship between tunnel spring water and crack |
图 4表明隧道涌水量随裂隙最大宽度的增加而增大,两者近似呈线性关系,这与裸洞时裂隙围岩下隧道涌水与裂隙宽度的立方成正比的关系有差异。究其原因,本文考虑了注浆与隧道支护结构,堵水结构联合作用减弱了围岩裂隙对涌水的影响。
同时隧道涌水量随裂隙分布参数β的增大而减小。究其原因,由式(20)可知,随β的增加,各裂隙宽度不断减小,进而导致隧道涌水降低。富水裂隙区隧道施工时,应通过注浆将最大裂隙宽度控制在合理范围内,避免隧址区地下水环境的破坏。
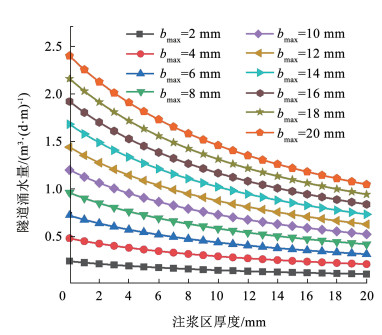
4.2 注浆区厚度确定注浆区渗透系数取1.25×10-5 m/s;注浆区与初期支护结构及二次支护结构渗透系数比值为15与20;裂隙数目N取10;裂隙分布参数β取0.3。由式(24)计算涌水量与注浆区厚度的关系,绘制曲线如图 5所示。
|
图 5 隧道涌水量与注浆圈厚度的关系 Fig. 5 Relationship between tunnel water volume and grout thickness |
图 5显示隧道涌水量随注浆区厚度的增加而不断降低,但敏感性逐渐减弱,帷幕注浆设计时应对注浆圈厚度进行优化。但注浆圈厚度影响分界点约为隧道半径的2倍,大于视围岩为均质且各向同性时计算的注浆圈厚度[28]。
4.3 注浆区渗透系数分析注浆区厚度取6 m;二次支护结构渗透系数为6.25×10-7 m/s;初期支护渗透系数为8.33×10-7 m/s;注浆区与二次支护结构渗透系数比值为λ;裂隙数目N取10;裂隙分布参数β取0.3。由式(24)计算涌水量与注浆区渗透系数的关系,绘制曲线如图 6所示。

|
图 6 隧道涌水量与注浆圈渗透系数的关系 Fig. 6 Relationship between tunnel water content and penetration coefficient of grouting |
图 6显示隧道涌水量随注浆圈渗透系数的下降而非线性降低。参数λ < 40时,注浆圈渗透系数对涌水量敏感性显著;参数λ>40时,继续降低注浆圈渗透系数对隧道涌水量影响较弱。
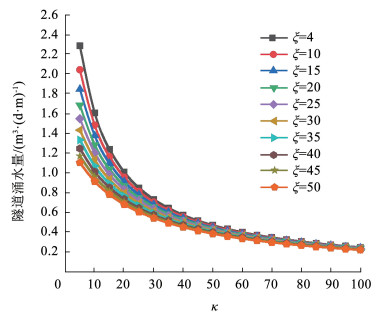
4.4 支护结构渗透系数分析注浆区厚度取6 m,渗透系数取1.25×10-5 m/s;注浆区与初期支护渗透系数比值为ξ;注浆区与二次支护结构渗透系数比值为κ;裂隙数目N取10;最大裂隙宽度为16 mm;裂隙分布参数β=0.3。由式(24)计算涌水量与支护结构渗透系数的关系,绘制曲线如图 7所示。
|
图 7 隧道涌水量与支护结构渗透系数的关系 Fig. 7 Relationship between tunnel water content and support structure penetration coefficient |
图 7表明,隧道排水量随初期支护及二次支护结构渗透系数的降低而非线性下降,其中参数ξ与κ宜分别取20与40。同时,初期支护背后的环向盲管等隧道排水系统极为重要,环向盲管一旦堵塞,由排水体系流出的水量急剧下降,防水板及二次衬砌承受的水头将增大。须定期对环向盲管进行检查,以防堵塞进而压裂防水板甚至二次衬砌,对隧道结构造成破坏。
5 结论基于地下水力学理论及流体质量守恒定律推导了涌水量计算式,揭示了各特征参数对富水裂隙区隧道涌水的影响规律。得出以下具体结论:
1) 构建了富水裂隙围岩下隧道涌水简化计算模型,推导了隧道涌水量计算式,通过退化分析及现场试验验证了富水裂隙围岩下隧道涌水简化计算模型构建的合理性及涌水量计算式推导的正确性。
2) 隧道涌水量随裂隙最大宽度的增加而增大,受堵水结构的联合制约,两者近似满足线性分布,富水裂隙区隧道施工时,应通过注浆控制最大裂隙宽度,避免隧址区地下水环境的破坏。
3) 注浆区厚度与隧道半径比值在2倍以内时,隧道涌水量受注浆区厚度的影响显著,该值大于视围岩为均质且各向同性时计算的注浆圈厚度,表明富水裂隙区隧道施工时可适当增加注浆圈厚度。
| [1] |
冯增朝, 赵阳升, 吕兆兴. 二维孔隙裂隙双重介质逾渗规律研究[J]. 物理学报, 2007, 56(5): 2796. FENG Zengchao, ZHAO Yangsheng, LÜ ZhaoXing. Study on percolation law of 2D porous and fractured double-medium[J]. Acta Physica Sinica, 2007, 56(5): 2796. |
| [2] |
张英, 李鹏, 郭奇峰, 等. 水力耦合裂隙岩体变形破坏机制研究进展[J]. 哈尔滨工业大学学报, 2020, 52(6): 21. ZHANG Ying, LI Peng, GUO Qifeng, et al. Research progress of deformation and failure mechanism in fractured rock mass under hydromechanical coupling[J]. Journal of Harbin Institute of Technology, 2020, 52(6): 21. DOI:10.11918/202003073 |
| [3] |
崔溦, 王利新, 江志安, 等. 基于修正立方定律的岩体粗糙裂隙网络注浆过程模拟研究[J]. 岩土力学, 2021, 42(8): 2250. CUI Wei, WANG Lixin, JIANG Zhian, et al. Numerical simulation of grouting process in rock mass rough fracture network based on corrected cubic law[J]. Rock and Soil Mechanics, 2021, 42(8): 2250. DOI:10.16285/j.rsm.2021.0007 |
| [4] |
陈益峰, 周创兵, 盛永清. 考虑峰后力学特性的岩石节理渗流广义立方定理[J]. 岩土力学, 2008(7): 1825. CHEN Yifeng, ZHOU Chuangbing, SHENG Yongqing. A generalized cubic law for seepage flow through rock joints considering post-peak mechanical response[J]. Rock and Soil Mechanics, 2008(7): 1825. DOI:10.16285/j.rsm.2008.07.031 |
| [5] |
ZHANG Y, CHAI J. Effect of surface morphology on fluid flow in rough fractures: a review[J]. Journal of Natural Gas Science and Engineering, 2020, 79: 103343. DOI:10.1016/j.jngse.2020.103343 |
| [6] |
潘东东, 李术才, 许振浩, 等. 考虑剪切接触与碎屑充填的裂隙渗流模型与数值分析[J]. 中南大学学报(自然科学版), 2019, 50(7): 1677. PAN Dongdong, LI Shucai, XU Zhenhao, et al. Seepage calculation model and numerical analysis of rock fracture considering effect of contact area and clastic rock[J]. Journal of Central South University (Science and Technology), 2019, 50(7): 1677. DOI:10.11817/j.issn.1672-7207.2019.07.022 |
| [7] |
甘磊, 马洪影, 沈振中. 下凹形态裂隙面粗糙程度表征及立方定律修正系数拟合[J]. 水利学报, 2021, 52(4): 420. GAN Lei, MA Hongying, SHEN Zhenzhong. Roughness characterization of concave fracture surface and coefficient fitting of modified cubic law[J]. Journal of Hydraulic Engineering, 2021, 52(4): 420. DOI:10.13243/j.cnki.slxb.20200692 |
| [8] |
牛玉龙, 王媛, 于可, 等. 裂隙网络非达西渗流REV及非达西系数张量研究[J]. 水利学报, 2020, 51(4): 468. NIU Yulong, WANG Yuan, YU Ke, et al. Non-Darcy seepage REV and non-Darcy coefficient tensor in fracture network[J]. Journal of Hydraulic Engineering, 2020, 51(4): 468. DOI:10.13243/j.cnki.slxb.20190646 |
| [9] |
刘日成, 蒋宇静, 李博, 等. 岩体裂隙网络非线性渗流特性研究[J]. 岩土力学, 2016, 37(10): 2817. LIU Richeng, JIANG Yujing, LI Bo, et al. Nonlinear seepage behaviors of fluid in fracture networks[J]. Rock and Soil Mechanics, 2016, 37(10): 2817. DOI:10.16285/j.rsm.2016.11.016 |
| [10] |
刘日成, 蒋宇静, 李树忱, 等. 交叉裂隙水力学开度的计算及非线性水力特性研究[J]. 岩土力学, 2015, 36(6): 1581. LIU Richeng, JIANG Yujing, LI Shuchen, et al. Study of nonlinear hydraulic characteristics and hydraulic aperture calculation of crossed fracture[J]. Rock and Soil Mechanics, 2015, 36(6): 1581. DOI:10.16285/j.rsm.2015.06.008 |
| [11] |
王刚, 王世斌, 李怀兴, 等. 考虑煤体孔-裂隙介尺度特征的水相渗流演化模型研究[J]. 岩石力学与工程学报, 2021, 44(8): 1547. WANG Gang, WANG Shibin, LI Huaixing, et al. Study on water phase seepage evolution model considering mesoscale characteristics of pore and fissure in coal[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 44(8): 1547. DOI:10.13722/j.cnki.jrme.2021.0050 |
| [12] |
高新强, 艾旭峰, 孔超. 高水压富水区裂隙岩体隧道渗流场的特征[J]. 中国铁道科学, 2016, 37(6): 42. GAO Xinqiang, AI Xufeng, KONG Chao. Characteristics of seepage field of fractured rock mass tunnel in high water pressure and rich water zone[J]. China Railway Science, 2016, 37(6): 42. DOI:10.3969/j.issn.1001-4632.2016.06.06 |
| [13] |
张庆松, 张连震, 刘人太, 等. 水泥-水玻璃浆液裂隙注浆扩散的室内试验研究[J]. 岩土力学, 2015, 36(8): 2159. ZHANG Qingsong, ZHANG Lianzhen, LIU Rentai, et al. Laboratory experimental study of cement-silicate slurry diffusion law of crack grouting with dynamic water[J]. Rock and Soil Mechanics, 2015, 36(8): 2159. DOI:10.16285/j.rsm.2015.08.005 |
| [14] |
俞文生, 李鹏, 张霄, 等. 可变倾角单裂隙动水注浆模型试验研究[J]. 岩土力学, 2014, 35(8): 2137. YU Wensheng, LI Peng, ZHANG Xiao, et al. Model test research on hydrodynamic grouting for single fracture with variable inclinations[J]. Rock and Soil Mechanics, 2014, 35(8): 2137. DOI:10.16285/j.rsm.2014.08.033 |
| [15] |
刘人太, 郑卓, 李术才, 等. 地下工程裂隙型涌水超前注浆治理方法[J]. 西南交通大学学报, 2019, 54(1): 48. LIU Rentai, ZHENG Zhuo, LI Shucai, et al. Pre-excavation grouting to prevent water inflow of jointed rock in underground construction[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 48. DOI:10.3969/j.issn.0258-2724.20170551 |
| [16] |
李术才, 郑卓, 刘人太, 等. 考虑浆-岩耦合效应的微裂隙注浆扩散机制分析[J]. 岩石力学与工程学报, 2017, 36(4): 812. LI Shucai, ZHENG Zhuo, LIU Rentai, et al. Analysis on fracture grouting mechanism considering grout-rock coupling effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 812. DOI:10.13722/j.cnki.jrme.2016.0765 |
| [17] |
李海燕, 胥洪彬, 李召峰, 等. 深部巷道断层涌水治理研究[J]. 采矿与安全工程学报, 2018, 35(3): 635. LI Haiyan, XU Hongbin, LI Zhaofeng. Study on treatment of fault water gushing in deep roadway[J]. Journal of Mining and Safety Engineering, 2018, 35(3): 635. DOI:10.13545/j.cnki.jmse.2018.03.026 |
| [18] |
何忱, 姚池, 邵玉龙, 等. 低裂隙密度条件下三维裂隙岩体的有效渗透性[J]. 清华大学学报(自然科学版), 2021, 61(8): 827. HE Chen, YAO Chi, SHAO Yulong, et al. Effective permeability of three-dimensional fractured rock with low fracture densities[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(8): 827. DOI:10.16511/j.cnki.qhdxxb.2021.25.014 |
| [19] |
张雨, 张顶立, 徐曈, 等. 水下隧道开挖面三维渗流场解析及涌水量预测分析[J]. 西南交通大学学报, 2021, 56(6): 1260. ZHANG Yu, ZHANG Dingli, XU Tong, et al. Analysis of three-dimensional seepage field and prediction of water inflow in underwater tunnel[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1260. DOI:10.3969/j.issn.0258-2724.20200397 |
| [20] |
EKER E, AKIN S. Lattice Boltzmann simulation of fluid flow in synthetic fractures[J]. Transport in Porous Media, 2006, 65(3): 363. DOI:10.1007/s11242-005-6085-4 |
| [21] |
蒋雅君, 李彬, 杨其新, 等. 隧道排水系统工作能力对衬砌水压力的影响探讨[J]. 铁道学报, 2020, 42(12): 179. JIANG Yajun, LI Bin, YANG Qixi, et al. Discussion on influence of working capacity of drainage system on water pressure acting on tunnel lining[J]. Journal of The China Rail Way Society, 2020, 42(12): 179. DOI:10.3969/j.issn.1001-8360.2020.12.023 |
| [22] |
李树忱, 李术才, 张京伟. 势问题的数值流形方法[J]. 岩土工程学报, 2006, 28(12): 2092. LI Shuchen, LI Shucai, ZHANG Jingwei. Numerical manifold method for the potential problem[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2092. |
| [23] |
雅· 贝尔. 地下水水力学[M]. 李竟生, 陈崇希, 译. 北京: 地质出版社, 1985 BEAR J. Ground water mechanic[M]. LI Jingsheng, CHEN chongxi, trans. Beijing: Geologic Publishing Company, 1985 |
| [24] |
朱红光, 谢和平, 易成, 等. 破断岩体裂隙的流体流动特性分析[J]. 岩石力学与工程学报, 2013, 32(4): 657. ZHU Hongguang, XIE Heping, YI Cheng, et al. Analysis of properties of fluid flow in rock fractures[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 657. |
| [25] |
GUSTAFSON G, FRANSSON A. The use of the Pareto distribution for fracture transmissivity assessment[J]. Hydrogeology Journal, 2006, 14(1/2): 15. DOI:10.1007/s10040-005-0440-y |
| [26] |
黄震, 朱术云, 赵奎, 等. 工程活动诱发的围岩结构变化对隧道突涌水的影响分析[J]. 岩土工程学报, 2018, 40(3): 449. HUANG Zhen, ZHU Shuyun, ZHAO Kui, et al. Influences of structural variation of host rock induced by engineering activities on water inrush of tunnels[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 449. DOI:10.11779/CJGE201803008 |
| [27] |
JOO E J, SHIN J H. Relationship between water pressure and inflow rate in underwater tunnels and buried pipes[J]. Geotechnique, 2013, 64(3): 226. DOI:10.1680/geot.12.P.185 |
| [28] |
潘以恒, 罗其奇, 周斌, 等. 半无限平面含注浆圈深埋隧道渗流场解析研究[J]. 浙江大学学报(工学版), 2018, 52(6): 1114. PAN Yiheng, LUO Qiqi, ZHOU Bin, et al. Analytical study on seepage field of deep tunnel with grouting circle in half plane[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(6): 1114. DOI:10.3785/j.issn.1008-973X.2018.06.010 |
 2024, Vol. 56
2024, Vol. 56


