2. 中国电建中南勘测设计研究院有限公司,长沙 410007;
3. 吉林大学 交通学院,长春 130000
2. POWERCHINA Zhongnan Engineering Corporation Limited, Changsha 410007, China;
3. Transportation College, Jilin University, Changchun 130000, China
为应对出行需求增长,缓解城市交通拥堵问题,国内大中城市常采取改扩建道路、新建地铁及快速路等举措来缓解区域交通压力。但这些占道施工所在路段往往成为区域交通运行的瓶颈,在施工期内严重干扰到区域交通运行,引发区域路网承载力下降。
城市道路网络容量是评价区域道路网络交通运行水平的重要指标,学者们就不同运行条件下的路网容量计算进行了相关研究。文献[1]探究了道路网络容量的主要影响因素,包括:路段通行能力、出行需求结构、服务水平要求、出行路径选择行为;文献[2]分析了出行者信息系统(ATIS)不同信息质量和市场渗透率对道路网络容量的影响;文献[3]构建了无人驾驶环境下考虑OD结构的路网容量模型;文献[4]基于路段服务水平约束开展了路网容量可靠性分析。文献[5]构建了考虑特定OD分布形态的路网容量双层规划模型,其在上层模型中引入了拥挤度约束来体现服务水平,并考虑了OD需求结构与路网的匹配程度。文献[6]考虑停车收费及供给政策,对城市路网容量进行评估,给出了需求不定下的路网容量模型,还有从信号配时[7]、新增路段[8]和关键扩容[9]等方面给路网容量带来的影响,这些研究集中在整体管控措施。而对于占道施工行为的影响,文献[10]将施工路段通行能力计算与Transcad模拟分配结合,给出了占道施工情况下,城市区域道路网络容量的计算模型。文献[11]通过高斯烟雨模型确定施工影响范围,结合时空消耗方式给出了施工情形下区域道路网络容量的计算模型。
综上,现阶段对于道路网容量的影响研究,较少从占道施工角度去研究对道路网络容量的影响。考虑占道施工对路网的影响主要体现在两方面,即路网容量降低和路网结构特征改变,本文从施工路段通行能力计算入手,开展占道施工影响下区域路网容量计算方法研究;同时,结合路网结构特征变化和路段饱和度分析,开展占道施工期关键路段识别方法研究,为有针对性地实施交通组织措施以提升路网容量提供依据。论文在理论研究方面可丰富道路网络容量计算理论与方法,在实际应用方面可为施工期交通管控方案的制定提供决策参考。
1 占道施工期路网容量计算 1.1 路网容量计算模型对于道路网络容量的定义,因研究方法与约束条件的不同而不同,例如由时空消耗法求解得到的网络容量不会考虑到出行行为和需求结构的约束。考虑到更多影响区域路网容量的因素,本文给出的网络容量定义为在道路条件与需求结构制约下,城市道路网络在单位时间内可以服务的最大机动车出行量。对于需求结构的选取,应当选择区域现状交通压力较大的时区所对应的需求结构,所得的网络容量更具备应用意义。
首先,定义道路路网为G=(N, A),其中N为节点集合,A为路段集合,a∈A。本研究采用双层规划理论,上层目标为最大网络流,下层为用户均衡分配的城市道路储备容量模型,具体的容量模型如下。
上层模型即求取最大出行量:
| $ \max u q_{r s}^0 $ | (1) |
下层模型为用户均衡UE分配出行:
| $ \min \sum\limits_{a \in A} \int_0^{x_a} t_a(x) \mathrm{d} x $ | (2) |
| $ \text{s.t.}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f_k^{r s} \geqslant 0 $ | (3) |
| $ x(a)=\sum\limits_{r, s} \sum\limits_k f_k^{r s} \delta_{a k}^{r s}, \forall a $ | (4) |
| $ x_a \leqslant C_a $ | (5) |
式中:u为储备容量乘子,qrs0为基础交通需求,ta(x)为路段a上的出行阻抗(本文采用BPR函数),xa为路段a的交通量,r、s分别为起点、终点标号,k为起终点间出行路径标号,fkrs为起点r到终点s间的路径k的流量,δakrs为0-1变量(当起点r到终点s间的路径k包含路段a时取δakrs=1,否则,δakrs=0),Ca为路段a的通行能力。
根据给出的网络容量定义及求解模型,可以得出影响网络容量的主要因素有:1)路段通行能力, 可通过式(5)约束来限制;2)出行者路径选择行为, 可在式(2)中选用用户最优(UE)来描述,而用户均衡假设出行者对整体路网有完整的了解,条件苛刻,在实际交通运行中,部分大型活动、交管措施(停车、拥挤区域收费)等也会改变区域内用户的出行选择;3)出行需求,对于式(1)中,上层给出的需求分布,各OD对间的流量比例直接影响分配结果,而影响网络容量的因素还有服务水平、交管措施等。
1.2 占道施工对路段通行能力的影响占道施工是指占用现状道路通行空间进行施工活动,为了隔离施工作业区与正常通行区域,会占用现有道路空间对作业区用安全隔离设施进行围挡。在《道路交通标志和标线设计规范》中将城市占道施工区域分为警示区、上游过渡区、缓冲区、作业区、下游过渡区和终止区共6个区域,如图 1所示。

|
图 1 施工作业区组成部分 Fig. 1 Components of construction area |
关于对居民出行活动的影响,过往研究集中在突发事件以及大型活动事件下对居民出行行为的影响,占道施工作为计划性作业活动,这里从通行能力的角度去研究占道施工对区域道路网络容量的影响,即施工前后路网的物理结构发生变化,不考虑需求结构和居民出行行为在施工前后的变化,影响通行能力约束,即通过式(5)来体现。
1.2.1 占道施工环境下通行能力影响因素分析1) 车道封闭形式
车道封闭形式主要包括:车道封闭数量与车道封闭位置,其中车道封闭数量直接限制通行能力。占道位置类型有“内侧占道”、“中间占道”及“外侧占道”,正常条件下,内侧与外侧车道驾驶人的驾驶行为会表现一定差异,相关研究表明,相对于外侧车道封闭,内侧车道封闭对通行能力的影响更大[9]。
2) 施工区限速对通行能力的影响
为提高施工区段行车的安全性,对所在区段进行限速是必要的,且相关研究表明,即使是未采取限速组织的施工路段,其平均行车速度下降超过6 km/h[12-13]。
在实际的施工区域交通组织方案中,对于施工区所在路段,主干路一般限速为40 km/h,次干路限速30~40 km/h,而支路一般限速为20~30 km/h。
3) 大型车比例对通行能力的折减
车辆在进入施工区路段时,会在过渡区参与强制换道,而公交车及施工车辆等大型车占用道路面积大,加减速较慢,在进行换道时会严重影响车流的速度,进而影响路段通行能力。
1.2.2 路段通行能力计算本文采用基于基本通行能力乘法修正的方法来计算路段通行能力,实际通行能力为基本通行能力与各影响因素折减系数乘积。
1) 正常条件下道路实际通行能力为
| $ C_{\mathrm{a}}=C_0 \times f_1 \times f_2 \times f_3 $ | (6) |
式中:Ca为正常条件下路段实际通行能力,pcu/h;C0为正常条件下路段基准通行能力,pcu/h;f1为路段通行能力的多车道影响折减系数;f2为路段通行能力的车道宽度影响折减系数;f3为路段通行能力的非机动车流影响折减系数。
正常道路条件下参照城市道路设计规范,车道数为1,2,3,4,5的折减系数分别为1,1.86,2.6,3.2,3.6;车道宽度为3.50 m,3.25 m,3.00 m,2.75 m的折减系数分别为1,0.93,0.85,0.77;非机动车车流对通行能力的影响折减系数取值主要取决于机非分隔设施与非机动车流量两方面,硬隔离和软隔离的折减系数分别为1和0.9,机非混行的折减系数为0.85,非机流量过剩的折减系数为0.5~0.85。
2) 施工条件下道路实际通行能力为
| $ C_{\mathrm{w}}=C_{\mathrm{s}} \times f_1 \times f_2 \times f_3 \times f_4 \times f_5 $ | (7) |
式中:Cw为占道施工期路段实际通行能力,pcu/h;Cs为占道施工期路段基准通行能力,pcu/h;f4为占道施工期路段通行能力的大型车影响折减系数;f5为占道施工期路段通行能力的的限速值影响折减系数。
上述影响因素中,限速值与大型车比例的影响可定量分析,而不同车道封闭形式直接影响上游过渡区交通流状态,各形式下通行能力量化关系较难确定,故选择各封闭形式下初始状态的通行能力为基准值来计算施工区段通行能力。
考虑各种施工封闭形式及交通条件无法在现实中同时获取,式(7)中的相关参数需通过VISSIM仿真软件确定,具体的仿真分析分为两个部分:设定基准仿真条件,确定各封闭形式下的道路通行能力基准值Cs;对各封闭形式下,设定不同的大型车比例、限速值仿真条件来确定与道路通行能力间的定量关系。
经过定义车辆组成、车流量输入、设置车速分布、设置冲突与减速区域等步骤,可获得占道施工路段的VISSIM仿真模型,见图 2。

|
图 2 施工区路段仿真 Fig. 2 Simulation of road section in construction area |
为验证仿真方法的可靠性,选取湖北省监利市北部近郊路段发展大道作为实例,该路段为双向四车道,每条机动车道宽度均为3.5 m,设计车速60 km/h,作业区限速40 km/h。由于经常有大中型货车通行,内侧车道沥青路面出现破损,故封闭内侧车道进行沥青路面翻新铺设,如图 3所示。

|
图 3 发展大道施工区段 Fig. 3 Construction section of Fazhan Avenue |
调查时段为2021年9月15日至9月17日期间12:30—13:30时段,该时段较多进城车流,施工区段车流多数时段处于排队状态,达到运行饱和状态。在作业区处选取一个观测断面记录单位时间内断面通过数,车流中大中型车辆主要以城乡客车与大中型货车为主,折算系数取为3,由断面通过流率得到的施工路段通行能力为1 245 pcu/h。
设定的基准条件为:正常道路行驶速度40~60 km/h,作业区限速40 km/h,区段长度设置见图 3,机动车道宽度3.5 m。作为城市次干路,相应驾驶行为参数设置为:前视最小距离为0 m,最大值为175 m,后视最小距离为0 m,最大值为125 m,走神持续时间为0 s,持续概率为0,跟车模式采用Wiedemann 74模型,平均停车间距(ax)为2 m,安全距离的附加部分(bx_add)为2,安全距离的倍数部分(bx_mult)为3。
输入不同交通量,仿真12次,每次连续运行4 200 s,取600~4 200 s间仿真结果,去除最大、最小值取平均值,得到仿真基准通行能力为1 501 pcu/h。观测时间内,共通行13辆大中型货车,大型车比例系数为10.44%,在该封闭形式下,限速值折减系数和大型车比例折减系数的仿真分析结果分别为0.937和0.921,进而得到仿真通行能力值为1 295 pcu/h,与实测值相比,其误差仅为4.02%,认为仿真结果可信度较高。
1.3 模型求解对于区域道路容量双层规划问题求解,作为非凸优化问题,求解算法种类很多实用性也不同,如直接搜索法、非数值优化方法与下降法等。而该双层规划模型上层问题仅储备容量乘子u,可以直接引入下层作为变量求解,而采用连续平均法(MSA)求解网络流分配的研究已经相当成熟,相对非数值优化方法、下降法等求解过程简便,计算效率更高。这里结合增量分配与连续平均法(MSA)来求解,通过增加u值,重复求解下层问题并返回上层约束,直至有路段达到通行能力约束,具体步骤如下。
步骤1 设定储备容量乘子u的初始值um=1,m=0,以及增量步长Δu0。
步骤2 采用MSW算法[14]分配需求量um增量,得到路段流量。分配步骤如下:
1) 在已有分配基础上,取零流时间进行一次分配,得到各路段交通量集合vam,m=1。
2) 更新各路段出行成本tm(a)。
3) 根据更新出行成本进行二次分配,确定搜索方向,得到各路段附加交通量ym(a),搜索方向Δtm(a)= ym(a)-xm(a)。
4) 更新路段流量, 其中d取1。
| $ x^{m+1}(a)=x^m(a)+\frac{m^d \Delta t^m(a)}{1^d+2^d+3^d+\cdots+m^d} $ | (8) |
5) 收敛判断。如果差值Δcam满足收敛要求,即
步骤3 如果现有流量未达到上层约束条件,令um+1=um+Δu0,返回步骤2。否则,取值增量步长
模型求解的流程如图 4所示。

|
图 4 算法流程 Fig. 4 Algorithm flow |
在城市道路网络日常运行中,部分路段由于通行能力、服务水平等因素的限制,制约了周边道路及区域路网的运行效率,而这些影响区域道路网络运行的瓶颈路段便是关键路段。当这些关键路段失效,即关键路段发生异常事件,会导致路网的连通性下降,承载能力降低。
国内外研究从不同角度给出了关键路段的定义[15]:1)从服务水平的角度分析,路网中最常发生拥堵的路段,即路段饱和度高的路段即为关键路段。2)从网络脆弱性角度分析,由于不利天气或突发事件导致某一路段无法通行,会引起路网交通运行混乱,降低路网总体运行效率和服务水平,该路段即为关键路段。3)在应急事件发生后,驾驶人会重新选择出行路径,各路径被选择的概率大于设定的阈值,即为关键路段。
对于城市道路网络关键路段的识别,可从两个角度进行:其一,通过复杂网络特性去分析,将道路网络抽象为拓扑图,从度、介数等特性指标来评估,可以模拟边和节点的破坏,分析对周边以及整体网络的影响来判断网络中节点、边的重要性。其二,通过实际道路网络交通运行情况去判别,根据交通量、运行速度、饱和度等交通流的运行指标去判别,或者拥堵时长、拥堵频率、排队长度等指标,从道路的脆弱性和可靠性去判别。
采用这些方法去进行关键路段识别,表征的重要度含义也有差异。道路网络作为现实网络,网络结构自身有物理条件限制,其网络流由居民的出行行为决定,有其特殊性,通过复杂网络特性去分析重要度,所得出来的结果并未有考虑现状道路网络的物理条件限制、需求结构等因素。
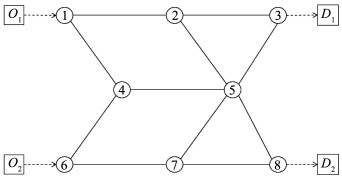
2.2 路段重要度计算在表示交通网络时,首先将其抽象化,采用原始图法将路网中的交叉口抽象为点,将路段抽象为边,将现实道路网络抽象为一个有权图集G=(N, A)。其中N是节点集合,A为路段集合,边权为对应路段自由流行程时间。
|
图 5 道路网络抽象结果 Fig. 5 Abstract results of road network |
关键路段的识别能在施工期间更有针对性地开展交通组织设计,传统的识别方法通常采用单一的复杂网络结构指标特性来作为重要度指标,但交通量等实际因素对路段的重要性也有很大影响。因此,本文综合从不同角度来表征关键路段的指标:边介值、网络效率变化率及路段饱和度,给出占道施工期路段重要度指标wa的计算公式为
| $ w_a=\frac{b_a}{\sum\limits_{a \in A} b_a}+\frac{p_a}{\sum\limits_{a \in A} p_a}+\frac{k_a}{\sum\limits_{a \in A} k_a} $ | (9) |
式中:ba为路段a的边介值,pa为路段a受攻击后对应网络效率的变化率,ka为路段a的饱和度。
边介值ba是指网络中任意两个节点间最短路径通过边a的数量与最短路径总数比值,常被用来表征边在网络信息流动中重要性与网络中心性,即
| $ b_a=\sum\limits_{i, j \in A} \frac{n_{i j}(a)}{n_{i j}} $ | (10) |
式中:nij(a)为经过边a的最短路径数,nij为节点ij间最短路径总数。
网络效率是表征整体网络的运输效率,衡量网络流动能力。在城市道路网中,交通事件的发生至使路段通过能力下降,即抽象网络中对应的边失效,从而使整个网络的连通性和通过效率降低。为了表现区域道路网络中各边对整体道路网络运输效率的影响,从而体现边的重要性,这里采用的攻击策略为:依次对各边进行攻击,即删除边,通过各边被删除前后网络效率变化幅度来表征。
| $ p_a=\frac{E-E_a}{E} $ | (11) |
| $ E=\frac{1}{N(N-1)} \sum\limits_{i, j \in v, i \neq j} \frac{1}{d_{i j}} $ | (12) |
式中:E为初始网络效率,Ea为对路段a进行蓄意破坏后的网络效率,N为节点总数,dij为节点由i至j的最短路径长度。
饱和度作为直接被用来评判路段服务水平的指标,对于饱和度ka的计算,流量采用网络容量计算过程中,对初始机动车出行需求即u=1时,进行分配得到的路段流量。
| $ k_a=\frac{x(a)_{i j}+x(a)_{j i}}{2 C_a} $ | (13) |
式中:x(a)ij为路段a由i点至j点流向的流量,x(a)ji为路段a由j点至i点流向的流量。
3 案例分析 3.1 道路网络选择以哈尔滨市阿城区中心城区道路网络为例,选取主次干路作为关键路段评估对象,共计94条路段,转化实际路网得到的网络拓扑如图 6所示。

|
图 6 道路网络拓扑结构 Fig. 6 Road network topology |
这里依据道路分布、土地利用及天然地貌等将阿城区中心区域分为36个交通小区,考虑到对外客流主要是沿绥满线和绥满公路的西北-东南方向客流,这里仅选取了两个外部小区,分别是西北方向的哈尔滨市中心城区四环内区域以及东南方向的尚志市及南部旅游区域,对于路网的交通需求数据,基于极智DaaS平台通过Hive SQL语言获取联通公司手机信令数据,区域用户覆盖率约为30%。经过去噪和扩样,2019年5月13日至2019年5月17日(周一至周五),日均居民跨交通小区出行总量42.043 3万人次,日均早高峰(7:00—9:00)出行人次约为6.617 3万人次,日均晚高峰(17:00—19:00)出行人次约为5.253 6万人次;早晚高峰时段出行量大,这与城市日常出行活动和交通调查相符。选用一周工作日晚高峰的手机信令数据,各小区的出行产生吸引量见表 1。
| 表 1 各小区的产生、吸引量 Tab. 1 Generation and attraction of each community |
2021年,阿城区完成两批次共计6个老旧小区的本体改造以及配套基础设施改建。在这些改造工程中,部分改造项目需要在外墙体进行施工,会占用外侧车道施工。这里模拟一期即北顺小区、祥泰小区、金城小区改造期间均占用外侧一车道进行施工,如图 7所示,其直接影响的路段分别为上京大街(金溪路至延川大街)、延川大街(解放大街至金都大街)、延川大街(民权大街至解放大街)。
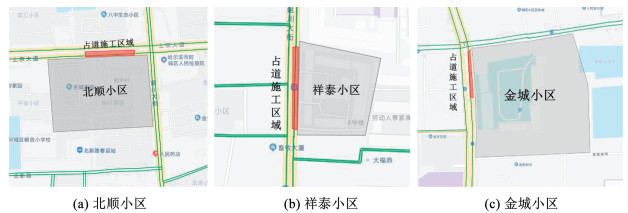
|
图 7 老旧小区改造占道形式 Fig. 7 Road occupation form for reconstruction of old residential areas |
对应的封闭形式分别为北顺小区单向四车道封闭最外侧车道、祥泰小区和金城小区单向三车道封闭最外侧车道。这里设定各封闭形式下基准交通条件为:正常道路行驶速度30~50 km/h,作业区限速20~40 km/h,警示区长度50 m,上游过渡区长度30 m,作业区长度100 m,大型车比例0%,机动车道宽度3.5 m。3条路段均为城市主干道,相应驾驶行为参数设置为:前视最小距离为0 m,最大值为200 m,后视最小距离为0 m,最大值为150 m,暂时走神的持续时间为0 s,持续概率为0,跟车模式采用Wiedemann 74模型,平均停车间距(ax)为2 m,安全距离的附加部分(bx_add)为2,安全距离的倍数部分(bx_mult)为3。仿真结果为:三车道封闭外侧一车道基准通行能力输入交通量为4 000 pcu/h,4 500 pcu/h,5 500 pcu/h,6 000 pcu/h时,仿真值分别为3 247 pcu/h,3 251 pcu/h,3 253 pcu/h,3 254 pcu/h;四车道封闭外侧一车道基准通行能力输入交通量为4 500 pcu/h,5 000 pcu/h,5 500 pcu/h,6 000 pcu/h,6 500 pcu/h时,仿真值分别为4 352 pcu/h,4 490 pcu/h,4 884 pcu/h,4 940 pcu/h,4 928 pcu/h。
3.2.2 限速值影响折减系数在仿真实验中,对限速值分别取20 km/h、25 km/h、30 km/h、35 km/h、40 km/h,对应的速度区间为10~20 km/h、15~25 km/h、20~30 km/h、25~35 km/h、30~40 km/h,占道施工期通行能力的限速值影响折减系数仿真试验结果如表 2所示。
| 表 2 限速值影响折减系数仿真结果 Tab. 2 Simulation results of reduction coefficient affected by speed limit value |
对限速值和折减系数进行回归分析,可以得折减系数y与限速值x之间有如下定量关系:
| $ y=-0.000\;2 x^2+0.025\;2+0.280\;7, R^2=0.998\;3 $ | (14) |
在仿真实验中,大型车比例分别取0%、0.05%、1%、2%、3%、5%、10%,所得的占道施工期通行能力大型车影响折减系数仿真结果如表 3所示。可以发现,随着大型车比例的上升,通行能力呈下降趋势。
| 表 3 大型车影响折减系数仿真结果 Tab. 3 Simulation results of large vehicle impact reduction coefficient |
对大型车比例和影响折减系数进行回归分析,可以得折减系数y与大型车比例x之间有如下线性关系:
| $ y=-0.009\;7 x+0.999\;7, R^2=0.998\;8 $ | (15) |
根据各小区施工期所占路段的交通量、交通组成及限速值,求得各小区对应施工路段的通行能力计算结果如表 4所示;阿城区中心城区其他道路通行能力计算结果如表 5所示。
| 表 4 施工区段通行能力 Tab. 4 Capacity of construction section |
| 表 5 其他道路通行能力计算结果 Tab. 5 Calculation results of other road capacity |
将基于手机信令得到的需求分布结果先分配,初始出行需求加载下,已经有部分路段V/C超过0.6,这里令储备容量乘子的增量步长Δu=0.1,但分配结果超过通行能力约束后,令储备容量乘子的增量步长Δu=0.02,对于原始OD得到的路网分配结果如图 8所示。

|
图 8 施工前路网容量加载分布图 Fig. 8 Road network capacity loading distribution before construction |
在第10次分配时,延川大街(北新路至民权大街段)流量超出了通行能力约束,得到的储备容量乘子u=1.46。加载施工期区段通行能力进行分配,得到分配结果如图 9所示。
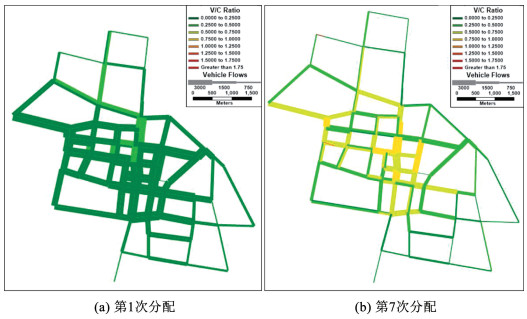
|
图 9 施工期路网容量加载分布图 Fig. 9 Road network capacity loading distribution during construction |
在第8次分配时,延川大街(解放大街-民权大街段)流量超出了通行能力约束,得到的储备容量乘子u=1.40。求得施工前,初始条件下阿城区中心城区道路网络容量为38 445 pcu/h,施工后阿城区中心城区道路网络容量为36 865 pcu/h,对比施工前后,道路网络容量值缩减了4.1%。
3.4 施工期关键路段识别 3.4.1 初始网络指标计算以Python为平台,调用网络分析工具库network、矩阵运算工具库numpy等。根据道路网络拓扑结构图,对各交叉口进行编号以及计算路段自由流行程时间,这里以路段自由流行程时间作为边权重,计算初始状态下区域道路网络边介值以及网络效率。
3.4.2 网络效率变化值计算本文的攻击策略是遍历网络对单边进行蓄意攻击,网络效率常被用来表征网络的运输效率,用作鲁棒性分析,这里选择各边被破坏后的网络效率变化幅度来表征相应边的重要性。初始网络效率计算为以路段自由流行程时间为权值的有权网络效率,后续表征边被破坏即将相应边权值调大做到隔断效果,遍历图一次只破坏一条边,每次攻击结果不对后续攻击产生影响,然后得到所有边被破坏后的网络效率值,得出各边对应网络效率变化率,综合得到指标计算结果如图 10所示。

|
图 10 路网各指标对比图 Fig. 10 Comparison diagram of various indicators of road network |
从图 10可以看出:部分路段的网络效率变化率为负值,这些路段均为连接外部小区路段及城区边缘路段,在删除这些路段后,网络效率反而得到了提升,即城市边缘、集散及末端道路被删除反而提升了城市道路网络的可达性。这些道路由于与整体路网联系不紧密,可以取消对其重要性的分析,这里将与节点度为1的节点连接的边不纳入重要度考虑范围,最终阿城区中心区域重要度排名前十的路段如表 6所示,这些路段均处于阿城区中心区域。
| 表 6 重要度排名前10的路段 Tab. 6 Top 10 sections in importance |
1) 考虑路段通行能力约束,构建了基于双层规划的占道施工影响下城市道路网络容量计算模型,上层求解最大储备容量乘子,下层为用户均衡,并针对该模型设计了算法。
2) 为给城市路网容量计算提供交通需求分配判别条件,基于各封闭形式下施工路段通行能力基准值,构建了考虑大型车及限速值影响的占道施工路段实际通行能力计算模型。
3) 综合考虑占道施工导致路网结构特征发生改变,以及施工路段通行能力减小而导致交通运行状态恶化,提出了占道施工影响下城市路网关键路段评估方法,为占道施工期交通组织提供了依据。选用哈尔滨市阿城区中心城区为案例,验证了模型与方法的适用性。
关于占道施工区段的通行能力计算,本文研究只是采用仿真软件单独分析每个影响因素与通行能力之间的定量关系,并未考虑到各因素间的交叉影响,给出的通行能力计算模型还需进一步完善。此外,交叉口延误作为行程时间的重要组成部分,在阻抗函数中应当予以考虑,后续可以进一步优化网络容量计算模型与求解算法。
| [1] |
朱吉双, 张宁. 城市道路网络承载能力影响因素分析[J]. 交通运输系统工程与信息, 2008(1): 92. ZHU Jishuang, ZHANG Ning. Analysis of factors in affecting the loading capacity of urban road networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2008(1): 92. DOI:10.16097/j.cnki.1009-6744.2008.01.011 |
| [2] |
方文彬, 单良慈, 黄中祥. ATIS对道路网络容量的影响[J]. 系统工程, 2015, 33(10): 155. FANG Wenbin, SHAN Liangci, HUANG Zhongxiang. The impact of ATIS on road network capacity[J]. Systems Engineering, 2015, 33(10): 155. |
| [3] |
黄中祥, 唐志强, 覃定明, 等. 无人驾驶环境下考虑OD结构的路网容量模型[J]. 中国公路学报, 2019, 32(12): 98. HUANG Zhongxiang, TANG Zhiqiang, QIN Dingming, et al. A road network reserve capacity model in the autonomous environment[J]. China Journal of Highway and Transport, 2019, 32(12): 98. |
| [4] |
方雅君, 郑长江, 马庚华, 等. 基于路段服务水平约束的路网容量可靠性分析[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(3): 502. FANG Yajun, ZHENG Changjiang, MA Genghua, et al. Reliability analysis of road network capacity based on service level constraints[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(3): 502. |
| [5] |
张晓婷, 吴兵. 考虑特定OD分布形态的路网容量双层规划模型[J]. 交通运输工程与信息学报, 2012, 10(4): 116. ZHANG Xiaoting, WU Bing. Bi-level programming model for the road network capacity based on the existed OD distribution[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 10(4): 116. |
| [6] |
杜牧青, 刘海生, 虞春滨. 考虑停车收费及供给政策的城市路网容量评估[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(6): 1052. DU Muqing, LIU Haisheng, YU Chunbin. Capacity evaluation of urban road network considering parking charge and supply policy[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(6): 1052. |
| [7] |
BASKAN O, CEYLAN H, OZAN C. A simultaneous solution for reserve capacity maximization and delay minimization problems in signalized road networks[J]. Journal of Advanced Transportation, 2019, 2019: 1. |
| [8] |
HAN F, CHENG L. Stochastic user equilibrium model with a tradable credit scheme and application in maximizing network reserve capacity[J]. Engineering Optimization, 2017, 49(4): 549. DOI:10.1080/0305215X.2016.1193357 |
| [9] |
MIANDOABCHI E, FARAHANI R Z. Optimizing reserve capacity of urban road networks in a discrete network design problem[J]. Advances in Engineering Software, 2011, 42(12): 1041. DOI:10.1016/j.advengsoft.2011.07.005 |
| [10] |
刘令. 占道施工对区域路网容量的影响研究[D]. 武汉: 华中科技大学, 2017 LIU Ling. Effects of work zones on road network capacity[D]. Wuhan: Huazhong University of Science and Technology, 2017 |
| [11] |
王熙煜. 城市道路施工作业影响下路网容量的计算及提升分析[D]. 西安: 长安大学, 2020 WANG Xiyu. The calculation of network capacity and analysis of improving under the influence of constructing urban road[D]. Xi'an: Chang'an University, 2020. DOI: 10.26976/d.cnki.gchau.2020.001160 |
| [12] |
邵长桥, 张兴宇, 罗凯, 等. 高速公路施工区通行能力研究综述[J]. 武汉理工大学学报(交通科学与工程版), 2021, 45(2): 207. SHAO Changqiao, ZHANG Xingyu, LUO Kai, et al. A review of traffic capacity in express way work zones[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2021, 45(2): 207. |
| [13] |
VON DER HEIDEN N, GEISTEFELDT J. Capacity of freeway work zones in Germany[J]. Transportation Research Procedia, 2016, 15: 233. DOI:10.1016/j.trpro.2016.06.020 |
| [14] |
李红莲. 可换乘条件下的城市多模式交通分配研究[D]. 北京: 北京交通大学, 2011 LI Honglian. Study on the urban multi-modal traffic assignment under the condition of inter-mode transfer[D]. Beijing: Beijing Jiaotong University, 2011 |
| [15] |
宋英华, 李玉枝, 霍非舟, 等. 城区内涝条件下城市公交-地铁双层交通网络的脆弱性分析[J]. 安全与环境工程, 2021, 28(2): 114. SONG Yinghua, LI Yuzhi, HUO Feizhou, et al. Vulnerability of two-layer traffic network of bus and subway under waterlogging condition based on complex network theory[J]. Safety and Environmental Engineering, 2021, 28(2): 114. |
 2024, Vol. 56
2024, Vol. 56


