2. 浙江大学 结构工程研究所,杭州 310058
2. Institute of Structural Engineering, Zhejiang University, Hangzhou 310058, China
现行规范考虑不利地形条件下水平风速的加速效应对输电线路设计的影响,但没有考虑竖向风速对输电线路设计的不利作用。竖向风速在山区地貌的流场中普遍存在,竖向风速的抬升作用将促进跳线的风偏响应,可能更易造成跳线风偏事故。
目前关于地形水平风速加速效应[1-5]的研究较为成熟和全面。相比之下,关于地形竖向风速的研究则较为稀少。文献[6]采用风洞试验结合数值模拟方法研究典型山地竖向平均风速分布特征,认为在1/3山高以上的迎风坡位置应当考虑竖向风速。文献[7]采用风洞试验获得某复杂山体的竖向平均风场特征,认为最大竖向平均风速发生在山腰位置,山顶和山脚存在较小的竖向平均风速,对于风荷载敏感的跳线结构影响较大。文献[8]通过现场实测得到某峡谷的三维风速时程,分析得到竖向风速的湍流强度、功率谱以及湍流积分尺度。
对于导线以及跳线风偏研究,需要对山地风场进行较为细致的考虑。文献[9]从竖向上升气流的角度研究山地风场对输电线路风偏的影响,通过有限元计算认为上相导线对上升气流较为敏感,竖向风速不可忽略。文献[10]采用有限元方法对实际输电线路的跳线风偏进行计算,认为考虑竖向风速共同作用时跳线风偏角会进一步增大。但是采用有限元计算的方法研究跳线风偏较为繁琐耗时,难以在工程应用中大量开展,而利用设计手册[11]提供的风偏计算公式更便于设计应用。文献[12]引入风荷载调整系数对设计手册提供的方法进行修正,能够精细考虑脉动风荷载的动力放大作用,但没有考虑竖向风速的影响。
本文基于规范中的风偏计算公式,提出了考虑竖向风速影响的跳线风偏状态方程。采用数值模拟方法获取跳线风偏事故地点的事故风速,验证跳线风偏状态方程的可靠性。最后根据跳线风偏状态方程分析竖向风速的变化对跳线风偏临界水平风速的影响,为改进跳线风偏计算方法提供借鉴。
1 考虑竖向风速的跳线风偏状态方程推导一般以跳线绝缘子串风偏位移作为验算跳线风偏的指标,但闪络事故通常是由于跳线绝缘间隙过小导致,而跳线绝缘子串无损伤。因此跳线风偏位移更能代表跳线的风偏情况,应将跳线与塔身的最小距离作为风偏指标。绕引跳线风偏立面示意如图 1所示,该图为侧视图,耐张绝缘子串2及另一半跳线与图中耐张绝缘子串1及跳线重叠。图中LH为横担长度,Ll为跳线与跳线挂点的最大水平距离,Lj为跳线到塔身的最小水平距离。显然最大风偏位移位于跳线上而非跳线与跳线绝缘子串的连接处。
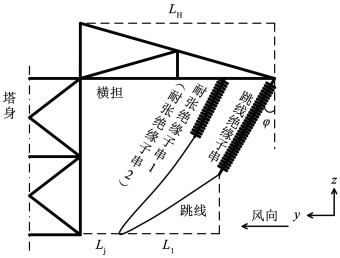
|
图 1 风偏立面示意图 Fig. 1 Vertical schematic diagram of wind-induced swing |
跳线绝缘子串和耐张绝缘子串间的两处跳线可分别视作直引跳线。本文根据规范推荐方法[13],以绕引跳线公式计算跳线绝缘子串风偏位移,再以直引跳线公式计算跳线最大风偏位移,并基于跳线风偏位移建立风偏状态函数:
| $ F_{\mathrm{j}}(V, \delta)=L_{\mathrm{j}}-L_{\text {cri }} $ | (1) |
式中:V为来流平均风速;δ为风攻角,表示来流平均风速与水平面间的夹角;Lcri为不发生闪络的最小电气间隙,按规范取1.2 m。显然,状态函数大于零,则表示不会发生风偏闪络,反之,则表示会发生风偏闪络。
由图 1几何关系可得,跳线与塔身最小距离为
| $ L_{\mathrm{j}}=L_{\mathrm{H}}-L_{\mathrm{s}} \sin \varphi-L_{\mathrm{l}} $ | (2) |
式中:Ls为跳线绝缘子串的长度,φ为跳线绝缘子串风偏角。
采用规范推荐的刚性直棒法计算绕引跳线绝缘子串风偏角,即将跳线绝缘子串视为刚性直棒,将跳线重力荷载和所受的风荷载集中作用于跳线挂点处。在山区地形影响下来流的竖向风速不可忽略[10],刚性直棒的受力分析示意图如图 2所示,基于静力平衡关系可得跳线绝缘子串风偏角计算公式为
| $ \varphi=\arctan \left(\frac{T_{\mathrm{y}}+0.5 G_{\mathrm{y}}+W_{\mathrm{y}}}{T_{\mathrm{z}}+0.5 G_{\mathrm{v}}+W_{\mathrm{v}}-\left(0.5 G_{\mathrm{z}}+W_{\mathrm{z}}\right)}\right) $ | (3) |
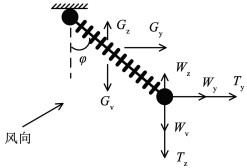
|
图 2 刚性直棒受力分析示意图 Fig. 2 Schematic diagram of force analysis of rigid bar |
式中:Gy和Gz分别为绝缘子串风荷载的水平分量和竖向分量,Wy和Wz分别为跳线风荷载的水平分量和竖向分量,Gv和Wv分别为绝缘子串和跳线的重力荷载,Tz和Ty分别为考虑挂线高差和横向张力影响的附加力。
附加力影响表现如下:当跳线绝缘子串两侧的跳线不平行时,跳线张力会合成横向张力;当跳线绝缘子串挂点和耐张绝缘子串挂点之间存在高差,跳线对两处挂点的作用力不相等。此时应考虑:
| $ T_y=2 T_{\mathrm{t}} \cos \omega $ | (4) |
| $ T_{\mathrm{z}}=2 T_{\mathrm{t}} \frac{h_{\mathrm{t}}}{l_{\mathrm{v}}} $ | (5) |
式中:Tt为有风状态下的跳线张力;ω为跳线与横担中线间的水平夹角;ht为跳线绝缘子串挂点与耐张绝缘子串挂点的高差;lV为跳线档距。
基于准定常假设,规范给出了跳线及绝缘子串的风荷载计算公式:
| $ F_{\mathrm{W}}=\alpha \beta_{\mathrm{c}} C_{\mathrm{D}} \cdot \frac{1}{2} \rho V^2 \sin ^2 \theta \cdot d \cdot l_{\mathrm{H}} $ | (6) |
| $ F_{\mathrm{G}}=\beta_{\mathrm{c}} \mu_{\mathrm{s}} \cdot \frac{1}{2} \rho V^2 \cdot A $ | (7) |
式中:FW和FG分别为跳线和绝缘子串风荷载;α为风压不均匀系数,取1.0;βc为风荷载调整系数,取1.4;CD为跳线阻力系数,当跳线直径大于17 mm时,取1.0,反之取1.1;ρ为空气密度;V为风速;θ为风向与跳线方向间的夹角;d为跳线计算外径;lH为跳线水平档距;μs为绝缘子串阻力系数;A为跳线绝缘子串迎风面积。
将风荷载转换到笛卡尔坐标系有
| $ \left[\begin{array}{ll} W_{\mathrm{y}} & W_{\mathrm{z}} \\ G_{\mathrm{y}} & G_{\mathrm{z}} \end{array}\right]=\left[\begin{array}{l} F_{\mathrm{W}} \\ F_{\mathrm{G}} \end{array}\right]\left[\begin{array}{ll} \cos \delta & \sin \delta \end{array}\right] $ | (8) |
耐张绝缘子串风偏角同样按刚性直棒法计算,得到耐张绝缘子串挂点与跳线绝缘子串挂点分别相对横担最外侧的方向矢量:
| $ \begin{gathered} \boldsymbol{R}_{\mathrm{n}}=\left[L_{\mathrm{n}} \cos \gamma_{\mathrm{n}} \cos \left(\frac{\psi}{2}+\varphi_{\mathrm{n}}\right)+L_{\mathrm{x} 0}, \right. \\ \left.L_{\mathrm{n}} \cos \gamma_{\mathrm{n}} \sin \left(\frac{\psi}{2}+\varphi_{\mathrm{n}}\right)+L_{\mathrm{y} 0}, -L_{\mathrm{n}} \sin \gamma_{\mathrm{n}}\right] \end{gathered} $ | (9) |
| $ R_{\mathrm{t}}=\left[0, L_{\mathrm{s}} \sin \varphi, -L_{\mathrm{s}} \cos \varphi\right] $ | (10) |
式中:Ln为耐张绝缘子串长度;γn为耐张绝缘子串与横担水平面间的竖向夹角;ψ为线路转角度数;φn为耐张绝缘子串风偏角;Lx0和Ly0分别为耐张绝缘子串上端与横担最外侧x和y向距离分量,分别取1.2 m和2 m。
在风荷载作用下,跳线将偏离竖直平面并在新的平面内达到静力平衡,图 3给出了跳线在风偏前后的静力平衡平面示意图。新静力平衡平面应平行于风荷载和重力荷载的合力方向。风荷载和重力荷载合力的单位方向矢量为
| $ r=\left[r_\text{x}, r_\text{y}, r_\text{z}\right]=\frac{\left[0, W_\text{y}, W_\text{z}-W_\text{v}\right]}{\sqrt{W_\text{y}^2+\left(W_\text{z}-W_\text{v}\right)^2}} $ | (11) |

|
图 3 跳线静力平衡平面 Fig. 3 Static equilibrium plane of jump line |
式中:rx,ry和rz分别为风荷载和重力荷载合力方向矢量对x轴,y轴和z轴的投影。
在跳线静力平衡平面内建立如图 3所示局部坐标系x′O′y′,按抛物线计算静力平衡构型
| $ y^{\prime}=a x^{\prime 2}+b x^{\prime}+c $ | (12) |
由于跳线张拉力极小,有风状态下跳线长度变化可以忽略。耐张绝缘子串的悬挂点位置会随两侧导线的运动而变化,计算可得两端挂点坐标[11]。式(12)中的系数可按下式计算:
| $ a=-\frac{S}{x_0^{\prime 2}} \sqrt{\frac{3\left(S^2-x_0^{\prime 2}-y_0^{\prime 2}\right)}{S^2+y_0^{\prime 2}}} $ | (13) |
| $ b=a x_0^{\prime}+\frac{y_0^{\prime}}{x_0^{\prime}} $ | (14) |
| $ c=y_0^{\prime} $ | (15) |
式中:S为跳线长度,x′0和y′0分别为抛物线对x′和y′轴的截距。
由风荷载和重力荷载合力矢量与挂点坐标可计算两截距:
| $ y_0^{\prime}=\frac{\left(\boldsymbol{R}_{\mathrm{n}}-\boldsymbol{R}_{\mathrm{t}}\right) \cdot \boldsymbol{r}^{\mathrm{T}}}{\boldsymbol{r} \cdot \boldsymbol{r}^{\mathrm{T}}} $ | (16) |
| $ x_0^{\prime}=\left\|y_0^{\prime} \boldsymbol{r}+\left(\boldsymbol{R}_{\mathrm{n}}-\boldsymbol{R}_{\mathrm{t}}\right)\right\| $ | (17) |
跳线与跳线绝缘子串挂点的最大水平距离为
| $ L_1=r_y \cdot\left(y_{\text {max }}^{\prime}-y_0^{\prime}\right)=-\frac{b^2}{4 a} r_y $ | (18) |
于2019年8月10日1:00时,事故塔绕引跳线发生风偏,位于东经121°8′14.23″,北纬28°26′32.72″,现场情况如图 4所示。图 4(a)为事故跳线示意图,展示事故跳线正常工作时的空间形态,正常情况下跳线将与塔身始终保持安全的绝缘间隙;图 4(b)为事故地点现场情况,绕引跳线悬挂于塔身脚钉上,跳线有断股,绝缘子串无损伤,说明当时事故风速大于风偏临界值。

|
图 4 事故线路及现场情况 Fig. 4 Accident line and site situation |
事故线路为500 kV四跨四分裂输电线路,线路示意图如图 5所示。故障杆塔塔型为JTS1(27)-21.0,导线跳线采用四分裂LGJ-630/45,耐张绝缘子采用FC300/195,引流线绝缘子采用FXBW-500/100,物理参数见表 1、2。事故地点按规范归为B类地貌。线路转角度数ψ取29°37′。
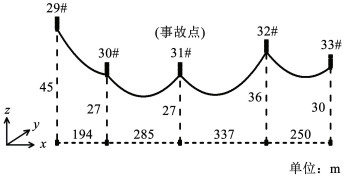
|
图 5 输电线路示意图 Fig. 5 Schematic diagram of transmission line |
| 表 1 LGJ630/45四分裂导线参数 Tab. 1 Parameters of four-bundled conductor LGJ630/45 |
| 表 2 绝缘子参数 Tab. 2 Parameters of insulator string |
事故发生时正值“利奇马”台风登陆期间,但事故地点缺乏气象资料,仅在其附近存在一处微气象站,二者相距1.9 km。因此事故发生时的实际风速需要通过微气象站数据反演得到。微气象站离地高度5 m,采集得到水平向10 min平均风速和平均风向。在事故发生前后的实测数据如图 6所示,其中部分时刻数据缺失。由图 6可得,事故发生期间平均风速和平均风向的变化较为剧烈。

|
图 6 微气象站实测数据 Fig. 6 The measured data of the micrometeorological station |
风向与事故地点的关系如图 7所示,由图中可得:342°风向下事故地点被一道山脊遮挡,而204°风向与跳线方向近乎平行,二者均较难引起跳线风偏。考虑台风期间风向变化较大,且事故发生是瞬间的,因此假设事故时风向为垂直跳线方向,即296°,平均风速取1∶ 02时刻的数据,即15.7 m/s。

|
图 7 事故点所处地形地貌 Fig. 7 Landform of the accident site |
事故地点的地形复杂多变,采用半径5 km的圆形区域作为真实地形计算范围,覆盖主要地形特征、事故地点以及微气象站,考虑了计算误差与地形范围的关系[14]。为确保CFD数值模拟结果更加可靠,将事故地点设为原点,使测点尽量靠近地形中央。真实地形边界会出现高程的突变,采用分段函数[15]进行过渡处理,过渡段宽度设为1 km。消除人造悬崖后的事故周边地形如图 8所示,地形既实现了平滑过渡,又保留了原始地貌特征。

|
图 8 事故周边地形展示 Fig. 8 The display of the terrain around the accident |
事故地点最高点为310 m。为保证流场充分发展,上游长度取5 km,下游长度取15 km,两边取3 km,计算域高度设为3 km。模型缩尺比为1∶ 1 000。
设置4种网格尺寸进行网格无关性检验,网格方案见表 3。水平向加速比定义为离山体表面水平向平均风速与来流对应高度处的风速比值。根据不同网格方案,比较同一地点10 m高度的水平向加速比,结果见图 9,可得方案1、方案2、方案3与方案4的误差分别为6.5%、3.2%和0.5%。综合考虑计算精度与计算能力,确定方案3作为网格划分方法,竖向网格增长率为1.07,水平向网格增长率为1.1,Y+控制在25~600之间。
| 表 3 网格方案 Tab. 3 Mesh scheme |

|
图 9 不同网格方案的测点水平向加速比 Fig. 9 Horizontal speed-up ratio of measuring points with different mesh schemes |
采用Realizable k-ε湍流模型,壁面函数选择Scalable Wall Function。计算域入口为速度入口,出口为自由出口,两侧与顶部为对称边界。计算域地面与真实地形表面为固定壁面,粗糙高度统一设为1 m。入口边界条件采用UDF进行设置[16],选用B类场地的风速剖面,参考点高度为5 m,参考点风速为15.7 m/s。
3 数值模拟与状态方程结果对比 3.1 数值模拟反演的事故风速为便于反演事故发生时事故地点的实际风速,将事故地点与微气象站点作为测点,计算296°风向下测点的风场规律。竖向风速比定义为离山体表面竖向平均风速与来流对应高度处的风速比值。事故地点与微气象站点的水平向加速比如图 10所示。由图 10可得:事故地点水平向加速比均大于1,说明存在明显的风场加速效应,最大加速比约为1.23,出现在离地10 m高度;微气象站点的水平向加速比均小于1,为水平风速减速区,原因是来流方向存在高山阻挡,二者高差约为230 m。事故地点与微气象站点的竖向风速比如图 11所示。由图 11可得:事故地点竖向风速整体为正,说明竖向风速方向向上,表现为升力;微气象站点近地面竖向风速为负;两处测点的竖向风速比绝对值均较小。综上所述:事故地点与微气象站点虽然仅相距1.9 km,但局部风环境有明显差异,不能直接采用微气象站的数据作为事故地点的风速结果。

|
图 10 测点水平向加速比 Fig. 10 Horizontal speed-up ratio of measuring points |
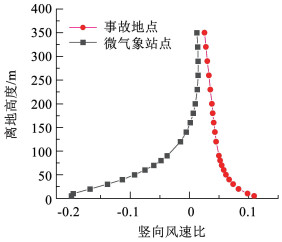
|
图 11 测点竖向风速比 Fig. 11 Vertical wind speed ratio of measuring points |
水平向加速比与竖向风速比均为无量纲参数,可用于反映不同地点风速剖面的内在联系。风速反演过程如下:通过微气象站点5 m高度处实测水平平均风速15.7 m/s得到来流B类风场5 m高度处水平平均风速为26.9 m/s,进一步可得B类风场27 m高度处水平平均风速为34.6 m/s,最后获得27 m高度处事故点水平平均风速为40.7 m/s,竖向平均风速为2.6 m/s,计算得到事故点风攻角约为3.6°。
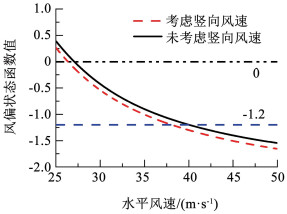
3.2 由风偏状态方程计算临界风速为使公式简洁明了,采用了全风速推导跳线风偏状态方程,而为便于比较,采用水平风速呈现结果。由式(1)可得考虑竖向风速影响的跳线风偏临界风速,风攻角按数值模拟结果的3.6°进行取值,采用试算法进行求解。图 12给出了来流水平风速为25~50 m/s的风偏状态函数值。结果表明:考虑竖向风速的风偏临界水平风速为26.32 m/s,未考虑竖向风速的风偏临界水平风速为27.07 m/s,后者略大于前者,说明考虑竖向风速影响的临界风速取值较为安全;二者较为接近,说明当竖向风速较小时,其对跳线风偏临界水平风速影响较弱。同时,提取风偏状态函数值为-1.2时的水平风速分别为38.0 m/s和40.0 m/s,说明事故风速下跳线会触碰塔身,与实际事故观测现象相匹配,证明跳线风偏状态方程合理有效。
|
图 12 不同水平风速下的风偏状态函数值 Fig. 12 The values of wind-induced swing state function at different levels of wind speed |
本次事故地点位于山顶附近,风速分量主要为水平方向,竖向风速分量较小。但山腰位置可能存在明显的竖向风速,此时风攻角较大,可能对跳线产生明显的竖向力。图 13展示了不同风攻角下的跳线风偏临界水平风速,随着风攻角在0~20°内增大,竖向风速逐渐增大,导致跳线风偏临界水平风速线性减小,降低可达16%。当风攻角为20°时,考虑竖向风速影响的跳线风偏临界水平风速为22.85 m/s,但不考虑该影响的跳线风偏临界水平风速为27.07 m/s,二者之比为1.18,说明存在竖向风速影响的输电线路更易发生跳线风偏事故,忽略竖向风速的影响可能低估跳线风偏响应,使得抗风偏设计较不安全。因此设计过程中需要考虑竖向风速的作用。

|
图 13 不同风攻角下的临界水平风速 Fig. 13 Critical horizontal wind speed under different wind attack angles |
本文以刚性直棒法及风荷载作用前后静力平衡平面的关系确定跳线处最大风偏位移值,提出了考虑竖向风速影响的跳线风偏状态方程,根据实际绕引跳线风偏事故验证跳线风偏状态方程的可靠性,探讨竖向风速对跳线风偏临界水平风速的影响,得出如下结论:
1) 通过数值模拟得到的事故风速大于跳线风偏状态方程计算得到的风偏临界风速,证明跳线风偏状态方程合理有效。
2) 当风攻角在0~20°内增大时,竖向风速逐渐增大,导致跳线风偏临界水平风速线性减小,降低可达16%。
3) 考虑竖向风速影响的跳线风偏计算方法可进一步完善规范中的设计要求,贴近输电塔线体系实际所处的流场状况,对于山区地貌的输电线路抗风设计具有显著的应用价值。
| [1] |
JACKSON P S, HUNT J C R. Turbulent wind flow over a low hill[J]. Quarterly Journal of the Royal Meteorological Society, 1975, 101(430): 929. DOI:10.1002/qj.49710143015 |
| [2] |
TAYLOR P A, LEE R J. Simple guidelines for estimating wind speed variations due to small scale topographic features[J]. Climatological Bulletin, 1984, 18(2): 3. |
| [3] |
沈国辉, 姚旦, 余世策, 等. 单山和双山风场特性的风洞试验[J]. 浙江大学学报(工学版), 2016, 50(5): 805. SHEN Guohui, YAO Dan, YU Shice, et al. Wind tunnel test of wind field characteristics on isolated hill and two adjacent hills[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(5): 805. DOI:10.3785/j.issn.1008-973X.2016.05.001 |
| [4] |
李正良, 徐姝亚, 肖正直, 等. 山地风速地形修正系数沿山坡的详细插值分布[J]. 湖南大学学报(自然科学版), 2016, 43(3): 23. LI Zhengliang, XU Shuya, XIAO Zhengzhi, et al. Detailed interpolation distribution of hilly wind topographic factor along hillside[J]. Journal of Hunan University (Natural Science), 2016, 43(3): 23. DOI:10.3969/j.issn.1674-2974.2016.03.004 |
| [5] |
楼文娟, 刘萌萌, 李正昊, 等. 峡谷地形平均风速特性与加速效应[J]. 湖南大学学报(自然科学版), 2016, 43(7): 8. LOU Wenjuan, LIU Mengmeng, LI Zhenghao, et al. Research on mean wind speed characteristics and speed-up effect in canyon terrain[J]. Journal of Hunan University (Natural Science), 2016, 43(7): 8. DOI:10.16339/j.cnki.hdxbzkb.2016.07.002 |
| [6] |
楼文娟, 梁洪超, 李正昊, 等. 典型山地地形竖向风速分布特征[J]. 空气动力学学报, 2018, 36(5): 791. LOU Wenjuan, LIANG Hongchao, LI Zhenghao, et al. Vertical wind velocity distribution in typical hilly terrain[J]. Acta Aerodynamica Sinica, 2018, 36(5): 791. DOI:10.7638/dlxxb-2016.0134 |
| [7] |
沈国辉, 翁文涛, 王轶文, 等. 某复杂山体的三维风场特征研究[J]. 振动与冲击, 2020, 39(4): 75. SHEN Guohui, WENG wentao, WANG Yiwen, et al. A study on three-dimensional wind field characteristics of a complex hill[J]. Journal of Vibration and Shock, 2020, 39(4): 75. DOI:10.13465/j.cnki.jvs.2020.04.009 |
| [8] |
YU C, LI Y, ZHANG M, et al. Wind characteristics along a bridge catwalk in a deep-cutting gorge from field measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 186: 94. DOI:10.1016/j.jweia.2018.12.022 |
| [9] |
楼文娟, 吴登国, 刘萌萌, 等. 山地风场特性及其对输电线路风偏响应的影响[J]. 土木工程学报, 2018, 51(10): 46. LOU Wenjuan, WU Dengguo, LIU Mengmeng, et al. Properties of mountainous terrain wind field and their influence on wind-induced swing of transmission lines[J]. China Civil Engineering Journal, 2018, 51(10): 46. DOI:10.15951/j.tmgcxb.2018.10.006 |
| [10] |
徐海巍, 楼文娟, 李天昊, 等. 微地形下输电线路跳线的风偏分析[J]. 浙江大学学报(工学版), 2017, 51(2): 264. XU Haiwei, LOU Wenjuan, LI Tianhao, et al. Wind-induced swing investigation on transmission line jumper wire under hilly terrain[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(2): 264. DOI:10.3785/j.issn.1008-973X.2017.02.006 |
| [11] |
张殿生. 电力工程高压送电线路设计手册[M]. 2版. 北京: 中国电力出版社, 2002: 103. ZHANG Diansheng. Electric power engineering design manual of high voltage transmission line[M]. 2nd ed.. Beijing: China Electric Power Press, 2002: 103. |
| [12] |
楼文娟, 周为政, 张跃龙, 等. 输电线路跳线风偏响应分析及手册计算方法修正[J]. 哈尔滨工业大学学报, 2021, 53(10): 79. LOU Wenjuan, ZHOU Weizheng, ZHANG Yuelong, et al. Wind-induced swing response analysis of jump line and modification of manual calculation method[J]. Journal of Harbin Institute of Technology, 2021, 53(10): 79. DOI:10.11918/202105117 |
| [13] |
邵天晓. 架空送电线路的电线力学计算[M]. 2版. 北京: 中国电力出版社, 2003: 33. SHAO Tianxiao. Mechanics calculation of electrical wire of overhead transmission lines[M]. 2nd ed.. Beijing: China Electric Power Press, 2003: 33. |
| [14] |
张希斌. 考虑复杂风环境影响的山地地形CFD数值模拟[D]. 合肥: 合肥工业大学, 2019 ZHANG Xibin. CFD numerical simulation of wind field over complex terrain[D]. Hefei: Hefei University of Technology, 2019 |
| [15] |
LIU Z, ISHIHARA T, HE X, et al. LES study on the turbulent flow fields over complex terrain covered by vegetation canopy[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 155: 60. DOI:10.1016/j.jweia.2016.05.002 |
| [16] |
李正昊, 楼文娟, 章李刚, 等. 地貌因素对垭口内风速影响的数值模拟[J]. 浙江大学学报(工学版), 2016, 50(5): 848. LI Zhenghao, LOU Wenjuan, ZHANG Ligang, et al. Numerical simulation of effects of topographic factors on wind speed in col[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(5): 848. DOI:10.3785/j.issn.1008-973X.2016.05.006 |
 2024, Vol. 56
2024, Vol. 56


