2. 湖南大学 土木工程学院,长沙 410082
2. School of Civil Engineering, Hunan University, Changsha 410082, China
斜拉索作为斜拉桥主要承重构件,在火灾、车船撞击等突发事故和腐蚀疲劳等累积损伤作用下,可发生拉索突然断裂事故,对桥梁的正常使用和行车安全造成极大安全威胁。当拉索失效后结构内力发生重分布,易引发连续倒塌等重大事故[1]。近年国内外发生了多起因桥梁拉索或吊杆断裂而引发的事故:2018年8月14日意大利莫兰迪大桥由于养护不当导致拉索和钢筋严重腐蚀,突然发生坍塌,造成重大人员伤亡;2014年10月29日汝郴高速公路赤石大桥施工过程中,因失火导致大桥9根拉索断裂,断索侧桥面严重下沉,桥梁损坏严重[2]。突发断索事故对桥梁结构安全和运营安全都会造成重要影响。
中国规范[3]建议设计中考虑单根斜拉索失效后,主梁最大应力不超过其设计应力10%。美国后张法协会[4]建议斜拉桥等缆索体系桥梁需能承受一根拉索损失带来的影响,建议将2倍拉索索力等效为断索静力效应反向施加于拉索端部。各国规范多采用基于动力放大系数的拟静力方法分析桥梁断索响应,其中动力放大系数DAF定义为
| $ \text { DAF }=\frac{D_{\text {dynamic, } \max }}{D_{\text {static, } \max }} $ | (1) |
式中: Ddynamic,max为断索作用下桥梁结构最大动力响应值,Dstatic, max为对应的最大静力响应值。
Wolff等[5]研究了多自由度体系在突加荷载作用下的动力响应,并推导了多自由度体系的静力应变能和动力放大系数之间的关系。文献[6-7]研究发现断索引起的全桥结构动力放大效应在非断索位置处常出现远大于静力响应两倍的现象,且该动力放大效应与桥梁结构固有特性、断索持时和索力退化模型等有关。
拉索破断的持时一般很短,断索事故对结构是一种瞬时冲击作用。断索过程中不但拉索索力是时变的,并且桥梁结构动力特性也会发生显著的变化。断索发生前桥梁为完整结构,而断索发生后桥梁模态特性将发生明显变化。晏班夫等[8]为了研究斜拉桥主要失效模式的关系,采用分枝-约界法对斜拉桥进行了拉索抗力衰减及拉索破断的模拟分析,发现了系统主要失效模式具有高度相关性以及拉索破断对剩余系统可靠度的影响规律。张建等[9]通过建立斜拉桥的有限元模型,分析了不同断索工况下对斜拉桥不同位置的影响程度。Minaei等[10]通过构建斜拉结构的整体结构动力模型,提出了一种简化的拉索破断力随时间变化的力学模型。Wu等[11]在考虑材料非线性和几何非线性的基础上,研究腐蚀对吊杆力学性能影响,提出对自锚式悬索桥提高克服意外情况能力的设计建议。Zhang等[12]通过现场检测和有限元模拟,详细研究了赤石大桥在火灾断索工况下的静力性能。Zhou等[13]基于索力突变模型,采用数值模拟方法分析了突发断索场景下斜拉桥的动力响应特征。
综上,现行桥梁规范主要采用动力放大系数方法,以静力方法估算突发断索下桥梁结构响应。该类方法无法反映断索作用下斜拉桥的动力响应特征,可能导致偏于不安全的分析结果。而现有针对断索的桥梁动力分析主要采用突加荷载方式,忽略了断索持续时间、不同断索模式及断索过程中索力和桥梁动力特性的时变特征。
为此,本文针对拉索破断作用下斜拉桥结构动力行为分析研究中的关键问题,提出了一种更为符合实际情况、可考虑拉索破断全过程特征和结构模态时变特性的斜拉桥动力响应分析方法。该方法可更全面和准确地模拟分析断索作用下斜拉桥动力行为全过程特征。依托桥例分析了典型断索场景下桥梁动力行为特征,研究了断索事故关键参数对桥梁动力响应的影响规律。所提出的分析方法可为突发断索作用下桥梁动力行为全过程模拟、车桥系统动力行为预测等相关研究提供参考。
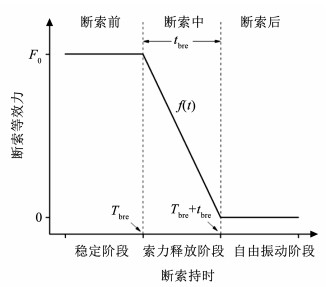
1 考虑模态更新的断索下斜拉桥动力分析方法 1.1 突发断索全过程的索力时变模型断索过程可分为断索前、断索中、断索后3个阶段,如图 1所示。
|
图 1 断索过程示意图 Fig. 1 Schematic diagram of cable breaking process |
如图 1所描述的实际拉索破断全过程这一极短时间过程,其中稳定阶段是指拉索受力破断的前一时刻,此时索力到达极限破断索力F0;索力释放阶段可近似认为索力呈线性衰减;当索力为0时拉索完成破断,系统开始自由振动。
现以函数f(t)表征t时刻下拉索剩余索力百分比,则拉索断裂全过程索力时程可表示为
| $ F(t)=\left\{\begin{array}{l} F_0, t<T_{\text {bre }} \\ {[1-f(t)] \cdot F_0, T_{\text {bre }} \leqslant t \leqslant T_{\text {bre }}+t_{\text {bre }}} \\ 0, t>T_{\text {bre }} \end{array}\right. $ | (2) |
式中:F(t)为断索作用力时程, F0为拉索初始力,Tbre为断索时刻,tbre为断索持时。
从国内外相关文献[13-17]研究结果发现,火灾、腐蚀、撞击等不同诱因导致的拉索破断均有不同的断索本构模型和断索持时取值,根据文献[14]对多种断索诱因下断索本构模型和断索持时参数下斜拉桥动力响应的比较分析研究结果,选取其最不利响应对应的本构简化模型和断索持时参数作为本文后继研究的基本模型和参数。该简化处理主要考虑对于结构设计或安全评估都偏于安全,可使所提方法具有更好的适用性。通过拉索恒应变率拉断试验模拟拉索强度破坏的试验研究,发现钢绞线上轴力呈三直线式释放,开始和结束两段直线斜率较小,轴力释放速率较缓;中间段直线斜率较大,轴力释放速率较快。该模型可较好地描述拉索突发破断的关键特征[15],结合文献[14]研究结果本文采用该索力释放模型。因三段直线斜率相差并不显著,进一步将三直线索力释放模型简化为单直线线性形式:
| $ f(t)=-\frac{1}{t_{\mathrm{bre}}} \cdot t+\frac{t_{\mathrm{bre}}+T_{\mathrm{bre}}}{t_{\mathrm{bre}}} $ | (3) |
根据Zhou等[13]的研究,断索持时tbre取为0.01 s。
1.2 基于模态更新的断索下桥梁动力分析模型基于有限单元法,将桥梁离散成由单元和节点组成的多自由度的结构体系,并在模态坐标下建立桥梁的运动方程。由于局部拉索断裂从而引起桥梁整体刚度改变较小,采用线性分析方法具有足够的精度[15]。
基于模态综合方法桥梁节点位移可表示为
| $ \begin{aligned} \boldsymbol{U}= & \sum\limits_{n=1}^N\left\{\varPhi_n\right\} q_n=\left\{\varPhi_1\right\} q_1+\left\{\varPhi_2\right\} q_2+\cdots+ \\ & \left\{\varPhi_N\right\} q_N=\boldsymbol{\varPhi} \boldsymbol{Q} \end{aligned} $ | (4) |
式中:U为各节点的位移向量;{Φi}为第i阶振型向量;qi为第i阶振型的广义坐标;Φ为振型矩阵;Q为广义坐标向量。
由振型向量关于质量矩阵和刚度矩阵的正交性,得到模态坐标下桥梁的运动方程为
| $ [M]\{\ddot{Q}\}+[C]\{\dot{Q}\}+[K]\{Q\}=\{F(t)\} $ | (5) |
式中:[M]、[C]、[K]分别为模态坐标下的桥梁质量、阻尼和刚度矩阵;{F(t)}为模态力向量。
通过式(2)和式(3)施加断索作用力,该力的作用方向沿着拉索且与原索力方向相反。设破断拉索在主梁上锚点为i节点,在主塔上锚点为j节点。ϕi, xn, b、ϕi, yn, b和ϕi, zn, b分别为主梁振型在i节点的x、y、z方向分量,ϕj, xn, b、ϕj, yn, b和ϕj, zn, b分别为主塔振型在j节点的x、y、z方向分量,fxb、fyb和fzb分别为作用在主梁上作用力的x、y、z方向分量,fxt、fyt和fzt分别为作用在主塔上作用力的x、y、z方向分量。则第n阶模态下的结构所受断索模态广义力为
| $ F_B^n(t)=\sum\limits_{I=x, y, z}\left(\phi_{i, I}^{n, b} f_I^b+\varphi_{j, I}^{n, t} f_I^t\right) $ | (6) |
设总共有N阶振型向量参与计算,则断索作用模态广义力向量为
| $ \{F(t)\}=\boldsymbol{F}_B(t)^{\mathrm{T}}=\left[F_B^1(t), F_B^2(t), \cdots, F_B^N(t)\right]^{\mathrm{T}} $ | (7) |
将式(7)代入到式(5),则突发断索下的桥梁运动方程为
| $ [M]\{\ddot{Q}\}+[C]\{\dot{Q}\}+[K]\{Q\}=\boldsymbol{F}_B(t)^{\mathrm{T}} $ | (8) |
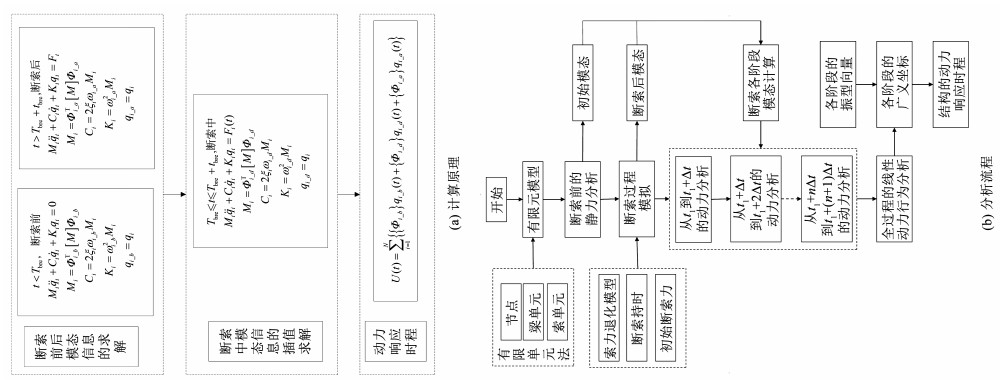
本文提出通过更新断索过程3个阶段(如图 1所示)的桥梁模态信息实现断索作用下桥梁动力行为的高精度模拟。基于模态信息更新的断索作用下斜拉桥动力响应计算原理和计算程序流程如图 2所示。主要过程可归纳为4个步骤:1)断索发生前结构完好,对该状态下桥梁结构有限元模型进行模态分析,基于得到的模态信息生成断索前阶段结构的广义质量、刚度和阻尼矩阵;2)断索发生后部分构件处于缺失状态,通过对移除对应拉索单元后的结构计算模型开展模态分析,更新模态信息用于生成断索后阶段桥梁结构的广义质量、刚度和阻尼矩阵;3)在断索发生时,以完整结构和移除拉索单元后结构的模态信息作为端点值,根据索力释放模型更新每个断索持时内时间步的模态信息,生成索力释放阶段结构的广义质量、刚度和阻尼矩阵;4)将断索全过程不同阶段求解动力方程获得的广义坐标解,乘以对应阶段下的振型向量再进行求和,可得到整个断索历程下结构动力响应时程。
|
图 2 断索下桥梁动力响应计算原理和分析流程 Fig. 2 Principle and flow chart of bridge dynamic response under cable breakage |
图 2(a)中下标b、d和a分别表示断索前、断索中和断索后结构的模态参数,其中断索中结构的模态参数通过插值获得;Tbre表示断索时刻;tbre表示断索持时。图 2(b)详细给出了基于所提方法进行计算程序编制的流程。基于上述分析原理和流程编制了对应的计算程序,可实现考虑不同断索初始力、断索持时和索力退化模型的多种断索场景下桥梁结构动力响应分析。
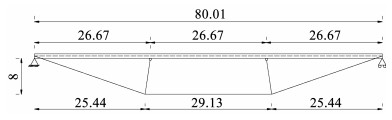
1.3 分析方法的验证为验证所提出突发断索下斜拉桥动力响应分析方法和程序的有效性和准确性,以文献[16]自锚式斜张索桥工程实例为对象,将本文方法与文献计算结果进行对比。该桥例由两根钢斜撑杆分成三跨,主梁为混凝土空心板,梁下斜张拉索由1860级钢绞线组成,通过两根撑杆实现偏转。撑杆与桥面铰接,与拉索固结。桥型总体布置见图 3所示,桥梁结构参数详见文献[16]。采用ANSYS建立该桥例有限元模型如图 4所示,考虑突发断索位置为中跨,主梁和撑杆采用空间梁单元模拟,拉索按实际参数采用索单元模拟。选取文献相同的断索方式和动力计算参数,设置中跨一根拉索破断,索力利用生死单元法以线性退化模型衰减,断索持时0.01 s,阻尼比ξ=2%。
|
图 3 桥例立面布置图(m) Fig. 3 Elevation layout of bridge example(m) |

|
图 4 桥例有限元模型和断索位置示意 Fig. 4 Finite element model of bridge and position diagram of broken cable |
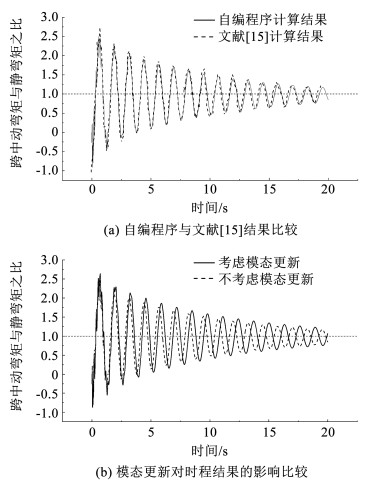
通过前述断索下桥梁动力响应分析原理自编程序,分别进行考虑模态更新和不考虑模态更新的断索全过程主梁跨中截面的动静弯矩之比时程的计算。将不考虑模态更新的时程结果与文献结果进行比较, 如图 5(a)所示,可见二者幅值和时程曲线均吻合良好,表明本文所提出方法和自编程序具有较高的准确性和适用性。图 5(b)为考虑模态更新和忽略模态变化时断索作用下桥梁结构动力响应的比较,可见考虑断索过程特征的模态更新方法较不考虑的情况结构响应峰值明显增大,增幅近10%,同时响应也出现略滞后现象。
|
图 5 断索下主梁跨中动静弯矩比时程比较 Fig. 5 Results of time-history comparison of moment ratio in middle span of main girder under cable break |
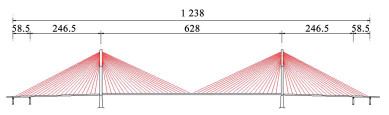
选取某跨长江双塔三跨斜拉桥为工程背景开展研究,主梁为宽37.2 m扁平钢箱梁,全桥布置20根× 8=160根斜拉索,拉索编号从中塔分别向江侧和岸侧进行编号,岸侧拉索编号为A1~A20,江侧拉索编号为J1~J20。主梁索距为12 m和15 m,塔上索距为1.75~2.5 m,全桥总体立面布置如图 6所示,更为详细的桥梁参数见文献[14]。
|
图 6 斜拉桥立面布置(m) Fig. 6 Elevation layout of cable-stayed bridge(m) |
通过ANSYS建立该桥空间有限元模型,塔、梁和桥墩采用空间梁单元模拟,拉索采用索单元模拟,模型如图 7所示。

|
图 7 斜拉桥有限元模型 Fig. 7 Finite element model of cable-stayed bridge |
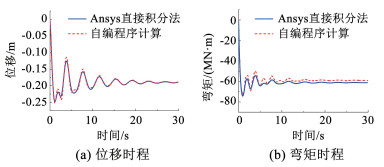
采用自编程序和ANSYS直接积分法对上述桥梁结构进行瞬态动力分析,考察断索作用对该桥例中跨跨中动力响应的影响。将紧邻跨中节点的一对拉索设置为断索,将其删除的同时施加一对相反力,再在0.01 s时间步内将该作用力以线性模式退化至零,计算得到中跨跨中节点竖向动位移时程、动弯矩时程如图 8所示。
|
图 8 斜拉桥动力响应时程比较 Fig. 8 Comparison of dynamic response time history of cable-stayed bridge under two methods |
采用Ansys直接积分法和自编程序振型叠加法下跨中节点的最终弯矩分别为-61.3、-59.1 MN · m,相对误差为3.5%,两种方法下动弯矩时程的衰减过程也比较接近。上述结果再次验证了自编程序的准确性和有效性。
2.2 突发断索作用下斜拉桥动力响应特征分析设定拉索成桥索力为断索初始力,断索持时0.01 s,采用线性索力退化模式,选取典型位置拉索突发破断工况进行分析,考察主梁边跨跨中、中跨跨中及全桥动力响应峰值分布和动力系数,讨论突发断索下斜拉桥动力响应特征。
首先,以边跨内侧a1号索断裂为例,通过Ansys分析并提取完好结构和a1号拉索缺失下桥梁结构模态信息。基于前述提出的考虑断索全过程的斜拉桥动力响应分析方法,计算得到主梁典型位置动力响应时程如图 9所示,全桥主梁动力响应峰值及局部动力放大系数分布如图 10、11所示。

|
图 9 a1拉索突发断裂下边跨跨中动力响应时程 Fig. 9 Time history of mid-span dynamic response under a1 cable burst fracture |
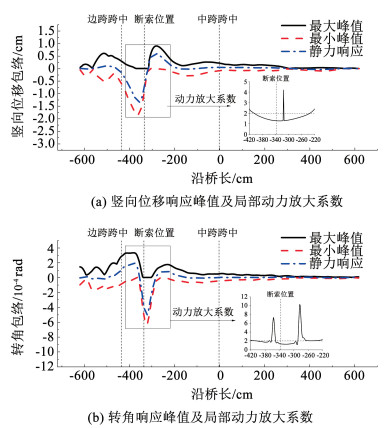
|
图 10 a1拉索破断下主梁位移和局部动力系数分布 Fig. 10 Displacement and local dynamic coefficient of main girder under a1 cable breakage |

|
图 11 全桥主梁内力包络及局部动力系数分布 Fig. 11 Internal force envelope and local dynamic coefficient distribution of main girder |
由图 9可以观察到,a1拉索断裂引起典型位置边跨跨中动力响应在开始即时达到峰值,动位移和动内力响应分别在10 s和5 s内趋于稳定。
由图 10、11结果,发现a1号索断裂引起边跨动力响应明显大于中跨,且主梁动位移和动内力响应峰值出现位置不同,但都出现在断索位置30 m以内。断索位置附近主梁截面虽动力响应幅值较大,但动力放大系数基本在2.0以内,远离断索位置截面的动力系数逐渐变大。
此外,为考察全跨典型位置断索事故对全桥动力响应的影响,分别选取边跨外侧a20、边跨中a9、中跨j1、中跨外侧j20拉索进行单根拉索破断工况分析。现将各工况下桥梁全跨主梁的动位移和动内力峰值进行比较,结果如图 12所示。

|
图 12 典型断索工况下全桥主梁在动力响应极值 Fig. 12 Extreme value of dynamic response of main girder under typical cable breakage condition |
从图 12结果可见,主塔附近a1、j1号短索由于初始索力小且靠近主塔,其断裂引起结构动力响应峰值除剪力外均较小;边跨外侧边索a20远离主塔,突发断裂引起的主梁动位移峰值较大,但动内力峰值均偏小;边跨中索a9位于跨中,其断裂对弯矩峰值影响较大,其他动力响应峰值偏小;中跨江侧边索j20远离主塔,断裂产生的动力响应峰值除剪力外均较大。综上可知,靠近主塔拉索的突发断裂引起的主梁剪力响应较大,跨中拉索断裂引起主梁弯矩响应较大,而外侧远离主塔边索初始索力最大,其破断引起的全桥主梁动位移和弯矩峰值均在断索位置附近取得,且幅值较大。
2.3 断索特征参数对斜拉桥动力响应影响分析不同诱因导致的突发断索事故,其断索过程关键参数存在显著差异。参考既有相关研究[14],选取断索持时这一关键参数对斜拉桥动力响应的影响进行分析。桥例及断索初始索力同本文前述,采用线性索力退化模型,通过改变上述参数应用所提出斜拉桥动力分析方法研究各参数对结构动力响应的影响规律。
多自由度体系在线性索力退化模式作用下结构某一阶振型广义坐标计算表达式[17]为
| $ Z_k=\frac{\left\{\psi_k\right\}^{\mathrm{T}}\left\{F_0\right\}}{M_k \omega_k^2}\left[1+\frac{1}{\pi \frac{t_r}{T_k}} \cdot\left|\sin \frac{\pi t_r}{T_k}\right|\right] $ | (9) |
式中:{ψk}表示第k阶振型向量,F0表示断索初始力,Mk表示第k阶广义质量,ωk表示第k阶圆频率,tr表示断索持时,Tk表示第k阶振型周期。由上式可见断索作用下结构的动力响应与断索持时和结构频率之比有关。
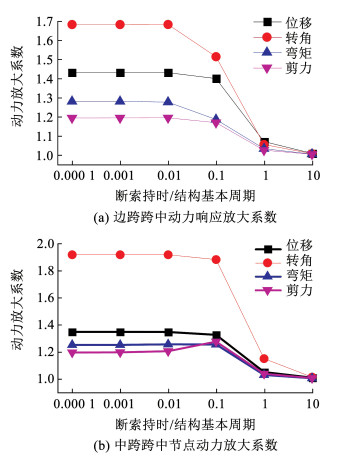
为研究断索持时对桥梁结构动力响应的影响,选取a9和j20号拉索突发破断工况,索力以线性模型释放,分析断索持时和结构频率比tr/Tk从0.000 1至10变化时,呈线性对数增长。分析得到a9拉索破断时边跨跨中和j20号拉索破断时中跨跨中位置的动力响应放大系数结果如图 13所示。
|
图 13 断索持时对边跨和中跨跨中动力放大系数的影响 Fig. 13 Effect of cable brearking duration on the amplification coefficient of dynamic response in middle of side-span and mid-span |
由图 13可见,当断索持时小于0.01倍结构基本周期时,结构响应动力放大系数基本不受断索持时影响;当断索持时处于0.01~1倍结构基本周期时,动力放大系数受断索持时变化影响明显,随持时的增加斜拉桥主梁典型断面(边跨与中跨跨中)响应的动力放大系数变小,且当持时小于0.1倍基本周期时,动力放大系数变化幅度较小;当断索持时大于结构基本周期时,结构动力放大系数变化较小且幅值均接近于1.0。此外,断索作用下边跨跨中和中跨跨中动位移响应的放大系数均大于动内力的放大系数,其中转角位移动力放大效应最为显著,处在1.7~1.9之间;弯矩和剪力动力放大系数在1.0~1.4之间。该桥为工程中常用的典型斜拉桥构造和布置形式,具有一定的代表性。基于本文所提方法,分析得到断索工况下桥例特征位置的各类响应动力放大系数分布规律、断索持时与结构基本周期之比对放大系数的影响规律,对于结构形式相似桥梁具有一定的普适性和参考价值。同时,桥例各类响应的动力放大系数可为同类桥型考虑突发断索的设计和事后结构评定等提供借鉴和参考。
3 结论针对拉索突发破断事故中斜拉桥动力行为计算分析问题,提出一种基于模态信息更新策略且考虑断索过程特征的突发断索条件下斜拉桥动力响应分析方法。依托桥例分析了不同典型断索场景下桥梁动力行为特征,研究了断索持时对桥梁动力响应的影响规律。主要研究结论如下:
1) 提出一种考虑断索全过程时变特征和桥梁模态时变特性的突发断索作用下斜拉桥动力响应分析方法,数值模拟验证分析表明该方法具有较好的精度和适用性。
2) 算例分析表明,单根拉索突发断裂作用下,斜拉桥主梁的动位移和动内力响应峰值不在同一位置,断索位置附近的截面的动力响应较为显著但动力放大效应较小;靠近主塔拉索的突发断裂引起的主梁剪力响应较大,跨中拉索断裂引起主梁弯矩响应较为突出;边索初始索力最大,其破断引起全桥主梁动位移和弯矩峰值较大且均发生在断索位置附近。
3) 断索持时和结构频率比是影响突发断索作用下斜拉桥动力响应的重要参数。算例分析表明当断索持时小于0.01倍结构基本周期时,桥梁典型截面动力响应的动力放大系数达到峰值,且不再受持时变化的影响;当断索持时处于0.01~1.0倍结构基本周期时,随着持时缩短结构响应的动力放大系数变大。
| [1] |
STAROSSEK U. Avoiding disproportionate collapse of major bridges[J]. Structural Engineering International, 2009, 19(3): 289. DOI:10.2749/101686609788957838 |
| [2] |
陈云鹤, 陈兵兵. 斜拉索断裂对斜拉桥动力性能的影响研究[J]. 国防交通工程与技术, 2009, 7(6): 13. CHEN Yunhe, CHEN Bingbing. Study of the effects of the breaking of cables on the dynamic performance of cable-stayed bridges[J]. Traffic Engineering and Technology for National Defence, 2009, 7(6): 13. DOI:10.3969/j.issn.1672-3953.2009.06.005 |
| [3] |
中华人民共和国交通运输部. 公路斜拉桥设计规范: JTG/T 3365-01—2020[S]. 北京: 人民交通出版社, 2020 Ministry of Transport of the People's Republic of China. Design code for highway cable-stayed bridges: JTG/T 3365-01—2020[S]. Beijing: People's Transportation Publishing House, 2020 |
| [4] |
文武松, 彭旭民. 斜拉索设计、试验与安装条例[J]. 国外桥梁, 1997(2): 6. WEN Wusong, PENG Xumin. Specification for design, experiment and installation of stayed-cable[J]. Guowai Qiaoliang, 1997(2): 6. |
| [5] |
WOLFF M, STAROSSEK U. Cable loss and progressive collapse in cable-stayed bridges[J]. Bridge Structures, 2009, 5(1): 17. DOI:10.1080/15732480902775615 |
| [6] |
RUIZ-TERAN A M, APARICIO A C. Dynamic amplification factors in cable-stayed structures[J]. Journal of Sound and Vibration, 2007, 300(1/2): 197. |
| [7] |
MOZOS C M, APARICIO A C. Parametric study on the dynamic response of cable stayed bridges to the sudden failure of a stay, Part Ⅱ: bending moment acting on thepylons and stress on the stays[J]. Engineering Structures, 2010, 32(10): 3301. DOI:10.1016/j.engstruct.2010.07.002 |
| [8] |
晏班夫, 孙雁峰, 邹祺祺. 考虑拉索抗力衰减及破断的斜拉桥可靠性分析[J]. 湖南大学学报(自然科学版), 2017, 44(9): 10. YAN Banfu, SUN Yanfeng, ZOU Qiqi. System reliability analysis on the cable-stayed bridge considering cable breakage and resistance degradation[J]. Journal of Hunan Universtiy (Natural Sciences), 2017, 44(9): 10. |
| [9] |
张建, 杨德灿, 舒鹏. 断索对大跨斜拉桥加劲梁内力的影响分析[J]. 交通科学与工程, 2019, 35(4): 47. ZHANG Jian, YANG Decan, SHU Peng. Analysis on the internal force of stiffening girder of long-span cable-stayed bridges to a cable loss[J]. Journal of Transport Science and Engineering, 2019, 35(4): 47. DOI:10.3969/j.issn.1674-599X.2019.04.008 |
| [10] |
MINAEI A, DANESHJOO F, GOICOLEA J M. Experimental and numerical study on cable breakage equivalent force in cable-stayed structures consisting of low-relaxation seven-wire steel strands[J]. Structures, 2020, 27: 595. DOI:10.1016/j.istruc.2020.05.028 |
| [11] |
WU G, QIU W, WU T. Nonlinear dynamic analysis of the self-anchored suspension bridge subjected to sudden breakage of a hanger[J]. Engineering Failure Analysis, 2019, 97: 701. DOI:10.1016/j.engfailanal.2019.01.028 |
| [12] |
ZHANG Y, FANG Z, JIANG R, et al. Static performance of a long-span concrete cable-stayed bridge subjected to multiple-cable loss during construction[J]. Journal of Bridge Engineering, 2020, 25(3): 04020002.1. |
| [13] |
ZHOU Y, CHEN S. Time-progressive dynamic assessment of abrupt cable-breakage events on cable-stayed bridges[J]. Journal of Bridge Engineering, 2014, 19(2): 159. DOI:10.1061/(ASCE)BE.1943-5592.0000517 |
| [14] |
陈逸民. 考虑突发断索事故的斜拉桥动力行为分析[D]. 哈尔滨: 哈尔滨工业大学, 2021: 22 CHEN Yimin. Dynamic behavior analysis of cable-stayed bridge considering sudden cable breakage accident[D]. Harbin: Harbin Institute of Technology, 2021: 22 |
| [15] |
MOZOS C M, APARICIO A C. Numerical and experimental study on the interaction cable structure during the failure of a stay in a cable stayed bridge[J]. Engineering Structures, 2011, 33(8): 2330. DOI:10.1016/j.engstruct.2011.04.006 |
| [16] |
RUIZ-TERAN A M, APARICIO A C. Response of under-deck cable-stayed bridges to the accidental breakage of stay cables[J]. Engineering Structures, 2009, 31(7): 1425. DOI:10.1016/j.engstruct.2009.02.027 |
| [17] |
MOZOS C M, APARICIO A C. Parametric study on the dynamic response of cable stayed bridges to the sudden failure of a stay, Part Ⅰ: bending moment acting on the deck[J]. Engineering Structures, 2010, 32(10): 32. |
 2024, Vol. 56
2024, Vol. 56


