2. 吉林省地质环境监测总站,长春 130000
2. Jinlin Geological Environment Monitoring Center, Changchun 130000, China
裂隙作为一种重要的不连续面广泛存在于岩体中,对岩体的结构及力学性质起重要作用,影响着岩体的强度和破坏模式。不同尺寸岩体试样包含的裂隙存在差异性,导致裂隙岩体的几何和力学参数存在明显的尺寸效应,当岩体参数达到基本稳定时的试样尺寸即为表征单元体(REV)[1]。表征单元体(REV)是能够反映材料统计平均性质的最小体积,从岩石材料的角度讲,它是表征岩体尺寸效应的参量[2-3]。在工程实践中,研究大尺度岩体所需要的力学参数来源主要是通过实验室测定小尺度岩体参数推算的,但是由于岩石材料的不均匀性和裂隙发育的随机性,这种方法的可靠性难以明确[4-5]。岩体尺寸效应的研究为获取大尺度岩体力学参数提供了一个新方法,它将岩块的实验数据与岩体的力学性质关联起来,在评估岩体力学性质方面具有重要意义[6],是获取岩体的等效参数的重要手段。
首先,当达到几何REV时,裂隙岩体在结构特性上就具有了统计学意义,结构稳定后,才能逐步达到能够用于工程计算和模拟的力学REV。众多学者用不同的几何参数探讨裂隙岩体的尺寸效应,可分为裂隙网络的几何特性和完整岩体的几何特性。前者包括裂隙的密度[7]、张开度[8]以及三维裂隙连通率[9-10]等;后者包括能够体现岩石完整性的块体百分比[11],表征岩体质量好坏和连续程度的岩石质量指标(RQD)[12],以及岩体结构发育程度的地质强度指标(GSI)[13]等。基于此,文献[14]进一步对块体百分比加以修正,提出块体体积综合百分比用以研究裂隙岩体的REV尺寸。以上研究均从几何角度对裂隙岩体的尺寸效应进行研究。
但在岩体工程计算中,掌握岩体的力学性质是合理计算的关键,离开材料力学性质谈REV没有任何意义[15]。因此,确定岩体的力学REV也至关重要。众多学者通过试验法、解析法和数值模拟法研究裂隙岩体的力学参数尺寸效应。文献[16]对现场岩体进行承压板试验和承载力试验进行变形模量的计算,求其REV尺寸,但受到试验设备及成本的限制,所测得的岩石面积分别仅有2 000 cm2和500 cm2。文献[17]通过3D打印技术制作裂隙网络类岩体试件,对120 cm以内的岩体进行单轴压缩试验研究尺寸效应。可见,试验法受到室内和现场条件的影响较大,在大尺度节理岩体的尺寸效应研究上受到限制。解析法将岩体的力学参数与岩石块体间的力学参数通过公式联系起来,提供了一种计算REV尺寸的途径。文献[18]依据中心极限定理推导了REV的数学表达式,其中涉及到了众多参数,例如,应力场、弹性形变势能、岩块及结构面的柔度矩阵、结构面的厚度等。解析法的公式多设计到的参数众多,且获取困难,这在一定程度上制约了其发展。随着计算机的发展,多种数值模拟技术被应用到裂隙岩体的尺寸效应研究中。文献[19-20]通过有限元方法对不同裂隙岩体进行REV特征分析,将岩体视为岩石和裂隙的二元结构。相对于上述有限元方法,离散元更加适用于非连续介质模型的模拟,也被应用到裂隙岩体的研究中。文献[21]采用Goodman节理单元模拟随机节理,通过数值模拟计算变形参数,最终将REV所对应的力学参数应用到的边坡的稳定性计算中。文献[22]运用颗粒流软件开展岩体单轴压缩试验,探究了直线型和分形节理模型峰值应力的尺寸效应,结果表明,二者在尺寸效应规律上较为一致。以上研究多从变形和抗压强度的角度对裂隙岩体的尺寸效应进行诸多研究。值得注意的是,剪切破坏也是边坡失稳的重要因素,当下滑力大于抗滑力时,就会产生滑移面导致边坡失稳,而滑动面的抗滑力主要由岩体的抗剪强度来提供。除此之外,在岩体工程连续介质模型的计算中抗剪强度指标也是必不可少的参数,尤其是在运用强度折减法时,主要是对内聚力内摩擦角进行折减,因此,研究岩体的剪切特性尺寸至关重要。然而目前多数抗剪强度尺寸效应的研究多集中在结构面上,关于岩体的相关研究较少。文献[23]通过室内和现场直剪试验对柱状节理玄武岩以抗剪强度参数为指标进行研究。由于受到试验条件的限制,仅对小尺度岩块进行了研究,研究的岩块最大尺寸为100 cm。数值模拟为大尺度岩体研究提供了途径。
鉴于此,本文基于三维裂隙网络通过颗粒流PFC3D软件进行大尺度裂隙岩体直剪试验数值模拟,从剪切特性的角度定量研究裂隙岩体的尺寸效应,探讨抗剪强度和相关参数的尺寸效应并确定REV尺寸,拟合力学参数和试样尺寸的函数关系。
1 坝肩岩体三维裂隙网络模拟现场结构面多以二维迹线的形式出露,baecher圆盘模型将三维空间内的裂隙视为薄圆盘,裂隙的特征参数可由圆盘模型简便且准确地表征,圆盘直径、方向分别表征裂隙的直径和产状。三维裂隙网络模拟即是在地质结构面现场采样的基础上,以概率理论为依据,利用迹长校正、直径估算等方法将二维迹线扩展为三维空间中的薄圆盘[24]。三维裂隙网络模拟基于蒙特卡洛原理,认为裂隙的特征参数在空间内服从某种特定的分布,将现场采样得到的随机性裂隙进行分布概率拟合,蒙特卡洛抽取随机数以逼近这种分布函数,即可得到与现场结构面分布一致的裂隙网络。
1.1 研究区概况怒江松塔水电站(图 1(a))位于青藏高原东南缘,区内地势总体北高南低,呈阶梯式下降,且具由西北向南东掀斜特征。坝址河段属中山-高山地貌单元,河谷主要呈较对称的“V”形,宽度为80~100 m,两岸岸坡坡度为30°~60°(图 1(b))。坝址区地质构造复杂,断裂较发育,为“入”字型构造体系,节理裂隙发育,可观察到岩脉侵入,如图 1(c)和1(d)所示。坝址区岩性主要为燕山晚期黑云二长花岗岩,粗粒变晶结构,整体块状构造。岩体受构造影响,轻微变质,岩石、矿物普遍碎裂,局部糜棱岩化,矿物定向分布形成片麻状和片理状构造等现象。大型水电站对坝肩岩体的承载能力及抗滑能力要求较高,其力学参数特别是抗剪能力的研究对工程的安全性至关重要,因此本文以西藏怒江松塔水电站右岸坝肩PDC3平硐内的裂隙岩体为例,开展三维裂隙网络模拟和直剪试验数值模拟以确定其剪切特性REV大小。现场结构面多以二维迹线的形式出露,采用矩形窗口法在右岸坝肩的平硐PDC3人工测量裂隙,共采集到裂隙247条。以二维迹线图的方式描述裂隙,如图 2所示。

|
图 1 研究区概况 Fig. 1 Overview of the research area |

|
图 2 裂隙二维迹线图 Fig. 2 Two-dimensional trace diagram of fracture |
采用文献[25]提出的QPSO-FCM全局优化算法对结构面产状进行优势分组,如表 1和图 3所示。划分优势组数为3组,3组裂隙数分别为31、37、179,第1组裂隙陡倾且与坡面大角度相交,第2、3组裂隙分别陡倾坡内和缓倾坡外。平均产状分别为180.3°∠89.8°、278.2°∠85°、118.1°∠32.2°。Fisher分布是表征裂隙产状最常用的概率分布。其概率密度函数为
| $ f(\theta, \varphi)=\frac{k \mathrm{e}^{k\cos \theta} \sin \theta}{4 \varphi \sinh k} $ | (1) |
| 表 1 三维裂隙网络模拟参数 Tab. 1 3D Fracture network simulation parameters |

|
图 3 裂隙优势分组结果 Fig. 3 Results of fracture grouping |
式中:θ为裂隙倾角,φ为裂隙倾向,k为Fisher常数。
Fisher常数k用于描述裂隙产状的离散程度,k值越大,裂隙产状越集中,反之,裂隙产状越离散。常数k计算公式为
| $ k=\frac{N-1}{N-\left|\overrightarrow{r_N}\right|} $ | (2) |
式中: N为裂隙数量,
由于采样窗口的限制,很难直接获取裂隙真实迹长,即裂隙迹长存在取样偏差,因此首先要对现场取样迹长进行校正[26]。迹长校正公式[27]为
| $ \mu=\frac{w h\left(1+R_0-R_2\right)}{\left(1-R_0+R_2\right)\left(w \sin \theta_0+h \cos \theta_0\right)} $ | (3) |
式中:w为采样窗口宽度,h为采样窗口高度,R0为两端相交型裂隙的占比,R2为两端可见型裂隙的占比,θ0为裂隙真倾角。
卡方检验用于对校正后的样本数据分布和标准分布之间的差异性进行判断,卡方值越小,表示越服从某种分布。对常见的迹长分布类型进行卡方检验,组1和组2的迹长服从正态分布,组3服从对数正态分布。基于校正后得到的迹长值,采用文献[28]提出的方法进行直径大小的估算。计算结果见表 1。
1.4 密度计算采用张量法计算裂隙在三维空间内的体积密度P32,计算公式[27]为
| $ P_{32}=\frac{4 \rho_i^1}{\pi E\left(D^2\right)} $ | (4) |
式中:P32为裂隙体积密度,ρi1为每组裂隙法向方向上裂隙间距的倒数,E(D2)为裂隙直径平方的期望值。
1.5 三维裂隙网络生成及验证利用PFC3D软件中DFN模块编制fish语言,基于蒙特卡洛原理将表 2中确定的裂隙参数组合,生成尺寸40 m×40 m×40 m的三维裂隙网络,包含34 250条裂隙,3组裂隙数分别为2 527、2 179以及29 544(图 4)。
| 表 2 数据对比 Tab. 2 Data comparison |

|
图 4 三维裂隙网络 Fig. 4 3D fracture network |
蒙特卡洛模拟按照裂隙参数随机地生成三维裂隙网络,因此模型具有一定随机性和误差,准确度还需要进一步检验。将三维裂隙网络中裂隙信息导出,进行直径分布拟合计算以及产状、密度的计算,与现场裂隙数据对比,以此来检验模型的准确度,见表 2。
2 等效岩体模型 2.1 等效岩体技术颗粒流中以平行黏结和光滑节理两大模型为基础构建等效岩体。颗粒被假设为刚性体,在颗粒间赋予平行黏结模型,在外力作用下相互运动,传递力和力矩,当颗粒间的接触被破坏时,单个颗粒本身不会发生破坏,而是在两个颗粒之间的平行黏结断裂处产生微裂纹,微裂纹积累导致破裂面产生,引起模型整体强度降低,这符合岩石材料的力学特性和破坏特征,可有效表征完整岩石的力学行为[29];光滑节理模型可反映结构面摩擦性质,摩擦行为通过将光滑节理模型分配给两侧颗粒之间所有的接触实现,允许颗粒穿过和滑动,更好地反映试样的脆性破坏特征[30-31]。等效岩体技术即将裂隙网络嵌入到完整岩石中,在完整岩石被裂隙交切部位的平行黏结模型替换为光滑节理模型,其原理见图 5。

|
图 5 等效岩体原理 Fig. 5 Schematic of equivalent rock mass |
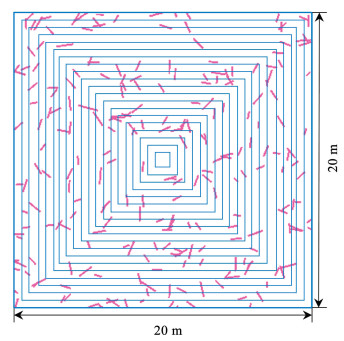
基于上述原理,将平行黏结和光滑节理模型中所涉及的细观参数与实验室所得的完整岩石及结构面的宏观力学参数对标,保证模型能够表征真实岩体。从裂隙网络中每隔1 m切割出一个正方体裂隙网络(图 6),同时,处于边界上的裂隙也切割处理,根据等效岩体技术,嵌入至相应尺寸的颗粒体模型中。
|
图 6 裂隙网络二维切割示意图 Fig. 6 2D Cutting diagram of fracture network |
细观力学参数表征模型的力学性质,当试样宏观力学参数与室内试验结果一致时,便可将该组参数用于实际计算模型根据试验结果统计,坝址区花岗岩单轴抗压强度平均值89 MPa,弹性模量30 GPa。结构面内摩擦系数0.70,内聚力0.10 MPa。
2.2.1 平行黏结模型参数标定文献[32-33]对颗粒尺寸和试样模型的大小关系作出了研究,分别认为模型高度与颗粒尺寸的比例大于100、125、200时对宏观力学参数和破坏模式影响较小,但二者只考虑了模型高径比为2∶ 1的情况。针对高径比1∶ 1时,考虑到颗粒数量对模拟速度的影响,将试样高度与颗粒尺寸的比例设置为62.5,把颗粒数量维持在一定范围内,保证模拟的效果和计算速率。由于不同尺寸模型中颗粒尺寸不一致,因此需要每一个模型都进行细观参数标定,采用试错法进行多次单轴压缩数值模拟试验不断地调整细观参数直到所得到的宏观力学参数与室内试验结果匹配。单轴压缩数值模拟试验如图 7所示。参数标定结果见表 3,标定的宏观参数与实验室力学试验结果误差均在可控范围内,可以用于表征完整花岗岩的力学性质。

|
图 7 单轴压缩数值模拟试验 Fig. 7 Numerical simulation test of uniaxial compression |
| 表 3 平行黏结模型细观参数 Tab. 3 Meso-parameters of parallel bonding model |
构建尺寸为0.1 m×0.1 m×0.1 m且包含贯通裂隙面的立方体试样,裂隙设置在试样的中间。剪切盒由8面“墙体”组成,其中,左右两侧均有两面“墙体”分别组成上下剪切盒,为了方便剪切试验的模拟,上下剪切盒之间设定微小间距。在进行直剪试验时,移动上剪切盒,同时对顶墙施加速度使法向压应力分别维持在1、2、3、4 MPa直至试样被剪坏,根据峰值抗剪强度画出抗剪强度包络线。通过不断地调整细观参数直至与室内结构面直剪试验结果匹配,求出内摩擦系数为0.693,内聚力为0.1 MPa,符合实验室试验结果,其中,法向刚度和切向刚度均为8×109 MPa,摩擦系数为0.8。另外,对于有胶结填充的黏结型裂隙,内聚力由摩擦系数、法向黏结强度和切向黏结强度共同提供,现场裂隙多为非黏结裂隙,其内聚力仅有摩擦系数提供,法向及切向黏结强度设为0。抗剪强度包络线如图 8所示。

|
图 8 裂隙抗剪强度包络线 Fig. 8 Envelope of fracture shear strength |
通过PFC3D对20个不同尺寸的等效岩体依次进行2、3、4 MPa正应力下的直剪试验,做出其抗剪强度包络线,求出内摩擦系数和内聚力。根据不同正应力下的抗剪强度,以及内摩擦系数和内聚力判断REV尺寸。
3.1 抗剪强度尺寸效应由不同尺寸的直剪试验求出其抗剪强度,得出抗剪强度τ与试样长度D的关系图,见图 9。从图 9可以看出,抗剪强度τ随试样长度D的变化而波动,说明试样的抗剪强度存在尺寸效应。在试样长度D为0~7 m时降低,7 m以后逐渐趋于稳定。计算结果局部出现波动,还需要具体判断指标来量化波动的大小以确定REV尺寸。设定差值变化率为量化指标,当差值变化率小于10%时确定为岩体的REV尺寸[34]。差值变化率计算公式为
| $ R_i=\left|\frac{P_i-P_{i-1}}{P_{i-1}}\right| $ | (5) |

|
图 9 不同正应力条件下抗剪强度τ与试样长度D的关系曲线 Fig. 9 Relationship curve between shear strength and sample length under different normal stress condition |
式中:Ri为差值变化率,Pi为第i个试样力学参数值,Pi-1为第i-1个试样力学参数值。
抗剪强度的差值变化率见图 10。由图 10可以看出,正应力σ为2、3、4 MPa时,试样尺寸在11 m× 11 m×11 m之后差值变化率均在10%以下,因此,确定裂隙岩体REV尺寸为11 m×11 m×11 m。

|
图 10 差值变化率 Fig. 10 Difference change rate |
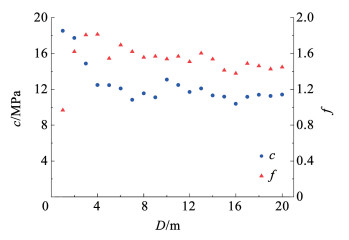
内摩擦系数和内聚力是表征岩体抗剪强度的重要参数。基于上述不同正应力下的抗剪强度,依据莫尔库伦理论求出不同尺寸试样抗剪强度参数,即内摩擦系数和内聚力。根据求得的内摩擦系数及内聚力分别做出其与试样尺寸的关系图,见图 11。
|
图 11 内摩擦系数f、内聚力c与试样长度D的关系 Fig. 11 Relationship between internal friction coefficient, cohesion andsample length |
由图 11可知,内摩擦系数f和内聚力c具有尺寸效应,且二者趋势不同:内摩擦系数f在试样长度D为0~4 m时逐渐增大,随后趋于稳定;在试样长度为0~6 m时,内聚力c逐渐减小,在9~11 m时亦有较大波动。同样采用差值变化率来量化波动的大小,以此作为确定REV的判断指标。内摩擦系数f及内聚力c的差值变化率见图 10。由图 10可知,内摩擦系数f在试样尺寸6 m×6 m×6 m以后的差值变化率均小于10%,因此,以内摩擦系数f为指标的REV尺寸为6 m×6 m×6 m。内聚力在试样尺寸11 m×11 m×11 m之后的试样的差值变化率均小于10%,判定以内聚力c为指标的REV尺寸为11 m×11 m×11 m。可见,以不同参数为指标确定的REV尺寸不尽相同,其中,依据内聚力和内摩擦系数求出的REV尺寸差别较大,内摩擦系数先达到稳定。
综合比较抗剪强度REV尺寸、内摩擦系数REV尺寸以及内聚力REV尺寸,选取11 m×11 m×11 m作为裂隙岩体的剪切特性REV尺寸。
3.3 剪切特性函数关系拟合为了探究剪切特性力学参数之间与试样尺寸之间是否存在某种规律,对不同尺寸、不同正应力下的抗剪强度以及内聚力和内摩擦系数分别进行函数拟合。
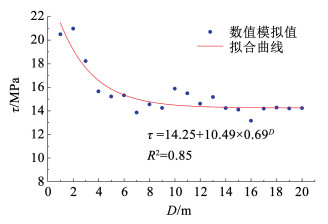
非线性回归拟合迭代计算表明,抗剪强度、内聚力以及内摩擦系数与试样尺寸之间均存在指数函数关系。由于篇幅限制,在此对抗剪强度的分析仅以2 MPa正应力为例,抗剪强度、内聚力以及内摩擦系数与试样尺寸之间拟合的相关系数分别为0.85、0.89、0.89,拟合程度较好,如图 12~14所示。拟合关系式分别为
| $ \tau=14.25+10.49 \times 0.69^D $ | (6) |
| $ c=11.39+12.25 \times 0.64^D $ | (7) |
| $ f=\left\{\begin{array}{l} 1.42+0.37+3.67 \times\left(0.013-\mathrm{e}^{-D / 0.69}\right), D<3 \\ 1.42+0.37 \mathrm{e}^{-(D-3) / 6.75}, D>3 \end{array}\right. $ | (8) |
|
图 12 抗剪强度τ与试样长度D拟合 Fig. 12 Fitting of shear strength and samplelength |

|
图 13 内聚力c与试样长度D拟合 Fig. 13 Fitting of cohesion and samplelength |

|
图 14 内摩擦系数f与试样长度D拟合 Fig. 14 Fitting of internal friction coefficient and samplelength |
式中:τ为抗剪强度,c为内聚力,f为内摩擦系数,D为试样长度。
根据以上拟合关系式可知,当试样尺寸趋于无穷时,抗剪强度、内聚力和内摩擦系数均会趋于一个定值,符合尺寸效应最终会使力学参数达到稳定的特征,这也验证了剪切特性尺寸效应的存在和函数关系式的合理性。并且抗剪强度和内聚力与试样尺寸的关系均可由式y=a+b×cx来表达,其中,y为抗剪强度/内聚力,x为试样长度,a, b, c为常数。
4 结论本文以怒江松塔水电站坝肩岩体为研究对象,基于蒙特卡洛原理构建了岩体结构三维网络模型,利用PFC3D实现了不同尺寸等效结构岩体的直剪模拟试验,从剪切特性角度揭示了复杂结构岩体的尺寸效应。其主要结论如下:
1) 研究区坝肩岩体的抗剪强度、内聚力、内摩擦角均存在明显的尺寸效应。试样尺寸在一定范围内时,抗剪强度、内聚力随试样尺寸的增大而增大,而内摩擦系数随试样尺寸的增大而减小。
2) 基于差值变化率定量分析剪切力学参数的变化程度以确定REV尺寸,结果表明抗剪强度、内聚力、内摩擦系数的REV尺寸不完全一致,针对不同岩体工程应分别考虑其影响。为安全起见,本文综合确定研究区坝肩岩体的剪切特性REV尺寸为11 m×11 m×11 m。
3) 通过非线性回归拟合分析,确定抗剪强度、内聚力、内摩擦系数与岩体试样尺寸之间近似存在指数函数关系,将为后续确定研究区坝基岩体抗剪强度参数提供参考。
| [1] |
安玉华, 王清. 基于三维裂隙网络的裂隙岩体表征单元体研究[J]. 岩土力学, 2012, 33(12): 3775. AN Yuhua, WANG Qing. Study on the unit body of fractured rock mass representation based on three-dimensional fracture network[J]. Geotechnical Mechanics, 2012, 33(12): 3775. DOI:10.16285/j.rsm.2012.12.024 |
| [2] |
朱万成, 张敏思, 张洪训, 等. 节理岩体表征单元体尺寸确定的数值模拟[J]. 岩土工程学报, 2013, 35(6): 1121. ZHU Wancheng, ZHANG Minsi, ZHANG Hongxun, et al. Numerical simulation of determination of unit size of jointed rock mass[J]. Journal of Geotechnical Engineering, 2013, 35(6): 1121. |
| [3] |
卢波, 葛修润, 朱冬林, 等. 节理岩体表征单元体的分形几何研究[J]. 岩石力学与工程学报, 2005, 24(8): 1355. LU Bo, GE Xiurun, ZHU Donglin, et al. Fractal geometry study of jointed rock mass[J]. Journal of Rock Mechanics and Engineering, 2005, 24(8): 1355. DOI:10.3321/j.issn:1000-6915.2005.08.013 |
| [4] |
HUANG M, LIU D, HONG C, et al. Representative sample sampling method for size effect experiment of jointed rock mass[J]. Geofluids, 2020, 2020: 1. DOI:10.1155/2020/8870387 |
| [5] |
YANG T, LIU H Y, TANG C A. Scale effect in macroscopic permeability of jointed rock mass using a coupled stress-damage-flow method[J]. Engineering Geology, 2017, 228: 121. DOI:10.1016/j.enggeo.2017.07.009 |
| [6] |
倪海江, 徐卫亚, 石安池, 等. 基于离散元的柱状节理岩体等效弹性模量尺寸效应研究[J]. 工程力学, 2015, 32(3): 90. NI Haijiang, XU Weiya, SHI Anchi, et al. Study on the size effect of equivalent elastic modulus of columnar jointed rock mass based on discrete element[J]. Engineering Mechanics, 2015, 32(3): 90. DOI:10.6052/j.issn.1000-4750.2013.09.0849 |
| [7] |
LIU Y, WANG Q, CHEN J, et al. Determination of geometrical REVs based on volumetric fracture intensity and statistical tests[J]. Applied Sciences-Basel, 2018, 8(5): 800. DOI:10.3390/app8050800 |
| [8] |
ZHAO M, SONG S, WANG F, et al. A method to interpret fracture aperture of rock slope using adaptive shape and unmanned aerial vehicle multi-angle nap-of-the-object photogrammetry[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2023, 224(23): 1674. DOI:10.1016/j.jrmge.2023.07.010 |
| [9] |
王晓明, 夏露, 郑银河, 等. 基于三维裂隙连通率的裂隙岩体表征单元体研究[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3297. WANG Xiaoming, XIA Lu, ZHENG Yinhe, et al. Study on the unit body of fractured rock mass based on three-dimensional fracture connectivity[J]. Journal of Rock Mechanics and Engineering, 2013, 32(Sup.2): 3297. |
| [10] |
SONG S, SUN F, CHEN J, et al. Determination of RVE size based on the 3D fracture persistence[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 2017, 50(1): 60. DOI:10.1144/qjegh2016-127 |
| [11] |
夏露, 刘晓非, 于青春. 基于块体化程度确定裂隙岩体表征单元体[J]. 岩土力学, 2010, 31(12): 3991. XIA Lu, LIU Xiaofei, YU Qingchun. Determination of representative unit of fractured rock mass based on the degree of blockiness[J]. Geotechnical Mechanics, 2010, 31(12): 3991. DOI:10.16285/j.rsm.2010.12.048 |
| [12] |
张文, 陈剑平, 苑晓青, 等. 基于三维裂隙网络的RQD尺寸效应与空间效应的研究[J]. 岩石力学与工程学报, 2012, 31(7): 1437. ZHANG Wen, CHEN Jianping, YUAN Xiaoqing, et al. Research on size effect and space effect of RQD based on three-dimensional fracture networ[J]. Journal of Rock Mechanics and Engineering, 2012, 31(7): 1437. DOI:10.3969/j.issn.1000-6915.2012.07.017 |
| [13] |
HUANG H, SHEN J, CHEN Q, et al. Estimation of REV for fractured rock masses based on geological strength index[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 126: 1. DOI:10.1016/j.ijrmms.2019.104179 |
| [14] |
CHEN Q, YIN T, NIU W, et al. Study of the geometrical size effect of a fractured rock mass based on the modified blockiness evaluation method[J]. Arabian Journal of Geosciences, 2018, 11(11): 286. DOI:10.1007/s12517-018-3645-9 |
| [15] |
向文飞, 周创兵. 裂隙岩体表征单元体研究进展[J]. 岩石力学与工程学报, 2005, 24(增刊2): 5686. XIANG Wenfei, ZHOU Chuangbing. Research progress of characterizing unit body of fractured rock mass[J]. Journal of Rock Mechanics and Engineering, 2005, 24(Sup.2): 5686. |
| [16] |
喻勇, 肖国强, 王法刚. 岩体变形模量的尺寸效应[J]. 岩土力学, 2003, 24(增刊1): 47. YU Yong, XIAO Guoqiang, WANG Fagang. Size effect of deformation modulus of rock mass[J]. Geotechnical Mechanics, 2003, 24(Sup.1): 47. DOI:10.16285/j.rsm.2003.s1.012 |
| [17] |
罗国立, 张科, 齐飞飞, 等. 基于3D打印的裂隙岩体力学特性尺寸效应及各向异性初探[J]. 岩土力学, 2023, 44(增刊1): 107. LUO Guoli, ZHANG Ke, QI Feifei, et al. A preliminary investigation on the size effect and anisotropy of mechanical properties of fractured rock body based on 3D printing[J]. Geotechnics, 2023, 44(Sup.1): 107. DOI:10.16285/j.rsm.2022.0757 |
| [18] |
周创兵, 於三大. 论岩体表征单元体积REV——岩体力学参数取值的一个基本问题[J]. 工程地质学报, 1999, 7(4): 332. ZHOU Chuanbing, YU Sanda. On the representative elementary volume of a rock mass, REV—a fundamental problem in the valuation of mechanical parameters of a rock mass[J]. Journal of Engineering Geology, 1999, 7(4): 332. DOI:10.3969/j.issn.1004-9665.1999.04.008 |
| [19] |
陈卫忠, 杨建平, 邹喜德, 等. 裂隙岩体宏观力学参数研究[J]. 岩石力学与工程学报, 2008, 27(8): 1569. CHEN Weizhong, YANG Jianping, ZOU Xide, et al. Study on macroscopic mechanical parameters of fractured rock mass[J]. Journal of Rock Mechanics and Engineering, 2008, 27(8): 1569. DOI:10.3321/j.issn:1000-6915.2008.08.005 |
| [20] |
杨建平, 陈卫忠, 戴永浩. 裂隙岩体变形模量尺寸效应研究Ⅰ: 有限元法[J]. 岩土力学, 2011, 32(5): 1538. YANG Jianping, CHEN Weizhong, DAI Yonghao. Study on size effect of deformation modulus of fractured rock mass Ⅰ: finite element method[J]. Geotechnical Mechanics, 2011, 32(5): 1538. DOI:10.3969/j.issn.1000-7598.2011.05.039 |
| [21] |
刘春. 岩体REV和力学参数的数值模拟[J]. 哈尔滨工业大学学报, 2009, 41(4): 236. LIU Chun. Numerical simulation of rock REV and mechanical parameters[J]. Journal of Harbin Institute of Technology, 2009, 41(4): 236. DOI:10.3321/j.issn:0367-6234.2009.04.055 |
| [22] |
王培涛, 刘操, 马驰, 等. 基于离散裂隙网络的岩体各向异性莫尔-库仑表征方法研究[J]. 岩石力学与工程学报, 2023, 42(增刊1): 3266. WANG Peitao, LIU Cao, MA Chi, et al. Anisotropic Mohr-Coulomb characterisation of rock body based on discrete fracture network[J]. Journal of Rock Mechanics and Engineering, 2023, 42(Sup.1): 3266. DOI:10.13722/j.cnki.jrme.2022.0627 |
| [23] |
刘顺桂, 池永翔, 王思敬, 等. 柱状节理玄武岩体抗剪强度参数尺寸效应研究[J]. 工程地质学报, 2009, 17(3): 367. LIU Shungui, CHI Yongxiang, WANG Sijing, et al. Study on size effect of shear strength parameters of columnar jointed basalt[J]. Journal of Engineering Geology, 2009, 17(3): 367. DOI:10.3969/j.issn.1004-9665.2009.03.014 |
| [24] |
陈剑平. 三维网络结构岩体力学架构与展望[J]. 工程地质学报, 2022, 30(1): 21. CHEN Jianping. Mechanical framework and prospect of rock mass with three-dimensional network structure[J]. Journal of Engineering Geology, 2022, 30(1): 21. DOI:10.13544/j.cnki.jeg.2021-0728 |
| [25] |
SONG S, WANG Q, CHEN J, et al. Fuzzy C-means clustering analysis based on quantum particle swarm optimization algorithm for the grouping of rock discontinuity sets[J]. KSCE Journal of Civil Engineering, 2016, 21(4): 1115. DOI:10.1007/s12205-016-1223-9 |
| [26] |
陈剑平. 岩体随机不连续面三维网络数值模拟技术[J]. 岩土工程学报, 2001, 23(4): 397. CHEN Jianping. Numerical simulation technology of three-dimensional network of random discontinuities in rock mass[J]. Journal of Geotechnical Engineering, 2001, 23(4): 397. DOI:10.3321/j.issn:1000-4548.2001.04.003 |
| [27] |
KULATILAKE P, WU T H. Estimation of mean trace length of discontinuities[J]. Rock Mechanics and Rock Engineering, 1984, 17(4): 215. DOI:10.1007/BF01032335 |
| [28] |
ODA M. Fabric tensor for discontinuous geological materials[J]. Soils and Founations, 1982, 22(4): 36. |
| [29] |
王浩然, 王志亮, 王昊辰, 等. 真三轴压缩下大理岩强度、变形与损伤特征数值[J]. 哈尔滨工业大学学报, 2022, 54(8): 100. WANG Haoran, WANG Zhiliang, WANG Haochen, et al. Strength, deformation and damage characteristics of marble under true triaxial compression[J]. Journal of Harbin Institute of Technology, 2022, 54(8): 100. DOI:10.11918/202110065 |
| [30] |
程毅, 丁耀胜, 李松龄, 等. 离散元光滑节理模型中颗粒"非正常重叠"的机理研究[J/OL]. 工程力学, 2023: 1(2023-03-27). http://kns.cnki.net/kcms/detail/11.2595.O3.20230325.1855.002.html CHENG Yi, DING Yaosheng, LI Songling, et al. Study on the mechanism of "abnormal overlap" of particles in discrete element smooth-joint model[J/OL]. Engineering Mechanics, 2023: 1(2023-03-27). http://kns.cnki.net/kcms/detail/11.2595.O3.20230325.1855.002.html |
| [31] |
殷鹏飞, 杨圣奇, 高峰, 等. 不同节理模型在层状复合岩石离散元模拟中的应用[J]. 采矿与安全工程学报, 2023, 40(1): 164. YIN Pengfei, YANG Shengqi, GAO Feng, et al. Application of different joint models in discrete element simulation of layered composite rocks[J]. Journal of Mining and Safety Engineering, 2023, 40(1): 164. DOI:10.13545/j.cnki.jmse.2021.0706 |
| [32] |
尹小涛, 郑亚娜, 马双科. 基于颗粒流数值试验的岩土材料内尺度比研究[J]. 岩土力学, 2011, 323(4): 1211. YIN Xiaotao, ZHENG Yana, MA Shuangke. Study of inner scale ratio of rock and soil material based on numerical tests of paritical flow code[J]. Geotechnical Mechanics, 2011, 323(4): 1211. DOI:10.16285/j.rsm.2011.04.017 |
| [33] |
宿辉, 杨家琦, 胡宝文, 等. 颗粒离散元岩石模型的颗粒尺寸效应研究[J]. 岩土力学, 2018, 39(12): 4642. SU Hui, YANG Jiaqi, HU Baowen, et al. Study of partical size effect of rock model based on partical discrete element method[J]. Geotechnical Mechanics, 2018, 39(12): 4642. DOI:10.16285/j.rsm.2017.0945 |
| [34] |
ZHOU Z, SUN J, LAI Y, et al. Study on size effect of jointed rock mass and influencing factors of the REV size based on the SRM method[J]. Tunnelling and Underground Space Technology, 2022, 127(9): 1. DOI:10.1016/j.tust.2022.104613 |
 2024, Vol. 56
2024, Vol. 56


