近年来,自然和人为灾害频发,城市路网交通疏散已经成为一个重要的课题。当突发事件发生时,确定合适安全的疏散计划是十分必要的。在疏散问题的影响因素研究中,段晓红等[1]考虑行程时间、交通负荷、路段长度等因素制定交通疏散策略,保证应急车辆调度和疏散救援路径的可靠性。Zhang等[2]基于交通网络系统弹性的特点,以最小化所有用户总行程时间为优化目标,生成突发事件下的路网交通疏散方案。Cassol等[3]以平均疏散时间、总疏散时间等作为疏散性能指标,制定不同仿真环境下的疏散计划并加以评估。分析发现,现有文献中路段的行程时间通常被认为是疏散过程中重要的影响因素,而少有学者结合交叉口车流冲突这一因素考虑。在应急疏散决策方面,部分学者从交通管理角度出发,考虑交叉口冲突消除、转向限制等交通组织策略[4],对路网交通疏散问题构建双层规划模型,上层确定合适的交通组织方案,下层进行用户均衡或系统最优的交通流分配[5]。还有学者从实时控制的角度,对交通疏散问题进行研究,通过调整信号配时方案来减少不同疏散方向冲突,从而提升疏散效率,例如Yuan等[6]以元胞传输模型模拟疏散网络的交通流演变规则,使用信号配时优化的策略来降低疏散全部交通所需的时间。上述的模型问题求解常使用元启发式算法,虽然能较快实现收敛,但是无法评判所求解与最优解的偏离程度。设定参数敏感性较高且操作性较强,每次运行结果的随机性较大,实际中运用较为困难。而拉格朗日松弛方法[7]可克服此类缺陷,利用优化目标上下界之间的相对差值来评价解的质量,具有调参处理方便、稳定性好等优点。此外,目前的研究大多为确定性规划问题,问题参数的设置往往是先验已知的,而参数改变产生的波动性对疏散计划的影响较大,可能导致模型不再适用。因此,基于不确定性的路网交通疏散策略研究更具现实意义。在疏散问题不确定性的研究方面,Lim等[8]考虑疏散撤离人员需求的不确定性,构建了一种分布式鲁棒机会约束模型来制定可靠的疏散策略。Yang等[9]以多优先级元胞传输模型为基础,基于疏散需求的不确定性搭建鲁棒优化模型,实现疏散响应决策。Lim等[10]则针对道路容量在应急规划时的随机不确定性场景,结合概率弧的容量约束构建最小成本网络流模型,确保疏散方案的可靠性。以往学者[11]探究的主要是应急疏散需求和道路容量不确定性的影响,往往忽略对交通出行成本不确定性的量化分析。
综上所述,目前考虑交叉口冲突风险因素的路网交通疏散研究较少,而疏散策略求解大多采用启发式算法,且现有针对疏散问题不确定性的研究主要表现在对疏散需求和道路容量的随机性考虑,较少涉及交通出行成本方面。基于此,本文提出一种考虑出行成本不确定性的路网交通疏散策略。通过创建新型时空耦合网络图,引入行程时间和冲突风险因素,从而对交通出行成本不确定性加以量化,结合边际约束搭建鲁棒优化模型,运用模型重构技术和改进的拉格朗日近似求解算法对模型进行优化求解,最后结合数值算例验证了模型的有效性。研究成果丰富了鲁棒优化和交通疏散决策相结合的有关理论,有助于降低突发事件造成的生命财产损失,可为应急指挥部门制定疏散处置方案提供依据。
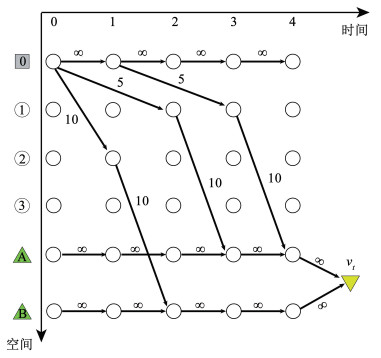
1 问题描述 1.1 时空耦合网络图创建本文基于路段出行和节点等待的时空逻辑关系,提出了一种新型时空耦合网络图的创建方法,进而对路网交通疏散问题加以建模。下面以图 1中的示例进行说明[12],G(N, A)表示物理网络,疏散起点编号为0,疏散需求为20,灾害发生时需要通过指定的计划将车辆从起点0疏散到安全终点编号为A和B的位置。0到1弧段的标注(2, 5)表示的是路段行程时间se=2和通行能力ue=5。

|
图 1 疏散网络 Fig. 1 Evacuation network |
时空网络图Gx=(Nx, Ax)的创建过程如下:1)首先,将疏散撤离的允许时长离散划分为多个等长的时间区间,即用步长集合H={1, …, T}表示,这里T为离散后的最大时间步。2)其次,在每一个时间步内,对道路网络的所有空间节点加以复制,即拓展成空间-时间节点(i, t)形式;同时物理弧段e=(i, j)用关联的时空弧代替, 即et=((i, t), (j, s)),其中,索引(i, t)表示的是i节点t时刻,(j, s)表示的是j节点s时刻,路段行程时间为se=s-t。3)所有的终点需要连接到一个超级虚拟终点vt=(z, T),用以接受所有的疏散交通车流的需求,连接的虚拟弧段通行能力设为无穷大,其出行时间置为0。
简要的疏散过程如图 2所示,其中弧段边标注的是通行能力。本文对时空耦合网络图作了改进,增加了时空通行弧和等待弧的连接。对于中间的时空节点来说,在原先单一行程时间弧et=((i, t), (j, s))的基础上,增加了(i, t)到节点(j, s-1)和(j, s+1)的通行弧,使得路段行程时间的可选择范围变大;另外,对中间时空节点添加了等待弧,符号表示为((i, t), (i, t+1))。因此,改进的时空耦合网络图能更好地描述路段延误和节点等待的状况。
|
图 2 时空耦合网络图 Fig. 2 Spatio-temporal coupling network graph |
时空弧段的成本(费用)通常表示为路段的行程时间,但是如果中间时空节点的汇入和流出涉及到多条路径流向,则可能会在该节点发生交通冲突。因此,需要对车流冲突风险干扰造成的不确定成本进行度量,记为冲突风险成本。
冲突风险成本定义为基准行程时间下出行效益的增减量。为避免时空出行成本中出现负值,定义冲突风险成本的波动值为
| $ \sigma_{e_t}=\mu_{e_t} \cdot p $ | (1) |
式中:μet为时空弧et索引的路段时间成本,p为冲突风险度量参数,取值为[0, 1],若取1,说明冲突风险成本产生的正负增益上限最大;若取0,说明不存在可波动的范围。为确定p值,本文提出了一种基于冲突信息积的冲突风险度量参数计算方法,流程如图 3所示。

|
图 3 冲突风险度量参数计算过程 Fig. 3 Computational process of conflict risk metric parameters |
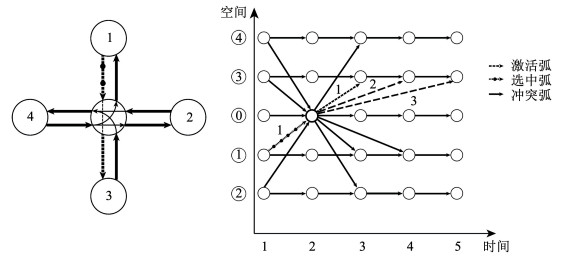
下面通过示例对计算过程说明(图 4),图 4左的中心节点编号为0,假设选中的时空弧索引为(1, 1, 0, 2),则:1)确定后序物理节点集合,以选中物理弧(1, 0)的后序节点3为例。由于时空节点(0, 2)对应后续到达节点3的时间不唯一,连接弧有多条,其中激活的转向弧(1, 0, 3)信息浓度是时空节点(0, 2)前后所有关联弧行程时间成本的倒数之积,则转向弧(1, 0, 3)信息浓度为
|
图 4 冲突风险度量参数计算示意 Fig. 4 Schematic calculation of conflict risk metric parameters |
本文所构建的模型以最小化总疏散交通的出行成本为目标,网络流守恒、通行能力等为约束,疏散策略需确定:合适的发车时间内从疏散起点出发到安全终点的车辆数,疏散起点出发到安全终点的疏散路径以及车道反转(lane reversal)的部署位置。为便于求解,模型需满足以下假设:1)疏散过程中道路网络上车辆的路段行程时间符合预定的区间范围;2)根据合理的预测手段可以事先得出疏散截止时间、路段阻塞时间、通行能力等相关参数。
2.1 目标函数以最小化总交通出行成本为优化目标,目标函数:
| $ \operatorname{Min} \sum\limits_{k \in \varepsilon} \sum\limits_{(i, t, j, s) \in A^x}\left(c_{i, t, j, s}^k \cdot x_{i, t, j, s}^k\right) $ | (2) |
式中:cki, t, j, s为疏散起点k从时空节点(i, t)到(j, s)的出行成本,xki, t, j, s为对应疏散的车流量。
2.2 约束条件| $ \sum\limits_{e \in \delta^{-}(v)} z_e^k-\sum\limits_{e \in \delta^{+}(v)} z_e^k=0, \forall v \in T, k \in \varepsilon $ | (3) |
| $ \begin{aligned} & \sum\limits_{(i, t, j, s) \in \delta^{-}(v)} x_{i, t, j, s}^k-\sum\limits_{\left(j, s, i^{\prime}, t^{\prime}\right) \in \delta^{+}(v)} x_{j, s, i^{\prime}, t^{\prime}}^k= \\ & \left\{\begin{array}{ll} -d_k, & v(j=k, s=1) \\ 0, & \text { 其他 } \end{array}, \forall v \in N^x \backslash\left\{v_t\right\}, k \in \varepsilon\right. \\ & \end{aligned} $ | (4) |
| $ \sum\limits_{k \in E} \sum\limits_{(i, t, j, s) \in \delta^{-}(v)} x_{i, t, j, s}^k=\sum\limits_{k \in \varepsilon} d_k, v=v_t $ | (5) |
| $ \sum\limits_{k \in \varepsilon} x_{i, t, j, s}^k \leqslant u_{i, j, t}, \forall(i, t, j, s) \in A^x \backslash A_c^x $ | (6) |
| $ \begin{gathered} \sum\limits_{k \in \varepsilon} x_{i, t, j, s}^k \leqslant y_{(j, i)} u_{j, i, t}+\left(1-y_{(i, j)}\right) u_{i, j, t}, \\ \forall(i, t, j, s) \in A_c^x \end{gathered} $ | (7) |
| $ y_{(i, j)}+y_{(j, i)} \leqslant 1, \forall(i, j) \in \hat{A}_c $ | (8) |
| $ x_{(i, t, j, s)}^k \leqslant u_{i, j, t} \cdot z_{(i, j)}^k, \forall(i, t, j, s) \in A^x, k \in \varepsilon $ | (9) |
| $ \sum\limits_{(i, j) \in A} w_{i, j}^{k, l} z_{i, j}^k \leqslant W_l^k, \forall k \in \varepsilon, l \in L $ | (10) |
式(3)为路径连续性约束,对于某一疏散路径的起点途径的任意中间节点来说,其前序和后序的激活路段的拓扑总数需保持一致。式(4)和式(5)是网络流守恒约束,对于疏散起点来说,对应的疏散需求等于出发的时空起点所连接的所有出度弧车流之和;对于疏散终点,由于终点的到达量未知,因此设置一个虚拟终点来连接。
式(6)、(7)分别代表的是不部署和可部署逆流操作的对应约束。当y(i, j)=1时,则y(j, i)=0,即路段(i, j)被部署逆流,路段通行能力为0,反向路段(j, i)的属性则是原两个方向的路段通行能力之和。式(8)说明的是对于一个双向车辆行驶的路段来说,最多仅允许一个方向被部署车道反转的逆流操作[15]。式(9)为路段-流量对应约束,如果道路网络的路段(i, j)不属于被激活使用的疏散路径序列,则从疏散起点出发的时空网络对应弧的车辆数为0。式(10)是边际约束,即各关联路段资源权重之和不超过各疏散起点对应路径资源权重的上限,具体测度可以是路径距离、行驶所需油耗或排放等。
本文涉及的决策变量:
| $ \begin{cases}x_e^k \geqslant 0, & \forall e \in A^x, k \in \varepsilon \\ y_e \in\{0, 1\}, & \forall e \in A_c \\ z_e^k \in\{0, 1\}, & \forall e \in A \cup A_{w v}\end{cases} $ | (11) |
文中详细的符号释义,可参见表 1。
| 表 1 符号说明 Tab. 1 Symbol description |
本文对目标函数中的成本系数进行了不确定性阐释[16],令疏散计划不因出行成本的不确定性而在实施过程中失去意义的同时,不过度影响目标函数的值。
2.3.1 预算不确定集不确定性的出行成本变量需借助不确定集来表达,这里以预算不确定集的形式来刻画,即
| $ \tilde{c}_{e_t}=\mu_{e_t}+\sigma_{e_t} r_{e_t} $ | (12) |
式中:
| $ R=\left\{r\mid\sum\limits_{e_t=1}^n \left|r_{e_t}\right| \leqslant \varGamma, r_{e_t} \in[-1, 1], \forall e_t=1, \cdots, n\right\} $ | (13) |
式中:ret为真实情况的波动程度,Γ为表现不确定性的预算参数,用于调节优化解的鲁棒性,以控制解的保守程度。换句话说,Γ的取值也反映出决策者对不确定性因素的态度。取值越大,说明对成本不确定性波动的顾虑越高,态度选择倾向越保守的情况。
2.3.2 min-max模型因此,考虑不确定性的鲁棒对应式(robust counterpart)表达为
| $ {\min _{x \in {\mathbb{R}^{|\varepsilon \times A^x|}}, y \in \{ 0, 1\} {n^\prime }, z \in \{ 0, 1\} {n^{\prime \prime }}}}{\max _{r \in \varepsilon }}\sum\limits_{{e_t} = 1}^n {\left( {{\sigma _{{e_t}}}{r_{{e_t}}}} \right)} {x_{{e_t}}} + \sum\limits_{{e_t} = 1}^{\left| {\varepsilon \times {A^x}} \right|} {\left( {{\mu _{{e_t}}}} \right)} {x_{{e_t}}} $ | (14) |
| $ \text { s. t. } \quad c(3-11) $ |
式中c(3-11)表示的是模型约束条件为文中公式(3)~(11),n′与n″分别对应的是对应决策变量下所属集合的空间长度,n为不确定参数集的空间长度,小于对应决策变量的集合,原因是考虑到存在部分时空弧始终无风险冲突的情况。
3 方法设计求解针对上述提出的鲁棒优化问题,先进行原模型重构[17],将其转换为等价的混合整数线性规划形式,进而选用改进拉格朗日松弛(adapted Lagrangian relaxation, ALR)方法加以求解。
3.1 原模型重构引入辅助变量来处理不确定集的绝对值约束,即
| $ r_{e_t}^{+}=\max \left\{0, r_{e_t}\right\} $ | (15) |
| $ r_{e_t}^{-}=\max \left\{0, -r_{e_t}\right\} $ | (16) |
则原模型等价于:
| $\begin{array}{c} {\min _{x \in {\mathbb{R}^{|\varepsilon \times A^x|}}\mid , y \in \left\{ {0, 1} \right\}n',z \in \left\{ {0, 1} \right\}n''}}{\max _{r_{{e_t}}^ + , {r_{e_t^ - }}}}\sum\limits_{{e_t} = 1}^n {\left[ {{\sigma _{{e_t}}}\left( {r_{{e_t}}^ + - } \right.} \right.} \\ \left. {\left. {r_{{e_t}}^ - } \right)} \right]{x_{{e_t}}} + \sum\limits_{{e_t} = 1}^{\left| {\varepsilon \times {A^x}} \right|} {\left( {{\mu _{{e_t}}}} \right)} {x_{{e_t}}}\end{array} $ | (17) |
| $ \sum\limits_{e_t=1}^n\left(r_{e_t}^{+}+r_{e_t}^{-}\right) \leqslant \varGamma $ | (18) |
| $ r_{e_t}^{+}, r_{e_t}^{-} \in[0, 1], \forall e_t=1, \cdots, n $ | (19) |
| $ \text { s. t. } \quad c(3-11) $ |
固定外层变量作为固定参数,将内层线性模型进行对偶,得到内层对偶模型为
| $\begin{array}{c} {\min _{\pi , \lambda , \theta }}\varGamma \pi + \sum\limits_{{e_t} = 1}^n {{\lambda _{{e_t}}}} + \sum\limits_{{e_t} = 1}^n {{\theta _{{e_t}}}} \\ \pi + {\lambda _{{e_t}}}\geqslant{\sigma _{{e_t}}}{x_{{e_t}}}, \forall {e_t} = 1, \cdots , n \\ \pi + {\theta _{{e_t}}} \geqslant- {\sigma _{{e_t}}}{x_{{e_t}}}, \forall {e_t} = 1, \cdots , n \\ \pi , {\lambda _{{e_t}}}, {\theta _{{e_t}}}\geqslant0, \forall {e_t} = 1, \cdots , n\end{array} $ |
上式对偶模型的所有变量均为0时,存在一个有界可行解,即强对偶条件成立。综上,原min-max问题可等价转化为
| $ \begin{array}{c} {\min _{x, y, z, \pi , \lambda , \theta }}\sum\limits_{{e_t} = 1}^{|\varepsilon \times {A^x}\mid } {\left( {{\mu _{{e_t}}}} \right)} {x_{{e_t}}} + \varGamma \pi + \sum\limits_{{e_t} = 1}^n {{\lambda _{{e_t}}}} + \sum\limits_{{e_t} = 1}^n {{\theta _{{e_t}}}} \\ \pi + {\lambda _{{e_t}}}\geqslant{\sigma _{{e_t}}}{x_{{e_t}}}, \forall {e_t} = 1, \cdots , n \\ \pi + {\theta _{{e_t}}} \geqslant- {\sigma _{{e_t}}}{x_{{e_t}}}, \forall {e_t} = 1, \cdots , n \\ \pi , {\lambda _{{e_t}}}, {\theta _{{e_t}}}\geqslant0, \forall {e_t} = 1, \cdots , n{\text{ }} \\ \end{array} $ |
| $ {\text{s}}{\text{.t}}{\text{. }}\quad c(3 - 11) $ |
经推导整理,本文的鲁棒优化问题可转化成等价的混合整数线性规划问题。
3.2 拉格朗日松弛对于混合整数线性规划问题,可采用拉格朗日松弛方法[7]松弛复杂约束,其思想是将原问题解耦为易求解的子问题,为原问题提供下界;并运用启发式算法构造原问题的可行解作为上界,不断更新上下界去收敛逼近高质量的解。
3.2.1 模型松弛为降低求解难度和保证松弛解质量,将边际约束加以松弛,则松弛问题的目标函数为
| $ \begin{array}{c} \mathit{\boldsymbol{L}}(\alpha ) = {\min _{x, y, z, \pi , \lambda , \theta }}\sum\limits_{i = 1}^{\left| {\varepsilon \times {A^x}} \right|} {{\mu _i}} {x_i} + \varGamma \pi + \sum\limits_{i = 1}^n {{\lambda _i}} + \hfill \\ \sum\limits_{i = 1}^n {{\theta _i}} + \sum\limits_{k \in \varepsilon , l \in \varepsilon } {\alpha _l^k} \left( {\sum\limits_{(i, j) \in A} {w_{i, j}^{k, l}} z_{i, j}^k - W_l^k} \right) \\ \end{array} $ | (20) |
相比对原问题作连续松弛的处理,拉格朗日松弛方法能够提升解的质量。根据弱对偶理论,对于任意给定的拉格朗日乘子,松弛问题的最优值是原问题的下界。为得到逼近原目标最优解的下界,其对偶问题应定义为最大化对偶函数的形式,即
| $ {\max _{\alpha \in {\mathbb{R}_ + }}}L(\alpha ) $ | (21) |
对于改进的次梯度法,求解步骤如下。
1) 参数初始化。令拉格朗日乘子α≥0,迭代次数i=0,上界UB=+∞、下界LB=-∞。
2) 子问题求解并求出目标上下界。对松弛子问题计算求解,进而代入松弛问题得出目标数值,从而更新原问题的模型下界(LB)并判断:如果松弛子问题的解对于原问题可行(即不违反松弛约束),代入并更新原问题的模型上界(UB);否则,构造启发式算法修复,寻找可行解来更新原模型上界。
3) 对偶问题求解。利用次梯度法求解对偶问题,即
| $ \alpha_l^k(i+1)=\alpha_l^k(i)+\delta(i) \cdot g_l^k(i) $ | (22) |
式中: g(i)为第i次迭代的次梯度,δ(i)为第i次迭代的步长。次梯度法作为经典的方法,存在收敛速度慢、效果差等问题,为提升收敛效率,本文改进步长[18]计算的方法,公式为
| $ \delta(i)=\alpha_i \frac{\delta(i-1)\|\tilde{g}(i-1)\|}{\|\tilde{g}(i)\|}, 0<\alpha_i<1, i=1, 2, \cdots $ | (23) |
原文αk为步长的设置参数,
4) 计算差值。输出上下界的相对差值(Gap),并结合终止条件判决,若收敛精度满足,算法中止;否则,返回第2)步继续。
设计流程如图 5所示。

|
图 5 算法流程 Fig. 5 Algorithm flow chart |
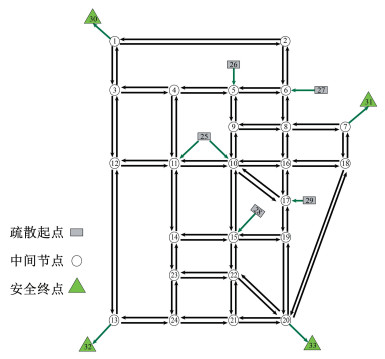
为验证模型及算法的有效性,本文选用SiouxFalls网络[2]来测试(图 6)并附加设定5个疏散起点,4个安全终点,疏散的时间步长间隔设为20 s,此外还包括有路段通行能力、道路长度、路段阻塞时间、截止出发时间、边际约束相关的路段资源权重等参数的设定。路段通行能力和道路长度可根据实际道路及交通条件设定,通过地图数据接口获取。路段阻塞时间[19]是路段因突发事件(如恶劣天气、交通事故等)可能发生交通中断的时刻,截止出发时间则结合实际疏散的限制时间确定。边际约束相关的路段资源权重[13]根据实际疏散要求,可以是路段长度、路段允许访问资源点数等。
|
图 6 测试网络算例 Fig. 6 Test network case |
实验设定3种确定性疏散问题的场景,并进行不同场景优化的效果对比。其中,场景编号越大,疏散总需求和疏散仿真运行的时间也在增加。经计算求解,结果见表 2。
| 表 2 确定性场景基准结果 Tab. 2 Deterministic scenario benchmark results |
3个场景下的不确定集规模大小n分别对应是31 000,63 805,97 775。假定Γ为500,收敛精度为10%,分析不同建模场景的不确定集规模对出行成本的影响。
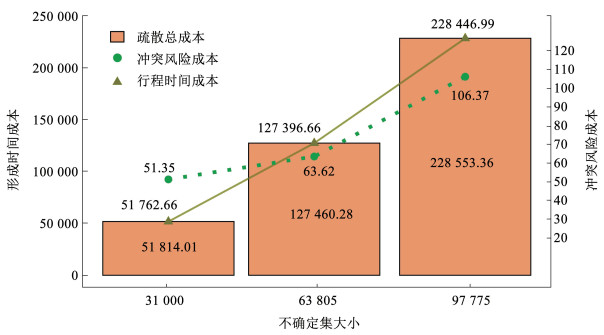
由图 7可知,随着不确定集和模型规模的增加,交通疏散的总行程时间成本和总冲突风险成本也增大。对于行程时间成本来说,不确定集规模小范围(31 000, 63 805)的增长速率为2.30,不确定集规模大范围(63 805, 97 775)的增长速率为2.97,增长速率提升约29.13%。对于冲突风险成本来说,不确定集规模的范围较小时,冲突风险成本从51.35增长到63.62,增长速率较慢;而不确定集规模的范围较大时,冲突风险成本从63.62增长到了106.37,增长速率较快,增速提升约236.46%。模型和不确定集的规模越大,疏散模型的总出行成本增速就越快,冲突风险成本的增速提高相比于行程时间成本的增速提高较为明显,约为8∶ 1。因此,在预算参数为定值的情况下,将不确定集大小与模型规模稳定在合理的范围内,能控制模型的不确定性成本维持在一定的水平。
|
图 7 不确定集规模对出行成本的影响 Fig. 7 Impact of uncertainty set size on travel cost |
以场景2为例,通过调节预算参数Γ,来分析对模型鲁棒性的影响。根据鲁棒性指标[13],为保证扰动下的解大概率可行,对违背不确定性的边界概率进行估计。这里的违背意味的是当目标成本系数不确定时,目标函数值较为敏感,优化效果不佳,即难以在可接受程度内制定疏散任务计划的含义,近似认为模型失效,结果见表 3。
| 表 3 预算参数对模型鲁棒性影响 Tab. 3 Effect of the budget parameter on model robustness |
表 3显示的是随着Γ取值增加,违背边界概率降低,解的鲁棒性增大,总出行成本呈现波动上升趋势。当取值过大时,如500以上,模型考虑的鲁棒性较强,违背概率较低,但目标函数最优性较差,偏离标称值在1 800以上;当取值过小时,如低于100,则违背概率值较高,在35%以上,模型鲁棒性较差,参数波动导致模型失效的可能性较大。因此,本实验Γ取值在300~400之间,模型综合性能评估较好,兼顾解的鲁棒性和最优性。
4.2 算法评估为说明改进拉格朗日松弛(ALR)方法的优点,选择场景1且假定Γ=300,与拉格朗日松弛方法(LR)作对比,结果如图 8所示。图 8表示的是在迭代过程中,ALR和LR方法的相对差值和步长大小的变化情况。分析发现,在第10次迭代的时候ALR完成收敛,而LR则是在第18次迭代才达到收敛,收敛速度较快。在收敛过程中,ALR的相对差值从10.72%逐渐减小到4.44%,LR则从17.63%到4.51%。在步长选择上,在前8次迭代时LR的步长搜索范围较大,数值振荡较明显,在0~40之间;而ALR步长数值的更新较为平稳,搜索范围在0~2之间,搜索方向更为精确。因此,ALR方法相比于LR方法的收敛速度和收敛精度明显较优。

|
图 8 不同方法的步长和相对差值对比 Fig. 8 Comparison of step size and gap for different methods |
为验证所述算法在更大规模算例中的适用性,本文选取南京部分路网(图 9),在两种疏散需求和疏散时间设置的场景下,对程序的运行时间、迭代收敛次数和相对差值的性能指标进行对比,结果见表 4。

|
图 9 南京部分路网示意图 Fig. 9 Schematic diagram of Nanjing partial road network |
| 表 4 不同方法在较大规模网络算例的性能指标对比 Tab. 4 Comparison of performance metrics for different methods in a larger-scale network case |
结果表明,相比于LR方法,ALR方法的迭代收敛次数和相对差值指标更小,且运行时间更少。不同场景对比下,ALR方法的运行时间相比LR方法分别减少了24.8%和11.1%,ALR方法的相对差值相比LR方法分别减少了13.0%和17.8%。在较大规模网络的算法性能测试中,随着问题规模的增大,运行时间和相对差值指标随之增加,ALR方法在收敛速度和收敛精度方面仍能表现出较为明显的优势。
5 结论本文在考虑出行成本不确定性的基础上,构建基于边际约束的城市路网交通疏散模型并设计算法求解验证,丰富了以往相关问题的理论研究,对现实中疏散策略的制定更具参考价值。得出主要结论如下:
1) 模型的总出行成本受不确定集大小和模型规模所影响,数值越大则行程时间和冲突风险成本增速均有提高,且冲突风险成本的增速提高值大于行程时间成本的增速提高值。
2) 场景2实验结果表明,预算参数控制在300~400之内,能较好地保证解的鲁棒性和最优性。
3) 所提出的ALR算法性能表现良好,能在一定的迭代次数内收敛到近似最优解。相比于传统LR方法,在收敛速度和收敛精度方面有一定的提升。
| [1] |
段晓红, 吴家新, 周芷晴. 基于层次蝙蝠算法的应急车辆调度与交通疏散协同决策[J]. 交通运输系统工程与信息, 2020, 20(2): 157. DUAN Xiaohong, WU Jiaxin, ZHOU Zhiqing. Collaborative decision-making of emergency vehicle scheduling and traffic evacuation based on bi-level bat algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(2): 157. |
| [2] |
ZHANG X, MAHADEVAN S, GOEBEL K. Network reconfiguration for increasing transportation system resilience under extreme events[J]. Risk Analysis, 2019, 39(9): 2054. DOI:10.1111/risa.13320 |
| [3] |
CASSOL V J, TESTA E S, JUNG C R, et al. Evaluating and optimizing evacuation plans for crowd egress[J]. IEEE Computer Graphics and Applications, 2017, 37(4): 60. DOI:10.1109/MCG.2017.3271454 |
| [4] |
LIU Y, LUO Z. A bi-level model for planning signalized and uninterrupted flow intersections in an evacuation network[J]. Computer-Aided Civil and Infrastructure Engineering, 2012, 27(10): 731. DOI:10.1111/j.1467-8667.2012.00778.x |
| [5] |
赵传林, 贺少松, 孙淑敏, 等. 基于理性疏忽理论的交通疏散网络双层优化模型[J]. 交通运输系统工程与信息, 2022, 22(2): 239. ZHAO Chuanlin, HE Shaosong, SUN Shumin, et al. Bi-level optimization model in transportation evacuation network based on rational inattention[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22(2): 239. |
| [6] |
YUAN Y, LIU Y, YU J. Trade-off between signal and cross-elimination strategies during evacuation traffic management[J]. Transportation Research Part C: Emerging Technologies, 2018, 97: 385. DOI:10.1016/j.trc.2018.10.013 |
| [7] |
FISHER M L. The Lagrangian relaxation method for solving integer programming problems[J]. Management Science, 1981, 27(1): 1. DOI:10.1287/mnsc.27.1.1 |
| [8] |
LIM G J, RUNGTA M, DAVISHAN A. A robust chance constraint programming approach for evacuation planning under uncertain demand distribution[J]. IISE Transactions, 2019, 51(6): 589. DOI:10.1080/24725854.2018.1533675 |
| [9] |
YANG M, LIU Y, YANG G. Robust optimization for a multiple-priority emergency evacuation problem under demand uncertainty[J]. Journal of Data, Information and Management, 2020, 2(4): 185. DOI:10.1007/s42488-019-00018-7 |
| [10] |
LIM G J, RUNGTA M, BAHARNEMATI M R. Reliability analysis of evacuation routes under capacity uncertainty of road links[J]. IIE Transactions, 2015, 47(1): 50. DOI:10.1080/0740817X.2014.905736 |
| [11] |
BAYRAM V. Optimization models for large scale network evacuation planning and management: a literature review[J]. Surveys in Operations Research and Management Science, 2016, 21(2): 63. DOI:10.1016/j.sorms.2016.11.001 |
| [12] |
PILLAC V, VAN HENTENRYCK P, EVEN C. A conflict-based path-generation heuristic for evacuation planning[J]. Transportation Research Part B: Methodological, 2016, 83: 139. |
| [13] |
WANG L, YANG L, GAO Z, et al. Evacuation planning for disaster responses: a stochastic programming framework[J]. Transportation Research Part C: Emerging Technologies, 2016, 69: 156. |
| [14] |
ESCRIBANO-MACIAS J J, ANGELOUDIS P, HAN K. Optimal design of rapid evacuation strategies in constrained urban transport networks[J]. Transportmetrica A: Transport Science, 2020, 16(3): 1092. |
| [15] |
WANG J W, WANG H F, ZHANG W J, et al. Evacuation planning based on the contraflow technique with consideration of evacuation priorities and traffic setup time[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 14(1): 481. |
| [16] |
BERTSIMAS D, SIM M. The price of robustness[J]. Operations Research, 2004, 52(1): 35. DOI:10.1287/opre.1030.0065 |
| [17] |
GORISSEN B L, YANIKOǦLU İ, DEN HERTOG D. A practical guide to robust optimization[J]. Omega, 2015, 53: 125. |
| [18] |
BRAGIN M A, LUH P B, YAN J H, et al. Convergence of the surrogate Lagrangian relaxation method[J]. Journal of Optimization Theory and Applications, 2015, 164(1): 180. |
| [19] |
HASAN M H, VAN HENTENRYCK P. Large-scale zone-based evacuation planning, Part Ⅱ: macroscopic and microscopic evaluations[J]. Networks, 2021, 77(2): 342. |
 2024, Vol. 56
2024, Vol. 56


