2. 生态安全屏障区交通网设施管控及循环修复技术交通运输行业重点实验室(长安大学),西安 710018
2. Key Laboratory of Transport Industry of Management, Control and Cycle Repair Technology for Traffic Network Facilities in Ecological Security Barrier Area(Chang′an University), Xi′an 710018, China
21世纪以来,伴随着中国公路网络的快速延伸,大量山区公路陆续建成通车,解决了广大偏远山区村镇的交通难题。然而,山区公路常伴随急弯、陡坡等不良线形路段,给安全行车埋下了严重隐患,亟需采取积极主动的防控措施来有效遏制道路交通事故的发生[1]。目前研究多关注单一车辆实体在过弯时的侧滑侧翻问题,多涉及驾驶行为、轨迹特性、速度预测等领域,进而依据不同指标进行安全风险预警[2-3]。而急弯路段中两个及以上车辆实体间若车速过快、车距过小、视距不足时同样易引发追尾事故[4],亟需深入分析该类事故,以提出针对性防控措施。
传统的交通事故研究多以往期事故数据等方向入手,而随着数据获取手段的不断更新,交通冲突分析技术逐渐成为主流。交通冲突技术作为一种交通事故风险量化分析方法,具有可获得性、直观、周期短、样本量大等优势[5],目前国内外已有大量针对交通冲突的相关研究,主要包括冲突判定及严重程度划分等方面[5-6],如文献[7]结合车辆运动信息建立了基于后侵入时间PET(post-encroachment time)算法的交通冲突识别模型;文献[8]利用车辆的精确位置及宽度来确定所有类型车辆间的关键相互作用,运用改进的碰撞时间MTTC (modified time to collision)模型对于所获取的相互作用中的交通冲突进行了识别;文献[9]利用高速公路上雷达传感器采集的追尾冲突TTC(time to collision)值作为输入,预测下一个时间间隔内的追尾碰撞风险。文献[10]通过对运动目标进行轨迹提取,利用神经网络预测车辆运动轨迹,结合碰撞概率评估冲突严重程度。综上,现有交通冲突研究多依据采集或预测的车辆轨迹数据,提取PET、TTC等指标以判别、预测冲突发生或划分冲突严重程度,借此可评估车-车间潜在碰撞事故。
目前针对交通冲突的研究成果较多,但大多仅考虑冲突是否发生及其严重程度,却忽视了对冲突微观过程及相关特征的探究。交通流运行过程中,运动车辆在安全状态与危险状态间具有过渡性[11],所引发的交通冲突呈现一定时空演化特征。急弯路段上车辆加减速频繁,易引发冲突,但目前研究多关注冲突的辨识[8]或预测[12-13],缺乏对其时空演化规律的深入研究。因此,本文以急弯路段为研究对象,通过实地调查获取交通流数据,提取车辆轨迹信息来判定车辆间追尾冲突,并着重探究不同类型冲突状态在入弯-出弯过程中的时空演化规律,以便针对性提出急弯路段车辆防追尾碰撞技术措施。
1 研究对象与数据获取 1.1 路段基本信息选定西安市灞桥区X101狄寨原路西安思源学院段急弯为研究路段,该弯道半径为46 m,曲线长为400 m、横坡度约为1°,根据《公路路线设计规范及条文说明(JTG D20—2006)》中的相关规定,该路段可被视为急弯路段。考虑到一般驾驶习惯,确定急弯路段起点上游50 m处为研究起点,将急弯路段结束点下游50 m作为研究终点,共长500 m。同时,直线-入弯缓和曲线交界点(OZH)、入弯缓和曲线-圆曲线交界点(OHY)、圆曲线中心点(OQZ)、圆曲线-出弯缓和曲线交界点(OYH))、出弯缓和曲线-直线交界点(OHZ))点作为标志点,这5个标志点所在断面分别为ZH、HY、QZ、YH、HZ标志断面,并以ZZ1、ZZ2断面为数据调查的起止点所在断面,如图 1所示。

|
图 1 急弯路段区域划分 Fig. 1 Zones of current sharp curve |
开展实地调查获取所研究急弯路段的交通流数据。选用大疆“DJI Air 2S”无人机升空至QZ断面120 m处悬停记录行车数据,共获得17段有效航拍视频, 总有效时长为119 min,并用Tracker软件处理视频,以获取不同类型车辆的时间、车辆坐标及相应的速度、加速度、车辆方位角、速度方位角。
1.3 车辆运动特征图 2给出了所研究急弯路段的车速与加速度空间分布状况,可见不同类型车辆过弯时均遵循先减速后加速的运动规律。

|
图 2 急弯路段车速分区段分布 Fig. 2 Distribution of speed zones oncurrent sharp curve |
由图 2(a)可知,在入弯缓和曲线段平均车速最小,在出弯直线段(HZ—ZZ2)段平均车速最大。由图 2(b)可知,急弯路段车辆加速度变化分为预减速、匀减速、匀速波动及加速4个阶段,分别对应图中0—ZH、ZH—HY、HY—QZ、QZ—YH段。
2 追尾冲突判别由图 2中采集数据分析结果可知,车辆因跟驰过弯且加减速频繁而易产生追尾冲突,故选用后侵入时间PET指标判别急弯路段的追尾冲突[14]。
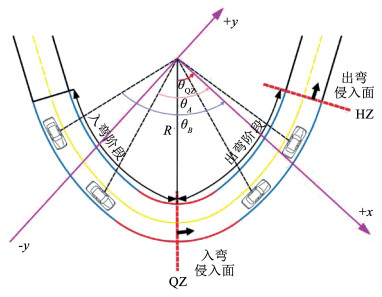
依据PET指标的定义,根据冲突先导车LV和冲突跟随车FV通过固定断面的时间差tFV-tLV建立急弯路段PET识别模型。由于车辆一般采用制动减速入弯和加速出弯的方式通过急弯路段,选取OQZ、OHZ点所在断面QZ、HZ作为入弯和出弯侵入面,见图 3,分别判定入弯和出弯车辆间的追尾冲突。
|
图 3 追尾冲突计算示意 Fig. 3 Rear-end conflict illustration |
假定在t时刻位于OQZ标志点上游的LV、FV间因近距离跟驰产生冲突,其地点车速分别为vLV(t)、vFV(t),忽略缓和曲线和圆曲线间的平曲线半径差异,假定车辆保持当前速度不变,可得t时刻入弯路段LV与FV间追尾冲突判别的PET模型:
| $ \mathrm{PET}_{\mathrm{LV}_{-} \mathrm{FV}_{-} \mathrm{en}}(t)=t_{\mathrm{FV}}-t_{\mathrm{LV}}=\frac{\pi r}{180}\left[\frac{\left|\theta_{\mathrm{QZ}}-\theta_{\mathrm{FV}}\right|}{v_{\mathrm{FV}}(t)}-\frac{\left|\theta_{\mathrm{QZ}}-\theta_{\mathrm{LV}}\right|}{v_{\mathrm{LV}}(t)}\right] $ | (1) |
式中:θQZ为QZ标志断面的方位角,(°);θLV、θFV分别为t时刻LV、FV的方位角,(°);r为平曲线半径均值,m。
对于出弯路段,以断面HZ替换断面QZ,同理可得t时刻出弯阶段LV与FV间追尾冲突判别的PET模型:
| $ \operatorname{PET}_{\mathrm{LV}_{-} \mathrm{FV} \_\mathrm{ex}}(t)=t_{\mathrm{FV}}-t_{\mathrm{LV}}=\frac{\pi r}{180}\left[\frac{\left|\theta_{\mathrm{HZ}}-\theta_{\mathrm{FV}}\right|}{v_{\mathrm{FV}}(t)}-\frac{\left|\theta_{\mathrm{HZ}}-\theta_{\mathrm{LV}}\right|}{v_{\mathrm{LV}}(t)}\right] $ | (2) |
式中θHZ为HZ标志断面的方位角,(°)。
以时刻t为基点、Δt=1/6 s为时间步长,计算LV与FV分别位于入弯和出弯路段的PET指标动态变化序列值。对于每一组车头间距小于50 m的近距离跟驰车对LV与FV间的两组PET序列,若其序列值随时间呈现上升或平稳的趋势,可判定该车对间不存在追尾冲突,反之则存在潜在追尾冲突。
3 追尾冲突动态演化 3.1 冲突类别划分根据入弯与出弯的PET序列值计算结果,共筛选出符合要求的追尾冲突车辆98对,冲突序列143组,提取出冲突关键帧数据共2 432帧,其中位于1~2.5 s之内的PET值最多,占比高达63.86%。根据冲突LV与FV的速度、加速度变化,将追尾冲突模式划分为T1~T13共13小类,如表 1所示,其中↗、—、↘依次表示增加、持平、减少3种趋势。模式T1~T3、T4~T6分别对应LV、FV均加速和均减速两种场景,可进一步归纳为大类Ⅰ、Ⅱ,其余模式T7~T13对应大类Ⅲ~Ⅸ。
| 表 1 急弯路段追尾冲突模式指标变化 Tab. 1 Changes in indicators for rear-end conflict patterns on current sharp curves |
由表 1可知,急弯路段出现的各类追尾冲突模式中大类Ⅱ、Ⅵ、Ⅰ、Ⅳ占比较高,分别为25.88%、22.38%、20.99%和13.99%,合计83.24%,剩余大类仅占约15%。其中,模式Ⅰ表征了LV、FV均加速情况,其中T2模式占据了大部分(14.69%),表明在LV、FV均加速导致的追尾冲突中FV加速度是关键影响因素;同样,模式Ⅱ表征了LV、FV均减速情况,其中T6模式占比最大(14.69%),表明在LV、FV均减速导致的追尾冲突中速度和加速度均有显著影响。
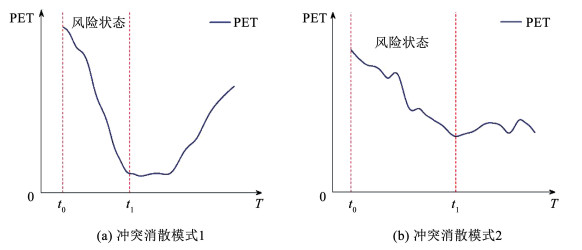
3.2 冲突演化过程 3.2.1 表征指标构建绘制追尾冲突PET序列值的变化曲线,发现PET变化包含两种类型,如图 4所示。
|
图 4 追尾冲突PET变化 Fig. 4 PET changes of rear-end conflict |
追尾冲突PET的消散模式可分为两种,如图 4(a)所示,第1种模式中追尾冲突过程中PET序列值快速下降,表明冲突FV追尾LV的时间距离越来越小,当PET减小到一定程度后出现上升趋势,即此时冲突FV追尾LV的时间距离开始增大,冲突开始消散。如图 4(b)所示,在第2种模式冲突发生时同样伴随着PET序列值的快速下降,当PET减小到一定程度后不再继续减小,而是保持相对稳定并上下波动,即代表冲突消散。
为细致刻画追尾冲突发生过程中PET序列值的动态变化幅度,定义指标DPET(derivative of PET),即PET的导数:
| $ \operatorname{DPET}(t+\Delta t)=\frac{\operatorname{PET}(t+\Delta t)-\operatorname{PET}(t)}{\Delta t} $ | (3) |
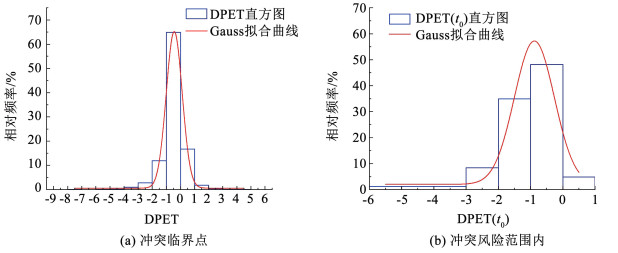
将LV与FV由安全状态转变为冲突风险状态的临界时刻定义为冲突临界点t0,即PET由上升或平稳分布开始快速下降的转折点,DPET由非负值转变成负值的零点;将由冲突风险状态恢复到安全驾驶状态的临界点定义为t1,即PET快速下降停止的转折点,DPET由负值转变成非负值的零点。图 5为DPET指标在冲突临界点和冲突风险范围内的分布情况。
|
图 5 DPET分布 Fig. 5 DPET distribution |
根据图 5(a)DPET值分布情况,在整个冲突风险范围内DPET值分布于(-1, 0)中的占比约65%,而小于-1的仅占约15%。在冲突临界点,DPET值位于(-1, 0)中的占比同样最多(48%),但相较整个冲突风险范围明显减少,而小于-1的占比有较大幅度的上升。
由图 5(b)可见,在冲突临界点DPET指标相对于整个冲突过程呈现更大的负值,随后逐渐下降至平缓。这是因为在风险时段内,LV与FV开始采取减速或加速操作,导致两车间相对速度等发生突变,产生更大的冲突风险;其后,随着驾驶人感知到风险并采取避险措施,PET值下降逐渐放缓,该时段的DPET值亦呈现出缓和趋势。
3.2.2 冲突临界点回归模型选取t0时刻6个指标速度vLV(t0)和vFV(t0)、加速度aLV(t0)和aFV(t0)、速度差Δv(t0)=vFV(t0)-vLV(t0)、减速度差Δa(t0)=aFV(t0)-aLV(t0)作为输入变量,列出了自变量与因变量间皮尔逊相关性的计算值,一般认为p<0.01呈现相关性、p<0.001呈现强相关性,由于篇幅限制,对于弱相关变量将不再标注。
| 表 2 冲突临界点变量统计 Tab. 2 Variable statistics for critical conflict point |
显然,t0时刻DPET(t0)仅与aLV(t0)、aFV(t0)、Δa(t0)显著相关,且与aLV(t0)正相关,而与aFV(t0)、Δa(t0)显著负相关[15],表明加速度尤其是aFV(t0)对追尾冲突的演化有重要影响。
以这6个指标为输入变量进行逐步回归分析,vFV(t0)与aFV(t0)被排除,其余4个指标均能显著影响DPET(t0)值(p<0.05),且VIF均小于5,表明各变量间不存在多重共线性[15]。回归分析模型见表 3,R2为0.710,表明所建立的模型能较好解释DPET(t0)值的变化。
| 表 3 DPET(t0)回归分析结果 Tab. 3 Results of DEPT regression analysis |
由表 3结果可知,vFV(t0)、aFV(t0)与Δv(t0)、Δa(t0)是引发该急弯路段追尾冲突的显著性影响因素,而vFV(t0)、Δa(t0)对PET值下降的影响更大,这说明控制FV安全运动状态能有效防控追尾冲突风险。
3.2.3 冲突风险状态回归模型针对急弯路段追尾冲突的4类主要冲突模式T2、T6、T8及T10,分别建立其冲突风险状态DPET指标的回归分析模型,量化上述6个输入因素的影响程度。表 4给出了各模式的描述变量统计及皮尔逊相关性分析结果。
| 表 4 典型追尾冲突模式状态变量统计 Tab. 4 Variable statistics of typical rear-end conflict modes |
由表 4可知,4类主要追尾冲突模式的风险状态时段内aLV、aFV、Δv、Δa 4个变量均与DPET值显著相关,且各变量的相关程度差异较大。表 5给出了各冲突模式下DPET的多元线性回归分析结果。
| 表 5 典型追尾冲突模式回归分析结果 Tab. 5 Regression results of typical rear-end conflict modes |
显然,对于各主要冲突模式均有3个不同显著变量能较好表征其DPET变化,且Δa在各模式中均对DPET有显著影响。此外,该指标在T2、T6、T10中标准化系数Beta绝对值最大,且与其他可解释变量的Beta值差距较大,说明Δa是这些模式中影响急弯路段追尾冲突的主要因素。在T8中,Δa和aFV两个变量的Beta绝对值均较大且差距极小,表明该模式下Δa与aFV对DPET变化的影响均较大,究其原因在于追尾冲突主要由aFV所引发,且难以被LV及时发现,因而导致DPET持续下降。图 6给出了4类典型冲突模式的DPET指标分布情况。

|
图 6 典型冲突模式的DPET指标分布 Fig. 6 DPET distribution of typical conflict modes |
由计算结果可知,如图 6(a)、6(b)、6(c)所示,T2、T6、T8的DPET指标较为接近(-0.376,-0.374,-0.357),但图 6(d)中T10的DPET指标存在较大差距(-0.601),表明T10的PET序列值下降最为快速,而其余3类模式的下降程度不存在显著差异。从T2、T6、T8的DPET演化看,分布于[-1, 0]中的比例约为65%,小于-1的占比均不到15%,而T10模式中小于-1的占比接近30%,表明T10模式出现PET序列值快速下降的概率远大于其他模式,这将导致该模式的追尾冲突危险性更大,亦是风险防范的着力点[16]。
3.3 冲突空间分布以临界冲突时刻t0对应的FV位置为坐标,分别提取冲突模式T2、T6、T8及T10,得到追尾冲突在急弯路段上的空间分布,如图 7所示。

|
图 7 急弯路段追尾冲突空间分布 Fig. 7 Spatial distribution of rear-end conflicts on current sharp curves |
由图 7可看出急弯路段追尾冲突分布呈现空间聚集性,以图 1中ZZ1点至ZZ2点方向为上行方向,从该方向看,主要集中在入弯缓和曲线上游(ZZ1—ZH段)、曲中标志断面下游(QZ—YH的前半段)及出弯缓和曲线下游(HZ—ZZ2段)3处,因此对t0时刻这3处的追尾冲突分别进行DPET(t0)指标的显著性检验,并列出了自变量与因变量间皮尔逊相关性的计算值,结果见表 6。
| 表 6 不同区段冲突临界点显著性检验 Tab. 6 Significance tests for conflict thresholds at different zones |
由回归分析结果可知,DPET(t0)在入弯缓和曲线上游受Δa和aFV的显著影响,其形成与进入缓和曲线上游的FV的减速大小有关,此时LV基本已完成减速,而此时aFV对冲突影响显著,同时Δa对冲突影响最为显著。DPET(t0)在曲中标志断面下游受Δa的影响最为显著,其形成与曲中断面后的加速行驶有关。DPET(t0)在曲线下游受Δa和aFV的显著影响,其形成与曲中断面后的加速行驶有关,且主要由于FV加速行驶导致的Δa,进而形成追尾冲突。
由表 6可见,LV的加速行为可降低追尾冲突风险,FV的加速行为则恰恰相反,但在3处冲突密集处,上述行为对追尾冲突风险的影响程度有明显差异,即Δv与Δa对冲突风险的影响存在空间差异性。这是因为在急弯不同区段中,LV与FV往往呈现不同的相对状态。当两车位于弯道前半段呈接近状态时,FV驾驶策略尚未完全确定,其速度、加速度等运动参数的变化幅度较大,但LV一般选择逐渐减速策略以通过弯道,此时FV更能对追尾冲突风险产生更显著的影响;当两车位于弯道后半段呈远离状态时,与上述情况相反,FV驾驶策略已定而LV驾驶策略开始出现变化,导致LV对追尾冲突风险的影响上升。
4 结论针对急弯路段追尾事故多发的特点,利用交通冲突技术,系统研究了急弯路段的追尾冲突及其演化机理,主要研究结论如下:
1) 在急弯路段九大类潜在追尾冲突模式中,发生频率最高的有四大类,包括Ⅱ(T6为主)、Ⅵ(T10)、Ⅰ(T2为主)、Ⅳ(T8),占比分别为25.88%、22.38%、20.99%和13.99%。
2) 加速度差Δa是急弯路段追尾冲突T2、T6、T10模式中引发DPET变化的首要因素,影响PET序列的下降程度;aFV与Δa对T8模式的DPET变化均有显著影响,但影响程度差异较小;T10模式的DPET均值最小,表明PET序列下降最为剧烈,危险性较高。
3) 急弯路段追尾冲突模式分布具有空间集聚性。T2主要分布于圆曲线下游,T6模式主要分布于入弯缓和曲线上游和出弯缓和曲线下游,T8模式与T10模式主要分布于圆曲线下游,少量分布于入弯缓和曲线段,这与急弯路段上车速变化特征一致。
本研究提出了急弯路段追尾冲突风险的时空分布甄别方法,对追尾事故防控有较高的理论指导价值,同时也为一般弯道及平直路段上冲突风险研究提供了借鉴思路。受时间所限,本研究仅对单个急弯路段的追尾冲突进行了系统研究,难以将结论移植至连续急弯、弯坡组合等其他事故多发路段,同时追尾冲突时空演化规律只考虑冲突发生的可能性,并未体现出潜在碰撞事故的严重程度。后续应拓展研究范围,可侧向冲突等纳入考虑,并研究连续弯道、回旋曲线等其他形式弯道的交通冲突相关问题,同时系统考量潜在碰撞事故的发生概率及严重程度。
| [1] |
WANG Y, PRATO C G. Determinants of injury severity for truck crashes on mountain expressways in China: a case-study with a partial proportional odds model[J]. Safety Science, 2019, 117: 100. DOI:10.1016/j.ssci.2019.04.011 |
| [2] |
XIN T, XU J, GAO C, et al. Research on the speed thresholds of trucks in a sharp turn based on dynamic rollover risk levels[J]. PLoS One, 2021, 16(8): e0256301. DOI:10.1371/journal.pone.0256301 |
| [3] |
XU J, LUO X, SHAO Y M. Vehicle trajectory at curved sections of two-lane mountain roads: a field study under natural driving conditions[J]. European Transport Research Review, 2018, 10(1): 12. DOI:10.1007/s12544-018-0284-x |
| [4] |
SALEEM T, PERSAUD B. Another look at the safety effects of horizontal curvature on rural two-lane highways[J]. Accident Analysis & Prevention, 2017, 106: 149. |
| [5] |
MINDERHOUD M M, BOVY P. Extended time-to-collision measures for road traffic safety assessment[J]. Accident Analysis & Prevention, 2001, 33(1): 89. |
| [6] |
戢晓峰, 谢世坤, 覃文文, 等. 基于轨迹数据的山区危险性弯道路段交通事故风险动态预测[J]. 中国公路学报, 2022, 35(4): 277. JI Xiaofeng, XIE Shikun, QIN Wenwen, et al. Dynamic prediction of traffic accident risk in risky curve sections based on vehicle trajectory data[J]. China Journal of Highway and Transport, 2022, 35(4): 277. |
| [7] |
马艳丽, 祁首铭, 吴昊天, 等. 基于PET算法的匝道合流区交通冲突识别模型[J]. 交通运输系统工程与信息, 2018, 18(2): 142. MA Yanli, QI Shouming, WU Haotian, et al. Traffic conflict identification model based on post encroachment time algorithm in ramp merging area[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(2): 142. |
| [8] |
CHARLY A, MATHEW T V. Estimation of traffic conflicts using precise lateral position and width of vehicles for safety assessment[J]. Accident Analysis & Prevention, 2019, 132: 105264. |
| [9] |
ORSINI F, GECCHELE G, ROSSI R, et al. A conflict-based approach for real-time road safety analysis: comparative evaluation with crash-based models[J]. Accident Analysis & Prevention, 2021, 161: 106382. |
| [10] |
姜雪娇, 郭唐仪. 基于轨迹数据的高速公路分流区冲突替代指标研究[J]. 交通信息与安全, 2016, 34(2): 39. JIANG Xuejiao, GUO Tangyi. Development of alternative indicators of conflict at freeway diverging area using trajectory data[J]. Journal of Transport Information and Safety, 2016, 34(2): 39. |
| [11] |
LI Y, WU D, LEE J, et al. Analysis of the transition condition of rear-end collisions using time-to-collision index and vehicle trajectory data[J]. Accident Analysis & Prevention, 2020, 144: 105676. |
| [12] |
柳本民, 廖岩枫, 涂辉招, 等. 基于模拟实验的低等级公路车辆过弯风险预测模型[J]. 同济大学学报(自然科学版), 2021, 49(4): 499. LIU Benmin, LIAO Yanfeng, TU Huizhao, et al. Risk prediction model of vehicle driving in small radius curves based on simulation experiment[J]. Journal of Tongji University (Natural Science), 2021, 49(4): 499. |
| [13] |
房锐, 张琪, 胡澄宇, 等. 基于风险矩阵的干线公路弯道路段交通冲突风险评估模型[J]. 交通运输系统工程与信息, 2021, 21(2): 166. FANG Rui, ZHANG Qi, HU Chengyu, et al. Risk assessment model based on risk matrix for traffic conflict on arterial highway bend section[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(2): 166. |
| [14] |
VOGEL K. A comparison of headway and time to collision as safety indicators[J]. Accident Analysis & Prevention, 2003, 35(3): 427. |
| [15] |
KUTNER M H, NACHTSHEIM C J, NETER J, et al. Applied linear regression models[M]. 4th ed. New York: McGraw-Hill Higher Education, 2004.
|
| [16] |
SHANGGUAN Q, FU T, WANG J, et al. Quantification of rear-end crash risk and analysis of its influencing factors based on a new surrogate safety measure[J]. Journal of Advanced Transportation, 2021, 2021: 5551273. |
 2024, Vol. 56
2024, Vol. 56


