2. 公路大型结构安全教育部工程研究中心(长安大学),西安 710064
2. Research Center of Highway Large Structure Engineering on Safety of Ministry of Education(Chang′an University), Xi′an 710064, China
交通荷载是桥梁的重要外部荷载之一,是影响桥梁构件使用寿命的重要荷载[1-2]。由于交通荷载贯穿于桥梁前期设计和后期运营的整个过程,对桥梁的设计、评估和养护都至关重要[3-5],因此对交通荷载的模拟一直是桥梁工程的重要内容。由于交通流的随机性,交通荷载也具有随机特性[6-8],这种随机性体现在车辆的组成和车辆的时空位置变化上。车辆组成的直观表现是车辆的轴载分布不同,车辆的时空位置变化由车辆在行驶过程中的加减速和变换道等微观交互行为确定。因此,要准确模拟桥梁上的随机车流荷载,车辆轴载模拟和车辆的微观交互行为模拟是两个重要内容。
常用的随机车流荷载模拟方法有Monte Carlo法[9-10](MC)和元胞自动机法[6-7, 11](cellular automata, CA),Monte Carlo法主要基于给定的车流宏观数理模型,通过随机抽样建立系列交通参数形成模拟车流,由于这种模拟方法难以模拟车辆之间的微观动态交互行为,因此难以考虑车辆交互形成的车辆时空位置变化。CA模型能够模拟车辆的微观交互行为,因此也被广泛用于随机车流荷载模拟。随机交通流模型最早由Wolfram提出,称为184模型[12],随后经过Nagel and Schreckenberg的改进,提出NS模型[13]和双车道NS模型[14],这些模型的发展都是为了更好地模拟交通微观特性,使模拟的交通流能更准确地反映实际交通流的微观特性。由于使用目标的不同,这些模型不关注车轴信息,所以将所有车辆(不论大小)统一限制在一个由道路离散产生的方形格子内(叫做元胞),通过定义一定的转换规则模拟车辆运动状态的变化。文献[7]首先将NS模型完整地应用到桥梁上用于车辆荷载的模拟中,并将车辆总重融入元胞,用集中力代替车辆荷载,分析了随机车流作用下的桥梁结构响应。文献[8, 15-17]将NS模型引入车桥耦合分析。在NS模型中,车流模拟均以道路离散后的元胞为基本核心元素,将车辆几何信息和运动信息与元胞结合,当元胞尺寸较大时,便不能准确模拟车辆尺寸和车辆间距,也不能准确模拟车辆轴载。为了模拟桥址处的随机交通荷载,文献[10]基于intelligent driver model(IDM)模型,采用Paramics系统分析了微观层面拥挤交通流下的中-大跨桥梁车辆荷载效应,在其模拟中,车辆荷载仍然采用车辆总重代替。
由于CA基本原理的限制,上述研究都只能将车辆限制在一个固定尺寸的元胞内,不能准确模拟车辆尺寸,因此不能反映实际车流中真实车间距等信息[18];同时由于只能用一个元胞模拟车辆,因此车辆荷载只能采用等效的集中荷载进行分析。为了得到准确的车辆荷载信息。文献[16-20]首先将考虑轴载的车辆荷载用于车桥耦合分析和结构评估中,但是其模拟的车流的随机性主要体现在车辆组成的随机性上,因此其更适用于小跨径桥梁。文献[21]建立了基于随机车流的车桥耦合程序,并基于随机车流作用下的桥梁响应并分析了冲击系数的取值规律。为了更准确地模拟车辆荷载,文献[22]首先对传统NS模型进行改进,将车辆的轴载信息融入到NS模型中,车辆不再局限在一个固定长度的元胞中,而是可以跨越多个元胞,轴载信息通过一系列参数进行定义,车辆位置采用车头所在的元胞对车辆进行定位,其运动状态仍然采用原始NS模型的状态更新规则进行更新,这种规则规定所有的车辆都只能采用统一的加减速值。在其后续的改进模型中[23],虽然引入了单位加速度来模拟加速,但所有车辆仍然只能采用相同的加速度,因此仍然不能反映不同车辆的不同的微观交互特性。文献[24]首先提出采用细化元胞的方式提高车辆荷载的精度,并推导了基于加速度的更新规则,但是该方法仍然局限在传统NS模型框架内,当元胞划分的较细时,模拟效率不高。
为准确模拟桥址处随机车流荷载,本文提出基于可变元胞和跟驰理论的新型元胞自动机模型。新型元胞自动机模型以车辆为核心,采用动态变化的元胞准确模拟车辆的几何尺寸、车间距和轴距。将轴载信息融入元胞,准确模拟车辆荷载。引入跟驰理论,推导基于加速度的车辆运动状态演化规则,计算每一辆车的专属加速度,准确模拟车辆之间的微观交互行为。建立基于WIM数据的车队生成方法,重构任意时段的实际车队。最后通过实例证明所提模型在随机车流荷载模拟中的可行性和准确性。
1 基于可变元胞与跟驰理论的元胞自动机模型 1.1 可变元胞定义与元胞转换本文提出在空间和时间上均离散的新型元胞自动机模型。与传统元胞自动机依赖于道路离散的固定元胞不同,本文提出的新型元胞自动机以车辆为核心元素,称为基于车辆的元胞自动机。元胞不再通过道路离散得到,而是将每辆车所在的道路空间位置都作为一个车辆元胞,没有车的道路空间作为空元胞,空元胞是车辆元胞的边界,是车间距的直接反映。车辆元胞状态可以用式(1)表达:
| $ \boldsymbol{C}_s=\left\{\boldsymbol{C}_m, \boldsymbol{M}, \boldsymbol{W}\right\} $ | (1) |
式中:
| $ \begin{gathered} \boldsymbol{C}_m=\left[c_f, c_r\right] \\ \boldsymbol{M}=\left[v_n, v_n^{\max }, v_n^{\text {EFDV }}, a_n^{\text {anti }}, a_n^{\max }, a_{\text {brake }}, T, T_n^{\mathrm{ETH}}, b\right] \\ \boldsymbol{W}=\left[G, k, o_r, o_f, q, \cdots, q^{k-1}, g^1, \cdots, g^k\right] \end{gathered} $ | (2) |
式中:Cs表示元胞状态,Cm表示位置参数,cf表示车辆元胞每一时步的开始位置,通过第一个车轴加前悬挂长度得到,cr表示车辆元胞每一时步的结束位置,通过最后一个车轴减后悬挂长度得到;M表示运动状态参数,包含当前速度vn、最大速度vnmax、自由流期望最大速度vnEFDV、每时步的期望加速度ananti、常规行驶状态下的最大加速度anmax、刹车减速度abrake、每时步的车头时距T、跟驰流期望车头时距TnETH和紧急刹车状态指征参数b;W表示车辆尺寸和轴载相关参数,G表示车辆总重,k表示车轴数,or和of分别表示车辆后悬挂长度和前悬挂长度,qk-1表示第k-1个车轴和第k个车轴的轴间距,gk表示第k个车轴的轴重。ananti根据状态演化规则计算得到;anmax需要人工定义,在实际模拟中,可以设置不同的限值,但其值必须小于车辆所能达到的极限最大加速度;b的取值只有0和1,当b=1时,表示该车辆处于紧急刹车状态,此时,车辆的减速度为紧急刹车减速度,当b=0时,表示该车辆处于正常行驶状态,车辆的加速度根据状态更新规则计算得到。
在车流模拟中,车辆元胞和空元胞都随着车辆位置的移动而更新,元胞更新可用图 1表示。提出的新型元胞与传统元胞不同,不依赖于通过道路离散产生的固定尺寸的晶格,能够准确反映车辆尺寸、轴间距和轴载信息。同时,在编程时,提出的模型只需要记录车辆元胞的信息即可完成对所有信息的记录,且信息矩阵的维度只与道路上车辆的数量有关。空元胞只是车间距的度量,没有运动特征。空元胞的距离信息也以通过相邻车辆元胞的车头和车尾参数计算得到,因此,编程时,空元胞不参与运算,以降低程序运算量,提高模拟效率。

|
图 1 元胞与元胞更新 Fig. 1 Cells and cell transition |
CA模型以加速度为核心指标对元胞运动状态进行更新,在提出的CA模型中,加速度的计算考虑了元胞当前速度、当前车间距和周围元胞的速度指标,因此,每个元胞状态的更新都受其周边车辆元胞的运动状态影响,这些对目标元胞的运动状态有影响的车辆元胞称为目标元胞的邻居元胞。在单车道模拟中,邻居元胞为当前车道的前一个车辆元胞。在多车道模拟中,车辆可能换道,邻居元胞为当前车道的前一个车辆元胞和相邻车道的前一个和后一个车辆元胞,邻居元胞如图 2所示。
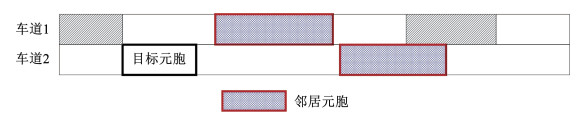
|
图 2 邻居元胞 Fig. 2 Neighbours |
为了准确描述车辆运动状态的不同,本文引入跟驰理论,并建立基于跟驰理论的状态演化规则。根据车头时距将车辆元胞的运动状态分为自由行驶和跟驰行驶两种状态。处于自由行驶的车辆元胞具有较大的车头时距,其运动状态不受前车运动状态影响,会以其期望的最大速度自由行驶;处于跟驰状态的车辆元胞具有较小的车头时距,其运动状态受车间距和前车速度影响,当车间距或者前车速度发生变化时,后车会动态调整其速度以便与前车保持合理的车间距和车速以避免撞车。
1.2.1 参数提取在推导新的状态更新规则时,首先需要先确定3个参数:1)跟驰状态确定指标;2)自由行驶状态期望最大速度vnEFDV;3)跟驰行驶状态期望车头时距TETH。跟驰状态确定指标决定了车流模拟过程中哪些车辆元胞将处于自由行驶和跟驰行驶,两种不同状态的车辆将采用不同的状态更新规则;vnEFDV是为了更准确的反映实际车流中自由行驶的车辆并非全部采用最大速度行驶的现象;TETH决定了处于跟驰流的车辆期望与前车保持的距离。
美国国家科学院交通研究委员会建议采用5 s作为判断车辆是否处于跟驰状态的指标阈值,为了考虑指标冗余性,同时避免固定指标引起状态转换时可能引发的局部震荡问题,本文采用5 s和6 s分别作为判断自由流和跟驰流的指标阈值,并规定当车辆元胞的车头时距小于5 s时,其进入跟驰状态,否则处于自由行驶状态;当处于跟驰状态的车辆元胞的车头时距大于6 s时,车辆元胞进入自由流状态。
vnEFDV和TnETH从WIM实测交通流数据中提取,这两个参数通过以下方式获得:1)通过WIM时,跟驰状态的车辆的当前车头时距即为其TnETH,自由行驶状态的车辆的当前速度即为其vnEFDV;2)所有车辆的vnEFDV和TnETH分别具有相同的概率分布。跟驰状态的车辆的vnEFDV和自由行驶状态的车辆的TnETH可以通过抽样获得,数据样本分别为通过WIM时自由行驶状态的车辆的vnEFDV和跟驰行驶状态的车辆的TnETH。
可以通过实测数据证明上述提取两个参数的过程的合理性。图 3(a)表示WIM系统两个月的车流数据中车头时距小于5 s的车辆的与前车的速度差,可以看到,大部分车辆的速度差小于4 m/s。假定后车具有平均车速25 m/s,以常规加速度2 m/s2加速至与前车速度相同,那么其车间距只缩小了4 m,车头时距只缩小了0.16 s,这样的差别几乎可以忽略。这说明,通过WIM系统时,处于跟驰状态的车辆处于稳定状态,因此取其当前车头时距作为其TnETH是合适的。图 3(b)表示WIM系统两个月的车流数据中车头时距大于10 s的车辆的当前速度,可以看到,大部分的车辆的速度小于28 m/s,说明并不是所有的车辆都会在不受干扰时以最大速度行驶,而是保持一个期望最大速度,因此取自由行驶状态车辆的当前速度作为其vnEFDV是合适的。

|
图 3 实测车辆速度统计结果 Fig. 3 Statistical results of velocity from WIM data |
根据车辆处于自由行驶和跟驰行驶两种不同状态,推导车辆元胞的状态更新加速度。首先对状态更新规则中的相关参数进行说明,如图 4所示。道路的坐标原点为模拟道路的起点,图中xn(t)表示车辆n在t时步的车头位置;Ln表示第n辆车的车长;gapn(t)表示第n辆车和第n-1辆车的车间距。

|
图 4 基本参数解释 Fig. 4 Explanation of basic parameters |
运动状态更新的基本时间单位为1 s,根据运动学基本原理,存在的基本关系有
| $ v_n(t+1)=v_n(t)+a_n(t+1) $ | (3) |
| $ x_n(t+1)=x_n(t)+v_n(t)+\frac{a_n(t+1)}{2} $ | (4) |
| $ x_{n-1}(t)-x_n(t)=\operatorname{gap}_n(t)+L_{n-1} $ | (5) |
式(3)表示速度更新,式(4)表示位置更新,式(5)表示相邻车辆元胞的空间关系。an(t+1)表示车辆n在t+1时步的加速度。
1) 自由行驶状态时,车辆期望提高速度以节省时间,同时又不希望速度过大以保证行驶安全,应该满足的条件为
| $ \begin{gathered} T_n^{\mathrm{ETH}} \cdot v_n(t)+L_{n-1} \leqslant x_{n-1}(t+1)- \\ x_n(t+1) \leqslant 5 v_n(t)+L_{n-1} \end{gathered} $ | (6) |
| $ v_n(t+1) \leqslant v_n^{\mathrm{EFDV}} $ | (7) |
| $ \left|a_n(t+1)\right| \leqslant a_n^{\max } $ | (8) |
式(6)表示自由流时,车辆期望提高速度以节省时间,同时又不希望速度过大以保证行驶安全;式(7)是速度边界条件,表示速度不能大于期望最大自由流速度;式(8)是加速度边界条件,表示加速度不应大于常规最大加速度。
根据式(3)~(8),并忽略an-1(t+1)以实现向量化加载提高模拟效率,则加速度应满足:
| $ a_n^{\text {anti }, \text { fre }}(t+1)=\max \left\{a_1, a_2\right\} $ | (9) |
式中ananti, fre(t+1)为自由行驶的车辆元胞的专属加速度,且
| $ \begin{aligned} &a_1=\max \left\{2\left[\operatorname{gap}_n(t)+v_{n-1}(t)-6 \cdot v_n(t)\right], -a_n^{\max }\right\}\\ &a_2=\min \left\{2 \left[\operatorname{gap}_n(t)+v_{n-1}(t)-\left(1+T_n^{\mathrm{ETH}}\right) \cdot\right.\right. \end{aligned} $ | (10) |
| $ \left.\left.v_n(t)\right], v_n^{\mathrm{EFDV}}-v_n(t), a_n^{\max }\right\} $ | (11) |
2) 跟驰行驶状态时,跟驰行驶应该满足两个目标:一是保持跟驰状态;二是在出现紧急状况时应该避免撞车。对于保持跟驰状态应满足:
| $ x_{n-1}(t+1)-x_n(t+1) \geqslant T_n^{\mathrm{ETH}} \cdot v_n(t)+L_{n-1} $ | (12) |
| $ v_n(t+1) \leqslant v_{n-1}(t+1) $ | (13) |
| $ \left|a_n(t+1)\right| \leqslant a_n^{\max } $ | (14) |
| $ v_n(t+1) \leqslant v_n^{\mathrm{EFDV}} $ | (15) |
式(12)表示跟驰车辆应该与前车保持期望车头时距;式(13)表示跟驰行驶的后车的速度不大于前车;式(14)表示加速度边界条件,实际加速度不大于加速度最大值;式(15)表示更新后的车辆速度应不大于自由流期望最大速度。
紧急制动考虑如下理想状态:假设在t+1时步,前车突然紧急刹车,并在i秒后将速度减至0 m/s。由于刹车灯的作用,后车发现前车刹车后也紧急刹车,并在i+n秒后将速度减至0 m/s,紧急刹车过程可以用图 5解释。

|
图 5 紧急制动模式 Fig. 5 Explanation of braking model |
在稳定的跟驰流中,后车的速度最终会与前车保持基本一致,或在前车速度附近波动,当前车紧急刹车,后车发现后也会紧急刹车。由于速度相近,发生紧急制动的车辆会在几乎相同时间内停车。考虑一般情况,城市道路最大车速120 km/h(33.3 m/s),当车辆以最大减速度(-8 m/s2)紧急刹车时,车辆将在4.2 s停车。本文取刹车时间为4 s,则刹车过程的行驶距离可以用以下公式描述:
| $ \begin{gather*} x_{n-1}(t+1+4)=x_{n-1}(t+1)+4 v_{n-1}(t+1)+ \\ (4-1) \cdot a_{\text {brake }}+\frac{4}{2} \cdot a_{\text {brake }} \end{gather*} $ | (16) |
| $ \begin{gather*} x_{n}(t+1+4)=x_{n}(t+1)+4 v_{n}(t+1)+ \\ (4-1) \cdot a_{\text {brake }}+\frac{4}{2} \cdot a_{\text {brake }} \end{gather*} $ | (17) |
为了避免撞车,停车后两车位置应该满足:
| $ x_{n-1}(t+1+4)-x_{n}(t+1+4) \geqslant L_{n-1}+S_{\text {safe }} $ | (18) |
式中Ssafe表示车辆停止时希望保持的安全距离。
同时,在t+1时刻,车辆应该具有减速空间:
| $ \begin{equation*} x_{n-1}(t+1)-x_{n}(t+1) \geqslant L_{n-1} \end{equation*} $ | (19) |
根据式(3)~(5)、(12)~(15)及式(16)~(19),并忽略an-1(t+1),跟驰状态车辆加速度应该满足:
| $ a_{n}^{\text {anti, fol }}(t+1)=\max \left\{\min \left\{a_{n}^{\mathrm{fol}, 1}, a_{n}^{\mathrm{fol}, 2}\right\}, a_{n}^{\mathrm{fol}, 3}\right\} $ | (20) |
| $ \begin{gather*} a_{n}^{\mathrm{fol}, 1}(t+1)=\min \left\{2 \left[\operatorname{gap}_{n}(t)+v_{n-1}(t)-\right.\right. \\ \left.v_{n}(t)-T_{n}^{\mathrm{ETH}} \cdot v_{n}(t)\right], \\ \left.v_{n-1}(t)-v_{n}(t), a_{n}^{\max }, v_{n}^{\mathrm{EFDV}}-v_{n}(t)\right\} \end{gather*} $ | (21) |
| $ \begin{gather*} a_{n}^{\mathrm{fol}, 2}=\min \left\{\frac{2}{3}\left[\operatorname{gap}_{n}(t)-S_{\text {safe }}+5\left(v_{n-1}(t)-v_{n}(t)\right)\right], \right. \\ \left.2\left[\operatorname{gap}_{n}(t)+v_{n-1}(t)-v_{n}(t)\right]\right\} \end{gather*} $ | (22) |
| $ a_{n}^{\mathrm{fol}, 2}(t+1)=-a_{n}^{\max } $ | (23) |
3) 紧急制动时,对于减速车辆,当车辆以期望最大减速度减速仍然不能避免相撞且不能换道时,触发紧急制动,即车辆运动满足下列条件时,触发紧急制动。
| $ x_{n-1}(t+1)-x_{n}(t+1) \leqslant L_{n-1}+S_{\text {safe }} \mid a_{n}(t+1)=-a_{n}^{\max } $ | (24) |
当车辆触发紧急制动时,车辆元胞的刹车状态指征参数b更新为1,车辆采用刹车加速度进行速度更新,直至运动状态不满足紧急制动条件。
4) 车辆行驶中会随机变速,当满足以下条件时,车辆随机变速。
| $ a_{n}^{\mathrm{R}}(t+1)=\left\{\begin{array}{l} \operatorname{rand}(-1, 1), \gamma \leqslant p_{\mathrm{d}} \\ 0, \gamma>p_{\mathrm{d}} \end{array}\right. $ | (25) |
式中:anR(t+1)表示随机加速度,γ表示生成的0~1之间的随机数,pd表示人工设定的随机变速概率指标。车辆的最终加速度为状态更新规则计算的加速度和随机加速度的综合。
5) 车辆行驶过程中会根据车间距换道,换道分为非必要性换道和必要性换道,非必要性换道指车辆在前方车辆速度较慢时,为追求更快的速度而发生的换道行为,必要性换道指在一定区间内必须实施的换道行为。必要性换道一般发生在匝道的分流、合流段等,桥梁一般不存在分流和合流段,因此本文只考虑非必要性换道。当满足以下条件时,车辆触发非必要换道条件,进行换道:
| $ \begin{equation*} a_{n}(t+1) \leqslant 0 \end{equation*} $ | (26) |
| $ x_{n-1}^{\mathrm{tar}}(t+1)-x_{n}(t+1) \geqslant T_{n}^{\mathrm{ETH}} \cdot v_{n}(t+1)+L_{n-1}^{\mathrm{tar}} $ | (27) |
| $ x_{n}(t+1)=x_{n}(t)+v_{n}(t)+\frac{1}{2} a_{n}^{\max }(t+1) $ | (128) |
| $ x_{n}(t)-x_{n}^{\mathrm{tar}}(t) \geqslant S^{\mathrm{tar}}-L_{n} $ | (29) |
式中:xn-1tar(t+1)表示目标车道的前车在t+1时步的位置,Ln-1tar表示目标车道的前车的车长,式(28)采用anmax(t+1)表示换道车辆期望以最大加速度尽快完成换道,Star表示换道车辆与目标车道的后车的车间距。Star因驾驶员的驾驶习惯不同而不同,目前没有实测数据或相关准则指导Star的取值。实际模拟中,研究人员可以根据实际需求设定不同的Star,当需要严格控制车辆换道时,可以将Star设置的较大,否则可以将Star设置的较小。
上述条件中,式(26)表示车辆在当前车道不能加速;式(27)、(28)表示车辆在目标车道可以加速,并且换道后,当前车辆与目标车道的前车的车头时距不小于跟驰状态期望车头时距;式(29)表示换道车辆与目标车道的后车具有足够的车间距。当满足上述条件时,车辆可以换道。
在目标车道上,换道车辆车头前的第一个车辆元胞为目标车道的前车邻居元胞,换道车辆的车头后的第一个车辆元胞为后车邻居元胞,换道车辆元胞与邻居车辆元胞的空间关系如图 6所示。

|
图 6 换道车辆与邻居元胞的空间关系 Fig. 6 Spatial correlation between lane-changing vehicle cell and neighbour cells |
本文虽然没有考虑必要性换道条件,但是可以对本文模型进行改进实现必要性换道的模拟,可以通过对车辆元胞增加更多的描述其驾驶目标的限制性变量来描述车辆的必要性换道需求,同时在换道条件中增加更多的位置限定条件和速度限定条件来准确模拟车辆的必要性换道。
1.3 基于实测WIM数据的发车规则本文提出基于实测WIM数据的发车规则,充分利用实测交通流信息,准确重构任意时段的车队信息,并提出基于车头时距的发车规则,重现实际车辆通过WIM的状态。基于实测数据的发车规则如下。
首先根据实测WIM数据直接生成车队:
| $ \boldsymbol{V}_{\text {pool }}=\left[\begin{array}{c} G_{1}, k_{1}, o_{1}^{r}, o_{1}^{f}, q_{1}^{1}, \cdots, q_{1}^{k_{1}-1}, g_{1}^{1}, \cdots, g_{1}^{k_{1}}, v_{1}, T_{1}, T_{1}^{\mathrm{ETH}}, v_{1}^{\mathrm{EFDV}}, I_{1} \\ \vdots \\ G_{i}, k_{i}, o_{i}^{r}, o_{i}^{f}, q_{i}^{1}, \cdots, q_{i}^{k_{i}-1}, g_{i}^{1}, \cdots, g_{i}^{k_{i}}, v_{i}^{0}, T_{i}^{0}, T_{i}^{\mathrm{ETH}}, v_{i}^{\mathrm{EFDV}}, I_{i} \\ \vdots \\ G_{n}, k_{n}, o_{n}^{r}, o_{n}^{f}, q_{n}^{1}, \cdots, q_{n}^{k_{n}-1}, g_{n}^{1}, \cdots, g_{n}^{k_{n}}, v_{n}, T_{n}, T_{n}^{\mathrm{ETH}}, v_{n}^{\mathrm{EFDV}}, I_{n} \end{array}\right] $ | (30) |
式中:Vpool表示车队,每行元素存储一辆车的所有信息;
然后按照顺序,当车辆满足式(31)时,车辆i将从入口将进入道路。
| $ T_{\mathrm{add} 0}+T_{i}^{0} \leqslant T_{t} $ | (31) |
式中:Tadd0为上次加车时间;Ti0为车辆i的初始车头时距;Tt为当前时步。
最后当车辆进入道路时,车辆初始位置通过式(32)确定。
| $ x_{i}=\left(T_{t}-T_{\text {add } 0}-T_{i}^{0}\right) \cdot v_{i}^{0} $ | (32) |
建立基于所提元胞自动机的随机车流荷载模拟方法,整体流程如图 7所示。首先基于WIM数据计算各车辆的车头时距,并确定各车辆的vnEFDV和TnETH;然后生成车队。当满足发车条件时,车辆进入道路,并依据提出的运动状态演化规则进行微观交互的模拟。

|
图 7 随机车流荷载模拟流程图 Fig. 7 Flowchart of stochastic traffic load simulation using the proposed model |
WIM数据为城市道路实测车流数据,共4车道,上下行各两车道,分为快车道和慢车道。根据WIM数据首先计算每辆车的车头时距、vnEFDV和TnETH,然后根据车辆出现顺序生成车辆队列。模拟24 h的车流以检验提出的模型的可靠性,模拟道路长度1 000 m,最大速度120 km/h,常规行驶期望最大加速度2 m/s2,常规行驶期望最大减速度-2 m/s2,紧急刹车减速度-8 m/s2,随机减速概率0.3,换道概率0.25。
2.2 车流宏观特性模拟验证图 8和图 9表示24 h两个车道的模拟车流和WIM数据的小时车流量和小时车辆总重对比结果。可以看到,模拟车流的小时车流量和小时车辆总重与WIM数据吻合较好,车流量和车辆总重均能反映实际车流的时段特性,可以准确反映车流的非平稳性,说明提出的新的基于实测数据的发车规则能准确模拟实际车流的宏观特性。
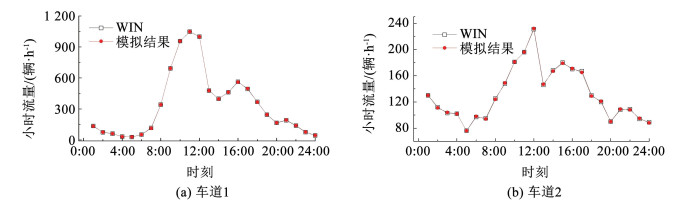
|
图 8 小时流量统计对比 Fig. 8 Comparison of hourly traffic volume |

|
图 9 小时总重对比 Fig. 9 Comparison of hourly gross weight |
通过提取模拟车流的典型场景中车辆的运动状态变化过程说明所提模型微观交互模拟的合理性,常规车流中的典型场景是加减速和变换道。图 10(a)表示车道2某时段的模拟车流的时空斑图,图中黑框部分表示车辆换道引起的加减速变换过程,黑框的放大图如图 10(b)。可以看到,在某时步突然有车换入该车道(具体表现为某辆车的时空轨迹不连续,如图 10 (b)空心圆),导致跟随其后面的车辆的车头时距发生变化,后车随即调整速度以适应这种变化,后车调整速度的具体表现为其时空轨迹改变原始路径,路径向右偏斜表示其单位时间内行驶的距离减小,即发生减速行为。

|
图 10 正常行驶时空斑图 Fig. 10 Spatial-temporal diagram of normal driving |
图 11表示典型场景下相邻两辆车的微观交互过程。车辆1进入道路后首先加速至其vnEFDV,其车头时距一直大于5 s,因此在自由行驶状态下一直保持其vnEFDV行驶。车辆2进入道路后首先加速至其vnEFDV,由于其速度大于前车速度,因此其车头数据不断减小。当其车头时距小于5 s时,进入跟驰状态,开始减速,直至与前车保持一定距离和合理的速度。模拟结果体现了WIM数据反映的自由流车辆不一定全部加速至最大速度行驶的事实。同时,车辆微观交互中加速度和速度的变化在合理范围内且体现了不同车辆加速度的独特性,车辆加速度依据车辆当前速度、前车速度和当前车间距计算得到,表明推导的动态演化规则的合理性。与文献[14]模型相比,本文提出的模型的模拟结果既能匹配WIM数据反映的事实,车辆的状态更新也更符合实际,表明本文模型的先进性。

|
图 11 速度和加速度更新(本文模型) Fig. 11 Evolution of acceleration and velocity(the proposed model) |
实际模拟车流没有触发紧急制动,为了验证提出的模型模拟车辆紧急制动的可行性,人工设定触发车辆紧急制动,车辆从开始制动至制动结束共持时15 s。图 12(a)表示紧急制动的时空斑图,图 12(b)表示图 12(a)方框中紧急制动期间相关车辆的时空斑图。可以看到,当前车开始紧急制动后,后车随着车头时距的改变其运动状态也相应发生变化,当后车进入跟驰状态时,也开始制动。制动车辆时空斑图表现为车辆轨迹斜率逐渐减小,当完全停止后,其斜率变为0,即车辆位置不再随着时间产生变化。制动结束时,所有减速至速度为0 m/s的车辆都以相同加速度2 m/s2开始启动,随后按照状态更新规则进行状态更新。
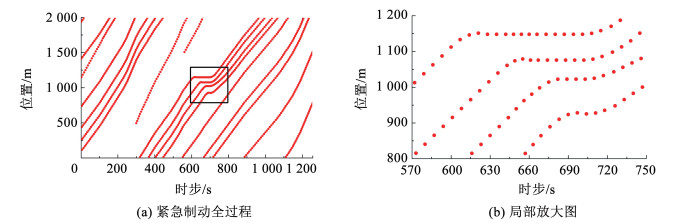
|
图 12 时空斑图-紧急制动过程 Fig. 12 Spatial-temporal diagram of sudden braking |
图 13展示了紧急制动期间,相关车辆的速度和加速度随着车头时距的变化过程。车辆1为开始制动车辆,车辆2为跟随车辆。当车辆1紧急刹车后,其速度逐渐减小至0 m/s;车辆2开始阶段车头时距大于5 s,处于自由行驶状态,当跟随车辆进入跟驰状态后也开始紧急刹车,直至停止。当制动结束,所有停止的车辆按照2 m/s2的加速度启动,然后按照更新规则计算每时步的加速度,完成状态更新。该过程完整模拟了车辆在不同行驶状态下的紧急刹车、停止和重启动过程,表明所提模型模拟紧急制动状况的可行性。

|
图 13 紧急制动过程速度和加速度变化 Fig. 13 Velocity and acceleration evolution in sudden braking |
为了验证提出的模型精确模拟车辆荷载的能力,不考虑变换道,重新模拟随机车流,并采用影响线加载的方式计算荷载效应。同时采用本文模型、传统NS模型和WIM数据计算荷载效应,并进行对比。为了避免不同车辆的轴载对结果的影响,采用20 m简支梁跨中弯矩作为对比效应。20 m简支梁的荷载效应由单辆车控制,因此通过对比20 m简支梁的荷载效应可以准确判断本文模型车辆荷载的模拟精度。采用WIM数据进行荷载效应计算时不考虑车辆的微观交互,设定所有车辆都采用通过WIM时的速度匀速行驶。在实际车流中很可能存在后车速度大于前车速度的状况,在这种情况下,匀速行驶的车辆有可能会因为车间距不断减小而发生撞车,从而影响计算结果。为了得到准确的荷载效应,当发现车辆的车间距小于当前速度时,将后车车速强制设为前车车速。为了准确获得极值荷载效应,将加载时步设为0.01 s,即每时步得到100个计算结果,然后选取绝对值最大的荷载效应作为每秒计算结果的代表值。
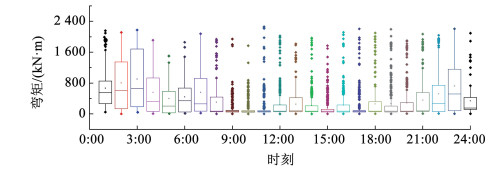
图 14~16给出基于WIM数据、本文模型和NS模型计算的24 h荷载效应的统计结果。可以看到,基于本文模型和WIM数据计算的荷载效应的统计分布几乎完全一致,基于NS模型的计算结果在最大值和分位值上均与WIM结果存在差异,这是由于NS模型只能以集中力的方式模拟车辆荷载。表 1给出第4、第10和第16小时的最大荷载效应的对比结果,以WIM结果为基准计算相对误差。第4、第10和第16小时的车流分别对应稀疏流、密集流和中等密集车流。可以看到,本文模型和WIM结果几乎完全一致,相对误差均小于0.1%,而NS模型与WIM结果最大相对误差接近8%。该结果说明,本文模型能准确的模拟车辆轴载。需要说明的是,荷载效应的相对误差受车辆轴间距的影响较大,当轴间距较小时,荷载效应相对误差较小,当轴间距较大时,相对误差也会变大。一般重车的车间距较大,因此当实际重车较多时,该相对误差还会更大。
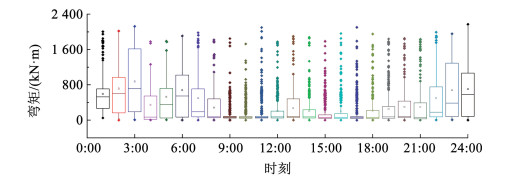
|
图 14 基于WIM数据计算的荷载效应小时统计箱形图 Fig. 14 Box plot of load effects using WIM data |

|
图 15 基于本文模型计算的荷载效应小时统计箱形图 Fig. 15 Box plot of load effects using the proposed model |
|
图 16 基于NS模型计算的荷载效应小时统计箱形图 Fig. 16 Box plot of load effects using NS model |
| 表 1 弯矩统计值对比 Tab. 1 Comparison of statistical results of bending moment |
从图 15还可以看到,统计结果的箱形图表现出明显的时变特性。各小时的最大荷载效应比较接近,但是不同小时的箱形图的箱体差异较大,这说明在各时段均存在重车,不同时段的车重(车型)表现出明显的差异性,在8:00—21:00时,车辆以小重量车为主,在其他时段,车辆以大重量车为主。该结果说明,本文提出的模型能重构时段车流,并准确反映时段车流的时变特性。
3 结论为实现桥址随机车流荷载的准确模拟,解决传统元胞自动机模型不能准确模拟车辆荷载与合理的微观交互行为的缺点,提出了基于可变元胞与跟驰理论的新型元胞自动机模型。采用实测WIM数据验证所提模型的可行性,得到以下结论:
1) 提出的可变元胞以车辆为核心,不依赖于传统的固定尺寸的元胞晶格,能精确反映实际车辆尺寸、轴间距等信息。结合融入的轴载信息,可以实现车辆荷载的精确模拟。
2) 提出的基于跟驰理论的状态更新规则能准确反映实际车流特性,并能计算每个车辆元胞的专属加速度,因此,模拟的车辆的微观交互也更符合实际车辆驾驶行为,得到的车辆的时空位置也更合理。
3) 基于WIM数据的车队重构规则能生成任意时段的真实车队,不受数据量的限制。结合提出的发车规则,可以重现实际车辆通过WIM系统时的状态,赋予模拟车流符合实际的初始运动状态。
4) 基于实测数据的发车规则和跟驰理论的转换规则保证了模拟车流中车辆时空位置的合理性,结合车辆元胞中精确的轴载信息,实现随机车流荷载的准确模拟。提出的元胞自动机模型可以实现桥址任意时段的随机车流荷载的模拟。
| [1] |
李光玲, 韩万水, 陈笑, 等. 风和随机车流下悬索桥伸缩缝纵向变形[J]. 交通运输工程学报, 2019, 19(5): 21. LI Guangling, HAN Wanshui, CHEN Xiao, et al. Longitudinal deformation of expansion joint of suspension bridge under wind and random traffic flow[J]. Journal of Traffic and Transportation Engineering, 2019, 19(5): 21. |
| [2] |
周军勇, 苏建旭, 齐飒. 基于元胞自动机微观模拟的随机车流与桥梁耦合振动数值研究[J]. 工程力学, 2021, 38(2): 187. ZHOU Junyong, SU Jianxu, QI Sa. Numerical investigation on random traffic-bridge coupled vibration using cellular automaton-based microscopic simulation[J]. Engineering Mechanics, 2021, 38(2): 187. |
| [3] |
韩万水, 闫君媛, 武隽, 等. 基于长期监测的特重车交通荷载特性及动态过桥分析[J]. 中国公路学报, 2014, 27(2): 54. HAN Wanshui, YAN Junyuan, WU Jun, et al. Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record[J]. China Journal of Highway and Transport, 2014, 27(2): 54. |
| [4] |
邓露, 何维, 俞扬, 等. 公路车-桥耦合振动的理论和应用研究进展[J]. 中国公路学报, 2018, 31(7): 38. DENG Lu, HE Wei, YU Yang, et al. Research progress in theory and applications of highway vehicle-bridge coupling vibration[J]. China Journal of Highway and Transport, 2018, 31(7): 38. |
| [5] |
刘焕举, 武隽, 刘宁, 等. 精细微观车流-桥梁耦合系统构建及伸缩缝纵向变形分析[J]. 中国公路学报, 2021, 34(12): 115. LIU Huanju, WU Jun, LIU Ning, et al. Construction of fine microscopic vehicle-bridge coupling system and analysis of longitudinal deformation of the expansion joint[J]. China Journal of Highway and Transport, 2021, 34(12): 115. |
| [6] |
武隽, 杨飞, 韩万水. 基于实测和CA模型的大跨桥梁车辆荷载模拟[J]. 铁道科学与工程学报, 2014, 11(4): 14. WU Jun, YANG Fei, HAN Wanshui. Vehicle load simulation for long-span bridge based on merging real-monitored data and cellular automaton model[J]. Journal of Railway Science and Engineering, 2014, 11(4): 14. |
| [7] |
CHEN S R, WU J. Modeling stochastic live load for long-span bridge based on microscopic traffic flow simulation[J]. Computers & Structures, 2011, 89(9/10): 813. |
| [8] |
ZHOU Y F, CHEN S R. Investigation of the live-load effects on long-span bridges under traffic flows[J]. Journal of Bridge Engineering, 2018, 23(5): 4018021. DOI:10.1061/(ASCE)BE.1943-5592.0001214 |
| [9] |
ENRIGHT B, OBRIEN E. Montecarlo simulation of extreme traffic loading on short and medium span bridges[J]. Structure & Infrastructure Engineering, 2013, 9(12): 1267. |
| [10] |
OBRIEN E, HAYRAPETOVA A, WALSH C. The use of micro-simulation for congested traffic load modeling of medium-and long-span bridges[J]. Structure and Infrastructure Engineering, 2012, 8(3): 269. DOI:10.1080/15732471003640477 |
| [11] |
杨飞. 基于实测数据与CA交通流模型的桥梁汽车荷载研究[D]. 西安: 长安大学, 2014 YANG Fei. Research on the bridge traffic loads based on the monitoring record and ca traffic model[D]. Xi'an: Chang'an University, 2014 |
| [12] |
WOLFRAM S. Statistical mechanics of cellular automata[J]. Reviews of Modern Physics, 1983, 55(3): 601. DOI:10.1103/RevModPhys.55.601 |
| [13] |
NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal De Physique I, 1992, 2(12): 2221. DOI:10.1051/jp2:1992262 |
| [14] |
NAGEL K, WOLF D E, WAGNER P, et al. Two-lane traffic rules for cellular automata: a systematic approach[J]. Physical Review E: Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1997, 58(2): 1425. |
| [15] |
XIONG Z L, ZHU J, ZHENG K F, et al. Framework of wind-traffic-bridge coupled analysis considering realistic traffic behavior and vehicle inertia force[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2020, 205: 104322. |
| [16] |
HAN W S, WU J, CAI C S, et al. Characteristics and dynamic impact of overloaded extra heavy trucks on typical highway bridges[J]. Journal of Bridge Engineering, 2015, 20(2): 5014011. DOI:10.1061/(ASCE)BE.1943-5592.0000666 |
| [17] |
HAN W S, YUAN Y G, XIE Q, et al. Reliability-based truck weight regulation of small-to medium-span bridges[J]. Journal of Bridge Engineering, 2017, 23(1): 4017101. |
| [18] |
HAN W S, YUAN Y G, HUANG P M, et al. Dynamic impact of heavy traffic load on typical t-beam bridges based onwim data[J]. Journal of Performance of Constructed Facilities, 2017, 31(3): 4017001. DOI:10.1061/(ASCE)CF.1943-5509.0000991 |
| [19] |
韩万水, 马麟, 汪炳, 等. 随机车流-桥梁系统耦合振动精细化分析与动态可视化[J]. 中国公路学报, 2013, 26(4): 78. HAN Wanshui, MA Lin, WANG Bing, et al. Refinement analysis and dynamic visualization of traffic-bridge coupling vibration system[J]. China Journal of Highway and Transport, 2013, 26(4): 78. |
| [20] |
韩万水, 武隽, 马麟, 等. 基于微观交通流模型的风-车-桥系统高真实度模拟[J]. 中国公路学报, 2015, 28(11): 37. HAN Wanshui, WU Jun, MA Lin, et al. High-fidelity simulation of wind-vehicle-bridge system based on microscopic traffic flow model[J]. China Journal of Highway and Transport, 2015, 28(11): 37. |
| [21] |
殷新锋, 邓露. 随机车流作用下桥梁冲击系数分析[J]. 湖南大学学报(自然科学版), 2015, 42(9): 68. YIN Xinfeng, DENG Lu. Impact factor analysis of bridges under random traffic loads[J]. Journal of Hunan University(Natural Sciences), 2015, 42(9): 68. |
| [22] |
阮欣, 金泽人, 周军勇, 等. 基于多元胞模型的桥梁车流合成及荷载模拟[J]. 同济大学学报(自然科学版), 2017, 45(7): 941. RUAN Xin, JIN Zeren, ZHOU Junyong, et al. Traffic flow generation and load simulation of bridges based on multi-cell cellular automaton[J]. Journal of Tongji University(Natural Science), 2017, 45(7): 941. |
| [23] |
RUAN X, ZHOU J Y, TU H Z, et al. An improved cellular automaton with axis information for microscopic traffic simulation[J]. Transportation Research Part C: Emerging Technologies, 2017, 78: 63. DOI:10.1016/j.trc.2017.02.023 |
| [24] |
张曦霖. 新型元胞自动机交通流荷载模型及其应用[D]. 西安: 长安大学, 2015 ZHANG Xilin. A new cellular automata model and it's application of traffic load[D]. Xi'an: Chang'an University, 2015 |
 2024, Vol. 56
2024, Vol. 56


