2. 地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059;
3. 中国兵器工业试验测试研究院,陕西 华阴 714200
2. Stake Key Laboratory of Geohazard Prevetion and Geoenvironment Protection (Chengdu University of Technology), Chengdu 610059, China;
3. Norinco Group Testing and Research Institute, Huayin 714200, Shaanxi, China
涵洞是基础设施中常见的地下构筑物,广泛应用于交通、水利和油汽输送等工程。随着涵洞修筑地质水文环境的恶化以及长期服役性能退化,涵洞结构安全问题日益突出。竖向土压力是涵洞结构设计考虑的主要荷载,也是影响涵洞结构安全的首要因素。根据埋设方式涵洞分为上埋式和沟埋式两类,众多学者基于饱和土力学对两类涵洞竖向土压力进行了系统研究[1-5]。然而,工程实践中遇到的土体大多处于非饱和状态[6-8],饱和状态仅是非饱和状态的一个特例,文献[9]对回填非饱和砂土的混凝土涵洞竖向土压力进行了现场实测,文献[10]获得了回填非饱和黏土时波纹管涵洞现场实测竖向土压力的分布特征,探讨非饱和土涵洞的竖向土压力计算方法,可完善并优化涵洞结构设计理论。
关于非饱和土结构物竖向土压力的理论研究,代表性进展有:文献[11]推导了4种给定吸力分布下非饱和土Trapdoor问题的松动土压力公式,文献[12]建立了线性吸力分布下非饱和土浅埋隧道竖向土压力的有效应力法解答,文献[13]提出了线性与均匀两种吸力分布下非饱和土上埋式涵洞的竖向土压力解析解。上述非饱和土竖向土压力公式均事先假定具体的吸力分布形式,难以反映土体类别、外界大气环境(降雨入渗、静水压力和水分蒸发)所引发的吸力大小与分布变化,在实际工程应用中存在一些不适用情形,亟需构建不受具体吸力分布形式限制的非饱和土涵洞竖向土压力解答。文献[14]基于吸应力理论创立了非饱和土的有效应力强度公式,结合达西定律得到稳态渗流下基质吸力和吸应力的理论表达式,已在非饱和土地基承载力、边坡稳定性等问题中得到实践与检验[15-16]。同时,涵洞回填土内部的土拱效应显著[17],假定圆弧小主应力轨迹是分析涵洞土拱效应的有效途径[18]。
因此,本文首先以圆弧小主应力轨迹描述非饱和回填土的土拱效应,推导涵洞滑移面处的土压力系数,继而基于非饱和土的有效应力强度公式和吸应力理论,分别建立稳态渗流下两类非饱和土涵洞的竖向土压力迭代解,给出应用步骤并进行对比验证与方法拓展,最后探讨涵洞竖向土压力迭代解的工程简化。
1 基本理论 1.1 力学模型鉴于涵洞长度多远大于其横断面尺寸、涵洞与回填土存在明显刚度差异以及两类涵洞不同的施工方法,图 1给出了平面应变状态下涵-土体系的两种受力模型,其中B为箱型涵洞的宽度,h为箱型涵洞的高度,H为从涵顶算起的填土高度, 地下水位Dw低于涵底,假定地基为刚体并忽略涵洞的结构变形, 上埋式涵洞内/外土柱的非饱和回填土相同,沟埋式涵洞内土柱为非饱和回填土、外土柱为原状地基土。

|
图 1 涵-土体系的受力模型 Fig. 1 Mechanical model of the culvert-soil system |
因为涵洞刚度大于回填土刚度,图 1(a)中上埋式涵洞内土柱沉降量小于外土柱沉降量而存在沉降差,进而外土柱对内土柱的摩擦力向下,当二者沉降量相等时出现等沉面及等沉面高度Hc。与上埋式涵洞内土柱摩擦力的方向相反,槽壁对图 1(b)中沟埋式涵洞内土柱的摩擦力向上。
1.2 非饱和土强度文献[14]定义的非饱和土有效应力σ′为
| $ \sigma^{\prime}=\left(\sigma-u_{\mathrm{a}}\right)-\sigma_{\mathrm{s}} $ | (1) |
式中:σ为总应力,ua为孔隙气压力,σ-ua为净法向应力,σs为吸应力。
将式(1)代入Mohr - Coulomb准则的有效应力公式得
| $ \tau_{\mathrm{f}}=c^{\prime}+\left(\sigma-u_{\mathrm{a}}\right) \tan \varphi^{\prime}-\sigma^{\mathrm{s}} \tan \varphi^{\prime} $ | (2) |
式中τf为土体抗剪强度,c′和φ′分别为饱和状态下土体的有效黏聚力、有效内摩擦角。
式(2)为非饱和土基于吸应力理论的抗剪强度公式,其中吸应力σs的表达式为
| $ \left\{\begin{array}{l} \sigma_{\mathrm{s}}=-\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right), u_{\mathrm{a}}-u_{\mathrm{w}} \leqslant 0 \\ \sigma_{\mathrm{s}}=-\frac{u_{\mathrm{a}}-u_{\mathrm{w}}}{\left\{1+\left[\alpha\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)\right]^{n}\right\}^{\frac{n-1}{n}}}, u_{\mathrm{a}}-u_{\mathrm{w}}>0 \end{array}\right. $ | (3) |
式中:uw为孔隙水压力,ua-uw为基质吸力,α近似为进气值的倒数,n为无量纲的常数。
文献[19]根据达西定理和Gardner模型求得稳态渗流下均质非饱和土的基质吸力为
| $ u_{\mathrm{a}}-u_{\mathrm{w}}=-\frac{1}{\alpha} \ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-\gamma_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right] $ | (4) |
式中:γw为水重度; ks为饱和渗透系数;q为稳态渗流量,存在水分蒸发(q>0)、静水压力(q=0)和降雨入渗(q < 0)3种情况;q/ks为无量纲量,代表最小水力坡降和渗流强弱。
将式(4)代入式(3),得稳态渗流下均质非饱和土的吸应力σs为
| $ \begin{equation*} \sigma^{\mathrm{s}}=\frac{1}{\alpha} \frac{\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]}{\left(1+\left\{-\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]\right\}^{n}\right)^{\frac{n-1}{n}}} \end{equation*} $ | (5) |
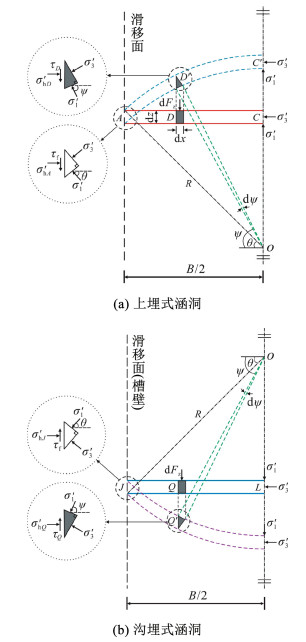
因涵-土体系左右受力对称,只取模型左侧一半进行分析。在图 2(a)中,上埋式涵洞内土柱回填土产生土拱负效应,所形成的小主应力轨迹为虚线上凸拱;在图 2(b)中,沟埋式涵洞回填土产生土拱正效应,所形成的小主应力轨迹为虚线下凸拱。假定两类涵洞不同深度处的小主应力轨迹均为圆弧,圆心在涵洞竖对称轴上。
|
图 2 小主应力轨迹 Fig. 2 Minor principal stress trajectory |
以图 2(a)中上埋式涵洞滑移面处的A点为例,图 3(a)给出了水平薄层单元达到极限平衡时的Mohr应力圆,将其纵坐标向左平移c′cot φ′转化为无黏性土,并在图 3(b)中标出A点应力。
新应力系的坐标为
| $ \left\{\begin{array}{l} \hat{\sigma}=\sigma^{\prime}+c^{\prime} \cot \varphi^{\prime} \\ \hat{\tau}=\tau \end{array}\right. $ | (6) |
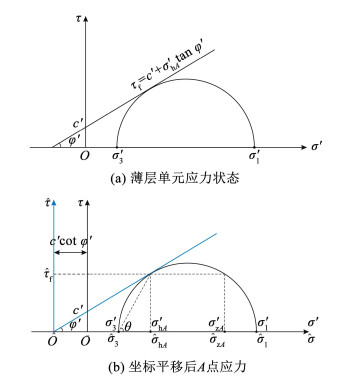
|
图 3 薄层单元应力状态及坐标平移后A点应力 Fig. 3 Stress state of a thin layer element and stresses of point A after translating coordinate axis |
式中
令N为图 3(b)中变换大主应力
| $ \begin{equation*} N=\frac{\hat{\sigma}_{1}}{\hat{\sigma}_{3}}=\frac{1+\sin \varphi^{\prime}}{1-\sin \varphi^{\prime}} \end{equation*} $ | (7) |
首先,在新应力系下由涵洞非饱和回填土拱效应与Mohr应力圆推导滑移面土压力系数;其次,分析水平薄层单元的竖向力平衡,考虑上埋式/沟埋式涵洞滑移面摩擦力的方向差异,结合非饱和土吸应力理论分别建立两类涵洞的竖向土压力迭代解,其中上埋式涵洞需确定等沉面高度;最后,给出应用两类涵洞竖向土压力迭代解的步骤,同时对涵洞力学模型假定进行了方法拓展。
2.1 上埋式涵洞 2.1.1 滑移面土压力系数根据图 2(a)中滑移面A点微元的力平衡,得A点的水平有效应力
| $ \begin{equation*} \sigma_{\mathrm{h}A}^{\prime}=\sigma_{1}^{\prime} \cos ^{2} \theta+\sigma_{3}^{\prime} \sin ^{2} \theta \end{equation*} $ | (8) |
式中θ为A点有效大主应力作用面与水平面的夹角,且θ=45°+φ′/2对应有效小主应力达到最大偏转、土拱效应充分发挥。
在新应力系下,任意D点对应图 2(a)中圆弧轨迹上D′点的变换水平应力
| $ \hat{\sigma}_{\mathrm{h} D}=\hat{\sigma}_{1} \cos ^{2} \psi+\hat{\sigma}_{3} \sin ^{2} \psi $ | (9) |
式中ψ为D点有效大主应力作用面与水平面的夹角,且θ≤ψ≤180°-θ。
将式(9)除以
| $ \hat{\sigma}_{\mathrm{z}D}=\hat{\sigma}_{1}\left(\sin ^{2} \psi+\cos ^{2} \psi/N\right) $ | (10) |
由式(10)角度积分得水平薄层单元的变换竖向力
| $ \hat{\sigma}_{\mathrm{z}}=\frac{\hat{F}_{\mathrm{z}}}{B}=\frac{\hat{F}_{\mathrm{z}}}{2 R \cos \theta}==\hat{\sigma}_{1}\left(1-\frac{N-1}{3 N} \cos ^{2} \theta\right) $ | (11) |
式中R=0.5B/cos θ为圆弧半径。
将A点的变换水平应力除以变换平均竖向应力式(11),得新应力系下滑移面土压力系数
| $ \hat{K}=\frac{\hat{\sigma}_{\mathrm{h}A}}{\hat{\sigma}_{\mathrm{z}}}=\frac{\sigma_{\mathrm{h}A}^{\prime}+c^{\prime} \cot \varphi^{\prime}}{\sigma_{\mathrm{z}}^{\prime}+c^{\prime} \cot \varphi^{\prime}}=\frac{3 N \cos ^{2} \theta+3 \sin ^{2} \theta}{3 N-(N-1) \cos ^{2} \theta} $ | (12) |
根据非饱和土的有效应力式(1),由式(12)得旧应力系下滑移面净水平应力σhA-ua为
| $ \sigma_{\mathrm{h} A}-u_{\mathrm{a}}=\hat{K}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+(1-\hat{K})\left(\sigma^{\mathrm{s}}-c^{\prime} \cot \varphi^{\prime}\right) $ | (13) |
式中(σz-ua)为深度z处的净竖向应力。
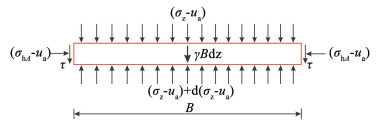
2.1.2 竖向土压力解答在图 2(a)深度z处(H-Hc≤z≤H)取一水平薄层单元,假定竖向土压力沿涵洞宽度方向为均匀分布,图 4为该单元的受力分析。
|
图 4 上埋式涵洞水平薄层单元 Fig. 4 Horizontal thin layer element for a positive buried culvert |
通过水平薄层单元的竖向力平衡得
| $ \gamma B \mathrm{~d} z+2 \tau \mathrm{d} z-B \mathrm{~d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)=0 $ | (14) |
式中γ为回填土的重度,τ为滑移面摩擦力。
在滑移面处非饱和土达到极限平衡,滑移面摩擦力τ等于土体抗剪强度τf,表明土拱效应已充分发挥即θ=45°+φ′/2,联合式(2)和式(13)得
| $ \begin{gather*} \tau=c^{\prime}+\left(\sigma_{\mathrm{h} A}-u_{\mathrm{a}}\right) \tan \varphi^{\prime}-\sigma^{\mathrm{s}} \tan \varphi^{\prime}= \\ \hat{K} \tan \varphi^{\prime}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}-\sigma^{\mathrm{s}}+c^{\prime} \cot \varphi^{\prime}\right) \end{gather*} $ | (15) |
将式(5)和式(15)代入式(14)得
| $\begin{array}{l} \frac{\mathrm{d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)}{\mathrm{d} z}-\frac{2 \hat{K} \tan \varphi^{\prime}}{B}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)=\gamma+\frac{2 \hat{K} c^{\prime}}{B}- \\ \frac{2 \hat{K} \tan \varphi^{\prime}}{\alpha B} \frac{\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]}{\left(1+\left\{-\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]\right\}^{n}\right)^{\frac{n-1}{n}}} \end{array} $ | (16) |
可见,式(16)为有关净竖向应力σz-ua的一阶线性非齐次微分方程,其通解为
| $ \begin{align*} \sigma_{\mathrm{z}}-u_{\mathrm{a}}= & C_{1} P(z)+\frac{Q(z)}{\alpha}- \\ & \frac{P(z)}{\alpha} \int P(-z) \mathrm{d} Q(z)-\frac{\gamma B+2 \hat{K} c^{\prime}}{2 \hat{K} \tan \varphi^{\prime}} \end{align*} $ | (17) |
式中:C1为积分常数,
由于对
| $ \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z+\Delta z}-\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{{z}}=\frac{\mathrm{d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)}{\mathrm{d} z} \Delta z $ | (18) |
式中Δz为深度迭代的步长,选取0.1、0.05或0.01 m以满足精度要求。
当存在等沉面时,式(18)以等沉面z=H-Hc处σz-ua=γ(H-Hc)为初值条件,迭代步数为Hc/Δz;不存在等沉面时,以填土面z=0处σz-ua=0为初值条件,迭代步数为H/Δz。
2.1.3 等沉面高度按土力学通常做法, 压缩变形计算时假定回填土为理想的线弹性体,记内土柱在深度z(>H-Hc)处的竖向土压力为(σz-ua)Ⅰ,外土柱在深度z处的竖向土压力(σz-ua)Ⅱ近似为
| $ \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{\mathrm{II}}=\gamma z $ | (19) |
由于内土柱竖向土压力大于土体自重而侧向膨胀,外土柱随之产生侧向压缩,内外土柱间的侧向压力可取为
| $ \left(\sigma_{\mathrm{h}}-u_{\mathrm{a}}\right)_{\mathrm{I}-\mathrm{II}}=\frac{\mu}{1-\mu} \cdot \frac{\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{\mathrm{I}}+\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{\mathrm{II}}}{2} $ | (20) |
式中:μ为回填土的泊松比,μ/(1-μ)为回填土的静止土压力系数。
根据分层总和法与广义Hooke定律,平面应变状态下内土柱的压缩量SⅠ为
| $ \begin{align*} S_{\mathrm{I}}= & \frac{1-\mu^{2}}{E} \cdot \frac{H_{\mathrm{c}}}{m_{1}} \sum\limits_{i=1}^{m_{1}}\left[\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}}-\right. \\ & 0.5\left(\frac{\mu}{1-\mu}\right)^{2}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}}- \\ & \left.0.5\left(\frac{\mu}{1-\mu}\right)^{2} \gamma\left(H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}\right)\right] \end{align*} $ | (21) |
式中: E为回填土的弹性模量,m1为等沉面至涵顶的回填土分层数。
取一侧外土柱范围L为箱型涵洞宽度B的1.5倍[9],外土柱的压缩量SⅡ包括涵顶以上和涵侧两部分,同理得平面应变状态下外土柱的压缩量SⅡ为
| $ \begin{align*} S_{\text {II }}= & \frac{1-\mu^{2}}{E} \cdot \frac{H_{\mathrm{c}}}{m_{1}} \sum\limits_{i=1}^{m_{1}}\left\{\gamma\left(H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}\right)-\right. \\ & 0.5\left(\frac{\mu}{1-\mu}\right)^{2}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}}- \\ & \left.0.5\left(\frac{\mu}{1-\mu}\right)^{2} \gamma\left(H-H_{\mathrm{c}}+i H_{\mathrm{c}}/m_{1}\right)\right\}+ \\ & \frac{1-\mu^{2}}{E} \cdot \frac{h}{m_{2}} \sum\limits_{j=1}^{m_{2}}\left\{\gamma\left(H+j h/m_{2}\right)-\right. \\ & 0.5\left(\frac{\mu}{1-\mu}\right)^{2}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H+j h/m_{2}}- \\ & \left.0.5\left(\frac{\mu}{1-\mu}\right)^{2} \gamma\left(H+j h/m_{2}\right)\right\} \end{align*} $ | (22) |
式中m2为涵顶至原地面的回填土分层数,对应涵侧外土柱的压缩变形。
当内土柱沉降量SⅠ等于外土柱沉降量SⅡ即SⅠ=SⅡ时,由式(21)=式(22)求出等沉面高度Hc,这在一定程度上体现了由土拱效应引起内/外土柱的竖向土压力变化。
2.2 沟埋式涵洞按照节2.1.1的分析思路,得图 2(b)中沟埋式涵洞滑移面处的净水平应力σhJ-ua为
| $ \begin{equation*} \sigma_{\mathrm{h} J}-u_{\mathrm{a}}=\hat{K}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+(1-\hat{K})\left(\sigma^{\mathrm{s}}-c^{\prime} \cot \varphi^{\prime}\right) \end{equation*} $ | (23) |
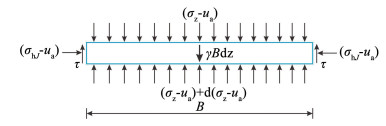
图 5为沟埋式涵洞水平薄层单元的受力情况,根据其竖向力平衡和2.1.2节求解步骤,得有关净竖向应力σz-ua的一阶线性非齐次微分方程为
| $ \begin{align*} & \frac{\mathrm{d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)}{\mathrm{d} z}+\frac{2 \hat{K} \tan \varphi^{\prime}}{B}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)=\gamma-\frac{2 \hat{K} c^{\prime}}{B}+ \\ & \frac{2 \hat{K} \tan \varphi^{\prime}}{\alpha B} \frac{\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]}{\left(1+\left\{-\ln \left[\left(1+\frac{q}{k_{\mathrm{s}}}\right) \mathrm{e}^{-r_{\mathrm{w}} \alpha\left(D_{\mathrm{w}}-z\right)}-\frac{q}{k_{\mathrm{s}}}\right]\right\}^{n}\right)^{\frac{n-1}{n}}} \end{align*} $ | (24) |
|
图 5 沟埋式涵洞水平薄层单元 Fig. 5 Horizontal thin layer element for a trench-buried culvert |
因式(24)的右边第3项积分在微分方程通解中不能显式表达,需结合填土面z=0处σz-ua=0的初值条件,由式(18)和式(24)迭代计算沟埋式涵洞的净竖向应力σz-ua,迭代步数为H/Δz。
2.3 应用步骤本文基于吸应力理论所建立的稳态渗流下非饱和土涵洞竖向土压力迭代解即式(16)、式(18)和式(24),可综合反映土体类别、水分蒸发(q>0)、降雨入渗(q < 0)和土拱效应(即新应力系下滑移面土压力系数
需注意的是,首先,以上均针对可忽略涵洞结构变形的刚性涵洞(管土相对刚度α≥1,如钢筋混凝土涵洞、碎石涵洞等),而柔性涵洞(管土相对刚度α < 1,如薄壁钢管涵洞、波纹管涵洞等)需考虑涵洞结构变形SG的影响,将刚性涵管结果乘以刚度影响系数ξ,且2.1.3节中等沉面形成条件变为SⅠ+SG=SⅡ。其中,α、ξ和SG的表达式[18, 20]为
| $ \left\{\begin{array}{l} \alpha=\frac{E_{\mathrm{p}}}{E_{0}}\left(\frac{t}{r}\right)^{3} \\ \xi=\alpha^{\frac{1}{6}}=\left(\frac{E_{\mathrm{p}}}{E_{0}}\right)^{\frac{1}{6}}\left(\frac{t}{r}\right)^{\frac{1}{2}} \\ S_{\mathrm{G}}=\frac{2 r^{4}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H}}{E_{\mathrm{p}} t^{3}} \end{array}\right. $ | (25) |
式中:EP为涵洞材料的弹性模量,E0为回填土的变形模量,t为涵洞壁厚,r=(B-t)/2为涵洞内半径。
其次,对于其他假定的方法拓展(上埋式涵洞):1)非刚性地基,将本文刚性地基结果乘以地基类型影响系数[20];2)竖向土压力分布的非线性,将本文均匀分布结果乘以圆弧小主应力轨迹的应力分布系数[18];3)非箱型涵洞,以涵高上下水平线、涵宽左右竖向线围成的矩形断面替代;4)地下水位在涵顶以上或涵顶以下而原地面以上,需区分地下水位以上为非饱和土、以下为饱和土。
3 对比验证通过对比涵洞顶部z=H处竖向土压力的现场实测数据[9-10]和有效应力法公式[12],以验证本文迭代解的正确性以及对非饱和土涵洞的适用性。
3.1 现场实测(非饱和砂土)文献[9]对高填方上埋式钢筋混凝土拱型涵洞的竖向土压力进行了现场测试,涵洞周围为非饱和砂土,最大填土高度为18 m,地下水位在原地面以下5 m处。文献[9]中实测涵顶竖向土压力集中系数随填土高度变化以及数值模拟回填土沉降等值线分布,验证了滑移面处土体已达到极限平衡、土拱效应充分发挥。图 6为本文计算涵顶竖向土压力(水分蒸发状态)与文献[9]现场实测的对比,等沉面高度Hc(蓝线)一并给出以选择迭代计算的初值条件(下同图 7),其中B=h=7.5 m,Dw=H+h+5,γ=20 kN/m3,c′=0 kPa,φ′=20°,E=30 MPa,μ=0.27;依据文献[19]设定α=0.2 kPa-1,n=4.2,ks=3×10-4 m/s,q=1.15×10-8 m/s。

|
图 6 与非饱和砂土现场实测竖向土压力的对比 Fig. 6 Comparisons with field-measured vertical earth pressure of unsaturated sands |
|
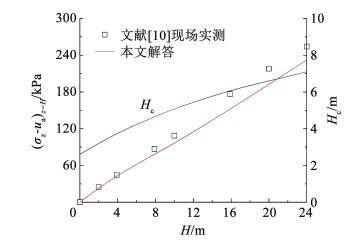
图 7 与非饱和黏土现场实测竖向土压力的对比 Fig. 7 Comparisons with field-measured vertical earth pressure of unsaturated clays |
由图 6可知,本文计算涵顶竖向土压力与文献[9]现场实测值吻合良好,平均相对误差绝对值为7.5%,表明式(16)和式(18)可用于分析非饱和砂土上埋式涵洞的竖向土压力。
3.2 现场实测(非饱和黏土)文献[10]开展了高填方上埋式波纹管涵洞竖向土压力的现场试验,回填土为非饱和黏土,最大填土高度为24 m,地下水位在原地面以下4 m处;文献[10]中涵顶沉降实测值随填土高度变化以及涵顶竖向土压力实测值出现区域集中,验证了滑移面处土体已达到极限平衡、土拱效应充分发挥。由式(25)得管土相对刚度α=3.5×10-4 < 1,可知属于柔性涵洞且刚度影响系数ξ=0.265。
图 7为本文涵顶竖向土压力计算值(水分蒸发状态)与文献[10]的实测值(填土高度H为0、2、4、8、10、16、20、24 m时涵顶实测土压力)对比,其中B=h=4.011 m,Dw=H+h+4,t=5.5 mm,Ep=2×105 MPa,γ=15.2 kN/m3,c′=35.8 kPa,φ′=24°,E=20 MPa,E0=12 MPa,μ=0.35;依据文献[19]设定α=0.005 kPa-1,n=1.4,ks=5×10-8 m/s,q=1.15×10-8 m/s。
由图 7可知,本文迭代解较好地预测了非饱和黏土上埋式柔性涵洞的涵顶竖向土压力,与现场实测的平均相对误差绝对值为8.2%,说明式(16)和式(18)对求解非饱和黏土涵洞竖向土压力具有一定的适用性。
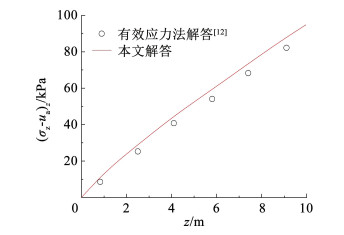
3.3 理论公式文献[12]基于非饱和土的Bishop有效应力原理,结合线性吸力分布(对应稳态渗流量q为零的静水压力状态),建立了非饱和土浅埋隧道竖向土压力的有效应力法解答。浅埋隧道可视为不存在涵槽的沟埋式涵洞,隧道上方土体受力情况与图 5类似。图 8为本文不同深度z处计算竖向土压力与文献[12]有效应力法解答的对比,其中B=h=10 m,Dw=10 m(地下水位在涵顶处),H=10 m(最大填土高度),γ=14.2 kN/m3,c′=0 kPa,φ′=30°,α= 0.246 kPa-1,n=1.461,ks=5×10-4 m/s,q=0 m/s。
|
图 8 与有效应力法解答的对比 Fig. 8 Comparisons with the solution of an effective stress method |
由图 8可知,本文计算竖向土压力与文献[12]的有效应力法解答接近且变化趋势一致,竖向土压力平均差异率的绝对值为10.7%,但本文计算竖向土压力均高于有效应力法解答,这是因为文献[12]假定滑移面土压力系数等于1,相比本文考虑土拱效应的滑移面土压力系数小于1,此假定使沟埋式涵洞内土柱回填土自重过多地转移给槽壁,进而有效应力法解答偏小。此外,本文可根据实际情况选取不同的稳态渗流量q,以分析降雨入渗和水分蒸发时的竖向土压力变化。
4 工程简化囿于迭代计算隐式和冗长,第2节涵洞竖向土压力迭代解在实际工程应用中欠缺简便性。因此,分析3类非饱和回填土吸应力沿深度的分布规律,提出可显式表达的涵洞竖向土压力简化实用公式,并进行准确性和合理性检验。
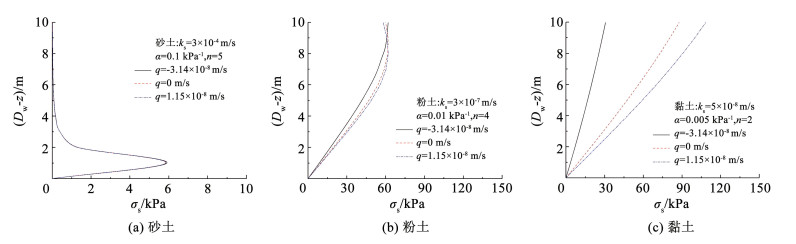
4.1 吸应力分布假定地下水位Dw=10 m,由式(5)得砂土、粉土和黏土的吸应力(取绝对值)沿深度的分布情况,如图 9所示。
|
图 9 吸应力分布 Fig. 9 Profiles of suction stress |
由图 9可知,砂土的吸应力很小且基本不受稳态渗流量q影响,而粉土和黏土的吸应力受稳态渗流量q影响较显著,尤其是黏土。此外,粉土的吸应力在地表下一定深度内呈现非线性变化,黏土的吸应力近似符合线性分布。
4.2 实用公式根据不同类型回填土的吸应力分布规律,以刚性涵洞为例对第2节竖向土压力迭代解进行实用性简化,柔性涵洞可按第2.3节修正。
对于砂土,因其吸应力σs很小而忽略即认为吸应力σs=0 kPa,此时对式(16)和式(24)积分得非饱和砂土涵洞竖向土压力的实用公式为
a) 上埋式涵洞
不存在等沉面时,
| $ \sigma_{\mathrm{z}}-u_{\mathrm{a}}=\frac{\gamma B}{2 \hat{K} \tan \varphi^{\prime}}\left(\mathrm{e}^{\frac{2 \hat{K} \tan \varphi^{\prime}}{B} z}-1\right) $ | (26) |
存在等沉面时,
| $ \begin{align*} \sigma_{\mathrm{z}}-u_{\mathrm{a}}= & \frac{\gamma B}{2 \hat{K} \tan \varphi^{\prime}}\left(\mathrm{e}^{\frac{2 \hat{K} \tan \varphi^{\prime}}{B}\left(z+H_{\mathrm{c}}-H\right)}-1\right)+ \\ & \gamma\left(H-H_{\mathrm{c}}\right) \mathrm{e}^{\frac{2 \hat{K} \tan \varphi^{\prime}}{B}\left(z+H_{\mathrm{c}}-H\right)} \end{align*} $ | (27) |
b) 沟埋式涵洞
| $ \sigma_{\mathrm{z}}-u_{\mathrm{a}}=\frac{\gamma B}{2 \hat{K} \tan \varphi^{\prime}}\left(1-\mathrm{e}^{-\frac{2 \hat{K} \tan \varphi^{\prime}}{B}}\right) $ | (28) |
对于粉土和黏土,假定吸应力σs沿深度线性减少且在地下水位Dw处为零。以填土面处的吸应力σs0为基准,深度z处的吸应力σs可表示为
| $ \sigma_{\mathrm{s}}=\sigma_{\mathrm{s} 0}\left(1-\frac{z}{D_{\mathrm{w}}}\right) $ | (29) |
式中
于是,结合式(29)对式(16)和式(24)积分得非饱和粉土或黏土涵洞竖向土压力的实用公式为
c) 上埋式涵洞
不存在等沉面时,
| $ \sigma_{\mathrm{z}}-u_{\mathrm{a}}=\frac{\gamma B+2 \hat{K} c^{\prime}+\left(\frac{B}{D_{\mathrm{w}}}-2 \hat{K} \tan \varphi^{\prime}\right) \sigma_{\mathrm{s} 0}}{2 \hat{K} \tan \varphi^{\prime}} \times\\ \;\;\;\;\;\;\;\;\;\;\;\left(\mathrm{e}^{\frac{2 \hat{\operatorname{Kan}} \varphi^{\prime}}{B} z}-1\right)-\frac{z}{D_{\mathrm{w}}} \sigma_{\mathrm{s} 0} $ | (30) |
存在等沉面时,
| $ \begin{aligned} \sigma_z-u_{\mathrm{a}}= &\frac{\gamma B+2 \hat{K} c^{\prime}+\left(\frac{B}{D_{\mathrm{w}}}-2 \hat{K} \tan \varphi^{\prime}\right) \sigma_{\mathrm{s} 0}}{2 \hat{K} \tan \varphi^{\prime}} \times \\ &\left(\mathrm{e}^{\frac{2 \hat{\mathrm{K}^{\prime a n} \varphi^{\prime}}}{B}\left(z+H_{\mathrm{c}}-H\right)}-1\right)+\gamma+\frac{\sigma_{\mathrm{s} 0}}{D_{\mathrm{w}}} \times \\ &\left(H-H_{\mathrm{c}}\right) \cdot \mathrm{e}^{\frac{2 \hat{\operatorname{Lan}} \varphi^{\prime}}{B}\left(z+H_{\mathrm{c}}-H\right)}-\frac{z}{D_{\mathrm{w}}} \sigma_{\mathrm{s} 0} \end{aligned} $ | (31) |
d) 沟埋式涵洞
| $ \begin{gather*} \sigma_{\mathrm{z}}-u_{\mathrm{a}}=\frac{\gamma B-2 \hat{K} c^{\prime}+\left(\frac{B}{D_{\mathrm{w}}}+2 \hat{K} \tan \varphi^{\prime}\right) \sigma_{\mathrm{s} 0}}{2 \hat{K} \tan \varphi^{\prime}} \times \\ \left(1-\mathrm{e}^{-\frac{2 \hat{K} \tan \varphi^{\prime}}{B}z}\right)-\frac{z}{D_{\mathrm{w}}} \sigma_{\mathrm{s} 0} \end{gather*} $ | (32) |
对式(27)与式(30)中的等沉面高度Hc,仍需由式(33)=式(34)即SⅠ=SⅡ确定。
| $ S_{\mathrm{I}}=\frac{1-\mu^2}{E} \int_{H-H_{\mathrm{c}}}^H\left[\begin{array}{l} \left(\sigma_z-u_{\mathrm{a}}\right)-\left(\frac{\mu}{1-\mu}\right)^2 \times \\ \frac{\left(\sigma_z-u_{\mathrm{a}}\right)+\gamma z}{2} \end{array}\right] \mathrm{d} z $ | (33) |
| $ S_{\mathrm{II}}=\frac{1-\mu^2}{E} \int_{H-H_{\mathrm{c}}}^{H+h}\left[\begin{array}{l} \gamma z-\left(\frac{\mu}{1-\mu}\right)^2 \times \\ \frac{\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+\gamma z}{2} \end{array}\right] \mathrm{d} z $ | (34) |
为说明上述涵洞竖向土压力实用公式的准确性,设定某刚性涵洞算例:涵洞的高度h为2.4 m,最大填土高度H为10 m;上埋式涵洞宽度B=2.4 m、沟埋式涵洞宽度B=5 m,地下水位在原地面以下2 m,3类非饱和回填土的参数按表 1取值。
| 表 1 非饱和回填土参数 Tab. 1 Unsaturated parameters of backfill soils |
图 10为涵洞竖向土压力实用公式与第2节迭代解的比较,右纵坐标和点划线代表竖向土压力差异率δ,红线对应上埋式涵洞,绿线对应沟埋式涵洞。

|
图 10 竖向土压力实用公式计算值与迭代解的比较 Fig. 10 Comparisons of vertical earth pressure calculated from a practical formulation and the iterative solution |
由图 10可知,上埋式涵洞由实用公式得到的竖向土压力相比迭代解略偏小,沟埋式涵洞由实用公式得到的竖向土压力相比迭代解略偏大,具体表现为:无论是上埋式还是沟埋式涵洞,图 10(a)、10(b)中砂土涵洞的竖向土压力差异率δ接近0%,图 10(c)、10(d)中粉土涵洞的竖向土压力差异率δ在±10%以内;对于图 10(e)、10(f)中黏土涵洞的竖向土压力差异率δ,上埋式涵洞在-5%以内,沟埋式涵洞在+10%以内。因此,所提涵洞竖向土压力实用公式对稳态渗流下3类非饱和回填土均具有较好的适用性。
另外,粉土吸力非线性分布使得上埋式粉土涵洞实用公式的竖向土压力偏小且差异率δ约为-10%,可将式(30)和式(31)乘以修正系数1.1以更好地应用于上埋式粉土涵洞。为验证所提非饱和土涵洞竖向土压力实用公式的预测合理性,将其计算竖向土压力与第3节中文献[9-10, 12]的实测和理论公式数据进行对比,如图 11所示。

|
图 11 竖向土压力实用公式计算值与文献数据的对比 Fig. 11 Comparisons of vertical earth pressure calculated from a practical formulation and the literatures |
由图 11可知,实用公式计算竖向土压力与上埋式砂土涵洞、上埋式黏土涵洞、沟埋式砂土涵洞的实测和理论公式数据吻合良好,平均相对误差绝对值分别为6.5%、9.6%和12.2%,精度与迭代解相当,表明竖向土压力实用公式可用于估算涵洞主要荷载。另外,未找到粉土涵洞和沟埋式黏土涵洞的竖向土压力实测数据,下一步将开展竖向土压力实用公式在粉土涵洞和沟埋式黏土涵洞中的应用合理性研究。
5 结论1) 结合非饱和土有效应力强度公式、吸应力理论和滑移面土压力系数,所建立的稳态渗流下涵洞竖向土压力迭代解与应用步骤能合理反映土体类别、土拱效应和外界大气环境变化下吸应力大小与分布的综合影响,并对所作假定给出了一些方法拓展。
2) 通过与文献现场实测和理论公式数据对比的良好吻合,验证了所得涵洞竖向土压力迭代解的正确性以及对非饱和土涵洞的适用性,进而基于吸应力沿深度分布规律,提出可显式表达的涵洞竖向土压力简化实用公式,用于估算不同稳态渗流下的涵洞主要荷载。
| [1] |
CRISTELO N, FELIX C, FIGUEIRAS J. Experimental behaviour of concrete box culverts-comparison with current codes of practice[J]. Canadian Geotechnical Journal, 2019, 56(7): 970. DOI:10.1139/cgj-2018-0506 |
| [2] |
TAO Q D, HE Z Y, JIA Y. Influence of filling properties and culvert structure parameters on the soil arching effect of upper-buried-type culverts[J]. Results in Physics, 2020, 16: 103003. DOI:10.1016/j.rinp.2020.103003 |
| [3] |
安宗文, 王莹莹, 张永明. 直槽沟埋式管道的垂直土压力计算模型[J]. 兰州理工大学学报, 2020, 46(5): 34. AN Zongwen, WANG Yingying, ZHANG Yongming. Vertical earth pressure calculation model for buried pipelines with straight grooves[J]. Journal of Lanzhou University of Technology, 2020, 46(5): 34. |
| [4] |
SOHRABPOUR A H, LONG M. Behaviour of intermediate stiffness culverts with recycled concrete aggregate backfill[J]. Tunnelling and Underground Space Technology, 2021, 115: 104061. DOI:10.1016/J.TUST.2021.104061 |
| [5] |
于金弘, 石长征, 伍鹤皋, 等. 大直径埋地钢管管顶土压力及其设计模型研究[J]. 岩土工程学报, 2022, 44(3): 514. YU Jinhong, SHI Changzheng, WU Hegao, et al. Soil pressures at top of large-diameter buried steel pipes and their design model[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(3): 514. DOI:10.11779/CJGE202203013 |
| [6] |
陈正汉, 郭楠. 非饱和土与特殊土力学及工程应用研究的新进展[J]. 岩土力学, 2019, 40(1): 1. CHEN Zhenghan, GUO Nan. New developments of mechanics and application for unsaturated soils and special soils[J]. Rock and Soil Mechanics, 2019, 40(1): 1. DOI:10.16285/j.rsm.2017.2577 |
| [7] |
GAO Y, SUN D A, ZHOU A N, et al. Predicting shear strength of unsaturated soils over wide suction range[J]. International Journal of Geomechanics, 2020, 20(2): 04019175. DOI:10.1061/(ASCE)GM.1943-5622.0001555 |
| [8] |
张常光, 吴凯, 康凌豪, 等. 非饱和土诱导减载涵洞的竖向土压力研究[J]. 哈尔滨工业大学学报, 2023, 55(2): 80. ZHANG Changguang, WU Kai, KANG Linghao, et al. Vertical earth pressure against an induced trench installation culvert in unsaturated soils[J]. Journal of Harbin Institute of Technology, 2023, 55(2): 80. DOI:10.11918/202204012 |
| [9] |
郑俊杰, 赵建斌, 陈保国. 高路堤下涵洞垂直土压力研究[J]. 岩土工程学报, 2009, 31(7): 1009. ZHENG Junjie, ZHAO Jianbin, CHEN Baoguo. Vertical earth pressure on culverts under high embankments[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1009. |
| [10] |
杨明辉, 方天云, 赵明华, 等. 高填方段波纹管涵垂直土压力试验及计算[J]. 公路交通科技, 2014, 31(4): 33. YANG Minghui, FANG Tianyun, ZHAO Minghua, et al. Test and calculation of vertical earth pressure on corrugated pipe culvert under high embankment[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 33. DOI:10.3969/j.issn.1002-0268.2004.04.006 |
| [11] |
蔺港, 孔令刚, 詹良通, 等. 基于太沙基土拱效应考虑基质吸力影响的松动土压力计算模型[J]. 岩土力学, 2015, 36(7): 2095. LIN Gang, KONG Linggang, ZHAN Liangtong, et al. An analytical model for loosening earth pressure considering matric suction based on Terzaghi soil arch effect[J]. Rock and Soil Mechanics, 2015, 36(7): 2095. DOI:10.16285/j.rsm.2015.07.035 |
| [12] |
FANG X, KIKUMOTO M, CUI Y. A theory of loosening earth pressure above a shallow tunnel in unsaturated ground[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(10): 1495. DOI:10.1002/nag.3072 |
| [13] |
张常光, 吴凯, 李宗辉, 等. 考虑中间主应力的非饱和土上埋式涵洞竖向土压力公式[J]. 建筑科学与工程学报, 2021, 38(6): 177. ZHANG Changguang, WU Kai, LI Zonghui, et al. Formulation of vertical earth pressure against positive buried culvert in unsaturated soils considering intermediate principal stress[J]. Journal of Architecture and Civil Engineering, 2021, 38(6): 177. DOI:10.19815/j.jace.2021.04092 |
| [14] |
LU N, LIKOS W J. Unsaturated soil mechanics[M]. New York: John Wiley and Sons, lnc., 2004.
|
| [15] |
VAHEDIFARD F, ROBINSON J D. Unified method for estimating the ultimate bearing capacity of shallow foundations in variably saturated soils under steady flow[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(4): 04015095. DOI:10.1061/(ASCE)GT.1943-5606.0001445 |
| [16] |
李梦姿, 蔡国庆, 李昊, 等. 考虑抗拉强度剪断的非饱和土无限边坡稳定性分析[J]. 岩土工程学报, 2020, 42(4): 705. LI Mengzi, CAI Guoqing, LI Hao, et al. Stability of infinite unsaturated soil slopes with tensile strength cut-off[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 705. DOI:10.11779/CJGE202004013 |
| [17] |
BARTLETT S F, LINGWALL B N, VASLESTAD J. Methods of protecting buried pipelines and culverts in transportation infrastructure using EPS geofoam[J]. Geotextiles and Geomembranes, 2015, 43: 450. DOI:10.1016/j.geotexmem.2015.04.019 |
| [18] |
张常光, 吴凯, 隋建浩. 基于小主应力轨迹的上埋式涵管竖向土压力非线性描述[J]. 岩土工程学报, 2021, 43(12): 2200. ZHANG Changguang, WU Kai, SUI Jianhao. Nonlinear descriptions of vertical earth pressure against positive buried pipelines based on minor principal stress trajectory[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(12): 2200. DOI:10.11779/CJGE202112006 |
| [19] |
LU N. Profiles of steady-state suction stress in unsaturated soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(10): 1063. DOI:10.1061/(ASCE)1090-0241(2004)130:10(1063) |
| [20] |
刘全林, 杨敏. 上埋式管道上竖向土压力计算的探讨[J]. 岩土力学, 2001, 22(2): 214. LIU Quanlin, YANG Min. Study of vertical earth pressure on positive buried pipelines[J]. Rock and Soil Mechanics, 2001, 22(2): 214. DOI:10.16285/j.rsm.2001.02.026 |
 2024, Vol. 56
2024, Vol. 56


