2. 东南大学 交通学院,南京 211189;
3. 长安大学 运输工程学院,西安 710064;
4. 南京理工大学 理学院,南京 210094
2. School of Transportation, Southeast University, Nanjing 211189, China;
3. College of Transportation Engineering, Chang′an University, Xi′an 710064, China;
4. College of Science, Nanjing University of Science and Technology, Nanjing 210094, China
水稳碎石(cement stabilized macadam, CSM)是一种由水泥、砂石料、水等在最佳含水量下拌合压实而成的复合材料,因其弹性变形小、承载能力强,在我国公路建设中常被用于修筑路面结构的基层[1]。作为典型的准脆性材料,CSM在服役过程中会因外界环境及荷载作用在结构内部产生局部微裂损伤,文献[2]研究表明,少量的微裂缺陷对结构的整体性能影响不显著,然而在疲劳荷载持续作用下,这些微裂纹会进一步发生跨尺度演化而导致结构断裂破坏。如何在结构发生破坏前对微裂纹进行有效修复是当今学术界与工程界所共同面临的热点问题[3]。
对于水泥稳定类材料而言,在一定条件下通过特定的物理化学反应可实现微裂纹的自修复[4],其作用机理主要包括结晶沉淀、膨胀填充等[5-6]。裂纹愈合是水泥后期持续水化作用和其他作用的结果,其中碳酸钙沉淀是混凝土结构中裂缝愈合的主要原因[7-8]。可见,自然状态下CSM材料的持续水泥水化反应、火山灰反应、氢氧化钙结晶及碳化反应均可引发自愈效果。通过添加膨胀剂、地聚物或微生物,还可实现自主的被动愈合[9-10]。而胶囊空管中预埋修复材料,细菌促进生成碳酸钙及形状记忆材料修复属于需要特殊工程设计的主动修复。通过掺加主动愈合材料可以极大地提高裂缝的自愈合程度,文献[11]研究发现,被动愈合能够完全修复的最大裂缝宽度小于60 μm,而主动修复措施能够完全愈合最大宽度为200 μm的裂纹。然而,目前对混凝土主动修复措施的研究大多关注于愈合材料的选取与修复系统的设计,但对触发机制的研究鲜有报道,特别是激发修复时机的选择还未形成统一的研究体系,有关微胶囊破裂的时机、形状记忆合金通电激励修复的时机、聚合物肌腱加热修复的时机等方面的问题亟待解决。
目前对混凝土材料愈合机制的研究普遍采用室内试验与数值手段相结合的方式进行。室内测试主要侧重于愈合材料的比选与自修复系统的设计,通过宏观试验结果进行愈合效果的评价[12-13]。而数值仿真手段可以在细微观尺度进行损伤及愈合行为的分析,进而阐明材料破坏的内在机理[14-17]。对于微裂纹尺度的损伤-愈合研究,数值方法可以方便地实现对材料局部损伤与愈合效应的分析,阐明愈合机制,并且局部的微裂损伤难以用宏观的连续损伤力学进行分析,建立细观尺度的损伤-愈合数值模型还可作为连续损伤-愈合力学模型的补充,这对探究CSM的愈合机制具有重要意义。
为了探究水稳碎石材料的愈合机制及最佳修复时机,本文基于自愈合混凝土的修复机理,建立了CSM材料的细观损伤-愈合模型,引入损伤因子模拟材料的局部损伤与愈合效应,确定模型的愈合变量,来表征荷载损伤的修复过程。通过虚拟SCB疲劳试验实现CSM试件不同程度的荷载损伤,讨论了不同损伤状态下的修复效果,分析初始损伤状态、愈合程度对修复效果的影响,并进一步研究CSM材料的最佳修复时机。
1 细观数值试件 1.1 SCB数值试件本文采用颗粒流程序PFC5.0构建二维SCB数值试件,试件直径为150 mm。为了提高模型的准确性,采用随机多边形表征骨料颗粒,将其二维形状视为4~10边形[18],并通过随机算法按照设计级配范围生成随机多边形骨料模板[19]。为了在满足精度的前提下提高模型的计算效率[20],模型中仅对粒径为1.18~19 mm的粗骨料进行模拟,而将小于1.18 mm的集料颗粒简化为砂浆基体。构建的虚拟SCB试件如图 1所示。
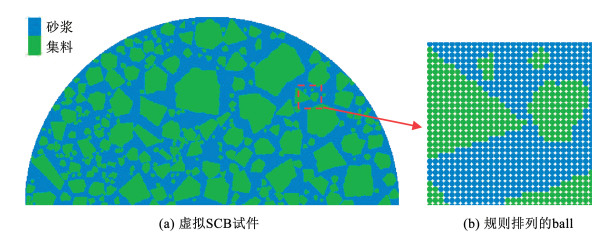
|
图 1 细观SCB模型 Fig. 1 Virtual SCB specimen |
DEM模型原本为离散颗粒单元的集合,采用接触模型将相邻离散颗粒黏结在一起,使数值模型可以反映实际材料的力学特征。本文将集料视为线弹性体,采用PFC5.0内置的线性接触黏结模型表征同一集料内部相邻ball之间的接触行为,砂浆为黏结材料,采用平行黏结模型表征砂浆ball之间及砂浆-集料界面处的接触行为。相邻集料颗粒之间的接触为无黏结的接触,采用黏结强度为0的线性接触黏结模型表示。本研究所涉及的主要模型参数有接触黏结的有效模量、刚度比及黏结强度,平行黏结的有效模量、刚度比与黏结强度。首先,基于粒子ball所属的材料分组(集料或砂浆),采用自定义的识别算法判断各相邻ball之间的接触分类:砂浆内部、同一集料内部、集料之间、砂浆-集料界面,然后按照设定的细观模型参数进行赋值。细观接触黏结模型分配情况如图 2所示。
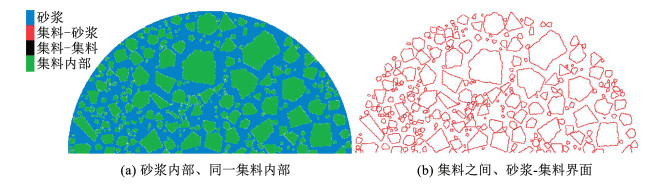
|
图 2 接触模型分配 Fig. 2 Contact phases in SCB model |
由于观测水平的限制,在细观尺度上很难实现对DEM模型参数的直接测量。目前细观参数确定的典型做法是将拟定参数进行反复的迭代调整,直至模拟荷载-位移曲线与试验结果相吻合[20-21]。本文以现有水泥砂浆[1, 22-23]和集料[24]研究成果为迭代初始值,基于水稳基层现场代表芯样的测试结果,采用参数反演确定模型细观参数。其中,室内SCB强度试验采用UTM-25试验机进行,两支座间距为120 mm,加载速率为0.86 mm/s。虚拟试验条件与其保持一致,并通过圆形墙体模拟加载和支撑单元。为了验证反演结果的准确性,同时设置了验证组(模拟测试2),根据两次模拟结果进一步校准反演参数。细观力学参数反演过程如图 3所示,表 1为最终确定的模型参数。由于试验结果有限,本文仅基于典型室内测试数据对模型进行了初步验证,在今后的研究中,还需增加用于模型参数反演的CSM基层样本数量,以期获得更加准确的模型参数,同时,还要开展除SCB加载模式外的其他加载条件下的模拟测试,对所建模型进行广泛的试验验证。

|
图 3 模型细观力学参数反演 Fig. 3 Meso-mechanical parameter inverse analysis |
| 表 1 DEM模型细观力学参数 Tab. 1 Meso-mechanical parameters in DEM model |
本文通过建立细观损伤-愈合模型来模拟CSM材料的局部损伤与愈合效应。对于CSM材料而言,荷载损伤主要表现为砂浆或砂浆与骨料界面处的性能退化[25],因此,可以通过平行黏结模型来实现对材料荷载损伤的模拟。在二维平行黏结模型中,利用“梁”理论计算粒子间的法向应力
| $ \bar{\sigma}=\frac{\bar{F}^{n}}{\bar{A}}+\frac{\left\|\bar{M}_{b}\right\| \bar{R}}{\bar{I}} $ | (1) |
| $ \bar{\tau}=\frac{\left\|\bar{F}^{s}\right\|}{\bar{A}} $ | (2) |
式中:
| $ \bar{A}=2 \bar{R} $ | (3) |
| $ \bar{I}=\frac{2}{3} \bar{R}^{3} $ | (4) |
| $ \bar{R}=\bar{\lambda} \min \left(R^{(1)}, R^{(2)}\right) $ | (5) |

|
图 4 基于平行黏结的荷载损伤示意 Fig. 4 Damage based on parallel bond contact |
DEM模型中,接触模型作为颗粒间连接的强度准则,控制着裂纹的产生,当连接受力超过强度极限时,黏结键会破坏消失,并伴随产生可见的实体微裂纹。值得注意的是,试样在荷载损伤过程中会同时出现开口裂纹和闭口裂纹[26],而开口裂纹比闭口裂纹更难愈合。文献[11]研究表明,主动修复措施能够实现宽度为200 μm的裂纹的愈合,因此,本文假定只有开口位移较小的开口裂纹(本文为小于0.2 mm)和闭口微裂纹才可以被修复。基于以上假定,损伤-愈合模型中制定如下损伤修复策略:1)采用黏结半径衰减但未发生断裂的黏结键来表征闭口微裂纹损伤,并通过调整黏结半径系数λ进行损伤的修复;2)对于因黏结键断裂而产生的开口裂纹损伤,首先采用最大间隙参数G来指定接触模型激活的范围(G=0.2 mm),然后根据式(6)判断相邻粒子的接触间距gc,若gc>G说明损伤为开口宽度较大的开口裂纹(大于0.2 mm),则无法进行修复,若gc≤G则通过在发生接触断裂的粒子间再生新的黏结键来实现损伤修复,新建黏结键的黏结半径系数λ由损伤愈合变量确定。损伤-愈合模型的修复策略如图 5所示,通过对开口微裂纹和闭口微裂纹的损伤分别进行修复,以使材料在局部获得新的力学性能提升,从而实现对损伤修复行为的模拟,但现实中CSM材料的损伤愈合效果还需考虑修复时间、修复剂材料等因素的影响,进一步研究中还需结合室内损伤愈合试验测试完善损伤修复策略。
| $ g_{c}=\sqrt[2]{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}-R^{(1)}-R^{(2)} $ | (6) |
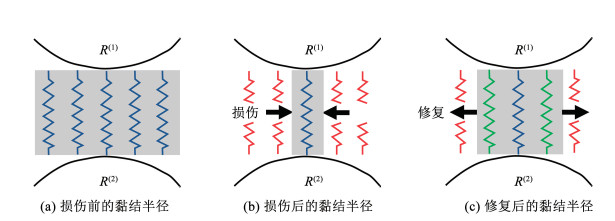
|
图 5 基于平行黏结的损伤修复示意 Fig. 5 Damage-healing based on parallel bond contact |
其中x1,x2,y1,y2分别是两个相邻粒子ball的圆心坐标。
2.2 损伤因子与宏观性能的关系以黏结半径系数λ作为损伤因子构造表征不同损伤程度的SCB数值试件,以探究损伤因子与宏观性能的关系。需要说明的是,此时材料的损伤为全局损伤,即所有的黏结半径均发生了同步衰减,这有别于实际荷载作用下的局部损伤。对构建的全局损伤试件进行SCB强度试验,采用位移控加载模式,加载速率为0.86 mm/s,测试结果如图 6所示。其中,SCB峰值能量ESCB是指试件达到破坏形变所需消耗的能量,其值为达到峰值荷载FSCB前的荷载-位移曲线下方的面积,用于表征材料的综合抗裂能力。可以看出损伤因子与宏观力学强度和断裂能之间具有良好的线性关系,这是由于黏结半径直接影响着粒子间的接触应力,在荷载作用下,黏结半径系数较小的接触模型更易达到强度极限而发生粒子间接触断裂,进而使材料整体强度降低,抗裂能力减弱。因此,通过控制黏结半径系数λ便可以完成对材料力学性能的调整,进而实现局部损伤和修复过程的有效模拟。

|
图 6 损伤因子与宏观力学性能的关系 Fig. 6 Relationship between damage factor and macroscopic mechanical properties |
在荷载作用下,材料的损伤并非全局的均匀损伤,而是局部的随机损伤,为了模拟CSM材料真实的荷载损伤状态,本文采用虚拟疲劳加载试验制备了具有局部损伤特征的数值试件。首先,基于Potyondy等[27]对岩石腐蚀损伤的数值研究,并参考宏观疲劳试验的应力-寿命关系指数模型,本文以黏结半径系数λ为损伤因子构建虚拟疲劳衰变模型,如式(7)所示。然后,通过自定义Fish函数将衰变模型嵌入到DEM运算的每个时间步中(式(8)),用于模拟CSM材料性能在疲劳荷载作用下的劣化过程。最后,通过虚拟疲劳加载试验,实现不同疲劳阶段的荷载损伤,用于损伤修复效果评估研究。
| $ \begin{gather*} \omega=\left\{\begin{array}{l} -\alpha_{1} \mathrm{e}^{\alpha_{2} \cdot \frac{\bar{\sigma}}{\sigma}}, 0<\bar{\sigma}<\sigma \\ -\infty, \bar{\sigma} \geqslant \sigma \end{array}\right. \end{gather*} $ | (7) |
| $ \bar{\lambda}_{t+\Delta t}=\bar{\lambda}_{t}+\omega \Delta t $ | (8) |
式中:ω为黏结半径系数的损伤率;σ为相邻粒子间的法向单位应力;σ为抗拉强度设定值;α1,α2为影响材料性能劣化速率的常数;Δt为计算时间步长,为1×10-6 s;
裂纹愈合同荷载损伤一样也具有一定的随机性,但为了便于对损伤修复效果进行定量评估,需要人为定义损伤修复水平。本文通过愈合系数α来表征单个砂浆或界面接触的黏结半径系数λ的修复水平,如式(9)所示。
| $ \bar{\lambda}_{\mathrm{H}}=\bar{\lambda}_{\mathrm{D}}+\left(1-\bar{\lambda}_{\mathrm{D}}\right) \times \alpha $ | (9) |
式中:λH为修复后的黏结半径系数;λD为损伤未修复时的黏结半径系数,对于黏结断裂的接触λD=0;α为黏结半径系数的愈合系数。首先,通过自定义Fish函数实现损伤状态的自动判别,获取接触间距gc与初始黏结半径系数λD参数,然后基于拟定的损伤修复策略建立新的接触黏结或者对黏结半径系数进行重新赋值,实现局部损伤的定量修复。本文选取的愈合系数α分别为0、0.2、0.4、0.6、0.8和1.0,其中,α=0代表损伤未修复,α=1代表损伤完全修复。
3.3 DEM模型的损伤及修复状态表征本文通过建立细观损伤及修复状态指标来实现对DEM模型的局部损伤及其修复水平的定量表征。在载荷作用下,材料出现损伤微裂纹而导致宏观性能劣化,传统损伤理论认为损伤为材料的总有效承载截面积的减小,其外在表现为结构承载能力的下降。对于细观损伤-愈合模型而言,材料性能劣化主要源于黏结半径的减小,因此,可以采用式(10)来定义DEM模型的损伤率d。同时,将损伤的愈合修复视为一种负损伤,又可采用式(11)定义愈合率h。
| $ d=\frac{A_{\mathrm{D}}}{A_{0}-A_{\mathrm{f}}}=\frac{\bar{\lambda}_{0}^{\text {sum }}-\bar{\lambda}_{\mathrm{D}}^{\text {sum }}}{\bar{\lambda}_{0}^{\text {sum }}-\bar{\lambda}_{\mathrm{f}}^{\text {sum }}}, 0 \leqslant d \leqslant 1 $ | (10) |
| $ h=\frac{A_{\mathrm{H}}}{A_{\mathrm{D}}}=\frac{\bar{\lambda}_{\mathrm{H}}^{\text {sum }}-\bar{\lambda}_{\mathrm{D}}^{\text {sum }}}{\bar{\lambda}_{0}^{\text {sum }}-\bar{\lambda}_{\mathrm{D}}^{\text {sum }}}, 0 \leqslant h \leqslant 1 $ | (11) |
式中:A0、Af、AD、AH分别为试件的初始有效承载截面积、完全断裂破坏时的有效承载截面积、发生损伤的承载截面积和得到愈合修复的承载截面积;
| $ d_{\text {net }}=d_{0}(1-h)=\frac{\bar{\lambda}_{0}^{\text {sum }}-\bar{\lambda}_{\mathrm{H}}^{\text {sum }}}{\bar{\lambda}_{0}^{\text {sum }}-\bar{\lambda}_{\mathrm{f}}^{\text {sum }}} $ | (12) |
式中:dnet为损伤试件修复后的有效损伤率, d0为损伤试件修复前的初始损伤率。
4 损伤修复效果影响分析 4.1 损伤修复效果评估本文以20次荷载循环作为一个损伤阶段,分别提取了虚拟试件全寿命期(140次荷载循环)内的7个疲劳阶段的损伤试件,用于建立不同的初始损伤状态。然后根据拟定的愈合系数(α=0, 0.2, 0.4, 0.6, 0.8, 1.0)完成损伤修复,最后通过测试不同损伤状态试件的虚拟SCB强度来进行修复效果评估,分析初始损伤状态、愈合程度对修复效果的影响。图 7为不同疲劳阶段及修复水平下的损伤状态评估结果,分别基于疲劳次数N和愈合系数α进行展示,其中α=0代表的是不同疲劳阶段试件的初始损伤状态,即损伤试件修复前的初始损伤率d0。可见,建立的有效损伤率评估指标可以很好地区分不同疲劳阶段和愈合程度下试件的细观损伤水平,随着疲劳次数的增加,有效损伤率dnet逐步增大; 随着愈合系数α的提高,有效损伤率dnet逐步降低至0附近。值得注意的是,图 7(a)中,当愈合系数α达到1.0时,即所有的可愈合损伤均得到了有效修复,但此时不同疲劳次数所对应的试件损伤率并不为0,分析认为,这是由于在疲劳加载过程中,试件内部出现了无法愈合的大裂纹损伤,导致最终的试件损伤无法实现完全愈合,且随着疲劳荷载的增加,这种无法修复的损伤也逐渐增多,这和实际情况相一致[28]。损伤状态的评估结果表明,有效损伤率dnet可以作为损伤及修复状态指标来表征细观损伤的修复过程,模拟局部损伤愈合行为,进而用于损伤修复效果的评估研究。

|
图 7 不同疲劳阶段及修复水平下的损伤状态评估结果 Fig. 7 Evaluation of damage at different fatigue stages and healing levels |
本研究是基于同一虚拟试件开展的损伤愈合虚拟测试,疲劳阶段和修复水平是影响试件损伤状态的主要因素,因此,本文主要开展不同疲劳阶段及愈合变量下的修复效果评估。图 8为不同疲劳阶段及修复水平对应的SCB峰值荷载,可见初始损伤状态及修复水平对SCB峰值荷载具有显著的影响。其中,SCB峰值荷载随疲劳荷载次数的变化具有非线性,在达到100次循环荷载之前,不同修复水平下的试件强度呈近似线性衰减,随后其强度衰减速度明显加快,在经历完剩余的30%的循环荷载作用之后,试件就发生了完全的断裂破坏。然而,不同疲劳阶段对应的SCB峰值荷载随修复水平的变化具有明显的线性,不同的是,针对不同疲劳阶段的损伤试件,其峰值荷载线性变化的速率不同,总体表现为疲劳初期的变化速率小,疲劳末期的变化速率大,但是在最后一个疲劳阶段中,其峰值荷载随愈合系数增大而提升的效果又出现了减缓的趋势。结果表明,修复后的损伤试件能承受较高的载荷强度,对于初始损伤程度较小的试件,这种提升效果不明显,对于初始损伤程度稍大的试件,其损伤修复效果较为显著,但当试件局部损伤累积到了一定程度(本文中达到了70%的疲劳寿命),局部损伤的愈合修复对结构整体强度的提升效果又会减弱。尽管在疲劳最后阶段实施完全的局部损伤修复(N=140, α=1.0),其SCB峰值荷载仍未得到明显的提升,这可能是由于此时试件内出现了过多的不可修复损伤,如图 7(a)所示, 这些损伤对宏观裂纹的贯通起到了明显主导作用,无论其余的局部微裂纹损伤是否被修复,在荷载作用下宏观裂纹的快速产生已经不可避免。损伤修复效果评估结果表明,初始损伤状态和愈合程度对修复效果的影响具有非线性,为了深入探究损伤修复作用对强度提升的发展规律,还需进一步开展损伤修复效果的影响分析研究,进而为最佳修复时机的选择提供依据。
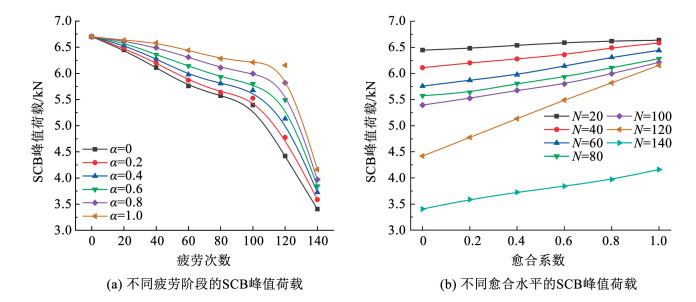
|
图 8 不同疲劳阶段及修复水平下的SCB峰值荷载 Fig. 8 SCB peak loads at different fatigue stages and healing levels |
基于所提出的细观损伤-愈合数值模型,讨论初始损伤状态和愈合程度对修复效果的影响。图 9为不同疲劳阶段和修复水平下测得的SCB荷载-位移曲线,可见,在相同修复水平下,随着疲劳次数的增加,试件的局部损伤增多,损伤试件的SCB峰值荷载降低,同时,试件的峰值形变也随之减小。反之,对于同一疲劳阶段的损伤试件,局部损伤状态相同,提高修复水平,可以显著提高材料的抗裂强度,同时,试件的破坏形变也随之增大。较高的SCB强度和较大的峰值形变表示试件在达到断裂破坏时可以吸收更多的断裂能量,具有更高的抗裂强度。无论试件的初始损伤程度和愈合水平如何变化,各荷载-位移曲线上升阶段均表现出了较好的一致性,说明材料的刚度并没有受到局部微裂纹损伤数量的增减变化而改变,其刚度水平是由材料的体积特性来决定[28],可以认为,破坏荷载高的试件其破坏形变也大,进而使试件在达到断裂时可以吸收更多的荷载能量,因此,可以直接采用破坏荷载值来反映试件局部损伤的修复效果。
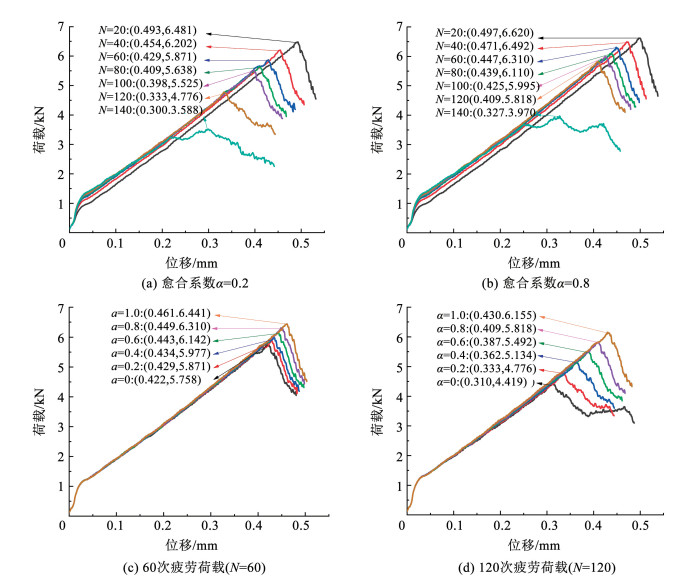
|
图 9 疲劳阶段和修复水平对SCB荷载-位移曲线的影响 Fig. 9 Effect of fatigue stage and healing level on SCB load-displacement curves |
进一步,本文基于SCB峰值荷载测试结果,通过建立强度折减率Rd和强度修复率Rh两个指标来表征初始损伤状态和愈合程度对修复效果的影响,如式(13)、(14)所示。
| $ R_{\mathrm{d}}=\frac{P_{0}-P_{\mathrm{D}}}{P_{0}} $ | (13) |
| $ R_{\mathrm{h}}=\frac{P_{\mathrm{H}}^{n}-P_{n}}{P_{0}-P_{n}} $ | (14) |
式中:P0为初始完好试件的SCB峰值荷载;PD为损伤试件的SCB峰值荷载;Pn为第n个疲劳阶段的损伤试件并未被修复时的SCB峰值荷载;PHn为第n个疲劳阶段的损伤试件但经过修复后的SCB峰值荷载。可见,强度折减率Rd是损伤试件基于初始完好状态的损伤程度评价,表征了试件损伤或损伤修复后的最终强度水平,强度修复率Rh是损伤试件基于初始损伤状态的损伤程度评价,表征了试件损伤修复后的强度提升程度。图 10和图 11分别为不同初始损伤状态和愈合程度所对应的修复效果,从图 10可以发现,对于不同的修复水平,随着试件初始损伤水平的提高,强度折减率Rd逐渐增大,在100次疲劳荷载之前,其上升速率较为缓慢,再进一步提升疲劳损伤水平,强度折减率Rd则急剧增加,对应的强度修复率Rh随疲劳次数增加而降低的过程也具有先慢后快的变化趋势,结果表明,在疲劳初始阶段(约70%的疲劳寿命),疲劳荷载对试件的损伤作用有限,其局部损伤对强度的衰减作用以及损伤修复对整体强度的提升效果均不太显著,当达到疲劳寿命的后期(约30%的疲劳寿命),由于局部损伤程度的加大,结构内部积累了足够的微裂纹损伤,可以有效促进宏观裂纹的扩展而形成断裂破坏,因此表现为较为显著的材料强度衰减效果。值得注意的是,在达到120次疲劳荷载时(约85%的疲劳寿命),强度修复率Rh出现了一个短暂上升过程,说明该疲劳阶段的损伤修复效果较其他疲劳阶段更为显著,分析认为,该阶段的微裂纹损伤水平为显著影响宏观强度降低的临界值,若不进行局部损伤的修复干预,则试件的力学性能就会显著下降,若对微裂纹损伤给予适当的修复处理,则材料性能会得到较大的提高,在之后的疲劳阶段中强度修复率Rh又显著降低,说明试件内已存在了较多的无法愈合裂纹而使局部损伤修复效果下降。由此可以认为,在100~120次疲劳荷载阶段进行损伤修复干预可以达到较佳的修复效果,且在同等修复水平下,可以达到疲劳寿命初期(20~40次疲劳荷载)时的修复效果, 如图 10(b)所示。因此,在疲劳中后期中,70%~85%的疲劳寿命为最佳的修复时机。

|
图 10 疲劳阶段对修复效果的影响 Fig. 10 Influence of fatigue stage on the healing effect |

|
图 11 修复水平对修复效果的影响 Fig. 11 Influence of healing level on the healing effect |
图 11是基于愈合系数α展示的修复效果变化过程,可以发现,对于相同初始损伤状态的试件而言,强度折减率Rd随着愈合系数α的提高而逐渐降低,强度修复率Rh随着愈合系数α的提高而增大,二者随修复水平的变化均呈现了明显的线性特征。强度折减率Rd变化对修复水平的敏感程度随着初始损伤水平的提高先增大后减小,其中当疲劳寿命阶段达到120次疲劳荷载时,修复水平对强度提升效果较为显著,而强度修复率Rh随修复水平变化的敏感程度总体保持一致,仅在临近断裂破坏的疲劳阶段(140次疲劳荷载),损伤修复水平变化对修复效果的影响程度较低,这是由于该疲劳阶段存在过多的无法愈合裂纹而使局部损伤修复效果下降。修复水平对修复效果影响的结果表明,对于不同初始损伤状态,试样的强度均随愈合水平的增大而提高,试件内局部可修复损伤数量越多,有效修复对强度的提升效果越明显,达到85%的疲劳寿命时,修复水平对损伤修复效果的影响达到最大,可以认为,在达到85%的疲劳寿命之前完成对局部损伤的有效修复对整体性能提升与结构寿命延续比较有益。此外,愈合水平及愈合材料的强度均与可用于有效修复裂纹损坏的愈合材料剂量有关,如果愈合材料的强度不够高,修复后的微裂纹容易重新裂开,如果愈合材料剂量不足,无法实现微裂纹的全局修复,修复后的微裂纹也容易重新断裂。因此,推荐使用高强且充足的愈合剂以最大程度提升损伤修复效果。由于考虑到裂纹修复会使结构内部出现局部的强度增高,进而出现应力集中的现象,具体的愈合剂强度比选还需作进一步研究。
综上分析认为,尽管在疲劳寿命初期,材料的局部损伤有限,此时进行微裂纹损伤修复可以较容易地使试件恢复到最初的强度水平,但考虑到最大化延续结构的整体使用寿命,且多数愈合机制的触发(如微胶囊破裂)具有“一次性”,因此,推荐在疲劳中后期使局部损伤累积达到一定程度时再实施损伤修复,因此,基于本文的数值分析,可认为70%~85%的疲劳寿命为CSM材料的最佳修复时机,此时,选择强度优良、数量充足的愈合剂可以最大程度地提升损伤修复效果。
5 结论本文基于DEM细观损伤-愈合模型对CSM材料的损伤-愈合行为进行了研究,通过不同损伤状态下的修复效果评估,分析了初始损伤状态、愈合程度对损伤修复效果的影响,确定了CSM材料的最佳修复时机。主要研究结论如下:
1) 所建立的细观损伤-愈合模型可以很好地用于模拟CSM材料的局部损伤与愈合效应,采用有效损伤率指标可以实现对CSM试件局部损伤及修复状态的细观评估。
2) 基于所构建的细观损伤-愈合模型,开展了损伤修复效果评估研究,结果表明,初始损伤状态和愈合程度对修复效果的影响具有非线性,70%~85%的疲劳寿命阶段,材料强度衰减速率开始加快,损伤修复对强度的提升效果增强。
3) 基于对损伤修复效果的数值分析,推荐将70%~85%的疲劳寿命作为CSM材料的最佳修复时机,此时,选择强度优良、数量充足的愈合剂可以最大程度地提升局部损伤修复效果。
| [1] |
赵晓康, 董侨, 陈雪琴, 等. 考虑初始缺陷的水泥基复合材料细观开裂研究[J]. 中国公路学报, 2020, 33(10): 230. ZHAO Xiaokang, DONG Qiao, CHEN Xueqin, et al. Mesoscale cracking of cement-treated composites with initial defects[J]. China Journal of Highway and Transport, 2020, 33(10): 230. DOI:10.19721/j.cnki.1001-7372.2020.10.017 |
| [2] |
ZHAO X K, DONG Q, CHEN X Q, et al. Influence of initial defects on the fatigue behaviour of cement-stabilized macadam base through DEM[J]. International Journal of Pavement Engineering, 2021, 23(14): 4845. DOI:10.1080/10298436.2021.1984473 |
| [3] |
裴建中. 道路工程学科前沿进展与道路交通系统的代际转换[J]. 中国公路学报, 2018, 31(11): 1. PEI Jianzhong. Progress of highway engineering and generation upgrading of highway transportation system[J]. China Journal of Highway and Transport, 2018, 31(11): 1. DOI:10.3969/j.issn.1001-7372.2018.11.001 |
| [4] |
李娜, 魏连雨, 张静. 基于微观结构分析的水泥稳定碎石微裂自愈性能[J]. 硅酸盐通报, 2018, 37(2): 578. LI Na, WEI Lianyu, ZHANG Jing. Self-healing properties of micro-cracks of cement stabilized macadam based on microstructure analysis[J]. Journal of the Chinese Ceramic Society, 2018, 37(2): 578. DOI:10.16552/j.cnki.issn1001-1625.2018.02.033 |
| [5] |
刘围, 丁华柱, 舒杨波, 等. 自愈合/自修复混凝土研究进展[J]. 四川建材, 2020, 46(7): 1. LIU Wei, DING Huazhu, SHU Yangbo, et al. Research progress of self-healing/self-repairing concrete[J]. Sichuan Building Materials, 2020, 46(7): 1. DOI:10.3969/j.issn.1672-4011.2020.07.001 |
| [6] |
DI CREDICO B, LEVI M, TURNI S. An efficient method for the output of new self-repairing materials through a reactive isocyanate encapsulation[J]. European Polymer Journal, 2013, 49(9): 2467. DOI:10.1016/j.eurpolymj.2013.02.006 |
| [7] |
孙道胜, 陈远远, 王爱国, 等. 自愈合和自修复混凝土的研究进展[J]. 材料导报, 2014, 28(11): 132. SUN Daosheng, CHEN Yuanyuan, WANG Aiguo, et al. Research progress of self-healing and self-repairing concrete[J]. Materials Reports, 2014, 28(11): 132. |
| [8] |
SUN X H, MIAO L C, YUAN J H, et al. Application of enzymatic calcification for dust control and rainfall erosion resistance improvement[J]. Science of the Total Environment, 2021, 759: 143468. DOI:10.1016/j.scitotenv.2020.143468 |
| [9] |
MIHASHI H, NISHIWAKI T. Development of engineered self-healing and self-repairing concrete state of the art report[J]. Journal of Advanced Concrete Technology, 2012, 10(5): 170. DOI:10.3151/jact.10.170 |
| [10] |
王立成, 邹凯. 混凝土微生物自愈合技术研究进展[J]. 硅酸盐学报, 2019, 47(11): 1652. WANG Licheng, ZOU Kai. Research progresses of microbial self-healing concrete[J]. Journal of the Chinese Ceramic Society, 2019, 47(11): 1652. DOI:10.14062/j.issn.0454-5648.2019.11.17 |
| [11] |
MUHAMMAD N Z, SHAFAGHAT A, KEYVANFAR A, et al. Tests and methods of evaluating the self-healing efficiency of concrete: a review[J]. Construction and Building Materials, 2016, 112: 1123. DOI:10.1080/09506608.2022.2145747 |
| [12] |
YANG Z X, HOLLER J, HE X D, et al. Laboratory assessment of a self-healing cementitious composite[J]. Transportation Research Record, 2010, 2142: 9. DOI:10.3141/2142-02 |
| [13] |
楠丁. 自愈合路面基层材料使用性能研究[D]. 长沙: 湖南大学, 2014 NAN Ding. A study on performance of self-healing materials for pavement base course[D]. Changsha: Hunan University, 2014 |
| [14] |
ZHU H H, ZHOU S, YAN Z G, et al. A two-dimensional micromechanical damage-healing model on microcrack-induced damage for microcapsule-enabled self-healing cementitious composites under compressive loading[J]. International Journal of Damage Mechanics, 2016, 25(5): 727. DOI:10.1177/1056789516641593 |
| [15] |
HERBST O, LUDING S. Modeling particulate self-healing materials and application to uni-axial compression[J]. International Journal of Fracture, 2008, 154(1/2): 87. DOI:10.1007/s10704-008-9299-y |
| [16] |
王泳丹, 刘子铭, 郝培文. 综论沥青的疲劳损伤自愈合行为: 理论研究, 评价方法, 影响因素, 数值模拟[J]. 材料导报, 2019, 33(9): 1517. WANG Yongdan, LIU Ziming, HAO Peiwen. Self-healing behavior of fatigue damage in asphalt binders: theoretical studies, evaluation approaches, influencing factors, numerical simulation[J]. Materials Reports, 2019, 33(9): 1517. DOI:10.11896/cldb.18040267 |
| [17] |
WANG G T, CHEN X Q, DONG Q, et al. Mechanical performance study of pervious concrete using steel slag aggregate through laboratory tests and numerical simulation[J]. Journal of Cleaner Production, 2020, 262: 121208. DOI:10.1016/j.jclepro.2020.121208 |
| [18] |
陈俊. 基于离散元方法的沥青混合料虚拟疲劳试验研究[D]. 南京: 东南大学, 2010 CHEN Jun. Virtual fatigue tests of asphalt mixture based on discrete element method[D]. Nanjing: Southeast University, 2010. DOI: 10.7666/d.Y1978213 |
| [19] |
赵晓康, 董侨, 肖源杰, 等. 基于细观非均质模型的水稳碎石基层材料疲劳开裂研究[J]. 中南大学学报(自然科学版), 2021, 52(9): 3132. ZHAO Xiaokang, DONG Qiao, XIAO Yuanjie, et al. Fatigue cracking of cement-treated composites with mesoscale heterogeneous model[J]. Journal of Central South University (Science and Technology), 2021, 52(9): 3132. DOI:10.11817/j.issn.1672-7207.2021.09.015 |
| [20] |
GONG L X, NIE L, XU Y, et al. Discrete element modelling of the mechanical behaviour of a sand-rubber mixture containing large rubber particles[J]. Construction and Building Materials, 2019, 205: 574. DOI:10.1016/j.conbuildmat.2019.01.214 |
| [21] |
DONG Q, ZHENG D B, ZHAO X K, et al. Mesoscale numerical simulation of fracture of cement treated base material during semi circular bending test with discrete element model[J]. Construction and Building Materials, 2020, 261: 119981. DOI:10.1016/j.conbuildmat.2020.119981 |
| [22] |
苏捷. 混凝土受压与受拉性能的尺寸效应研究[D]. 长沙: 湖南大学, 2013 SU Jie. Research on the size effect of concrete behavior in compression and tension[D]. Changsha: Hunan University, 2013 |
| [23] |
汪维学. 采用圆弧Ⅰ型截面试件测量砂浆直接抗拉强度的研究[D]. 天津: 天津大学, 2009 WANG Weixue. Study on the direct tensile strength of mortar with Arc-I shaped test piece[D]. Tianjin: Tianjin University, 2009. DOI: 10.7666/d.y1675027 |
| [24] |
李惠惠. 基于离散元方法的乳化沥青冷再生混合料疲劳性能研究[D]. 哈尔滨: 东北林业大学, 2018 LI Huihui. Study on fatigue performance of emulsified asphalt cold recycled mixture based on discrete element method[D]. Harbin: Northeast Forestry University, 2018 |
| [25] |
CHEN X Q, YUAN J W, DONG Q, et al. Meso-scale cracking behavior of cement treated base material[J]. Construction and Building Materials, 2020, 239: 117823. DOI:10.1016/j.conbuildmat.2019.117823 |
| [26] |
ZHOU S, ZHU H H, YAN Z G, et al. A micromechanical study of the breakage mechanism of microcapsules in concrete using PFC2D[J]. Construction and Building Materials, 2016, 115: 452. DOI:10.1016/j.conbuildmat.2016.04.067 |
| [27] |
POTYONDY D O, CUNDALL P. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329. |
| [28] |
ZHOU S, ZHU H H, JU J W, et al. Modeling microcapsule-enabled self-healing cementitious composite materials using discrete element method[J]. International Journal of Damage Mechanics, 2017, 26(2): 340. DOI:10.1177/1056789516688835 |
 2024, Vol. 56
2024, Vol. 56


