能源安全是关系国家经济社会发展的重要基石,中国能源安全离不开煤炭能源供给的保障[1-2]。然而,随着中国浅部煤炭逐渐枯竭,资源开采向深部转移已成为必然趋势,受深部开采“三高一扰动”因素的影响,越来越多的巷道转为动压巷道,加之工作面采动引起的卸荷作用,导致动压巷道围岩应力环境恶化,群死群伤的恶性事故频发。因此,研究三维动静组合加载下煤岩动力学特性及动力扰动后卸荷破坏特征,对控制巷道变形失稳,保证煤炭安全高效开采具有重要意义。
针对深部煤岩“高应力+强扰动”的环境,国内外学者借助霍普金森压杆系统(split Hopkinson pressure bar,SHPB)开展了动静加载下煤岩力学特性[3-5]、能量耗散[6-8]、破坏特征[9-11]的研究。如李夕兵等[3]指出岩石动抗压强度随轴压增大,呈先增后减趋势。宫凤强等[4]借助SHPB装置开展三维动静组合实验。结果表明: 轴压促进裂纹发育,弱化岩石承载能力;围压抑制裂纹萌生,强化承载能力。吴拥政等[5]对长径比0.5~1.0的煤样开展三轴冲击实验,结果表明煤样峰值应力的长径比效应随应变率增加越显著。一方面,煤炭开采与能量释放密切相关,金解放等[6]开展红砂岩冲击实验,研究了应变率、轴压对试样能耗特性及破坏模式的影响。尹土兵等[7]、刘少虹等[8]深入探讨了动静加载下煤岩能耗特征,认为温度、应力波幅值导致煤岩能耗特征显著变化。另一方面,随着岩石力学的研究深入,部分学者重视并研究了“高应力+开挖卸荷+动力扰动”下煤岩力学特性,如叶洲元等[9]探讨了预加静载卸载后的砂岩动力学特性,发现动抗压强度随轴压先增后减,与围压呈正相关。王春等[10]通过研究卸荷速率,指出岩块破坏粒度随卸荷速率增大而增大,卸荷速率促进岩样破坏转向剪切破坏。Gong等[11]采用动态强度弱化因子量化围压卸荷造成的强度弱化。
部分学者在煤岩动态本构模型领域取得了丰硕成果。单仁亮等[12]结合ZWT本构模型[13],引入损伤体元件,表征无烟煤塑性流动特征。郭德勇等[14]研究了低-中-高应变率下煤岩响应特征,优化了元件型本构模型适用范围。解北京等[15]考虑了煤岩组合体的应变率及损伤特性,构建7参数层叠本构模型。上述研究集中于一维动静组合加载,且构建模型仅考虑单因素,未考虑因素交互作用。
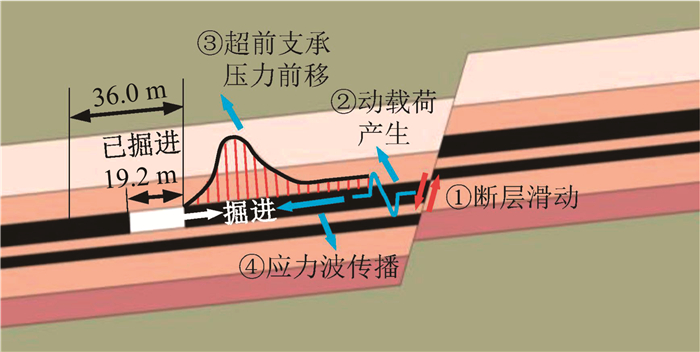
此外,煤岩力学研究成果集中于“高应力+动力扰动”、“高应力+开挖卸荷+动力扰动”,即动静组合、三维静载荷-卸荷-冲击,关于深部动压巷道面临的“三轴应力+动力扰动+开挖卸荷”应力环境的研究存在不足,如图 1所示。在井下巷道掘进时,邻近断层受地应力影响,导致断层滑动等地质扰动,即前方煤体处于“三轴应力+动力扰动”环境。随着巷道及掘进面的推进,煤岩受超前支承压力前移的影响,存在不同程度的应力卸荷。因此,本文利用SHPB系统,探究不同应变率、轴压下煤样动力学特性及卸荷破坏特征,并综合因素交互作用、Weibull分布、Drucker-Prager(D-P)准则,借助响应曲面法构建回归方程,修正动静加载下的强度统计损伤本构模型,以期为深部巷道围岩控制提供一定参考。
1 实验概况 1.1 试样制备实验煤样取自有冲击地压灾害的内蒙古鄂尔多斯某煤矿3-1煤层,埋深772 m(平均水平主应力24.0 MPa,垂直应力17.0 MPa)。选取外观完好、结构完整的大块煤取样,保证试样均质性和结果可靠性。同时,根据中国岩石力学与工程学会规程,按照长径比L/D=1.0制备Ф50 mm×50 mm标准圆柱形煤样。试样两端需切割、打磨抛光,保证试样两端不平行度小于0.02 mm,垂直试样轴线方向的最大偏离度小于0.25 °。制备完好的标准试样如图 2所示,物理力学参数见表 1。

|
图 2 部分标准煤样 Fig. 2 Partial standard coal samples |
| 表 1 煤样基础参数数据 Tab. 1 Basic parameter data of coal samples |
实验依托中国矿业大学(北京)煤岩动载破坏参数测试实验室Ф50 mm分离式霍普金森压杆系统(SHPB)。SHPB实验系统如图 3所示。

|
图 3 SHPB实验装置示意 Fig. 3 Schematic diagram of SHPB experimental device |
该装置主要由撞击杆(圆柱形子弹Φ50 mm×400 mm)、入射杆(Φ50 mm×3 000 mm)、透射杆(Φ50 mm×2 500 mm)、吸能杆(Φ50 mm×1 000 mm) 组成,其中杆件材质为低碳弹簧钢,弹性模量为206 GPa,密度为7 740 kg/m3,弹性波速为5 410 m/s,泊松比为0.35。实验系统采用压缩空气为动力源(空气压缩机最低冲击气压为0.1 MPa),借助橡胶圆片整形器(Φ10 mm×1 mm),形成正弦波加载。同时,利用粘贴于入射杆与透射杆中部的AF2-1普通应变片采集脉冲信号,并通过LK2017超动态应变仪和数据采集系统获取试样入射、透射、反射信号。另外,实验前应校准仪器共轴,并在试样表面均匀涂抹少量凡士林,减少端面摩擦影响[16]。
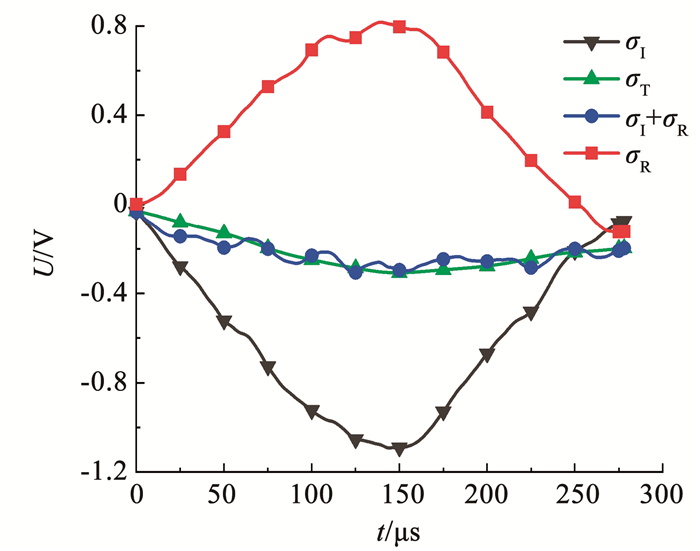
1.3 方案及应力平衡应力平衡为检验SHPB实验结果可靠的前提条件[17]。为满足这一要求,在数据处理前,应对采集的数据开展应力平衡检验。文献[18-19]认为试样两端面应力差与端面平均应力之比不超过5%时,即达到应力均匀。图 4为典型的三维动静加载下煤样应力平衡曲线。由图 4可知,入射σI、反射应力σR之和与透射应力σT基本相等,证明三维动静加载下试样处于应力平衡。另外,基于地应力测试结果及SHPB系统性能,设置实验方案见表 2。
|
图 4 应力平衡曲线 Fig. 4 Stress balance curve |
| 表 2 实验方案 Tab. 2 Experimental scheme |
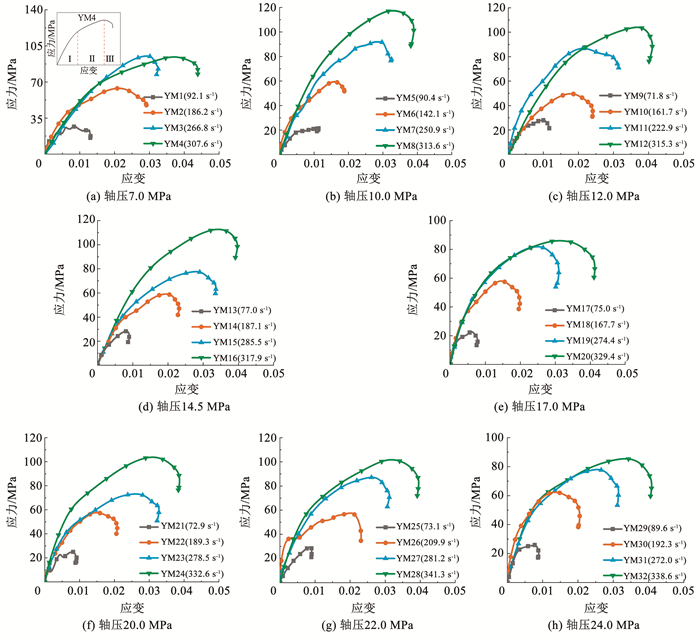
由于三维动静加载实验结束后开展卸荷实验研究,因此煤样动力学响应行为不受卸荷方式的影响。图 5中固定围压Pw为24.0 MPa、8种轴压Pz分别为7.0、10.0、12.0、14.5、17.0、20.0、22.0、24.0 MPa (轴围比为0.3~1.0,即轴压/围压)、冲击气压Pd为0.1~0.6 MPa下煤样动态应力-应变曲线。由图 5可见,不同轴压、冲击气压的煤样动力学响应特征基本一致,应力-应变曲线具有显著的非线性特征,包括线弹性、塑性屈服、卸载阶段。为明确煤样的阶段性力学特征,以YM4为例,阐述煤样动力学性能,具体如图 5(a)所示。
|
图 5 动态应力-应变曲线 Fig. 5 Dynamic stress-strain curve |
由图 5(a)可知,煤样动态应力-应变曲线的阶段性特征如下。
1) 线弹性阶段Ⅰ。对比文献[9]可知,动静组合加载下的煤样应力-应变曲线基本不存在下凹阶段。一方面,预先施加的轴围压,导致煤样内部结构裂隙受载闭合。另一方面,冲击加载历程短暂,冲击速度较快,造成曲线无明显压密阶段。
2) 塑性屈服阶段Ⅱ。当应力增长至弹性极限值时,应力-应变不符合Hooke定律。原因在于试样内部次生裂隙萌生、发育,进而贯通原生裂隙,导致部分应力-应变曲线出现屈服阶段,但整体动抗压强度保持增长趋势。
3) 卸载阶段Ⅲ。随着应变的增长,煤样应力迅速降低,其内部损伤变形、宏观缺陷增加,导致煤样承载能力显著下降,力学性能劣化严重。
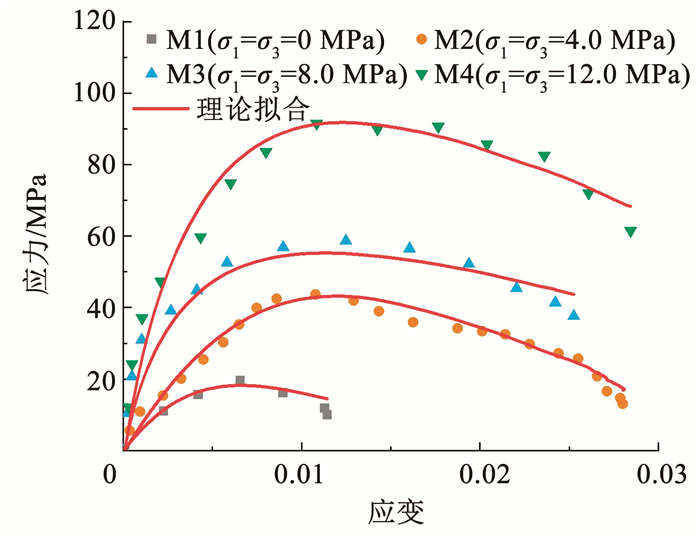
2.2 动抗压强度特征由文献[20]可知,动抗压强度σm随应变率
| $ \sigma_{\mathrm{m}}=a \dot{\varepsilon}^b $ | (1) |
式中, a、b为动抗压强度相关拟合参数。
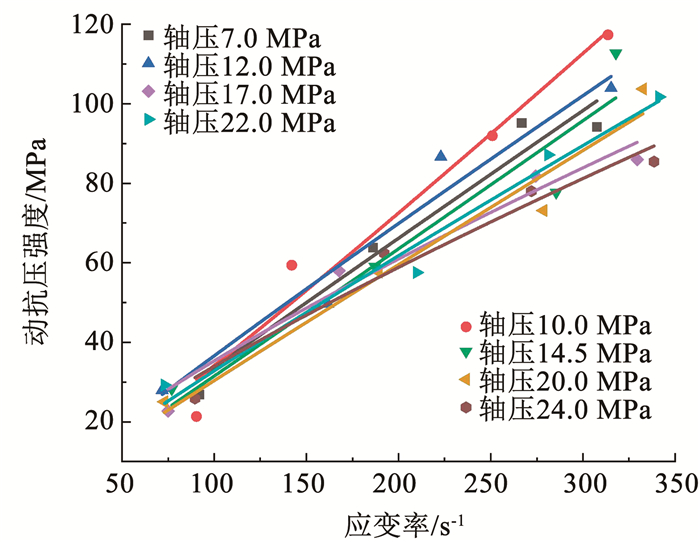
图 6为轴压7.0~24.0 MPa下煤样动抗压强度与应变率(71.8~341.3 s-1)关系曲线。由图 6可见,煤样动抗压强度与应变率呈显著正相关,且幂函数拟合效果较好(R2≥0.87),但不同轴压下煤样抗压强度与应变率拟合参量差异显著。随着试样承受轴压变化,相同应变率间隔下,拟合曲线抗压强度增幅差异显著。其中,轴压为7.0、10.0、12.0、14.5 MPa时,曲线曲率较高,即静载轴压较小时,煤样的抗压强度对应变率变化更为敏感。
|
图 6 应变率与动抗压强度关系 Fig. 6 Relationship between strain rate and compressive strength |
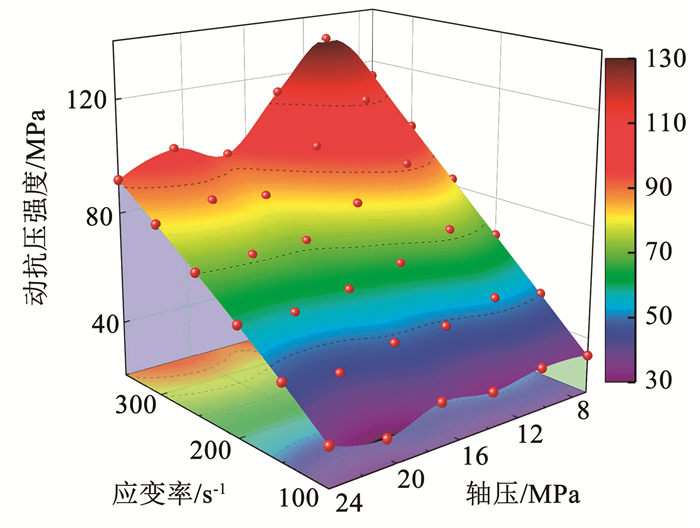
为明确煤样的轴压效应,基于文献[5]解耦轴压及应变率效应,选取应变率100.0、150.0、200.0、250.0、300.0、350.0 s-1,结合表 3参数,获得应变率100.0~350.0 s-1下煤样动抗压强度,如图 7所示。
| 表 3 拟合参数值 Tab. 3 Fitting parameter values |
|
图 7 轴压与动抗压强度关系 Fig. 7 Relationship between axial pressure and dynamic compressive strength |
由图 7可知,三维动静加载中轴压控制作用包括:当轴压7.0~10.0 MPa,煤内部原生裂隙、孔隙受压闭合,受轴压约束颗粒摩擦力显著增强,导致致密性、抗压强度等相应提高。其次,随着轴压增大至12.0~20.0 MPa,煤内部薄弱面受载变形、破坏,造成裂隙萌生、扩展、贯通,即煤样受冲击载荷作用前已存在大量裂纹,因此抗压强度随轴压增大显著减小。最终,当轴压增至22.0~24.0 MPa时,动抗压强度-轴压曲线呈小范围波动,原因在于煤样基本达到三向稳定受力状态,其受力、变形趋于一致,导致承载力小范围增长,但受损伤变形影响,整体仍呈下降趋势。
2.3 因素交互作用由图 6、7可知,轴压、应变率对煤样动抗压强度影响显著。为探究因素交互作用对煤样力学性能的影响,引入响应曲面法(response surface methodology,RSM)中的中心复合试验法(central composite design,CCD)设计方案[21],构建非线性响应面模型,以期表征轴压、应变率与动抗压强度关系。其中,为满足RSM-CCD试验设计的需要(因素梯度变化),响应曲面以轴围比A、应变率B为影响因素,动抗压强度为响应值。方案及编码水平见表 4、5。
| 表 4 中心复合试验因素及水平 Tab. 4 Factors and levels of central composite test method |
| 表 5 响应曲面试验设计方案 Tab. 5 Design scheme of response surface test |
借助Design-Expert 13.0软件开展轴围比、应变率与动抗压强度关系的拟合模型分析见表 6。由表 6可知,三次多项式模型(cubic)的失拟项(lack of fit,LOF)、校正值(adjusted)、预测值(predicted)最大,模型P < 0.000 1,故选用三次多项式模型。
| 表 6 模型匹配度分析 Tab. 6 Model matching analysis |
获得动抗压强度σm与A、B的回归方程为
| $ \begin{aligned} \sigma_{\mathrm{m}}= & -287.24+1409.42 A+0.25 B-4.50 A B- \\ & 1407.65 A^2+0.0067 B^2+6.47 A^2 B-0.0097 A B^2 \end{aligned} $ | (2) |
为反映试验因素及交互因素的显著性,开展方差分析见表 7。表中: F为均方差与误差的比值,可反映因素显著性;PE(pure error)为纯误差, P为显著性判断指标,其中: #(P>0.050 0)为不显著, **(P < 0.050 0)为显著, ***(P < 0.000 1)为极显著。
| 表 7 回归模型方差分析 Tab. 7 Analysis of variance of regression model |
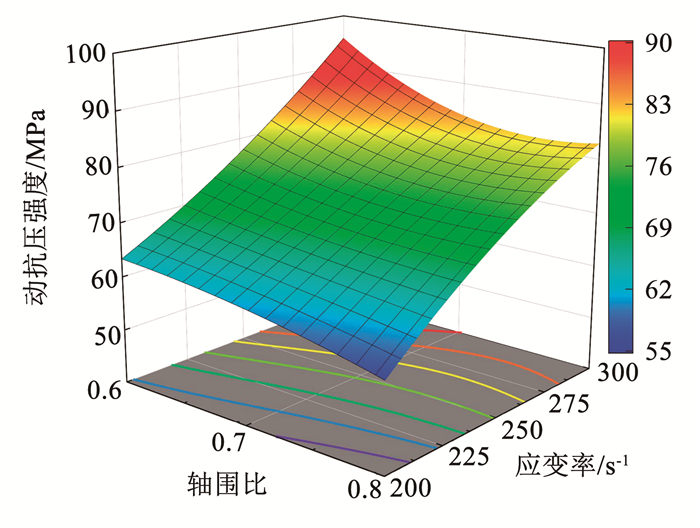
由表 7可知,A3、B3为不显著项,B2、AB为显著项,A、B、A2、A2B、AB2为极显著项,模型P < 0.000 1,表明回归模型显著,可用于响应值分析与预测。同时,根据模型因素F值,交互项影响:A2B>AB2>AB、单因素项影响:B>A2>A>B2。根据式(2) 绘制响应面,可直观分析轴压、应变率对动抗压强度的交互影响,如图 8所示。
|
图 8 动抗压强度响应曲面 Fig. 8 Response surface of compressive strength |
文献[21]指出响应面坡度反映单一因素是否显著,曲面陡峭为显著,反之不显著;等高线形状反映交互作用是否显著,曲线呈椭圆形为显著,反之不显著。由图 8可知,当轴压一定时,煤样动抗压强度随着应变率增加而显著增长,呈近似线性增长趋势;当应变率为200.0 s-1时,动抗压强度随轴压增加而降低。同时,不同轴压下煤样动抗压强度变化幅度存在显著差异,但整体保持下降,即响应面结果与图 6一致。另外,部分等高线呈椭圆状,表明轴压与应变率交互显著,即二者耦合作用无法忽略。
3 动态本构模型 3.1 模型构建 3.1.1 Weibull分布在动静加载实验中,煤样的破坏主要由内部微缺陷的萌生、发育造成。为分析煤样细观损伤,假设煤样由无数足够小的微元集合体构成,可容纳大量微缺陷,损伤过程连续,满足各向同性损伤。同时,为量化煤岩内部微元强度、表征损伤随机分布的特点,假设各微元强度F均符合Weibull分布[22],则概率密度函数P(F)为
| $ P(F)=\frac{m}{F_0}\left(\frac{F}{F_0}\right)^{m-1} \exp \left[-\left(\frac{F}{F_0}\right)^m\right] $ | (3) |
式中F0、m为Weibull参数。为分析煤内部微元破坏特性,定义损伤变量D为
| $ D=\int_0^F P(x) \mathrm{d} x=1-\exp \left[-\left(\frac{F}{F_0}\right)^m\right] $ | (4) |
文献[23]指出D-P准则综合考虑了中间主应力、静水压力作用,克服了M-C准则的缺点,可用于表征煤岩材料微元体强度。则基于D-P准则的微元体强度表达式为:
| $ F=\alpha I_1+J_2^{1 / 2} $ | (5) |
| $ \left\{\begin{array}{l} \alpha=\frac{\sin \varphi}{\sqrt{9+3 \sin ^2 \varphi}} \\ I_1=\sigma_1^*+\sigma_2^*+\sigma_3^* \\ J_2=\frac{1}{6}\left[\left(\sigma_1^*-\sigma_2^*\right)^2+\left(\sigma_2^*-\sigma_3^*\right)^2+\left(\sigma_3^*-\sigma_1^*\right)^2\right] \end{array}\right. $ | (6) |
式中:I1、J2为应力张量的第1不变量、应力偏量的第2不变量,α为强度参数,φ为内摩擦角,σ1、σ2、σ3为名义应力,μ为泊松比,E为初始弹性模量,ε1为轴向应变,εm为峰值应变。
当损伤体的有效应力σi*表达式为
| $ \sigma_i^*=\sigma_i /(1-D) $ | (7) |
式中:i为应力方向,1为轴向,2、3为侧向。
由胡克定律可知,试样轴向应变ε1为
| $ \varepsilon_1=\frac{1}{E}\left(\sigma_1^*-\mu \sigma_2^*-\mu \sigma_3^*\right) $ | (8) |
鉴于实验过程中σ2*=σ3*、σ2=σ3=24.0 MPa、ε1=ε,联立式(5)~(8),则微元强度F为
| $ F=E \varepsilon \frac{\left[\left(\alpha+\frac{1}{\sqrt{3}}\right)\left(\sigma+\sigma_1\right)+\left(2 \alpha-\frac{1}{\sqrt{3}}\right) \sigma_3\right]}{\left(\sigma+\sigma_1\right)-2 \mu \sigma_3} $ | (9) |
基于应变等效假设[24],获得三轴煤样冲击压缩作用下的动态损伤本构模型为
| $ \sigma=E \varepsilon(1-D)-\sigma_1+2 \mu \sigma_3 $ | (10) |
由式(4)、(10)可知,F0、m为本构模型的关键参数[23-24],二者可通过三轴压缩应力-应变曲线的极值点(εm,σm)、式(10)求导获得,计算如下:
| $ F_0=E \varepsilon_{\mathrm{m}} \frac{\left[\left(\alpha+\frac{1}{\sqrt{3}}\right)\left(\sigma_{\mathrm{m}}+\sigma_1\right)+\left(2 \alpha-\frac{1}{\sqrt{3}}\right) \sigma_3\right]}{\left(\sigma_{\mathrm{m}}+\sigma_1\right)-2 \mu \sigma_3}\sqrt[m]{m} $ | (11) |
| $ m=-\frac{1}{\ln \left(\sigma_{\mathrm{m}} / E \varepsilon_{\mathrm{m}}\right)} $ | (12) |
由表 7、图 8可知,煤样动抗压强度不仅受轴压、应变率单一因素影响,且二者交互作用显著。为体现轴压、应变率交互作用对煤样力学特性的影响,根据轴压与轴围比关系及式(2),建立σm与σ1、
| $ \begin{aligned} \sigma_{\mathrm{m}}= & -287.24+58.73 \sigma_1+0.25 \dot{\varepsilon}- \\ & 0.19 \sigma_1 \dot{\varepsilon}-2.44 \sigma_1^2-0.007 \dot{\varepsilon}^2+ \\ & 0.11 \sigma_1^2 \dot{\varepsilon}-0.004 \sigma_1 \dot{\varepsilon}^2 \end{aligned} $ | (13) |
将式(9)~(13)联立化简,获得基于Weibull分布、D-P准则、因素交互作用的三维静载下煤样冲击统计损伤本构模型为
| $ \sigma = \underbrace {E\varepsilon \exp {{\left( { - \frac{F}{{{F_0}}}} \right)}^m}}_{动静因素 + 因素交互} - \underbrace {{\sigma _1}}_{轴压\\因素} + \underbrace {2\mu {\sigma _3}}_{围压\\因素} $ | (14) |
式中F、F0、σm表达式见式(9)、(11)、(13)。
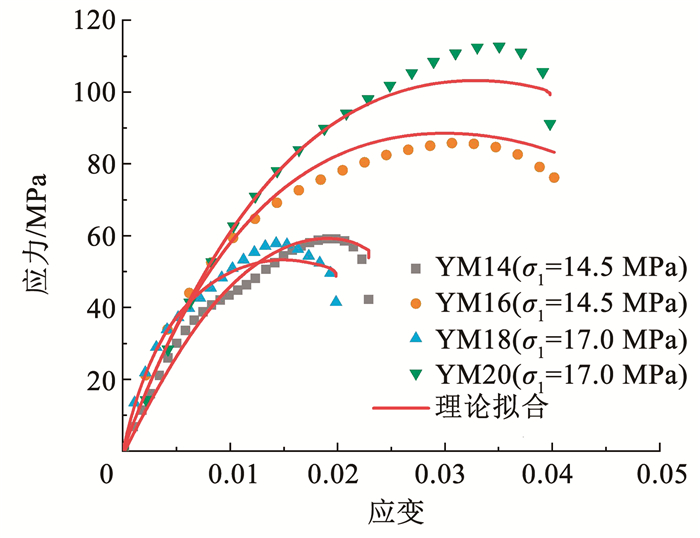
3.3 模型验证基于煤样统计损伤本构模型及动静组合实验结果,明确模型参数见表 8。同时,借助式(14)、表 8计算求解不同轴压、应变率下煤样应力-应变曲线,实验与理论对比曲线如图 9所示。
| 表 8 本构模型拟合参数 Tab. 8 Fitting parameters of constitutive model |
|
图 9 煤样实验和理论应力-应变曲线 Fig. 9 Coal sample test and theoretical stress-strain curve |
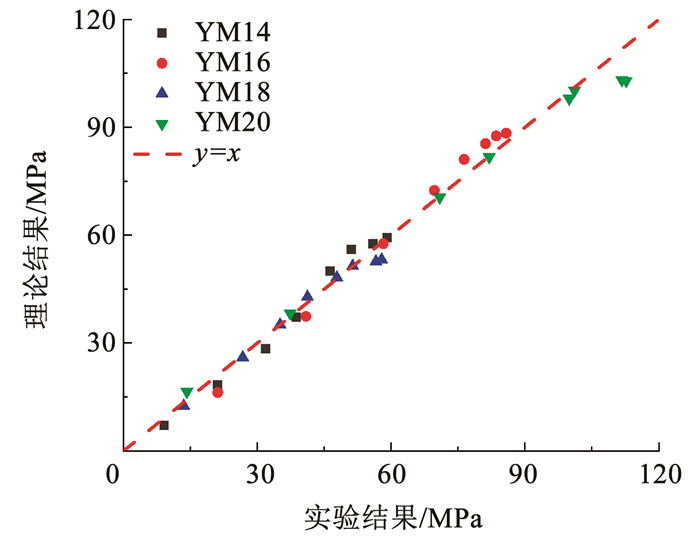
由表 8、图 9可知,实验结果与理论曲线的相关系数R2≥0.88。结果表明,综合Weibull分布、D-P准则、因素交互作用,构建的损伤本构模型精度较高,可表征三维静载下煤样冲击压缩性能,直观体现轴压及应变率效应。同时,模型参数包括σ3、σ1、σm、
|
图 10 理论与实验结果对比 Fig. 10 Comparison of theoretical and experimental results |
为验证实验本构模型拟合效果,运用三维动静组合冲击损伤模型对文献[25]的冲击实验数据开展理论拟合。拟合结果及参数如图 11、表 9所示。
| 表 9 本构模型拟合参数 Tab. 9 Fitting parameters of constitutive model |
由图 11、表 9的实验与理论曲线拟合结果及参数可知,实验构建的本构模型不仅能够描述内蒙古鄂尔多斯煤矿煤样的动态冲击力学性质,也能较好拟合其他煤岩材料的动态冲击试验结果。
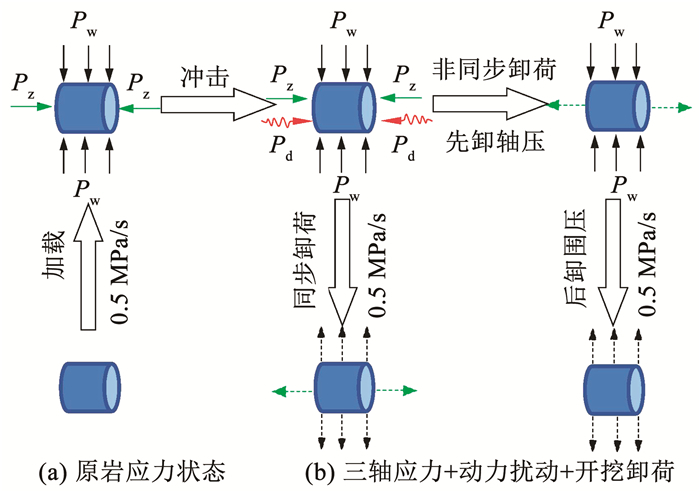
4 动静加载后卸荷破坏特征煤宏观破坏的本质是受动静载荷等因素,煤内部原生及次生缺陷(孔隙、裂隙、节理等)不断萌生、扩展、贯通,进而导致失稳破坏的结果。由于煤样内部结构复杂多样、随机分布,受载荷作用破坏形态多样,如层裂、剪切、压碎、表面剥离、周边破碎等。为探讨深部煤岩“三轴应力+动力扰动+卸荷”的力学特征,借助加卸荷电液伺服装置(如图 12所示),在常规三维动静组合加载后增加卸荷实验,对比轴压、冲击气压、卸荷方式对煤样破坏特征的影响及机制。卸荷实验及具体方案如图 13、表 10所示。

|
图 12 加卸荷电液伺服装置 Fig. 12 Loading and unloading electro-hydraulic servo device |
|
图 13 卸荷实验示意 Fig. 13 Schematic diagram of unloading experiment |
| 表 10 卸荷实验方案 Tab. 10 Unloading test scheme |
同步卸荷指将轴围载荷同时卸载,可忽略卸载效应的影响,仅探究三维动静加载实验对于煤样的破坏影响,操作步骤见表 11。同步卸荷后煤样破坏特征(上端面为入射端,下端面为透射端),如图 14~16所示。
| 表 11 同步卸荷操作步骤 Tab. 11 Synchronous unloading operation steps |

|
图 14 冲击气压0.6 MPa下煤样破坏特征 Fig. 14 Coal sample failure characteristics under impact pressure of 0.6 MPa |

|
图 15 层裂示意 Fig. 15 Schematic diagram of spallation |

|
图 16 不同冲击气压-同步卸荷下煤样破坏特征 Fig. 16 Failure characteristics of coal samples under different impact pressures and synchronous unloading |
实验选取最大冲击气压0.6 MPa、轴压7.0~24.0 MPa开展同步卸荷对煤样破坏特征研究,如图 14所示。
由图 14可知,当轴压小于14.5 MPa时,煤样发生典型动态破坏,主要形式为层裂式拉伸破坏,且层裂程度随着轴压增大,逐渐减小,即负相关趋势;同时,当轴压大于14.5 MPa时,煤样受轴围压作用,煤样内部裂隙闭合程度逐渐加深,宏观表现为煤样表面未发生破坏。
根据最大正拉应力瞬间断裂准则,若加载波为正弦波,波阵面波峰为σ0、层裂临界应力σc,当正拉应力超过临界应力,则发生断裂(如图 15所示),即波峰应力值近似为最大正拉应力,关系如下:
| $ 2 \sigma_0 \geqslant \sigma_{\mathrm{c}} $ | (15) |
结合应力波传播理论可知,同步卸荷时层裂程度随轴压的增大而减小,原因可能在于:压缩加载波、卸载反射波作用于煤样径向方向,在层裂区域形成拉伸界面。当煤样受轴围压作用时,随着轴压的增加,煤样组合抗压强度相应提高,导致拉伸界面后移。当拉伸界面不作用于煤样,其产生的拉应力无法影响煤样,即煤样的层裂临界应力未达到,造成层裂现象难以发生。
4.1.2 冲击气压-同步卸荷的影响图 16为同步卸荷-轴压17.0、20.0、22.0、24.0 MPa煤样在不同冲击气压梯度下的破坏特征。当轴压高于14.5 MPa,煤样保持完整,未发生明显破坏。结合图 14可知,层裂现象的出现与轴压、冲击气压存在显著关联,以轴压14.5 MPa为分界点,低于该数值存在层裂破坏的可能。
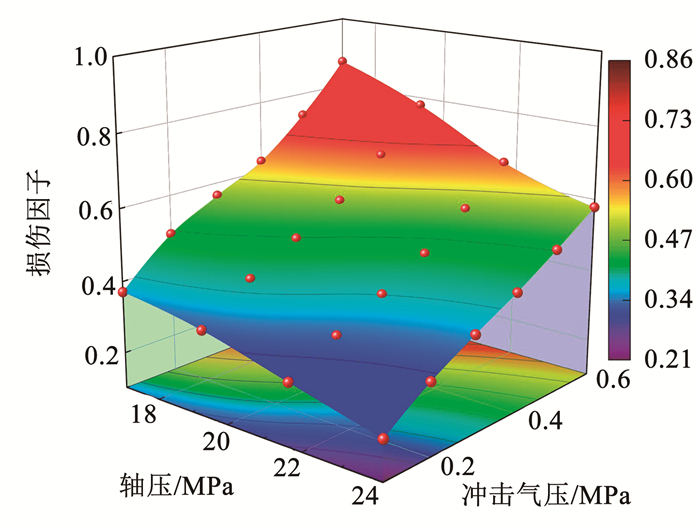
为表征图 16、17中同步卸荷煤样的损伤,以试样冲击前、后的纵波波速定义冲击损伤,计算如下:
| $ D_{\mathrm{t}}=1-\frac{V_{\mathrm{P}}^{\prime 2}}{V_{\mathrm{P}}^2} $ | (16) |
|
图 17 不同冲击气压-同步卸荷下煤样损伤规律 Fig. 17 Coal sample damage rule under different impact pressures and synchronous unloading |
式中:VP为损伤前试样纵波波速,V′P为损伤后试样纵波波速。
结合图 16、17可知,轴压17.0~24.0 MPa下试样内部损伤差异显著,损伤因子D随轴压增大而减小,随冲击气压的增大呈显著上升趋势。结果表明轴围压、冲击气压造成煤样内部一定损伤,但试样结构未呈现整体失稳破坏,原因可能在于轴围压造成煤样组合强度提高,损伤降低,无法造成显著破坏。
4.2 非同步卸荷后煤样破坏特征非同步卸荷指首先卸载轴压,后卸载围压,探究卸载效应的影响,操作步骤见表 12。同步卸荷后煤样破坏特征(上端面为入射端,下端面为透射端),如图 18、19所示。
| 表 12 非同步卸荷操作步骤 Tab. 12 Operation steps of asynchronous unloading |

|
图 18 冲击气压0.1 MPa下煤样破坏特征 Fig. 18 Damage characteristics of coal sample under impact pressure of 0.1 MPa |

|
图 19 不同冲击气压-非同步卸荷下煤样破坏特征 Fig. 19 Failure characteristics of coal samples under different shock pressures and asynchronous unloading |
由于非同步卸荷下煤样的承载能力较低,选取实验最小冲击气压0.1 MPa、轴压7.0~24.0 MPa开展非同步卸荷对煤样破坏特征研究,如图 18所示。
由图 18可知,非同步卸荷导致煤样破坏程度随轴压增大而显著增加。其中,轴压14.5 MPa为临界压剪破碎状态,存在剪切裂纹及表面剥离现象。随着轴压增加至17.0~24.0 MPa,卸载轴压导致煤样整体粉碎性破坏,部分碎块呈明显剪切破坏造成的楔形块体,且轴压为20.0~24.0 MPa时的块体破坏效果更为显著,同时掺杂部分碎屑粉末。
4.2.2 冲击气压-非同步卸荷的影响图 19为煤样在轴压7.0、10.0、12.0、14.5 MPa、冲击气压0.1~0.6 MPa下的非同步卸荷破坏特征。
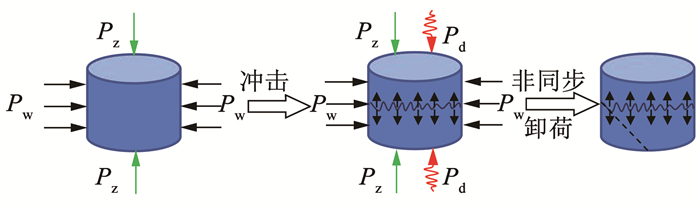
由图 19可知,轴压7.0~14.5 MPa、气压0.1~0.6 MPa时煤样破坏形式主要表现为整体完整、层裂、压剪、层裂-压剪混合破坏。其中,当冲击气压0.1~0.2 MPa、轴压7.0~12.0 MPa时(直线区域),试样处于弱冲击-低轴围压,未达到层裂/压剪破坏条件,表现为煤样无宏观破坏;当冲击气压0.4~0.6 MPa、轴压7.0~12.0 MPa时(短划线区域),试样处于强冲击-低轴围压,仅达到层裂应力范围,此阶段表现为层裂破坏,层裂的拉伸界面随冲击气压的增大而后移;当冲击气压0.1~0.2 MPa、轴压14.5 MPa时(圆点线区域),试样处于弱冲击-中间应力,未达到层裂临界应力,煤样破坏形式为压剪破坏;当冲击气压为0.4~0.6 MPa、轴压14.5 MPa时(长划线区域),试样达到层裂-压剪破坏条件,破坏形式为拉伸-剪切破坏,即先层裂,后压裂。同时,为研究煤样“层裂-压剪”混合破坏机制,绘制非同步卸荷破坏示意图,如图 20所示。
|
图 20 “层裂-压剪”混合破坏形式 Fig. 20 "Spallation compression shear" mixed failure mode |
结合图 20可知,受煤体泊松效应影响,非同步卸荷中煤样卸荷作用等价于卸荷方向施加拉应力,逐步解除抑制微裂纹扩展作用,进而导致煤样扩容效果显著加剧[26]。同时,受卸荷速率影响,煤样破坏过程中轴压未直接降低至0,即非同步卸荷状态下的破坏为围压侧限抑制作用下的破坏效果,具体表现为单轴、三轴的中间状态,造成冲击气压0.4~0.6 MPa、轴压14.5 MPa试样出现层裂-压剪复合破坏状态。对比同步卸荷可知,二者虽均可造成煤样失稳破坏,但应力卸荷路径不同,卸荷方式的不同导致煤样破坏过程显著差异。除此之外,该破坏模式与矿山开采中巷道围岩“层裂-压剪”混合破坏形式相似(动静扰动+卸荷),一定程度上揭示了深部动压巷道“三轴应力+动力扰动+开挖卸荷”下围岩破坏模式的形成原因。
同时,由于煤岩冲击破坏SHPB实验条件有限,实验并未考虑围压、卸荷速率影响,即围压梯度下的煤岩动力学特性、围压+应变率的交互作用及卸荷破坏特征有待进一步研究。
5 结论1) 煤样动抗压强度与应变率呈幂函数增长趋势, 动抗压强度随轴压增加呈先增加后减小趋势。响应面结果表明,三轴动静加载实验中轴压A、应变率B影响显著,二者交互作用影响显著,其中交互项影响为A2B>AB2>AB, 单因素项影响为B>A2>A>B2。
2) 借助Weibull分布、D-P准则,基于轴围压、冲击载荷作用,构建煤样强度型统计损伤模型,并借助RSM-CCD获得考虑因素交互作用的回归方程(R2≥0.88),修正后的本构模型可反映应变率、轴压的单一及因素交互作用。
3) 冲击加载后同步卸荷的煤样以层裂式拉伸破坏为主,拉伸破坏界面随轴压增大而后移直至消失,无法形成层裂破坏;非同步卸荷下煤样破坏形式包括整体完整、层裂、压剪破坏、层裂-压剪混合破坏。其中,当冲击气压0.4~0.6 MPa、轴压14.5 MPa时,非同步卸荷煤样表现为“层裂+压剪”混合式破坏。
| [1] |
刘峰, 郭林峰, 赵路正. 双碳背景下煤炭安全区间与绿色低碳技术路径[J]. 煤炭学报, 2022, 47(1): 1. LIU Feng, GUO Linfeng, ZHAO Luzheng. Research on coal safety range and green low-carbon technology path under the dual-carbon background[J]. Journal of China Coal Society, 2022, 47(1): 1. DOI:10.13225/j.cnki.jccs.YG22.0016 |
| [2] |
谢和平, 任世华, 谢亚辰, 等. 碳中和目标下煤炭行业发展机遇[J]. 煤炭学报, 2021, 46(7): 2197. XIE Heping, REN Shihua, XIE Yachen, et al. Development opportunities of the coal industry towards the goal of carbon neutrality[J]. Journal of China Coal Society, 2021, 46(7): 2197. DOI:10.13225/j.cnki.jccs.2021.0973 |
| [3] |
李夕兵, 宫凤强, ZHAOJ, 等. 一维动静组合加载下岩石冲击破坏试验研究[J]. 岩石力学与工程学报, 2010, 29(2): 251. LI Xibing, GONG Fengqiang, ZHAO J, et al. Test study of impact failure of rock subjected to one-dimensional coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 251. |
| [4] |
宫凤强, 李夕兵, 刘希灵. 三维动静组合加载下岩石力学特性试验初探[J]. 岩石力学与工程学报, 2011, 30(6): 1179. GONG Fengqiang, LI Xibing, LIU Xiling. Preliminary experimental study of characteristics of rock subjected to 3D coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(6): 1179. |
| [5] |
吴拥政, 孙卓越, 付玉凯. 三维动静加载下不同长径比煤样力学特性及能量耗散规律[J]. 岩石力学与工程学报, 2022, 41(5): 877. WU Yongzheng, SUN Zhuoyue, FU Yukai. Mechanical properties and energy dissipation laws of coal samples with different length-to-diameter ratios under 3D coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(5): 877. DOI:10.13722/j.cnki.jrme.2021.0920 |
| [6] |
金解放, 吴越, 张睿, 等. 冲击速度和轴向静载对红砂岩破碎及能耗的影响[J]. 爆炸与冲击, 2020, 40(10): 39. JIN Jiefang, WU Yue, ZHANG Rui, et al. Effect of impact velocity and axial static stress on fragmentation and energy dissipation of red sandstone[J]. Explosion and Shock Waves, 2020, 40(10): 39. DOI:10.11883/bzycj-2019-0479 |
| [7] |
尹土兵, 李夕兵, 叶洲元, 等. 温-压耦合及动力扰动下岩石破碎的能量耗散[J]. 岩石力学与工程学报, 2013, 32(6): 1197. YIN Tubing, LI Xibing, YE Zhouyuan, et al. Energy dissipation of rock fracture under thermo-mechanical coupling and dynamic disturbances[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1197. DOI:10.3969/j.issn.1000-6915.2013.06.013 |
| [8] |
刘少虹, 毛德兵, 齐庆新, 等. 动静加载下组合煤岩的应力波传播机制与能量耗散[J]. 煤炭学报, 2014, 39(Sup.1): 15. LIU Shaohong, MAO Debing, QI Qingxin, et al. Under static loading stress wave propagation mechanism and energy dissipation in compound coal-rock[J]. Journal of China Coal Society, 2014, 39(Sup.1): 15. DOI:10.13225/j.cnki.jccs.2013.0411 |
| [9] |
叶洲元, 赵伏军, 周子龙. 动静组合载荷下卸荷岩石力学特性分析[J]. 岩土工程学报, 2013, 35(3): 454. YE Zhouyuan, ZHAO Fujun, ZHOU Zilong. Mechanical characteristics of unloading rock under coupled dynamic and static loads[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 454. |
| [10] |
王春, 程露萍, 唐礼忠, 等. 高静荷载下卸载速率对岩石动力学特性及破坏模式的影响[J]. 岩石力学与工程学报, 2019, 38(2): 217. WANG Chun, CHENG Luping, TANG Lizhong, et al. Effects of the unloading rate on dynamic characteristic and failure modes of rock under high static loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(2): 217. DOI:10.13722/j.cnki.jrme.2018.0954 |
| [11] |
GONG Fengqiang, ZHONG Wenhui, GAO Mingzhong, et al. Dynamic characteristics of high stressed red sandstone subjected to unloading and impact loads[J]. Journal of Central South University, 2022, 29(2): 596. DOI:10.1007/s11771-022-4944-6 |
| [12] |
单仁亮, 程瑞强, 高文蛟. 云驾岭煤矿无烟煤的动态本构模型研究[J]. 岩石力学与工程学报, 2006, 25(11): 2258. SHAN Renliang, CHENG Ruiqiang, GAO Wenjiao. Study on dynamic constitutive model of anthracite of yunjialing coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2258. DOI:10.3321/j.issn:1000-6915.2006.11.014 |
| [13] |
王礼立, PLUVINAGEG, LABIBESK. 冲击载荷下高聚物动态本构关系对粘弹性波传播特性的影响[J]. 宁波大学学报(理工版), 1995, 8(3): 30. WANG Lili, PLUVINAGE G, LABIBES K. The influence of dynamic constitutive relations of polymers at impact loading on the viscoelastic wave propagation character[J]. Journal of Ningbo University(Natural Science & Engineering Edition), 1995, 8(3): 30. |
| [14] |
郭德勇, 吕鹏飞, 赵杰超, 等. 煤岩冲击变形破坏特性及其本构模型[J]. 煤炭学报, 2018, 43(8): 2233. GUO Deyong, LÜ Pengfei, ZHAO Jiechao, et al. Deformation and damage characteristics and constitutive model of coal and rock under impact loading[J]. Journal of China Coal Society, 2018, 43(8): 2233. DOI:10.13225/j.cnki.jccs.2018.0300 |
| [15] |
解北京, 严正. 基于层叠模型组合煤岩体动态力学本构模型[J]. 煤炭学报, 2019, 44(2): 463. XIE Beijing, YAN Zheng. Dynamic mechanical constitutive model of combined coal-rock mass based on overlay model[J]. Journal of China Coal Society, 2019, 44(2): 463. DOI:10.13225/j.cnki.jccs.2018.1007 |
| [16] |
KONG Xiangguo, LI Shugang, WANG Enyuan, et al. Experimental and numerical investigations on dynamic mechanical responses and failure process of gas-bearing coal under impact load[J]. Soil Dynamics and Earthquake Engineering, 2021, 142: 106579. DOI:10.1016/j.soildyn.2021.106579 |
| [17] |
DAI Feng, HUANG Sheng, XIA Kaiwen, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar[J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 657. DOI:10.1007/s00603-010-0091-8 |
| [18] |
孟庆山, 范超, 曾卫星, 等. 南沙群岛珊瑚礁灰岩的动态力学性能试验[J]. 岩土力学, 2019, 40(1): 183. MENG Qingshan, FAN Chao, ZENG Weixing, et al. Tests on dynamic properties of coral-reef limestone in South China Sea[J]. Rock and Soil Mechanics, 2019, 40(1): 183. DOI:10.16285/j.rsm.2017.1271 |
| [19] |
丰平, 张庆明, 陈利, 等. SHPB测试中斜坡加载对应力均匀性和恒应变率的影响分析[J]. 北京理工大学学报, 2010, 30(5): 513. FENG Ping, ZHANG Qingming, CHEN Li, et al. Influence of incident pulse of slope on stress uniformity and constant strain rate in SHPB test[J]. Transactions of Beijing Institute of Technology, 2010, 30(5): 513. DOI:10.15918/j.tbit1001-0645.2010.05.010 |
| [20] |
闻磊, 梁旭黎, 冯文杰, 等. 冲击损伤砂岩动静组合加载力学特性研究[J]. 岩土力学, 2020, 41(11): 3540. WEN Lei, LIANG Xuli, FENG Wenjie, et al. An investigation of the mechanical properties of sandstone under coupled static and dynamic loading[J]. Rock and Soil Mechanics, 2020, 41(11): 3540. DOI:10.16285/j.rsm.2020.0214 |
| [21] |
王志航, 白二雷, 许金余, 等. 基于响应曲面法的纳米颗粒增强水泥浆体制备研究[J]. 硅酸盐通报, 2021, 40(12): 3918. WANG Zhihang, BAI Erlei, XU Jinyu, et al. Preparation of nano-particles reinforced cement paste based on response surface method[J]. Bulletin of the Chinese Ceramic Society, 2021, 40(12): 3918. DOI:10.16552/j.cnki.issn1001-1625.20211101.001 |
| [22] |
解北京, 栾铮, 陈冬新, 等. 不同长径比煤样动力学特征及本构模型[J]. 矿业科学学报, 2023, 8(2): 190. XIE Beijing, LUAN Zheng, CHEN Dongxin, et al. Dynamic characteristics and constitutive model of coal samples with different length diameter ratio[J]. Journal of Mining Science and Technology, 2023, 8(2): 190. DOI:10.19606/j.cnki.jmst.2023.02.006 |
| [23] |
王登科, 刘淑敏, 魏建平, 等. 冲击破坏条件下煤的强度型统计损伤本构模型与分析[J]. 煤炭学报, 2016, 41(12): 3024. WANG Dengke, LIU Shumin, WEI Jianping, et al. Analysis and strength statistical damage constitutive model of coal under impacting failure[J]. Journal of China Coal Society, 2016, 41(12): 3024. DOI:10.13225/j.cnki.jccs.2016.0540 |
| [24] |
王恩元, 孔祥国, 何学秋, 等. 冲击载荷下三轴煤体动力学分析及损伤本构方程[J]. 煤炭学报, 2019, 44(7): 2049. WANG Enyuan, KONG Xiangguo, HE Xueqiu, et al. Dynamics analysis and damage constitute equation of triaxial coal mass under impact load[J]. Journal of China Coal Society, 2019, 44(7): 2049. DOI:10.13225/j.cnki.jccs.2018.1314 |
| [25] |
XUE Yang, LIU Xiaohui, ZHAO Rui, et al. Investigation on triaxial dynamic model based on the energy theory of bedding coal rock under triaxial impact compression[J]. Shock and Vibration, 2021, 2021: 5537341. DOI:10.1155/2021/5537341 |
| [26] |
冯友良, 鞠文君. 加卸荷应力路径下巷帮煤体力学特性与损伤破坏研究[J]. 煤炭科学技术, 2019, 47(4): 210. FENG Youliang, JU Wenjun. Study on mechanical characteristics and damage failure of coal mass from roadway side wall under loading and unloading stress path[J]. Coal Science and Technology, 2019, 47(4): 210. DOI:10.13199/j.cnki.cst.2019.04.035 |
 2024, Vol. 56
2024, Vol. 56